В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Формула массы тела в физике
Содержание:
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. {n} m_{i}(1)$$
{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.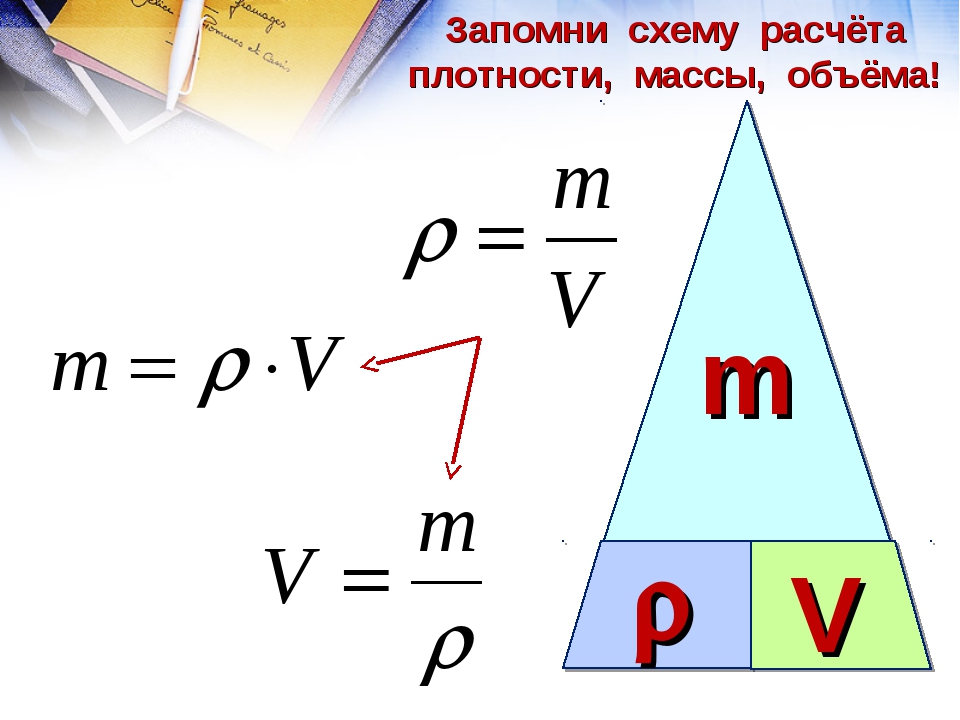 {2}}}}$$
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$\rho$ Cu=8900 кг/м
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Формула массы тела в физике
Содержание:
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. {n} m_{i}(1)$$
{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. {2}}}}$$
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$\rho$
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Формула массы тела в физике
Содержание:
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. {n} m_{i}(1)$$
{n} m_{i}(1)$$
В классической механике считают:
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. {2}}}}$$
{2}}}}$$
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$\rho$
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Масса покоя или инертная масса?
Масса покоя или инертная масса?УДК. 12:531.18+51]
Масса покоя или инертная масса?
Р. И. Храпко
Исключение из современных учебников
физики инертной массы и замена ее массой покоя
представляется ошибкой. Эта тема была поднята
автором в статье [1,2].
Здесь приведены дополнительные рассуждения в
подтверждение такого тезиса.
Эта тема была поднята
автором в статье [1,2].
Здесь приведены дополнительные рассуждения в
подтверждение такого тезиса.
Конец 20-го века ознаменовался великой путаницей с физическим понятием “масса тела”.
1. Масса покоя
В начале века, до создания теории относительности, было все ясно. Массой тела, m, называлось количество вещества тела, и в то же время масса являлась мерой инертности тела. Инертность тела определяет его “количество движения” при заданной скорости v движения, то есть коэффициент пропорциональности в формуле
P = mv. (1)
P – количество движения или, по-научному, импульс тела, а коэффициент
Но массу как меру инертности тела можно определять и с помощью формулы
F = ma: (2)
чем больше масса, тем меньше ускорение тела при
заданной силе. Значение массы по формулам (1) и (2)
получалось одно и то же, потому что формула (2)
является следствием формулы (1), если инертная
масса не зависит от времени и скорости.
Значение массы по формулам (1) и (2)
получалось одно и то же, потому что формула (2)
является следствием формулы (1), если инертная
масса не зависит от времени и скорости.
То же значение массы можно было получить, взвесив тело, то есть измерив силу притяжения к земле или к любому другому заданному телу (масса которого обозначена M). В законе тяготения Ньютона фигурирует та же самая масса m,
, (3)
но тут она называется гравитационной (пассивной) массой. В этом выражается эквивалентность инертной и гравитационной массы. Благодаря этой эквивалентности ускорение свободного падения, как известно, не зависит от природы и массы тела:
(4)
2. Инертная масса
Однако при создании теории
относительности выяснилось, что никакое тело
нельзя разогнать до скорости света, потому что
при приближении скорости тела к скорости света
ускорение тела уменьшается до нуля, как бы ни
была велика ускоряющая сила. Другими словами,
выяснилось, что инертность тела возрастает до
бесконечности при приближении его скорости к
скорости света, хотя “количество вещества”
тела, очевидно, остается при этом неизменным.
Другими словами,
выяснилось, что инертность тела возрастает до
бесконечности при приближении его скорости к
скорости света, хотя “количество вещества”
тела, очевидно, остается при этом неизменным.
Выскажемся точнее по поводу увеличения инертности тела. Теория относительности показала, что импульс тела P при любых скоростях остается параллелен скорости v. Поэтому формулу P = mv можно сохранить неизменной при больших скоростях, если принять, что коэффициент m, то есть инертная масса, увеличивается с ростом скорости по закону
, (5)
то есть для импульса тела справедливо выражение
. (6)
В этих формулах m0 – это то значение массы
рассматриваемого тела, о котором говорилось
вначале, то есть значение, которое можно получить
после того, как тело затормозят до достаточно
малой скорости. Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
. Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
“до теории относительности” корректна.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
“до теории относительности” корректна.
Для того, чтобы подчеркнуть, что инертная масса m зависит от скорости, ее называют иногда “релятивистской” массой: она оказывается различной с точки зрения различных наблюдателей, если эти наблюдатели движутся друг относительно друга. Однако существует выделенное значение инертной массы, именно, значение, которое наблюдает неподвижный относительно тела наблюдатель. Другими словами, масса покоя является выделенным значением инертной массы. Такое свойство инертной массы аналогично свойству времени: одни и те же часы имеют разную скорость хода с точки зрения различных наблюдателей. Однако существует собственная скорость хода часов.
При желании проверить формулу (6) вы
должны измерить скорость v тела, а потом измерить импульс тела. Для этого следует затормозить тело некоторой
преградой, все время замеряя силу F(t), с которой при торможении тело
будет действовать на преграду, а потом
проинтегрировать. Импульс, как известно, равен
Для этого следует затормозить тело некоторой
преградой, все время замеряя силу F(t), с которой при торможении тело
будет действовать на преграду, а потом
проинтегрировать. Импульс, как известно, равен
(7)
Эта процедура, по сути, задает операционное определение инертной массы.
Заметим, что формулы (5) и (6) остаются справедливыми и для объекта, у которого нет массы покоя, m0 = 0, например, для фотона или нейтрино (если предположить, что масса покоя нейтрино равна нулю). Такие объекты обладают инертной массой и импульсом, но должны двигаться со скоростью света, их нельзя остановить, они исчезают при остановке. Тем не менее, несмотря на постоянство скорости движения, величина их инертной массы оказывается различной с точки зрения различных наблюдателей. Однако в этом случае не существует какого либо выделенного значения инертной массы. Либо, можно сказать, выделенное значение равно нулю.
Увеличение инертности тела при
больших скоростях мы объяснили уменьшением
ускорения при большой скорости. При этом мы
сослались на формулу (2). И это допустимо. Однако
именно в силу увеличения инертной массы с ростом
скорости тела формула (2) при некоторых условиях
изменяет свой вид. Это объясняется тем, что при
фиксированном ускорении сила, если она имеет
составляющую вдоль скорости, должна обеспечить
не только возрастание скорости уже имеющейся
массы
При этом мы
сослались на формулу (2). И это допустимо. Однако
именно в силу увеличения инертной массы с ростом
скорости тела формула (2) при некоторых условиях
изменяет свой вид. Это объясняется тем, что при
фиксированном ускорении сила, если она имеет
составляющую вдоль скорости, должна обеспечить
не только возрастание скорости уже имеющейся
массы
, (5)
она должна обеспечить возрастание самой массы:
. (8)
Коэффициент
называют иногда продольной массой [3] .
Если сила перпендикулярна скорости и, значит, не изменяет величину скорости и инертной массы, то формула F = ma сохраняет свой вид:
. (9)
Последнее обстоятельство позволило Р.
Фейнману предложить простой способ
операционного определения инертной массы,
основанный на формуле (9) и справедливый для любой
скорости. “Массу можно измерить так: просто
привязать предмет на веревочке, крутить его с
определенной скоростью и измерять ту силу,
которая необходима, чтобы удержать его. ” [4]
” [4]
При произвольном направлении силы относительно скорости тела коэффициент пропорциональности в формуле (2) следует рассматривать как некий оператор (тензор), превращающий вектор a в вектор F: F = a. Оператор зависит от величины и направления скорости тела и, вообще говоря, изменяет направление вектора. Это нетрудно принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело – это внешний по отношению к телу фактор. Понятно, что результат воздействия силы, то есть ускорение a тела, может зависеть от соотношения направлений векторов F и v.
3. Гравитационная масса
Одновременно теория относительности показала, что не только инертность тела, но и его вес увеличивается с ростом скорости, причем по тому же закону (5) в соответствии с эквивалентностью инертной и гравитационной массы. Поэтому формула (8) для тела, падающего вниз со скоростью v, выглядит, грубо говоря, так:
= .
Точная формула для ускорения может быть получена в рамках общей теории относительности, как показано в конце статьи:
, . (10)
Эта формула является релятивистским аналогом формулы (4).
4. Энергия
Теория относительности показала далее, что прирост инертной массы, m – m0, умноженный на квадрат скорости света, равен как раз кинетической энергии тела:
(m √ m0)c2 = Ek. (11)
Поэтому, если приписать покоящемуся телу энергию покоя E0 = m0c2, то полная энергия E = E0 + Ek тела оказывается пропорциональной инертной массе:
E = mc2 (12)
Эта знаменитая формула Эйнштейна провозглашает эквивалентность инертной массы и энергии. Два, доселе различных понятия, соединяются в одно.
Заметим, что формула (12), как и формулы
(5) и (6) остается справедлива и для объекта, у
которого нет массы и энергии покоя, m0 = 0.
При желании проверить формулу (11) и одновременно убедиться в справедливости теории относительности вы должны измерить инертную массу и массу покоя тела как было объяснено выше, и, кроме того, измерить кинетическую энергию тела. Для этого следует при торможении тела упомянутой преградой все время замерять силу, с которой тело будет действовать на преграду в процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать. Кинетическая энергия, равная, как известно, в данном случае работе, вычисляется по формуле
.
Здесь F(l)dl – скалярное произведение силы на инфинитезимальный вектор смещения преграды. Все это рассказано в [5] .
Формула (11) связывает инертную массу, массу покоя и кинетическую энергию. Используя формулу (6) для вычисления разности m2 √ P2/c2, легко связать инертную массу, массу покоя и импульс:
. (13)
(13)
Для частиц с нулевой массой покоя получаем mc = P или E = Pc.
5. Система тел
При объединении нескольких тел в систему тел, как известно, их импульсы и их инертные массы складываются. Для двух тел это выглядит так:
P = P1 + P2, m = m1 + m2. (14)
Другими словами, импульс и инертная масса аддитивны. Не так обстоит дело с массой покоя. Из формул (13), (14) следует, что масса покоя пары тел с массами покоя m01, m02 равна не сумме m01 + m02, а сложному выражению, зависящему от импульсов P1, P2:
. (15)
Таким образом, масса покоя, вообще
говоря, не аддитивна. Например, пара фотонов, не
имеющих массу покоя, имеет массу покоя, если
фотоны летят в разные стороны, и не имеет массу
покоя, если фотоны летят в одну и ту же сторону.
Тем не менее, все три величины, P, m, m0, подчиняются закону сохранения, то есть не изменяются со временем для замкнутой системы.
Однако ввиду неаддитивности массы покоя, на наш взгляд, нецелесообразно рассматривать массу покоя системы тел. Имеет смысл говорить лишь о сумме масс покоя отдельных тел системы. В действительности именно так поступают на практике. Когда говорят, что при неупругих соударениях увеличивается масса покоя, имеют ввиду не массу покоя системы, которая удивительным образом сохраняется неизменной при соударениях благодаря неаддитивности, а сравнивают именно сумму масс покоя тел до столкновения и массу покоя после столкновения. Точно так же, когда говорят о дефекте массы покоя при ядерных реакциях, имеют в виду не массу покоя, определяемую формулой (15), а сумму масс покоя частей системы.
6. Сравнение масс
Теперь уместно задать вопрос.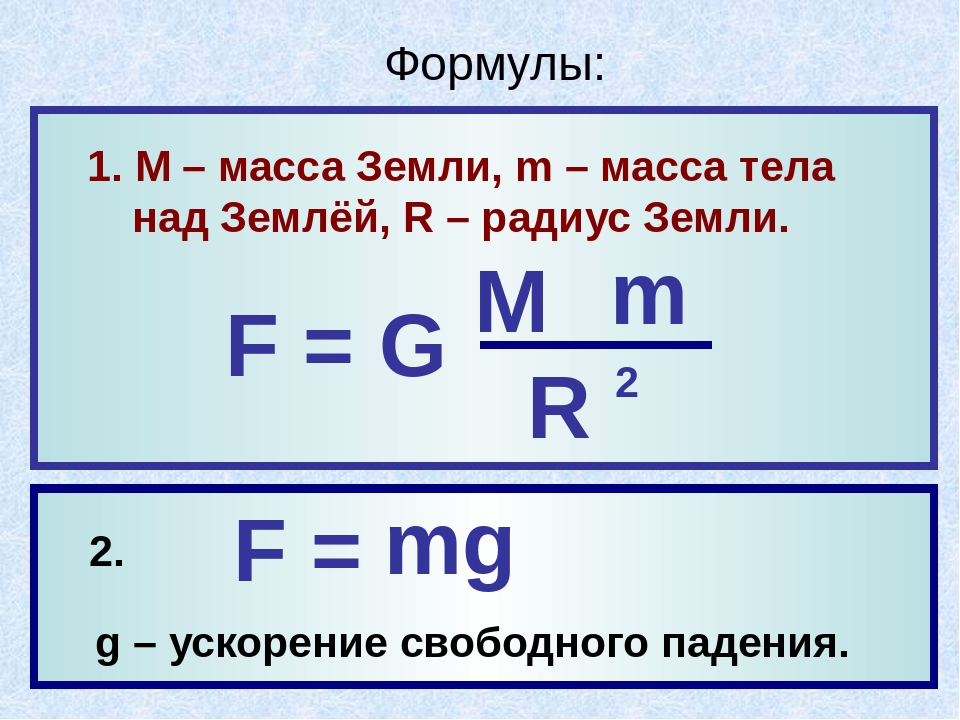 Какую из
двух масс, массу покоя или инертную массу следует
назвать простым словом масса, обозначить буквой m без индексов и тем самым признать
“главной” массой. Это – не терминологическая
проблема. Здесь имеется серьезная
психологическая подоплека.
Какую из
двух масс, массу покоя или инертную массу следует
назвать простым словом масса, обозначить буквой m без индексов и тем самым признать
“главной” массой. Это – не терминологическая
проблема. Здесь имеется серьезная
психологическая подоплека.
Чтобы решить, какая из масс – главная, перечислим еще раз свойства обеих масс.
Масса покоя является постоянной
величиной для данного тела и выражает
“количество вещества тела”. Она
соответствует привычному дорелятивисткому
ньютоновскому представлению о массе. Но она не
эквивалентна энергии, не эквивалентна
гравитационной массе, она не аддитивна и поэтому
не используется как характеристика системы тел или частиц. Это последнее обстоятельство
вызывает путаницу (см. [1] , стр. 1365) и мешает
проявлению закона сохранения массы покоя. Фотоны
и частицы, движущиеся со скоростью света, не
обладают массой покоя. Операционное определение
массы покоя частицы предполагает торможение ее
до малой скорости без использования информации о
текущем состоянии частицы.
Инертная масса это – релятивистская масса. Она принимает различное значение для различных наблюдателей, аналогично тому, как скорость хода часов оказывается различной относительно различных наблюдателей. Инертная масса эквивалентна энергии и гравитационной массе, она аддитивна и подчиняется закону сохранения. Инертной массой обладают частицы, не имеющие массы покоя. Операционное определение инертной массы основано на простой формуле P = mv.
На наш взгляд, инертную массу следует называть массой и обозначать m, как это и делалось в настоящей статье.
7. Психологическая подоплека
К сожалению, большое количество физиков считает массу покоя главной и обозначает ее m а не m0, а инертную массу дискриминирует и оставляет без обозначения, что вносит дополнительную путаницу, поскольку из-за этого порой бывает трудно понять, о какой массе идет речь.
Эти физики соглашаются, например, с тем, что
масса газа увеличивается при нагревании, потому
что увеличивается содержащаяся в нем энергия, но
психологический барьер мешает им попросту
объяснить это увеличение ростом массы отдельных
молекул вследствие увеличения их тепловой
скорости.
Эти физики жертвуют представлением о массе как мере инертности в пользу ярлыка, прикрепляемого к каждой частице с информацией о неизменном “количестве вещества”, потому что ярлык соответствует их привычному ньютоновскому представлению о массе. Они считают, например, что излучение, которое, согласно Эйнштейну [6] , “переносит инерцию между излучающими и поглощающими телами”, не имеет массы, поскольку к излучению невозможно прикрепить ярлык.
Инертная масса отсутствует в издаваемых сейчас стандартных учебниках физики в России (И.В.Савельев) и за рубежом [7,8], а также в популярной литературе [9] . Этот факт, однако, скрыт тем обстоятельством, что сторонники массы покоя настойчиво называют массу покоя не массой покоя, а просто массой, словом, которое ассоциируется с мерой инерции.
Главная психологическая трудность заключается
в том, чтобы отождествить массу и энергию
(которая изменяется), чтобы принять эти две
сущности, как одну. Легко принять формулу E0 = m0c2 для
покоящегося тела. Труднее принять
справедливость формулы E = mc2 для любой скорости. Замечательная
формула E= mc2 представляется,
например, Л.Б. Окуню “безобразной” [10] .
Труднее принять
справедливость формулы E = mc2 для любой скорости. Замечательная
формула E= mc2 представляется,
например, Л.Б. Окуню “безобразной” [10] .
Сторонники массы покоя, видимо, не в состоянии
принять идею инертной, релятивистской массы так
же, как ранее противники теории относительности
не могли принять относительность времени. Ведь
время жизни астронавта или нестабильной частицы
изменяется так же, как изменяется их инертная
масса: . Здесь уместно процитировать М.
Планка: “Великая научная идея редко внедряется
путем постепенного убеждения и обращения своих
противников, редко бывает, что Савл становится
Павлом. В действительности дело происходит так,
что оппоненты постепенно вымирают, а растущее
поколение с самого начала осваивается с новой
идеей.” [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
“Известия вузов. Физика”, “Квант”, “American Journal of Physics”,
“Physics Education” (Bristol), “Physics Today”.
Физика”, “Квант”, “American Journal of Physics”,
“Physics Education” (Bristol), “Physics Today”.
8. Шварцшильдовское пространство
Мы получим здесь формулу (10), рассмотрев пространство-время Шварцшильда общей теории относительности с выражением для интервала s [12] :
.
Уравнения радиальной геодезической линии могут быть получены по общей формуле, использующей коэффициенты связности :
, (16)
. (17)
Первый интеграл уравнения (16) легко находится:
. (18)
Запишем теперь выражение для ускорения a, учитывая (18) и то, что соотношения между расстоянием l и временем , с одной стороны, и координатами r, t, с другой, даются формулами
, :
.
Выразив таким образом ускорение a через , мы можем теперь воспользоваться уравнением (17), а затем, вернувшись к l и , получить окончательно
, . (10)
(10)
Список литературы
1. Храпко Р. И. Что есть масса? // Успехи физических наук. – 2000, N12. √ с.1363-1366.
2. Храпко Р. И. Что есть масса? – http://www.mai.ru. Труды МАИ, Вып.2.
3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. – М.: ГИТТЛ, 1951.- 547 с.
4. Фейнман Р. и др. Фейнмановские лекции по физике. Т. 1. – М.: Мир, 1965. √ 232 с.
5. Храпко Р. И., Спирин Г.Г., Разоренов В. М. Механика. – М.: МАИ, 1993. √ 89 с.
6. Эйнштейн А. Зависит ли инерция тела от содержащейся в нем энергии. // Принцип относительности. – ОНТИ, 1935.- с.175-178.
7. Resnick R., Halliday D., Krane K. S. Physics. V.1 – N.Y.: J. Wiley, 1992.-592p.
8. Alonso M., Finn E. J. Physics – N.Y.: Addison-Wesley, 1995.-496p.
9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.-
631c. Русский перевод: Тейлор Э. Ф.,
Уилер Дж. А. Физика пространства-времени. √ М.:
Мир, 1971. – 612c.
– 612c.
10. Окунь Л. Б. Понятие массы. // Успехи физических наук. – 1989, т. 158. – с.512-530.
11. Планк М. Происхождение научных идей и влияние их на развитие науки./ М. Планк.// Сборник статей к столетию со дня рождения Макса Планка. – М.: АНСССР, 1958.- с.52.
12. Ландау Л.Д., Лифшиц Е.М. Теория поля. – М.: Наука, 1973.- 504с.
Как решать 2 задание ЕГЭ по физике, примеры решения (Ростов-на-Дону)
Из последних КИМов ЕГЭ по физике следует, что задание 2 относится к разделу «Динамика» и может содержать расчетные задачи по следующим темам: «Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения».
Основные формулы, которые необходимо знать для успешного решения задания 2.
Сила тяжести |
|
m – масса тела g=10 м/с2 – ускорение свободного падения |
Сила упругости |
|
Δx – удлинение пружины k – коэффициент жесткости пружины |
Сила трения |
|
µ – коэффициент трения N – сила реакции опоры |
Сила Архимеда (выталкивающая сила) |
|
V – объём погруженной части тела g=10 м/с2 – ускорение свободного падения |
Сила притяжения между телами (закон Всемирного тяготения) |
|
G = 6,67*10-11 Н*м2/кг2 – гравитационная постоянная m1 и m2 - массы взаимодействующих тел r – расстояние между телами |
Второй закон Ньютона |
|
m – масса тела R – равнодействующая всех сил, действующих на тело a – ускорение, с которым движется тело под действием этих сил |
При решении задач из раздела «Динамика» желательно придерживаться следующего алгоритма решения:
1. Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.
Сделать рисунок, на котором указать вектора всех сил, действующих на
тело.
2. Если тело двигается с ускорением, указать направление этого ускорения. Если тело покоится или двигается равномерно, его ускорение a=0.
3. Составить уравнение движения (второй закон Ньютона) для рассматриваемого тела в его векторном виде.
3. Выбрать систему координат и спроецировать полученное уравнение на выбранные оси координат.
4. Расшифровать неизвестные величины, вошедшие в уравнение движения.
5. Решить полученную систему уравнений.
Задание
2
– это расчётные задачи базового уровня сложности, и для решения
некоторых из них этот алгоритм будет чересчур подробным и
перегруженным, так как их можно решить и без вспомогательного рисунка
или даже без записи второго закона Ньютона. Это касается, например,
заданий, в которых на тело действует только одна сила. Но привычка
решать задания по приведенному выше алгоритму поможет ученикам
успешно справиться с расчетными задачами по разделу «Динамика»
повышенного и высокого уровней сложности – такие задания могут
стоять в ЕГЭ под номерами 25 и 29.
Ответом на задание 2 является число, именно его нужно вписать в бланк ответов 1, не указывая единицы измерения.
Примеры решения
1. (ЕГЭ-2019)
Пружина жёсткостью 2*104 Н/м одним концом закреплена в штативе. На какую величину она растянется под действием силы 400 Н?
Ответ: ___________________________ см.
Решение:
Сделаем чертёж
Пружина под действием силы F привели в растянутое состояние. Кроме растягивающей силы F и силы упругости , стремящейся вернуть пружину в нерастянутое состояние, больше никакие силы на нее не действуют.
Запишем проекции сил на вертикальную ось Oy
F=Fупр
По закону Гука, сила упругости Fупр = k *Δx, следовательно,
k
– коэффициент
жёсткости пружины,
Δx
– её
удлинение.
Выразим величину растяжения пружины
Ответ: 2
(ЕГЭ – 2020. Вариант 1 досрочного ЕГЭ)
Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.
Ответ: _______ .
Решение:
Силу трения можно найти по формуле
Fтр= µN,
где N – сила реакции опоры, или по-другому нормальная составляющая силы воздействия тела на плоскость.
Ответ: 0,25.
(ЕГЭ – 2020. Демонстрационный вариант)
Два
одинаковых маленьких шарика массой m
каждый,
расстояние между центрами которых равно r,
притягиваются друг к другу с силами, равными по модулю 0,2 пН. Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?
Каков
модуль сил гравитационного притяжения двух других шариков, если масса
каждого из них равна 2m,
а расстояние между их центрами равно 2r?
Ответ: _______ пН.
Решение:
По закону Всемирного тяготения шары массами m1и m2, находящиеся друг от друга на расстоянии r, притягиваются друг к другу с силой
.
В первом случае
Во втором случае
Ответ: 0,2
(ЕГЭ – 2019. Демонстрационный вариант)
По горизонтальному полу по прямой равномерно тянут ящик, приложив к нему горизонтальную силу 35 Н. Коэффициент трения скольжения между полом и ящиком равен 0,25. Чему равна масса ящика?
Ответ _______ кг.
Решение:
Сделаем
чертёж, на котором обозначим все силы, действующие на тело.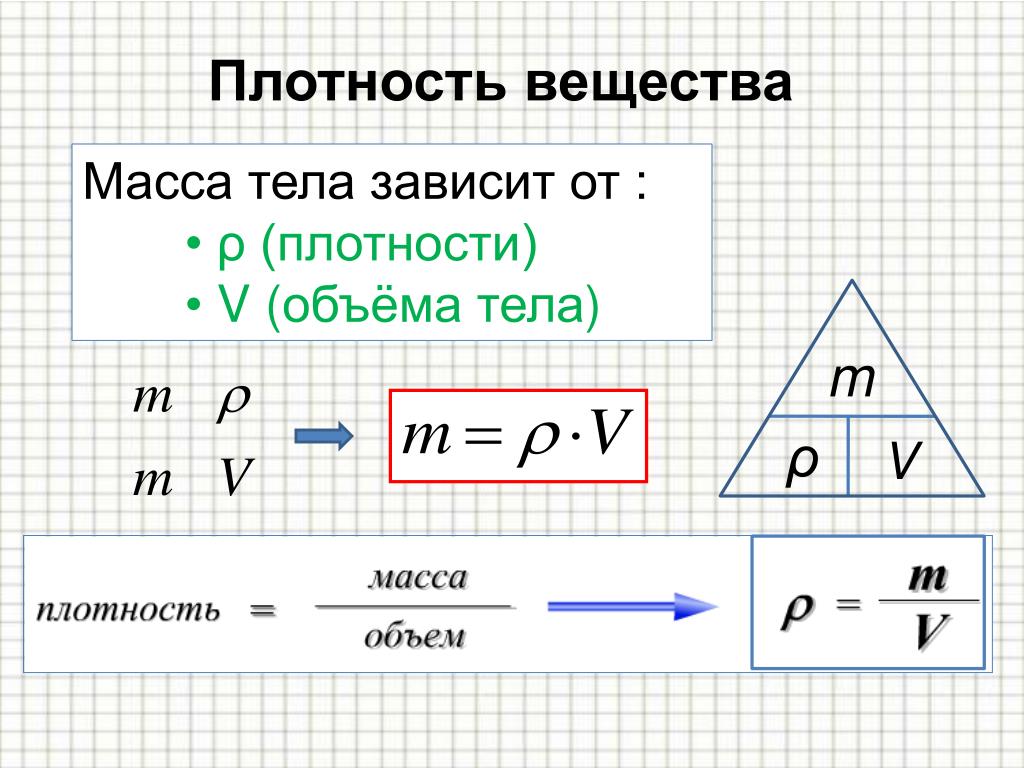
По второму закону Ньютона, равнодействующая всех сил, действующих на тело, будет равна нулю, так как по условию задачи тело движется равномерно, то есть ускорение тела a=0.
Запишем это в проекциях на оси Ox и Oy
Ox: Fтр – F = 0,
Oy: N – m g=0.
Откуда N = mg, следовательно,
Fтр = µ N = µ mg.
Масса тела
Ответ: 14
(ЕГЭ – 2018)
К пружине подвесили груз массой 150 г, вследствие чего пружина удлинилась на 1 см. Чему будет равно удлинение этой пружины, если к ней подвесить груз 450 г?
Ответ: __________ см.
Решение:
Переведём единицы измерения физических величин в систему СИ
m1
=
150 г = 0,15 кг, m2
=
450 г = 0,45 кг, Δx=1
см = 0,01 м.
Сделаем чертёж, на котором обозначим все силы, действующие на тело.
На тело действует сила тяжести (Fт = mg), направленная вертикально вниз, и сила упругости со стороны пружины (Fупр = k Δx), направленная вертикально вверх.
В проекции на вертикальную ось Oy.
Fт =Fупр
mg = kΔx (1)
k – коэффициент жёсткости пружины, Δx – её удлинение.
Найдём, чему равен коэффициент жёсткости пружины
Выразим из выражения (1) удлинение пружины во втором случае
Ответ: 3
РЕКОМЕНДУЕМЫЕ ТОВАРЫ
Формулы для вычисления массы тел различной формы
9.05.2013 // Владимир ТруновЭто странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т. е. следующая статья будет называться «Масса полой детали»).
е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4.
 Масса сегмента шара
Масса сегмента шараОбъем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
Что такое формула массы?
Масса – это свойство физических объектов и мера устойчивости этого тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от реляционных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством , которое объект имеет независимо от его отношения к другим вещам.Массу объекта можно рассчитать несколькими способами:
- масса = плотность × объем (m = ρV) . Плотность – это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса = сила ÷ ускорение (м = F / a) . Согласно второму закону Ньютона (F = ma) ускорение объекта прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающая приложение постоянной силы, обратно пропорциональна массе.
- масса = вес ÷ ускорение свободного падения (м = Вт / г). Вес – это произведение ускорения массы в гравитационном поле. В зависимости от силы ускорения свободного падения вес будет разным.

Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в других единицах, как джоуль (Дж) ньютона (Н). Есть и другие способы вычисления массы объекта, но эти три формулы являются наиболее распространенными.
m = ρV
m = W / g
m = F / a
Единицы массы
Единица измерения массы, принятая в системе СИ, килограмм (кг). Килограмм – единственная основная единица СИ, имеющая в названии префикс (килограмм). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре плавления. В 1889 году килограмм был переопределен как масса International Kilogram Prototype (IPK), физического артефакта, который должен был быть универсальной эталонной массой для килограмма.Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятый ИПК представляет собой цилиндр высотой 39 мм из специального сплава платины.
«Слова тоже имеют подлинную сущность – массу, вес и удельный вес». – Тим О’Брайен
По состоянию на 2018 год килограмм является единственной единицей системы СИ, в которой физический объект является опорным значением. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка.В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за пересмотр определения килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года.
Способы расчета массы
на основе плотности и объема
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше у него массы на единицу объема.
Например, вода имеет плотность 977 кг / м 3 при стандартной температуре и давлении. То есть один кубометр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть образец воды размером 0,7 м 3 . Какова масса этого образца?
То есть один кубометр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть образец воды размером 0,7 м 3 . Какова масса этого образца?
Решение для массы дает:
m = ρV
m = (0,7 м 3 ) (977 кг / м 3 ) = 683 кг
0.5 кубометров воды при стандартной температуре и давлении имели бы массу 683 кг.
Некоторые объекты невероятно плотные. Например, нейтронная звезда имеет среднюю плотность 1,1 x 10 18 кг / м 3 . Одна чайная ложка нейтронной звезды на Земле будет весить около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может сокрушить только своим весом ». – Hans Von Seeckt
От силы и ускорения
Свойство массы также понимается как мера сопротивления физического объекта ускорению под действием внешней силы. Это понятие массы иногда называют инерционной массой . Инерция – это тенденция движущегося тела продолжать движение в постоянном состоянии, поэтому инерционная масса – это мера того, сколько инерции имеет тело и насколько сложно изменить его состояние движения. Связь между массой, силой и ускорением выражается вторым законом движения Ньютона F = ma. Это математическое соотношение говорит нам, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Это понятие массы иногда называют инерционной массой . Инерция – это тенденция движущегося тела продолжать движение в постоянном состоянии, поэтому инерционная масса – это мера того, сколько инерции имеет тело и насколько сложно изменить его состояние движения. Связь между массой, силой и ускорением выражается вторым законом движения Ньютона F = ma. Это математическое соотношение говорит нам, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, предположим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м / с 2 . Какая масса у металлического куба? Мы можем вычислить массу, разделив величину силы на величину ускорения:
м = F / a
м = (748 Н) / (21 м / с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35.62 кг.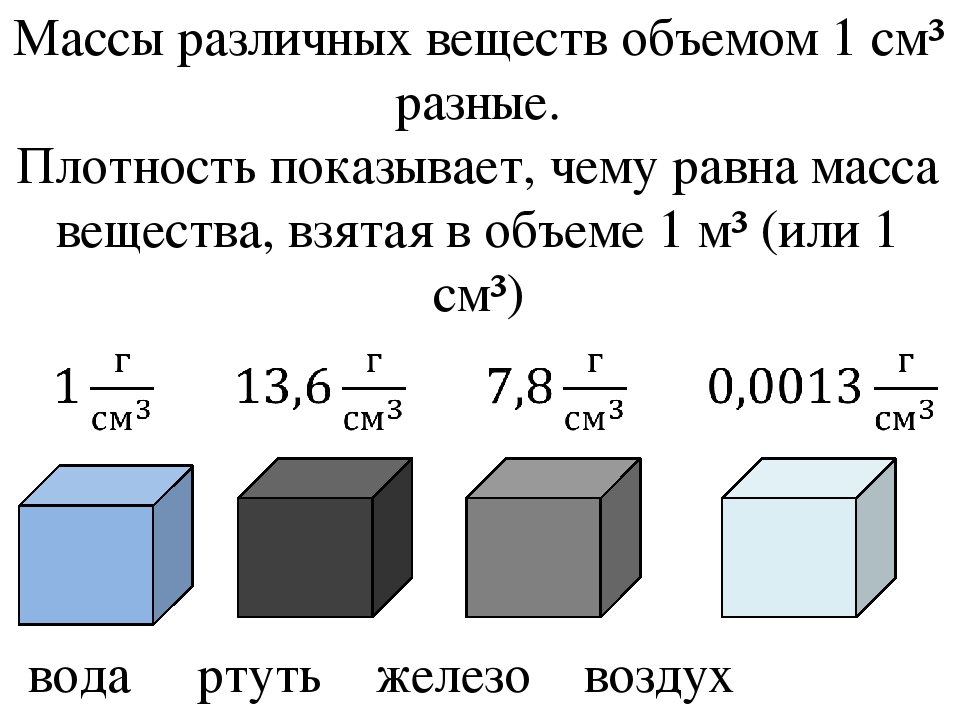
From Вес
Строго говоря, вес и масса – разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, но в физических науках они имеют разные значения. Масса – неизменное свойство, которое не меняется от места к месту. Вес – это мера силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, то есть Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Связь между массой и весом определяется выражением W = mg, где g – мера ускорения свободного падения. Точное значение g различается в зависимости от местоположения. На Земле g имеет значение приблизительно 9,81 м / с 2 , а на Луне g составляет около 1,6 м / с 2 . Выражение W = мг дает вес в ньютонах, в то время как повседневное понимание веса дано в фунтах (фунтах), коэффициент преобразования из ньютонов в фунты составляет около 1 Н = 0,22 фунта.
Например, на поверхности Земли где g = 9.81 м / с 2 , объект весом 50 кг будет иметь вес в фунтах:
W = (50 кг) (9,81 м / с 2 ) = 490,5N
Преобразование ньютонов в фунты дает:
490,5 Н (0,22 фунта / 1 Н) ≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м / с 2 , объект весом 50 кг будет весить:
W = 50 (кг) ( 1,6 м / с 2 ) (0,22 фунта / 1 Н) ≈ 18 фунтов
Тот же объект весом 50 кг весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как:
180 фунтов (1N / 0,22 фунта) = 818,18N
818,18N = м (9,81 м / с 2 )
м = 818,18N / (9,81 м / с 2 ) ≈ 83,4 кг
Таким образом, тело на Земле весом 180 фунтов имеет массу около 84,3 кг.
Эквивалентность массы и энергии
В течение очень долгого времени ученые считали, что массу объекта можно считать полностью независимой от других его свойств.Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E = mc 2 , где c – скорость света в вакууме.
E = mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c = 3 000 000 м / с, c 2 является чрезвычайно большим фактором.Следовательно, даже крошечный кусочек массы содержит огромное количество внутренней энергии. Чтобы рассмотреть вопрос в перспективе, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам в тротиловом эквиваленте – силе атомной бомбы в Хиросиме.
«Любой дурак может знать. Дело в том, чтобы понять ». – Альберт Эйнштейн
В определенных физических процессах, таких как ядерное деление или движение тела в сильном гравитационном поле, материя преобразуется в энергию и выделяется в виде большого количества света и тепла.В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, выделяющейся во время таких реакций.
Скажем, 30 кг урана (Ur) загружают в ядерный реактор. Во время деления примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг составляет 0,3 кг. Подставив это в уравнение Эйнштейна, мы получим:
E = (0,3 кг) (3,000,000) 2 = (0,3) (8,98755179 × 10 16 ) = 2,69626554 × 10 16 J
Полное преобразование всего 0 .3 кг (0,6 фунта) вещества превращаются в энергию, выделяя 2,69626554 × 10 16 Дж энергии. Это примерно столько же, сколько взорвано более 6 миллионов тонн тротила (12 миллиардов фунтов), чего достаточно, чтобы полностью сравнять с землей даже самые большие города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, некоторая реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. Сколько массы было преобразовано в энергию во время этого процесса? Используя нашу удобную формулу эквивалентности массы и энергии, мы можем определить:
1.6178 × 10 16 J = м (8,98755179 × 10 16 )
(1,6178 × 10 16 ) / 8,98755179 × 10 16 ) = м
м ≈ 0,18 кг
Таким образом, примерно 0,18 кг масса была преобразована в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы со своими уравнениями, описывающими поведение элементарных частиц.В частности, их уравнения предсказывали, что определенные частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может быть образована взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют некоторую энергию.Поле Хиггса преобразует эту энергию в массу-энергию, которая проявляется как масса свойства, которую мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса приведет к созданию новой частицы, крошечного бозона, получившего название бозона Хиггса. Ускоритель элементарных частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглерт были удостоены Нобелевской премии по физике за их теоретические работы по частице.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.
Формула массы: определение и примеры – видео и стенограмма урока
Расчет и измерение массы
Есть два способа определить массу объекта. Первый метод включает в себя немного математики. Масса вводится в физику Второй закон движения Ньютона . В этом законе Ньютон утверждает, что когда вы складываете все силы, действующие на объект, называемые суммой сил или чистой силой, и эта сумма не равна нулю, то этот объект ускоряется.Этот закон гласит, что сила, действующая на объект, пропорциональна ускорению, испытываемому объектом. Это означает, что если сила увеличивается, ускорение увеличивается, и наоборот, если сила уменьшается, то ускорение уменьшается. Константа пропорциональности силы и ускорения называется массой. Более конкретно, это называется инертной массой.
Инерционная масса определяется как сопротивление объекта ускорению. Это означает, что чем больше инерционная масса, тем труднее ускорить этот объект.Давайте снова посмотрим на наши шары для боулинга и пинг-понга. Если я приложу одинаковую силу к обоим шарам, какой объект будет иметь большее ускорение? Ответ – шар для пинг-понга, потому что он имеет меньшую инерционную массу и, следовательно, его будет легче ускорить, чем шар для пинг-понга, чем шар для боулинга. Эта система уравнений дает нам формулу для расчета массы объекта, если мы знаем силу, действующую на него, и ускорение объекта:
Если я приложу одинаковую силу к обоим шарам, какой объект будет иметь большее ускорение? Ответ – шар для пинг-понга, потому что он имеет меньшую инерционную массу и, следовательно, его будет легче ускорить, чем шар для пинг-понга, чем шар для боулинга. Эта система уравнений дает нам формулу для расчета массы объекта, если мы знаем силу, действующую на него, и ускорение объекта:
Чистая сила объекта равна массе, умноженной на ускорение.Массу можно рассчитать, разделив чистую силу, действующую на объект, на его ускорение. Говоря о чистой силе, мы используем единицы килограмм-метр на секунду в квадрате. Это также известно как Ньютон. Единицами измерения ускорения являются квадратные метры в секунду, а единицей измерения массы – килограммы.
Давайте сделаем пример. Вы толкаете тележку на 8,0 Ньютона, заставляя ее ускоряться со скоростью 0,50 м / с / с. Какая масса у корзины покупок?
Какая масса у корзины покупок?
Мы знаем, что масса равна чистой силе, деленной на ускорение. Мы знаем, что чистая сила равна 8 Ньютонам, или 8 килограммам на секунду в квадрате. Ускорение составляет 0,5 метра в секунду в квадрате. Метры в секунду в квадрате компенсируют друг друга, и затем мы делим 8 на 0,5, что означает, что мы получаем массу в 16 килограммов. Как видите, если вы знаете силу, действующую на объект, и ускорение, возникающее в результате этой силы, вы сможете рассчитать массу объекта.
Для большинства объектов вам не нужно знать силу или ускорение, если у вас есть масштаб. Второй метод, используемый для определения массы объекта, – это просто поставить объект на весы. Если на весах указаны граммы или килограммы, это измерение массы. Любая шкала с фунтами измеряет вес, который, как мы теперь знаем, представляет собой совершенно другое измерение. Конечно, для некоторых объектов, таких как корабль или автомобиль, очень сложно найти масштаб для таких массивных объектов. Затем в этих случаях вы можете разрабатывать эксперименты, в которых вы прикладываете к объекту известную силу, а затем измеряете результирующее ускорение. Затем вы можете определить массу большого объекта.
Затем в этих случаях вы можете разрабатывать эксперименты, в которых вы прикладываете к объекту известную силу, а затем измеряете результирующее ускорение. Затем вы можете определить массу большого объекта.
Резюме урока
Масса – это мера того, сколько материала находится в объекте. Более формально масса или инерционная масса – это мера сопротивления ускорению. Чем больше инерционная масса, тем труднее разогнать объект. Мы можем либо измерить массу с помощью шкалы, либо вычислить массу объекта.Однако, чтобы рассчитать массу объекта, нам нужно знать силу, действующую на объект, и результирующее ускорение.
5.3 Формула массы | Вводная химия
Цели обучения
К концу этого раздела вы сможете:
- Вычислить формулы масс для ковалентных и ионных соединений
Мы можем утверждать, что современная химическая наука началась, когда ученые начали изучать как количественные, так и качественные аспекты химии.Например, атомная теория Дальтона была попыткой объяснить результаты измерений, которые позволили ему вычислить относительные массы элементов, объединенных в различные соединения. Понимание взаимосвязи между массами атомов и химическими формулами соединений позволяет количественно описывать состав веществ.
Понимание взаимосвязи между массами атомов и химическими формулами соединений позволяет количественно описывать состав веществ.
Формула массы
В предыдущей главе мы описали развитие атомной единицы массы, концепцию средних атомных масс и использование химических формул для представления элементного состава веществ.Эти идеи могут быть расширены для вычисления формулы массы вещества путем суммирования средних атомных масс всех атомов, представленных в формуле вещества.
Формула массы ковалентных веществ
Для ковалентных веществ формула представляет количество и типы атомов, составляющих одну молекулу вещества; следовательно, формульную массу можно правильно называть молекулярной массой. Рассмотрим хлороформ (CHCl 3 ), ковалентное соединение, которое когда-то использовалось в качестве хирургического анестетика, а теперь в основном используется для производства «антипригарного» полимера, тефлона.Молекулярная формула хлороформа указывает на то, что одна молекула содержит один атом углерода, один атом водорода и три атома хлора. Таким образом, средняя молекулярная масса молекулы хлороформа равна сумме средних атомных масс этих атомов. На рисунке 1 показаны расчеты, использованные для определения молекулярной массы хлороформа, которая составляет 119,37 а.е.м.
Таким образом, средняя молекулярная масса молекулы хлороформа равна сумме средних атомных масс этих атомов. На рисунке 1 показаны расчеты, использованные для определения молекулярной массы хлороформа, которая составляет 119,37 а.е.м.
Рис. 1. Средняя масса молекулы хлороформа, CHCl 3 , составляет 119,37 а.е.м., что является суммой средних атомных масс каждого из составляющих ее атомов.Модель показывает молекулярную структуру хлороформа.
Аналогичным образом, молекулярная масса молекулы аспирина, C 9 H 8 O 4 , представляет собой сумму атомных масс девяти атомов углерода, восьми атомов водорода и четырех атомов кислорода, что составляет 180,15 а.е.м. (Фигура 2).
Рис. 2. Средняя масса молекулы аспирина составляет 180,15 а.е.м. Модель показывает молекулярную структуру аспирина, C 9 H 8 O 4 .
Пример 1:
Расчет молекулярной массы ковалентного соединения Ибупрофен, C 13 H 18 O 2 , представляет собой ковалентное соединение и активный ингредиент в нескольких популярных безрецептурных обезболивающих, таких как Адвил и Мотрин. Какова молекулярная масса (а.е.м.) этого соединения?
Какова молекулярная масса (а.е.м.) этого соединения?
Молекулы этого соединения состоят из 13 атомов углерода, 18 атомов водорода и 2 атомов кислорода. Таким образом, в соответствии с описанным выше подходом средняя молекулярная масса этого соединения составляет:
Ацетаминофен, C 8 H 9 NO 2 , представляет собой ковалентное соединение и активный ингредиент в нескольких популярных безрецептурных обезболивающих, таких как тайленол.Какова молекулярная масса (а.е.м.) этого соединения?
Формула массы для ионных соединений
Ионные соединения состоят из дискретных катионов и анионов, объединенных в соотношении, чтобы получить электрически нейтральное объемное вещество. Формульная масса для ионного соединения рассчитывается так же, как формульная масса для ковалентных соединений: путем суммирования средних атомных масс всех атомов в формуле соединения. Однако имейте в виду, что формула ионного соединения не представляет собой состав дискретной молекулы, поэтому ее нельзя правильно называть «молекулярной массой».”
Однако имейте в виду, что формула ионного соединения не представляет собой состав дискретной молекулы, поэтому ее нельзя правильно называть «молекулярной массой».”
В качестве примера рассмотрим хлорид натрия, NaCl, химическое название обычной поваренной соли. Хлорид натрия – это ионное соединение, состоящее из катионов натрия Na + и анионов хлора Cl – , объединенных в соотношении 1: 1. Расчетная масса этого соединения составляет 58,44 а.е.м. (см. Рисунок 3).
Рис. 3. Поваренная соль NaCl содержит набор ионов натрия и хлорида, объединенных в соотношении 1: 1. Его формульная масса составляет 58,44 а.е.м.
Обратите внимание, что в этом расчете использовались средние массы нейтральных атомов натрия и хлора, а не массы катионов натрия и анионов хлора.Такой подход вполне приемлем при вычислении формульной массы ионного соединения. Несмотря на то, что катион натрия имеет немного меньшую массу, чем атом натрия (поскольку у него отсутствует электрон), это различие будет компенсировано тем фактом, что анион хлорида немного массивнее атома хлорида (из-за дополнительного электрона). . Более того, масса электрона ничтожно мала по сравнению с массой типичного атома. Даже при вычислении массы изолированного иона недостающие или дополнительные электроны, как правило, можно игнорировать, поскольку их вклад в общую массу пренебрежимо мал и отражается только в незначительных цифрах, которые будут потеряны при правильном округлении вычисленной массы.Несколько исключений из этого правила – очень легкие ионы, полученные из элементов с точно известными атомными массами.
Пример 2:
Расчет формулы массы ионного соединенияСульфат алюминия, Al 2 (SO 4 ) 3 , представляет собой ионное соединение, которое используется в производстве бумаги и в различных процессах очистки воды. Какова формула массы (а.е.м.) этого соединения?
Покажи ответ Формула этого соединения показывает, что оно содержит ионы Al 3+ и SO 4 2- в сочетании в соотношении 2: 3.Для вычисления формулы массы полезно переписать формулу в более простом формате: Al 2 S 3 O 12 . Следуя описанному выше подходу, формула массы для этого соединения рассчитывается следующим образом:
Фосфат кальция, Ca 3 (PO 4 ) 2 , представляет собой ионное соединение и обычный агент против слеживания, добавляемый в пищевые продукты. Какова формула массы (а.е.м.) фосфата кальция?
Основные понятия и краткое изложение
Формульная масса вещества – это сумма средних атомных масс каждого атома, представленного в химической формуле, и выражается в атомных единицах массы.Формульная масса ковалентного соединения также называется молекулярной массой.
Глоссарий
формула масса: сумма средних масс всех атомов, представленных в химической формуле; для ковалентных соединений это также молекулярная масса
молярная масса: масса в граммах на 1 моль вещества
Формула массы: определение и пример расчета
Масса по формуле молекулы (также известная как масса по формуле ) – это сумма атомных масс атомов в эмпирической формуле соединения.Формула веса дается в атомных единицах массы (а.е.м.).
Пример и расчет
Молекулярная формула глюкозы: C 6 H 12 O 6 , поэтому эмпирическая формула CH 2 O.
Формула массы глюкозы составляет 12 + 2 (1) +16 = 30 а.е.м.
Определение относительной формулы массы
Вы должны знать родственный термин – относительная масса по формуле (относительный вес по формуле). Это просто означает, что расчет выполняется с использованием значений относительной атомной массы элементов, которые основаны на естественном изотопном соотношении элементов, обнаруженных в атмосфере и коре Земли.Поскольку относительный атомный вес является безразмерным значением, относительная масса по формуле технически не имеет каких-либо единиц. Однако часто используются граммы. Если относительная формульная масса дана в граммах, то она рассчитана на 1 моль вещества. Обозначение относительной формулы массы – M r , и она рассчитывается путем сложения значений A r всех атомов в формуле соединения.
Пример расчета относительной массы по формуле
Найдите относительную формулу массы оксида углерода, CO.
Относительная атомная масса углерода равна 12, а кислорода – 16, поэтому относительная масса по формуле:
12 + 16 = 28
Чтобы найти относительную формульную массу оксида натрия, Na 2 O, вы умножаете относительную атомную массу натрия на ее нижний индекс и прибавляете полученное значение к относительной атомной массе кислорода:
(23 х 2) + 16 = 62
Один моль оксида натрия имеет относительную формульную массу 62 грамма.
Грамм Формула Масса
Масса по формуле в граммах – это количество соединения с такой же массой в граммах, что и масса по формуле в а.е.м.Это сумма атомных масс всех атомов в формуле, независимо от того, является ли соединение молекулярным. Масса по формуле грамма рассчитывается как:
грамм формула масса = масса растворенного вещества / формула масса растворенного вещества
Обычно вас просят указать массу по формуле в граммах на 1 моль вещества.
Пример
Найти по формуле грамма масса 1 моля KAl (SO 4 ) 2 · 12H 2 O.
Помните, умножьте значения атомных единиц массы атомов на их индексы.Коэффициенты умножаются на все последующее. В данном примере это означает, что имеется 2 сульфат-аниона согласно нижнему индексу и 12 молекул воды согласно коэффициенту.
1 K = 39
1 Al = 27
2 (SO 4 ) = 2 (32 + [16 x 4]) = 192
12 H 2 O = 12 (2 + 16) = 216
Итак, масса по формуле грамма составляет 474 г.
Источник
- Paul, Hiemenz C .; Тимоти, Лодж П. (2007). Химия полимеров (2-е изд.). Бока-Ратон: CRC P, 2007. 336, 338–339.
Вес объекта определяется как сила тяжести на объекте и может быть рассчитана как масса, умноженная на ускорение свободного падения, w = mg. Поскольку вес – это сила, ее единицей СИ является ньютон. Для объекта, находящегося в свободном падении, когда на него действует только сила тяжести, выражение для веса следует из второго закона Ньютона. Вы можете спросить, как и многие, «Почему вы умножаете массу на ускорение свободного падения, когда масса покоится на столе?». Значение g позволяет определить чистую силу тяжести, если было в свободном падении, а чистая сила тяжести равна весу. Другой подход состоит в том, чтобы считать “g” мерой интенсивности гравитационного поля в Ньютонах / кг в вашем местоположении. Вы можете рассматривать вес как меру массы в кг, умноженную на интенсивность гравитационного поля, 9.8 Ньютонов / кг при стандартных условиях. Данные можно ввести в любое из полей ниже. Затем щелкните за пределами поля, чтобы обновить другие количества. У поверхности Земли, где g = 9,8 м / с 2 :
| Индекс А как насчет состояния невесомости? |
Формула атомной массы
Атомная масса элемента равна средневзвешенному значению изотопов этого элемента.Изотопы – это атомы, которые имеют один и тот же атомный номер (количество протонов), но другое количество нейтронов. Число протонов определяет идентичность атома, а изотопы имеют одинаковые атомные номера, поэтому атомы принадлежат к одному элементу. Число нейтронов не равно, поэтому массы изотопов не будут одинаковыми. Атомная масса измеряется в атомных единицах массы (а.е.м.), где одна а.е.м. примерно эквивалентна массе отдельного протона или нейтрона.
Изотопы элемента не встречаются в природе в равных процентах, поэтому для определения атомной массы элемента необходимо использовать средневзвешенное значение.Изотопы, встречающиеся в более высоких процентах, будут иметь большее влияние на атомную массу, в то время как изотопы, встречающиеся в более низких процентах, будут иметь меньший эффект.
Атомная масса находится путем умножения массы изотопа на его относительное содержание, а затем сложения индивидуальных масс вместе.
Вопросы по формуле атомной массы:
1. Рассчитайте атомную массу хлора, используя информацию, представленную в следующей таблице.
Ответ:
Чтобы найти атомную массу хлора, атомная масса каждого изотопа умножается на относительное содержание (процентное содержание в десятичной форме), а затем индивидуальные массы складываются.
34,96885 x 0,7578 = 26,50
36,96590 x 0,2422 = 8,95
26,50 + 8,95 = 35,45
Атомная масса хлора 35,45 а.е.м.
2. Рассчитайте атомную массу никеля, используя информацию, представленную в следующей таблице.
Ответ:
Чтобы найти атомную массу никеля, атомная масса каждого изотопа умножается на относительное содержание (процентное содержание в десятичной форме), а затем индивидуальные массы складываются.
57,93535 x 0,680769 = 39,4406
59,93079 x 0,262231 = 15,7157
60,93 · 106 x 0,011399 = 0,69455
61,92835 x 0,036345 = 2,2508
63,92797 x 0,009256 = 0,59172
39,4406 + 15,7157 + 0,69455 + 2,2508 + 0,59172 = 58,69337
Атомная масса никеля равна 58,69337 а.е.м.
Массово-мольные расчеты Учебное пособие по химии
Ключевые понятия
- 1 моль чистого вещества имеет массу, равную его молекулярной массе (1) , выраженной в граммах.
Она известна как молярная масса M и измеряется в г моль -1 (граммы на моль вещества).
- Взаимосвязь между молярной массой, массой и молями может быть выражена математическим уравнением, как показано ниже:
г моль -1 = г ÷ моль
молярная масса = масса ÷ моль
M = m ÷ n
где:
M = молярная масса чистого вещества (измеряется в г · моль -1 )
m = масса чистого вещества (измеряется в граммах, г)
n = количество чистого вещества (измеряется в молях, моль) - Это математическое уравнение можно преобразовать в следующее:
п = м ÷ М
моль = масса ÷ молярная массам = n × M
масса = моль × молярная масса - Для расчета молей чистого вещества: n = m ÷ M
- Для расчета массы чистого вещества: m = n × M
- Для расчета молярной массы чистого вещества: M = m ÷ n
Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!
Расчет массы чистого вещества (m = нМ)
1 моль чистого вещества определяется как имеющий массу в граммах, равную его относительной молекулярной массе.
Эта величина известна как молярная масса (символ M).
Итак, масса 1 моля чистого вещества = относительная молекулярная масса в граммах.
А, масса 1 моля чистого вещества = молярная масса чистого вещества (г моль -1 )
Или, масса 1 моля = M (г моль -1 )
В таблице ниже указана масса 1 моля ряда обычных чистых веществ:
| название | молекулярная формула | относительная молекулярная масса | молярная масса (г моль -1 ) | масса 1 моль (г) | |||||
|---|---|---|---|---|---|---|---|---|---|
| газообразный гелий | He | 4.003 | 4,003 г моль -1 | 4,003 г | |||||
| газообразный кислород | O 2 | 2 × 16,00 = 32,00 | 32,00 г моль -1 | 321 | 321 | углекислый газCO 2 | 12,01 + (2 × 16,00) = 44,01 | 44,01 г моль -1 | 44,01 г |
| жидкая вода | H 2 O | (2 × 1,008) + 16.00 = 18,016 | 18,016 г моль -1 | 18,016 г |
Из таблицы видно, что 1 моль воды имеет массу 18,016 грамма, что не очень много (примерно по массе воды в паре маленьких кубиков льда, которые вы бы сделали в своей семейной морозильной камере).
А что, если бы у вас было 10 молей воды? Какой будет масса 10 молей воды?
Если 1 моль воды имеет массу 18,016 г, то 10 моль воды должны иметь массу в десять раз больше:
масса 10 моль воды = 10 × масса 1 моля воды
масса 10 моль воды = 10 × 18.016 = 180,16 г (примерно масса воды, которую можно налить в небольшой стакан)
Итак, если бы у нас было только ½ моля воды, какая масса воды была бы у нас?
Если 1 моль воды имеет массу 18,016 г, то ½ моля воды должно иметь ½ массы:
масса ½ моля воды = ½ × масса 1 моля воды
масса ½ моля воды = ½ × 18,016 = 9,008 г
В обоих приведенных выше примерах мы можем вычислить массу воды в граммах, умножив количество молей воды на массу 1 моля воды в граммах:
масса воды = моль воды × масса 1 моля воды
, поскольку масса 1 моля воды в граммах известна как его молярная масса, мы можем записать:
масса воды = моль воды × молярная масса воды
В таблице ниже сравнивается масса различных количеств воды в молях, и данные представлены в виде графика справа:
| ||||||||||||||||||||||||||||||||
| Из данных в таблице мы можем обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна молям вещества, умноженным на массу 1 моля вещества: масса = моль × масса 1 моля и поскольку масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль) масса (г) = моль × молярная масса (г моль -1 ) м = n × M | На приведенном выше графике показана прямая линия, проходящая через начало координат (0,0), поэтому уравнение для прямой выглядит следующим образом: y = наклон × x где y – масса воды (г) и x – моль воды (моль) и наклон (уклон) линии = вертикальный подъем ÷ горизонтальный ход = 270.24 г ÷ 15 моль = 18,016 г моль -1 = молярная масса воды (г моль -1 ) Итак, уравнение для этой линии: масса (H 2 O) = молярная масса (H 2 O) × моль (H 2 O) В целом: масса (г) = молярная масса (г-моль -1 ) × моль (моль) |
Выполните следующие действия, чтобы рассчитать массу чистого вещества с учетом количества вещества в молях:
- Извлеките данные из вопроса:
масса = m =? (единицы – граммы)
родинок = n = запишите, что вам говорят в вопросе
молярная масса = M = запишите, что вам говорят в вопросе (единицы измерения: г моль -1 )
(вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу) - Проверить единицы на соответствие и при необходимости преобразовать:
Количество вещества должно быть в молях (моль)!
Если количество указано в миллимолях (ммоль), разделите его на 1000, чтобы получить количество в молях (моль).
Если количество указано в микромолях (мкмоль), разделите его на 1 000 000, чтобы получить количество в молях (моль).
Если количество указано в километрах (кмоль), умножьте его на 1000, чтобы получить количество в молях (моль). - Напишите математическое уравнение (математическую формулу):
масса = моль × молярная масса
или
м = n × M - Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
Расчет молей чистого вещества (n = m / M)
В приведенном выше обсуждении мы обнаружили, что можем рассчитать массу чистого вещества, используя моль и молярную массу вещества:
масса (г) = моль (моль) × молярная масса (г-моль -1 )
Как бы мы вычислили количество молей чистого вещества, если бы мы знали массу вещества?
(a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на молярную массу:
| масса | = | моль × | |||||||||||||||||||||||||||
| молярная масса | 2 молярная масса | 2 молярная масса
| мы знаем массу в единицах | грамм (г) |
| мы знаем молярную массу в единицах | грамм на моль (г моль -1 ) |
| нам нужно найти моль в единицах | моль (моль) |
При проверке единиц мы видим, что деление молярной массы на массу даст нам количество в единицах «моль -1 ».
молярная масса / масса = г моль -1 / г = моль -1
Если мы перевернем это вверх дном (в математических терминах, возьмем обратную величину), мы получим количество в единицах “моль”, которое нам и нужно:
масса / молярная масса = г / г моль -1 = моль
так
моль = масса ÷ молярная масса
п = м ÷ М
Выполните следующие действия, чтобы рассчитать количество чистого вещества в молях с учетом массы вещества:
- Извлеките данные из вопроса:
масса = м = запишите, что вам говорят в вопросе
моль = n =? (единицы моль)
молярная масса = M = запишите, что вам говорят в вопросе (единицы измерения: г моль -1 )
(вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу) - Проверить единицы на соответствие и при необходимости преобразовать:
Масса должна быть в граммах!
Если масса указана в миллиграммах (мг), разделите ее на 1000, чтобы получить массу в граммах (г).
Если масса дана в микрограммах (мкг), разделите ее на 1000000, чтобы получить массу в граммах (г).
Если масса указана в килограммах (кг), умножьте ее на 1000, чтобы получить массу в граммах (г). - Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
п = м ÷ М - Подставьте значения и решите уравнение, чтобы найти количество молей веществ (моль).
Расчет молярной массы чистого вещества (M = m / n)
Что, если бы вы знали количество чистого вещества в молях и его массу?
Не могли бы вы вычислить его молярную массу?
Напомним, что масса = моль × молярная масса или m = n × M
(a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на моли:
| масса | = | |
| моль |
молярная масса = масса ÷ моль
M = m ÷ n
(b) Мы могли бы использовать некоторую логику:
Изучая единицы измерения, мы видим, что, разделив массу в граммах на количество в молях, мы приходим к количеству единиц в граммах на моль (г моль -1 ), которые являются единицами измерения молярной массы.
Следовательно, молярная масса (г моль -1 ) = масса (г) ÷ моль (моль)
или вы можете написать
M = m × n
Выполните следующие действия, чтобы рассчитать молярную массу чистого вещества с учетом количества вещества в молях и массы вещества:
- Извлеките данные из вопроса:
масса = м = запишите, что вам говорят в вопросе
родинок = n = запишите, что вам говорят в вопросе
молярная масса = M =? (ед.гмоль -1 ) - Проверить единицы на соответствие и при необходимости преобразовать:
Масса должна быть в граммах (г)!
Количество, моль, должно быть в молях (моль)! - Напишите математическое уравнение (математическую формулу):
молярная масса = масса ÷ моль
или
M = m ÷ n - Подставьте значения и решите уравнение, чтобы найти молярную массу вещества в граммах на моль.
Рабочие примеры расчета массы, молей, молярной массы
Рабочий пример: масса = моль × молярная масса (m = n × M)
Рассчитайте массу 0,25 моля воды, H 2 O.
- Извлеките данные из вопроса:
моль = n = 0,25 моль
молярная масса = M = (2 × 1,008) + 16,00 = 18,016 г моль -1 (рассчитано с использованием периодической таблицы)
масса = m =? грамм - Проверить данные на соответствие:
Количество воды в молях (моль)? Да.
Преобразовывать это не нужно. - Напишите математическое уравнение (математическую формулу):
масса = моль × молярная масса
или
м = n × M - Подставьте значения в уравнение и решите для массы (г):
масса = m = 0,25 × 18,016 = 4,504 г
Работает Пример: моль = масса & разделить молярную массу (n = m / M)
Вычислите количество кислородного газа, O 2 , в молях, присутствующее в 124.5 г газообразного кислорода.
- Извлеките данные из вопроса:
масса = m = 124,5 г
молярная масса = M = 2 × 16,00 = 32,00 г моль -1 (рассчитано с использованием периодической таблицы)
моль = n =? моль - Проверить данные на соответствие:
Масса газообразного кислорода выражена в граммах (г)? Да.
Преобразовывать это не нужно. - Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
п = м ÷ М - Подставьте значения в уравнение и решите, чтобы найти количество молей газообразного кислорода:
моль = n = 124.5 ÷ 32,00 = 3,89 моль
Работает Пример: молярная масса = масса ÷ моль (M = m / n)
Вычислите молярную массу чистого вещества, если масса 1,75 моль вещества составляет 29,79 г.
- Извлеките данные из вопроса:
масса = m = 29,79 г
моль = n = 1,75 моль - Проверить данные на соответствие:
Масса в граммах (г)? Да.Нам не нужно это преобразовывать.
Количество вещества в молях (моль)? Да. Нам не нужно это преобразовывать. - Напишите уравнение:
молярная масса = масса ÷ моль
или
M = m ÷ n - Подставьте значения в уравнение и решите для молярной массы:
молярная масса = M = 29,79 ÷ 1,75 = 17,02 г моль -1
Решение задач с использованием молей, массы и молярной массы
Проблема: Карбонат кальция, CaCO 3 , является важным промышленным химическим веществом.У химика Криса есть нечистый образец карбоната кальция. Масса загрязненного образца составляет 0,1250 кг, и он состоит из 87,00% (по массе) карбоната кальция. Прежде чем Крис сможет использовать этот карбонат кальция в химической реакции, Крису необходимо знать количество в молях карбоната кальция, присутствующего в этом образце.
Рассчитайте количество карбоната кальция в молях, присутствующее в этом загрязненном образце карбоната кальция.
Решение проблемы с использованием модели StoPGoPS для решения проблем:
| СТОП! | Сформулируйте вопрос. | Что вас просят сделать? Рассчитать количество карбоната кальция в молях n (CaCO 3 ) = моль карбоната кальция =? моль |
| ПАУЗА! | План. | Какой химический принцип вам нужно будет применить? Применить стехометрию (n = m ÷ M) Какую информацию (данные) вам предоставили? Шаг 1: Напишите математическое уравнение для расчета молей карбоната кальция: n (моль) = m (г) ÷ M (г-моль -1 ) Шаг 2: Рассчитайте массу карбоната кальция в образце в килограммах (кг). масса карбоната кальция (кг) = 87,00% массы образца (кг) Шаг 3: Преобразовать массу карбоната кальция в килограммах (кг) в массу в граммах (г). m (CaCO 3 ) в граммах = m (CaCO 3 ) в кг × 1000 г / кг Шаг 4: Рассчитайте молярную массу карбоната кальция (используйте Периодическую таблицу, чтобы найти молярную массу каждого элемента): молярная масса = M (CaCO 3 ) = M (Ca) + M (C) + [3 × M (O)] = Шаг 5: Подставьте значения m (CaCO 3 ) в граммах и M (CaCO 3 ) в г · моль -1 в математическое уравнение и решите для n (моль) n (моль) = m (г) ÷ M (г-моль -1 ) |
| Вперед! | Следуйте плану. | Шаг 1: Напишите математическое уравнение для расчета молей карбоната кальция: n (моль) = m (г) ÷ M (г-моль -1 ) Шаг 2: Рассчитайте массу карбоната кальция в образце в килограммах (кг). масса карбоната кальция (кг) = 87.00% массы образца (кг) Шаг 3: Преобразовать массу карбоната кальция в килограммах (кг) в массу в граммах (г). m (CaCO 3 ) в граммах = m (CaCO 3 ) в кг × 1000 г / кг Шаг 4: Рассчитайте молярную массу карбоната кальция (используйте Периодическую таблицу, чтобы найти молярную массу каждого элемента): молярная масса = M (CaCO 3 ) = M (Ca) + M (C) + [3 × M (O)] Шаг 5: Подставьте значения m (CaCO 3 ) в граммах и M (CaCO 3 ) в г · моль -1 в математическое уравнение и решите для n (моль) n (CaCO 3 ) = m (CaCO 3 ) ÷ M (CaCO 3 ) |
| ПАУЗА! | Поразмышляйте над правдоподобием. | Вы ответили на заданный вопрос? Да, мы рассчитали количество молей карбоната кальция в образце. Разумно ли ваше решение вопроса?
|

