Чему равен момент инерции материальной точки: 20. Момент инерции материальной точки, системы материальных точек, твердого тела относительно оси.

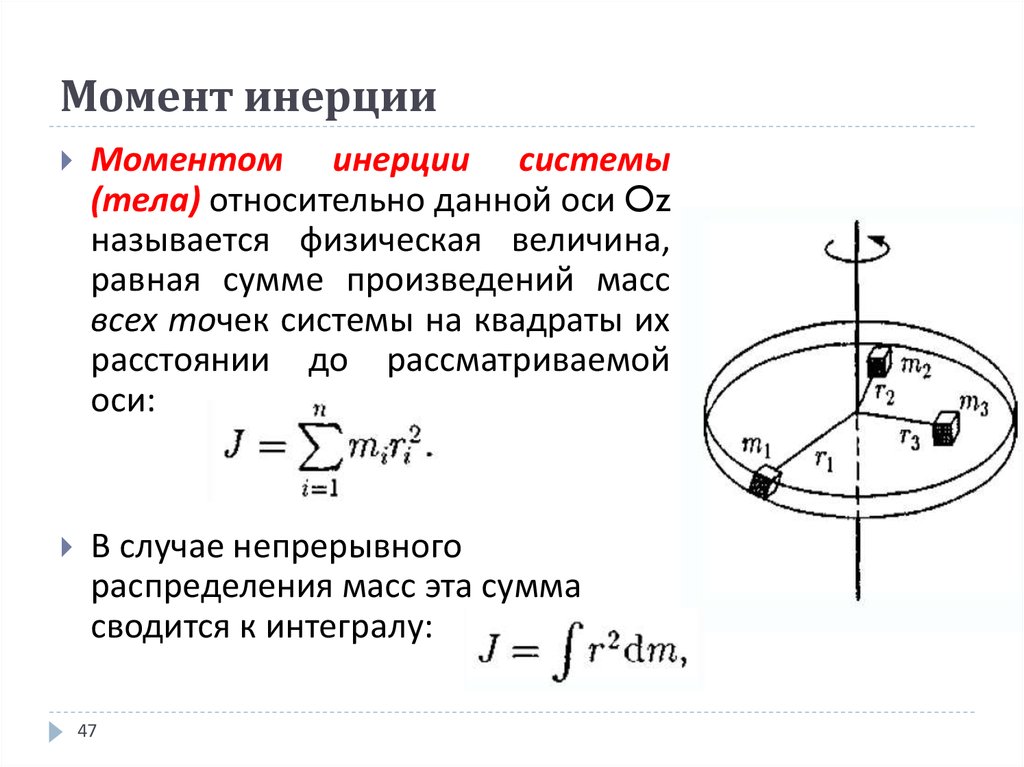
Момент инерции системы материальных точек

1. Главная страница 🏠
2. 📚 Библиотека
3. 👉 Механика 👈
4. Лекции по динамике вращательного движения
5. Момент инерции системы материальных точек

Нужна помощь в написании работы?

Узнать стоимость

 

Тело можно представить состоящим из большого числа м.т., тогда момент инерции системы м.

т. равен:

                                                        ,                                                    

где   – масса i – ой м.т.

         – ее расстояние до полюса О.

Моментом инерции системы м.т. или тела относительно полюса называют алгебраическую сумму произведений масс м.т., из которых состоит тело, на квадрат расстояния их до полюса О.

 

Поможем написать любую работу на аналогичную тему

• Реферат

  Момент инерции системы материальных точек

  От 250 руб

• Контрольная работа

  Момент инерции системы материальных точек

  От 250 руб

• Курсовая работа

  Момент инерции системы материальных точек

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Поделись с друзьями

• Содержание
• Материалы 1
• Меню

Момент инерции материальной точки, 

Момент инерции системы материальных точек

Момент силы

Момент импульса материальной точки

Связь вектора момента силы и момента импульса

Связь момента инерции, момента силы и момента импульса и ЗСМИ

Работа, совершаемая телом при вращении.

Кинетическая энергия вращающегося тела

Материалы по теме:

Момент инерции материальной точки,  Лекция

Добавить в избранное (необходима авторизация)

КИНЕТИЧЕСКИЙ МОМЕНТ • Большая российская энциклопедия

Авторы: В. А. Самсонов

КИНЕТИ́ЧЕСКИЙ МОМЕ́НТ, век­тор­ная ди­на­мич. ме­ра ме­ха­нич. дви­же­ния. К. м. $\boldsymbol G$ ма­те­ри­аль­ной точ­ки от­но­си­тель­но не­по­движ­ной сис­те­мы ко­ор­ди­нат с на­ча­лом в точ­ке $O$ ра­вен $\boldsymbol G=\boldsymbol r \times m\boldsymbol v$, где $m$ – мас­са точ­ки, $\boldsymbol r$ – её ра­ди­ус-век­тор, $\boldsymbol v$ – ско­рость. К. м. ма­те­ри­аль­ной точ­ки на­зы­ва­ет­ся так­же мо­мен­том им­пуль­са или мо­мен­том ко­ли­че­ст­ва дви­же­ния. К. м. сис­те­мы ма­те­ри­аль­ных то­чек ра­вен гео­мет­рич. сум­ме К. м. всех то­чек сис­те­мы.

К. м. твёр­до­го те­ла, со­вер­шаю­ще­го по­сту­па­тель­ное дви­же­ние от­но­си­тель­но точ­ки $O$, оп­ре­де­ля­ет­ся мгно­вен­ны­ми по­ло­же­ни­ем и ско­ро­стью цен­тра масс те­ла: $\boldsymbol G=\boldsymbol r_\text{c} \times m\boldsymbol v_\text{c}$, где $m$ – мас­са те­ла, $\boldsymbol r_\text{c}$ – ра­ди­ус-век­тор цен­тра масс, $\boldsymbol v_\text{c}$ – ско­рость цен­тра масс. Для те­ла, вра­щаю­ще­го­ся во­круг не­под­виж­ной оси $Oz$, К. м. от­но­си­тель­но этой оси ра­вен про­из­ве­де­нию мо­мен­та инер­ции $I_z$ от­но­си­тель­но этой оси на уг­ло­вую ско­рость $\omega$ вра­ще­ния те­ла: $G_z=I_z \omega$. Для слу­чая вра­ще­ния те­ла во­круг не­под­виж­ной точ­ки $O$ К. м. те­ла от­но­си­тель­но точ­ки $O$ удоб­но за­да­вать в гл. осях инер­ции, свя­зан­ных с те­лом: $\boldsymbol G=\{I_x\omega_x,I_y\omega_y, I_z\omega_z\}$, где $I_x$, $I_y$, $I_z$ – мо­мен­ты инер­ции от­но­си­тель­но со­от­вет­ст­вую­щих осей, $\omega_x$, $\omega_y$, $\omega_z$ – про­ек­ции век­то­ра уг­ло­вой ско­ро­сти $\boldsymbol \omega$. Век­тор $\boldsymbol G$ кол­ли­неа­рен век­то­ру $\boldsymbol \omega$ лишь в тех слу­ча­ях, ко­гда по­след­ний на­прав­лен вдоль од­ной из гл. осей инер­ции. К. м. те­ла от­но­ситель­но лю­бой оси, про­хо­дя­щей че­рез точ­ку $O$ (в ча­ст­но­сти, мгно­вен­ной оси вра­ще­ния), ра­вен про­ек­ции $\boldsymbol G$ на эту ось. Для слу­чая про­из­воль­но­го дви­же­ния те­ла К. м. те­ла от­но­си­тель­но точ­ки $O$ вы­чис­ля­ет­ся по фор­му­ле $\boldsymbol G=\boldsymbol r_\text{c} \times m \boldsymbol v_\text{c}+ \boldsymbol G_\text{c}$, где $\boldsymbol G_\text{c}=\{I_{cx}\omega_x, I_{cy}\omega_y,I_{cz}\omega_z\}$ – К. м. вра­ще­ния те­ла во­круг его цен­тра масс.

К. м. – од­но из важ­ней­ших по­ня­тий клас­сич. ме­ха­ни­ки, ко­то­рое ис­поль­зу­ет­ся в осн. для опи­са­ния эво­лю­ции вра­ща­тель­но­го дви­же­ния те­ла под дей­ст­ви­ем при­ло­жен­ной к не­му си­лы. В этом слу­чае, со­глас­но тео­ре­ме об из­ме­не­нии К. м. (см. Ди­на­ми­ка), по­след­ний мо­жет из­менять своё на­прав­ле­ние. Это при­во­дит к т. н. ги­ро­ско­пи­че­ским эф­фек­там, при ко­то­рых ось вра­щаю­ще­го­ся те­ла по­во­ра­чи­ва­ет­ся в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном на­прав­ле­нию си­лы.

Си­лы, дей­ст­вую­щие ме­ж­ду точ­ка­ми сис­те­мы, не из­ме­ня­ют К. м. сис­те­мы, но мо­гут из­ме­нить кон­фи­гу­ра­цию сис­те­мы и уг­ло­вую ско­рость её вра­ще­ния. Так, при прыж­ках в во­ду с выш­ки спорт­смен груп­пи­ру­ет­ся для то­го, что­бы умень­шить мо­мент инер­ции сво­его те­ла и со­от­вет­ст­вен­но уве­ли­чить ско­рость вра­ще­ния за счёт по­сто­ян­ст­ва К. м. При рас­прям­ле­нии те­ла спорт­сме­на уг­ло­вая ско­рость вра­ще­ния за­мет­но па­да­ет, об­лег­чая ус­ло­вия вхо­да в во­ду.

Калькулятор момента инерции масс

Создано Kenneth Alambra

Последнее обновление: 31 августа 2022 г.

Содержание:

• Что такое момент инерции?
• Уравнение и таблица момента инерции
• Таблица момента инерции
• Как пользоваться калькулятором момента инерции такие фигуры, как сферы, прямоугольные призмы, цилиндрические объекты и многое другое.

  Продолжайте читать, чтобы узнать о:

  • Что такое момент инерции;
  • Как рассчитать момент инерции;
  • Уравнение момента инерции масс;
  • Таблица моментов инерции масс; и
  • Как использовать этот калькулятор момента инерции массы.

  Что такое момент инерции?

  Массовый момент инерции — это величина крутящего момента или момента, необходимого для того, чтобы заставить объект вращаться или испытывать угловое ускорение вокруг оси.

  Момент инерции массы объекта дает нам представление о том, какую инерцию вращения объект может иметь относительно произвольной оси вращения. Чем больше момент инерции объекта, тем труднее ему набрать вращательную кинетическую энергию или тем труднее остановить вращение.

  Чтобы узнать, что такое момент инерции объекта, возьмите произведение крутящего момента, необходимого для вращения этого объекта, и расстояния приложенного крутящего момента от оси вращения. Однако есть гораздо лучший и правильный способ сделать это, и мы обсудим его в следующем разделе этого текста. 92\times dm)I=∫(r2×dm)

  Таблица момента инерции

  Затем мы можем использовать интегрирование формулы момента инерции для получения других формул для объектов, которые имеют определенные формы, такие как куб, цилиндр, сфера и и так далее, как показано в таблице моментов инерции масс ниже:

  94 фута 4. Вы можете узнать больше о втором моменте площади, взглянув на наш отдельный калькулятор момента инерции.

  Как использовать этот калькулятор момента инерции массы

  Вот шаги, которые вы можете выполнить при использовании нашего калькулятора момента инерции массы:

  1. Выберите фигуру , которая соответствует форме объекта, для которого вы хотите найти момент массы инерции. Вы можете выбрать из более чем 20 фигур в нашем инструменте.
  2. Введите массу вашего объекта.
  3. Введите значение расстояния , которое требует ввести наш калькулятор. Это расстояние зависит от выбранной вами фигуры. Наш калькулятор момента инерции массы будет использовать это измерение для определения плеча момента или расстояния, rrr, подходящего для выбранного вами объекта.

  И все! Наш момент инерции массы уже будет отображать момент инерции массы относительно оси (или различных осей), в зависимости от выбранной вами фигуры. Вы также можете изменить единицы измерения момента инерции, щелкнув стрелку раскрывающегося списка рядом с рассчитанным значением.

  Кеннет Аламбра

  Карта механики – Момент инерции массы

  Момент инерции массы представляет сопротивление тела угловым ускорениям вокруг оси, точно так же, как масса представляет сопротивление тела линейным ускорениям. Это представлено в уравнении с вращательной версией второго закона Ньютона.

  №	Фигура и моменты инерции
  #1 – шар . Твердый шар радиусом r и массой m с осью вращения, проходящей через его центр.
  #2 – Круглые пяльцы . Тонкий круглый обруч радиуса r и массы m, через центр которого проходят три оси вращения: параллельные осям x, y или z.
  #3 – Прямоугольный . Сплошной прямоугольный параллелепипед длины l, ширины w, высоты h и массы m, через центр которого проходят четыре оси вращения: параллельные длине l, ширине w, высоте h или наибольшей диагонали d.
  #4 – Цилиндр . Сплошной цилиндр радиуса r, высоты h и массы m, через центр которого проходят три оси вращения: параллельные осям x, y и z.
  #5 – Цилиндрическая трубка . Цилиндрическая труба с внутренним радиусом r₁, внешним радиусом r₂, высотой h и массой m с тремя осями вращения, проходящими через ее центр: параллельно осям x, y и z.
  #6 – Цилиндрическая оболочка . Цилиндрическая оболочка радиусом r и массой m с осью вращения, проходящей через ее центр параллельно высоте.
  #7 – Диск . Тонкий сплошной диск радиусом r и массой m, через центр которого проходят три оси вращения: параллельные осям x, y или z.
  #8 – Додекаэдр . Сплошной и полый правильный додекаэдр (двенадцать плоских граней) со стороной s и массой m с осью вращения, проходящей через его центр и одну из вершин.
  	где:
  #9 – Эллипсоид . Сплошной эллипсоид с полуосями a, b, c и массой m, через центр которого проходят три оси вращения: параллельные полуосям a, b или c.
  #10 Сплошной и полый правильный икосаэдр (двадцать плоских граней) со стороной s и массой m с осью вращения, проходящей через его центр и одну из вершин.
  	где:
  #11 – Равнобедренный треугольник . Равнобедренный треугольник массы m, угла при вершине 2β и длины общей стороны L с осью вращения, проходящей через вершину перпендикулярно плоскости.
  #12 – Октаэдр . Сплошной и полый правильный октаэдр (восемь плоских граней) со стороной s и массой m с осью вращения, проходящей через его центр и одну из вершин.
  #13 – Масса точек . Точка массы m на расстоянии r от оси вращения.
  #14 – Прямоугольная пластина . Тонкая прямоугольная пластина длиной l, шириной w и массой m с осью вращения, проходящей через ее центр перпендикулярно плоскости.
  #15 – Правильный многоугольник . Плоский правильный многоугольник с n вершинами, радиусом описанной окружности R и массой m с осью вращения, проходящей через его центр, перпендикулярно плоскости. Радиус R можно выразить стороной s.
  #16 – Правый круговой конус (полый) . Полый прямоугольный конус радиуса r, высоты h и массы m с тремя осями вращения, проходящими через его центр: параллельно осям x, y или z.
  #17 – Правый круговой конус (сплошной) . Сплошной прямоугольный конус радиуса r, высоты h и массы m с тремя осями вращения, проходящими через его центр: параллельно осям x, y или z.
  #18 – Стержень . Стержень длины L и массы m с двумя осями вращения: вокруг центра и на одном конце.
  #19 – Сфера . Полая сфера радиуса r и массы m с осью вращения, проходящей через ее центр.
  #20 – Сферическая оболочка . Сферическая оболочка внутреннего радиуса r₁, внешнего радиуса r₂ и массы m с осью вращения, проходящей через ее центр.
  #21 – Тетраэдр . Сплошной и полый правильный тетраэдр (четыре плоские грани) со стороной s и массой m с осью вращения, проходящей через его центр и одну из вершин.
  Тор малого радиуса a, большого радиуса b и массы m с осями вращения, проходящими через его центр: перпендикулярно большому диаметру и параллельно большому диаметру.

  \[F=m a\]

  \[M=I \альфа\]

  Так же, как и момент инерции площади, момент инерции массы можно рассчитать с помощью интегралов моментов или с помощью метода составных частей и теоремы о параллельных осях. На этой странице будет обсуждаться только метод интеграции, так как метод составных частей обсуждается на отдельной странице.

  Момент инерции массы и угловые ускорения

  Момент инерции массы представляет собой интеграл момента, а именно второй, полярный, интеграл момента массы. Чтобы понять, почему это связано с моментами и угловыми ускорениями, мы начнем с изучения точечной массы на конце безмассовой палки, как показано ниже. Представьте, что мы хотим повернуть палку вокруг левого конца, приложив к ней момент. Мы хотим связать приложенный момент к угловому ускорению палки относительно этой точки.

  Точка массы на конце безмассовой палочки. Мы пытаемся повернуть массу вокруг ее левого конца, прикладывая к ней момент.

  Чтобы связать момент и угловое ускорение, нам нужно начать с традиционной формы второго закона Ньютона, утверждающего, что сила, действующая на точечную массу палкой, будет равна массе, умноженной на ускорение точечной массы (F = м а). В этом случае момент будет связан с силой в том смысле, что сила, действующая на массу, умноженная на длину палки (d), равна моменту. Мы также можем связать линейное ускорение массы в том смысле, что линейное ускорение равно угловому ускорению, умноженному на длину стержня (d). Если мы возьмем эти две замены и поместим их в исходное уравнение F = m, мы можем получить уравнение, которое связывает момент и угловое ускорение для нашего сценария. Упрощенная версия этого нового соотношения гласит, что момент будет равен массе, умноженной на квадрат расстояния, умноженный на угловое ускорение. Этот член, умноженный на квадрат расстояния (относящийся к моменту и угловому ускорению), формирует основу для массового момента инерции. 92)*\альфа\]

  Делая последний шаг, твердые тела с массой, распределенной по объему, подобны бесконечному количеству малых масс вокруг оси вращения. Вместо безмассовых палочек, удерживающих все на месте, масса просто удерживается на месте материалом вокруг нее. Чтобы связать момент и угловое ускорение в этом случае, мы используем интегрирование, чтобы сложить бесконечное число малой массы, умноженной на квадрат расстояния.

  Аппроксимируя твердое тело как бесконечное число бесконечно малых масс, связанных с осью вращения, мы можем суммировать все массы, умноженные на квадрат расстояния, с интегрированием. 92)\]

  Вычисление момента инерции масс путем интегрирования

  Первым шагом в вычислении момента инерции масс является определение оси вращения, которую вы будете использовать. В отличие от массы, момент инерции массы зависит от точки и оси , вокруг которой мы вращаемся. Мы можем легко продемонстрировать это с чем-то вроде метлы, где в зависимости от положения и направления оси, вокруг которой мы вращаемся, может быть более или менее трудно вращать метлу.

  Момент инерции массы будет варьироваться в зависимости от точки и направления оси вращения.

  После выбора оси вращения полезно нарисовать фигуру с включенной осью вращения. Это полярный интеграл, поэтому мы возьмем массовый интеграл, исходящий наружу от этой оси вращения.

  Кроме того, мы интегрируем по массе, и масса в любой заданной точке будет равна плотности, умноженной на объем. Если исследуемый объект имеет однородную плотность, как это часто бывает, мы можем вынести эту константу плотности за пределы интеграла, оставив интеграл от расширения объема. Плотность в этих случаях указывается редко, но если вы можете определить общую массу и общий объем, вы также можете это использовать. Если мы поместим все это в исходное уравнение, которое у нас было выше, мы получим следующее. 92)\]

  Для полярного интеграла нам нужно определить dV в терминах радиуса (r), движущегося наружу от оси вращения. Скорость изменения объема (dV) будет равна площади цилиндрической поверхности при заданном радиусе, умноженной на скорость, с которой этот радиус увеличивается (dr).