Что такое золотое сечение и правда ли оно повсюду
18 июля 2021 Ликбез Жизнь
Спойлер: это лишь красивая математическая легенда.
Что такое золотое сечение
Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.
Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.
1 / 0
«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons
2 / 0
«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons
Золотое сечение тесно связано с числами Фибоначчи.
Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.
Почему золотое сечение так популярно
Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.
Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».
Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще.
Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.
Его можно встретить в природе
Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.
Часть растения эониума. Фото: Max Ronnersjö / Wikimedia CommonsЕго обнаруживают в произведениях архитектуры и искусства
Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.
Почему универсальность золотого сечения — миф
Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.
Божественность золотого сечения преувеличивается
Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.
Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.
В природе золотое сечение не так уж распространено
Его находят далеко не везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие. У них больше витков, и расстояние между ними меньше.
Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:
1 / 0
Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons
2 / 0
Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons
В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.
В искусстве оно тоже встречается не так уж часто
Изучение 565 картин выдающихся художников показало, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.
Археологические исследования не подтверждают и того, что древние греки могли использовать золотое сечение при постройке Парфенона.
Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.
Кому золотое сечение может быть полезно на самом деле
Современная математика использует золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.
Фрактальная форма кочана капусты Романеско. Фото: Ivar Leidus / Wikimedia CommonsЗнание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.
Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.
Читайте также 💆♂️👩🔬
- Продолжите последовательность! 10 мини-задач для разминки мозга
- Как округлять числа
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- Гимнастика для ума: 10 увлекательных задач с числами
- 10 увлекательных задач от советского математика
Фи и пи .
Стоунхендж и пирамиды ЕгиптаЗолотая пропорция — геометрическая конструкция, широко использовавшаяся в греческой архитектуре. Это также натуральная пропорция, воплощенная в знаменитой прогрессии чисел ряда Фибоначчи, названной так по фамилии итальянского математика. Это ряд 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… и т д, в котором каждое последующее число равно сумме двух предыдущих (На пример, 1+1=2; 2+1=3, 3+2=5 и тд.). В природе этот ряд проявляется среди прочего в спиральном рисунке семян подсолнечника и в еловой шишке Если посчитать семена, то они выстроятся в ряд Фибоначчи. Он также выявляется в стадиях роста раковины наутилуса.
Золотая пропорция, или фи (φ), получается путем деления одного числа из ряда Фибоначчи на предшествующее число. Чем больше числа этого ряда, тем выше точность фи. Например, при делении 144 на 89 получаем 1,6 179 775 то есть число, которое подобно пи дает цепочку десятичных знаков, тянущуюся до бесконечности без явного повторения.
Число пи (π) используется для вычисления различных характеристик круга. В Древнем Египте оно выражалось отношением 22:7. Сегодня его значение определяется с точностью до четырех десятичных знаков 3,1416.
Великая пирамида воплощает как фи, так и пи простым способом. Во-первых, сумма четырех сторон основания пирамиды равна длине окружности круга, радиус которого равен ее высоте (рис. 23). Это можно продемонстрировать с помощью отношения 7:11 высоты к основанию. Формула вычисления окружности круга 2πr, где:
r — радиус. В нашем случае равен 7 единицам, а мы принимаем за 22:7.
2 х (22:7) х 7 = 44 единицы.
Итак, раз каждая сторона равняется 11 единицам, тогда сумма всех четырех сторон равна:
11 + 11 + 11 + 11 = 11×4, то есть опять же 44 единицам.
Золотая пропорция фи присутствует и в отношении основания пирамиды и длины ее апофемы или склона (рис. 24). Теорема Пифагора гласит, что квадрат гипотенузы — в данном случае откоса — равен сумме квадратов двух других сторон, иными словами, высоты и половины основания. Таким образом, длина гипотенузы или ската является корнем квадратным из 7,02
Разумеется, эти отношения могли вовсе не попасть в поле зрения древних египтян. Отношение высоты Великой пирамиды к ее основанию -7:11 — могло быть выбрано по совершенно иным соображениям. Но точность и изысканность конструкции пирамиды означает, что архитекторы должны были понимать, что такие отношения подразумеваются в том, что они строили.
Фи: Золотое сечение | Live Science
Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать партнерскую комиссию.
Вот как это работает.
На протяжении столетий вокруг фи росло множество преданий, таких как представление о том, что оно символизирует совершенную красоту или уникально встречается в природе. Но многое из этого не имеет под собой реальной основы.
Определение фи
Фи можно определить, взяв палку и разломив ее на две части. Если соотношение между этими двумя частями такое же, как соотношение между общей палочкой и большим сегментом, говорят, что пропорции находятся в золотом сечении. Это было впервые описано греческим математиком Евклидом, хотя, по словам математика, он называл это «делением в крайнем и среднем отношении».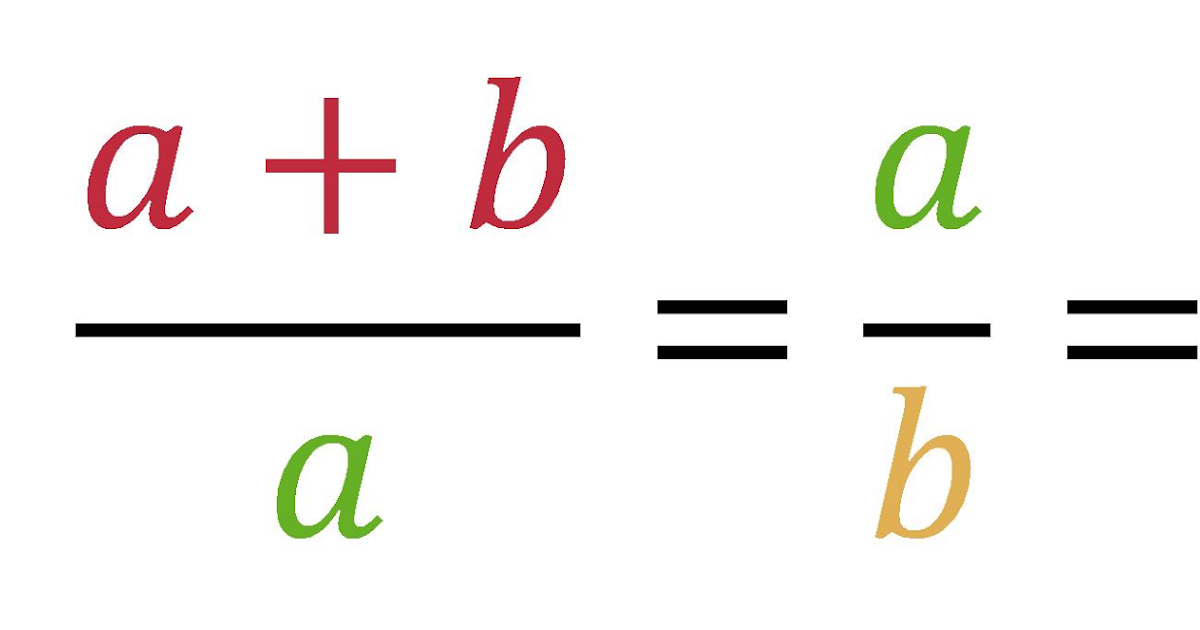
2 = phi + 1
Это представление можно преобразовать в квадратное уравнение с двумя решениями: (1 + √5)/2 и (1 – √5)/2. Первое решение дает положительное иррациональное число 1,6180339887… (точки означают, что числа продолжаются вечно), и это обычно то, что известно как фи. Отрицательное решение равно -0,6180339887… (обратите внимание, что числа после запятой совпадают) и иногда называется малым фи.
Последний и довольно элегантный способ представления фи выглядит следующим образом: 90,5 * 0,5 + 0,5
Это пять, возведенные в половинную степень, умноженное на половину плюс половина.
Связанный: 11 самых красивых математических уравнений
Phi тесно связан с последовательностью Фибоначчи , в которой каждое последующее число в последовательности находится путем сложения двух предыдущих чисел. Эта последовательность идет 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Это также связано со многими заблуждениями.
Взяв соотношение последовательных чисел Фибоначчи, вы можете все ближе и ближе приближаться к фи. Интересно, что если вы продолжите последовательность Фибоначчи в обратном направлении, то есть до нуля и до отрицательных чисел, отношение этих чисел будет все ближе и ближе приближать вас к отрицательному решению, маленькому фи -0,6180339887…
Существует ли золотое сечение в природа?
Хотя люди знали о фи уже давно, известность о нем пришла лишь в последние столетия. Итальянский математик эпохи Возрождения Лука Пачоли написал книгу под названием «De Divina Proportione» («Божественная пропорция») в 1509 году.по словам Нотта, это обсуждало и популяризировало фи.
Пачоли использовал рисунки, сделанные Леонардо да Винчи , которые включали фи, и возможно, что да Винчи был первым, кто назвал его «sectio aurea» (латинское «золотое сечение»). Только в 1800-х годах американский математик Марк Барр использовал греческую букву Φ (фи) для обозначения этого числа.
Как свидетельствуют другие названия числа, такие как божественная пропорция и золотое сечение, фи приписывается многим чудесным свойствам. Писатель Дэн Браун включил в свой бестселлер «Код да Винчи» (Doubleday, 2000) длинный отрывок, в котором главный герой обсуждает, как фи представляет собой идеал красоты, который можно найти на протяжении всей истории. Более трезвые ученые обычно опровергают такие утверждения.
Например, энтузиасты фи часто упоминают, что некоторые размеры Великой пирамиды Гизы , такие как длина основания и/или высота, находятся в золотом сечении. Другие утверждают, что греки использовали фи при проектировании Парфенона или в своих прекрасных скульптурах.
Энтузиасты Фи любят указывать на то, что пирамиды Гизы, построенные между 2589 и 2504 годами до нашей эры, были построены в соответствии с золотым сечением. Но измерения по своей природе неточны и произвольны, поэтому пирамиды не являются точными примерами золотого сечения. (Изображение предоставлено Дэном Брекволдтом (открывается в новой вкладке) Shutterstock (открывается в новой вкладке)) Но, как указал Марковски в своей статье 1992 года в College Mathematics Journal под названием «Заблуждения о золотом сечении»: «измерения реальных объектов могут быть только приблизительными.
Поверхности реальных объектов никогда не бывает идеально ровным». Далее он написал, что неточности в точности измерений приводят к большим неточностям, когда эти измерения переводятся в отношения, поэтому заявления о древних зданиях или произведениях искусства, соответствующих фи, следует воспринимать с большой долей скептицизма.
Часто говорят, что размеры архитектурных шедевров близки к фи, но, как заметил Марковский, иногда это означает, что люди просто ищут отношение, которое дает 1,6, и называют это число фи. Найти два отрезка, отношение которых равно 1,6, не представляет особой сложности. Выбор места для измерения может быть произвольным и при необходимости корректироваться, чтобы приблизить значения к фи.
Попытки найти фи в человеческом теле также приводят к подобным заблуждениям. В недавнем исследовании утверждалось, что золотое сечение найдено в различных пропорциях человеческого черепа. Но как сказал Дейл Риттер, ведущий преподаватель анатомии человека в Медицинской школе Альперта (AMS) Университета Брауна в Род-Айленде, 9 лет.
«Я считаю, что основная проблема с этой статьей заключается в том, что в ней очень мало (а возможно, и нет) науки… с таким количеством костей и так много интересных мест на этих костях, я полагаю, что там было бы по крайней мере несколько “золотых сечений” где-либо еще в человеческой скелетной системе .
Связанный: Фотографии: Большие числа, определяющие Вселенную
И хотя говорят, что фи широко распространена в природе, ее значение преувеличено. Лепестки цветов часто имеют числа Фибоначчи, например, пять или восемь, а семена сосновых шишек вырастают наружу по спирали чисел Фибоначчи. Но существует столько же растений, которые не следуют этому правилу, сколько и тех, которые ему следуют, Кит Девлин, математик из Стэнфордского университета, рассказал Live Science .
Люди утверждают, что морские раковины, такие как раковины наутилуса, обладают свойствами, в которых скрывается фи.
Но, как указывает Девлин на своем веб-сайте
Хотя фи, безусловно, интересная математическая идея, именно мы, люди, придаем значение вещам, которые находим во Вселенной. Сторонник, смотрящий через очки цвета фи, может видеть золотое сечение повсюду. Но всегда полезно выйти за рамки конкретной точки зрения и спросить, действительно ли мир соответствует нашему ограниченному пониманию.
Дополнительные ресурсы:
- Вот полезное поясняющее видео о золотом сечении из
- Узнайте больше о мифе о золотом сечении в природе от GoldenNumber.net .
- Посмотрите объяснение Академии Хана о золотом сечении.
Адам Манн — независимый журналист с более чем десятилетним стажем, специализирующийся на астрономии и физике.
Он имеет степень бакалавра астрофизики Калифорнийского университета в Беркли. Его работы публиковались в New Yorker, New York Times, National Geographic, Wall Street Journal, Wired, Nature, Science и многих других изданиях. Он живет в Окленде, штат Калифорния, где любит кататься на велосипеде.
Что означает имя Фидиакс?
Phi — иррациональная математическая константа, приблизительно равная 1,618.., часто обозначаемая греческой буквой φ. Другими часто используемыми названиями для Фи являются: Золотое сечение, Экстремальное и среднее отношение, Божественная пропорция и Золотое сечение. Phi — это встречающееся в природе соотношение, которое демонстрирует эстетически приятные свойства. Его можно увидеть на протяжении всей истории и природы в некоторых из самых почитаемых сооружений.
Фи можно выразить с помощью следующего уравнения:
Соотношения между этими величинами находятся в соотношении Фи, если верно следующее:
Алгебраически это можно рассчитать с помощью следующего уравнения:
Фидий (480 г.
до н.э. – 430 г. до н.э.) был известным греческим архитектором, художником и скульптором. . Именно Фидий, тщательно изучив эту математическую аномалию, решил представить это безупречное соотношение греческой буквой фи (φ). Использование фи в пространственной пропорциональности можно увидеть в работах Фидия, таких как Статуя Зевса в Олимпии (одно из семи чудес древнего мира), Афина Парфенос и Афина Промахос. На протяжении всей истории многие другие художники, архитекторы, математики, музыканты и инженеры использовали Фи в своих творениях. Несколько исполнителей: Платон, Евклид, Фибоначчи, Иоганн Кеплер, Роджер Пенроуз, Леонардо да Винчи и египтяне.
Многие встречающиеся в природе структуры также имеют Фи в своей конструкции. Некоторые из этих структур включают пропорции человеческого тела, расположение ветвей вдоль стеблей растений, расположение семян подсолнечника, сосновых шишек, листьев, ДНК и морских раковин, таких как наутилус.
Фи широко представлена в некоторых из самых интересных объектов и в некоторых из самых захватывающих дух природных красот, известных человеку.
Это символ элегантности, и его свойства будут продолжать проявляться и реализовываться во времени.
Phidiax представляет Phi с помощью элегантного дизайна программного обеспечения. Естественная красота проявляется в различных случаях в природе. От повторяющихся и предсказуемых паттернов, основанных на соотношениях (Phi — 1,618.., Pi — 3.14..), обладающих безупречными свойствами, до кажущихся случайными изображений (фракталов, снежинок), алгоритмы которых определяются физикой, — наш мир управляется математическими законами.
Осязаемое применение Золотого сечения (Phi) подтверждается наблюдением за природными структурами, такими как сосновые шишки, подсолнухи, ананасы и раковина наутилуса.
Как определение элегантности, Phi был засвидетельствован как метод пропорции в различных произведениях искусства и архитектуры, включая структуры Акрополя, статуи Парфенона Фидия, Мону Лизу Леонардо да Винчи, Таинство Тайной Вечери Сальвадора Дали. , египетские храмы. Они считаются произведениями искусства по целому ряду причин, включая элегантность и эстетически приятный внешний вид.
Обычно наблюдатель смотрит на изображения, обращенные наружу, и воспринимает произведения искусства с бурей эмоций. Не требуется натренированного глаза, чтобы извлечь смысл из этих произведений. Однако понимание тонкостей, в том числе пространственных отношений, стоящих за тем, что видно в этих произведениях искусства и человеке, само по себе является редким искусством.
В Phidiax мы находим похожие параллели в архитектуре и дизайне программного обеспечения. Мы уделяем самое пристальное внимание деталям, которые делают наши поставки красноречивыми. Phidiax стремится к тому, чтобы наши произведения искусства удовлетворяли обращенным вовне требованиям, которые эффективно находили отклик у наших клиентов, в то время как направленный внутрь оркестр компонентов работал согласованно.
«X» в Phidiax означает расширяемость. В программной и системной архитектуре расширяемость — это методология, при реализации которой учитывается будущий рост. Это принцип построения программных компонентов, которые служат поддержкой для будущего улучшения системы.