Что характеризует и от чего зависит момент инерции: Национальный исследовательский университет «Высшая школа экономики»

9. Момент инерции твердого тела

Из формулы (7.24) видно, что угловое ускорение, сообщаемое телу вращающим моментом, зависит от момента инерции тела; чем больше момент инерции, тем меньше угловое ускорение. Следовательно, момент инерции характеризует инерционные свойства тела при вращательном движении, как и масса при поступательном движении. В отличие от массы тела момент инерции зависит от радиуса окружности, описываемой точкой приложения силы, а, следовательно, от выбора оси вращения.

Из формулы следует, что единицей измерения момента инерции является кг.мІ.

Из определения момента инерции

(7.25)

видно, что момент инерции есть величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей:

(7.26)

Момент инерции существует безотносительно к вращению. Каждое тело независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси.

Для неоднородных тел и тел неправильной формы момент инерции определяют экспериментально, а для однородных тел геометрически правильной формы – посредством интегрирования.

Как было ранее указано, в силу формулы (7.3) элементарная масса равна произведению плотности тела в данной точке на соответствующий элементарный объем: _.

Следовательно, момент инерции можно представить в виде: _.

Если плотность  тела постоянна, её можно вынести за знак суммы задача нахождения моментов инерции сводится к интегрированию:

(7.27)

Интегралы в (7.27) берутся по всему объему тела. Величины  и r в этих интегралах являются функциями точки.

В качестве примера вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 7.10).

Рис. 7.10.

Разобьем диск на кольцевые слои толщиной . Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном . Объем такого слоя равен , где – толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова, (7.27) можем вынести за знак интеграла: , где – радиус диска.

Так как масса диска , то получим

(7.28)

Для однородных и симметричных тел обычно основной осью вращения является ось симметрии. В этом случае момент инерции, как мы видели, легко вычисляется.

Для некоторых тел правильной формы значение моментов инерции относительно осей, проходящих через центр их симметрии приведены в таблице 2.

Таблица 2

Форма тела	Расположение оси	Величина момента инерции
Обруч
Цилиндр
Шар
Примечание: m – масса тела, R0 – его радиус

Рассмотрим произвольное тело и две параллельные друг другу оси, одна из которых (ось С) проходит через центр масс тела, а другая (ось О) отстоит от первой на расстояние а (рис.

7.11). Выберем оси координат и так, как показано на рис. 7.11.

Рис. 7.11

Момент инерции относительно оси О определяется выражением

Разобьем это выражение на три суммы:

Первая сумма представляет собой момент инерции относительно оси, проходящей через центр масс. Сумма дает массу тела . Наконец, , где – координата центра масс, которая при сделанном выборе начала координат равна нулю. Таким образом, мы приходим к соотношению:

(7.29)

Это соотношение выражает теорему Штейнера, которая гласит, что момент инерции относительно произвольной оси равен сумме момента инерции

относительно оси, параллельной данной и проходящей через центр масс тела, и произведением массы т тела на квадрат расстояния а между осями.

В соответствии с теоремой Штейнера момент инерции диска относительно оси ОґОґ, отстоящей на расстоянии от оси, проходящей через центр масс, равен найденному нами моменту инерции (7. 28) относительно оси, проходящей через центр диска, плюс : .

формула. Момент инерции тела :: SYL.ru

Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.

Что такое вращение с точки зрения физики?

Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:

• Движение колеса автомобиля или велосипеда.
• Вращение лопастей вертолета или вентилятора.
• Движение нашей планеты вокруг оси и вокруг Солнца.

Какие физические величины характеризуют процесс вращения?

Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:

• r – расстояние до оси материальной точки массой m.
• ω и α – угловая скорость и ускорение, соответственно. Первая величина показывает, на сколько радиан (градусов) поворачивается тело вокруг оси за одну секунду, вторая величина описывает скорость изменения во времени первой.
• L – момент импульса, который подобен аналогичной характеристике при линейном движении.
• I – момент инерции тела. Эта величина рассматривается ниже в статье подробно.
• M – момент силы. Он характеризует степень изменения величины L, если приложена внешняя сила.

Перечисленные величины связаны друг с другом следующими формулами вращательного движения:

1. L = I*ω

2. M = I*α

Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.

Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.

Откуда появляется величина I?

В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r. Эта ситуация приведена на рисунке.

Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:

L = r*p = r*m*v, поскольку p = m*v

Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:

v = ω*r => L = m*r²*ω

Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:

I = m*r² => L = I*ω

То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.

Общая формула для величины I тела

Выражение для момента инерции массой m материальной точки является базовым, то есть оно позволяет рассчитать эту величину для любого тела, имеющего произвольную форму и неоднородное распределение массы в нем. Для этого необходимо разбить рассматриваемый объект на маленькие элементы массой m_i (целое число i – номер элемента), затем, умножить каждый из них на квадрат расстояния r_i² до оси, вокруг которой рассматривают вращение, и сложить полученные результаты. Описанную методику нахождения величины I можно записать математически так:

I = ∑_i(m_i*r_i²)

Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:

I = ∫_m(r_i²*dm)

Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:

I = ρ*∫_V(r_i²*dV)

Все три формулы используются для вычисления момента инерции тела.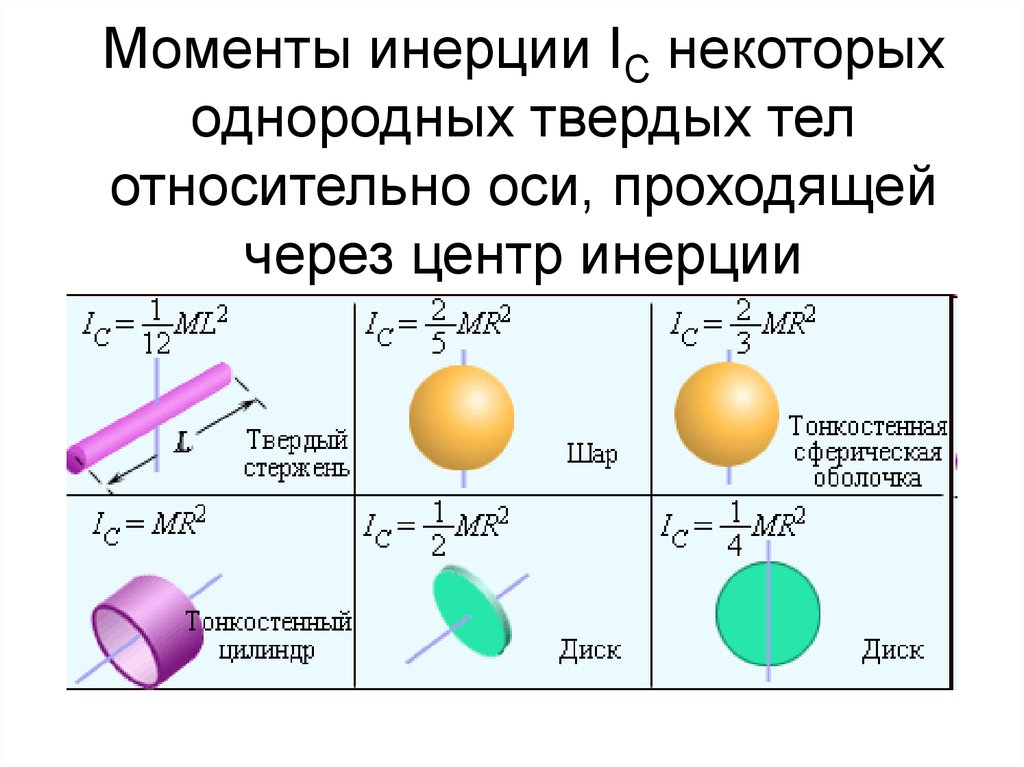 При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.

Свойства величины I и ее физический смысл

Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:

• она является аддитивной, то есть полный момент инерции системы можно представить, как сумму моментов отдельных ее частей;
• она зависит от распределения массы внутри системы, а также от расстояния до оси вращения, чем больше последнее, тем больше I;
• она не зависит от действующих на систему моментов сил M и от скорости вращения ω.

Физический смысл I заключается в том, насколько сильно система препятствует любому изменению скорости ее вращения, то есть момент инерции характеризует степень “плавности” возникающих ускорений. Например, колесо велосипеда можно легко раскрутить до больших угловых скоростей и также легко его остановить, но чтобы изменить вращение маховика на коленвале автомобиля, понадобится приложить значительное усилие и некоторое время. В первом случае имеет место система с маленьким моментом инерции, во втором – с большим.

Значение I некоторых тел для оси вращения, проходящей через центр масс

Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:

• Стержень. Ось вращения проходит перпендикулярно ему. I = m*L²/12, где L – длина стержня.
• Диск произвольной толщины. Момент инерции с осью вращения, проходящей перпендикулярно его плоскости через центр масс, вычисляется так: I = m*R²/2, где R – радиус диска.
• Шар. В виду высокой симметрии этой фигуры, для любого положения оси, проходящей через ее центр, I = 2/5*m*R², здесь R – шара радиус.

Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.

Задача на расчет значения I для системы с дискретным распределением массы

Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.

Поскольку массой стержня можно пренебречь, тогда необходимо рассчитать момент I для каждого груза и сложить полученные результаты, чтобы получить полный момент системы. Согласно условию задачи от оси груз массой 2 кг находится на расстоянии 0,15 м (0,25-0,1), груз 3 кг – 0,05 м (0,25-0,20), груз 1,5 кг – 0,25 м. Воспользовавшись формулой для момента I материальной точки, получаем:

I = I₁+I₂+I₃ = m₁*r₁² + m₂*r₂² + m₃*r₃² = 2*(0,15)²+3*(0,05)²+1,5*(0,25)² = 0,14 625 кг*м².

Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.

Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:

M = I*α

Поскольку α = Δω/Δt и M = r*F, где r – длина плеча, получаем:

r*F = I*Δω/Δt => Δω = r*F*Δt/I

Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:

Δω = r*F*Δt/I = 0,25*50*10/0,14625 = 854,7 рад/с

Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:

f = Δω/(2*pi) = 854,7/(2*3,1416) = 136 с^-1

Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.

Расчет значения I для стержня, когда ось проходит через его конец

Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.

Воспользуемся общим выражением для I:

I = ρ*∫_V(r_i²*dV)

Разбивая рассматриваемый объект на элементарные объемы, заметим, что dV может быть записано, как dr*S, где S – площадь сечения стержня, а dr – толщина элемента разбиения. Подставляя это выражение в формулу, имеем:

I = ρ*S*∫_L(r²*dr)

Этот интеграл вычислить достаточно просто, получаем:

I = ρ*S* (r³/3)∣₀^L => I = ρ*S*L³/3

Поскольку объем стержня равен S*L, а масса – ρ*S*L, то получаем конечную формулу:

Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L²/3/(m*L²/12)=4).

Moment of Inertia Lab – Физика B. Karpowicz

Название: Moment of Inertia Lab
Дата: 3/3/15
Партнер:

Steph Kinsella

Цель

Цель этой лаборатории заключалась в том, чтобы определить момент инерции объекта, используя как геометрические формулы, так и величины углового движения.

Теория

Момент инерции — это свойство любого катящегося или вращающегося объекта, которое измеряет сопротивление объекта изменению направления вращения.

Чтобы вычислить момент инерции геометрически, необходимо идентифицировать формы объектов. Поскольку объект состоит из двух одинаковых форм (полого цилиндра или кольца и сплошного цилиндра или диска), можно использовать следующие уравнения для однородных объектов. Момент инерции предназначен для расчета всего объекта, поэтому уравнения складываются вместе, чтобы получить:

Используя величины углового движения, необходимо вывести дополнительное уравнение. Используя взаимосвязь между крутящим моментом и моментом инерции, а также диаграмму свободного тела для устройства и отметив, что сила, вызывающая крутящий момент, является натяжением, верно следующее: Тогда, просуммировав силы и подставив величину натяжения обратно в вышеприведенное уравнение, получим:

Наконец, подставив соотношение между угловым и тангенциальным ускорением в исходное соотношение, мы получим окончательное уравнение.

Экспериментальная техника

После расчетов необходимо измерить массы и радиусы диска и кольца, а также радиусы основания датчика вращательного движения. Устройство, установленное, как показано ниже, должно иметь диск, плотно сидящий на датчике движения, и кольцо, закрепленное на диске.

Нить плотно обматывается вокруг основания системы и подводится к шкиву под параллельным углом, чтобы уменьшить ненужное трение.

К концу струны прикреплена подвеска, которая может упасть, заставляя систему наверху вращаться. Массы меняются с каждым испытанием эксперимента, чтобы получить множество различных точек данных.

С помощью Data Studio измеряется скорость вращения и определяется ускорение вращения путем нахождения наклона графика зависимости скорости от времени.

Данные

Измеренная масса кольца составила 0 .122 кг .
Измеренная масса диска составила 0 ,465 кг .
Измеренный внутренний диаметр кольца составил 5,070 см, что дает внутренний радиус 0,02535 м .
Внешний диаметр кольца составил 7,335 см, что делает внешний радиус 0,03668 м .
Измеренный диаметр диска составил 9,230 см, что делает радиус диска 0,04615 м .
Диаметр части датчика вращательного движения, вокруг которой вращается система, был измерен и составил 4,520 см, что составляет ее радиус

0,0226 м 92.   Пример расчета также показан ниже.

Наконец, процентная разница между геометрическими и измеренными значениями составила 0,647%.

Заключение

Целью данной лабораторной работы было определение момента инерции системы кольцо-диск двумя методами. Геометрически момент инерции оказался равным 92.   Процентная разница между двумя значениями составила 0,647%

.

Небольшая ошибка может быть связана с нашей классификацией шкива. Мы рассматривали шкив как невесомую систему без трения, хотя на самом деле это не так. Шкив создает небольшое трение о струну. Он также имеет свою массу и, следовательно, свой момент инерции, который должен быть включен в геометрический расчет, но для наших целей его не было.

Ссылки

Джанколи, Д. (2009). Физика для ученых и инженеров  (4-е изд.). Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall.
Lahs Physics (без даты). Получено 6 октября 2014 г. с сайта www.lahsphysics.weebly.com
Момент инерции. (н.д.). Получено 8 марта 2015 г. с http://www.engineeringtoolbox.com/moment-inertia-torque-d_913.html

Расчеты размеров двигателя

Правильный выбор размера и выбор двигателя для вашего оборудования являются ключом к обеспечению производительности и надежности и стоимость оборудования. В дополнение к приведенной ниже информации по правильному подбору двигателя, Oriental Motor предлагает онлайн-инструменты для подбора двигателя, а также помощь сотрудников службы технической поддержки.

Наш персонал службы технической поддержки всегда готов помочь вам правильно определить размеры и выбрать двигатель в соответствии с вашими индивидуальными потребностями. Просто позвоните по номеру 1-800-GO-VEXTA (468-3982) (с понедельника по пятницу с 7:30 до 17:00 по тихоокеанскому времени).

Процедура выбора

Первым шагом является определение приводного механизма для вашего оборудования. Некоторыми примерами являются прямое вращение, шариковый винт, ремень и шкив или рейка и шестерня. Наряду с типом приводного механизма необходимо также определить размеры, массу, коэффициент трения и т. д., необходимые для расчета нагрузки:

• Размеры и масса (или плотность) груза
• Размеры и масса (или плотность) каждой части
• Коэффициент трения поверхности скольжения каждой движущейся части

Далее необходимо определить требуемые характеристики оборудования:

• Скорость работы и время работы
• Расстояние позиционирования и время позиционирования
• Резолюция
• Точность остановки
• Удержание позиции
• Электропитание и напряжение
• Операционная среда
• Особые характеристики и требования, такие как; Разомкнутый цикл, замкнутый цикл, программируемый, обратная связь, рейтинг IP, утверждения агента и т. д.

Чтобы определить требуемую производительность двигателя, необходимо рассчитать три фактора; Момент инерции, крутящий момент и скорость. (См. приведенные ниже разделы по расчетам для каждого из них.)

После того, как вы рассчитаете инерцию, крутящий момент и скорость двигателя, вы выберете тип двигателя на основе требуемых характеристик. Oriental Motor предлагает широкий ассортимент шаговых двигателей, серводвигателей, двигателей переменного тока и бесщеточных двигателей для удовлетворения конкретных потребностей вашего оборудования.

Наконец, после выбора типа двигателя вы сделаете окончательное определение двигателя, подтвердив, что характеристики выбранного двигателя (и редуктора, если применимо) удовлетворяют всем требованиям, таким как механическая прочность, время разгона и момент разгона.

Расчет размера двигателя

При расчете размера двигателя необходимо рассчитать три фактора; Момент инерции, крутящий момент и скорость.

Момент инерции

Момент инерции является мерой сопротивления объекта изменениям скорости его вращения.

Когда объект просто сидит без движения, момент инерции равен 0.

Когда вы пытаетесь заставить его двигаться, это означает, что вы хотите изменить скорость объекта от 0 до любой, будет момент инерции эффект.

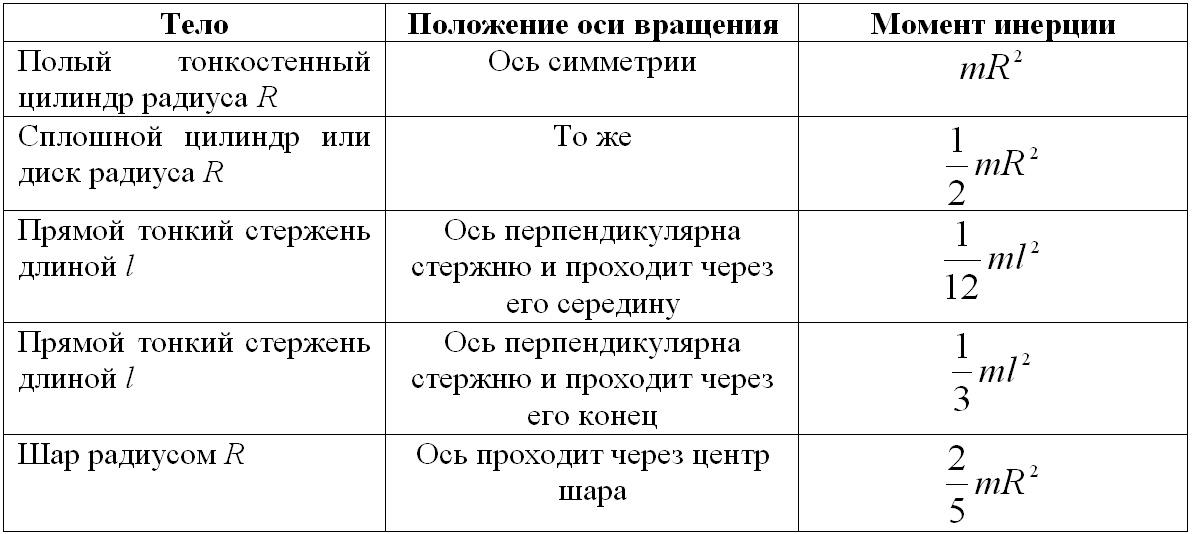
Фундаментальная инерция (J) Уравнение :

Момент расчета инерции для вращающегося объекта

Момент расчета инерции для цилиндра

0002 Момент расчета инерции для пологого цилиндра

Момент расчета инерции для оси вне центра

Момент инерции Расчет для прямоугольной колонны

Moment interia Dildalar

Momentia intardia Dildia. для объекта в линейном движении

Единицы измерения момента инерции

Единицы инерции обычно используются двумя способами:  унция-дюйм²  и  унций-в-сек² . Первое включает гравитацию, второе — только массу.

Теоретически инерция является фактором массы, поэтому она не должна включать гравитацию, однако практически мы не можем легко измерить массу на Земле.

Oriental Motor обычно обеспечивает инерцию в унциях на дюйм². Затем, когда мы рассчитываем крутящий момент ускорения в разделе «Расчет крутящего момента», мы делим общую инерцию на силу тяжести.

Гравитация = 386 дюймов/с²

• oz-in²  = Инерция в зависимости от веса
• унций-в-сек²  = инерция, основанная на массе

Расчет преобразования унций на дюйм² в унции на секунду²

Крутящий момент

Крутящий момент — это тенденция силы вращать объект вокруг оси. Крутящий момент состоит из двух компонентов; составляющая нагрузки (постоянная) и составляющая ускорения.

Составляющая момента нагрузки обычно возникает из-за трения и/или силы тяжести и всегда действует на двигатель. Этот компонент обычно можно определить путем расчета или путем установки динамометрического ключа на систему и считывания значения крутящего момента. Когда это невозможно измерить, мы используем некоторые уравнения для расчета приблизительного значения.

Однако ускоряющий момент воздействует на двигатель только при его ускорении или торможении. Когда двигатель работает с постоянной скоростью, этот компонент исчезает. Измерение составляющей ускорения сложно, не говоря уже об опасности. Если вы хотите, чтобы нагрузка достигла нужной скорости в течение 50 миллисекунд, вполне вероятно, что динамометрический ключ слетит. Поэтому вычисляем составляющую ускорения. Эта составляющая является функцией инерции системы и скорости ускорения. Итак, как только мы определим эти значения, мы сможем вычислить момент ускорения.

Момент нагрузки ( T )

Момент нагрузки очень прост.

Как вы видите, крутящий момент в этом уравнении является произведением силы и расстояния между силой и центром вращения. Например, если вы хотите удерживать силу, действующую на конец шкива, T  = F x r . Таким образом, расчет крутящего момента нагрузки определяет силу в системе и логическое расстояние между валом двигателя и местом, где действует сила.

Когда механика становится сложной, нам нужно преобразовать F и r, чтобы она соответствовала механике.

Крутящий момент при нагрузке – фактическое измерение

Если вы можете измерить силу, это самый точный способ найти силу, поскольку он учитывает эффективность и коэффициент трения каждой детали.

FB  = Сила, когда главный вал начинает вращаться

Силы

Существует три типа сил; вертикальные, горизонтальные и наклонные. Сила меняется в зависимости от того, как она действует.

Расчет вертикальной силы

Расчет горизонтальной силы

Расчеты сил с наклоном

Расчет Torque Torque Torque.

Расчет крутящего момента при нагрузке — канатная или ременная передача, реечный привод

Момент ускорения

Как упоминалось ранее, момент ускорения состоит из инерции и коэффициента ускорения. Зная эти два значения, мы можем рассчитать момент ускорения.

Расчет момента ускорения (  Ta  )

Если скорость двигателя изменяется, всегда необходимо устанавливать момент ускорения или момент торможения.

Основная формула одинакова для всех двигателей. Однако используйте приведенные ниже формулы при расчете ускоряющего момента для шаговых двигателей или серводвигателей на основе импульсной скорости.

Общая формула для всех двигателей

При расчете крутящего момента для шаговых или серводвигателей на основе импульсной скорости

Существует два основных профиля движения. Операция ускорения/торможения является наиболее распространенной. Когда рабочая скорость низкая и инерция нагрузки мала, можно использовать операцию пуска/останова.

Расчет требуемого крутящего момента (  TM  )

Требуемый крутящий момент рассчитывается путем умножения суммы момента нагрузки и момента ускорения на коэффициент безопасности.

Расчет эффективного крутящего момента нагрузки ( Trms  ) для серводвигателей и бесколлекторных двигателей серии BX

Если требуемый крутящий момент двигателя меняется с течением времени, определите, может ли двигатель использоваться, путем расчета эффективной нагрузки крутящий момент. Эффективный момент нагрузки становится особенно важным для режимов работы, таких как операции с быстрым циклом, где часто происходит ускорение/замедление. Рассчитайте эффективный крутящий момент нагрузки при выборе серводвигателей или бесщеточных двигателей серии BX.

Скорость

Скорость определяется путем вычисления расстояния, деленного на время.