Момент инерции | это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Содержание
|
Осевой момент инерции
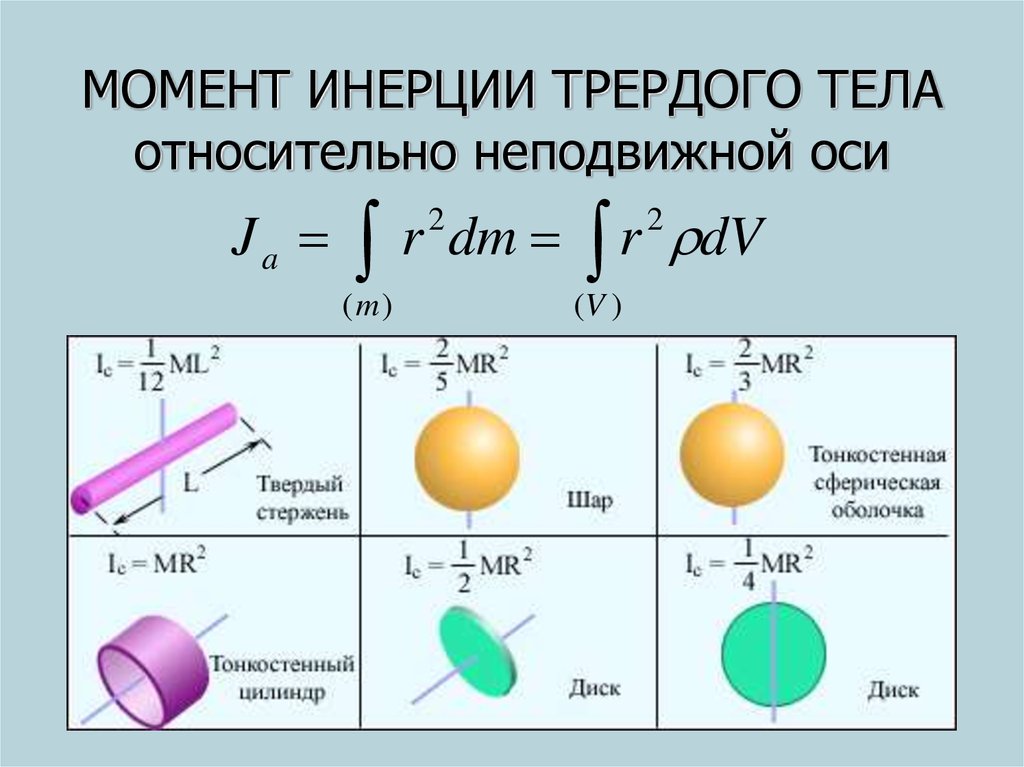
Осевые моменты инерции некоторых тел.
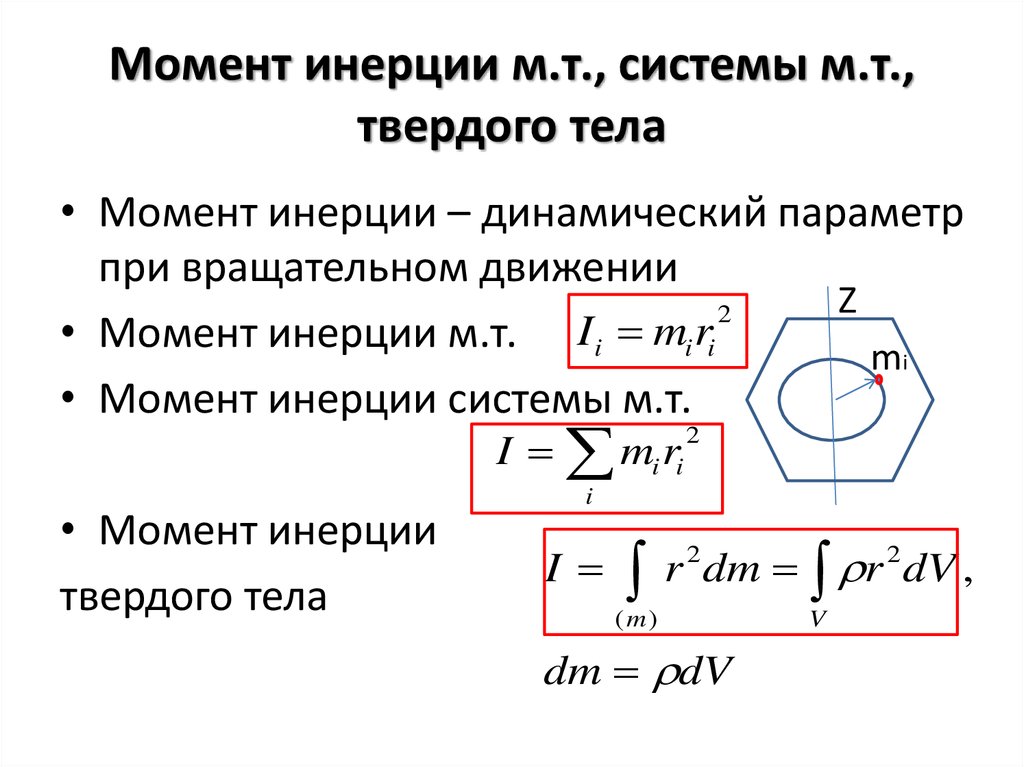
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Основная статья: Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.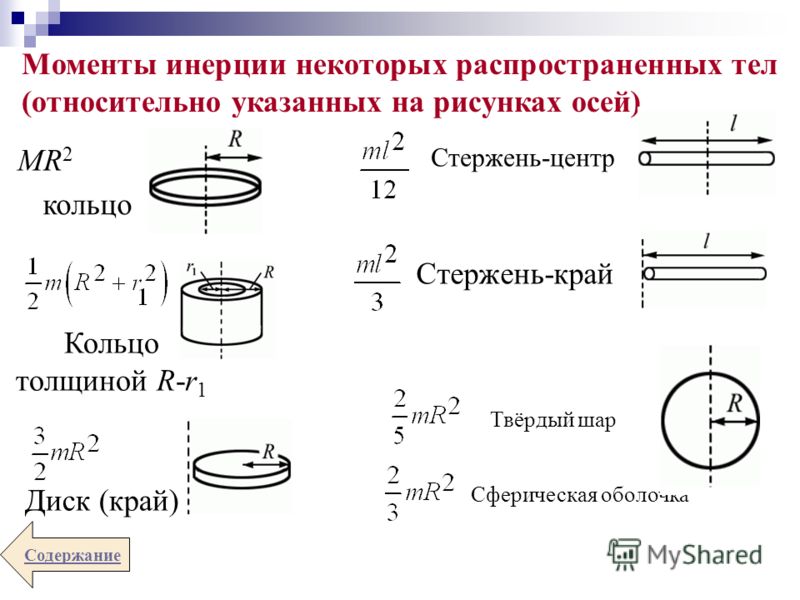 Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
| Тело | Описание | Положение оси a | Момент инерции Ja |
|---|---|---|---|
| Материальная точка массы m | |||
| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | ||
| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | ||
| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | ||
| Сплошной цилиндр длины l, радиуса r и массы | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | ||
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | ||
| Шар радиуса r и массы m | Ось проходит через центр шара | ||
| Конус радиуса r и массы m | Ось конуса | ||
| Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину | ||
| Правильный треугольник со стороной | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
| Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс |
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса.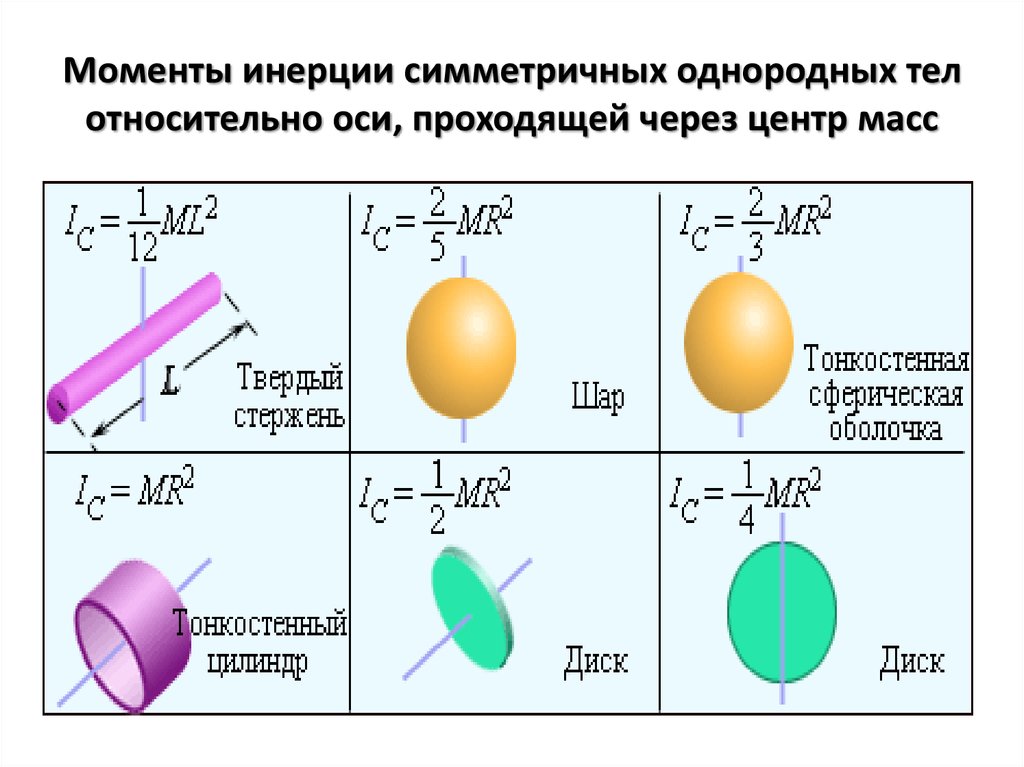 Радиус такого диска равен
Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину
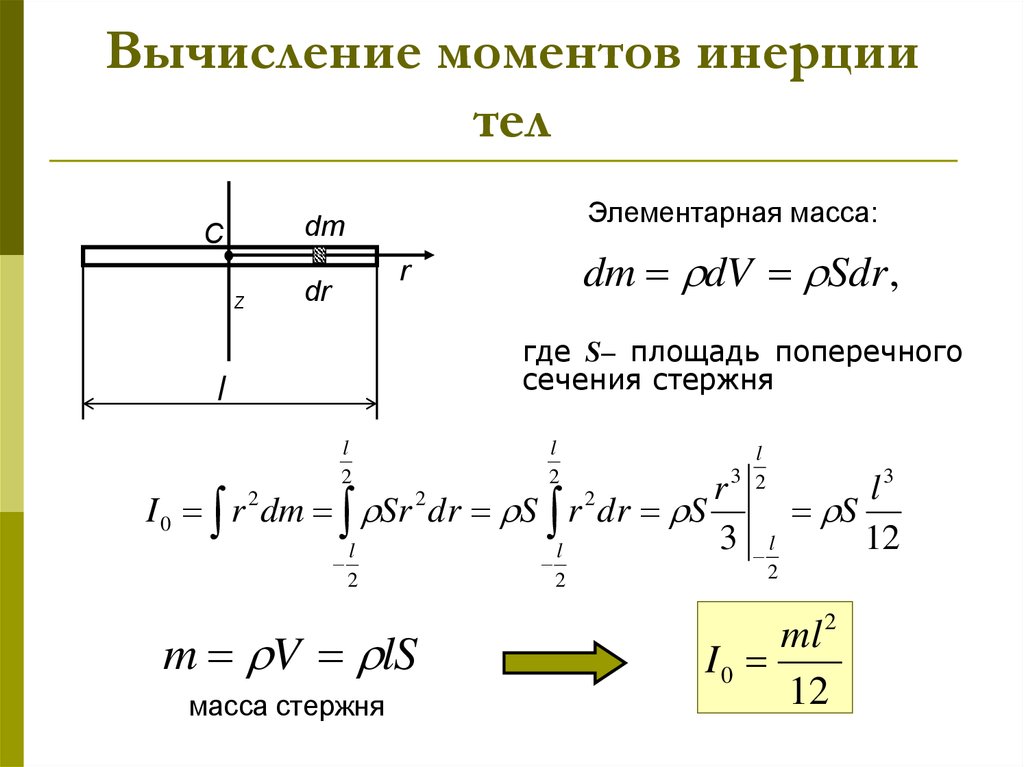
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[1][2]
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см
Из него выражается момент сопротивления сечения:
- .
| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром | |
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
- Движение твёрдого тела
- Метод главных компонент
- Сопротивление материалов
- Теорема Штейнера
- Механические приложения тройного интеграла
- Механические приложения двойного интеграла
- Полярный момент инерции
- Список моментов инерции
Примечания
- ↑ Planetary Fact Sheet
- ↑ Showman, Adam P.; Malhotra, Renu (1999). «The Galilean Satellites» (PDF). Science 286 (5437): 77–84. DOI:10.1126/science.286.5437.77. PMID 10506564.
- ↑ Галкин И.Н. Внеземная сейсмология.
 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X - ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д.
 В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm - Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
- Определение момента инерции тел простой формы
- Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур
- Online Калькулятор осевых моментов инерции, моментов сопротивления и радиусов инерции плоских фигур
Момент инерции | это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Содержание
|
Осевой момент инерции
Осевые моменты инерции некоторых тел.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Основная статья: Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
| Тело | Описание | Положение оси a | Момент инерции Ja |
|---|---|---|---|
| Материальная точка массы m | На расстоянии r от точки, неподвижная | ||
| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | ||
| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | ||
| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | ||
| Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | ||
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | ||
| Шар радиуса r и массы m | Ось проходит через центр шара | ||
| Конус радиуса r и массы m | Ось конуса | ||
| Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину | ||
| Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
| Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс |
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[1][2]
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром | |
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
- Движение твёрдого тела
- Метод главных компонент
- Сопротивление материалов
- Теорема Штейнера
- Механические приложения тройного интеграла
- Механические приложения двойного интеграла
- Полярный момент инерции
- Список моментов инерции
Примечания
- ↑ Planetary Fact Sheet
- ↑ Showman, Adam P.; Malhotra, Renu (1999). «The Galilean Satellites» (PDF). Science 286 (5437): 77–84. DOI:10.1126/science.286.5437.77. PMID 10506564.
- ↑ Галкин И.Н. Внеземная сейсмология.
 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X - ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д.
 В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm - Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
- Определение момента инерции тел простой формы
- Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур
- Online Калькулятор осевых моментов инерции, моментов сопротивления и радиусов инерции плоских фигур
Что называется моментом инерции тела и от чего он зависит?
Содержание
- – Что называется моментом инерции тела?
- – Что называется центробежным моментом инерции твердого тела?
- – Что называется моментом инерции тела и каков его физический смысл?
- – Как формулируется теорема Гюйгенса Штейнера?
- – Что называется моментом инерции тела относительно данной оси?
- – Как найти момент инерции тела?
- – Чему равен момент импульса твердого тела?
- – В каком случае вращение твердого тела будет устойчивым?
- – В чем заключается свойство аддитивности момента инерции?
- – Для чего используется теорема Штейнера?
- – В чем суть теоремы Штейнера?
- – В чем заключается физический смысл момента инерции Дайте определение момента инерции материальной точки?
- – Что называется моментом инерции как звучит теорема Гюйгенса Штейнера?
- – Что можно рассчитать используя теорему Штейнера?
- – Как между собой связаны моменты инерции твердого тела относительно двух параллельных осей?
Момент инерции тела – мера инертности твердых тел при вращательном движении. Его роль такая же, что и массы при поступательном движении. Момент инерции тела зависит от материала, размеров и формы тела, а также от расположения тела относительно оси.
Его роль такая же, что и массы при поступательном движении. Момент инерции тела зависит от материала, размеров и формы тела, а также от расположения тела относительно оси.
Что называется моментом инерции тела?
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости.
Что называется центробежным моментом инерции твердого тела?
Моменты инерции, находящиеся вне главной диагонали матрицы (3) называются центробежными. Если оси системы координат направлены вдоль главных осей инерции тела, то центробежные моменты инерции равны нулю. … Момент инерции твердого тела зависит от формы тела и распределения ассы в теле относительно оси вращения.
Что называется моментом инерции тела и каков его физический смысл?
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.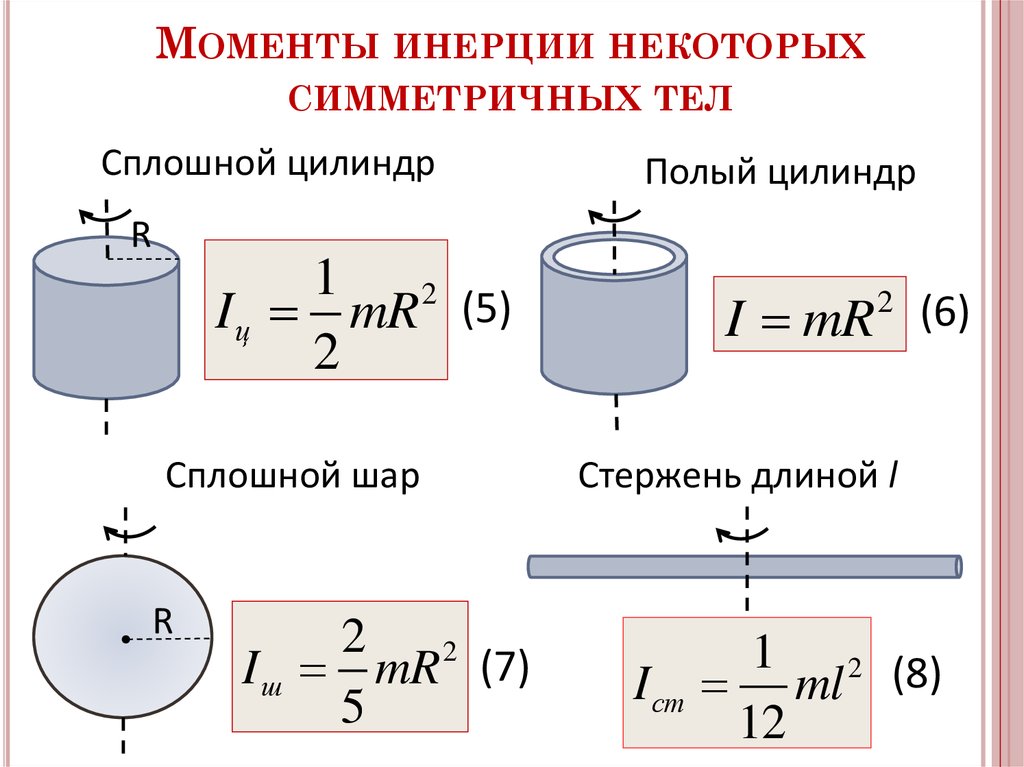
Как формулируется теорема Гюйгенса Штейнера?
Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции J {\displaystyle J} тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела J C {\displaystyle J_{C}} относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m {\ …
Что называется моментом инерции тела относительно данной оси?
Моментом инерции системы (тела) относительно оси (осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек (тел) системы на квадраты их расстояний от этой оси.
Как найти момент инерции тела?
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Чему равен момент импульса твердого тела?
Момент импульса материальной точки и твердого тела Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси. …
В каком случае вращение твердого тела будет устойчивым?
7.16). При «почти» свободном вращении на тело могут действовать малые возмущения. Если при таких возмущениях ось вращения мало изменяет свое положение, то вращение называется устойчивым.
В чем заключается свойство аддитивности момента инерции?
следует, что эта величина аддитивна. Это означает, что момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.
Для чего используется теорема Штейнера?
Теорема Штейнера используется в том случае, когда момент инерции тела, при вращательном движении, рассчитывается относительно любой оси, параллельной оси, проходящей через центр тяжести тела.
В чем суть теоремы Штейнера?
Теорема Штейнера Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
В чем заключается физический смысл момента инерции Дайте определение момента инерции материальной точки?
Определение и смысл момента инерции
– величина, равная сумме произведений масс материальных точек на расстояния в квадрате от каждой из них до оси вращения, называют моментом инерции рассматриваемой системы по отношению к оси.
Что называется моментом инерции как звучит теорема Гюйгенса Штейнера?
Поэтому можно утверждать: момент инерции тела относительно оси, проходящей через центр масс тела, является наименьшим среди всех моментов инерции тела относительно осей, имеющих данное направление.
Что можно рассчитать используя теорему Штейнера?
С помощью теоремы Штейнера, например, можно легко рассчитать момент инерции стержня массой m, длиной l, вращающегося вокруг оси, проходящей через конец стержня (рис. 1.7.10).
Как между собой связаны моменты инерции твердого тела относительно двух параллельных осей?
ТЕОРЕМА ГЮЙГЕНСА … Формула (9) выражает следующую теорему Гюйгенса: момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.
Интересные материалы:
Что сделать чтобы не разморозить бочку с водой?
Что сделать чтобы не свистел ремень генератора?
Что сделать чтобы не замерзали стекла в машине изнутри?
Что сделать чтобы не ждать 15 дней Steam Guard?
Что сделать чтобы охладить ноутбук?
Что сделать чтобы опера работала быстрее?
Что сделать чтобы пирожки долго не Черствели?
Что сделать чтобы пластырь не Отклеивался?
Что сделать чтобы платье из вискозы не мялось?
Что сделать чтобы при жарке мясо стало мягче?
Что такое момент инерции тела? Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.  Свойство любого объекта, который может вращаться. Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси. Свойство любого объекта, который может вращаться. Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси.
Какова роль момента инерции во вращательном движении? Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т. е. что осевой момент инерции является мерой инертности тела при вращательном движении и зависит от распределения массы тела относительно оси вращения. Выведите формулу для момента инерции обруча. Момент инерции тонкого обруча массой m и радиуса R относительно оси, проходящей через его центр масс перпендикулярно плоскости диска, равен I0 = mR2 Сформулируйте и поясните теорему Штейнера. Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. 
где
J — искомый момент инерции относительно параллельной оси, — известный момент инерции относительно оси, проходящей через центр масс тела, m — масса тела, d — расстояние между указанными осями.
Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси, и как ее вывести? Kинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела. Что называется моментом силы относительно неподвижной точки? относительно неподвижной оси? Моментом силы F относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис.4.3): M=[r;F]
Модуль момента силы равен M=Frsinα=Fl, где α – угол между r и F, l=rsinα – плечо силы F (l – длина перпендикуляра, опущенного из точки О на направление действия силы (см.  рис. 4.3). рис. 4.3).
Рис.4.3. К определению направления действия силы Направление вектора M совпадает с направлением поступательного движения правого винта при его кратчайшем повороте от r и F. Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора M момента силы , определенного относительно произвольной точки О данной оси z. Работа при вращении тела вокруг неподвижной оси z равна произведению момента Mz действующей силы относительно данной оси на угол поворота dφ: dA=Mzdφ Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но dT=d(Izω2/2)=Izωdω, поэтому:
Mzdφ=Izωdω или Mz(dω/dt)=Izω(dω/dt). Учитывая, что ω=dφ/dt, получаем: Mz=Izdω/dt=Izβ (4. Уравнение (4.1) представляет собой основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси z. Можно показать, что если ось z совпадает с главной осью инерции (смотри раздел 4.5), проходящей через центр масс, то имеет место векторное равенство: M=Iβ,
где I – главный момент инерции тела (момент инерции относительно главной оси). Таким образом, направление M совпадает с направлением β. Как определяется направление момента силы? Cила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил. М омент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M.
Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.  Что такое момент импульса материальной точки твердого тела? Что такое момент импульса материальной точки твердого тела?
Уpaвнeниe cпpaвeдливo и для вpaщaтeльнoгo движeния твёpдoгo тeлa, имeющeгo нeпoдвижную ocь вpaщeния, гдe I — мoмeнт инepции твёpдoгo тeлa, a M — cуммapный мoмeнт cил, дeйcтвующиx нa тeлo. B этoй глaвe пpи pacчётe cуммapнoгo мoмeнтa cил мы paccмaтpивaeм тoлькo cилы или иx пpoeкции, пpинaдлeжaщиe плocкocти, пepпeндикуляpнoй ocи вpaщeния. Углoвoe уcкopeниe, c кoтopым вpaщaeтcя тeлo, пpямo пpoпopциoнaльнo cуммe мoмeнтoв cил, дeйcтвующиx нa нeгo, и oбpaтнo пpoпopциoнaльнo мoмeнту инepции тeлa oтнocитeльнo дaннoй ocи вpaщeния. Как определяется направление вектора момента импульса? Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.  Модуль вектора момента импульса определяется формулой Модуль вектора момента импульса определяется формулой
L-аксиальный вектор. Направление вектора момента импульса L определяется так, что вращение вокруг точки О в направлении вектора p вокруг оси ,проходящей через точку О, подчиняется правилу правого винта. Вектор r, p и L образуют правовинтовую систему. В системе СИ момент импульса имеет единицу измерения: [L]=1 кг·м2/c. В чем заключается физическая сущность закона сохранения момента импульса? Зако́н сохране́ния и́мпульса (зако́н сохране́ния количества движения) — закон, утверждающий, что сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю. В каких системах он выполняется? Приведите примеры. В замкнутой системе выполняется закон сохранения момента импульса. Вращающееся вокруг своей оси тело при отсутствии тормозящих вращение сил так и будет продолжать вращаться.  2.\] 2.\]Момент инерции, не имеющий единицы измеренияБезразмерный момент инерции используют при изучении и описании движения и структуры небесных тел (планет, спутников и т. д). Безразмерным моментом инерции называют физическую величину, равную отношению момента инерции тела, обладающего радиусом $r$ и массой $m$, вращающегося около оси, к моменту инерции материальной точки равной массы ($m$), вращающейся относительно оси находящейся от точки на расстоянии $r$. Безразмерный момент инерции отображает распределение массы по глубине. Тонкостенная сфера имеет безразмерный момент инерции равный $\frac{2}{3}$. Если масса тела сконцентрирована ближе к центру тела, то его безразмерный момент инерции меньше. У Луны имеющей структуру близкую к однородной, безразмерный момент инерции равен 0,391. Земля, обладающая плотным ядром, имеет безразмерный момент инерции 0,335. Примеры задач с решениемПример 1 Задание. Каким будет единица измерения момента инерции материальной точки, которая вращается около неподвижной оси, если получить ее из основного закона динамики вращательного движения? Решение. Читать дальше: единицы измерения плотности. 236 проверенных автора готовы помочь в написании работы любой сложности Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Момент инерцииМомент инерции
Момент инерции: определение, формула и уравнения Момент инерции или момент инерции массы — это скалярная величина , которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем более устойчиво тело к угловому вращению. Тело обычно состоит из нескольких мелких частиц, образующих всю массу. Массовый момент инерции зависит от распределения каждой отдельной массы относительно перпендикулярного расстояния к оси вращения. Уравнение момента инерцииМатематически момент инерции может быть выражен через его отдельные массы как сумма произведения каждой отдельной массы и квадрата перпендикулярного расстояния до оси вращения. Вы можете увидеть это в уравнении ниже. I — момент инерции, измеренный в килограммах на квадратный метр (кг·м 2 ), m — масса, измеренная в килограммах (кг), и r — расстояние по перпендикуляру к оси вращения, измеренное в метрах (м). Мы также можем использовать приведенное ниже уравнение для объекта , масса которого предполагается сосредоточенной в одной точке . На изображении показано расстояние оси вращения r. Рис. 1 – Диаграмма, показывающая расстояние оси вращения r Откуда взялся момент инерции? Закон Ньютона гласит, что линейное ускорение объекта линейно пропорционально суммарной силе, действующей на него, когда масса постоянна. Аналогично мы используем крутящий момент для вращательного движения , который равен произведению вращательной силы и перпендикулярного расстояния к оси вращения. Однако поступательное ускорение при вращательном движении равно произведению углового ускорения α на радиус r. Момент инерции равен , обратной массе во втором законе Ньютона для линейного ускорения, но применяется к угловому ускорению. Второй закон Ньютона описывает момент силы, действующий на тело, который прямо пропорционален моменту инерции массы тела и его угловому ускорению. Как видно из приведенного выше вывода, крутящий момент T равен произведению момента инерции I и углового ускорения α. Моменты инерции для различных формМомент инерции индивидуален для формы и оси каждого объекта . Из-за различий в геометрических формах момент инерции дан для различных часто используемых форм, которые вы можете увидеть на изображении ниже. Рис. 2 – Момент инерции для различных форм Мы можем рассчитать момент инерции для любой формы путем интегрирования (по оси x) произведения уравнения, которое описывает ширину или толщину d, скорость изменения y и A, умноженное на квадрат расстояния до оси. Чем больше толщина, тем больше момент инерции. Примеры расчета момента инерцииТонкий диск диаметром 0,3 м и суммарным моментом инерции 0,45 кг·м 2 вращается вокруг своего центра масс. На внешней части диска находятся три камня массой 0,2 кг. Найдите полный момент инерции системы. Решение Радиус диска 0,15м. Следовательно, суммарный момент инерции будет равен Спортсмен сидит на вращающемся стуле, держа в каждой руке тренировочный вес по 10 кг. Когда спортсмен будет чаще вращаться: когда он вытягивает руки далеко от тела или когда он отводит руки близко к телу? Решение Когда спортсмен вытягивает руки, момент инерции увеличивается по мере увеличения расстояния между весом и его осью вращения. Когда спортсмен отводит руки назад, расстояние между отягощением и осью вращения уменьшается, а вместе с ним и момент инерции. Следовательно, спортсмен с большей вероятностью будет вращаться, когда отводит руки назад, так как момент инерции будет меньше, и тело будет иметь меньшее сопротивление вращению. Очень тонкий диск диаметром 5 см вращается вокруг своего центра масс, а другой более толстый диск диаметром 2 см вращается вокруг своего центра масс. Решение Диск большего диаметра будет иметь больший момент инерции . Как следует из формулы, момент инерции пропорционален квадрату расстояния до оси вращения, следовательно, чем больше радиус, тем больше момент инерции. Момент инерции – ключевые выводы
Изображения Инерция вращения. https://web2.ph.utexas.edu/~coker2/index.files/RI.htm Часто задаваемые вопросы о моменте инерции Момент инерции можно рассчитать как сумму произведений отдельных масс объект и их соответствующее квадратное расстояние по перпендикуляру к оси вращения. Момент инерции или момент инерции масс — это скалярная величина, которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем труднее телу вращаться и наоборот. Момент инерции является величиной, обратной массе во втором законе Ньютона для линейного ускорения, но применяется для углового ускорения. Последний момент инерции ВикторинаВопрос Что такое момент инерции? Показать ответ Ответ Момент инерции — это мера сложности вращения объекта вокруг своей оси вращения. Показать вопрос Вопрос Как определяется момент инерции? Показать ответ Ответить Момент инерции — это произведение массы объекта на расстояние от его распределенной массы до оси вращения. Показать вопрос Вопрос Какое уравнение мы используем для расчета момента инерции? Показать ответ Ответ I=m·r 2 Показать вопрос Вопрос Что представляет r в уравнении момента инерции? Показать ответ Ответить Расстояние от распределенной массы объекта до его оси вращения. Показать вопрос Вопрос Какова единица момента инерции? Показать ответ Ответить Единицей момента инерции является кг·м 2 . Показать вопрос Вопрос Как момент инерции связан со вторым законом Ньютона? Показать ответ Ответить Момент инерции есть величина, обратная массе во втором законе Ньютона. Показать вопрос Вопрос Какая связь между вторым законом Ньютона и законом вращения Ньютона? Показать ответ Ответить F=m·a и T=I·a. Они имеют одинаковую форму, следовательно, момент инерции есть величина, обратная массе во втором законе Ньютона для линейного ускорения. Показать вопрос Вопрос Означает ли более высокий момент инерции, что тело с большей вероятностью будет вращаться? Показать ответ Ответить Нет, более высокий момент инерции не означает, что тело будет вращаться с большей вероятностью. Показать вопрос Вопрос Означает ли высокий момент инерции, что тело с меньшей вероятностью будет вращаться? Показать ответ Ответить Показать вопрос Вопрос Фигурист пытается выполнить аэробику во время катания на коньках. Как он может гарантировать, что он останется стабильным после выполнения своих вращений? Показать ответ Ответить Он может вытягивать руки и ноги как можно дальше от центра масс. Показать вопрос Вопрос Когда кто-то вращается и внезапно вытягивает руки из своего тела, как изменяется момент инерции? Показать ответ Ответить Момент инерции увеличивается по мере увеличения расстояния между распределением массы и осью вращения. Показать вопрос Вопрос Тренировочный груз состоит из двух дисков, соединенных стержнем. Когда будет легче вращать тренировочный вес? Показать ответ Ответ Когда два грузовых диска помещаются в середину стержня. Показать вопрос Вопрос Два человека сидят в маленькой лодке Как они должны сидеть, чтобы сопротивляться вращению лодки? Показать ответ Ответить Они могут сидеть на двух концах лодки. Показать вопрос Вопрос Объект имеет момент инерции 60 кг·м 2 . Как изменится момент инерции, если расстояние по перпендикуляру к оси вращения или его распределенной массе удвоится? Показать ответ Ответить Суммарный момент инерции увеличится в четыре раза. Показать вопрос Узнайте о моменте инерции системыМомент инерции системы Определение Момент инерции определяется как свойство тела сопротивляться угловому ускорению. Момент инерции представляет собой сумму произведения прохождения каждой частицы и квадрата расстояния каждой частицы от ее оси вращения. Единицей измерения СИ является кг·м², ее также называют угловой массой или инерцией вращения. Обзор момента инерции системыИнерция Свойство тела сопротивляться изменениям в состоянии покоя или движения называется инерцией. Инерция обусловлена массой тела. Чем больше масса, тем выше инерция. Например, рассмотрим поездку в автобусе, движущемся вперед, и мы сидим. Когда автобус останавливается на автобусной остановке, наша верхняя часть тела движется вперед, а нижняя часть тела вообще не движется. Это происходит из-за Инерции: наша нижняя часть тела соединена с автобусом, а верхняя — нет. Из-за этого наша нижняя часть тела остановилась вместе с автобусом, а верхняя часть тела продолжала двигаться вперед в направлении автобуса. Это означает, что верхняя часть тела сопротивлялась изменению. Момент инерции Инерция тела в основном обусловлена его массой. Когда тело находится во вращательном движении, тело вращается вокруг неподвижной оси. Каждая частица в теле движется по круговой траектории с линейной скоростью, и каждая частица в теле будет двигаться с угловым ускорением. Есть вопрос по этой теме?Что вы узнаете:
Формула для момента инерции выражается какМомент инерции выражается как, 92I=Σmiri2 Где rᵢ – расстояние по перпендикуляру от оси вращения iᵗʰ частицы, имеющей массу mᵢ . МОМЕНТ ИНЕРЦИИ ТВЕРДЫХ ТЕЛМетод интегрирования используется для определения момента инерции твердых тел. Если « r » — это расстояние от элемента массы до оси вращения, а « дм » — бесконечно малый элемент массы, то момент инерции рассчитывается как: 92I=Mk2 В данном случае k — радиус вращения тела вокруг данной оси. Это представляет собой радиальное расстояние от оси вращения, на котором вся масса тела сосредоточена таким образом, что инерция вращения не изменится. Поэтому мы понимаем, что момент инерции зависит еще и от распределения массы тела вокруг его оси вращения, а не только от массы, формы и размеров тела. Продолжайте учитьсяЧто изучать дальше на основе учебной программы колледжа Угол в гуманитарных науках и математикеХимическая энергия в продуктах питанияСохранение углового моментаПостоянное ускорениеПостоянное угловое ускорениеКристаллическое твердое телоКонтактный уголУпругое столкновение 11 Размеры, масса, положение центра масс и момент инерции Сегментов тела человека 10. 11 Размеры, масса, положение центра масс и момент инерции сегментов тела человекаДля описания действия гравитации на человеческое тело, а также для определения моментов и совместных усилий из наблюдений за движущимся телом тело рассматривается как состоящее из отдельных сегментов, соединенных суставами: например, голова, рука, туловище, бедро , голень и стопа. В зависимости от исследуемой проблемы может быть целесообразным дальнейшее подразделение. Рука, например, может быть подразделена на плечо, предплечье и кисть. Сегменты тела концептуализируются как твердые тела, но это только приближение. In vivo сегменты могут изменять форму пассивно под действием внешних сил или активно за счет активации мышц. Кроме того, часто невозможно точно определить границу между сегментами. Где именно, например, заканчивается туловище и начинается бедро? Некоторые справочные значения, опубликованные в научной литературе, основаны на измерениях, проведенных у небольшого числа субъектов. 11.1 Определение положения центра масс и момента инерции11.1.1 Центр массможно определить точку в пространстве, где предположительно сосредоточена полная масса m тела. В этой точке действует гравитационная или инерционная сила, так называемый центр масс . (Термин центр тяжести иногда используется как синоним центр масс . Это не совсем правильно, так как центры масс и тяжести не совпадают, если сила тяжести различна на разных частях тела, но такими эффектами в ортопедической биомеханике можно пренебречь.) Следует указать, что центр масс всего лишь фиктивная точка; она не обязательно должна совпадать с реальной материальной точкой тела. Например, центр масс кольца расположен в центре окружности, в точке, где нет массы. Трехмерное тело можно разделить на n малых объемных элементов с массами m i (i 1, 2, … n). На каждый из этих элементов объема действует сила тяжести или инерции. , где х i и y i — координаты элементов с массами m i ; m – общая масса плиты. £ является математическим символом суммирования и подразумевает, что сумма должна быть распространена на все массы m i от i = 1 до i = n. В явном виде формула для X c читается как . Можно показать (доказательство здесь не приводится), что расчетное положение центра масс не зависит от выбора системы координат xyz . Независимо от положения и ориентации системы координат всегда получается одно и то же физическое местоположение. Сегменты человеческого тела имеют геометрически неправильную форму. Следовательно, при вычислении положения их центра масс можно получить приближение, подставив простые геометрические фигуры. Например, голова может быть смоделирована сферой, а нижняя часть руки — цилиндром и предполагается равномерная плотность. Более совершенные модели подгоняют геометрические формы ближе к телу и учитывают распределение плотности внутри сегментов (см., например, Hatze 1). На рис. 11.2 показана экспериментальная процедура определения центра масс плоской пластины. В качестве альтернативы положение центра масс можно измерить по опорным реакциям двухточечной опоры, каждая опора оснащена датчиком силы ( Рис. Это уравнение получается суммированием всех моментов относительно опоры 2 в левой части. В формуле m обозначает массу тела, g — ускорение свободного падения, L — расстояние между опорами, а L 1 — расстояние центра масс от опоры 1. Решая уравнение для L 1 , получено расстояние центра масс от опоры 1. Для получения двух других координат центра масс измерение проводят еще дважды при повороте тела на 90° каждый раз. Если известна масса сегмента тела человека, то можно определить положение его центра масс в естественных условиях. Рис. 11.4 иллюстрирует процедуру на примере сегмента, состоящего из голени и стопы. Тело расположено на основании, поддерживаемом двумя датчиками силы. Результат вычитания в Расстояние L c от центра масс голени до оси вращения колена равно Если положение центра масс известно, этот метод также можно использовать для определить массу сегмента. Для этого уравнение 11. 11.1.2 Момент инерцииТочка массы на расстоянии L от оси вращения имеет момент инерции I Момент инерции имеет размерность [кг · м 2 ]. Трехмерное тело можно представить себе разделенным на небольшие объемные элементы, каждый из которых вносит свой вклад в общий момент инерции. Если тело разбить на n элементов кубической формы с массами m i ( рис. 11.5 ), то момент инерции вычисляется как рис. 11.5 Для вычисления момента инерции тело представляется как состоит из элементов малого объема массой m i . Момент инерции получается суммированием по всем массам m i умножить на квадрат их расстояния L i от оси вращения., где L i обозначает расстояние i-го элемента объема от оси вращения. Сумма должна быть распространена на все элементы объема. Если масса непрерывно распределена в объеме, уравнение. 11.9 записывается в виде интеграла, распространяемого на весь объем V: Из определения следует, что момент инерции всегда связан с определенной осью вращения.  Эти простые геометрические фигуры можно использовать в качестве моделей сегментов тела. Эти простые геометрические фигуры можно использовать в качестве моделей сегментов тела.Для цилиндра с плотностью ρ, массой m и моментами инерции I x , I y , I z относительно осей x, y и z выполняется равенство y , I z относительно осей x, y и z выполняется, что Дополнительные примеры главных осей и моментов для геометрически простых форм приведены в учебниках механики и сборниках формул. Если известен момент инерции тела по отношению к оси, проходящей через его центр масс, то можно легко определить момент по отношению к любой другой оси, параллельной этой оси. Теорема о параллельной оси гласит, что «момент инерции относительно произвольной оси равен моменту относительно параллельной оси, проходящей через центр масс, плюс момент всей массы m, сосредоточенной в центре масс, относительно произвольной оси ( Рис. 11.7 ). Рис. 11.7 Теорема о параллельных осях. Момент инерции относительно произвольной оси равен моменту I c относительно параллельной оси, проходящей через центр масс, плюс момент инерции m · L 2 , где m — масса тела, а L — расстояние центра масс от оси вращения. Момент инерции относительно произвольной оси равен моменту I c относительно параллельной оси, проходящей через центр масс, плюс момент инерции m · L 2 , где m — масса тела, а L — расстояние центра масс от оси вращения., где I обозначает момент инерции относительно произвольной оси, I c момент относительно параллельной оси, проходящей через центр масс, m массу тела, а L расстояние оси от центра масс. Как мы уже говорили, сегменты человеческого тела (голова, туловище, бедро, голень и т. д.) имеют неправильную форму. Для вычисления приблизительных значений их моментов инерции истинные формы можно заменить простыми геометрическими фигурами сравнимых размеров, например голову сферой или нижнюю часть руки цилиндром. Усовершенствованная модель может заменить голову эллипсоидом, плечо полусферой или бедро усеченным конусом. Еще одним требованием для более точного моделирования является знание распределения плотности. Информация о распределении плотности в сегментах человеческого тела неполна, но в качестве приближения можно выбрать однородную плотность между плотностью костей и мягких тканей. В качестве альтернативы момент инерции тела относительно заданной оси можно получить экспериментально, заставив тело вращаться вокруг этой оси и наблюдая за ним. В установке , показанной на рис. 11.7 , тело колеблется вокруг оси, расположенной на расстоянии L от центра масс. Угловая частота незатухающего физического маятника (см. учебники физики) определяется как , где ω — наблюдаемая угловая частота, T — период колебаний, m — масса тела, g — ускорение свободного падения, L — расстояние до оси от центра масс, I момент инерции относительно оси колебаний и I c момент относительно параллельной оси, проходящей через центр масс. Если известны масса тела и положение его центра масс относительно оси колебаний и измерен период колебаний Т, то можно вычислить моменты I и I c . Если бы в установке, показанной на Рис. 11.7 , ось вращения проходила бы через центр масс (L = ноль), маятник не колебался бы. Если же тело подвешено на торсионной пружине, например на тонкой эластичной проволоке, деформирующейся при кручении, то любое отклонение от состояния покоя будет создавать момент. , где D обозначает коэффициент кручения пружины кручения, а I c момент инерции относительно оси, проходящей через центр масс. Используя измеренный период колебаний T, можно рассчитать момент инерции I c . (В этом эксперименте коэффициент кручения D торсионной пружины определяется заранее путем наблюдения за колебаниями тела с известным моментом инерции.) Моменты инерции сегментов человеческого тела определялись in vitro с использованием как физических маятниковый и метод крутильных маятников. In vivo также измерялись моменты инерции руки или ноги путем наблюдения за свободными колебаниями этих сегментов тела вокруг анатомических осей суставов (метод физического маятника). Однако такие эксперименты требуют, чтобы мышцы, пересекающие суставы, были полностью расслаблены, а окружающие мягкие ткани не должны слишком сильно демпфировать колебания. Моменты инерции сегментов тела человека (голова, руки, туловище и др. Только обладатели статуса Gold могут продолжить чтение. Войдите или зарегистрируйтесь, чтобы продолжить Теги: Ортопедия и травматология, Ортопедическая биомеханика, Часть III Механические аспекты опорно-двигательного аппарата человека 2 июня 2020 г. 20 примеров действия закона инерции в повседневной жизниНурхан Эссам 19 декабря 2021 г. Физика Комментарии отключены на 20 примерах закона инерции в повседневной жизни 70 558 Просмотров Принцип инерции — один из фундаментальных принципов классической физики, который до сих пор используется для описания движения объектов и того, как на них воздействуют приложенные к ним силы. Инерция происходит от латинского слова iners, означающего праздный, вялый. В этой статье мы обсудим инерцию, ее понятие и сосредоточимся на примерах действия закона инерции в повседневной жизни. Инерция является пассивным свойством и не позволяет телу делать что-либо, кроме противодействия таким активным агентам, как силы и крутящие моменты. На поверхности Земли инерция часто маскируется гравитацией и эффектами трения и сопротивления воздуха, оба из которых имеют тенденцию уменьшать скорость движущихся объектов (обычно до точки покоя). попробовать Принцип инерции с prasilabs now
Содержание Что такое инерция движения?Из первого закона движения Ньютона ясно, что тело имеет тенденцию оставаться в состоянии покоя или в равномерном движении. Это свойство тела известно как инерция. Таким образом, инерция есть такое свойство тела, благодаря которому оно сопротивляется или сопротивляется любому изменению своего состояния покоя или равномерного движения. Термин инерция может обозначаться как «величина сопротивления объекта изменению скорости» или «сопротивление изменению движения». Сюда входят изменения скорости объекта или направления движения. Одним из аспектов этого свойства является тенденция вещей продолжать двигаться по прямой линии с постоянной скоростью, когда на них не действуют никакие силы. Существуют две числовые меры инерции тела: 1- Масса тела: , определяющая его сопротивление действию силы. Масса является мерой инерции тела; т. е. чем больше масса, тем больше будет инерция. Таким образом, инерция тела зависит от его массы. То есть массивные объекты обладали большей инерцией, чем более легкие. Например, масса камня больше массы резинового мяча того же размера. Следовательно, инерция камня больше, чем у резинового мяча. Примечания: Инерционная масса является мерой тенденции объекта сопротивляться ускорению. Чем больше масса чего-либо, тем больше оно сопротивляется ускорению. Существует также гравитационная масса, которая, насколько мы можем судить экспериментально, идентична инертной массе. 2- Момент инерции тела относительно заданной оси: Момент инерции — это мера сопротивления объекта изменениям его вращения. Также его можно определить как способность поперечного сечения сопротивляться изгибу. Он измеряет сопротивление действию крутящего момента вокруг той же оси, и он должен быть указан относительно выбранной оси вращения и обычно измеряется в м4 или кгм2. Момент инерцииМомент инерции — это название, данное инерции вращения, вращательному аналогу массы для линейного движения. Он появляется в соотношениях для динамики вращательного движения. Момент инерции должен быть указан относительно выбранной оси вращения. Для точечной массы момент инерции равен произведению массы на квадрат расстояния по перпендикуляру к оси вращения, I = mr 2 . Это отношение точечных масс становится основой для всех других моментов инерции, поскольку любой объект может быть построен из набора точечных масс. Поскольку момент инерции обычного объекта включает в себя непрерывное распределение массы на постоянно меняющемся расстоянии от любой оси вращения, расчет моментов инерции обычно включает исчисление, дисциплину математики, которая может обрабатывать такие непрерывные переменные. Момент инерции играет ту же роль в угловом движении, что и масса в линейном движении. Можно заметить, что момент инерции зависит не только от массы m, но и от r². Концепция инерции Концепция инерции является фундаментальной концепцией в физике. Он связан с другими фундаментальными понятиями, такими как: – Понятие состояния : состояние системы может быть механическим (статическим, кинематическим, динамическим и деформационным), термодинамическим, электромагнитным и т. д. Состояние системы определяется параметрами состояния. – Понятие взаимодействия. – Понятие процесса (преобразования) : В зависимости от характера системы. Процесс заключается в переходе системы из одного состояния в другое. Согласно принципу причинности, процесс является следствием взаимодействия. В зависимости от природы систем и природы подразумеваемых состояний существует множество типов процессов: механические (равновесие, движение и деформация), электромагнитные, гравитационные, химические, термодинамические и т. Посетите наши виртуальные лаборатории и окунитесь в виртуальный мир научного образования Попробуйте виртуальную лабораторию PraxiLabs БЕСПЛАТНО! Типы инерции с примерами Свойство тела сопротивляться любому изменению своего состояния покоя называется инерцией покоя. Примеры инерции покоя в нашей повседневной жизниТеперь мы покажем несколько примеров закона инерции
Объект будет двигаться с той же скоростью, пока на него не подействует сила. Свойство тела сопротивляться любому изменению своего состояния равномерного движения называется инерцией движения. Виртуальные лаборатории Praxilabs включают ряд научных онлайн-экспериментов по физике, химии и биологии. Начните работу с Praxilabs БЕСПЛАТНО Примеры закона инерции в повседневной жизни (инерция движения)
Объект будет двигаться в том же направлении, если на него не действует сила. Свойство тела сопротивляться любому изменению направления движения называется инерцией направления. 5 Примеры инерции направления1-Если вы прыгаете с движущегося автомобиля или автобуса, ваше тело продолжает двигаться в направлении транспортного средства. Когда ваши ноги касаются земли, земля воздействует на ваши ноги, и они перестают двигаться. Вы упадете, потому что верхняя часть вашего тела не остановилась, и вы упадете в том направлении, в котором двигались. 2-Частицы воды, прилипшие к велосипедной шине, отлетают по касательной всякий раз, когда водитель преодолевает поворот; пассажиры испытывают силу, действующую от центра кривой. 3-Когда водитель автобуса преодолевает поворот на дороге, пассажиры падают к центру поворота дороги. Всякий раз, когда водитель движется по кривой, на пассажиров действует сила, действующая в направлении от центра кривой; это происходит из-за стремления пассажиров продолжать движение по прямой. 4-Когда вы перемешиваете кофе или чай и останавливаетесь, вихревое движение продолжается по инерции. 5-Спутники (устанавливающие орбиту вокруг Земли) продолжают движение по своей траектории по инерции. Пояснительное видео к примерам действия закона инерции в повседневной жизни Важность инерции в нашей повседневной жизни день, не задаваясь вопросом. У него много важных применений:
Одним из хороших примеров закона инерции в повседневной жизни является то, что тело игрока, быстро бегущего по полю, стремится сохранить это движение, если мышечная сила не может его преодолеть. эта инерция. Фигурист, скользящий по льду, будет продолжать скользить с той же скоростью и в том же направлении, если не будет действовать внешняя сила. В гимнастике спортсмены постоянно меняют конфигурацию своего тела. При увеличении радиуса от оси вращения увеличивается момент инерции, что замедляет скорость вращения. Если спортсмен хочет увеличить скорость вращения, то он должен уменьшить радиус, приблизив сегменты тела к оси вращения, тем самым уменьшив радиус и момент инерции. Виртуальные лаборатории PraxiLabs по механической физикеВиртуальные научные лаборатории PraxiLabs позволяют проводить различные лабораторные эксперименты по физике, химии и биологии онлайн в любое время и в любом месте. Создайте бесплатную учетную запись и попробуйте виртуальные лаборатории по механике, которые объясняют законы движения Ньютона и закон инерции. Попробуйте виртуальные 3D-лаборатории прямо сейчас О Нурхан ЭссамПредыдущий Павильон PraxiLabs в Египте Праздничная выставка «Способность отличаться» Присутствовал президент Абдель Фаттах Эль-Сиси Next PraxiLabs теперь находится в Университете Низва Проверьте также «Сила» — один из очень важных терминов, используемых в физике. Законы физики занимают видное место в нашей повседневной жизни, поскольку они пронизывают, управляют и … Законы движения Ньютона — это три физических закона, на которых основывается наука о кинематике. Эти … Подробные пояснения и задачи – Lambda GeeksВ статье рассматривается связь между крутящим моментом и моментом инерции вращающегося тела и ее решаемые задачи. Крутящий момент и момент инерции поддерживают тело при вращательном движении. Когда на тело наводится крутящий момент, оно начинает ускоряться обратно пропорционально его моменту инерции. Вот почему крутящий момент, передаваемый телу, является произведением его момента инерции и углового ускорения. Законы движения Ньютона выражают, что тело остается неподвижным или движется из одной точки в другую с определенной скоростью; если на него не действует внешняя сила . Это означает, что тело получает ускорение в зависимости от его полной массы и силы приложенной внешней силы. Используя принцип Ньютона во вращательном движении, когда крутящий момент или момент силы создается на неподвижном или движущемся теле, оно инициирует угловое ускорение. Вот почему каждое твердое тело, совершая вращательное движение вокруг своей оси, несет угловое ускорение, когда индуцируется крутящий момент. Из предыдущих статей мы поняли, что инерция — это свойство тела, которое представляет тенденцию тела сопротивляться движению . Вот почему инерция обратно пропорциональна ускорению тела . Следовательно, первый закон движения Ньютона также называется законом инерции 90 270. Крутящий момент и момент инерции Каждая частица внутри такого вращающегося тела имеет свою массу, и все они вращаются вокруг центральной оси вращения тела. Следовательно, величина крутящего момента, необходимая для ускорения частиц внутри тела, зависит от распределения массы всего тела. Величина тела, выражающая распределение массы, называется « моментом инерции» . (кредит: Shutterstock) При вращательном движении величина инерции рассматривается как момент инерции тела, определяемый путем интегрирования полных масс частиц M и их расстояний R от его ось вращения. Следовательно, момент инерции тела (I) равен I = MR 2 . Взаимосвязь крутящего момента и момента инерцииЗаконы движения Ньютона связывают крутящий момент и момент инерции при вращательном движении. Когда мы включаем вентилятор, мы наводим на него крутящий момент. Теперь ускорение вентилятора будет зависеть от того, какой момент инерции имеет вентилятор и какой крутящий момент нам нужно создать. Момент инерции – это вращательная масса тела, а крутящий момент – вращательная сила, действующая на него. Крутящий момент τ, который необходимо приложить к телу, пропорционален как угловому ускорению, так и моменту инерции. Утверждение дает связь между крутящим моментом и моментом инерции как 15 рад/с 2 чтобы тело имело момент инерции 5 кгм 2 ? Дано : I = 5 кгм 2 α = 15 рад/с 2 Найти : τ =? Формула : τ = I α Раствор : . Круч должен индуцировать тело, чтобы повернуть его на 15 RAD/S 2. и момент инерции , τ= I α Подставляя все значения, τ = 5 x 15 τ= 75 Крутящий момент, необходимый для вращения тела, составляет 75 Нм. Какой крутящий момент должен возникнуть на расстоянии 2 м от тела массой 4 кг, чтобы оно вращалось со скоростью 5 рад/с 2 ?Дано : M = 4 кг R = 2 M α = 5 RAD/S 2 4 до нахождения : : : : : : : : – до нахождения : до : до : до : . Формула : τ = I α Решение : Крутящий момент, необходимый для корпуса, рассчитывается как τ = Iα Но момент инерции диска равен I = MR 2 . τ = MR 2 α Заменить все значения, τ = 4 x 2 2 x 5 τ = 4 x 5 τ = 8016 кузов 80 Нм. Формула крутящего момента и момента инерцииФормула крутящего момента и момента инерции легко определяется путем замены линейного эквивалента в формуле закона движения Ньютона его угловым эквивалентом. Крутящий момент τ является угловым эквивалентом приложенной силы F, а момент инерции I является угловым эквивалентом массы m. Следовательно, закон движения Ньютона (F = ma) для вращательного движения принимает вид: τ = Iα угловой момент. Вращательное движение также подчиняется законам движения Ньютона. Угловой импульс углового импульса тела при индуцированном крутящем моменте определяется как L = r x PГде P – линейный импульс 1 . т. е. P = mv L = r x mv Соотношение между линейной скоростью v и угловой скоростью ω равно Но мистер 2 срок тела момент инерции (I). L = I ω Мы узнали, что крутящий момент, действующий на тело, представляет собой скорость изменения углового момента . τ = DL/DT Заменить Аглоумическая формула момента , τ = diω/dt τ = IDω/DT Термин Dω/DT – Accelerator Наконец, крутящий момент получается из момента инерции, τ = lα Читать о крутящем моменте и скорости Диск массой 0,1 кг и радиусом 1 м вращается со скоростью 2 рад/с 2. Момент инерции диска равен I = 1/ 2мр 2 . Рассчитайте крутящий момент, действующий на диск.Дано : M = 0,1 кг R = 1 M α = 2 рад/с 2 до нахождения: до нахождения: до нахождения: до нахождения: до нахождения: до |

 также
также
 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X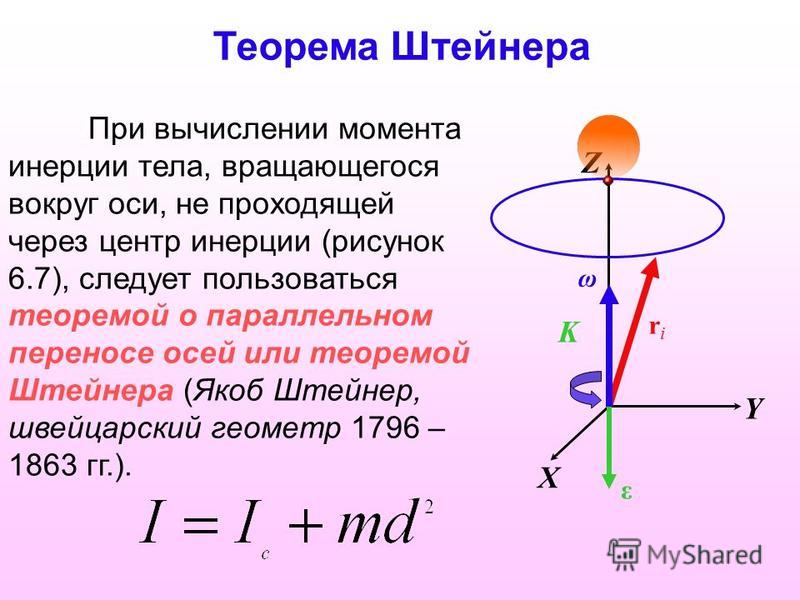 В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm

 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X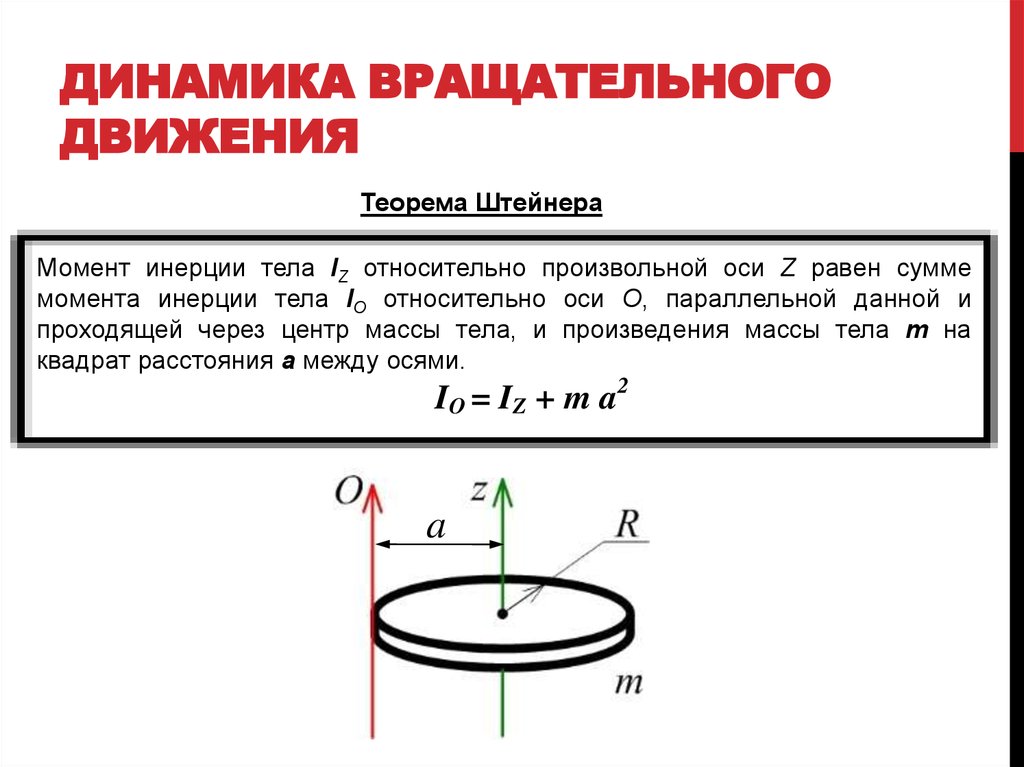 В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm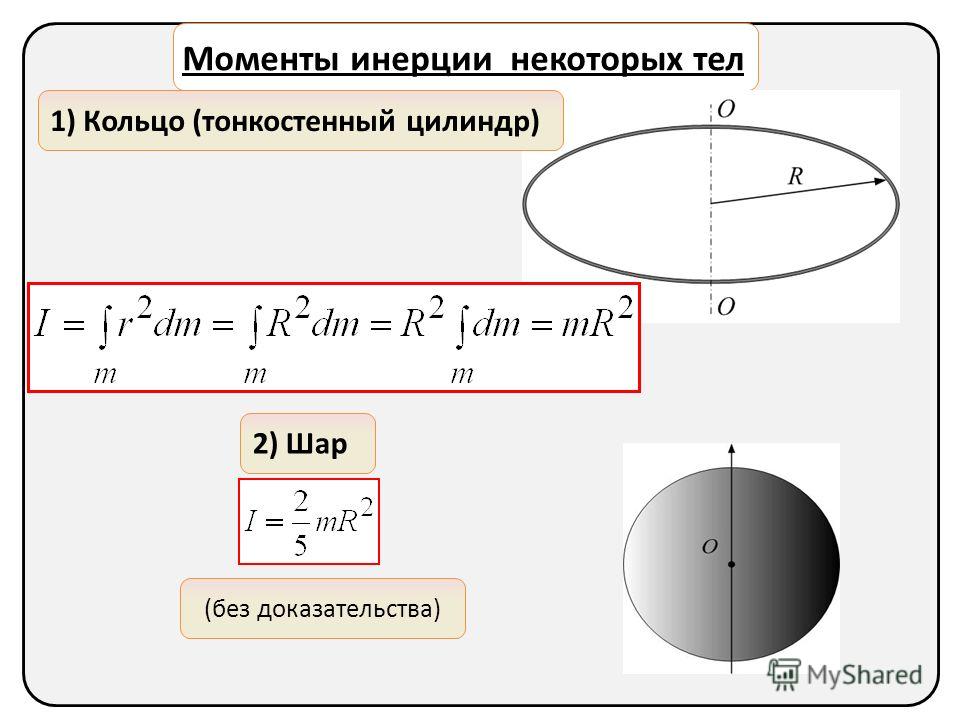 1)
1)
 2$
2$ ..
..
 Характеризует вращательное действие силы на твёрдое тело.
Характеризует вращательное действие силы на твёрдое тело. Разбиение можно производить до тех пор, пока движение не станет прямолинейным, а сила постоянной │dr│=ds.. Работа, совершенная силой на данном участке определяется по представленной формуле dA=F· dS· cos £= = │F│·│dr│· cos £=(F;dr)=Ft·dS A=F·S· cos £=Ft·S . Таким образом работа переменной силы на участке траектории равна сумме элементарных работ на отдельных малых участках пути A=SdA=SFt·dS= =S(F·dr).
Разбиение можно производить до тех пор, пока движение не станет прямолинейным, а сила постоянной │dr│=ds.. Работа, совершенная силой на данном участке определяется по представленной формуле dA=F· dS· cos £= = │F│·│dr│· cos £=(F;dr)=Ft·dS A=F·S· cos £=Ft·S . Таким образом работа переменной силы на участке траектории равна сумме элементарных работ на отдельных малых участках пути A=SdA=SFt·dS= =S(F·dr). ..
.. Если нить натянута вниз так, что радиус равен половине первоначального радиуса, то закон сохранения углового момента диктует, что мяч должен иметь четырехкратную угловую скорость. Это связано с тем, что произведение момента инерции и угловой скорости должно оставаться постоянным, а уменьшение радиуса вдвое уменьшает момент инерции в четыре раза.
Если нить натянута вниз так, что радиус равен половине первоначального радиуса, то закон сохранения углового момента диктует, что мяч должен иметь четырехкратную угловую скорость. Это связано с тем, что произведение момента инерции и угловой скорости должно оставаться постоянным, а уменьшение радиуса вдвое уменьшает момент инерции в четыре раза.
 Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл.
Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл. Поскольку момент инерции точечной массы определяется как
Поскольку момент инерции точечной массы определяется как
 Однако в физике мы обычно предполагаем, что масса объекта сосредоточена в одной точке, называемой центр масс .
Однако в физике мы обычно предполагаем, что масса объекта сосредоточена в одной точке, называемой центр масс . Мы можем сформулировать это с помощью приведенного ниже уравнения, где F t — результирующая сила, m — масса объекта, а t — поступательное ускорение .
Мы можем сформулировать это с помощью приведенного ниже уравнения, где F t — результирующая сила, m — масса объекта, а t — поступательное ускорение . 
 Мы можем рассчитать момент инерции каждого камня как
Мы можем рассчитать момент инерции каждого камня как Какой из двух дисков имеет больший момент инерции?
Какой из двух дисков имеет больший момент инерции?




 Когда тело сопротивляется угловому ускорению, это свойство называется моментом инерции. Он рассчитывается как сумма произведения массы каждой частицы в теле на квадрат расстояния частицы от оси ее вращения.
Когда тело сопротивляется угловому ускорению, это свойство называется моментом инерции. Он рассчитывается как сумма произведения массы каждой частицы в теле на квадрат расстояния частицы от оси ее вращения.
 1055/b-0036-140426
1055/b-0036-140426 Причина в том, что некоторые значения необходимо определять in vitro из образцов вскрытия, которых может не быть в большом количестве. По этой причине приведенные ниже числа для массы, размеров, положения центра масс и момента инерции сегментов тела не являются репрезентативными для обоих полов и всех возрастных групп. Их следует рассматривать как оценочные. Они примерно правильные, но в индивидуальном случае возможны отклонения в зависимости от пола, возраста и телосложения. Для простоты эталонные значения часто приводятся не в абсолютных единицах, а в относительных, на метр роста или на килограмм массы тела. Это избавляет от необходимости указывать значения отдельно для людей разного роста или массы тела; однако индивидуальные различия в телосложении игнорируются. Неопределенности в значениях влияют на все исследования, в которых эти данные используются в качестве входных значений, например, анализ походки. Если в результатах требуется высокая точность, соответствующие лица должны быть измерены заранее.
Причина в том, что некоторые значения необходимо определять in vitro из образцов вскрытия, которых может не быть в большом количестве. По этой причине приведенные ниже числа для массы, размеров, положения центра масс и момента инерции сегментов тела не являются репрезентативными для обоих полов и всех возрастных групп. Их следует рассматривать как оценочные. Они примерно правильные, но в индивидуальном случае возможны отклонения в зависимости от пола, возраста и телосложения. Для простоты эталонные значения часто приводятся не в абсолютных единицах, а в относительных, на метр роста или на килограмм массы тела. Это избавляет от необходимости указывать значения отдельно для людей разного роста или массы тела; однако индивидуальные различия в телосложении игнорируются. Неопределенности в значениях влияют на все исследования, в которых эти данные используются в качестве входных значений, например, анализ походки. Если в результатах требуется высокая точность, соответствующие лица должны быть измерены заранее.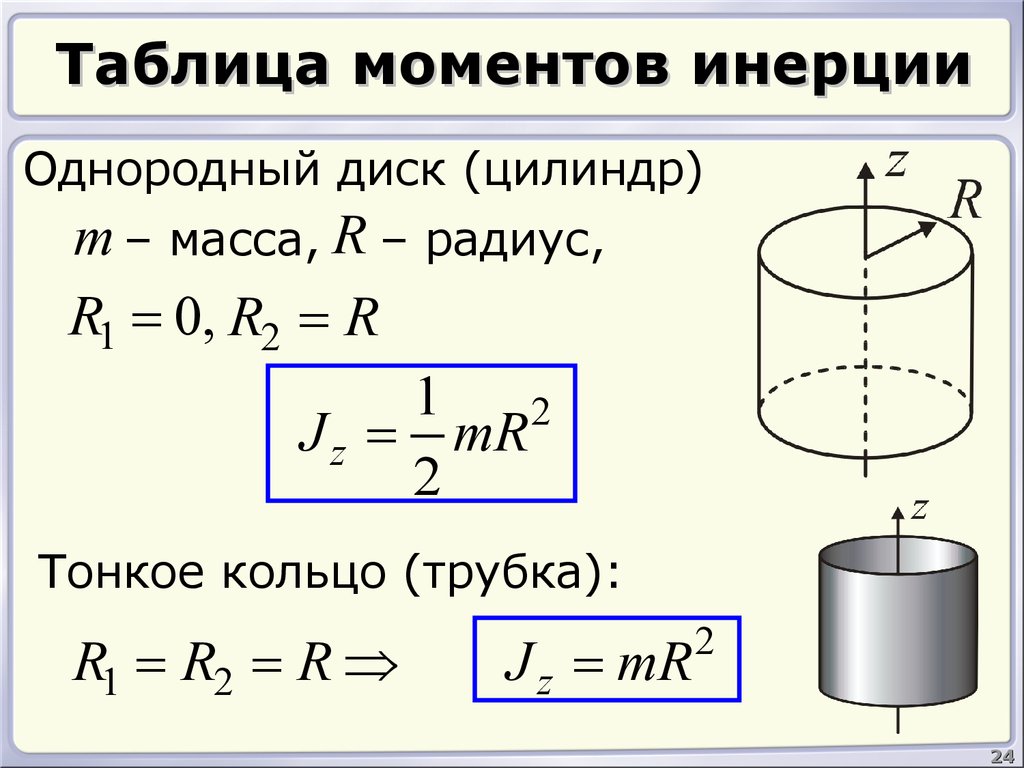
 Рис. 11.1 иллюстрирует расчет положения центра масс на примере плоской пластины. Для целей расчета пластина разбита на n малых квадратных элементов с массами m i . X- и y-координаты центра масс X c и Y c рассчитываются как
Рис. 11.1 иллюстрирует расчет положения центра масс на примере плоской пластины. Для целей расчета пластина разбита на n малых квадратных элементов с массами m i . X- и y-координаты центра масс X c и Y c рассчитываются как Если нужно вычислить положение центра масс трехмерного тела, мы представляем тело разделенным на маленькие кубы. Х с и Y c затем рассчитывают, как указано выше. Координата Z c центра масс получается из
Если нужно вычислить положение центра масс трехмерного тела, мы представляем тело разделенным на маленькие кубы. Х с и Y c затем рассчитывают, как указано выше. Координата Z c центра масс получается из Если пластина подвешена на нити, прикрепленной к произвольной точке Р на ее ободе, то известно, что в статическом равновесии ее центр масс расположен перпендикулярно ниже точки Р. (Если бы это было не так, пластина колебалась бы вперед и назад и положение покоя не будет достигнуто.) Если пластина подвешена в двух разных точках, положение центра масс определяется пересечением перпендикуляров, проходящих через точки подвеса. Центр масс трехмерного тела можно получить, подвешивая тело к трем неколлинеарным точкам (точкам, не лежащим на одной линии).
Если пластина подвешена на нити, прикрепленной к произвольной точке Р на ее ободе, то известно, что в статическом равновесии ее центр масс расположен перпендикулярно ниже точки Р. (Если бы это было не так, пластина колебалась бы вперед и назад и положение покоя не будет достигнуто.) Если пластина подвешена в двух разных точках, положение центра масс определяется пересечением перпендикуляров, проходящих через точки подвеса. Центр масс трехмерного тела можно получить, подвешивая тело к трем неколлинеарным точкам (точкам, не лежащим на одной линии). 11.3 ). В равновесии моментов датчик силы 1 с правой стороны установки измеряет силу как
11.3 ). В равновесии моментов датчик силы 1 с правой стороны установки измеряет силу как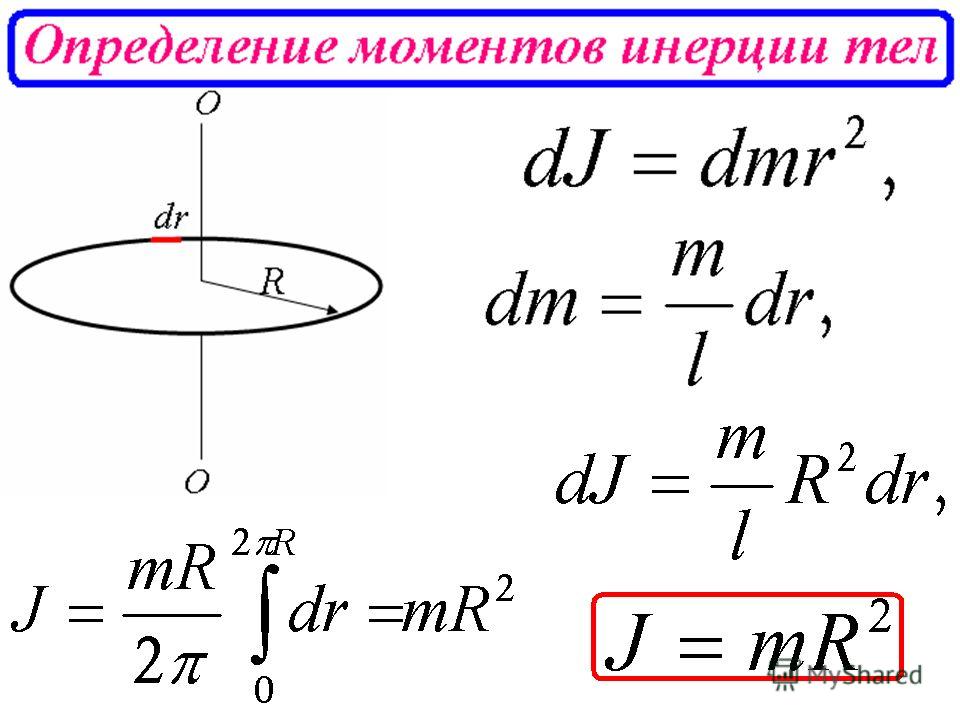 Массу голени и стопы обозначают m. Величина силы F 1 на датчик 1 измеряется в исходном состоянии i (колено согнуто 90°) и в конечном состоянии f (колено вытянуто). Относительно точки приложения силы F 2 суммы моментов (все силы, обозначенные их модулями) читаются как
Массу голени и стопы обозначают m. Величина силы F 1 на датчик 1 измеряется в исходном состоянии i (колено согнуто 90°) и в конечном состоянии f (колено вытянуто). Относительно точки приложения силы F 2 суммы моментов (все силы, обозначенные их модулями) читаются как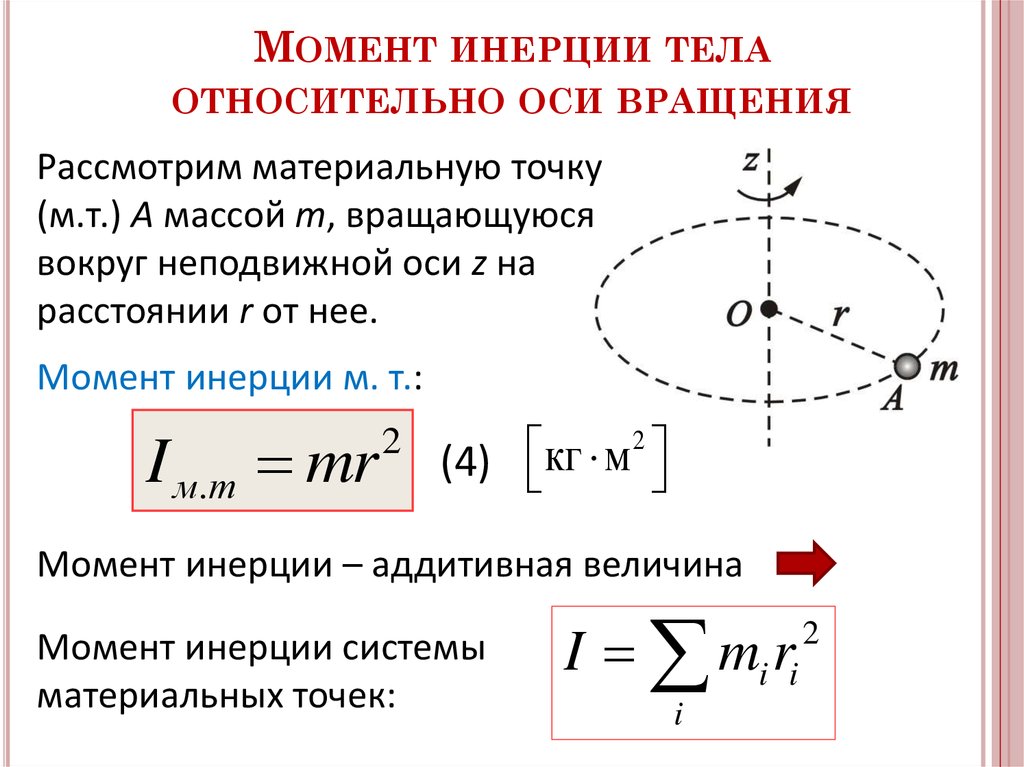 7 нужно решить относительно m.
7 нужно решить относительно m. При изменении оси изменяется и момент инерции. Поскольку количество осей неограниченно, существует также неограниченное количество моментов инерции. Если, однако, ограничиться рассмотрением осей, проходящих через центр масс, то это множество осей может быть уменьшено до трех 9 .0711 главные моменты инерции . Главные моменты — это моменты по отношению к трем взаимно перпендикулярным осям, проходящим через центр масс: главным осям. Можно показать (доказательство здесь не приводится), что момент инерции относительно любой оси, проходящей через центр масс, можно вычислить, если известны три главных момента. Для тел типа шаров, цилиндров или прямоугольных параллелепипедов, симметричных относительно некоторых осей, главные оси совпадают с осями симметрии. Например, На рис. 11.6 показаны направления главных осей и соответствующие им главные моменты инерции, полученные путем интегрирования, для сферы и цилиндра с равномерным распределением масс.
При изменении оси изменяется и момент инерции. Поскольку количество осей неограниченно, существует также неограниченное количество моментов инерции. Если, однако, ограничиться рассмотрением осей, проходящих через центр масс, то это множество осей может быть уменьшено до трех 9 .0711 главные моменты инерции . Главные моменты — это моменты по отношению к трем взаимно перпендикулярным осям, проходящим через центр масс: главным осям. Можно показать (доказательство здесь не приводится), что момент инерции относительно любой оси, проходящей через центр масс, можно вычислить, если известны три главных момента. Для тел типа шаров, цилиндров или прямоугольных параллелепипедов, симметричных относительно некоторых осей, главные оси совпадают с осями симметрии. Например, На рис. 11.6 показаны направления главных осей и соответствующие им главные моменты инерции, полученные путем интегрирования, для сферы и цилиндра с равномерным распределением масс.
 При этом тело совершит вращательные колебания с частотой
При этом тело совершит вращательные колебания с частотой ) обычно не приводят в единицах килограмм на квадратный метр [кг·м 2 ]. Вместо этого радиус вращения i дается в метрах [м]. По радиусу вращения i и массе сегмента m s момент инерции I можно рассчитать как мода. Это предполагает, что сегменты тела людей с разной массой тела геометрически подобны. В действительности это верно лишь приблизительно — вспомните, например, о различиях формы бедра у разных людей. Иногда указан относительный радиус инерции и отн ; это равно радиусу вращения, деленному на длину сегмента. Указание относительного радиуса вращения имеет то преимущество, что для каждого сегмента тела достаточно одного числа для количественной оценки момента инерции у людей разного роста.
) обычно не приводят в единицах килограмм на квадратный метр [кг·м 2 ]. Вместо этого радиус вращения i дается в метрах [м]. По радиусу вращения i и массе сегмента m s момент инерции I можно рассчитать как мода. Это предполагает, что сегменты тела людей с разной массой тела геометрически подобны. В действительности это верно лишь приблизительно — вспомните, например, о различиях формы бедра у разных людей. Иногда указан относительный радиус инерции и отн ; это равно радиусу вращения, деленному на длину сегмента. Указание относительного радиуса вращения имеет то преимущество, что для каждого сегмента тела достаточно одного числа для количественной оценки момента инерции у людей разного роста. | Опубликовано drzezo в ОРТОПЕДИЧЕСКАЯ | Комментарии отключены на 11 размерах, массе, расположении центра масс и моменте инерции сегментов человеческого тела
| Опубликовано drzezo в ОРТОПЕДИЧЕСКАЯ | Комментарии отключены на 11 размерах, массе, расположении центра масс и моменте инерции сегментов человеческого тела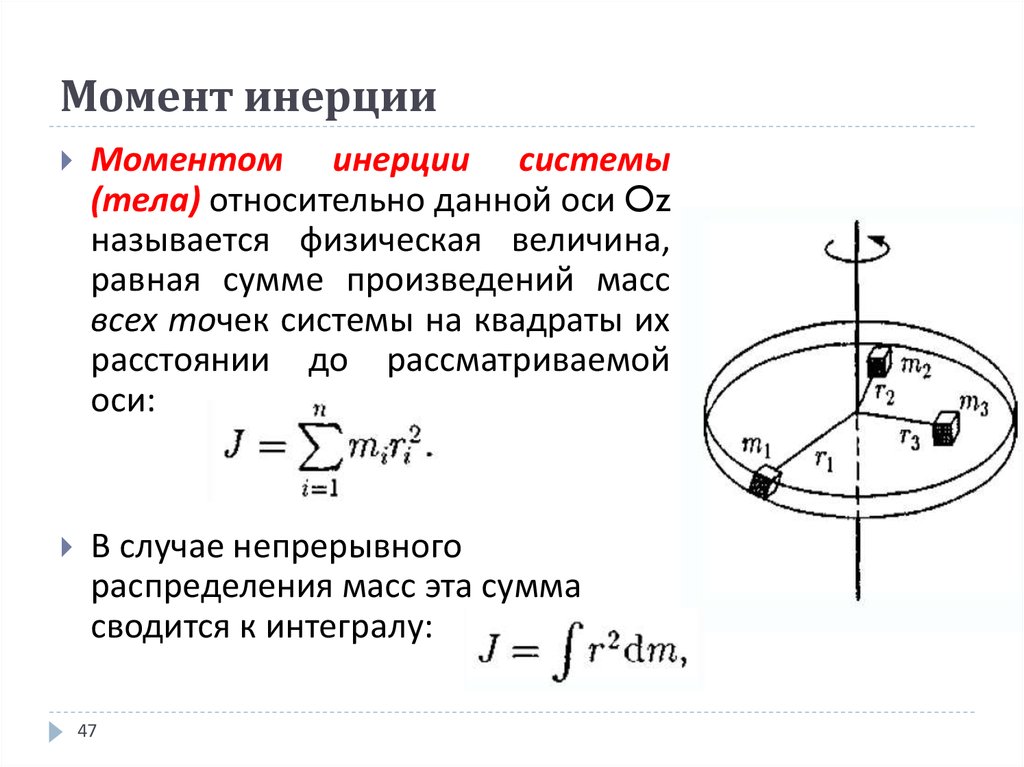 Это ввело философа Аристотеля в заблуждение, и он решил, что объекты могут двигаться только до тех пор, пока к ним применяется сила.
Это ввело философа Аристотеля в заблуждение, и он решил, что объекты могут двигаться только до тех пор, пока к ним применяется сила.

 Так как момент инерции точечной массы определяется как
Так как момент инерции точечной массы определяется как д.
д. Таким образом, пассажир падает назад.
Таким образом, пассажир падает назад. Попробуйте прямо сейчас!
Попробуйте прямо сейчас! 

 .
.
 Всегда и везде …
Всегда и везде …
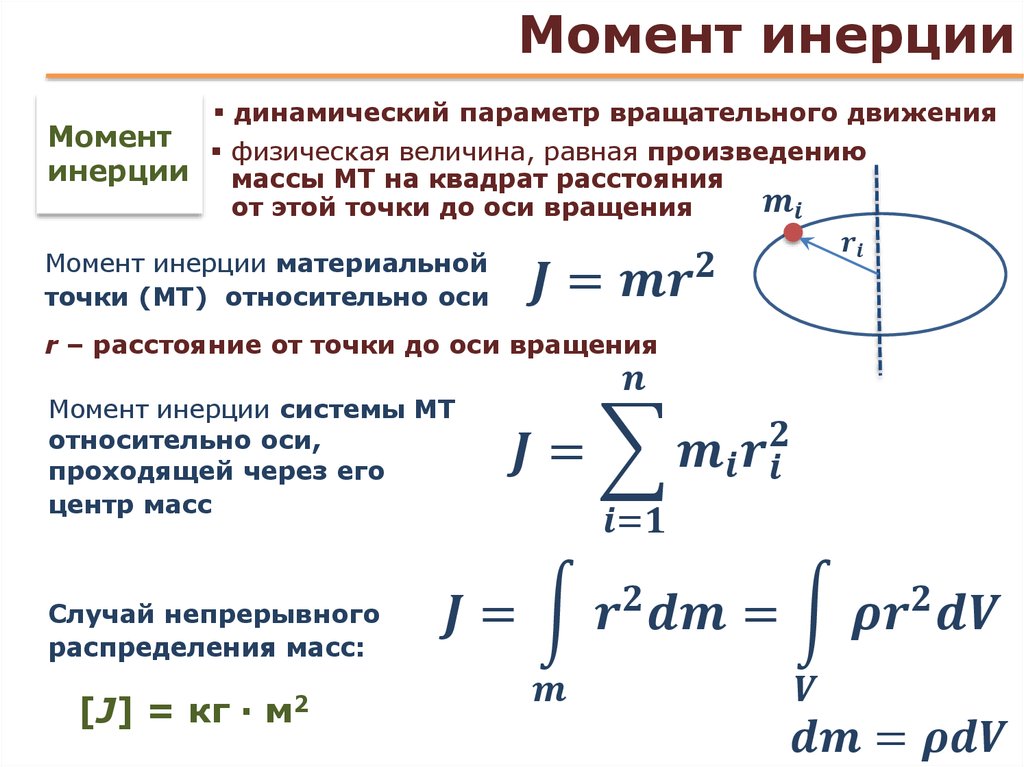
 Но момент инерции I уменьшает угловое ускорение α тела.
Но момент инерции I уменьшает угловое ускорение α тела.