Что такое архимедова сила: Архимедова сила — урок. Физика, 7 класс.

Архимедова сила | СПАДИЛО

Определение

Архимедова сила (выталкивающая сила, подъемная сила) — сила, с которой жидкость или газ выталкивают погруженное в них тело.

Полезно знать и понимать!

• Причина возникновения выталкивающей силы: нижняя грань тела находится на большей глубине, чем верхняя, поэтому давление жидкости снизу больше, чем сверху. Из-за разницы в давлениях возникает выталкивающая сила.
• Архимедова сила всегда направлена вертикально вверх.
• Архимедова сила равна разности сил давления на нижнюю и верхнюю грани:

F_A = F_H – F_B

• Также выталкивающая сила равна разности веса тела в воздухе и веса тела в жидкости:

F_A = P_возд – P_ж

• Модуль выталкивающей силы определяется с помощью закона Архимеда.

Закон Архимеда

Выталкивающая сила равна весу вытесненной жидкости.

F_A = P_ж

Частные случаи определения архимедовой силы

Полное погружение
	Архимедова сила равна произведению плотности жидкости, объема тела и ускорения свободного падения: FA = ρжVтg Vт — объем погруженного в жидкость тела.
Неполное погружение
	Архимедова сила равна произведению плотности жидкости, объема погруженной части тела и ускорения свободного падения: FA = ρжVп.ч.g Vп.ч. — объем погруженной в жидкость части тела.

Внимание! Если тело погружено в газ, то в формуле нужно использовать плотность этого газа.

Пример №1. При взвешивании груза в воздухе показание динамометра равно 1 Н. При опускании груза в воду показание динамометра уменьшается до 0,6 Н. Найдите значение выталкивающей силы.

Выталкивающая сила равна разности веса тела в воздухе и веса тело в воде. Следовательно:

F_A = P_возд – P_ж = 1 – 0,6 = 0,4 (Н)

Воздухоплавание

Подъемной силой воздушного шара служит архимедова сила, равная:

F_A = ρ_воздV_шg

Подъемной силе противостоят сила тяжести и сила сопротивления воздуха:

F_тяж = (M_шара + m_газа + m_корз + m_груза)g

F_сопр

Управление шаром:

•  чтобы взлететь, шар заполняют нагретым воздухом или газом, плотность которого меньше плотности окружающего воздуха;
• чтобы увеличить высоту полета, с шара сбрасывают балласт;
•  чтобы спуститься на землю, газ охлаждают.

Пример №2. Аэростат объемом 1000 м³ заполнен гелием. Плотность гелия 0,18 кг/м³, плотность воздуха 1,29 кг/м³. Какая выталкивающая сила действует на аэростат?

Выталкивающая сила зависит только от плотности окружающей среды и объема погруженного в него тела. Так как аэростат погружен в воздух полностью:

F_A = ρ_вV_тg = 1,29∙1000∙10 = 12,9 (кН)

Архимедова сила и законы Ньютона

Если тело полностью погружено в жидкость (или газ):

• Архимедова сила равна: F_A = ρ_жV_тg.
• Сила тяжести, действующая на тело: F_тяж = mg = ρ_тV_тg.

Частный случай

Определить минимальную массу груза, который следует положить на плоскую однородную льдину площадью S, чтобы она полностью погрузилась в воду. Толщина льдины h, а плотность льда ρ_л, плотность воды ρ_в.

Второй закон Ньютона в векторной форме для льдины, полностью погруженной в воду (она не тонет и не всплывает):

→FA+→Fтяж=0

Так как эти силы направлены в противоположные стороны:

F_A = F_тяж

Архимедова сила, действующая только на льдину, равна:

F_A = ρ_вV_лg

Сила тяжести равна сумме масс льдины и груза:

F_тяж = (m_л + m_гр)g

Массу льдины можно выразить через произведение ее плотности на объем, равные произведению ее площади на толщину:

m_л = ρ_лSh

Пример №3. Какую силу надо приложить, чтобы поднять под водой камень, масса которого 30 кг, а объем 12 000 см³?

12 000 куб. см = 0,012 куб. м

Чтобы поднять под водой камень, потребуется сила, равная разности силе тяжести и архимедовой силы, действующей на этот камень:

F = F_тяж – F_A = mg – ρ_вV_тg = 30∙10 – 1000∙0,012∙10 = 180 (Н)

Условия плавания тел

На любое тело, погруженное в жидкость или газ, действуют две противоположно направленные силы: сила тяжести и архимедова сила.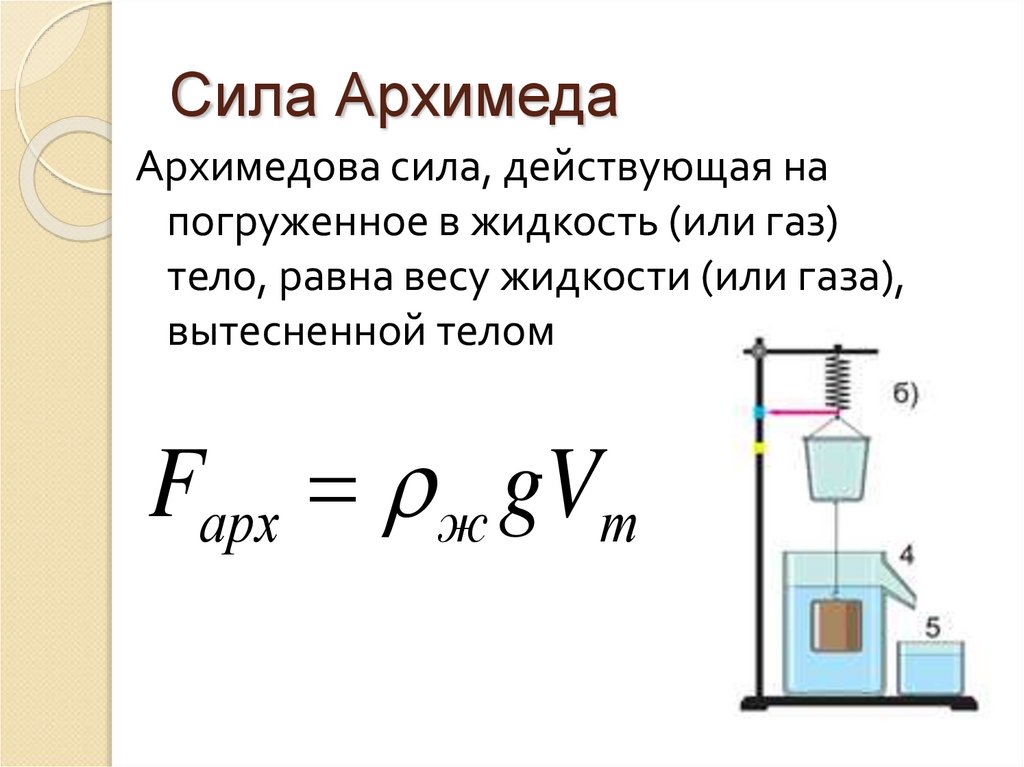 Направление движения тела зависит от того, какая из этих сил больше по модулю:

• Тело тонет, если: mg > F_A; ρ_т > ρ_ж.
• Тело плавает в толще среды, если: mg = F_A ; ρ_т = ρ_ж.
• Тело всплывает, если: mg < F_A; ρ_т < ρ_ж.

Внимание! Тело, имеющее плотность меньшую, чем плотность жидкости, в которой оно плавает, будет находиться на поверхности, погрузившись в жидкость частично.

Если тело плавает на поверхности:

• Архимедова сила и сила тяжести, действующие на него, равны: F_A= F_тяж.
• Сила тяжести равна: F_тяж = mg = ρ_тV_тg.
• Архимедова сила равна: F_A = ρ_жV_п.ч.g .
• Взаимосвязь между объемом и высотой тела правильной формы: V = Sh.

Варианты условий задач на условия плавания тел

Сплошное тело объемом Vт плавает в воде. Причем под водой находится 3/4 его объема. Определите силу тяжести, действующую на тело. Плотность воды ρв.	Второй закон Ньютона в векторной форме: →FA+→Fтяж=0 Отсюда (проекция на вертикальную ось): FA = Fтяж Fтяж = 3ρвVтg/4
Какая часть (в процентах) айсберга находится под водой? Плотность льда ρл, а воды ρв.	Второй закон Ньютона в векторной форме: →FA+→Fтяж=0 Отсюда (проекция на вертикальную ось): FA = Fтяж Отсюда: ρлVлg = ρвVп.ч.g Ускорение свободного падения взаимоуничтожается. Чтобы найти погруженную часть айсберга в процентах, нужно: Vп.ч.Vл..=ρлρв.. Найденное отношение остается умножить на 100%.
Полое тело плотностью ρтплавает в воде, погрузившись на 1/5 своего объема. Найдите объем полости Vп, если объем тела Vт, а плотность воды ρв.	Второй закон Ньютона в векторной форме: →FA+→Fтяж=0 Отсюда (проекция на вертикальную ось): FA = Fтяж Отсюда: ρвVп.ч.g = ρт(Vт – Vп)g Преобразовав выражение, получим: Vп=Vт(5ρт−ρв)5ρт..

Пример №4. Кубик массой 40 г и объемом 250 см³ плавает на поверхности воды. Найдите значение выталкивающей силы, действующей на кубик.

40 г = 0,04 кг

250 см³ = 250∙10^–6 м³

Так как тело плавает, Архимедова сила будет равна по модулю силе тяжести, которая определяется формулой:

F_A = F_тяж = 0,04∙10 = 0,4 (Н)

Задание EF18524

Деревянный шарик плавает в стакане с водой. Как изменятся сила тяжести и архимедова сила, действующие на шарик, если он будет плавать в подсолнечном масле?

Для каждой величины определите соответствующий характер изменения:

1. Увеличится.
2. Уменьшиться.
3. Не изменится.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

---

Алгоритм решения

1. Записать условие плавания тел.
2. На основании условия плавания тел сделать вывод о том, как изменятся указанные физические величины.

Решение

По условию задачи деревянный шарик плавает на поверхности воды. Но это возможно, лишь когда архимедова сила равна силе тяжести:

F_Aв = F_тяж

Если шарик будет плавать в подсолнечном масле, также можно применить условие плавания тел:

F_Aм = F_тяж

Сила тяжести зависит только от массы тела, которая остается неизменной. Поэтому сила тяжести тоже не меняется. Но из этого следует:

F_Aв = F_Aм

Это возможно благодаря тому, что объем погруженной части шарика в масло будет больше объема погруженной части шарика в воду. Этим компенсируется разница в плотностях жидкостей, но архимедова сила при этом остается неизменной.

Верный ответ: 33.

Ответ: 33

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18477

Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В его распоряжении имеется установка, состоящая из ёмкости с водой и сплошного деревянного шарика объёмом 30 см³. Какая из следующих установок необходима ещё ученику для того, чтобы на опыте обнаружить зависимость силы Архимеда от объёма тела?

№ установки	Жидкость, налитая в ёмкость	Объём шарика	Материал, из которого сделан шарик
1	вода	30 см3	сталь
2	вода	20 см3	дерево
3	керосин	20 см3	дерево
4	подсолнечное масло	30 см3	сталь

Ответ:

а) установка № 1

б) установка № 2

в) установка № 3

г) установка № 4

---

Алгоритм решения

1. Сделать анализ задачи. Определить, какие величины в опыте остаются постоянными.
2. Определить, какие величины должны быть в опыте переменными.

Решение

Ученик изучает силу Архимеда, действующую на тела, полностью погружённые в жидкость. В формулировке слово «жидкость» используется в единственном числе. Следовательно, жидкость во всех опытах будет одной и той же (плотность жидкости будет постоянной). У ученика уже есть установка, в которую входит емкость с водой. Поэтому во второй установке в качестве жидкости тоже должна использоваться вода. Варианты 3 и 4 исключаются.

В формулировки задачи также говорится о «телах». Они могут быть выполнены из разных материалов, и они могут иметь разный объем. Но известно, что архимедова сила зависит только от объема тела. Поэтому во второй установке нужно использовать тело другого объема. В вариантах 1 и 2 этому условию соответствует деревянный шарик объемом 20 куб. см (так как в первой установке используется шарик объемом 30 куб. см).

Отсюда верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22696

Необходимо экспериментально изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости.

Какие две установки следует использовать для проведения такого исследования?

---

Алгоритм решения

1. Установить цели опыта.
2. Сделать вывод о том, какие величины в опыте должны быть постоянными, а какие — переменными.
3. Выбрать установки, соответствующие выводу.

Решение

В опыте нужно изучить зависимость силы Архимеда, действующей на тело, погружённое в жидкость, от плотности жидкости. Это значит, что плотность жидкости — величина переменная. Все остальные величины при этом должны оставаться постоянным. Поэтому нам нужны установки с разными жидкостями, но одинаковыми телами. Этому условию соответствуют две установки: «а» и «д».

Ответ: ад

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18057

На границе раздела двух несмешивающихся жидкостей, имеющих плотности ρ₁ = 400 кг/м³ и ρ₂ = 2ρ₁, плавает шарик (см. рисунок). Какой должна быть плотность шарика ρ, чтобы выше границы раздела жидкостей была одна четверть его объёма?

---

Алгоритм решения

1.Записать исходные данные.

2.Выполнить рисунок.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в проекции на ось ординат.

5.Выполнить общее решение.

6.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Плотность первой жидкости: ρ₁ = 400 кг/м³.

• Плотность второй жидкости: ρ₂ = 2ρ₁.

• Объем шарика: V.

• Объем шарика выше границы раздела двух жидкостей: V₁ = V/4.

• Объем шарика выше границы раздела двух жидкостей: V₂ = 3V/4.

Построим рисунок и укажем все силы, действующие на шарик:

Запишем второй закон Ньютона в векторном виде:

m→g+→FA1+→FA2=0

Запишем второй закон Ньютона в виде проекции на ось ординат:

mg=FA1+FA2

Выразим массу тела через его объем и плотность, выразим выталкивающие силы через закон Архимеда и получим:

ρVg=ρ1gV1+ρ2gV2

Преобразуем выражение, сократив ускорение свободного падения и подставив выражения для объемов погруженных в жидкости частей тела, а также выражение для плотности второй жидкости:

ρV=ρ1V4..+2ρ13V4..

Объемы сокращаются. Остается:

ρ=ρ14..+2ρ134..=7ρ14..=7·4004..=700 (кгм3..)

.

.

.

.

Ответ: 700

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 8. 4k

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3. 1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5. 2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

АРХИМЕДОВА СИЛА

Архимедова сила является частным случаем массы или объемной силы . Под массовыми (объемными) силами понимаются силы, действующие на каждый элемент объема или массы тела. В механике сплошных сред масса вводится исходя из объемной плотности ρ(x _i , t), определяемой для каждого момента времени t и любой точки пространства x _i Масса в объеме v в момент времени t имеет интеграл ρ (x _i , t)dV.

Точно так же механика сплошных сред занимается не самими силами, а плотностью сил и их распределением в пространстве и во времени.

Таким образом, плотность распределения объемных сил ∫ _v (x _i , t) в данной точке среды x _i можно интерпретировать как отношение основного вектора сил, приложенных к малому объему включая точку x _i , к массе объема, когда последняя стремится к нулю.

В качестве примера объемных сил можно рассмотреть силу тяжести ρ dV, где ρ — среднее значение плотности в объеме dV, вектор ускорения свободного падения. Другие примеры включают центробежные силы или электромагнитные силы, действующие на жидкость, несущую электрический заряд.

Градиент давления является аналогом объемной силы (взятой с обратным знаком), действующей на жидкий элемент, если само давление изменяется от точки к точке. Если выделить в жидкости некоторый объем, то сила, действующая на этот объем, равна интегралу −∫pdA, где dA — элемент поверхности, где интеграл берется по поверхности, окружающей этот объем. Преобразуя поверхностный интеграл в объемный, находим

Последний интеграл представляет собой объемную силу, действующую на весь объем.

Тот факт, что в уравнение движения входит не само давление, а только его градиент, показывает, что величина давления в жидкости определяется только относительно произвольной постоянной.

Если внешняя объемная сила = dV, где – сила, отнесенная к единице массы, а F _A – сила, действующая на объем V со стороны окружающей среды через граничную поверхность A, то сумма сил, действующих на отделенную объем будет следующим

Сила считается известной функцией времени и пространства. Если поле связано с потенциалом Φ, который не зависит от времени, то Φ = −grad Φ.

В гидромеханике во многих практически интересных случаях главная движущая сила обусловлена ​​наличием поля температуры или концентрации. Изменение температуры или концентрации приводит к изменению плотности; это приводит к развитию выталкивающей силы, которая образуется из-за наличия объемного силового поля. Выталкивающая сила также называется 9.0003 Архимед или гидростатическая подъемная сила . При малых перепадах температуры зависимость плотности жидкости от температуры можно принять линейной, т.е. при температуре Т ₀ ; β – коэффициент объемного расширения. Произведение β _g называют также параметром плавучести.

В случае гравитационного поля горячее вещество движется под действием силы Архимеда F = (ρ − ρ ₀ )gV относительно более холодного вещества в направлении, противоположном направлению силы тяжести. Интенсивность конвекции зависит от разницы температур между слоями, теплопроводности и вязкости среды.

Правда ли, что Архимед сформулировал свой знаменитый принцип на основе наблюдения, которое он сделал, погружаясь в ванну? | Office for Science and Society

Принцип Архимеда гласит, что любой объект, полностью или частично погруженный в жидкость, поднимается вверх под действием силы, равной весу жидкости, вытесненной этим объектом. Но. не открытие принципа, названного в его честь, заставило греческого математика, физика и изобретателя бежать обнаженным по улице с криком «Эврика», что означает «я нашел это». То, что он якобы нашел, было решением проблемы, поставленной перед ним королем Сиракуз Иероном, который подозревал, что ювелир, которому было поручено сделать ему золотую корону, заменил часть золота серебром. Как можно определить, была ли корона из чистого золота, недоумевал король?

Как гласит история, ответ пришел к Архимеду, когда он заметил, что уровень воды в ванне поднимается, когда он погружается в нее. Это привело его к выводу, что тело, погруженное в воду, вытесняет объем воды, равный его собственному объему, а это означает, что объем любого предмета неправильной формы, который тонет в воде, может быть определен по объему вытесненной воды. Затем, разделив вес этого объекта на его объем, можно рассчитать его плотность. Когда дело дошло до короны, Архимед предположил, что можно определить, была ли она подмешана с другим металлом, сравнив ее плотность с плотностью чистого золота. По крайней мере, так гласит история. Сомнительно, насколько можно полагаться на это объяснение, поскольку мы впервые слышим об этом от римского архитектора и инженера Витрувия в I веке до нашей эры, примерно через двести лет после того, как предположительно произошел момент эврики. Хотя это повествование может быть несколько фантастичным, нет сомнения, что Архимед действительно сформулировал принцип плавучести, который, среди прочего, объясняет, почему корабли плавают.

Давайте начнем с воображаемого приключения с маской и трубкой. Вы видите красивый коралл на глубине около двадцати футов и решаете нырнуть, чтобы рассмотреть его поближе. Но чем глубже вы погружаетесь, тем большую силу вы чувствуете, толкая вас вверх к поверхности. Это означает, что сила, направленная вниз из-за вашего веса плюс давление воды на вас сверху, меньше, чем сила, оказываемая водой на нижнюю часть вашего тела, толкающая вас вверх, которая называется «выталкивающей силой».

Теперь представьте, что мы можем в какой-то момент нажать кнопку паузы во время погружения и каким-то волшебным образом удалить ваше тело и заменить его водой. Эта вода имеет такой же объем, какой занимало ваше тело, но не такой же вес. Однако эта замещающая вода испытывает такое же давление снизу, то есть ту же выталкивающую силу, что и ваше тело, поскольку давление воды зависит исключительно от глубины. Но объем воды, заменивший ваше тело, имеет определенный вес, толкающий вниз. Поскольку вы теперь неподвижны, направленная вниз сила должна равняться восходящей силе или плавучести. Но так как эта направленная вниз сила создается весом воды, занимающей тот же объем, что и ваше тело, то вывод состоит в том, что выталкивающая сила должна равняться весу воды, вытесненной вашим телом. И здесь мы имеем принцип Архимеда, а именно, что направленная вверх сила, действующая на тело, погруженное в жидкость, равна весу вытесненной жидкости.

Как же тогда это объясняет, почему корабль плавает? Для плавучести восходящая сила воды, то есть выталкивающая сила, должна быть равна направленной вниз силе веса корабля. Когда корабль опускается на воду, он будет вытеснять все больше и больше воды, пока вес вытесненной воды не сравняется с весом корабля. В этот момент он всплывает. Если на корабль будет навалено больше веса, он будет опускаться все ниже и ниже, пока вес вытесняемой им воды не станет меньше веса корабля, после чего он утонет. Но так как корабли построены таким образом, что имеют большие объемы пустого пространства, то объем вытесняемой ими воды будет весить больше, чем корабль, так как вода тяжелее воздуха. Это также объясняет, почему корабль будет плавать выше в соленой воде, чем в пресной. Поскольку соленая вода тяжелее из-за содержания соли, меньший объем должен быть вытеснен, чтобы сравняться с весом корабля. Если вы задавались вопросом, почему в Мертвом море практически невозможно утонуть, то это из-за его поразительного содержания соли, составляющего около 34%. Вам не нужно погружаться слишком глубоко, чтобы вытеснить объем воды, равный вашему весу. Я надеюсь, что все эти разговоры о погружении не оставили у вас ощущения, что вы прыгаете выше головы.