Что такое давление физика: Давление — урок. Физика, 7 класс.

в теории и на практике

Рассказываем, что такое давление, как оно рассчитывается и где мы сталкиваемся с ним каждый день.

Теория: что говорит нам физика

Любое вещество в условиях гравитации оказывает давление. По определению это:

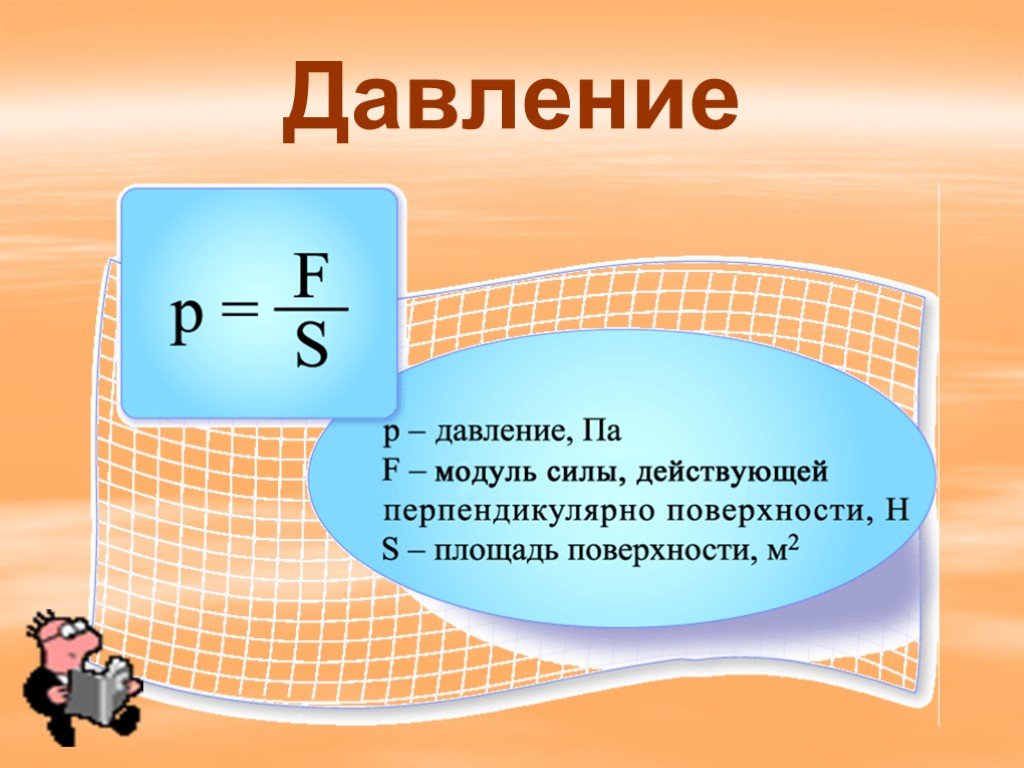
Физическая величина, которая выражает воздействие силы на единицу площади поверхности.

В международной системе СИ (от франц. ‘Le Système International d’Unités’, SI) давление измеряется в Паскалях (Па) и обозначается буквой p. 

Формула, вытекающая из определения, выглядит так:

 

Давление твердых тел, жидкости и газа проходит по-разному.

У твердого тела в условиях гравитации есть точка опоры. Все давление приходится на нее, а значит, оно неравномерно.

Жидкость и газ заполняют сосуд и оказывают давление не только на его дно, но и на стенки (а газ — и на крышку). Если надавить на любую точку заполненного сосуда (предположим, это полиэтиленовый пакет), то давление равномерно передастся во всех направлениях: вниз, вверх и вбок. Это закон Паскаля.

Гидростатическое давление

Это давление столбика жидкости (точнее, его веса) на дно сосуда. Отсюда можно вывести новую формулу:

 

У поверхности жидкости ее давление на стенки сосуда будет практически равно нулю (так как чем ближе к поверхности, тем меньше вес жидкости), а ближе ко дну будет действовать формула ρgh.

Давление (любое, не только гидростатическое) может отсутствовать только в вакууме, потому что в нем нет вещества, которое могло бы его создавать. Абсолютный вакуум не достижим или достижим только в искусственных условиях, так как даже в космосе есть минимальная концентрация молекул — а значит, есть и давление, но в ничтожных количествах. 

Также в науке есть понятие «физический вакуум», которое означает лишенное вещества пространство. Заполненное квантовым полем, оно все же не может быть охарактеризовано как «абсолютная пустота», так как в этих условиях постоянно рождаются и исчезают виртуальные частицы.

Практика: давление в реальной жизни

Давление — это не всегда больно и неприятно. С некоторыми его видами мы сталкиваемся каждый день, едва ли задумываясь об этом.

Атмосферное давление

Атмосфера любой планеты состоит из газов и удерживается гравитацией. Высота атмосферы Земли — примерно 100 км.

Так как на газ действует гравитация, у воздуха тоже есть вес. Логично предположить, что у поверхности планеты он будет тяжелее, чем на вершине горы. Давление этой 100-километровой массы на поверхность планеты (а заодно и нас) называется атмосферным.

Атмосферное давление, кроме Паскалей, может измеряться в миллиметрах ртутного столба и атмосферах.

В нормальном состоянии человек не обращает внимания на атмосферное давление, потому что оно компенсируется внутренним.

Артериальное давление

Огромный вес воздуха должен был бы нас раздавить, если бы в нас не было крови, которая оказывает внутреннее давление на сосуды.

В данном случае — на артерии.

Кровь движется в сосудах не равномерно, а толчками — под воздействием сокращения сердечной мышцы. Загадочные цифры «120/90» — это фиксация превышения давления крови на стенки сосудов над атмосферным давлением, где «120» — максимальное значение в момент сокращения сердца (систолическое давление), а «90» — минимальное значение (диастолическое).

Давление — основная величина в термодинамике, и понять, что это значит, не так уж и сложно. Но если учитель или преподаватель давит слишком сильно, наш студенческий сервис поможет справиться с контрольной, лабораторной, курсовой и любой другой работой. Ждем вас в FenixHelp!

Давление для чайников: определение, объяснение простыми словами

Никому не нравится быть под давлением. И не важно, под каким. Об этом спела еще группа Queen вместе с Дэвидом Боуи в своем знаменитом сингле “Under pressure”. Что такое давление? Как понять давление? В чем оно измеряется, какими приборами и методами, куда направлено и на что давит. Ответы на эти и другие вопросы – в нашей статье про давление в физике и не только.

Давление в физике

Если преподаватель давит на вас, задавая каверзные задачки, мы сделаем так, чтобы вы смогли верно на них ответить. Ведь понимание самой сути вещей – ключ к успеху! Итак, что такое давление в физике?

По определению:

Давление – скалярная физическая величина, равная силе, действующей на единицу площади поверхности.

В международной системе СИ измеряется в Паскалях и обозначается буквой p. Единица измерения давления – 1 Паскаль. Русское обозначение – Па, международное – Pa.

Согласно определению, чтобы найти давление, нужно силу разделить на площадь.

Любая жидкость или газ, помещенный в сосуд, оказывает на стенки сосуда давление. Например, борщ в кастрюле действует на ее дно и стены с некоторым давлением. Формула определения давления жидкости:

где g – ускорение свободного падения в гравитационном поле земли, h – высота столба борща в кастрюле, греческая буква «ро» – плотность борща.

Одно из важнейших свойств жидкостей – изотропность. Это значит, что по закону Паскаля во всех направлениях жидкости производимое ею давление передается одинаково. Кстати, подробнее о жидкостях, их свойствах и движении читайте в нашем материале про уравнение Бернулли.

Наиболее распространенный в быту прибор для определения давления – барометр. Но в чем измеряют давление? Кроме паскаля существуют и другие внесистемные единицы измерения:

• атмосфера;
• миллиметр ртутного столба;
• миллиметр водяного столба;
• метр водяного столба;
• килограмм-сила.

В зависимости от контекста применяются разные внесистемные единицы.

Например, когда вы слушаете или читаете прогноз погоды, там и речи не идет о паскалях.  Говорят о миллиметрах ртутного столба. Один миллиметр ртутного столба – это 133 Паскаля. Если вы ездите за рулем, то наверное знаете, что нормальное давление в колесах легкового автомобиля – около двух

атмосфер.

 

Давление в шинах – это давление газа. Оно обусловлено столкновениями молекул воздуха с поверхностью шины

 

Атмосферное давление

Атмосфера – это газ, точнее, смесь газов, которая удерживается у Земли благодаря гравитации. Атмосфера переходит в межпланетное пространство постепенно, а ее высота – примерно 100 километров.

Как понимать выражение «атмосферное давление»? Над каждым квадратным метром земной поверхности находится стокилометровый столб газа.  Конечно, воздух прозрачен и приятен, но у него есть масса, которая давит на поверхность земли. Это и есть атмосферное давление.

Нормальное атмосферное давление принято считать равным 101325 Па. Это давление на уровне мирового океана при температуре 0 градусов Цельсия. Такое же давление при этой же температуре оказывает на свое основание столб ртути высотой 766 миллиметров.

Чем больше высота над уровнем моря, тем ниже атмосферное давление. Например, на вершине горы Джомолунгма оно составляет всего одну четвертую от нормального атмосферного давления.

 

Эверест. На его вершине давление в 4 раза меньше, чем у подножия

 

Артериальное давление

Еще один пример, где мы сталкиваемся с давлением в повседневной жизни – это измерение кровяного давления.

Артериальное давление – это кровяное давление, т.е. давление, которое кровь оказывает на стенки сосудов, в данном случае – артерий.

Если вы измерили артериальное давление и оно у вас 120 на 80, то все хорошо. Если 90 на 50

или 240 на 180, то вам уже точно будет неинтересно разбираться, в чем это давление измеряется и что это вообще значит.

 

Артериальное давление – давление крови на стенки артерий

 

Тем не менее, возникает вопрос:  120 на 80 чего именно? Паскалей, миллиметров ртутного столба, атмосфер или еще каких-то единиц измерения?

Артериальное давление измеряется в миллиметрах ртутного столба. Оно определяет превышение давления жидкости в кровеносной системе над атмосферным давлением.

Кровь оказывает давление на сосуды и тем самым компенсирует действие атмосферного давления. Будь иначе, нас бы просто раздавило огромной массой воздуха над нами.

Но почему в измерении артериального давления две цифры?

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Дело в том, что кровь движется в сосудах не равномерно, а толчками. Первая цифра (120) называется систолическим давлением. Это давление на стенки сосудов в момент сокращения сердечной мышцы, его величина – наибольшая. Вторая цифра (80) определяет наименьшее значение и называется диастолическим давлением.

При измерении фиксируются значения систолического и диастолического давлений. Например, для здорового человека типичное значение артериального давления составляет 120 на 80 миллиметров ртутного столба.

Это означает, что систолическое давление равно 120 мм. рт. ст., а диастолическое – 80 мм рт. ст. Разница между систолическим и диастолическим давлениями называется пульсовым давлением.

Физический вакуум

Вакуум – это отсутствие давления. Точнее, практически полное его отсутствие. Абсолютный вакуум является приближением, как идеальный газ в термодинамике и материальная точка в механике.

В зависимости от концентрации вещества различают низкий, средний и высокий вакуум.  Наилучшее приближение к физическому вакууму – космическое пространство, в котором концентрация молекул и давление минимальны.

 

В космосе наблюдается почти полное отсутствие давления

 

Давление – основной термодинамический параметр состояния системы. Определить давление воздуха или другого газа можно не только по приборам, но и пользуясь уравнениями, формулами и законами термодинамики. А если у вас нет времени разбираться, студенческий сервис поможет решить любую задачу на определение давления.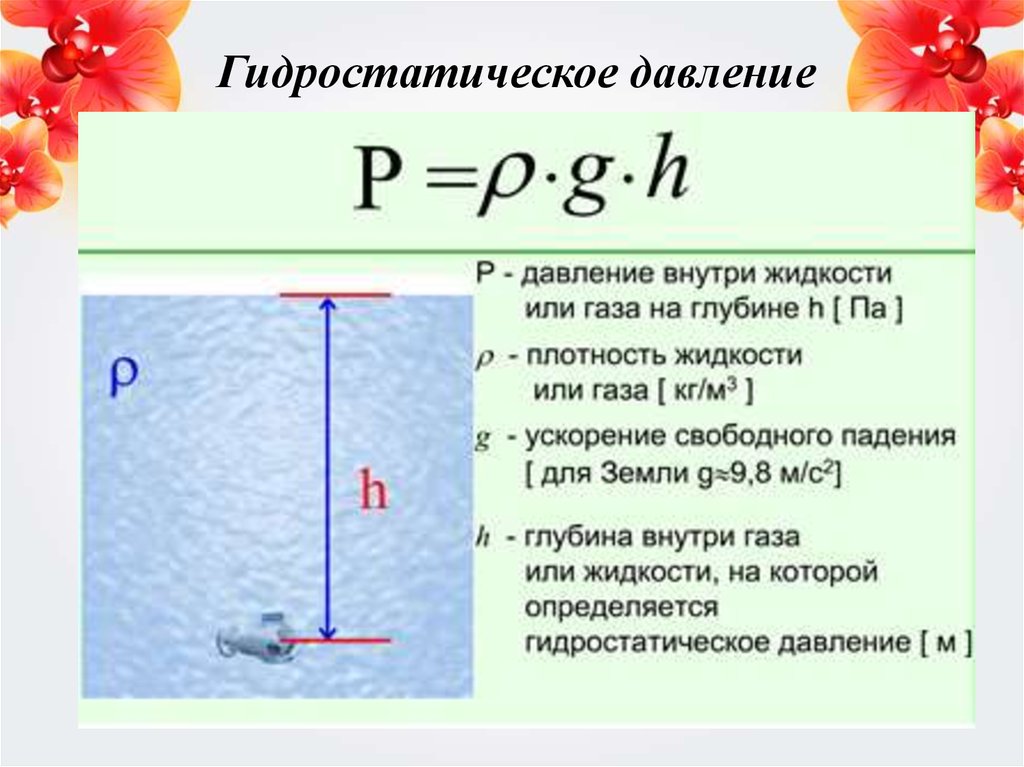

14.3: Жидкости, плотность и давление (часть 2)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

6553

• OpenStax
• OpenStax

Изменение давления с глубиной в жидкости постоянной плотности

Давление определяется для всех состояний вещества, но оно особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, приспосабливаясь к горизонтальной силе. Сила, приложенная перпендикулярно поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что в каждой точке внутри жидкости в направлении наружу возникает сила реакции, уравновешивающая силу, действующую на молекулы на границе.

Рассмотрим жидкость постоянной плотности, как показано на рисунке \(\PageIndex{1}\). Давление на дне контейнера обусловлено давлением атмосферы (p ₀ ) плюс давлением веса жидкости. Давление жидкости равно весу жидкости, деленному на площадь. Вес жидкости равен произведению ее массы на ускорение свободного падения.

Рисунок \(\PageIndex{1}\): Дно этого контейнера выдерживает весь вес жидкости в нем. Вертикальные стороны не могут воздействовать на жидкость восходящей силой (поскольку она не может противостоять сдвигающей силе), поэтому дно должно поддерживать все это.

Поскольку плотность постоянна, вес можно рассчитать, используя плотность:

\[w = mg = \rho Vg = \rho Ahg \ldotp\]

Таким образом, давление на дне сосуда равно атмосферному давление, добавленное к весу жидкости, деленному на площадь:

\[p = p_{0} + \frac{\rho Ahg}{A} = p_{0} + \rho hg \ldotp\]

Это уравнение подходит только для давления на глубине для жидкости с постоянной плотностью

Давление на глубине для жидкости с постоянной плотностью

Давление на глубине в жидкости постоянной плотности равно атмосферному давлению плюс давление, обусловленное весом жидкости, или

\[p = p_{0} + \rho hg, \label {14. 4}\]

Где p — давление на определенной глубине, p ₀ — атмосферное давление, \(\rho\) — плотность жидкости, g — ускорение свободного падения и h – глубина.

Рисунок \(\PageIndex{2}\): Плотина «Три ущелья», воздвигнутая на реке Янцзы в центральном Китае в 2008 г., создала массивное водохранилище, в котором оказались перемещены более миллиона человек. (кредит: «Le Grand Portage»/Flickr)

Пример 14.1: Какую силу должна выдерживать плотина?

Рассмотрим давление и силу, действующие на плотину, удерживающую резервуар с водой (рис. \(\PageIndex{2}\)). Предположим, что ширина плотины составляет 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? б) Рассчитайте силу, действующую на плотину.

Среднее давление p из-за веса воды равно давлению на средней глубине h, равной 40,0 м, поскольку давление увеличивается линейно с глубиной. Сила, действующая на плотину со стороны воды, равна среднему давлению, умноженному на площадь контакта, F = pA.

9{10}\; М \ldotp \end{split}$$

Значение

Хотя эта сила кажется большой, она мала по сравнению с 1,96 x 10 ¹³ Н веса воды в резервуаре. На самом деле это всего лишь 0,0800% веса.

Упражнение 14.1

Если водохранилище в примере \(\PageIndex{1}\) покрывает вдвое большую площадь, но остается на той же глубине, нужно ли перепроектировать плотину?

Давление в статической жидкости в однородном гравитационном поле

A статическая жидкость — это жидкость, которая не находится в движении. В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке будет реагировать на результирующую силу и ускоряться.

Давление в любой точке статической жидкости зависит только от глубины в этой точке. Как обсуждалось, давление в жидкости вблизи Земли меняется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности. Это разумное приближение для таких жидкостей, как вода, где требуются большие силы для сжатия жидкости или изменения объема. В плавательном бассейне, например, плотность приблизительно постоянна, и вода на дне очень мало сжимается под весом воды наверху. Однако путешествие в атмосферу — это совсем другая ситуация. Плотность воздуха начинает значительно меняться уже на небольшом расстоянии от поверхности Земли.

Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость с плотностью \(\rho\) на поверхности Земли, мы должны начать с предположения, что плотность жидкости непостоянна. Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, расположенная ближе к поверхности, из-за веса жидкости над ней. Следовательно, давление, рассчитанное на заданной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.

Представьте тонкий элемент жидкости на глубине h, как показано на рисунке \(\PageIndex{3}\). Пусть элемент имеет площадь поперечного сечения A и высоту \(\Delta\)y. Силы, действующие на элемент, обусловлены давлением p(y) над ним и p(y + \(\Delta\)y) под ним. Вес самого элемента также показан на диаграмме свободного тела.

Рисунок \(\PageIndex{3}\): Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.

Поскольку элемент жидкости между y и y + \(\Delta\)y не ускоряется, силы уравновешены. Используя декартову ось y, ориентированную вверх, мы находим следующее уравнение для y-компоненты:

\[p(y + \Delta y)A – p(y)A – g \Delta m = 0(\Delta y < 0) \ldotp \label{14.6}\]

Обратите внимание, что если элемент имеет ненулевую y-компоненту ускорения, правая часть не будет равна нулю, а вместо этого будет массой, умноженной на y-ускорение . Массу элемента можно записать через плотность жидкости и объем элементов:

\[\Delta m = |\rho A \Delta y| = – \rho A \Delta y \quad (\Delta y < 0) \ldotp\]

Поместив это выражение для \(\Delta\)m в уравнение \ref{14.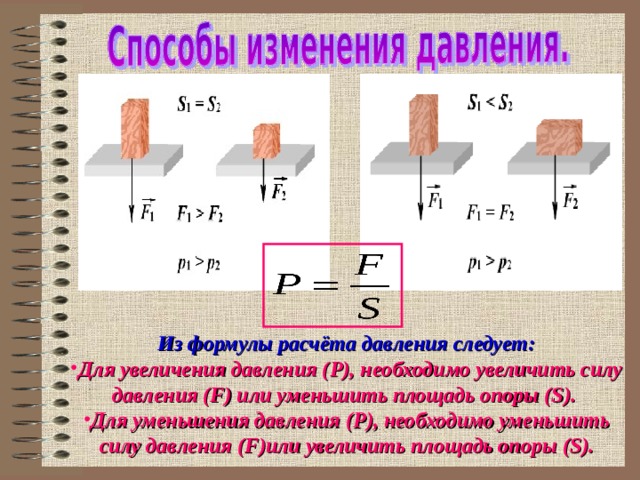 6}, а затем разделив обе части на A\( \Delta\)y, находим

\[\frac{p(y + \Delta y) – p(y)}{\Delta y} = – \rho g \ldotp \label{14.7}\]

Беря предел бесконечно малому элементу \(\Delta\)y → 0, мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:

\[\frac{dp}{dy} = – \rho g \ldotp \label{14.8}\]

Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, постоянна ли плотность \(\rho\) или изменяется с глубиной; то есть функция \(\rho\)(y).

Если диапазон анализируемых глубин не слишком велик, плотность можно считать постоянной. Но если диапазон глубин достаточно велик для заметного изменения плотности, как, например, в случае с атмосферой, плотность существенно меняется с глубиной. В этом случае мы не можем использовать приближение постоянной плотности. 9{-h} \rho gdy \\ p – p_{0} & = \rho gh \\ p & = p_{0} + \rho gh \ldotp \end{split} \label{14. 9}\]

Отсюда , давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс \(\rho\)gh, если плотность жидкости постоянна по высоте, как мы нашли ранее.

Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы сосуда. Таким образом, в сосуде, где жидкость может свободно перемещаться в различных частях, уровень жидкости во всех частях остается на одном уровне, независимо от формы, как показано на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Если жидкость может свободно течь между частями сосуда, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление на дне каждой колонны одинаково; если бы это было не то же самое, жидкость текла бы до тех пор, пока давления не сравнялись бы.

Изменение атмосферного давления с высотой

Изменение атмосферного давления с высотой представляет особый интерес. Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна. (Мы обсудим закон идеального газа в одной из последующих глав, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p(y) — атмосферное давление на высоте y. Плотность \(\rho\) в точке у, температура Т по шкале Кельвина (К) и масса m молекулы воздуха связаны с абсолютным давлением по закону идеального газа в виде0034

\[p = \rho \frac{k_{B} T}{m}\; (атмосфера), \label{14.10}\]

, где k _B — постоянная Больцмана, которая имеет значение 1,38 x 10 ⁻²³ Дж/К.

Возможно, вы встречали закон идеального газа в форме pV = nRT, где n — число молей, а R — газовая постоянная. Здесь тот же закон записан в другой форме, но с использованием плотности \(\rho\) вместо объема V. Следовательно, если давление p меняется с высотой, то меняется и плотность \(\rho\). Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как 9{- \alpha y} \ldotp\]

Таким образом, атмосферное давление падает экспоненциально с высотой, поскольку ось y направлена ​​вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря. Давление падает в \(\frac{1}{e}\), когда высота равна \(\frac{1}{\alpha}\), что дает нам физическую интерпретацию для \(\alpha\) : Константа \(\frac{1}{\alpha}\) представляет собой шкалу длины, которая характеризует изменение давления в зависимости от высоты и часто называется высотой шкалы давления. 9{-23}\; Дж/К) \times (300\; K)} = \frac{1}{8800\; m} \ldotp\]

Следовательно, на каждые 8800 метров атмосферное давление падает в 1/e раз, или примерно на треть своего значения. Это дает нам лишь приблизительную оценку фактической ситуации, поскольку мы предполагали постоянную температуру и постоянную g на столь больших расстояниях от Земли, и ни одно из этих утверждений в действительности не верно.

Направление давления в жидкости

Давление жидкости не имеет направления, поскольку является скалярной величиной, тогда как силы давления имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности. Причина в том, что жидкости не могут противостоять силам сдвига или оказывать на них силы сдвига. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление оказывается перпендикулярно поверхностям любого объекта в жидкости. На рисунке \(\PageIndex{5}\) показано давление, оказываемое воздухом на стенки шины и водой на тело пловца.

Рисунок \(\PageIndex{5}\): (a) Давление внутри этой шины действует перпендикулярно ко всем поверхностям, с которыми она контактирует. Стрелки представляют направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода потекла бы в пространство, которое он занимает, если бы его там не было. Стрелки представляют направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы внизу больше из-за большей глубины, что дает сеть вверх или выталкивающую силу. Суммарная вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.

---

Эта страница под названием 14.3: Fluids, Density, and Pressure (Part 2) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. плотность
   2. жидкости
   3. давление
   4. источник@https://openstax.