Лекция по высшей математике”Дифференциал функции”(для 26 гр.)
Дифференциал функции
Пусть функция дифференцируема на отрезке . Производная этой функции в некоторой точке отрезка определяется равенством: . Тогда, по теореме о связи функции, её предела и бесконечно малой функции, можно записать , где при , или .
Приращение функции состоит из двух слагаемых, из которых первое есть так называемая главная часть приращения, линейная относительно .
Дифференциалом функции в точке называется главная часть её приращения, которая равна произведению производной функции на приращение аргумента, и обозначается или : .
Дифференциал называют также дифференциалом первого порядка.
Дифференциал независимой переменной равен приращению этой переменной: и тогда , дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Пример 1. Найти дифференциал функции .
Решение: По формуле находим
.
Основные теоремы о дифференциалах. Таблица дифференциалов.
Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяется формулами:
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточной переменной на дифференциал этой промежуточной переменной.
Таблица дифференциалов
Применение дифференциала в приближенных вычислениях
.
Пример 2. Вычислить приближенно .
Решение. Рассмотрим функцию f(x)=arctg x.
По формуле имеем:,
т.е..Так как , то при и получаем:
Производные высших порядков.
Производная у’ = f ‘(х) функции у = f (x) есть также функция от х и называется производной первого порядка.
Если
функция f ‘(х) дифференцируема, то ее производная называется производной второго порядка и
обозначается у” (или f ¢¢(x), , , ).
Итак,
у” = (y¢ )¢.
Производная от производной второго порядка, если она существует, называется производной третьего порядка
Производной n -го порядка (или n -й производной) называется производная от производной
(n – 1) порядка: у(n) = (y(n – 1))¢ .
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (у V или у(5) – производная пятого порядка).
Пример . Найти производную 13-го порядка функции у = sin x
Решение: у’ = (sin x)¢ = cos x = , у” = (y¢)¢ = (cos x)¢ = – sin x = ,
у‘” = (y¢¢)¢ = (– sin x)¢ = – cos x = ,у(13) =
Механический смысл производной второго порядка
Вторая
производная от пути по времени есть величина ускорения прямолинейного движения
точки, т.
е. =
Дифференциалы высших порядков.
Определение. Дифференциал от дифференциала функции называется ее вторым дифференциалом или дифференциалом второго порядка. Обозначение: d²y=d(dy).
При вычислении второго дифференциала учтем, что dx не зависит от х и при дифференцировании выносится за знак производной как постоянный множитель.
Итак, d²y=d(dy)=d(f΄(x)dx)=(f΄(x)dx)΄dx=(f΄(x))΄(dx)²=f΄΄(x)dx².
Подобным же образом можно найти третий дифференциал от данной функции:
Определение. Дифференциалом n-го порядка называется первый дифференциал от дифференциала (n-1)-го порядка: dny = d(dn-1y) = (f(n-1)(x)dn-1x)΄ = f(n)(x)dnx.
Свойства дифференциалов высших порядков.
1. Производную любого порядка можно представить как отношение дифференциалов соответствующего порядка: .
2. Дифференциалы высших порядков не обладают свойством инвариантности.
Покажем это на примере второго дифференциала. Если y=F(φ(x))=F(u), где u=φ(x), то d²y=d(F΄(u)du). Но du=φ΄(x)dx зависит от х, поэтому d²y=d(F΄(u))du+Fu΄(u)d(du)=F΄΄uu(u)(du)²+Fu΄(u)
Возрастание и убывание функций
Напомним, что функция y = f (x) называется возрастающей
(убывающей) на промежутке Х, если для любых x1, x2 ∈ X и x2 > x1 верно
неравенство f (x2 ) > f (x1 ) ( f (x2 ) < f (x1 ) ).
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.
Возрастание и убывание функции характеризуется значением ее производной : если в некотором интервале >0, то функция возрастает, а если <0, то функция убывает в этом интервале.
Теорема (необходимое условие монотонности функции).
Определение. Точка х0 называется точкой максимума функции f (x) , если в некоторой окрестности точки х0 выполняется неравенство f
Определение. Точка х1 называется точкой минимума функции f (x) , если в некоторой окрестности точки х1 выполняется неравенство f (x) ≥ f (x1 ) (рис. 11).
Значение функции в точках х0 и х1 называются соответственно максимумом и минимумом функции. Мак-
симум и минимум функции объединяются общим названием экстремума функции
Необходимое условие экстремума . Для того чтобы функция y = f (x) имела экстремум в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю f ′(x0 ) = 0 или не существовала.
Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются критическими (или стационарными). Обращаем внимание на то, что эти точки должны входить в область определения функции.
Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая. Очень важно заметить, что обратное утверждение не верно. Критическая точка вовсе не обязательно будет точкой экстремума.
Правило исследования функции на экстремум.
Чтобы найти точки экстремума функции , в которых она непрерывна, нужно:
1.
Найти производную и
критические точки, в которых =0 или не существует, а сама функция непрерывна,
и которые лежат внутри области определения функции.
2а. Определить знак слева и справа от каждой критической точки.
Если при переходе аргумента х через критическую точку хо:
1) меняет знак с + на -, то хо есть точка максимума;
2) меняет знак с – на +, то хо есть точка минимума;
3) не меняет знака, то в точке хо нет экстремума.
Иногда проще исследовать критические точки, где , по знаку второй производной, – вместо правила 2а можно пользоваться следующим правилом:
2б. Найти вторую производную и определить ее знак в каждой критической точке.
Если в критической точке хо, где :
1) >0, то хо есть точка максимума;2) <0, то хо есть точка минимума;
3) =0, то вопрос о наличии экстремума в точке хо остается открытым. Такую критическую точку, как и всякую другую, можно исследовать по правилу 2а.
Далее
следует найти экстремумы функции, т.е. вычислить значения функции в найденных
точках экстремума.
Выпуклость функции. Точки перегиба
Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.
Точкой перегиба называется точка на кривой, где меняется направление ее выпуклости.
Направление выпуклости кривой характеризуется знаком второй производной : если в некотором интервале >0, то кривая выпукла вниз, а если <0, то кривая выпукла вверх в этом интервале.
Абсциссы точек перегиба кривой , или графика функции f(x), являются точками экстремума производной . Поэтому их можно найти по следующему правилу:
1. Найти и точки х, в которых =0 или не существует, а кривая непрерывна и которые лежат внутри области ее расположения.
2.
Определить знак слева и
справа от каждой из этих точек. Исследуемая точка х будет абсциссой точки
перегиба, если по разные стороны от нее имеет разные знаки.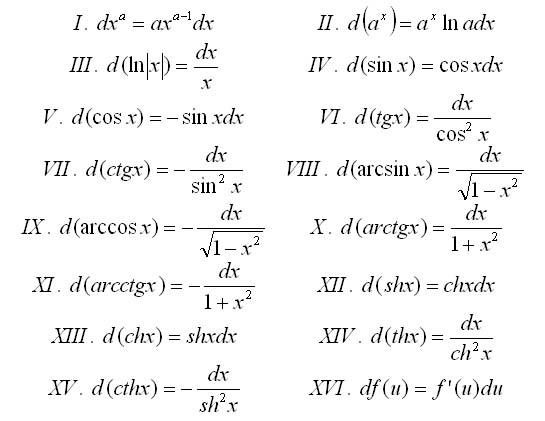
Интервалы, где кривая выпукла вверх и где она выпукла вниз, определяются из условия, что их границами могут быть только абсциссы точек перегиба, точки разрыва и граничные точки области расположения кривой.
Асимптоты
Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат.
Для нахождения асимптот пользуются следующими положениями:
а) если при х=а кривая имеет бесконечный разрыв, т.е. если при , то прямая х=а является вертикальной асимптотой;
б) если при существует конечный предел функции , т.е. , то прямая y=b горизонтальная асимптота графика функции ;
3) если существуют конечные пределы и , то прямая у = kx + b является наклонной асимптотой графика функции .
Правило исследования функции на экстремум с помощью второй производной:
1.Находят первую производную f ‘ (x).
2.Находят действительные корни уравнения f
‘(x)=0 (критические точки).
3.Находят вторую производную f ” (x).
4.Во вторую производную подставляют поочередно все критические значения; если при этой подстановке вторая производная окажется положительной, то в этой точке функция имеет минимум; если же вторая производная окажется отрицательной, то функция имеет максимум. Если при подстановке получится нуль, то исследование нужно продолжить с помощью первой производной.
Например 1. Исследовать на экстремум функцию у = 1/3х3 – 2х2 +3х + 1.
Решение:
1)Находим производную у’ = х2– 4х + 3;
2)Решаем уравнение х2– 4х + 3= 0, его корни х1 = 1, х2 = 3 – критические точки;
– |
| ||
|
| ||
1 | 3 | х |
|
3.
Определяя знак у’, находим экстремум; при х = 1функция
достигает максимума, а при х =3 функция достигает минимума.
4. Находим значение функции в точках экстремума у(1) =7/3, у(3) =1.
Например 2. Исследовать на экстремум с помощью второй производной функцию
у = 1/3х3 – 5/2 х2 + 6х.
Решение:
1.Находим производную у’ = х2– 5х + 6;
2.Решаем уравнение х2– 5х + 6 = 0, его корних1 = 2, х2 = 3 – критические точки;
3.Находим вторую производную у” = 2х – 5;
4.Во вторую производную подставляем поочередно критические значения:
у”(2)= 2∙2 – 5 = – 1< 0, при х1 = 2 имеем максимум, равный у(2) =14/3 ;
5.Т.к. у”(3)= 2∙3 – 5 = 1 > 0, то при х2 = 3 имеем минимум у(3) = 4,5 .
Задания для самостоятельной работы.
1. Найти производные второго порядка от функций: а) у = 3х4 +5х3 + 2х2 – х, б) у =(2х + 5)3.
2. Найти дифференциал второго порядка для функций: а) у = sin x∙ ln 3x, б) у = 6х +2,5х6
3. Дана функция f(x)= sin3х. Найти f “(- p/2 ), f “(0).
4. Дана функция f(x)= х∙ех. Найти f ‘”(-3), f ‘”(2), f ‘”(0).
5. Исследовать на экстремум функции: а)f(x)= 2х3 + 6х2– 18х + 120,б) у = 3х4 – 4х3.
6. Исследовать на выпуклость, вогнутость и точки перегиба функции:
а) у = х3 – 3х2 + 1, б) у = – х3 + 3х2.
7.
Найти промежутки выпуклости и вогнутости кривой у
= х4 – 2х3 + 36х2 – х + 7.
8. Найти интервалы выпуклости и точки перегиба графика функции y = x(x −1)3 .
4.20. Дифференциал функции
Понятие дифференциала функции тесно связано с понятием ее производной. Как и производная функции, дифференциал функции принадлежит к числу важнейших понятий математического анализа и введен в математику Ньютоном и Лейбницем параллельно с понятием производной.
Вспомним определение производной функции в некоторой фиксированной точке X (§ 1, формулы 1.5 и 1.6):
(5.1)
Здесь – приращение аргумента X, а – соответствующее приращение функции Y.
Будем считать, что данная функция дифференцируема в рассматриваемой фиксированной точке X. То есть будем считать, что производная в этой точке существует и конечна. Тогда, согласно (5.1),
при (5.2)
А это значит, что при малых значениях будем иметь:
(5.3)
Причем приближенные равенства (5.3) будут тем точнее, чем меньше (и соответственно чем меньше ).
А теперь будем считать приращение аргумента функции не просто малым, а Бесконечно малым, и назовем его Дифференциалом аргумента x. Введем (следуя Лейбницу) для него и специальное обозначение:
Dx – дифференциал аргумента X. (5.4)
Таким образом, Дифференциал Dx аргумента X – это бесконечно малое приращение этого аргумента. Конечно, только что введенное понятие дифференциала переменной X – математическая абстракция (она сродни диаметру точки или толщине линии). Но математика постоянно пользуется абстракциями, поэтому еще одна абстракция пугать нас не должна.
Если приращение аргумента X бесконечно мало (), то и приращение функции Y тоже будет бесконечно мало. Обозначим его символом Dy и будем называть Дифференциалом функции Y. Так как , то
– дифференциал функции Y. (5.5)
Если теперь в приближенных равенствах (5.3) заменить малые, но конечные и на бесконечно малые Dx и Dy, то эти равенства станут Точными.
(5.6)
Оба равенства (5.6) имеют важный смысл. Первое из них дает выражение производной функции Y через отношение дифференциалов Dy и Dx функции и аргумента. А второе дает выражение дифференциала функции Dy через производную функции и дифференциал аргумента Dx.
Кстати, если учесть, что , то последнее равенство (5.6) можно записать подробнее:
(5.7)
А если еще учесть исходное выражение (5.5) для дифференциала функции , то из последнего равенства получаем:
(5.8)
Равенство (5.8) позволяет записать значение функции в точке , бесконечно близкой к точке X, через значение функции и ее производной в самой точке X. Эта формула имеет большое теоретическое значение.
Если в равенстве (5.8) заменить бесконечно малое Dx на малое, но конечное , то вместо точного оно станет приближенным:
(5.9)
Равенство (5.9) называется Простейшим вариантом формулы Тейлора. Эта приближенная формула тем точнее, чем меньше .
Она используется для приближенного вычисления значения по значениям и . У формулы (5.9) имеется и ясный геометрический смысл – мы его укажем в следующем параграфе. Там же мы приведем и полный вариант формулы Тейлора.
В частности, применяя эту формулу для функций ; ; ; , и т. д., получим следующие интересные формулы для производства приближенных вычислений:
1) ; ( – в радианах) 2) ; (5.10)
3) ; ;
4) ; ;
В частности, используя последнюю формулу, получим:
.
Для сравнения: точное значение . То есть приближенное значение , полученное вручную, отличается от его точного значения лишь в четвертом знаке после запятой.
Вернемся все же к формулам (5.6) и (5.7), служащим для нахождения дифференциала функции . На базе этих формул можно установить следующие
| < Предыдущая | Следующая > |
|---|
многомерное исчисление – Что такое дифференциальная форма?
Прежде чем говорить о дифференциальных формах, нам нужно поговорить о многообразиях и векторных полях.
\infty(M)$, область значений которой равна $\mathbb R$, и которая удовлетворяет следующим трем свойствам: :
- $v(f+g)=v(f)+v(g)$
- $v(\лямбда f)=\лямбда v(f)$
- $v(fg)=v(f)g(x)+f(x)v(g)$
Где $f$ и $g$ — гладкие функции на $M$, а $\lambda$ — действительное число (обратите внимание на то, что похоже на правило произведения). Что это значит и как это связано с векторами, какими мы их привыкли видеть? Мы привыкли видеть векторы, определяемые набором компонентов. Но проблема в том, что эти координаты зависят от системы координат, которую мы выбираем для использования. Определение, которое я только что дал, не подходит. Но если вам нравятся координаты, не волнуйтесь; мы можем переходить между этими двумя определениями. Если ваши координаты $(x_1,\cdots,x_n)$ и ваш вектор, выраженный в евклидовых координатах в точке $x$, равен $v=(v_1,\cdots,v_n)$, мы можем записать вектор как объект форма, которую я определил выше, написав $$v=v_1\frac{\partial}{\partial x_1}+\cdots+v_n\frac{\partial}{\partial x_n}.
$$ Он может действовать на функцию $f $ дифференцированием: $$v(f)=v_1\frac{\partial f}{\partial x_1}(x)+\cdots+v_n\frac{\partial f}{\partial x_n}(x).$$ Легко заметить, что это удовлетворяет каждому из трех вышеперечисленных свойств. 9\infty(M)$ такое, что
- $X(f+g)=X(f)+X(g)$
- $Х(\лямбда f)=\лямбда X(f)$
- $X(fg)=X(f)g+fX(g)$
Если вам будет проще, то можно представить себе вектор как маленькую стрелку, касающуюся некоторой поверхности, а векторное поле — как набор таких стрелок, покрывающих многообразие. Это естественный образ для размышления, но на практике он оказывается довольно бесполезным. Но поскольку это «неформальная дискуссия», продолжайте.
Наконец мы готовы определить дифференциальную форму.
Дифференциальной $k$-формой на $n$-мерном гладком многообразии $M$ называется любая полилинейная функция $\omega$, принимающая на вход $k$ гладких векторных полей на $M$, $X_1,\cdots,X_k $ и выводит скалярную функцию на $M$ так, что $$\omega(X_1,\cdots,X_i,\cdots,X_j,\cdots,X_k)=-\omega(X_1,\cdots,X_j,\cdots,X_i ,\cdots,X_k).
$$ Последнее свойство называется антисимметрией .
Так что же стоит за таким объектом? Насколько мне известно, наиболее важным применением дифференциальных форм является интегрирование на многообразиях. Возможно, была какая-то другая причина для их первоначального открытия и определения, но это то, для чего они используются. Когда вы думаете об интеграции, вы думаете о вычислении площади и объема. В $n$-мерном многообразии мы можем захотеть измерить объем или площадь любого подмногообразия в $n$ с любой размерностью, меньшей или равной $n$. Учитывая систему координат на $M$, дифференциальная $k$-форма говорит нам, как измерить $k$-мерный объем в соответствии с этой системой координат. Предполагая, что вы прошли курс многомерного исчисления, вы, вероятно, помните изображение элемента объема со сферическими координатами.
Картинки, подобные этой, также дают нам некоторое представление о том, как работают дифференциальные формы. На рисунке отмечены бесконечно малые изменения в направлениях $\theta$, $\phi$ и $r$ и показано, как мы можем вычислить бесконечно малый объем, выметаемый этими изменениями.
Вместо этого мы могли бы рассмотреть три векторных поля, векторы которых в каждой точке касаются направлений $\theta$, $\phi$ и $r$ соответственно. Дифференциальная 3-форма объединила бы эти три векторных поля в один и тот же элемент объема.
Почему антисимметрия? Антисимметрия позволяет нам учитывать ориентации. Опять же, если вы изучали многомерное исчисление, вы знаете, что при интегрировании по поверхности в трехмерном пространстве обычно важно отметить, в каком направлении находятся векторы нормалей к поверхности. Но если наша поверхность находится в пространстве 4 или более измерений, в каждой точке нет уникального направления нормали, поэтому вместо этого мы используем порядок наших координат для определения ориентации. Если мы поменяем две координаты, мы поменяем ориентацию. Мы получим тот же результат от интегрирования, за исключением того, что знак будет обратным.
Надеюсь, я ответил на некоторые ваши вопросы.
Дифференциал – Математическая энциклопедия
Основная линейная часть приращения функции.
1) Действительнозначная функция $ f $ вещественной переменной $ x $ называется дифференцируемой в точке $ x $ если она определена в некоторой окрестности этой точки и существует число $ A $ так что приращение
$$ \Delta y = f ( x + \Delta x ) – f ( x) $$
можно записать(если точка $ x + \Delta x $ лежит в этой окрестности) в виде
$$ \Дельта у = А \Дельта х + \омега , $$
где $ \omega / \Delta x \rightarrow 0 $
как $ \Delta x \rightarrow 0 $.
Здесь $A\Deltax$
обычно обозначается $dy$
и называется дифференциалом $f$
в $х$.
Для заданного $ x $
дифференциал $dy$
пропорциональна $ \Delta x $,
т.е. является линейной функцией от $\Delta x $.
По определению при $ \Delta x \rightarrow 0 $
дополнительный член $ \omega $
бесконечно мала более высокого порядка, чем $ \Delta x $(
а также чем $dy$
если $A \neq 0 $).
Вот почему говорят, что дифференциал является основной частью приращения функции.
9{ \prime } ( x ) = dy / dx $,
т. е. производная равна отношению дифференциалов $dy$
и $дх$.
Если $A\neq0$,
тогда $ \Delta y / dy \rightarrow 1 $
как $ \Delta x \rightarrow 0 $,
т. е. если $ A \neq 0 $,
тогда $ \Delta y $
и $ды$
являются бесконечно малыми того же порядка, что и $ \Delta x \rightarrow 0 $;
этот факт, наряду с простой структурой дифференциала (т.е. линейностью по отношению к $\Delta x $),
часто используется в приближенных вычислениях, предполагая, что $ \Delta y \ приблизительно dy $
для малых $ \Delta x $.
Например, если требуется вычислить $ f ( x + \Delta x ) $
по известному $f(x)$
когда $ \Delta x $
мало, предполагается, что
9{ \prime } ( x _ {0} ) \Delta x $.
Правая часть представляет собой значение дифференциала функции $f$
в точке $ x _ {0} $
соответствующее значению $ \Delta x $
рассматривается. Таким образом, дифференциал идентичен соответствующему приращению ординаты касательной к кривой $ y = f ( x) $(
ср. отрезок $NT$
на рис. а). Здесь $\omega = \Delta y – dy$,
то есть значение $ | \омега | $
совпадает с длиной отрезка $TS$.
Рисунок: d031810a
2) Определения дифференцируемости и дифференциала легко распространяются на вещественнозначные функции от $ n $
реальные переменные.
Таким образом, в случае $ n = 2 $
говорят, что вещественнозначная функция дифференцируема в точке $(x,y)$
по обеим переменным $ x $
и $ у $
если она определена в некоторой окрестности этой точки и если ее полное приращение
$$ \Delta z = f (x + \Delta x, y + \Delta y) – f (x, y) $$ 9{2} } $; предполагается, что точка $ ( x + \Delta x , y + \Delta y ) $ принадлежит упомянутой выше окрестности (рис. б).
Рисунок: d031810b
Вводится обозначение
$$ d z = d f ( x , y ) = A \Delta x + B \Delta y; $$
$ дз $
называется полным дифференциалом или просто дифференциалом функции $f$
в точке $(x,y)$(
иногда добавляется фраза «по обеим переменным x и y»). Для заданной точки $(x,y)$
дифференциал $ dz $
является линейной функцией от $ \Delta x $
и $ \Delta y $;
разница $\alpha=\Delta z – dz$
бесконечно мала более высокого порядка, чем $\rho$.
В этом смысле $dz$
— главная линейная часть приращения $\Delta z$.
9{ \prime } ( x , y ) dy $
является частным дифференциалом по $y$.
{ \prime } $
непрерывны или б) $A$
и $В$
всюду дифференцируемы в $D$
по обеим переменным $ x $
и $y$[7], [8].
См. также Дифференциальное исчисление для дифференциалов вещественных функций одной или нескольких действительных переменных и для дифференциалов высших порядков.
3) Пусть функция $f$ быть определено на некотором множестве $ E $ действительных чисел, пусть $ x $ — предельная точка этого множества, пусть $x\inE$, $ x + \Delta x \in E $, $ \Delta y = A \Delta x + \alpha $, где $ \alpha / \Delta x \rightarrow 0 $ если $ \Delta x \rightarrow 0 $; то функция $f$ называется дифференцируемым по множеству $E$ в $х$, а $ dy = A \Delta x $ называется его дифференциалом по множеству $ E $ в $х$. Это обобщение дифференциала действительнозначной функции одной действительной переменной. К специальным видам этого обобщения относятся дифференциалы в концах интервала, внутри которого функция определена, и аппроксимативный дифференциал (ср. Приближенная дифференцируемость).
Аналогичным образом вводятся дифференциалы по множеству для вещественнозначных функций нескольких действительных переменных.
4) Все определения дифференцируемости и дифференциала, данные выше, почти без изменений могут быть распространены на комплекснозначные функции одной или нескольких действительных переменных; к вещественнозначным и комплекснозначным вектор-функциям одной или нескольких действительных переменных; и к комплексным функциям и вектор-функциям одной или нескольких комплексных переменных. В функциональном анализе они распространяются на функции точек абстрактного пространства. Можно говорить о дифференцируемости и о дифференциале функции множества по некоторой мере.
Ссылки
| [1] | Г.П. Толстов, “Элементы математического анализа”, 1–2 , Москва (1974) (на русском языке) Fichtenholz, “Differential und Integralrechnung”, 1 , Deutsch. Verlag Wissenschaft. (1964 г.)0167 |
| [3] | L.D. Kudryavtsev, “Mathematical analysis” , 1 , Moscow (1973) (In Russian) MR1617334 MR1070567 MR1070566 MR1070565 MR0866891 MR0767983 MR0767982 MR0628614 MR0619214 Zbl 1080. 00002 Zbl 1080.00001 Zbl 1060.26002 Zbl 0869.00003 Zbl 0696.26002 Zbl 0703.26001 Zbl 0609.00001 Zbl 0632.26001 Zbl 0485.26002 Zbl 0485.26001 |
| [4] | С.М. Никольский, “Курс математического анализа”, 1 , МИР (1977) (Translated from Russian) Zbl 0397.00003 Zbl 0384.00004 |
| [5] | W. Rudin, “Principles of mathematical analysis” , McGraw-Hill (1953) MR0055409 Zbl 0052.05301 |
| [6] | A.N. Колмогоров, С.В. Фомин, “Элементы теории функций и функционального анализа”, 1–2 , Graylock (1957–1961) (Перевод с русского)6 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
| [7] | G.P. Толстов, “О криволинейных и повторных интегралах”, , Тр. Инст. Стеклов. , 35 (1950) (на русском языке) MR44612 |
| [8] | Г. П. Толстов, «О полном дифференциале», УМН. наук , 3 : 5 (1948) стр. 167–170 MR0027044 |
Комментарии
См. также Дифференциация; Дифференциация отображения.
Для дифференциации функций набора см. Установить функцию; Теорема Радона–Никодима, [a7].
Для обобщения функций между абстрактными пространствами см. также производную Фреше; Производная Гато.
Для производной функции $ f : \mathbf C \rightarrow \mathbf C $ см. Аналитическая функция.
Каталожные номера
| [a1] | Т.М. Apostol, “Calculus” , 1–2 , Blaisdell (1964) MR1908007 MR1182316 MR1182315 MR0595410 MR1536963 MR1535772 MR0271732 MR0248290 MR0247001 MR0261376 MR0250092 MR0236734 MR0236733 MR0214705 MR1532185 MR1531712 MR0087718 Zbl 0123.25902 |
| [a2] | T.M. Апостол, “Математический анализ”, Addison-Wesley (1974) MR0344384 Zbl 0309.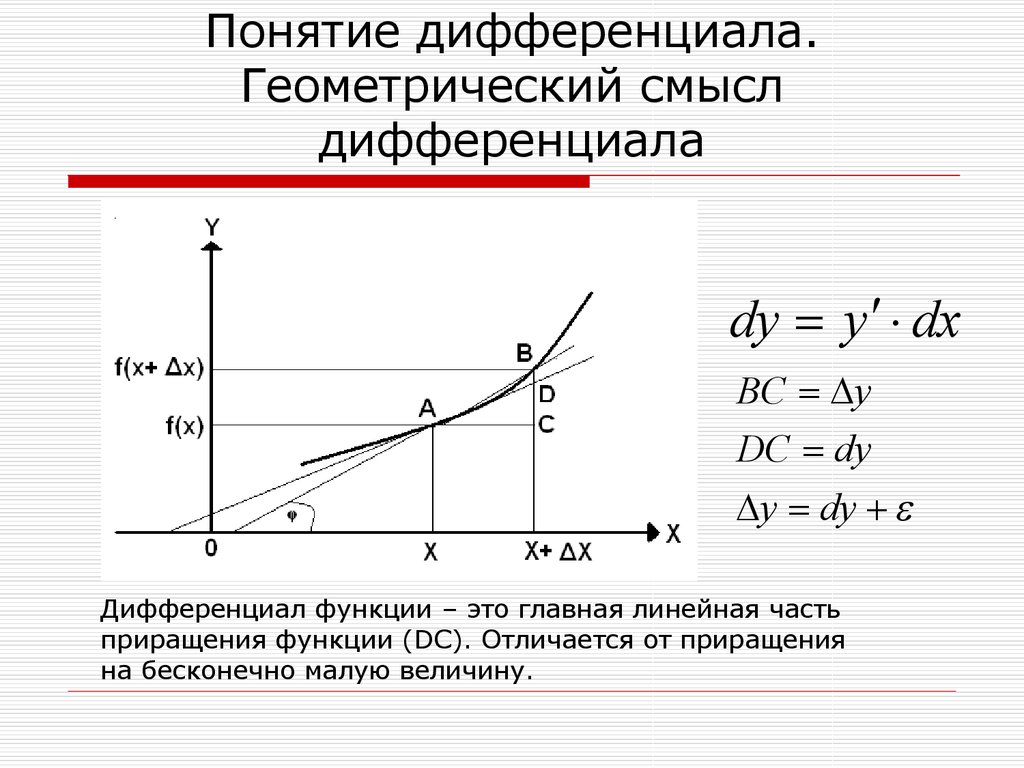 |