Квадратная матрица | это… Что такое Квадратная матрица?
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.
Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.
Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).
Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.
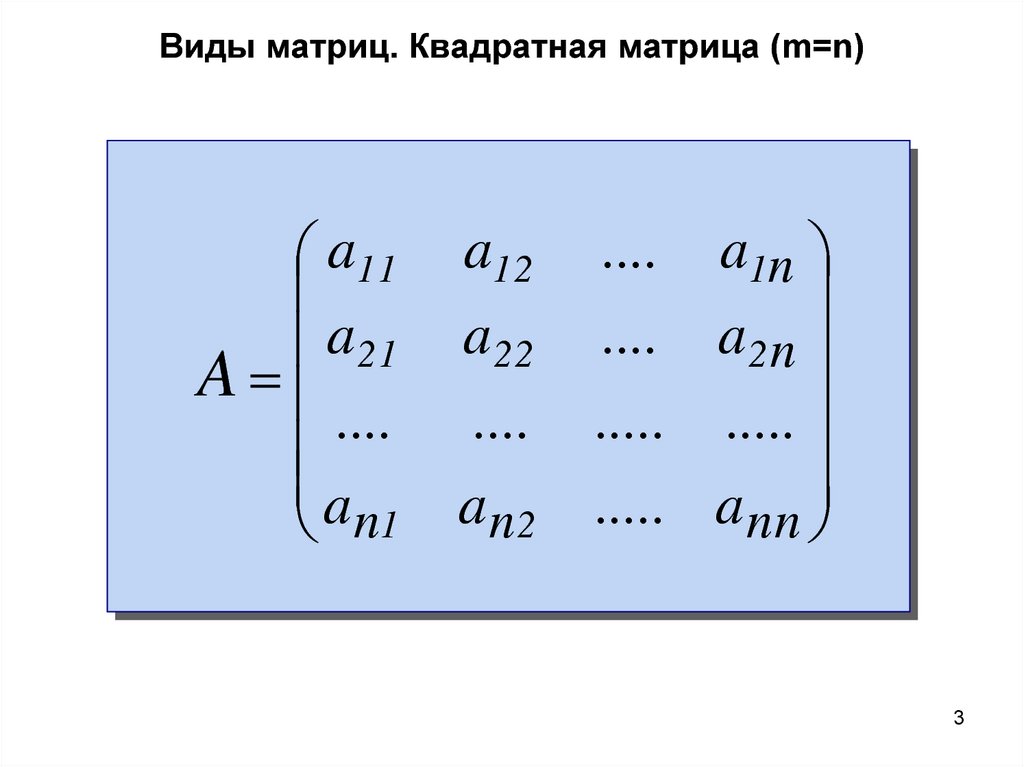
У каждого элемента матрицы есть 2 нижних индекса (aij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.
Содержание
|
История
Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.
Матрица как запись коэффициентов системы линейных уравнений
Систему из m уравнений с n неизвестными
можно представить в матричном виде
и тогда всю систему можно записать так:
- AX = B,
где A имеет смысл таблицы коэффициентов aij системы уравнений.
Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A – 1, поскольку умножив обе части уравнения на эту матрицу слева
- A – 1AX = A – 1
A − 1A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений
- X = A – 1B.
Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.
Операции над матрицами
Пусть aij — элементы матрицы A, а bij — элементы матрицы B.
Линейные операции:
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы
- bij = λaij
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
- cij = aij + bij
Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой
- cij = aij – bij
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть
- A + Θ = A
Все элементы нулевой матрицы равны нулю.
Нелинейные операции:
Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
| cij = | ∑ | aikbkj |
| k |
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.
Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.
Возводить в степень можно только квадратные матрицы.
Транспонирование матрицы (обозначение: AT) — операция, при которой матрица отражается относительно главной диагонали, то есть
Если A — матрица размера , то AT — матрица размера
Квадратная матрица и смежные определения
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно
- EA = AE = A
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A – 1 такова, что если умножить матрицу на неё, то получится единичная матрица:
- AA − 1 = E
Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.
Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.
Свойства матриц
- A + (B + C) = (A + B) + C
- A + B = B + A
- A(BC) = (AB)C
- A(B + C) = AB + AC
- (B + C)A =
- (AT)T = A
- (A * B)T = BT * AT
Элементарные преобразования матриц
Основная статья: Элементарные преобразования матрицы
Элементарными преобразованиями строк матрицы называются следующие преобразования:
- Умножение строки на число отличное от нуля
- Прибавление одной строки к другой строке
Элементарные преобразование столбцов матрицы определяются аналогично.
Типы матриц
- Антиперестановочная: AB = − BA
- Единичная
- Блочно-диагональная
- Ганкелева
- Верхнетреугольная
- Вырожденная
- Диагональная
- Трёхдиагональная
- Заполненная — в вычислительной математике матрица, которая практически не содержит нулей. Такую матрицу приходится хранить в памяти целиком. Антоним: разреженная.
- Квадратной называют матрицу, количество строк в которой равно количеству столбцов. Для квадратных матриц существует определитель.
- Кососимметрическая
- Нижнетреугольная
- Нулевая
- Ортогональная
- Перестановочная: AB = BA
- Разреженная — в вычислительной математике матрица, содержащая много нулей. Организовав подходящую структуру данных, вычисления с разреженными матрицами можно проводить очень быстро.
 Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.
Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная. - Симметричная
- Симметричная матрица A положительно определена (A > 0), если значения у всех ее главных угловых миноров Ak > 0
- Симметричная матрица
- Теплицева
- Треугольная
- Эрмитова
- Циркулянт
- Унитарная
- Унимодулярная
Матрица линейного оператора
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис . Пусть — произвольный вектор. Тогда его можно разложить по этому базису:
- ,
где xk — координаты вектора в выбранном базисе.
Здесь и далее предполагается суммирование по немым индексам.
Пусть — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим
- .
Вектора также разложим в выбранном базисе, получим
- ,
где — j-я координата k-го вектора из .
Подставим разложение в предыдущую формулу, получим
- .
Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец xk даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.
См. также
- Норма матрицы
- Определитель матрицы
- Массив — тип данных в программировании, соответствующий многомерной матрице.
- Разрежённый массив — компьютерная форма представления матриц со множеством нулей.
- Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.
Литература
- Дж. Голуб, Ч.Ван Лоун Матричные вычисления. — М.: Мир, 1999 (djvu).
- Беллман Р. Введение в теорию матриц. — М.: Мир, 1969 (djvu).
- Гантмахер Ф. Р. Теория матриц (2-е издание). — М.: Наука, 1966 (djvu).
- Ланкастер П. Теория матриц. — М.: Наука, 1973 (djvu).
- Соколов Н. П. Пространственные матрицы и их приложения. — М.: ГИФМЛ, 1960 (djvu).
Ссылки
- Операции над матрицами онлайн
Квадратная матрица | это… Что такое Квадратная матрица?
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др. ) между ним и другими подобными объектами.
) между ним и другими подобными объектами.
Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.
Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями «||…||»).
Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.
У каждого элемента матрицы есть 2 нижних индекса (aij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов.
Содержание
|
История
Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.
Матрица как запись коэффициентов системы линейных уравнений
Систему из m уравнений с n неизвестными
можно представить в матричном виде
и тогда всю систему можно записать так:
- AX = B,
где A имеет смысл таблицы коэффициентов aij системы уравнений.
Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A – 1, поскольку умножив обе части уравнения на эту матрицу слева
- A – 1AX = A – 1B
A − 1A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений
И это даёт возможность получить столбец корней уравнений
- X = A – 1B.
Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.
Операции над матрицами
Пусть aij — элементы матрицы A, а bij — элементы матрицы B.
Линейные операции:
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен
- bij = λaij
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
- cij = aij + bij
Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой
- cij = aij – bij
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть
- A + Θ = A
Все элементы нулевой матрицы равны нулю.
Нелинейные операции:
Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
| cij = | ∑ | aikbkj |
| k |
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.
Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.
Возводить в степень можно только квадратные матрицы.
Транспонирование матрицы (обозначение: AT) — операция, при которой матрица отражается относительно главной диагонали, то есть
Если A — матрица размера , то AT — матрица размера
Квадратная матрица и смежные определения
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно
- EA = AE = A
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A – 1 такова, что если умножить матрицу на неё, то получится единичная матрица:
- AA − 1 = E
Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.
Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.
Свойства матриц
- A + (B + C) = (A + B) + C
- A + B = B + A
- A(BC) = (AB)C
- A(B + C) = AB + AC
- (B + C)A = BA + CA
- (AT)T = A
- (A * B)T = BT * AT
Элементарные преобразования матриц
Основная статья: Элементарные преобразования матрицы
Элементарными преобразованиями строк матрицы называются следующие преобразования:
- Умножение строки на число отличное от нуля
- Прибавление одной строки к другой строке
Элементарные преобразование столбцов матрицы определяются аналогично.
Типы матриц
- Антиперестановочная: AB = − BA
- Единичная
- Блочно-диагональная
- Ганкелева
- Верхнетреугольная
- Вырожденная
- Диагональная
- Трёхдиагональная
- Заполненная — в вычислительной математике матрица, которая практически не содержит нулей. Такую матрицу приходится хранить в памяти целиком. Антоним: разреженная.
- Квадратной называют матрицу, количество строк в которой равно количеству столбцов. Для квадратных матриц существует определитель.
- Кососимметрическая
- Нижнетреугольная
- Нормальная
- Нулевая
- Ортогональная
- Перестановочная: AB = BA
- Разреженная — в вычислительной математике матрица, содержащая много нулей. Организовав подходящую структуру данных, вычисления с разреженными матрицами можно проводить очень быстро.
 Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.
Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная. - Симметричная
- Симметричная матрица A положительно определена (A > 0), если значения у всех ее главных угловых миноров Ak > 0
- Симметричная матрица A отрицательно определена (A < 0), если матрица ( − A) положительно определена, то есть если для любого k главный минор k-го порядка Ak имеет знак ( − 1)k
- Теплицева
- Треугольная
- Эрмитова
- Циркулянт
- Унитарная
- Унимодулярная
Матрица линейного оператора
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.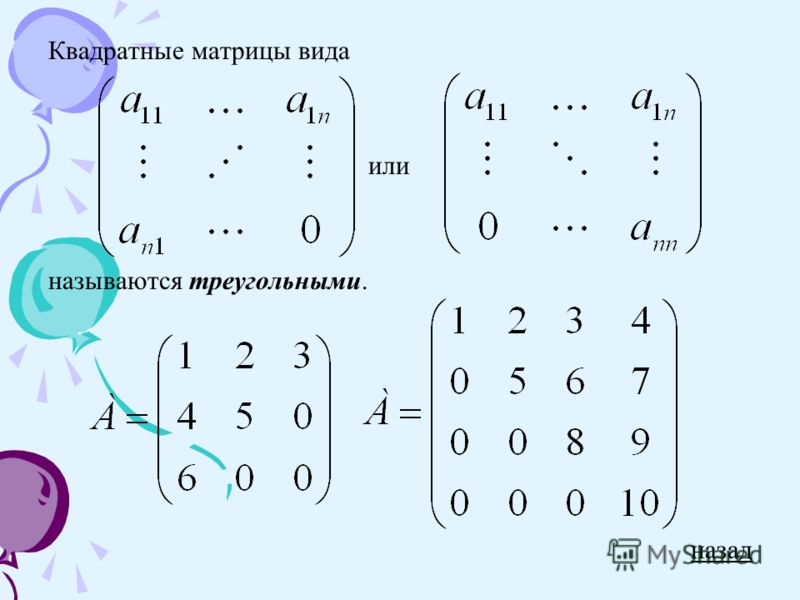
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис . Пусть — произвольный вектор. Тогда его можно разложить по этому базису:
- ,
где xk — координаты вектора в выбранном базисе.
Здесь и далее предполагается суммирование по немым индексам.
Пусть — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим
- .
Вектора также разложим в выбранном базисе, получим
- ,
где — j-я координата k-го вектора из .
Подставим разложение в предыдущую формулу, получим
- .
Выражение , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица при умножении на столбец xk даёт в результате координаты вектора , возникшего от действия оператора на вектор , что и требовалось получить.
См. также
- Норма матрицы
- Определитель матрицы
- Массив — тип данных в программировании, соответствующий многомерной матрице.
- Разрежённый массив — компьютерная форма представления матриц со множеством нулей.
- Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.
Литература
- Дж. Голуб, Ч.Ван Лоун Матричные вычисления. — М.: Мир, 1999 (djvu).
- Беллман Р. Введение в теорию матриц. — М.: Мир, 1969 (djvu).
- Гантмахер Ф. Р. Теория матриц (2-е издание). — М.: Наука, 1966 (djvu).
- Ланкастер П. Теория матриц. — М.: Наука, 1973 (djvu).
- Соколов Н. П. Пространственные матрицы и их приложения. — М.: ГИФМЛ, 1960 (djvu).
Ссылки
- Операции над матрицами онлайн
Квадратная матрица – определение, примеры, операции
Квадратная матрица является важным форматом матрицы и имеет идеальное квадратное число элементов. В нем одинаковое количество строк и столбцов, поэтому его порядок имеет вид n × n. Все матричные операции транспонирования, определителя, сопряжения, инверсии и математические операции над матрицами применимы и к квадратной матрице.
В нем одинаковое количество строк и столбцов, поэтому его порядок имеет вид n × n. Все матричные операции транспонирования, определителя, сопряжения, инверсии и математические операции над матрицами применимы и к квадратной матрице.
Квадратная матрица имеет особое применение при решении квадратных уравнений с двумя переменными. Здесь мы изучим различные свойства квадратной матрицы и попытаемся понять, как выполнять математические операции над этими матрицами.
| 1. | Что такое квадратная матрица? |
| 2. | Транспонирование квадратной матрицы |
| 3. | Определитель квадратной матрицы |
| 4. | Обратная квадратная матрица |
| 5. | Операции с матрицами |
| 6. | Важные термины, относящиеся к квадратной матрице |
| 7. | Примеры на квадратной матрице |
8. | Практические вопросы |
| 9. | Часто задаваемые вопросы о квадратной матрице |
Что такое квадратная матрица?
Квадратная матрица — это матрица с равным количеством строк и столбцов. Его порядок имеет вид n x n. Кроме того, произведение этих строк и столбцов дает количество элементов в квадратной матрице. Следовательно, количество элементов в нем всегда является совершенным квадратным числом. Типичная квадратная матрица выглядит следующим образом.
\(A_{n,n} = \begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{ 2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\)
Вот несколько примеров квадратных матриц .
- \(\left(\begin{массив}{ll}
-1&2\\
3 и 4
\end{array}\right)\) — квадратная матрица порядка 2×2 (или просто порядка 2).
Он имеет 2×2 = 4 элемента. - \(\ влево(\begin{массив}{ccc}
3&-6&2\
2 и 3 и 6 \
6 и 2 и -3
\end{array}\right)\) — квадратная матрица порядка 3×3 (или просто порядка 3).
Он имеет 3×3 = 9 элементов.
Транспонирование квадратной матрицы
Матрица, полученная преобразованием строк в столбцы и столбцов в строки, называется транспонированием данной матрицы. Как правило, порядок матрицы изменяется при преобразовании ее в транспонированную. Для матрицы порядка m × n транспонирование матрицы имеет порядок n × m. Здесь для квадратной матрицы транспонированная матрица имеет тот же порядок, что и данная матрица.
A = \(\begin{pmatrix}a & b & c\\d&e&f\\g&h&i\end{pmatrix}\) A T = \(\begin{pmatrix}a & d & g\\b&e&h\\c&f&i \end{pmatrix}\)
Попробуем разобраться в двух важных терминах, связанных с транспонированием матрицы. Квадратная матрица, транспонирование которой равно данной матрице, называется симметричной матрицей. Квадратная матрица, транспонирование которой равно отрицательному значению данной матрицы, называется кососимметричной матрицей.
Симметричная матрица: A T = A
Кососимметричная матрица: A T = -A
Определитель квадратной матрицы
Определитель квадратной матрицы представляет собой одно числовое значение или суммарное значение, представляющее весь набор элементов матрицы. Определитель матрицы порядка 2 × 2 можно легко вычислить по формуле. Определитель матрицы порядка 2 × 2 равен разности произведения диагональных элементов матрицы. Это можно наблюдать в приведенной ниже работе.
Определитель матрицы порядка 2 × 2 можно легко вычислить по формуле. Определитель матрицы порядка 2 × 2 равен разности произведения диагональных элементов матрицы. Это можно наблюдать в приведенной ниже работе.
A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\)
|A| = ad – bc
Кроме того, давайте проверим несколько матриц, которые были названы на основе значений их определителей. Матрица, определитель которой равен нулю, называется сингулярной матрицей (|A| = 0). Для сингулярной матрицы обратной матрицы не существует. А матрица, значение определителя которой не равно нулю, называется невырожденной матрицей (|A| ≠ 0).
Обратная квадратная матрица
Обратная квадратная матрица используется для деления одной матрицы на другую матрицу. Чтобы найти обратную матрицу, нужно сначала найти определитель матрицы. Затем вычисляется сопряжение квадратной матрицы. Наконец, обратное получается путем деления присоединенной матрицы на определитель квадратной матрицы.
A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) A -1 = \(\dfrac{1}{|A|}.Adj A\) = \ (\frac{1}{ad – bc}\begin{pmatrix}d &-b\\\\-c&a\end{pmatrix}\)
Попробуем рассмотреть важный термин, относящийся к обратной матрице. Квадратная матрица называется ортогональной матрицей, если ее выворот равен обратному.
Ортогональная матрица: A T = A -1
Матричные операции с квадратной матрицей
Математические операции сложения, вычитания и умножения также можно выполнять над двумя квадратными матрицами. Для сложения или вычитания соответствующие элементы добавляются для получения результирующей матрицы. Сложение матриц следует коммутативному свойству (A + B = B + A).
A + B = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) + \(\begin{pmatrix}1 &2\\\\3&4\end{pmatrix }\) = \(\begin{pmatrix}a \pm1 &b \pm2\\\\c \pm3&d \pm4\end{pmatrix}\)
Умножение матричного скаляра очень просто. Для умножения квадратной матрицы на константу каждый элемент матрицы умножается на константу.
Для умножения квадратной матрицы на константу каждый элемент матрицы умножается на константу.
kA = k\(\begin{pmatrix}a &b \\\\c &d \end{pmatrix}\) = \(\begin{pmatrix}ka &kb \\\\kc &kd \end{pmatrix}\)
Умножение двух квадратных матриц включает в себя последовательность шагов. Рассмотрим две квадратные матрицы порядка 2 × 2. Здесь мы рассматриваем элементы строки в первой матрице и элементы столбца во второй матрице. Следующие расчеты показывают последовательность вычислений, связанных с процессом умножения матриц.
Важные термины, относящиеся к квадратной матрице
Давайте проверим несколько важных терминов, относящихся к квадратной матрице, которые помогут нам глубже понять концепцию квадратной матрицы.
- Порядок матрицы: это произведение строк и столбцов в матрице. Квадратная матрица имеет равное количество строк и столбцов и имеет порядок n × n.
- След матрицы: равен сумме диагональных элементов квадратной матрицы.

- Матрица идентичности: это квадратная матрица с единицами в качестве диагональных элементов, а все остальные элементы – нули.
- Скалярная матрица: Квадратная матрица, имеющая то же число, что и все ее диагональные элементы, а все остальные элементы равны нулю.
- Симметричная матрица: Матрица, транспонирование которой равно данной матрице, называется симметричной матрицей.
- Кососимметричная матрица: Матрица, транспонирование которой равно отрицательному значению той же матрицы, называется кососимметричной матрицей.
- Ортогональная матрица: Матрица называется ортогональной, если обратная матрица равна транспонированной матрице.
☛ Похожие темы:
- Калькулятор сложения матриц
- Умножение матриц
- Матричная формула
Часто задаваемые вопросы о квадратной матрице
Что такое определение квадратной матрицы?
Квадратная матрица — это матрица, в которой количество строк равно количеству столбцов. Например, матрицы порядка 2×2, 3×3, 4×4 и т. д. являются квадратными матрицами. Матрицы порядка 2×3, 3×2, 4×5 и т. д. НЕ являются квадратными матрицами (это прямоугольные матрицы).
Например, матрицы порядка 2×2, 3×3, 4×4 и т. д. являются квадратными матрицами. Матрицы порядка 2×3, 3×2, 4×5 и т. д. НЕ являются квадратными матрицами (это прямоугольные матрицы).
Как найти обратную квадратную матрицу?
Обратная квадратная матрица получается после нахождения определителя и сопряженной матрицы данной матрицы. Для матрицы A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) ее определитель равен |A| = ad – bc и Adj A =\( \begin{pmatrix}d &-b\\\\-c&a\end{pmatrix}\). Комбинируя эти два понятия, матрица, обратная A -1 = \(\dfrac{1}{|A|}.Adj A\) = \(\frac{1}{ad – bc}\begin{ pmatrix}d &-b\\\\-c&a\end{pmatrix}\). Обратная матрица возможна только для невырожденных матриц. Несингулярная матрица — это матрица, определитель которой не равен нулю |A| ≠ 0,
Как определить, обратима ли квадратная матрица?
Квадратная матрица обратима, только если определитель матрицы не равен нулю |A| ≠ 0. Для матрицы A = \(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) ее определитель равен |A| = объявление – до н.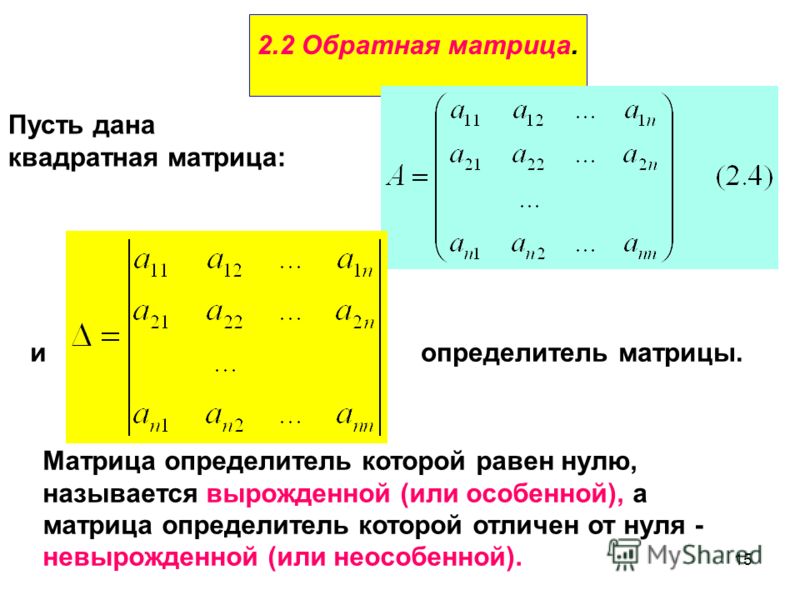 э. Для матриц, имеющих |A| = 0, обратного ему не существует.
э. Для матриц, имеющих |A| = 0, обратного ему не существует.
Как умножать квадратные матрицы?
Две квадратные матрицы можно перемножить, если обе матрицы одного порядка. Рассматриваются строки первой матрицы и рассматриваются столбцы второй матрицы для умножения.
Как найти определитель квадратной матрицы?
Определитель квадратной матрицы порядка 2 × 2 равен разности произведения элементов первой диагонали и второй диагонали. Для матрицы A = \(\begin{pmatrix}a &b\\ \\c&d\end{pmatrix}\). его определитель равен |A| = объявление – до н.э.
Что такое матрица магического квадрата?
Матрица магического квадрата — это квадратная матрица, имеющая нечетное количество строк и столбцов (n), так что сумма элементов в каждой строке, столбце или диагонали равна. Эта сумма элементов равна n(n 2 + 1)/2.
Каков порядок квадратной матрицы?
Квадратная матрица имеет порядок n × n и имеет одинаковое количество строк и столбцов. Количество элементов в квадратной матрице можно вычислить по ее порядку и оно равно числу квадратов n 2 .
Количество элементов в квадратной матрице можно вычислить по ее порядку и оно равно числу квадратов n 2 .
Что такое транспонирование квадратной матрицы?
Транспонирование квадратной матрицы получается путем записи элементов строки данной матрицы в виде элементов столбца. Для матрицы A = \(\begin{pmatrix}a & b & c\\c&e&f\\g&h&i\end{pmatrix}\) ее транспонирование равно A T = \(\begin{pmatrix}a & d & g\\b&e&h\\c&f&i\end{pmatrix}\). Элементы первой строки данной матрицы были записаны в первый столбец, а элементы второй строки матрицы были записаны во второй столбец, чтобы получить транспонированную матрицу.
Что такое невырожденная квадратная матрица?
Несингулярная матрица имеет ненулевое значение определителя (|A| ≠ 0. Для матрицы A =\(\begin{pmatrix}a &b\\\\c&d\end{pmatrix}\) Условие для того, чтобы это была невырожденная матрица, таково: ad – bc ≠ 0. Обратная заданная квадратная матрица существует только в том случае, если это невырожденная матрица. 0003
0003
Квадратная матрица — определение, операции, свойства и примеры
Матрица определяется как прямоугольный массив чисел, расположенных в строках и столбцах. Размер матрицы можно определить по количеству строк и столбцов в ней. Говорят, что матрица представляет собой матрицу «m на n», если она имеет «m» строк и «n» столбцов и записана как матрица «m × n». Например, если порядок матрицы «4 × 3», то она имеет четыре строки и три столбца. У нас есть различные типы матриц, такие как прямоугольные матрицы, квадратные матрицы, треугольные матрицы, симметричные матрицы и т. д.
Что такое квадратная матрица?
Квадратная матрица определяется как матрица, имеющая одинаковое количество строк и столбцов. Порядок квадратной матрицы, которая имеет «n» строк и «n» столбцов, равен «n × n». Количество элементов в матрице можно определить произведением количества строк и столбцов в матрице. Таким образом, количество элементов в квадратной матрице всегда является совершенным квадратным числом. Если сложить или перемножить любые две квадратные матрицы одного порядка, порядок результирующей матрицы останется прежним.
Если сложить или перемножить любые две квадратные матрицы одного порядка, порядок результирующей матрицы останется прежним.
Примеры квадратной матрицы
Ниже приведены некоторые распространенные примеры квадратных матриц разного порядка:
- Следующая матрица является квадратной матрицей порядка «2 × 2», т. е. данная матрица имеет две строки и две строки. столбцы.
- Следующая матрица представляет собой квадратную матрицу порядка «3 × 3», т. е. данная матрица имеет три строки и три столбца.
- Следующая матрица представляет собой квадратную матрицу порядка «n × n», т. е. данная матрица имеет «n» строк и «n» столбцов.
Свойства квадратной матрицы
Ниже приведены некоторые важные свойства квадратной матрицы:
- В каждой квадратной матрице количество строк и столбцов одинаково.
- Сумма всех элементов главной диагонали в квадратной матрице определяется как след матрицы.

- Значение определителя можно определить только для квадратных матриц.
- Если определитель квадратной матрицы равен нулю, то матрица называется вырожденной, а невырожденной, если ее определитель не равен нулю.
- Если главные диагональные элементы квадратной матрицы – единицы, а остальные элементы – нули, то матрица называется единичной.
- Порядок квадратной матрицы и ее транспонирования одинаковы.
- Мы можем выполнять различные операции над квадратной матрицей, такие как сложение, умножение, обращение и т. д.
Типы квадратных матриц
У нас есть различные типы квадратных матриц, такие как единичные матрицы, сингулярные матрицы, невырожденные матрицы, симметричные матрицы и т. д.
- Вырожденная матрица: Если определитель квадратной матрицы равен нулю, то матрица называется вырожденной матрицей.
«A» является квадратной матрицей порядка «n × n» и называется сингулярной матрицей, если |A| = 0.

- Скалярная матрица: Скалярная матрица представляет собой квадратную матрицу, главные диагональные элементы которой равны, а остальные элементы равны нулю.
- Единичная матрица: Единичная матрица — это квадратная матрица, элементы главной диагонали которой равны единицам, а остальные элементы — нулям.
- Симметричная матрица: Симметричная матрица — это квадратная матрица, транспонирование которой совпадает с исходной матрицей.
«A» является квадратной матрицей порядка «n × n» и называется симметричной матрицей, если A T = A .
- Кососимметричная матрица: Кососимметричная матрица — это квадратная матрица, транспонирование которой равно отрицательному значению исходной матрицы.
«A» является квадратной матрицей порядка «n × n» и называется симметричной матрицей, если А Т = -А .
- Ортогональная матрица: Ортогональная матрица — это квадратная матрица, обратная сторона которой равна транспонированной матрице.
«A» является квадратной матрицей порядка «n × n» и называется ортогональной матрицей, если A -1 = A T .
Сложение и вычитание квадратных матриц
С квадратной матрицей можно выполнять различные математические операции, такие как сложение, умножение и т. д. При сложении или вычитании двух квадратных матриц одного порядка результирующая матрица получается, когда соответствующие элементы добавляются или вычитаются.
Если две квадратные матрицы порядка «2 × 2», то .
- Если A и B — две квадратные матрицы одного порядка, то A + B = B + A.
Умножение квадратных матриц
затем
.
Определитель квадратной матрицы
Определитель квадратной матрицы — это скалярное значение или суммарное значение, представляющее весь набор элементов матрицы. Определитель квадратной матрицы «2 × 2» можно легко определить по формуле, представляющей собой разность произведения главных диагональных элементов матрицы.
Определитель квадратной матрицы «2 × 2» можно легко определить по формуле, представляющей собой разность произведения главных диагональных элементов матрицы.
Если является квадратной матрицей порядка «2 × 2», то формула для вычисления ее определителя задается следующим образом:
|A| или det A = [ad – bc]
Обратная квадратная матрица
Обратная операция может быть выполнена на квадратной матрице. Разделение матрицы может быть достигнуто с помощью обратной матрицы. Обратная матрица находится после вычисления определителя квадратной матрицы. После этого находится сопряженная квадратная матрица. Тогда обратное вычисляется как
A -1 = прил. А / |А|
Также проверьте: Миноры и сомножители определителей
Решенные примеры на квадратной матрице
Пример 1: Вычислите определитель квадратной матрицы, приведенной ниже.
Решение:
Данная матрица,
|P| = (-3 × 0) – (–2 × 5)
|P| = 0 – (–10) = 10
Следовательно, определитель данной матрицы равен 10,
Пример 2: Определите, является ли приведенная ниже матрица вырожденной или нет.
Решение:
Чтобы определить, является ли приведенная ниже матрица вырожденной или нет, мы должны вычислить ее определитель.
|Б| = (4 × 4) – (0 × 0) = 16 ≠ 0
Поскольку определитель данной матрицы не равен нулю, данная матрица невырожденная.
Пример 3: Определите обратную матрицу, приведенную ниже.
Решение:
IF, то
Пример 4: Узнайте, приведена ли матрица, приведенная ниже, или нет.
Решение:
«A» является квадратной матрицей порядка «n × n» и называется симметричной матрицей, если A T = A.
Данная матрица,
≠ AПоскольку AT ≠ A, данная квадратная матрица несимметрична.
Часто задаваемые вопросы о квадратной матрице
Вопрос 1.

 Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.
Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная. также
также Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.
Частные случаи: диагональная, трёхдиагональная, жорданова. Антоним: заполненная.