Примеры линейных элементов электрических цепей
Метод эквивалентных схем
Метод применяется, когда НС
работают на прямолинейных участках
своих ВАХ. Суть метода заключается в
замене НС эквивалентной схемой, состоящей
из ЭДС и линейного сопротивления.
Условием эквивалентности служит
равенство напряжений на НС и на
эквивалентной схеме при одинаковых
токах. Пусть ВАХ НС имеет прямолинейный
участок (рис.2.3,а), заключенный между
точками а и
b.
Продолжим этот участок до пересечения
с осью напряжений и определим величину
U.
Тогда для произвольной
точки с на
прямолинейном участке можно записать:
U = U+cd*mU
=
=U+ed
*tgα*mU
=
U+*tgα*mU=
U+I
*tgα*mR
= U+IRд
.
Этому уравнению соответствует
схема, показанная на рис.2.3,б. Действительно,
по второму закону Кирхгофа для этой
схемы можно записать U
– IRд
= U.
Если продолжение прямолинейного
участка ВАХ пересекает ось напряжений
при отрицательных значениях величиной
U
(рис.2.3,в),
то для произвольной точки с
на прямолинейном участке можно записать:
U = — U+ cd*mU
= — U
+ IRд и тогда эквивалентная
схема принимает вид, показанный на
рис.2.3,г.
Если в сложной цепи все НС работают
на прямолинейных участках своих ВАХ,
то их можно позаменять эквивалентными
схемами. В результате цепь становится
линейной и её можно рассчитать любым
известным методом расчета сложных
линейных цепей постоянного тока (МУП,
МКТ, МЭГ и т.д.). Однако нужно следить за
тем, чтобы рабочая точка не выходила за
пределы прямолинйного учаска ВАХ.
Нелинейные отношения повторения
Гост 2.709-89 ескд. обозначения условные проводов и контактных соединений электрических элементов, оборудования и участков цепей в электрических схемах
Нелинейное отношение повторения определяет последовательные условия последовательности как нелинейная функция предыдущих условий. Примеры нелинейных отношений повторения — логистическая карта и отношения, которые определяют различные последовательности Hofstadter.
Нелинейные дискретные модели, которые представляют широкий класс нелинейных отношений повторения, включают NARMAX (Нелинейное Авторегрессивное Скользящее среднее значение с внешними входами) модель и связанные нелинейные системные идентификационные и аналитические процедуры. Эти подходы могут использоваться, чтобы изучить широкий класс сложных нелинейных поведений во время, частоту и пространственно-временные области.
Нелинейные алгебраические уравнения
Нелинейные алгебраические уравнения, которые также называют многочленными уравнениями, определены, равняя полиномиалы к нолю. Например,
Например,
Для единственного многочленного уравнения находящие корень алгоритмы могут использоваться, чтобы найти решения уравнения (т.е., наборы ценностей для переменных, которые удовлетворяют уравнение). Однако
системы алгебраических уравнений более сложны; их исследование — одна мотивация для области алгебраической геометрии, трудной отрасли современной математики. Даже трудно решить, есть ли у данной алгебраической системы сложные решения (см. Nullstellensatz Хилберта). Тем не менее, в случае систем с конечным числом сложных решений, эти системы многочленных уравнений теперь хорошо поняты, и эффективные методы существуют для решения их.
1 2 3 4
Расчет электрических цепей
А что можно сказать о графиках 1,2 и 4? Какие элементы характеризуют эти графики?
Нелинейный элемент в любой точке ВАХ характеризуется статическим сопротивлением, которое равно отношению напряжения к току, соответствующих этой точке (рис. 18). Например, для точки а:
Кроме статического сопротивления нелинейный элемент характеризуется дифференциальным сопротивлением, под которым понимается отношение бесконечно малого или весьма малого приращения напряжения ∆U к соответствующему приращению ∆I (рис. 18). Например, для точки а ВАХ можно записать
18). Например, для точки а ВАХ можно записать
где β – угол наклона касательной, проведенной через точку а.
Данные формулы составляют основу аналитического метода расчета простейших нелинейных цепей.
Рассмотрим примеры. Если статическое сопротивление нелинейного элемента при напряжении U1=20 В равно 5 Ом, то сила тока I1 составит…
1 А
Статическое сопротивление нелинейного элемента при токе 2 А составит…
5 Ом
Вывод по третьему вопросу: различают линейные и нелинейные элементы электрической цепи. В нелинейных элементах не выполняется закон Ома. Нелинейные элементы характеризуются в каждой точке ВАХ статическим и дифференцированным сопротивлением. К нелинейным элементам относятся все полупроводниковые приборы, газоразрядные лампы и лампы накаливания.
Вопрос № 4. Графический метод расчета нелинейных
электрических цепей (15 мин. )
)
Для расчета нелинейных электрических цепей применяются графический и аналитический методы расчета. Графический метод более простой и его мы и рассмотрим более подробно.
Пусть источник ЭДС Е с внутренним сопротивлением r питает два последовательно соединенных нелинейных элемента или сопротивления НС1 и НС2. Известны Е, r, ВАХ 1 НС1 и ВАХ 2 НС2. Требуется определить ток в цепи Iн, падения напряжения на внутреннем сопротивлении источника и на нелинейных элементах.
Сначала строим ВАХ линейного элемента r. Это прямая, проходящая через начало координат. Напряжение U, падающее на сопротивления контура, определяется выражением
Чтобы построить зависимость U=f(I), необходимо сложить графически ВАХ 0, 1 и 2, суммируя ординаты, соответствующие одной абсциссе, затем другой и т. д. Получаем кривую 3, представляющую собой ВАХ всей цепи. Использую эту ВАХ, находим ток в цепи Iн, соответствующее напряжению U=E. Затем, используя найденное значение тока, по ВАХ 0, 1 и 2 находим искомые напряжение U, U1, U2 (рис. 19).
д. Получаем кривую 3, представляющую собой ВАХ всей цепи. Использую эту ВАХ, находим ток в цепи Iн, соответствующее напряжению U=E. Затем, используя найденное значение тока, по ВАХ 0, 1 и 2 находим искомые напряжение U, U1, U2 (рис. 19).
Пусть источник ЭДС Е с внутренним сопротивлением r питает два параллельно соединенных нелинейных элемента или сопротивления НС1 и НС2, ВАХ которых известны. Требуется определить ток в ветвях цепи I1 и I2, падения напряжения на внутреннем сопротивлении источника и на нелинейных элементах.
Строим ВАХ Iн =f (Uab) . Для этого складываем графически ВАХ 1 и 2, суммируя абсциссы, соответствующие одной ординате, затем другой ординате и т.д. Строим ВАХ всей цепи (кривая 0,1,2). Для этого складываем графически ВАХ и 1,2, суммируя ординаты, соответствующие определенным абсциссам.
Для этого складываем графически ВАХ 1 и 2, суммируя абсциссы, соответствующие одной ординате, затем другой ординате и т.д. Строим ВАХ всей цепи (кривая 0,1,2). Для этого складываем графически ВАХ и 1,2, суммируя ординаты, соответствующие определенным абсциссам.
Рассмотрим следующие примеры.
При последовательном соединении нелинейных сопротивлений с характеристиками R1 и R2, если характеристика эквивалентного сопротивления RЭ…
пройдет ниже характеристики R1
пройдет выше характеристики R1
пройдет, соответствуя характеристике R1
пройдет ниже характеристики R2
При последовательном соединении линейного и нелинейного сопротивлений с характеристиками а и б характеристика эквивалентного сопротивления…
пройдет ниже характеристики а
пройдет выше характеристики а
пройдет, соответствуя характеристике а
пройдет ниже характеристики б
Вывод по четвертому вопросу: нелинейные электрические цепи постоянного тока составляют основу электронных цепей. Существует два метода их расчете: аналитический и графический. Графический метод расчета позволяет более просто определить все необходимые параметры нелинейной цепи.
Существует два метода их расчете: аналитический и графический. Графический метод расчета позволяет более просто определить все необходимые параметры нелинейной цепи.
Классификация электрических цепей
Буквенные обозначения элементов на электрических схемах
По назначению электрические цепи бывают:
- Силовые электрические цепи;
- Электрические цепи управления;
- Электрические цепи измерения;
Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.
Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.
Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.
Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.
ШАГОВЫЙ НЕЛИНЕЙНЫЙ ПРОЦЕССОР
Шаговый нелинейный процессор предназначен для решения физически и геометрически нелинейных, а также контактных задач.
В линейных задачах существует прямая пропорциональность между нагрузками и перемещениями в следствие малости перемещений, а также между напряжениями (усилиями) и деформациями в следствие линейного закона Гука. Поэтому для линейных задач справедлив принцип суперпозиции и независимости действия сил.
В физически нелинейных задачах отсутствует прямая пропорциональность между напряжениями и деформациями. Материал конструкции подчиняется нелинейному закону деформирования. Закон деформирования может быть и несимметричным – с различными пределами сопротивления растяжению и сжатию.
В геометрически нелинейных задачах отсутствует прямая пропорциональность между нагрузками и перемещениями. На практике наибольшее распространение имеет случай больших перемещений при малых деформациях.
В задачах конструктивной нелинейности имеет место изменение расчетной схемы по мере деформирования конструкции – например, в момент достижения некоторой точкой конструкции определенной величины прогиба возникает контакт этой точки с опорой.
Для решения таких задач шаговый нелинейный процессор организует процесс пошагового нагружения конструкции и обеспечивает решение линеаризованной системы уравнений на каждом шаге для текущего приращения вектора узловых нагрузок, сформированного для конкретного нагружения.
Шаговый нелинейный процессор позволяет получить напряженно-деформированное состояние для мономатериальных и для биматериальных, в частности железобетонных, конструкций.
Моделирование физической нелинейности производится с помощью конечных элементов, оперирующих библиотекой законов деформирования материалов.
Моделирование геометрической нелинейности производится с помощью конечных элементов, учитывающих изменение геометрии конструкции и возникновение мембранной группы напряжений (усилий), что позволяет рассчитывать мембранные и вантовые конструкции.
Моделирование конструктивной нелинейности обеспечивается наличием специальных конечных элементов односторонних связей.
Матрица жесткости линеаризованной физически нелинейной системы формируется на основании переменных интегральных жесткостей, получаемых в точках интегрирования, как по сечению, так и по конечному элементу при решении линейной задачи на каждом шаге. Сечение конечного элемента в точках интегрирования дробится на ряд элементарных подобластей, в центрах которых определяются новые значения жесткостных характеристик в соответствии с заданной диаграммой деформирования. На каждом шаге решается линеаризованная задача с формированием векторов перемещений, усилий (напряжений) и новых жесткостей по касательному модулю деформации для следующего шага.
При расчете геометрически нелинейных систем считается, что закон Гука соблюдается. На каждом шаге происходит учет мембранной группы усилий (для стержней – учет продольной силы) при построении матрицы жесткости.
Для решения нелинейных задач необходимо задавать информацию о количество шагов и коэффициентах к нагрузке. Схема может содержать несколько нагружений, из которых может быть сформирована последовательность (история) нагружений.
Схема может содержать несколько нагружений, из которых может быть сформирована последовательность (история) нагружений.
Для решения геометрически нелинейных задач реализован автоматический выбор шага нагружения.
Это нравится:ДаНет
Метки
- алгоритм расчет цепей при несинусоидальных периодических воздействиях
- алгоритм расчета цепей периодического несинусоидального тока
- баланс мощностей
- ВАХ нелинейного элемента
- Векторная диаграмма
- ветви связи
- взаимная индуктивность
- взаимная проводимость
- вольт-амперная характеристика нелинейного элемента
- второй закон Кирхгофа
- второй закон Кирхгофа для магнитных цепей
- входная проводимость
- гармоники напряжения
- гармоники тока
- Генератор напряжения
- генератор тока
- главные контуры
- графический метод расчета нелинейных электрических цепей
- динамическое сопротивление
- дифференциальное сопротивление
- емкость двухпроводной линии
- емкость коаксиального кабеля
- емкость конденсатора
- емкость однопроводной линии
- емкость плоского конденсатора
- емкость цилиндрического конденсатора
- закон Ампера
- закон Био Савара Лапласа
- закон Ома
- закон полного тока
- закон электромагнитной индукции
- Законы Кирхгофа
- индуктивность
- индуктивность двухпроводной линии
- индуктивность однопроводной линии
- индуктивность соленоида
- катушка со сталью
- Конденсатор в цепи постоянного тока
- контурные токи
- коэффициент амплитуды
- коэффициент гармоник
- коэффициент искажения
- коэффициент магнитной связи
- коэффициент мощности трансформатора
- коэффициент трансформации
- коэффициент формы
- кусочно-линейная аппроксимация
- магнитная постоянная
- магнитная цепь
- магнитный поток рассеяния
- метод активного двухполюсника
- метод двух узлов
- метод контурных токов
- метод наложения
- метод узловых напряжений
- метод узловых потенциалов
- метод эквивалентного генератора
- метод эквивалентного источника ЭДС
- Метод эквивалентных преобразований
- методы расчета магнитных цепей
- независимые контуры
- нелинейный элемент
- несинусоидальный периодический ток
- обобщенный закон Ома
- опорный узел
- основной магнитный поток
- параллельное соединение конденсаторов
- первый закон Кирхгофа
- первый закон Кирхгофа для магнитных цепей
- последовательное соединение конденсаторов
- последовательный колебательный контур
- постоянная составляющая тока
- потери в меди
- потери в стали
- приведенный трансформатор
- Примеры расчета схем при несинусоидальных периодических воздействиях
- принцип взаимности
- принцип компенсации
- расчет гармоник тока
- расчет магнитной цепи
- расчет нелинейных цепей постоянного тока
- расчет цепей несинусоидального тока
- Расчет цепи конденсаторов
- расчет цепи с несинусоидальными периодическими источниками
- Резонанс в электрической цепи
- решение задач магнитные цепи
- сила Ампера
- сила Лоренца
- Символический метод
- собственная проводимость
- статическое сопротивление
- сферический конденсатор
- теорема об эквивалентном источнике
- теорема Тевенена
- топографическая диаграмма
- Трансформаторы
- трехфазная система
- удельная энергия магнитного поля
- уравнения трансформатора
- Цепи с конденсаторами
- частичные токи
- чередование фаз
- ЭДС самоиндукции
- эквивалентная схема трансформатора
- электрическая постоянная
- электроемкость
- энергия магнитного поля
Элементы электрических цепей
Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.
Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.
Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.
Существуют условные обозначения для изображения элементов цепи на схемах.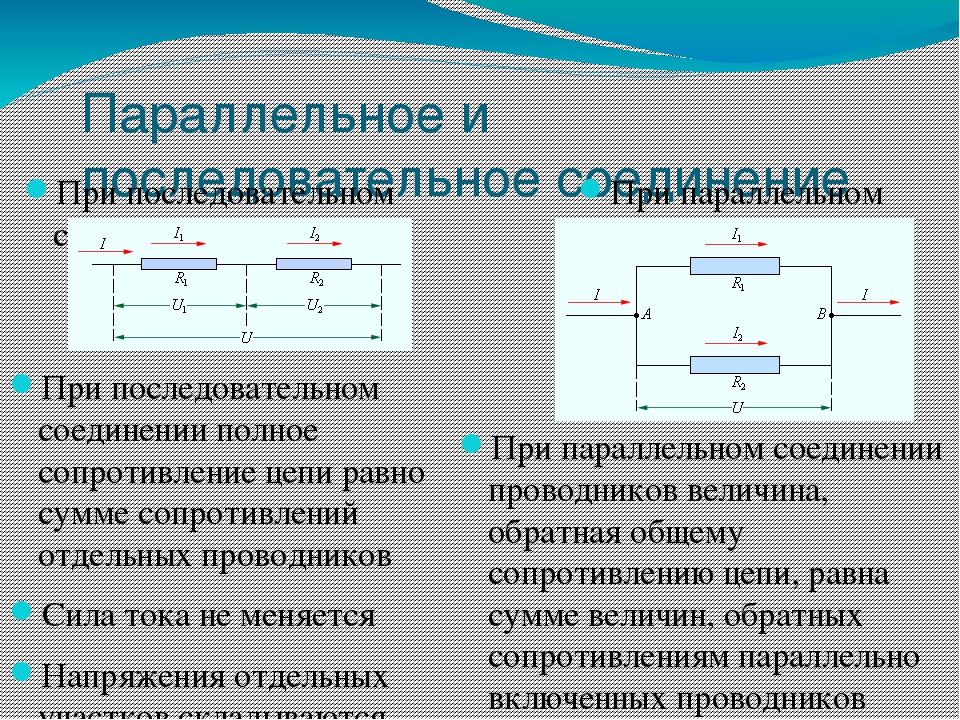
Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.
Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.
Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.
При решении задач и анализе схем используют следующие понятия:
- Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
- Узел – соединение ветвей цепи;
- Контур – последовательность ветвей, которая образует замкнутый путь.
 При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
Чтобы понять, что есть что, взглянем на рисунок:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
1.1. Нелинейные элементы и их характеристики. Способы аппроксимации характеристик нелинейных элементов
В общем случае нелинейная цепь описывается оператором преобразования Wнц:
uвых(t) = Wнц[Uвх(t),t], (1.1)
для которого свойство линейности не выполняется. В состав такой цепи входят один или несколько нелинейных элементов (НЭ). Различают резистивные и реактивные НЭ. В качестве резистивных НЭ выступают транзисторы, полупроводниковые диоды, электронные лампы. Примером реактивного НЭ является варикап.
При анализе НЭ предполагается, что переходные процессы в НЭ заканчиваются практически с окончанием изменения входного сигнала, т.е. НЭ является безынерционным.
В подавляющем большинстве задач радиотехники рассматриваются резистивные безынерционные НЭ. В таких элементах в качестве входного сигнала выступает напряжение, а в качестве выходного – ток, протекающий по элементу. На Рис.1.1 показаны: нелинейный двухполюсник – полупроводниковый диод и четырехполюсник, которым может быть представлен транзистор. Основной характеристикой НЭ является его вольт-амперная характеристика (ВАХ), т.е. зависимость тока, протекающего через НЭ, от приложенного к нему напряжения:
В таких элементах в качестве входного сигнала выступает напряжение, а в качестве выходного – ток, протекающий по элементу. На Рис.1.1 показаны: нелинейный двухполюсник – полупроводниковый диод и четырехполюсник, которым может быть представлен транзистор. Основной характеристикой НЭ является его вольт-амперная характеристика (ВАХ), т.е. зависимость тока, протекающего через НЭ, от приложенного к нему напряжения:
Другими характеристиками НЭ являются (Рис 1.2):
– статическое сопротивление или сопротивление НЭ по постоянному току:
, (1.2)
– статическая крутизна:
, (1.3)
– дифференциальное сопротивление:
, (1.4)
– дифференциальная крутизна:
. (1.5)
Статическая крутизна пропорциональна тангенсу угла α, а динамическая тангенсу угла β – угла наклона касательной ВАХ в рабочей точке.
Замена истинной (реальной) ВАХ приближенно представляющей функцией называется аппроксимацией характеристики.
Степенная аппроксимация – представление ВАХ в виде ряда Тейлора в окрестности рабочей точки (I, U):
i=f(u)=a+a1(u-U)+a2(u-U)2+… (1. 6)
6)
Кусочно-линейная аппроксимация – представление ВАХ отрезками прямых с различными наклонами. На практике ограничиваются двумя отрезками:
(1.7)
Здесь – напряжение начала характеристики;
– крутизна наклона характеристики;
Аппроксимации (1.6) и (1.7) показаны на Рис. 1.3.
1.3. Анализ преобразования гармонического сигнала НЭ при кусочно-линейной аппроксимации ВАХ
При кусочно-линейной аппроксимации вольт-амперная характеристика описывается выражением (1.7). Так же, как и в предыдущем случае, входной сигнал представляет собой сумму напряжения смещения U и гармонического сигнала (выражение 1.8).
На Рис. 1.5 изображена вольт-амперная характеристика, а также графики входного сигнала и тока, протекающего через нелинейный элемент.
Ток, протекающий через НЭ имеет вид периодической последовательности импульсов косинусоидальной формы, ограниченных по амплитуде.
Подстановка (1.8) в (1.7) дает следующее выражение для тока:
(1. 15)
15)
Вводится специальный параметр – угол отсечки θ, определяемый из соотношения:
.
Откуда:
. (1.16)
В соответствии с этим величина 2θ равна длительности одного импульса, выраженного в угловой мере, т.е. ωτи = 2θ.
Для определения спектрального состава тока необходимо провести разложение периодической последовательности косинусоидальных импульсов в ряд Фурье, которое приводит к следующему результату:
i(t)=I+I1cosωt+ I2cos2ωt+…+ Ikcoskωt ,
где I=SUmγ(θ), I1=SUmγ1(θ), I2=SUmγ2(θ) , … , Ik=SUmγk(θ), — амплитуды соответствующих гармоник,
γ(θ), γ1(θ), γ2(θ), … , γk(θ), – функции Берга.
Значения функций Берга рассчитаны для различный значений K и Θ и сведены в таблицу (табулированы).
Зависимости γk(θ) показывают, как изменяется амплитуда к-той гармоники тока, если амплитуда входного сигнала постоянна, а угол отсечки изменяется за счет изменения напряжения смещения .
Для получения наибольшей амплитуды желаемой гармоники тока необходимо обеспечить оптимальный угол отсечки. Так, например для второй гармоники при , оптимальный угол отсечки Θ=90.
Графический метод
Метод применяется для расчета
цепей, содержащих только один источник,
а НС, ВАХ которых задана графиками,
соединены последовательно, параллельно
или смешано.
1.
Расчет последовательного
соединения. Пусть
последовательно соединены два НС
(рис.2.4,а), ВАХ которых заданы графиками.
Известно также приложенное к схеме
напряжение, а требуется определить ток
в цепи и напряжения на элементах U1
и
U2.
На основании второго
закона Кирхгофа можно записать
U
= U1
+ U2.
(1)
Это выражение и положено в основу
решения. На рис.2.4,б кроме заданных ВАХ
НС строим зависимость I(U1+U2).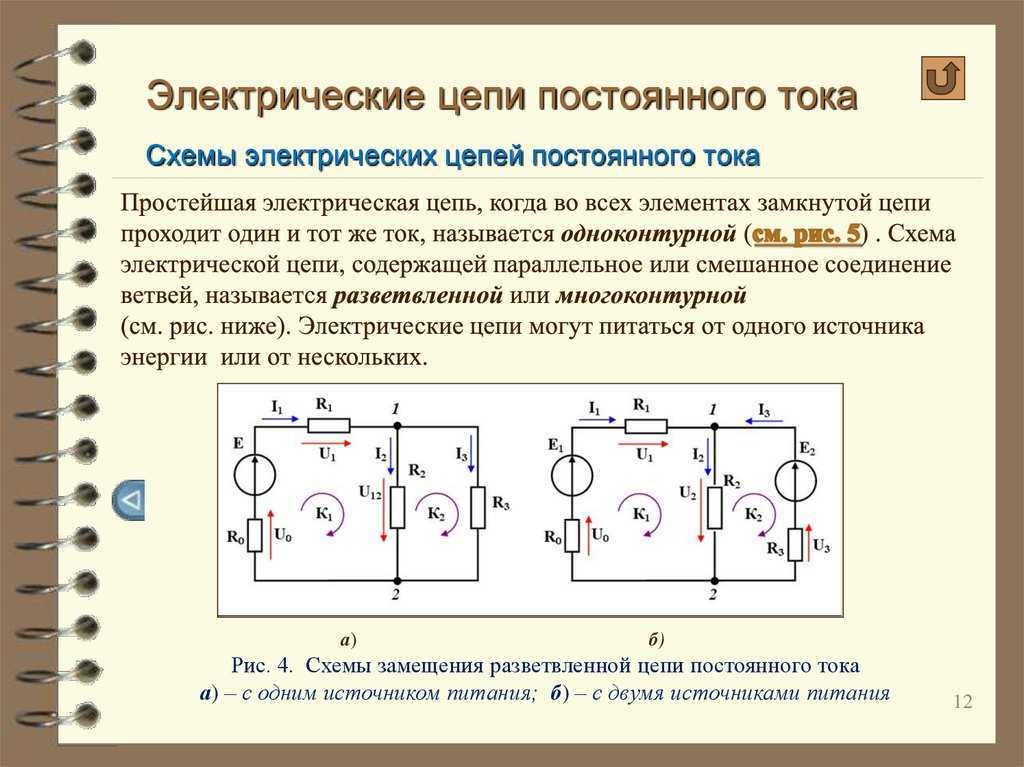
Задаваясь
различными значениями тока и суммируя
соответствующие значения U1
и U2.
Эта зависимость представляет собой
ВАХ всей цепи. Откладывая
заданное напряжение, по ВАХ всей цепи
определяем ток, а по ВАХ НС – U1
и U2
сответстенно.
Определив эти величины, легко рассчитать
другие, например, мощности, потребляемые
НС: Р1=IU1;
P2=IU2:
или их статические
сопротивления. Аналогично
может быть произведен расчет
последовательного соединения большего
числа НС.
Существует
второй способ расчета последовательного
соединения. Он
также основан на использовании соотношения
(1), из которого необходимо выразить либо
U1,
либо U2.
Например, U1=
U—U2
и построить зависимость I(U-U2)
(рис2. 5). Она является зеркальным
5). Она является зеркальным
изображением ВАХ второго элемента
относительно вертикали, проведенной
через точку, соответствующую заданному
напряжению, поэтому легко может быть
построена. Точка пересечения ВАХ первого
элемента и кривой I(U-U2)
дает решение, определяющее I,
U1
и U2.
Особенно эффективен второй способ в
случае, когда один из элементов является
линейным. Тогда зависимость I(U-U2)
является линейной и строится по двум
точкам (ХХ и КЗ).
2. Расчет параллельного
соединения. Пусть параллельно
соединены два НС (рис.2.6,а), ВАХ которых
заданы графиками (рис.2.6,б). Если задано
подведенное напряжение, а требуется
определить токи, то по ВАХ элементов
находятся I1
и I2,
а
I=I1+I2.
(2)
Значительно сложнее решается
задача, когда задан ток в неразветвленной
части цепи, а остальные токи и входное
напряжение нужно определить. В этом
В этом
случае на основании (2) строится ВАХ
параллельного по заданной величине I
определяется U,
а также I1
и I2.
Метод двух узлов
Даны ВАХ каждого
элемента
Порядок расчета:
1. Строим
ВАХ отдельных ветвей I1(Uab),
I2(Uab),
I3(Uab)
1.1. Запишем
выражения ВАХ (II закон Кирхгофа)
Uab
= Е1 — Uнэ1
Uab
= Е2 — Uнэ2
Uab= Uнэ3
1.2. Строим ВАХ
Используем
правила последовательного соединения.
Задаем
различные значениятоков I1,
находим Uнэ1,
строим ВАХ I1(Vab)
(I1
Uнэ1
Uab
= Е1 — Uнэ1)
2. Запишем
выражения для I
закона Кирхгофа
I1
+ I2
= I3
I1
+ I2
= f(Uab)
Нужно
1 и 2 ветви заменить эквивалентной.
3.
Строим
ВАХ
I1
+ I2
= f(Uab).
Используем
правила построения параллельносоединенных
ветвей.
Задаем
значение Uab,
определяем I1
и I2
от Uab
по ВАХ и используя II
закон Кирхгофа строим ВАХ I1
+ I2.
4.
Определяем точку рабочего режима и
напряжение Uab.
Точка
рабочего режима находится на пересечении
ВАХ I1
+ I2
= f
и I3(Uab),
т.к. здесь выполняется I
закон Кирхгофа I1
+ I2
= I3.
5. Определяем
токи в параллельных ветвях.
Нелинейные
резистивные элементы при переменных
токах и напряжениях.
Инерционные
и безинерционные нелинейные сопротивления
Инерционность
определяется скоростью протекания
физических процессов в нелинейных
элементах. Например, лампа накаливания,
Например, лампа накаливания,
по которой протекает переменный ток 50
Гц
Принимая во внимание, что скорость
наростания температуры длится
1 с, то следет вывод, что лампа накаливания
не реагирует на мгновенное изменение
тока в течение секунды и поэтому
нелинейную ВАХ инерционных элементов
записывают для действующих значений.
Значительно быстрее физические процессы
протекают в полупроводниковых элементах
(диодах)
Расчет
разветвленных цепей с инерционными
нелинейными
элементами,
у которых ВАХ спрведливы для действующих
значений
I3
U3
R3C
=
I3
выбираем произвольно, для которого с
помощью ВАХ выбираем U3
и R3C
= . Далее определяем напряжение U
на входе соответственно выбранному
значению I3.
Сравниваем полученное напряжение со
значением на входе. При несовпадении
При несовпадении
корректируем и производим расчет, пока
не не совпадут.
1)
Z1
= r1
+ jXL
Z2
= r2
— jXC2
Z3
= r3C
+ jXL3
2)
U23
= I3Z3
3)
I2
= U23/Z2
4)
I1
= I2
+ I3
5) U
= I1Z1
+ U23
Сравниваем
полученное напряжение со значением на
входе. При несовпадении корректируем
и производим расчет, пока не совпадут.
Электрические цепи
Рассмотрим самую простую электрическую цепь. Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Ток может течь только по замкнутой цепи. Дадим еще одно определение:
Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.
Кстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.
По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.
Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.
Нелинейные элементы и их вольт-амперные характеристики.

Графики, которые полученны экспериментально, представляют вольт-амперные характеристики I(U) электрических свойств нелинейных элементов, в графиках отображается зависимость тока от напряжения, для которых иногда составляется приближенная эмпирическая формула, являющаяся удобной для произведения расчетов.
У неуправляемых нелинейных элементов имеется только одна вольт-амперная характеристика, а управляемые содержат в себе целое семейство таких характеристик и основными параметрами которых являются управляющие факторы.
Электрическое сопротивление у линейных элементов является постоянным, поэтому их вольт-амперная характеристика — проходящая через начало координат — прямая линия (рис.1, а).
Относительно осей координат на симметричные и несимметричные разделяются вольт-амперные характеристики нелинейных элементов, имеющие различную форму (рис.1 ,б, в).
Не приводит к изменению значения тока перемена направления напряжения у нелинейных элементов, имеющих симметричную вольт-амперную характеристику (симметричных элементов), а разные токи будут при одинаковом абсолютном значении напряжения, направленного в противоположные стороны, у нелинейных элементов с несимметричной вольт-амперной характеристикой (несимметричных элементов). В электрических цепях переменного и постоянного тока поэтому применяются нелинейные симметричные элементы, а для преобразования переменного тока в ток постоянного направления в цепях переменного тока используются нелинейные несимметричные элементы.
В электрических цепях переменного и постоянного тока поэтому применяются нелинейные симметричные элементы, а для преобразования переменного тока в ток постоянного направления в цепях переменного тока используются нелинейные несимметричные элементы.
Оцените статью:
контрольные вопросы – Контрольные вопросы Что такое линейный и нелинейный элемент в электрической цепи
Скачать 92.66 Kb.
|
С этим файлом связано 1 файл(ов). 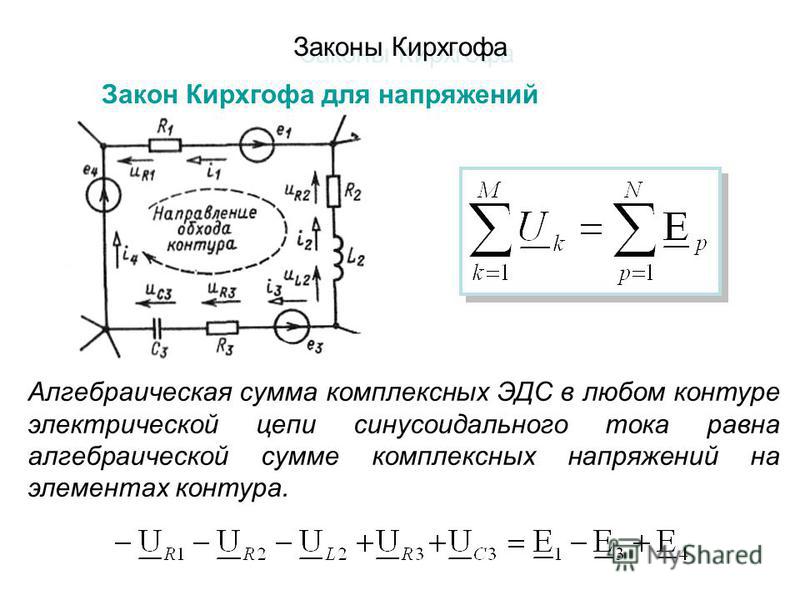 Среди них: 275710.ppt. Среди них: 275710.ppt.Показать все связанные файлы Подборка по базе: Экзаменационные вопросы по ЕНКМ_ddee3d7db06d0df6c667cea154487c08, искусство задачть вопросы.docx, Психология труда (ответы на вопросы).docx, 1 раб вопросы.docx, экз. вопросы лечфак 19-20 (1).doc, Тестовые вопросы к разделу 1.pdf, Штрыков Р.Р. ( земельное право ) ответы на вопросы.docx, Ответы на вопросы по физике.docx, Задачи_и_контрольные вопросы_по_математике_для_студентов_2_семес, Ответы на вопросы всех коллоквиумов.docx Контрольные вопросы 1.Что такое линейный и нелинейный элемент в электрической цепи? Линейным элементом или нагрузкой называют такой, сопротивление которого R, при любых значениях тока через него, остается постоянным, а вольтамперная характеристика представляет собой прямую линию. Нелинейным элементом называют такой, сопротивление которого R непостоянно и зависит от величины тока, проходящего через. 2. Привести примеры линейных и нелинейных элементов электрических цепей и вид их вольтамперных характеристик. Линейные элементы Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью. Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется. Кроме того речь может идти не только об элементах, обладающих чисто активными сопротивлениями R, но и о линейных индуктивностях L и емкостях C, где постоянными будут зависимость магнитного потока от тока – Ф(I) и зависимость заряда конденсатора от напряжения между его обкладками – q(U). Яркий пример линейного элемента — проволочный резистор. Нелинейные элементы Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью. Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется. В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи не линеен. 3.Как по показаниям амперметра и вольтметра можно определить величину сопротивления участка электрической цепи постоянного тока? Подключив вольтметр параллельно данному участку, а амперметр последовательно, разделить показания вольтметра на показания амперметра. 4.В каких единицах измеряются сила тока, напряжение и сопротивление? Сила тока измеряется в амперах, измеряется в вольтах, сопротивление измеряется в омах . 5. Нарисуйте схемы для измерения методом амперметра и вольтметра больших и малых электрических сопротивлений. 6.Для исследуемых электрических цепей запишите уравнения по законам Кирхгофа. 1 Закон Кирхгофа: I – I1 – I2 = 0 2 Закон Кирхгофа: E = I1*R1 + I2*R23 |
Работа № 1 – 2. ЛИНЕЙНАЯ ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ
ПОСТОЯННОГО ТОКА
Цель работы
Получение навыков сборки простых электрических пеней, включения в электрическую цепь измерительных приборов. Научиться измерять токи и напряжения, убедиться в соблюдении законов Ома и Кирхгофа в линейной электрической цепи.
Перечень минимодулей
| Наименование минимодулей | Количество |
| Резистор 2 Вт 68 Ом | |
| Резистор 2 Вт 150 Ом | |
| Резистор 2 Вт 330 Ом |
Пояснения к работе
Электрическая цепь, состоящая из элементов, вольтамперные характеристики которых являются прямыми линиями, называется линейной электрической цепью, а элементы, из которых состоит цепь, – линейными элементами.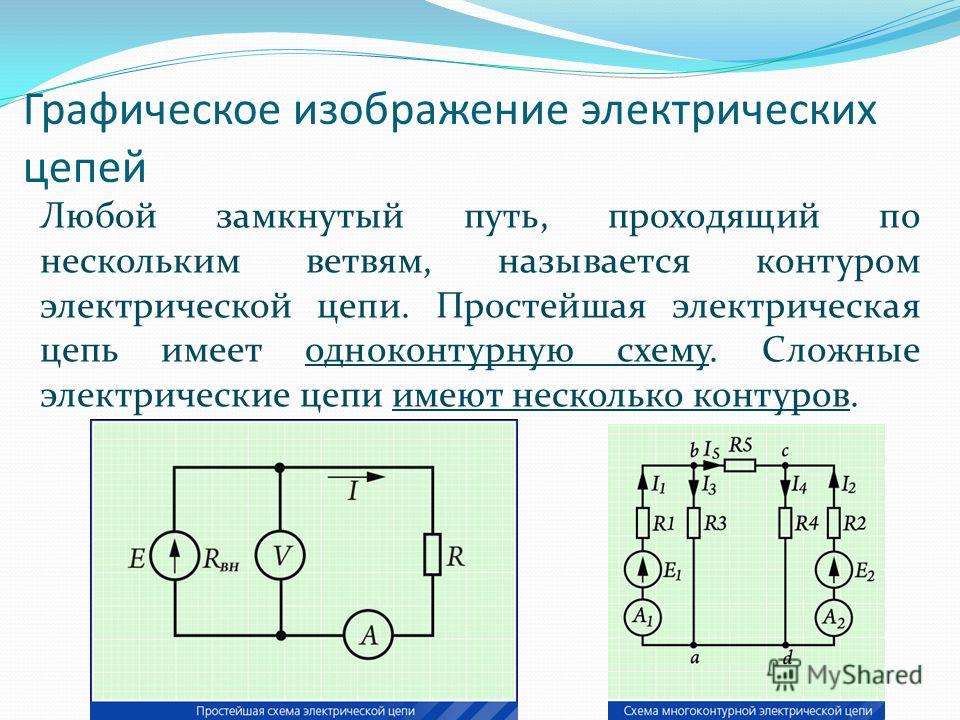
Соединение в электрической цени, при котором через все элементы протекает один и тот же ток, называется последовательным соединением. Эквивалентное сопротивление RЭ последовательной цепи постоянного тока равно сумме сопротивлений отдельных участков: RЭ= R1+ R2.
Напряжение на отдельном участке в соответствии с законом Ома пропорционально сопротивлению этого участка: U1=IR1; U2=IR2.
Напряжение U на входе последовательной цепи в соответствии со вторым законом Кирхгофа равно сумме напряжений на отдельных участках: U = U
При параллельном соединении двух или нескольких элементов напряжение на них одно и то же, так как выводы этих элементов подключены к одним и тем же узлам. Токи в отдельных элементах определяются по закону Ома: I1=U/R1; I2=U/R2.
В соответствии с первым законом Кирхгофа ток I в неразветвленной части цепи равен сумме токов всех параллельных ветвей: I=I1+I2.
Проводимость параллельного соединения равна сумме проводимостей отдельных участков: I/RЭ=I1/R1+I2/R2.
Порядок выполнения работы
3.1. Ознакомиться с лабораторной установкой. Собрать линейную электрическую цепь с последовательным соединением резисторов (рис. 1). Для измерения тока использовать вход 5 модуля ввода – вывода (гнезда Х25, Х26). Для измерения напряжений Ul, U2, U использовать входы 1, 2, 3 модуля ввода – вывода на пределе 30 В (гнезда Х9 и Х10, X11 и Х12, Х13 и Х14, соответственно).
Рис. 1.
Загрузить программу автоматического управления Delta Profi.
В левом верхнем углу и окне программы выбрать меню «Работы». Одинарный щелчок левой кнопкой мыши приводит к появлению контекстного меню, в котором надо выбрать раздел «Электрические цепи (мини)».
В появившемся списке работ выбрать «Работа 1 – 2. Простейшие линейные электрические цепи постоянного тока» и открыть вкладку «С последовательным соединением резисторов». На экране ПК отображается электрическая схема и набор виртуальных измерительных приборов, необходимых в данном эксперименте.
Запустить программу в работу, нажатием кнопки «Пуск» ► или командой главного меню «Управление – Пуск» или горячей клавишей F5.
Включить электропитание стенда (автоматический выключатель QF модуля питания, который выключается только в конце лабораторной работы) и модуля «Ввод – вывод».
3.2. На модуле питания включить источник постоянного напряжения (SA1). Измерить ток в цепи, величину напряжения U на входе цепи и напряжения U1 и U2 на резисторах R1 и R2. Результаты измерений занести в табл. I. Выключить источник питания (S.A.1).
3.3. Заменить резистор R2=330 Ом на резистор, заданный преподавателем, и повторить п. 3.2.
Остановить программу, нажатием кнопки «Стоп» ▀ или командой главного меню «Управление – Стоп» или горячей клавишей F6.
3.4. Собрать электрическую цепь с параллельным соединением резисторов (рис. 2). Для измерения тока использовать входы 5, 6, 7 модуля ввода – вывода (гнезда Х25 и Х26, Х27 и Х28, Х29 и Х30, соответственно). Для измерения напряжения U использовать вход 1 модуля ввода – вывода на пределе 30 В (гнезда Х9 и Х10). Представить схему для проверки преподавателю.
3.5. Загрузить программу автоматического управления Delta Profi.
В левом верхнем углу в окне программы выбрать меню «Работы». Одинарный щелчок левой кнопкой мыши приводит к появлению контекстного меню, в котором надо выбрать раздел «Электрические цепи и основы электроники».
В появившемся списке работ выбрать «Работа 1 – 2. Простейшие линейные электрические цепи постоянного тока» и открыть вкладку «С параллельным соединением резисторов» На экране ПК отображается электрическая схема и набор виртуальных измерительных приборов, необходимых в данном эксперименте.
Рис. 2.
Запустить программу в работу, нажатием кнопки «Пуск» ► или командой главного меню «Управление – Пуск» или горячей клавишей F5.
3.6. На модуле питания включить источник постоянного напряжения (SA1). Измерить напряжение и токи на всех участках цепи. Результаты занести в табл. Включить источник постоянного напряжения (SA1).
Таблица 1.
| Последовательное соединение | Параллельное соединение | ||||||||
| U, В | U1, В | U2, В | U=U1+U2, В | 11, мА | U, В | 11, мА | 12, мА | 13, мА | 11=12+13, мА |
3. 7. Заменить резистор R2=330 Ом на резистор, заданный преподавателем и повторить п. 3.6.
7. Заменить резистор R2=330 Ом на резистор, заданный преподавателем и повторить п. 3.6.
Остановить программу, нажатием кнопки «Стоп» ▀ или командой главного меню «Управление – Стоп» или горячей клавишей F6.
3.8. Проверить выполнение баланса мощностей.
3.9. Сделать выводы о выполнении законов Кирхгофа и о применении закона Ома в линейной электрической цепи постоянного тока.
3.10. Объяснить, используя законы Ома и Кирхгофа, изменение режима работы цепи и отдельных потребителей при изменении величины резистора R2.
3.11. Собрать линейную цепь со смешанным соединением резисторов (рис. 3).
Рис. 3.
Для измерения тока использовать входы 5, 6, 7 модуля ввода – вывода (гнездо Х25 и Х26, Х27 и Х28, Х29 и Х30, соответственно). Для измерения напряжений на отдельных участках иен и использовать вход 1 модуля ввода – вывода на пределе 30 В (гнезда Х9 и Х10).
Представить схему для проверки преподавателю.
3.12. Загрузить программу автоматического управления Delеa Profi.
В левом верхнем углу в окне программы выбрать меню «Работы». Одинарный шелчок левой кнопкой мыши приводит к появлению контекстного меню, в котором надо выбрать раздел «Электрические цени (мини)».
В появившемся списке работ выбрать «Работа 1 – 2. Простейшие линейные электрические цепи постоянного тока» и открыть вкладку «Со сметанным соединением резисторов». На экране ПК отображается электрическая схема и набор виртуальных измерительных приборов, необходимых в данном эксперименте.
Запустить программу в работу, нажатием кнопки «Пуск» или командой главного меню «Управление – Пуск» или горячей клавишей F5.
3.13 Включить питание и измерить напряжения и токи на всех участках цепи. Результаты занести в табл. 2. Выключить источник постоянного напряжения.
Таблица 2
| U, В | U1, В | U23, В | U= U1+ U2, В | 11, мА | 12, мА | 13, мА | 11-12+13, мА |
3. 14. Заменить резистор R3=330 Ом на резистор, заданный преподавателем, и повторить п.3.13.
14. Заменить резистор R3=330 Ом на резистор, заданный преподавателем, и повторить п.3.13.
Остановить программу, нажатием кнопки «Стоп» ▀ или командой главного меню «Управление – Стоп» или горячей клавишей F6.
3.15. Объяснить, используя законы Ома и Кирхгофа, изменение режима работы исследуемой цепи и отдельных потребителей при изменении величины резистора R3.
3.16. Используя мультиметр в режиме измерения сопротивления, измерить значения сопротивления R1, R2, R3. Результаты измерений занести в табл. 3.
В конце лабораторной работы выключить стенд (автоматический выключатель QF модуля питания).
3.17. По результатам измерений (п.3.13.) вычислить значения сопротивлений R1, R2, R3. Результаты расчетов занести в табл. 3.
Таблица 3
| Резистор | Измерено мультиметром | Вычислено |
| R1, Ом | ||
| R2, Ом | ||
| R3, Ом |
3. 18. Проверить выполнение баланса мощностей.
18. Проверить выполнение баланса мощностей.
3.19. Сделать выводы о выполнении законов Кирхгофа и о применении закона Ома в линейной электрической цепи постоянного тока.
Содержание отчета
Отчет по работе должен содержать:
а) наименование работы и цель работы;
б) схемы экспериментов и таблицы полученных экспериментальных данных;
в) результаты расчетов;
г) объяснить, используя законы Ома и Кирхгофа, зависимость режимов работы каждого потребителя при изменении величины параметра одного из них.
д) выводы по работе.
5. Контрольные вопросы
1. Что такое «линейный элемент» в электрической цепи?
2. Привести примеры линейных элементов электрических цепей.
3. В каких единицах измеряются сила тока, напряжение, мощность и сопротивление?
4. Как по показаниям амперметра и вольтметра можно определить величину сопротивления участка электрической цепи постоянного тока и потребляемую им мощность?
Как по показаниям амперметра и вольтметра можно определить величину сопротивления участка электрической цепи постоянного тока и потребляемую им мощность?
5. Нарисуйте схемы для измерения методом амперметра и вольтметра больших и малых электрических сопротивлений.
6. Как определить величину эквивалентного сопротивления при последовательном соединении резисторов?
7. Как определить величину эквивалентного сопротивления при параллельном соединении резисторов?
8. Для исследуемых электрических цепей запишите уравнения по законам Кирхгофа.
9. В чем заключается баланс мощностей в цепи постоянного тока?
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем…
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? – задался я вопросом. ..
..
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Типы электрических элементов » Теория сетей
Электрические элементы подразделяются на несколько категорий:
- Активные и пассивные элементы.
- Линейные и нелинейные элементы.
- Односторонние и двусторонние элементы.
- Временные и неизменяемые во времени элементы/схемы.
- Модель сосредоточенных и распределенных элементов.
Итак, давайте обсудим каждый из них один за другим.
Активные и пассивные элементы Активный элементЭто свойство активного элемента. Если какой-либо электрический элемент обладает хотя бы одним из этих свойств, он называется активным элементом.
- Активные элементы обеспечивают питание электрической цепи в течение длительного времени.

- Активные элементы могут управлять потоком заряда в цепи.
- Способен усиливать мощность сигнала (напряжения или тока).
- Для работы требуется внешний источник.
Примеры активных элементов:
- Источники напряжения, источники тока, генераторы
- Транзисторы (такие как BJT, MOSFET, FET, JEFT) – Транзисторы используются для усиления электрических сигналов. Таким образом, это активный элемент.
- Диоды (например, стабилитроны, фотодиоды, диоды Шоттки, светодиоды).
Идеальный независимый источник напряжения — это активный элемент, обеспечивающий заданное напряжение, полностью независимое от других элементов схемы.
Идеальный источник напряжения подает в цепь ток, необходимый для поддержания напряжения на клеммах. Пример: Батареи, генераторы можно рассматривать как приближение к идеальным независимым источникам напряжения. В реальной жизни существуют практические независимые источники напряжения, которые мы обсудим в этой статье позже. На приведенном ниже рис. (а) и (б) дан рисунок идеального независимого источника напряжения.
На приведенном ниже рис. (а) и (б) дан рисунок идеального независимого источника напряжения.
Идеальный независимый источник тока — это активный элемент, обеспечивающий заданный ток, полностью независимый от других элементов цепи.
Другими словами, идеальный источник тока подает в цепь любое напряжение, необходимое для поддержания заданного тока. Пример: генератор Ван де Граафа может обеспечивать один и тот же небольшой ток практически при любом уровне электрического потенциала, это пример почти идеального источника тока. На рисунке ниже приведена схема идеального независимого источника тока.
Идеальный зависимый источникИдеальный зависимый источник — это активный элемент, в котором величина источника управляется другим напряжением или током. Существует четыре возможных типа зависимых источников.
- Источник напряжения, управляемый напряжением: (VCVS) – Источник напряжения, управляемый напряжением, — это источник напряжения, который управляется другим напряжением в другом месте цепи.
 Обычно обозначается как V=AV c , где V c – управляющее напряжение, а A – коэффициент усиления. Пример: идеализированный усилитель.
Обычно обозначается как V=AV c , где V c – управляющее напряжение, а A – коэффициент усиления. Пример: идеализированный усилитель. - Источник напряжения с регулируемым током (CCVS) – это источник напряжения, значение которого контролируется током в другом месте цепи. Его выход обычно задается как V=AI c , где A — коэффициент усиления, а I c — управляющий ток.
- Источник тока, управляемый напряжением (VCCS) – Это источник тока, значение которого контролируется напряжением в другом месте цепи. Его выход обычно задается как I=AV c , где A — коэффициент усиления, а V c — управляющее напряжение.
Источник тока, управляемый током (CCCS)- Источник тока, управляемый током, — это источник тока, значение которого управляется другим током в другом месте цепи. Обычно обозначается I=AI c , где I c управляет током.
 Пример: БЖТ.
Пример: БЖТ.
Практически источник напряжения имеет конечное значение внутреннего сопротивления (импеданса). Мы представляем это путем последовательного подключения внутреннего сопротивления к идеальному источнику напряжения [показан на рисунке выше №. (д)].
Разница между реальным и идеальным источником напряжения:
Идеальный источник напряжения
- Значение внутреннего сопротивления равно нулю, что означает отсутствие внутреннего сопротивления.
- Он будет производить любой ток для поддержания заданного напряжения на клеммах. Таким образом, идеальный источник напряжения может поставлять бесконечное количество энергии.
- Обеспечивает постоянное напряжение независимо от типа нагрузки.
- V AB =V [Из приведенного выше рисунка №. (e)], так как внутреннее сопротивление равно нулю.
Практический источник напряжения
- Он имеет некоторое конечное внутреннее сопротивление, соединенное последовательно.
 Когда значение внутреннего сопротивления приближается к нулю, он начинает становиться идеальным источником напряжения.
Когда значение внутреннего сопротивления приближается к нулю, он начинает становиться идеальным источником напряжения. - Он не может обеспечить неограниченный ток.
- Он не может обеспечить постоянное напряжение на клеммах для каждой нагрузки из-за падения напряжения из-за внутреннего сопротивления.
- V AB =V-IR [Из приведенного выше рисунка №. (д)], где R≠0.
Практически источник тока также имеет конечное значение внутреннего сопротивления. Мы представляем это, подключив внутреннее сопротивление параллельно с идеальным источником тока [показан на рисунке выше №. (е)].
Разница между реальным и идеальным источником тока:
Идеальный источник тока
- Значение внутреннего сопротивления бесконечно. Таким образом, весь ток проходит через нагрузку.
- Он будет производить любое напряжение для поддержания заданного тока.
 Таким образом, идеальный источник тока может обеспечить бесконечное количество энергии.
Таким образом, идеальный источник тока может обеспечить бесконечное количество энергии. - Обеспечивает определенный ток независимо от типа нагрузки.
- I(выход)=i, потому что внутреннее сопротивление бесконечно. (е)]
Практический источник тока
- Он имеет некоторое конечное внутреннее сопротивление, соединенное параллельно. Когда значение внутреннего сопротивления приближается к бесконечности, он начинает становиться идеальным источником тока.
- Он не может обеспечить неограниченную мощность, потому что по мере увеличения V AB выходной ток уменьшается. (е)]
- Невозможно обеспечить одинаковый выходной ток для каждого типа нагрузки из-за разделения тока.
- I(выход)=i-(V AB /R), где значение R не бесконечно. [рис. (е)]
- Пассивные элементы не способны сами по себе обеспечивать энергию.
- Использует и хранит энергию в цепи.

- Используется для накопления энергии, разрядки, генерации, фильтрации и фазового сдвига.
- Для работы не требуется внешний источник.
- Он не может контролировать или усиливать сигнал.
Примеры пассивных элементов:
- Резистор: Резистор рассеивает энергию в виде тепла в цепи, поэтому он является пассивным элементом.
- Конденсатор: Конденсатор накапливает электрическую энергию в виде электрического поля, а также иногда разряжает энергию. Таким образом, это пассивный элемент.
- Индуктор: Индуктор накапливает электрическую энергию в виде магнитного поля. Следовательно, это пассивный элемент.
Как определить, является ли электрический элемент активным или пассивным, анализируя график его ВАХ? Прежде чем это узнать, давайте узнаем, что такое V-I характеристики электрического элемента?
ВАХ показывают соотношение между напряжением на элементе и током через него. Если часть графика характеристик V-I элемента лежит во втором и четвертом квадранте, то это активный элемент, в противном случае — пассивный элемент.
Если часть графика характеристик V-I элемента лежит во втором и четвертом квадранте, то это активный элемент, в противном случае — пассивный элемент.
Функция является линейной, если она обладает следующими свойствами:
- Однородность (масштабирование) : f(ax)=af(x)
- Аддитивность : f(x1+x2) =f(x1)+f(x2)
Когда входы и выходы представляют собой одиночные числа, функция, обладающая свойством масштабирования, также автоматически обладает аддитивностью. Резисторы, конденсаторы и катушки индуктивности 90 243 являются линейными 90 244 , поскольку они обладают свойством масштабирования.
Линейный элементТе электрические элементы, ВАХ которых являются линейными, называются линейными элементами. Например, резистор, конденсатор, катушка индуктивности, трансформатор и т. д.
Резистор может быть линейным или нелинейным. Линейный резистор следует закону Ома, в то время как нелинейный резистор не подчиняется закону Ома.
V(I)=IR
проверим линейно или нет
Однородность: V(aI)=aIR=aV(I).
Аддитивность: V(I1+I2)= (I1+I2)R = I1R+I2R = V(I1)+V(I2).
Следовательно, V=IR следует линейному свойству. Аналогично для конденсатора и катушки индуктивности.
Линейная цепьЭлектрические цепи — это цепи, параметры которых (резистор, изолятор, конденсатор) постоянны. Другими словами, чей параметр не меняется в зависимости от тока и напряжения. Ток, протекающий через линейную цепь, прямо пропорционален приложенному напряжению или наоборот.
Нелинейный элементТе электрические элементы, ВАХ которых не являются линейными, называются нелинейными элементами. Например, нелинейные резисторы, транзисторы, диоды, электронные лампы, катушки индуктивности с железным сердечником, другие полупроводниковые устройства, трансформаторы и т. д. Нелинейные элементы не подчиняются закону ОМ.
Нелинейная цепь Электрические цепи, содержащие нелинейный элемент, называются нелинейными цепями. Другими словами, параметр нелинейной цепи изменяется во времени.
Другими словами, параметр нелинейной цепи изменяется во времени.
Если график ВАХ электрического элемента представляет собой прямую линию, проходящую через начало координат, то он называется линейным элементом, в противном случае – нелинейным элементом.
Элемент односторонний и двустороннийЭлемент односторонний
- Свойства односторонних элементов изменяются при изменении направления питающего напряжения или тока.
- Позволяет проводить ток только в одном направлении.
- Пример: Диод, транзистор
Двусторонний элемент
- Свойства двусторонних элементов не меняются при изменении направления питающего напряжения или тока.
- Проводимость тока в обоих направлениях в элементе с одинаковой величиной.
- Пример: резистор, конденсатор, катушка индуктивности и т.
 д.
д.
Если вольт-амперная характеристика электрического элемента симметрична относительно начала координат (т. е. первый и третий квадранты симметричны, а второй и четвертый квадранты симметричны), то двусторонний элемент, в противном случае односторонний.
Изменяемые во времени и неизменяющиеся во времени элементы/цепиКогда вольт-амперная характеристика цепи или элемента изменяется со временем, тогда цепь или этот элемент называется изменяющейся во времени, в противном случае – неизменной во времени.
Модель сосредоточенных и распределенных элементовМодель сосредоточенных элементов
- Когда мы берем значения электрических элементов, считая, что они сосредоточены в точке.
- Мы используем его, когда размер электрического элемента очень мал по сравнению с длиной волны напряжения и тока.

- Электрическая цепь, в которой используется модель с сосредоточенными элементами, называется моделью с сосредоточенными параметрами.
- Используется в электронной схеме
Модель распределенных элементов
- Основана на рассмотрении электрических элементов, распределенных в пространстве.
- Мы используем его, когда размер электрического элемента сравним с длиной волны напряжения и тока.
- Электрическая цепь, в которой используется модель распределенных элементов, называется моделью распределенной цепи.
- Используется в линиях передачи и распределения.
Полезный анализ линейной электрической цепи и теоремы — Wira Electrical
Линейная электрическая цепь очень поможет нам, если мы столкнемся с более сложной цепью для анализа.
Основное преимущество анализа цепи с использованием законов Кирхгофа, как мы делали это раньше, заключается в том, что мы можем анализировать цепь, не вмешиваясь в ее первоначальную конфигурацию.
Основным недостатком является то, что для большой и сложной схемы требуются утомительные вычисления.
Обязательно сначала прочтите, что такое электрическая цепь постоянного тока.
Рост областей применения электрических цепей привел к эволюции от простых схем к сложным.
Чтобы справиться со сложностью, инженеры на протяжении многих лет разработали некоторые теоремы, упрощающие анализ цепей.
К таким теоремам относятся:
- Теорема Тевенина
- Теорема Нортона
Поскольку эти теоремы применимы клинейная схема , мы сначала обсудим концепцию линейности схемы.
В дополнение к теоремам о цепях мы обсудим концепции:
- Суперпозиции
- Преобразования источника
- Максимальной передачи мощности
Свойства линейной электрической цепи эффект. Хотя это свойство применимо ко многим элементам схемы, на этот раз мы ограничим его применимость резисторами.
Свойство представляет собой комбинацию свойства однородности (масштабирования) и свойства аддитивности.
Свойство однородности требует, чтобы если ввод (также называемый возбуждением ) умножался на константу, то вывод (также называемый откликом ) умножался на ту же константу.
Например, для резистора закон Ома связывает вход i с выходом v ,
| (1) |
Если ток увеличить на константу k , то напряжение соответственно возрастет на k ; то есть
| (2) |
Свойство аддитивности требует, чтобы ответ на сумму входных данных был суммой откликов на каждый вход, примененный отдельно. Используя соотношение напряжения и тока резистора, если
| (3a) |
and
| (3b) |
then applying ( i 1 + i 2 ) gives
| (4) |
Мы говорим, что резистор является линейным элементом, потому что зависимость напряжение-ток удовлетворяет свойствам однородности и аддитивности.
В общем случае цепь является линейной, если она одновременно аддитивная и однородная. Линейная цепь состоит только из линейных элементов, линейных зависимых источников и независимых источников.
Линейная схема — это схема, выход которой линейно связан (или прямо пропорционален) входу.
В этой книге мы рассматриваем только линейные цепи. Обратите внимание, что поскольку p = i 2 R = v 2 /R (что делает его квадратичной, а не линейной функцией), связь между мощностью и напряжением (или током) нелинейна.
Следовательно, теоремы, изложенные в этой главе, неприменимы к мощности.
Чтобы проиллюстрировать принцип линейности, рассмотрим линейную схему, показанную на рис.(1). Линейная цепь не имеет внутри себя независимых источников.
Возбуждается от источника напряжения v с , который служит входом.
Рисунок 1. Линейная цепь Линейная цепь |
Цепь нагружена нагрузкой Р . Мы можем взять текущий i через R в качестве выхода. Предположим, что v с = 10 В дает i = 2 А. i = 1 мА должно быть из-за v s = 5 мВ.
Читайте также: неинвертирующий операционный усилитель
Примеры схем линейности
Чтобы лучше понять, давайте рассмотрим примеры ниже:
1. Для схемы на рисунке. (2), найдите I O , когда V x = 12 В и V S = 24 V.
Solution :
Applying KVL to the two loops, we get
| (1.1) |
(1. 2) 2) |
Но v x = 2 i 1 . Уравнение (1,2) становится
| (1,3) |
Добавление (1,1) и (1,3). = 12 В,
Когда v с = 24 В,
Показывает, что при удвоении исходного значения I или двойные.
2. Предположим, что I o = 1 А, и с помощью линейности найдем фактическое значение I o в схеме на рисунке (3).
| Figure 3 |
Solution :
If I o = 1 A, then V 1 = (3 + 5)I o = 8 В и I 1 = В 1 /4 = 2 А . Применение KCL в узле 1 дает
Применение KCL в узле 2 дает
Следовательно, Is = 5 A. Это показывает, что если принять Io = 1, то Is = 5 A, фактический ток источника 15 A даст Io = 3 A, поскольку фактическое значение.
Это показывает, что если принять Io = 1, то Is = 5 A, фактический ток источника 15 A даст Io = 3 A, поскольку фактическое значение.
Как выполнить анализ цепи линейности
Ключевые выводы
Понимание концепции линейности цепи.
Узнайте, как выполнять анализ цепи на линейность.
Определите, являются ли цепи, управляемые переменным током, линейными.
У меня была фобия надувания воздушных шаров с тех пор, как в детстве один из них взорвался прямо мне в лицо. В то время как воздушный шар легко расширить, накачав в него больше воздуха, трудно оценить, когда остановиться, прежде чем он в конечном итоге лопнет.
Это похоже на то, когда ток и напряжение помещаются в цепь — очень важно знать их взаимосвязь и то, как они повлияют на работу цепи. Вот почему понимание линейности схемы и выполнение анализа линейности схемы важны в процессе проектирования печатной платы.
Вот почему понимание линейности схемы и выполнение анализа линейности схемы важны в процессе проектирования печатной платы.
Что такое линейность цепи?
Прежде чем проводить анализ цепи на линейность, необходимо понять ее линейность. В электронике линейная цепь состоит из элементов внутри резистора, что приводит к пропорциональному соотношению между напряжением и током.
Резисторы считаются линейным элементом. При включении в цепь ток через резистор изменяется пропорционально падающему на него напряжению. Связь между напряжением и током может быть выражена линейным уравнением ax + b = 0. Катушки индуктивности и конденсаторы также считаются линейными элементами.
Зависимость между напряжением и током в резисторе.
Как насчет нелинейной цепи? Как он реагирует на текущие изменения? Этот тип цепи состоит из одного или нескольких нелинейных компонентов, которые не удовлетворяют линейному уравнению. Изменения, внесенные в один параметр, не отражаются пропорционально в другом параметре. Диод – хороший пример.
Изменения, внесенные в один параметр, не отражаются пропорционально в другом параметре. Диод – хороший пример.
Нелинейная ВАХ диода.
Рассмотрим приведенную выше диаграмму вольт-амперных характеристик диода. При прямом смещении ток не течет между 0 В и напряжением перехода, которое составляет около 0,7 В для силикона. Как только напряжение превышает напряжение перехода, ток резко возрастает.
Диод также демонстрирует нелинейность при работе в конфигурации с обратным смещением, при этом небольшая утечка контрастирует с большим током пробоя. Другие нелинейные элементы включают транзисторы, трансформаторы и SCR.
Линейные схемы разрешимы для любой постоянной времени. Однако нелинейные схемы имеют много решений или вообще не имеют решений.
Выполнение анализа линейности цепей
Для анализа линейных цепей требуются базовые знания в области электроники, в частности, законы Ома и законы Кирхгофа. Закон Ома определяет соотношение между напряжением, током и сопротивлением по следующей формуле:
Закон Ома определяет соотношение между напряжением, током и сопротивлением по следующей формуле:
В = IR
Когда известны любые два параметра, можно рассчитать третий.
Часто линейная цепь состоит из множества элементов, соединенных последовательно, параллельно или из комбинации того и другого. Вот когда законы Кирхгофа становятся полезными. Первый закон Кирхгофа, или закон тока Кирхгофа, гласит, что общий ток, входящий в узел, равен сумме, выходящей из него.
Законы Кирхгофа о напряжении и токе
Между тем, второй закон Кирхгофа, или закон Кирхгофа о напряжении, утверждает, что сумма всех разностей потенциалов в замкнутом контуре равна нулю. Используя оба закона Кирхгофа, вы можете решать сложные линейные схемы, составляя уравнения для каждой из подсхем.
Вот пример.
Пример линейной схемы.
Вышеупомянутая схема состоит из резисторов, расположенных в параллельно-последовательной конфигурации. Зная напряжение и сопротивление, можно рассчитать ток, протекающий по каждой петле.
Зная напряжение и сопротивление, можно рассчитать ток, протекающий по каждой петле.
Согласно KVL, два уравнения для каждой петли могут быть определены следующим образом:
Таким образом, I1 и I2 могут быть решены следующим образом:
Линейны ли цепи переменного тока?
Часто цепи переменного тока могут быть ошибочно приняты за нелинейные, поскольку линейность цепи определяется соотношением между напряжением и током. Хотя сигнал переменного тока меняется со временем, он по-прежнему демонстрирует линейную зависимость между такими элементами, как резисторы, конденсаторы и катушки индуктивности. Следовательно, цепи, управляемые переменным током, являются линейными.
В то время как анализ линейности цепей довольно прост, вычисления могут быть утомительными, если у вас есть слои вложенных подсхем. Вы сэкономите драгоценное время с правильным программным обеспечением. Cadence PSpice Designer — это полноценный инструмент сквозного проектирования, позволяющий быстро и эффективно анализировать схемы.

 При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.
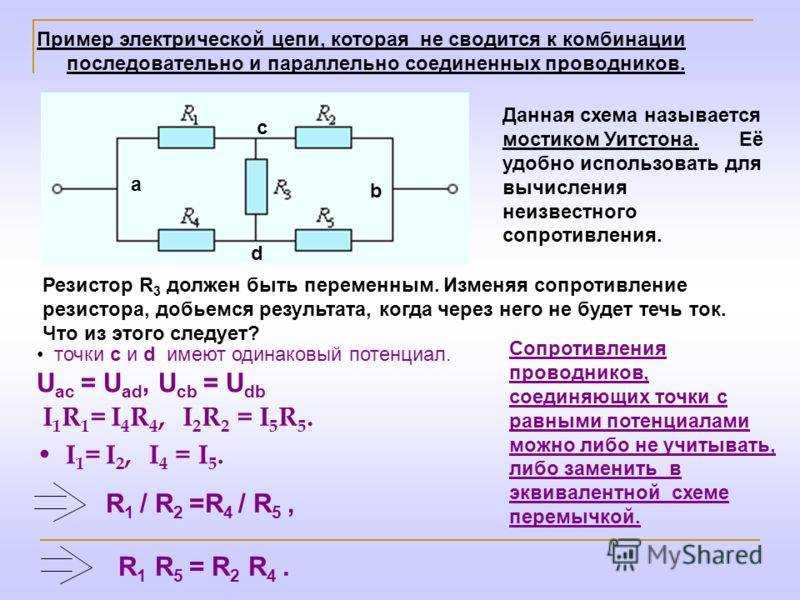 Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.
Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.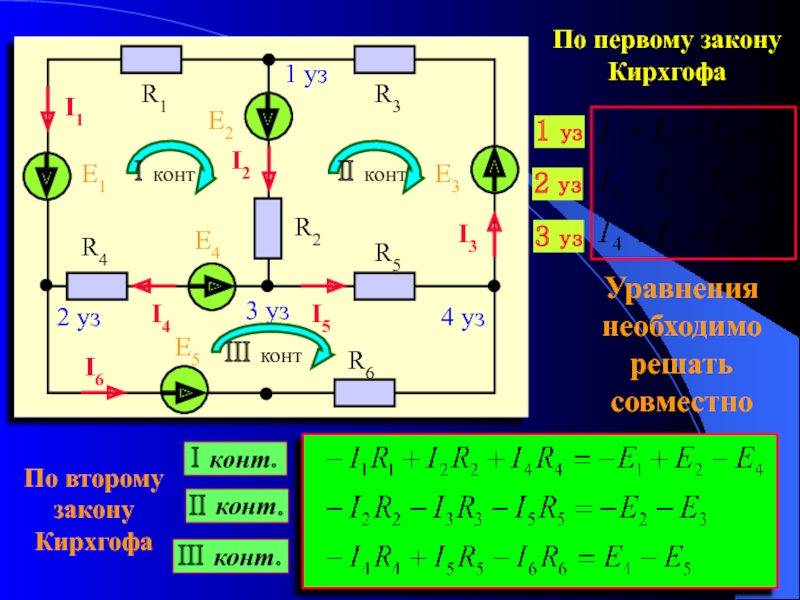 Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.
Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.

 Обычно обозначается как V=AV c , где V c – управляющее напряжение, а A – коэффициент усиления. Пример: идеализированный усилитель.
Обычно обозначается как V=AV c , где V c – управляющее напряжение, а A – коэффициент усиления. Пример: идеализированный усилитель. Пример: БЖТ.
Пример: БЖТ. Когда значение внутреннего сопротивления приближается к нулю, он начинает становиться идеальным источником напряжения.
Когда значение внутреннего сопротивления приближается к нулю, он начинает становиться идеальным источником напряжения. Таким образом, идеальный источник тока может обеспечить бесконечное количество энергии.
Таким образом, идеальный источник тока может обеспечить бесконечное количество энергии.
 д.
д.