Что такое мгновенная скорость и ускорение: Мгновенная скорость и ускорение это - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Физика Мгновенная скорость. Сложение скоростей

Материалы к уроку

Конспект урока

Ни одно тело не может двигаться все время с постоянной скоростью. Трогаясь с места, велосипедист увеличивает свою скорость. Далее в течение какого-то промежутка времени он движется с постоянной или почти постоянной скоростью, но все же когда-нибудь ему придется остановиться. Для этого велосипедист тормозит – уменьшает скорость движения до нуля. При этом за одинаковые промежутки времени он перемещается на различные расстояния, то есть движется неравномерно. В каждой точке траектории значения скорости велосипедиста разные.
Скорость тела в данной точке траектории или в данный момент называют мгновенной скоростью. Необходимо уметь рассчитывать мгновенную скорость в данный момент времени для того, чтобы задать неравномерное движение.
Чтобы понять, что же такое мгновенная скорость, представим себе, что велосипедист, трогаясь с места, ускоряется в течение 20 секунд. Если найти отношение перемещения велосипедиста во время разгона к времени разгона, мы получим среднюю скорость на этом участке пути. Но это не значит, что в каждый момент времени реальная скорость велосипедиста была именно такой. Напротив, в начале пути скорость была равна нулю, а в конце разгона скорость была гораздо больше полученной средней скорости.

Если же мы разделим участок пути, на котором скорость увеличивалась, на две равные по времени части и вычислим среднюю скорость для каждого участка отдельно, то мы получим совершенно разные значения средней скорости для каждого участка. Средняя скорость на первом участке будет меньше, чем на втором.
Если разделить все время разгона на 10 равных частей и вычислить средние скорости для каждого участка отдельно, то мы получим, что средняя скорость на первом участке совсем невелика, на втором – больше, на третьем – еще больше.

А на десятом участке средняя скорость будет самая большая. Это и понятно – ведь велосипедист разгоняется. Такие значения скоростей будут гораздо точнее характеризовать неравномерное движение, чем средняя скорость на всем участке.
Но все же скорость на каждом из десяти участков в любой момент времени будет равна средней скорости на этом участке лишь приближенно. Реальная скорость в начале участка будет меньше средней, а в конце участка больше.
Если разделить все время разгона на 20 равных частей и вычислить средние скорости для каждого участка, то мы получим значения средних скоростей для каждого участка. Эти значения будут еще точнее характеризовать движение.
Чем меньше будут эти временные промежутки, тем меньше будет отличие между скоростями соседних участков и тем точнее будут значения этих скоростей.
Если устремить промежуток времени к нулю, то отношение малого перемещения к малому промежутку времени, в течение которого это перемещение произошло, будет стремиться к определенному значению.

Это и есть мгновенная скорость точки в данный момент времени.
Мгновенная скорость точки – это предел отношения перемещения точки к промежутку времени, в течение которого это перемещение произошло, при устремлении промежутка времени к нулю.
Мгновенная скорость всегда направлена по касательной к траектории движения. В этом можно наглядно убедиться, посмотрев на любые отделяющиеся от вращающегося тела части. К примеру, грязь, вылетающая из-под колес автомобиля, она отделяется от колеса и летит вдоль линии, касательной к поверхности колеса, так как кусочки грязи в момент отрыва имеют скорость равную скорости поверхности колеса. Аналогичным примером может служить процесс заточки ножа при помощи точильного круга. Вылетающие искры будут двигаться по касательной к поверхности круга.
Понятие мгновенной скорости относится к точке. В дальнейшем, когда мы будем говорить о скорости движения тела, будем иметь в виду скорость какой-либо точки этого тела.
Механическое движение относительно: тело вполне может покоиться в одной системе отсчета и при этом двигаться в другой системе отсчета с одной скоростью, а в третьей системе с другой скоростью.

Траектория движения одного и того же тела в разных системах отсчета также будет различной. Рассмотрим пример, человек лежит в поезде, который в свою очередь движется относительно Земли. В этом примере человек относительно поезда имеет нулевую скорость, а относительно Земли будет двигаться со скоростью движения поезда. Некоторая точка, находящаяся на пропеллере летящего вертолета, описывает окружность в системе отсчета, связанной с вертолетом, а в системе отсчета, связанной с посадочной площадкой, находящейся на поверхности Земли, та же самая точка будет описывать уже не окружность, а винтовую линию.
Перемещение тела, пройденный им путь, а также его скорость тоже изменяются, если мы переходим от одной системы отсчета к другой. Пассажир поезда неподвижен относительно движущегося поезда, перемещение и путь человека по отношению к поезду равны нулю. Но по отношению к деревьям или зданиям, расположенным вдоль железной дороги, они имеют некоторые ненулевые значения.

Решая практические задачи, достаточно часто требуется вычислить перемещение либо скорость тела в некоторой системе отсчета, если значения этих величин уже известны, но относительно другой системы отсчета.

Рассмотрим пример. Для того чтобы составить расписание движения теплохода, необходимо знать его скорость в системе отсчета, связанной с берегом и скорость течения реки тоже относительно берега. Предположим, что теплоход, плывущий по реке, имеет определенную собственную скорость. Тогда в системе отсчета, связанной с берегом, при движении теплохода вниз по течению реки модуль его скорости будет больше, а при движении вверх против течения – меньше собственной скорости теплохода.
Скорость течения реки относительно берега измерить достаточно просто, вычислить скорость теплохода относительно воды тоже не составит труда. Теперь зная все необходимые величины, мы можем вычислить скорость движения теплохода относительно берега. Так как скорость является величиной векторной, скорость теплохода относительно берега будет равна векторной сумме вектора скорости движения теплохода в системе отсчета, связанной с водой в реке и вектором скорости течения воды. Если теплоход движется по течению, то векторы скорости теплохода относительно воды и воды относительно берега сонаправлены.

Соответственно проекции этих векторов будут иметь одинаковые знаки, поэтому модуль вектора суммы векторов будет больше модуля вектора скорости теплохода относительно воды в реке. Если же теплоход идет против течения реки, то вектор скорости теплохода относительно воды будет направлен противоположно вектору скорости течения воды. Проекции этих векторов будут иметь противоположные знаки, значит, модуль вектора суммы векторов будет меньше модуля вектора собственной скорости теплохода.
Это подтверждается нашими наблюдениями: что теплоход, идущий по течению, движется относительно берега значительно быстрее, такого же теплохода, движущегося против течения воды в реке.
Эти рассуждения можно распространить на любое тело, движущееся в подвижной системе отсчета. Если тело движется в системе отсчета К1, которая сама движется относительно другой системы отсчета К2, то скорость движения этого тела относительно системы К2 равна геометрической сумме скорости тела в системе К1 и скорости движения системы отсчета К1 относительно системы отсчета К2.

Это и есть закон сложения скоростей.
Закон сложения скоростей можно получить и по-другому. Мы уже изучали закон сложения перемещений. В нем говорится о том, что перемещение тела в подвижной системе отсчета относительно неподвижной системы отсчета равно геометрической сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной.
Разделим обе части этого уравнения на промежуток времени, в течение которого происходило перемещение. В результате имеем, что отношение перемещения тела относительно неподвижной системы отсчета к промежутку времени равно отношению перемещения тела относительно подвижной системы отсчета к промежутку времени плюс отношению перемещения самой подвижной системы относительно неподвижной к тому же промежутку времени.

Согласно определению, отношение перемещения к промежутку времени, в течение которого оно произошло, равно скорости тела. Отсюда следует, что скорость тела, движущегося в подвижной системе отсчета относительно неподвижной, равна геометрической сумме скорости подвижной системы отсчета относительно неподвижной и скорости тела в подвижной системе отсчета.

Как любое векторное уравнение, закон сложения скоростей для движения на плоскости можно записать как два уравнения для сложения проекций скоростей. Проекция вектора скорости тела на ось Х относительно системы отсчета К2 равна сумме проекции на ось Х вектора скорости тела относительно системы К1 и проекции на ось Х скорости системы отсчета К1 относительно системы отсчета К2. Проекция вектора скорости тела на ось Y относительно системы отсчета К2 равна сумме проекции на ось Y вектора скорости тела относительно системы К1 и проекции на ось Y скорости системы отсчета К1 относительно системы отсчета К2.
Проекции скоростей складываются алгебраически.

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Мгновенная скорость.

Ускорение. Движение с постоянным ускорением.

Мгновенная скорость Учитель: Клименко Ольга Анатольевна 2019

Содержание 1.Титульный лист 2.Содержание 3.Мгновенная скорость 1-6 слайд 4.Ускорение 7-10 слайд 6.Движение с постоянным ускорением 10-19 слайд 7.Спасибо за внимание

Скорость тела в данной точке траектории в данный момент времени называется мгновенной скоростью.

Чтобы определить мгновенную скорость нужно:

1. Измерить среднюю скорость за интервал времени от t до t+ ∆ t

2 . Принять, что средняя скорость за этот промежуток примерно равна скорости в момент времени t .

Чем меньше промежуток времени, тем точнее определена скорость. ( ∆ t→0)

к предельному значению

или

Мгновенной скоростью называется предел отношения перемещения к интервалу времени, в течение которого это перемещение произошло, если интервал времени стремится к нулю.

направлена по касательной

Частный случай- равномерное прямолинейное движение: направление скорости совпадает с траекторией в направлении вектора перемещения.

Проекции вектора скорости на координатные оси.

Модуль вектора скорости

Ускорение

Ускорение это величина,

характеризующая быстроту изменения скорости.

A 2

A 1

вектор скорости в точке А 1

вектор скорости в точке А 2 через промежуток времени ∆ t=t 2 -t 1

вектор изменения скорости

вектор среднего ускорения за время ∆ t

Ускорением называется предел отношения изменения скорости к промежутку времени ∆ t , в течении которого это изменение произошло, если интервал времени ∆ t стремится к нулю.

или

Векторное уравнение при движении на плоскости эквивалентно двум уравнениям для проекций вектора на координатные оси

Равнопеременное движение-движение с постоянным ускорением.

Равноускоренное- модуль скорости увеличивается с течением времени.

Равнозамедленное- модуль скорости уменьшается с течением времени.

Движение с постоянным ускорением совершается в одной плоскости

модуль вектора скорости

Скорость при равнопеременном движении

Вектор мгновенной скорости

Векторное уравнение

при движении

на плоскости эквивалентно

двум уравнениям

для проекций вектора

на координатные оси

Графическое представление равнопеременного движения

Графики модуля и проекции ускорения

a 1 a 1 0 t a X a 1X 0 t 0 X -a 2X a 2 a 1 “

a 2

a 2 a 1

a 1

a X

a 1X

-a 2X

a 2 a 1

Ускоренное

Ускоренное движение

Замедленное

Замедленное движение

График зависимости проекции скорости от времени υ X = υ X (t)

tg α↑ =a ↑ Модуль ускорения численно равен тангенсу угла наклона графика υ x = υ x (t) “

υ X

∆ υ

υ 0

∆ t

α ↑ =tg α↑ =a ↑

Модуль ускорения численно равен тангенсу угла наклона графика υ x = υ x (t)

Спасибо за внимание

Видео: среднее и мгновенное ускорение

Стенограмма видео

В этом видео мы узнаем о среднем и мгновенном ускорении. Что это за термины, как они относятся к скорости и положению, и как использовать их практически в решении проблемы.

Когда мы начнем, представьте, что вы находитесь в гоночная трасса, наблюдающая за тем, как ваш любимый гонщик соревнуется в гонке чемпионата. После нескольких часов вождения все машины доходят до своего последнего круга по ипподрому. К сожалению, ваш любимый водитель нет впереди. И вы начинаете задаваться вопросом, если все другие автомобили сохраняют свою текущую скорость, тогда было бы возможно даже для вашего водителю, чтобы разогнаться и пересечь финишную черту первым? Это вопрос, который нам нужно понять ускорение, чтобы иметь возможность ответить.

Ускорение — это временная скорость изменение скорости. Это означает, что если бы мы хотели решить среднее ускорение объекта, затем через некоторый интервал времени, начиная с 𝑡 начальным и заканчивающимся 𝑡 конечным, мы бы вычли скорость объекта в начальное время от скорости объекта в конечное время и разделить это на разница во времени всего.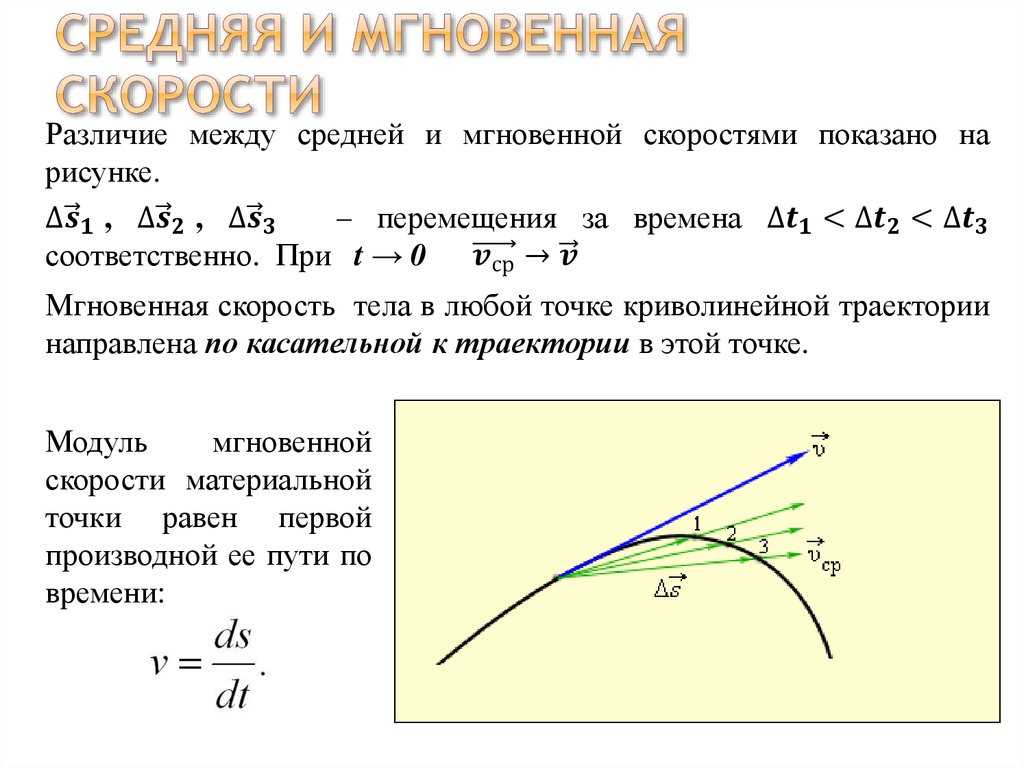

Если бы мы распространили это понятие на рассчитать мгновенное ускорение, то есть ускорение в определенной точке время, то мы намеренно сократили бы разрыв между окончательным и начальным время, все меньше и меньше, пока этот временной дифференциал не приблизился к нулю. Теперь мы знаем, что мгновенно ускорение равно производной скорости по времени. И мы можем вспомнить, что мгновенная скорость дается как производная по времени от положения.

Итак, теперь у нас есть три члена, положение, скорость и ускорение, которые связаны друг с другом. Мы могли бы почти думать об этом как о лестнице, где позиция находится на верхней ступени, скорость — на следующей ступени, а разгон ниже. Чтобы перейти от положения к скорости, мы возьмем производную по времени. И точно так же, чтобы получить от скорости вплоть до разгона. И если бы мы хотели двигаться вверх по ступени лестницы, скажем, от ускорения к скорости, то мы берем интеграл от ускорение по времени. И аналогично, чтобы получить из скорости позиционировать.

Кстати, эти три термина — не единственные термины, описывающие движение. Если бы мы потратили время производной ускорения, мы приходим к менее известному термину, известному как рывок. Если бы мы ехали в машине, чья ускорение менялось, то этот термин, рывок, мог бы быть хорошим описанием того, как это будет чувствоваться. Тем не менее, положение, скорость и ускорение покрывает большую часть интересующего нас движения. Теперь, когда мы знаем, как вычислить среднее и мгновенное ускорение, давайте попрактикуемся в использовании этих концепции.

Скаковая лошадь проезжает через стартовые ворота разгоняются из состояния покоя до скорости 15,0 м/с за счет запад, во временном интервале 1,80 секунды. Найдите средний показатель скаковой лошади ускорение. Предположим, что восток соответствует положительное смещение.

Мы хотим найти среднее ускорение скаковой лошади за этот 1,80-секундный интервал времени. Мы можем назвать этот интервал времени Δ𝑡. И мы можем назвать конечную скорость скаковой лошади, 15,0 метров в секунду, 𝑣 саб 𝑓. Если мы назовем 𝑎 sub avg средним ускорение скаковой лошади, мы можем написать, что оно равно ускорению скаковой лошади. конечная скорость минус его начальная скорость на Δ𝑡, время, которое потребовалось, чтобы сделать это изменение скорости.

Так как лошадь проезжала начальные ворота, мы можем считать, что 𝑣 sub 𝑖 равно нулю. А так как у нас есть 𝑣 sub 𝑓 и Δ𝑡 в постановке задачи, мы почти готовы решить для 𝑎 sub avg. Единственный момент, который мы хотим сохранить разум в том, что это вектор. И поэтому оно могло иметь положительное или отрицательное значение.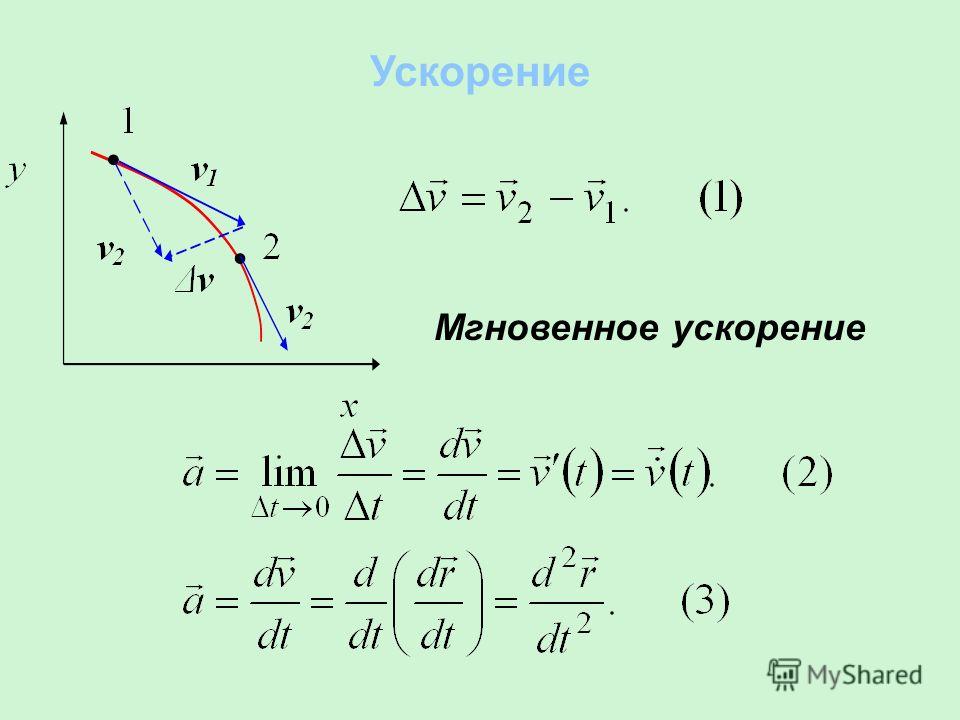

Нам сказали, что наша скорость 𝑣 sub 𝑓, находится в западном направлении, но это движение на восток – это движение, которое мы можем рассматривать в положительном направлении. Итак, это означает, что мы можем вставить знак минус перед нашей конечной скоростью скаковой лошади. Ведь он движется в отрицательное направление, согласно нашему соглашению. Итак, ускорение в среднем равно минус 15,0 м/с, деленное на 1,80 сек, или минус 8,33 м/с. вторая в квадрате. Это среднее ускорение скаковая лошадь.

Теперь давайте рассмотрим упражнение, которое позволяет найти мгновенное ускорение, а также мгновенную скорость.

Положение частицы вдоль 𝑥-ось изменяется со временем согласно уравнению 𝑥 как функция 𝑡 равна 1,5 минус 3,3𝑡 квадратных метра. Какова скорость частица в 𝑡 равна 2,7 секунды? Какова скорость частица в 𝑡 равна 4,3 секунды? Какое ускорение у частица в 𝑡 равна 2,7 секунды? Какое ускорение у частица в 𝑡 равна 4,3 секунды?

Итак, учитывая уравнение, описывающее положение частицы как функцию времени, мы хотим решить для мгновенного скорость и мгновенное ускорение при двух разных значениях времени, 𝑡 равно 2,7 секунд, а 𝑡 равно 4,3 секунды. Мы можем назвать значения, которые мы хотим решить для 𝑣 2,7 секунды, 𝑣 4,3 секунды, 𝑎 2,7 секунды и 𝑎 4,3 секунды.

Учитывая эту информацию, мы можем Напомним, что существует зависимость между положением, скоростью и ускорение. Мгновенная скорость равна производная положения по времени. И мгновенное ускорение равно равна производной скорости по времени, которая также равна второму времени производная положения. Поскольку нам дана позиция нашу частицу по времени, давайте продифференцируем ее дважды, чтобы найти мгновенная скорость и мгновенное ускорение.

Мгновенная скорость как функция времени равна производной по времени от 1,5 минус 3,3𝑡 в квадрате метров. Вычисляя эту производную, мы найдите его равным минус 6,6 метра в секунду. Это говорит нам о том, что для решения скорость, когда 𝑡 равно 2,7 секунды и когда 𝑡 равно 4,3 секунды, нам нужно только подставьте эти значения времени в это общее выражение. Когда мы делаем, к двум значительным цифры, скорость в 2,7 секунды составляет минус 18 метров в секунду, а скорость скорость в 4,3 секунды составляет минус 28 метров в секунду.

Теперь переходим к решению ускорение при этих двух конкретных значениях времени. Вспоминая, что ускорение равно производной скорости по времени, мы можем записать это ускорение как функция времени равна производной по времени от отрицательных 6,6𝑡 метров на второй. Мы находим, что эта производная есть постоянная, отрицательная 6,6 метра в секунду в квадрате. Это означает, что для любого значения времени это будет нашим ускорением. Поэтому ускорение на 2,7 секунд равно ускорению в 4,3 секунды, что равно минус 6,6 метров в секунду в квадрате. Вот такое ускорение у этих два значения времени.

Подведем итоги. что мы узнали о среднем и мгновенном ускорении. Ускорение равно времени скорость изменения скорости. То есть это вектор. Среднее ускорение равно скорость объекта в некоторый последний момент времени минус скорость того же объекта в начальный момент времени все делится на этот интервал времени, 𝑡 конечный минус 𝑡 начальный.

Мгновенное ускорение равно к производной скорости по времени, 𝑑𝑣 𝑑𝑡. Эти два уравнения связанный. Поскольку временной интервал между 𝑡 final и 𝑡 initial становятся все меньше и меньше, приближаясь к нулю, среднее ускорение приближается к мгновенному ускорению.

И ускорение связано с скорость и положение через производные по времени. Дан один из этих трех величины, мы можем найти остальные, интегрируя или дифференцируя по отношению к 𝑡. Как правило, когда мы знаем объект положение, скорость и ускорение как функцию времени, мы можем понять его движение полностью.