Что такое модуль и направление вектора скорости: найдите модуль и направление вектора скорости точки, если при равномерном движении по оси ox

3, если при темп … ературе T1=293 K его относительная влажность 90%,а температура воздуха понизилась до T2=288K (p нас 20° =17,3 г/м3 p нас 15° =12,8 г/м3). 2.Относительная влажность воздуха при температуре t1=15°C была 96%. Если количество водяного пара в воздухе увеличится вдвое, а его температура повысится до t2=25°C (p нас 15° = 12,8 г/м3, а 25°С 23 г/м3) то относительная влажность воздуха составит… %. 3. Относительная влажность воздуха в помещении при температуре t1=10°C 25%. Если температуру воздуха повысить до t2=30°С (p 10 =9, 41 г/м3 p 30 = 30 г/м3), а количество водяного пара в помещении увеличить вдвое то относительная влажность воздуха составит… %.

Почему компоненты воздуха (азот, кислород и другие) не просачиваются на поверхность Земли даже в безветренную погоду?​

Положительно заряженная частица с зарядом q = ? и массой 3.34 * 10 в -27 влетает в однородноеэлектрическое поле с напряженностью 50 кн/кл так, что век … тор начальной скоростисовпадает по направлению с вектором напряженности электрического поля.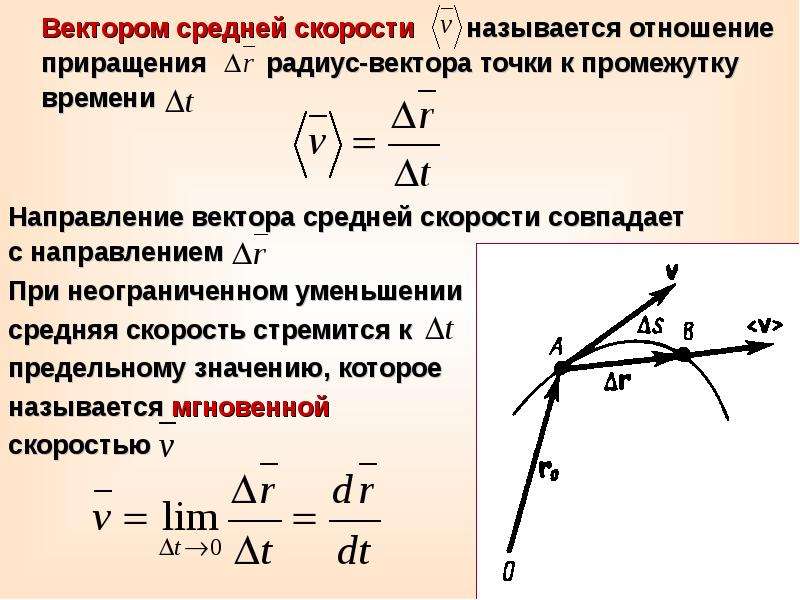

Завремя 1.7 мкс скорость частицы увеличивается от начальной скорости 230 км/c до скорости 43 * 10 в квадрате км/cОпределите значение величины, обозначенной ?Дано: m = 3.34 * 10 в -27E = 50 кн/клt = 1.7 мкс U0 = 230 км/с U = 43.10 в 2 км/cНайти: qПОМОГИТЕ ПОЖАЛУЙСТА ДАМ 30 БАЛЛОВ!

В вершинах прямоугольного треугольника ABC (угол C – прямой) находятся заряды qA = 8нкл, qB =2 нкл, qC =3,5 нкл . Длины катетов AC и BC равны соответс … твенно a = 20см и b = ? Сила, действующая на заряд qC со стороны зарядов qA и qB равна F = 11,7 мкн. Определите значение величины, обозначенной ? Дано: qA = 8 нкл qB = 2 нкл qC = 3,5 нкл а = 20 см F = 11,7 мкн Найти: b ПОЖАЛУЙСТА ПОМОГИТЕ, ДАМ 30 БАЛЛОВ!

на какой высоте кинетическая энергия брошенной вверх палки равна её потенциальной энергии если начальная скорость палки равна 14м/с?​

Физика 7 класс!! 30 баллов

Определение направления и модуля скорости

Определение направления и модуля скорости  [c. 53]

Решение, Для определения угловой скорости шестерни / надо найти скорость ее точки Е. Эту скорость найдем, пользуясь тем, что такую же скорость имеет точка Е шестерни 2. Для шестерни 2 известны направление и модуль скорости точки А  

[c.139]

Теперь перейдем к определению направления и модуля угловой скорости. В соответствии с формулой (12.10), скорость точки С равна  [c.225]

Для определения направления (знака) угловой скорости звена 2 переносим вектор скорости Усв в точку С и рассматриваем движение точки С относительно точки В в направлении скорости Усв. В данном примере вращение отрезка СВ, а следовательно, и угловая скорость (02 направлены против хода часовой стрелки, т. е. сог имеет знак плюс. Определяем модуль угловой скорости звена 3   [c.37]

Итак, у вектора скорости во время движения могут меняться и направление, и модуль.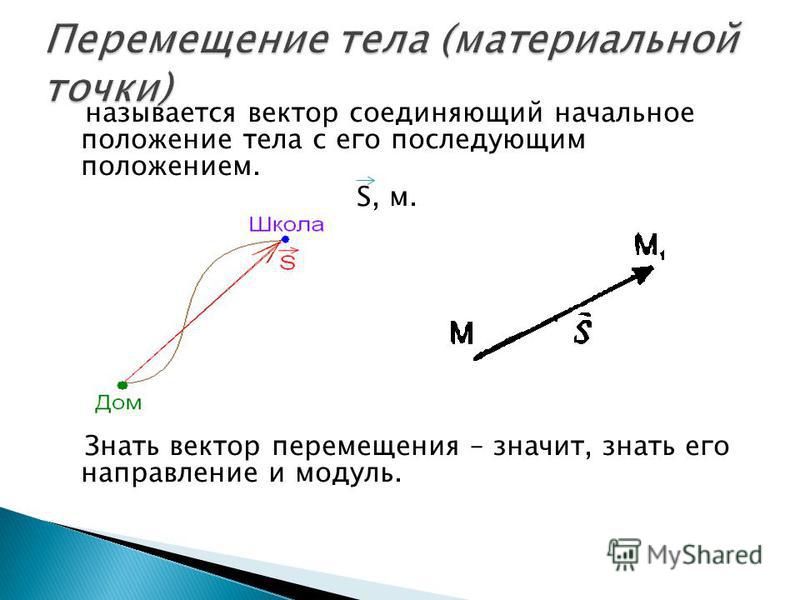 Для определения этих изменений вектора скорости оказывается необходимым рассмотрение траектории и за-  [c.66]

П р и м е р 2. Тело движется равномерно по траектории произвольной формы. По определению равномерного движения модуль скорости в таком движении постоянен. Все изменения скорости определяются только изменением ее направления. Следовательно, в равномерном движении по любой траектории тангенциальное ускорение всегда равно нулю, и полное ускорение все время совпадает с нормальным  

[c.68]

При прямолинейном движении вектор скорости v все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь численно при криволинейном движении кроме числового значения все время изменяется и направление вектора скорости точки. Размерность скорости LIT, т. е. длина/время в качестве единиц измерения применяют обычно м/с или км/ч. Вопрос об определении модуля скорости будет рассмотрен в 40 и 42.  [c.100]

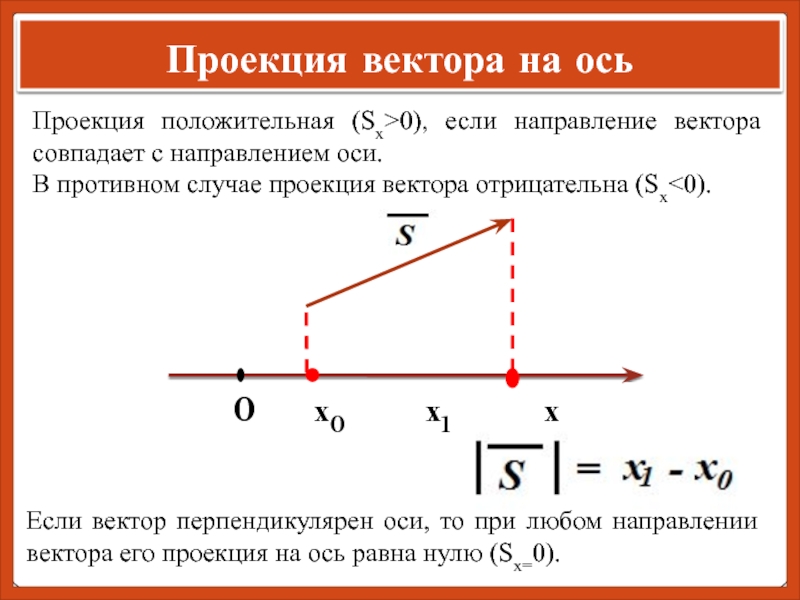
Для определения проекции скорости на ось мы умножали на направляющий косинус не вектор, а его модуль, его абсолютную величину. Проекция скорости на ось (как и алгебраическая скорость точки) не является вектором, так как не имеет собственного направления, а вполне определяется величиной проекции, направлением оси и знаком + или — . Проекция на ось вектора скорости (как и всякого другого вектора) АВ положительна (рис. 9, а) (+ аЬ), если угол между положительным направлением оси и направлением вектора АВ острый, и отрицательна (рис. 9, б)  

[c.30]

Если точка переменит свое движение на возвратное, например, если точка совершает колебательные движения на каком-либо участке кривой, то обычно не меняют положительного направления естественных осей, а приписывают скорости знак минус, если точка движется н сторону уменьшения дуговой координаты. Так в естественном способе задания движения точки, вместо модуля скорости появилась алгебраическая скорость , по абсолютной величине равная модулю, но имеющая собственный знак ( + или — ). Это обстоятельство сказывается и на определении касательного ускорения точки при естественном способе задания ее движения.

 [c.39]

Нормальное ускорение соответствует изменению вектора скорости перпендикулярно его направлению, и для определения нормального ускорения надо спроецировать вектор ускорения на главную нормаль, а для этого в нашем случае плоской траектории надо модуль ускорения помножить на sin б = sin (а — aj   [c.43]

Указания к решению задач. Среди задач, относящихся к этому параграфу, следует обратить внимание на такие задачи, в которых требуется исследовать движения плоских механизмов, состоящих из нескольких звеньев. Механизм при решении задачи надо изображать на чертеже в том положении, для которого требуется определить скорости соответствующих точек. При этом необходимо последовательно рассмотреть движение отдельных звеньев механизма, начиная с того звена, движение которого по условию задачи задано, и при переходе от одного звена к другому определить скорости тех точек, которые являются общими для этих двух звеньев механизма. Рассматривая движение отдельного звена механизма, нужно выбрать две точки этого звена, скорости которых известны по направлению, а скорость одной из этих точек известна и по модулю.

По этим данным можно найти положение мгновенного центра скоростей рассматриваемого звена. Картина распределения скоростей точек этого звена находится тогда, как при чистом вращении. Следует подчеркнуть, что мгновенный центр скоростей и угловую скорость можно находить только для каждого звена в отдельности, так как каждое звено имеет в каждый момент свой мгновенный центр скоростей и свою угловую скорость. В ряде случаев целесообразно определение скоростей точек рассматриваемого звена механизма производить с помощью теоремы о равенстве проекций скоростей концов неизменяемого отрезка на его направ-   [c.333]

Таким образом, нам известна по модулю и направлению скорость VA точки А шатуна АС и известно направление скорости ис другой точки С этого шатуна. Для определения модуля скорости ис удобнее воспользоваться теоремой о равенстве проекций скоростей концов отрезка на его направление. Принимая точку А, скорость которой известна по модулю и направлению, за полюс, будем иметь  [c. 342]

Одновременно с определением модулей скоростей точек находим их направления, а также направления вращений звеньев механизма. Например, по направлению скорости точки А и положению мгновенного центра скоростей Рав устанавливаем, что вращение звена АВ происходит по часовой стрелке. Поэтому скорость точки В при данном положении механизма направлена вверх.  

[c.115]

Векторное уравнение (4.9) равносильно двум скалярным уравнениям его можно заменить двумя уравнениями проекций векторов на координатные оси, лежащие в плоскости векторов. Следовательно, из уравнения (4.9) можно найти модули скоростей Ос и v в. Они находятся графическим построением треугольника векторов. Для этого из точки Ь проводим линию, перпендикулярную БС, а из полюса р — линию, перпендикулярную СО. В пересечении этих направлений находится точка с — конец вектора Ус — искомой скорости точки С. Вектор скорости Усв изображается отрезком сЬ, причем стрелка вектора направлена к точке с, соответствующей первой букве индекса.

Скорость вве по модулю равна скорости Усв и направлена в противоположную сторону. Поэтому вектор скорости УВД также изображается отрезком Ьс=сЬ, но стрелка вектора направлена к точке Ь (первой букве индекса). Для того чтобы указанное правило определения векторов скоростей соблюдалось, индексы у векторов скоростей в уравнениях следует располагать в принятой последовательности. Например, в уравнении (4.9) сперва идет индекс С, затем В и далее СВ.   [c.37]

Для увеличения объема информации при определении физикомеханических свойств измеряют скорости УЗ-волн различных типов. Для этого применяют ЭМА-преобразователи, обеспечивающие повышенную точность измерения ввиду отсутствия слоев контактной жидкости. При использовании ЭМ.А.-преобразователей можно излучать и принимать одновременно три волны — продольную и две поперечные. Измеряют скорости и коэффициенты затухания для каждой волны, в результате чего определяют упругие постоянные, главные направления кристаллических осей и текстуру материала (т. е. преимущественное направление кристаллитов). Измерение таким методом упругой анизотропии позволяет оценивать некоторые технологические параметры металлических листов (например штампуемость). Аналогичный способ применяют для определения модуля упругости покрытий.  [c.418]

Т. е. скорости Vp перемещения мгновенного центра скоростей в неподвижной и подвижной плоскостях равны между собой как по направлению так и по модулю (не следует, конечно, смешивать этих скоростей со скоростью точки фигуры, совпадающей в данный момент с мгновенным центром скоростей последняя равна нулю в силу самого определения понятия мгновенного центра скоростей). Первое обстоятельство говорит  [c.100]

В качестве примера решим задачу об определении констант преобразователя движения, приняв k —– 2. В этом случае находим, что вращение звеньев 6 1 будет происходить в противоположных направлениях, а модули средней угловой скорости звена 6 и скорости звена 1 будут равны. В соответствии с формулами (12) и (15) Л4 = 1, а й = 2. Согласно уравнениям (16) константы с d будут связаны единственной зависимостью  [c.222]

Неизменность направления скорости в прямолинейном движении значительно упрощает решение задач, так как позволяет ограничиться только определением модуля и знака скорости.  [c.58]

Весьма часто приходится по известной абсолютной скорости точки определять ее составляющие, т. е. производить разложение абсолютной скорости. Подобно тому как задача сложения скоростей аналогична задаче сложения двух сил, приложенных к одной точке, так и обратная ей задача разложения абсолютной скорости точки на переносную и относительную скорости полностью аналогична задаче разложения силы на две сходящиеся составляющие ( 9). Решение этих задач будет правильным в том случае, когда абсолютная скорость представляет собой диагональ параллелограмма, построенного на векторах переносной и относительной скоростей точки. Так как по данной диагонали можно построить бесчисленное множество параллелограммов, то, подобно задаче разложения силы, задача разложения скорости точки в общем случае является неопределенной.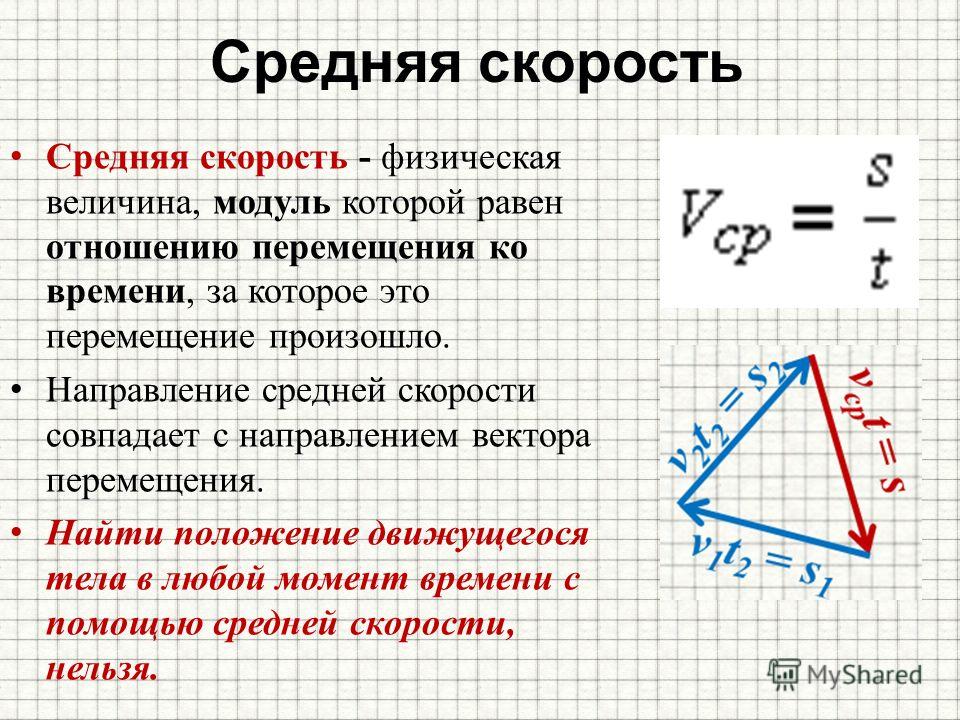 Для определенности решения этой задачи требуется задание двух дополнительных условий (или направления составляющих скоростей, или модуля и направления одной из них и т. д.).  [c.231]

В данном случае перпендикуляры, восставленные в точках А ц В фигуры к направлениям их скоростей, сливаются в одну прямую и для определения положения мгновенного центра скоростей нужно знать скорости двух точек фигуры не только по направлению, но и по модулю.  [c.244]

Следует отметить, что определение содержания связующего проводилось в соответствии с методикой, изложенной в нашей работе [132]. Расчет статического модуля упругости проводился по корреляционному уравнению, приведенному в табл. 14, по измеренным значениям скорости продольных волн в трубах. Трубы диаметром от 700 до 2000 мм испытывались в производственных условиях предприятий, выпускающих эти трубы. Для таких труб весьма важна количественная оценка неравномерности распределения модуля упругости и определения направлений, в которых модуль уп-  [c. 122]

Для ИХ определения необходимо сделать измерения скоростей распространения ультразвуковых волн в шести неэквивалентных кристаллографических направлениях [100], [010], [001], [ПО], [101], [011] (см. работу [101]). В направлении [010] моноклинного кристалла все три упругие волны, распространяющиеся вдоль него, являются чистыми. Кроме того, вдоль направлений [ООП, [101], [100] из трех волн одна, с поляризацией вдоль оси [010], является чисто сдвиговой. Эффективная жесткость для этих трех типов волн непосредственно определяет модули и С44.  [c.265]

За редкими исключениями, давление в рассматриваемых случаях настолько мало, что энтальпия активации практически равна энергии активации. Она зависит, однако, от приложенного напряжения сдвига, которое способствует развитию прямой реакции (-f) и затормаживает обратную реакцию (—), предопределяя таким образом величину и направление скорости деформации. Поскольку зависимость энтальпии активации от напряжения проявляется как сила, действующая на дислокации и способствующая протеканию реакции, она также зависит от наличия субструктуры Хотя в определенных случаях такие механизмы могут определяться диффузионными процессами, энтальпия активации практически нечувствительна к температуре в других случаях она зависит от температуры так же, как и модуль сдвига. Частотный фактор /+, включающий энтропию активации, также зависит от т, Т и 81. Влияние температуры на /+ обычно невелико по сравнению с ее влиянием на экспоненциальный член Больцмана. Как и во всех задачах по кинетике реакций, истинная скорость процесса определяется как разность между скоростями прямой и обратной реакций, что и обусловливает наличие двух членов в уравнении (1), определяющем истинную скорость ползучести, обусловленную развитием /-того процесса.  [c.249]

Однако модель бесконечно длинного сопла, используемая в теоретических исследованиях, не слишком пригодна для вычисления решений, определенных в конечной области и воспроизводящих течения реального газа с учетом всех действующих факторов. Адекватная интерпретация граничных условий, осуществляющихся в действительности на входе в сопло представляет собой важную проблему. Строго говоря, эта проблема находится вне рамок модели идеального газа. Наиболее простая умозрительная интерпретация состоит в формулировке граничного условия либо для аргумента, либо для модуля скорости во входном сечении аэродинамической трубы. Что касается прямой задачи, то для нее установлена единственность решения при условии выравнивания направления потока, т. е. аргумента скорости (см. гл. 3, 15).  [c.86]

Величину X, приведенную здесь, и модуль жесткости II называют постоянными Ламе. В упругом теле деформация сдвига, определяемая модулем жесткости, также распространяется с определенной скоростью, причем направление сдвига перпендикулярно направлению распространения, в связи с чем это распространение называется поперечной волной. Скорость поперечной волны получаем из выражения  [c.247]

Известны Va (модуль и направление), V (модуль и направление), направления Vba (перпендикулярно ВА ) и Fb (перпендикулярно ВС У Неизвестными величинами будут модули скоростей Vba и Vвс, поскольку для их определения необходимо знать угловые скорости звеньев 2 и 3.  [c.145]

Чтобы задать скорость ), аналогично паре сил в статике, требуются только три величины две — для задания направления и одна — для определения модуля скорости или момента пары сил Открытию этой аналогии мы обязаны Пуансо.  [c.207]

Если известны ускорения двух точек А и В плоской фигуры по модулю и направлению в какой-либо момент времени, то путем проецирования соотношения (23) на два взаимно перпендикулярных направления, одно из которых удобно направить по А В, получим два уравнения для определения угловой скорости и углового ускорения (см. п. 4 8).  [c.169]

Две такие величины вам известны — это скорость и сила. Для определения каждой из них нужно указывать направление и модуль. Они подчинаются правилу векторного сложения. Условимся обозначать векторы или одной латинской полужирной буквой, или двумя буквами начала и конца вектора со стрелкой над ними. Например, вектор скорости может быть обозначен или aS, вектор силы — F или D (рис. 1.20).  [c.28]

Определение ускорения точки. Если материальная точка движется прямолинейно и равномерно, то во всех местах её траектории характер траектории будет один и тот же, направление движения будет одно и то же и скорость будет одна и та же следовательно, при такого рода движении никакого изменения движения быть не может.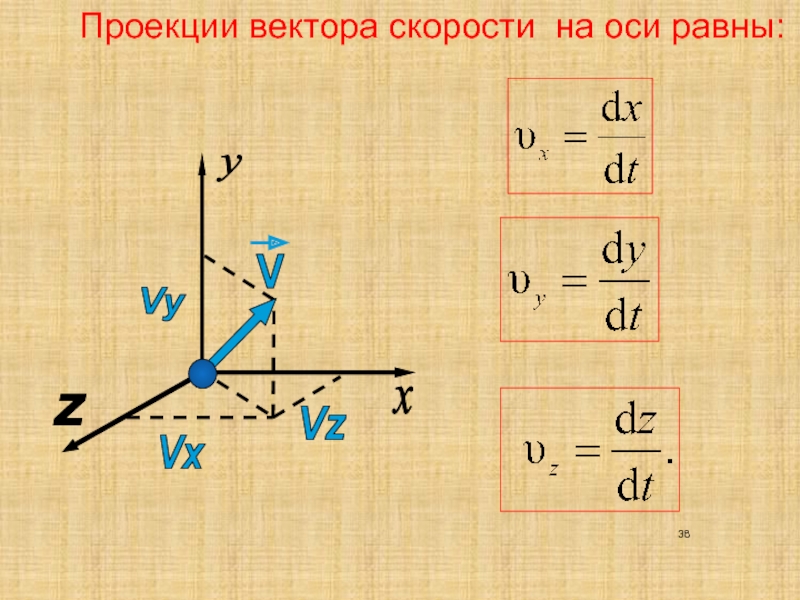 Чтобы имело место изменение движения, скорость точки должна изменяться с течением времени. Изменение вектора скорости может происходить или так, что направление скорости остаётся неизменным, а меняется лишь модуль вектора скорости, или так, что модуль вектора скорости остаётся неизменным, а меняется лишь направление скорости, или, наконец, так, что меняются одновременно и модуль и направление вектора скорости. Чтобы сразу в одной картине представить изменение вектора скорости точки, применяют следующее построение. Пусть будет (С) — траектория точки А построим во всех точках этой траектории векторы скорости v точки А, Возьмём какую-нибудь произвольную точку О пространства и перенесём в неё параллельно самим себе все векторы скорости v точки А геометрическое место концов векторов Zf представит некоторую линию, которая называется годографом скоростей. Так как согласно построению радиусы-векторы годографа суть векторы скорости точки Л, то непосредственно на годографе мы можем не только увидеть, но и измерять изменения направления и модуля вектора скорости точки А. 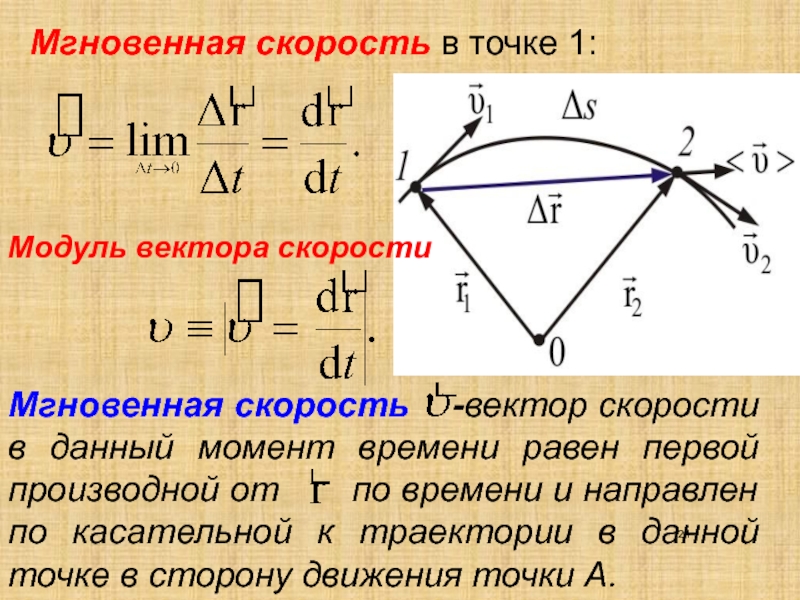Отнесём движение точки А к прямоугольной системе Oxyz осей координат пусть будут  [c.248]

Частные случаи определения положения мгновенного центра скоростей плоской фигуры. Прежде всего рассмотрим случай, когда скорости оа и ов двух точек Ам В параллельны друг другу,, и при этом линия АВ не перпендикулярна к о а и, следовательно, к Ув(рис.206). При этом из теоремы о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, следует, что 1) с05а=0дС05 р, но а=р, поэтому оа=ов и, следовательно, ии=ув- Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент времени должны быть равны друг другу и по модулю и по направлению. Такое состояние движения плоской фигуры называют мгновенно-поступательным.  [c.331]

Таким образои, элементарная работа силы равна произведению модуля элементарного перемещения на проекцию силы на направление этого перемещения. Исходя из этого определения элементарной работы можно утверждать, что работа силы характеризует то действие силы, которым определяется изменение модуля скорости точки приложения этой силы. В самом деле, если разложить силу Р на составляющие Р и Р , то изменять модуль скорости точки приложения силы Р будет только касательная составляющая Р , сообщающая этой точке касательное ускорение. Нормальная же составляющая Р или изменяет направление вектора скорости (сообщает точке приложения силы Р нормальное ускорение), или, если сила Р действует на несвободную материальную точку, изменяет давление этой точки на связь. На модуль вектора скорости точки приложения силы Р составляющая Р не влияет, т. е. сила Р не будет совершать работу.  [c.624]

Для определения периода и направления вращения Венеры использовано различие лучевых скоростей отд. участков вращающейся поверхности, к-рое приводит благодаря Доплера эффекту к уширению спектральной линии отражённых сигналов. Величина этого ушнренин цропорц. угл. скорости вращения планеты относительно наземного наблюдателя. Это вращение складывается из собств. вращения планеты в инерциальной системе координат и переносного движения системы координат относительно наземного наблюдателя. Результирующее изменение модуля угл. скорости вращения Венеры относительно наземного наблюдателя, вычисленное для неск. значений периода вращения планеты, представлено на рис. 2. На этом же графике нанесены эксперим. точки, полученные по  [c.217]

Рис. 2. Определение периода и направления вращення Венеры по наблюдениям вариаций тшврения спектра отражённых волн. Кривые представляют иаменение модуля угловой скорости а видимого вращения Венеры, вычисленное для ряда значений периода Т в предположении, что ось вращения планеты перпендикулярна плоскости её орбиты. Экспериментальные точки лучше всего согласуются с кривой, соответствующей обратному вращению Венеры с периодом около 300 сут.

Интересной в теоретическом отношении является работа [151], в которой получены зависимости для определения упругих постоянных, вещественных и мнимых частей комплексных модулей и коэффициентов Пуассона в оротропном и изотропном слоях по скоростям распространения и декремента затухания продольных и сдвиговых колебаний. Для определения всех упругих параметров ортотропной пластины необходимо экспериментально определить скорости продольных волн вдоль главных направлений и скорость сдвиговых колебаний в одном главном направлении и под углом 45° к нему. Комплексные составляющие модулей и коэффициентов Пуассона определяются по скоростям и декрементам затухания колебаний. Однако в этой работе совершенно не затрагивается задача онределе-  [c.71]

Данное определение соответствует понятию о работе, как о характеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу F на составляющие F и то изменять модуль скорости точки будет только составляюшая F,, сообщающая точке касательное ускорение. Составляющая же или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном движении, изменяет давление на связь. На модуль скорости составляющая влиять не будет, т. е., как говорят, сила F не будет производить работу .  [c.268]

Используя основные свойства мгновенного центра скоростей, можно определить его положение и в других случаях. На рис. 11.12, а показано, как находится эта точка, когда известны направления скоростей двух точек. Из точек А В восставлены перпендикуляры к Ул и ц- Точка Р находится на их пересечении. Если скорости точек Л и Б параллельны и ЛБ J v , то для определения мгновенного центра сЙЬростей следует воспользоваться свойством пропорциональности модулей скоростей расстояниям точек до мгновенного центра скоростей. На рис. 11.12, б и е показано, как находится мгновенный центр в этих случаях. На рис. 11.12, г показан случай, когда Vg и Ул параллельны, но Ул не перпендикулярна отрезку АВ. Очевидно, что в этом случае прямые, перпендикулярные Ул и Ув, пересекаются в бесконечности и мгновенного центра скоростей не существует. В самом деле, на основании теоремы о проекциях скоростей имеем УлС08а = УвС05а. Отсюда Ул = Vb и Уд = Ув. Из формулы (11.7) следует, что  [c.202]

При определении скорости любой точки тела, совершающего плоское движение, используем соотношение Ув =У -кохр = Уд +(охБА = Уд + вА в которое входят следующие параметры модуль скорости точки В, направление скорости точки В, модуль скорости точки А, направление скорости точки А, угловая скорость тела, взаимное расположение точек А и В.  [c.105]

Используя основные свойства мгновенного центра скоростей, можно определить его положение и в других случаях. На рис. 11.12, о показано, как находится эта точка, когда известны направления скоростей двух точек. Из точек А и В восставлены перпендикуляры к Уд и Vg. Точка Р находится на их пересечении. Если скорости точек А и В параллельны и i4B X Уд, то для определения мгновенного центра скоростей следует воспользоваться свойством пропорциональности модулей скоростей расстояниям точек до мпювен-ного центра скоростей. На рис. 11.12, б и в показано, как находится мгновенный центр в этнх случаях. На рис. 11.12, г показан случай, когда Ув и Уд параллельны, но Уд не перпендикулярна отрезку АВ. Очевид1ю, что в этом случае прямые, перпендикулярные Уд и Уе, пересекаются в бесконечности и мгновенного цеитра скоростей не существует. В самом деле, иа основании теоремы о проекциях скоростей имеем Кд os а = к,, os а. Отсюда = i>o и д = Ув. Из формулы (11.7) следует, что при этом л X ЛВ = О, т. е. угловая скорость фигуры равна нулю (w = 0). Значит, в данный момент временн скорости всех точек плоской фигуры равны по модулю и направлению к, следовательно, точки, линейная скорость которой равна пулю, не yute TeyeT.  [c.174]

---

Как определяется модуль и направление скорость точки при координатном способе задания движения?

, , Таким образом, проекции скорости на неподвижные декартовы оси координат равны первым производным по времени от соответствующих координат движущейся точки. Из равенств следует, что проекции скорости точки на координатные оси равны скорости проекций этой точки на те же оси. Зная проекции вектора скорости точки, найдём его модуль: .

Для определения направления вектора скорости воспользуемся направляющими косинусами:

, , .

4. Какая зависимость существует между радиус-вектором движущейся точки и вектором ускорения точки? Как направлен вектор ускорения криволинейного движения точки по отношению к её траектории, в какой плоскости он лежит?

, при стремлении к нулю получаем следующий предел: , этот предел называют ускорение точки в данный момент времени. Так как вектор скорости есть первая производная радиус-вектора точки по времени, то: . Таким образом, ускорение точки в данный момент времени, есть векторная величина, равная первой производной от вектора скорости или второй производной от радиус-вектора по времени.

Установим теперь положение вектора относительно траектории. Отметим, что плоскость треугольника МАВ, образованного векторами , и , при будет поворачиваться вокруг вектора , т.е. вокруг касательной к траектории в точке М, и займёт в пределе определённое предельной положение. Это предельное положение плоскости МАВ называется соприкасающейся плоскостью в точке М траектории. Вектор среднего ускорения направлен так же, как и , т.е. в сторону вогнутости кривой, и всё время находиться в плоскости треугольника МАВ. Предел вектора при есть вектор , который расположен в предельном положении треугольника МАВ, т.е. в соприкасающейся плоскости траектории точки М. Итак, вектор полного ускорения точки находиться в соприкасающейся плоскости траектории точки М направлен в сторону вогнутости траектории.

5. Как определяется модуль и ускорение точки при координатном способе задания движения?

Разложим радиус вектор по ортам декартовой системы координат: . Теперь дважды дифференцируем равенство по времени. В результате получим разложение ускорения по ортам i, j, k: , разложение можно представить так: , где , , – проекции вектора ускорения на оси координат. То есть, проекции вектора ускорения на неподвижные оси координат равны первым производным по времени от соответствующих проекций вектора скорости или вторым производным от соответствующих координат точки. По этим проекциям определяем величину вектора ускорения: .

6. Какие оси называются естественными осями? Дайте из определения и приведите соответствующий рисунок.

Единичный вектор касательной – , нормали – , бинормали – . Через эти векторы проходят плоскости: (, ) – соприкасающаяся, (,) – нормальная, (,) – спрямляющая. Три взаимно перпендикулярных направления, которые определяются векторам , , , образуют естественную систему координат, или так называемый естественный (подвижный) трёхгранник. Оси этой системы координат называются естественными осями (касательная, нормаль, бинормаль).

– Единичный вектор всегда направлен в сторону вогнутости кривой.

– Предельное положение секущей, проходящей через две точки кривой M и , когда стремиться к M, называется касательной к кривой в точке M. Единичным вектором этой касательной является вектор . Плоскость, образованная взаимно перпендикулярными векторами и называется соприкасающейся.

– Единичный вектор нормали всегда направлен в сторону вогнутости кривой, а геометрическое место нормалей к данной кривой называют нормальной плоскостью.

Как вычислить модуль скорости

Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько стремительно тело передвигается в пространстве. Перемещение полагает метаморфоза координат.

Инструкция

1. Введите систему координат, касательно которой вы будете определять направление и модуль скорости . Если в задаче теснее задана формула зависимости скорости от времени, вводить систему координат не надобно – предполагается, что она теснее есть.

2. По имеющейся функции зависимости скорости от времени дозволено обнаружить значение скорости в всякий момент времени t. Пускай, скажем, v=2t?+5t-3. Если требуется обнаружить модуль скорости в момент времени t=1, примитивно подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.

3. Когда задача требует обнаружить скорость в исходный момент времени, подставьте в функцию t=0. Таким же образом дозволено обнаружить время, подставив вестимую скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t?+5t-3=0. Отсель t=[-5±?(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а от того что время не может быть негативным, остается только t=1/2.

4. Изредка в задачах уравнение скорости дается в завуалированной форме. Скажем, в условии сказано, что тело двигалось равноускоренно с негативным убыстрением -2 м/с?, а в первоначальный момент скорость тела составляла 10 м/с. Негативное убыстрение обозначает, что тело равномерно замедлялось. Из этих условий дозволено составить уравнение для скорости : v=10-2t. С всей секундой скорость будет уменьшаться на 2 м/с, пока тело не остановится. В конце пути скорость обнулится, следственно легко обнаружить всеобщее время движения: 10-2t=0, откуда t=5 секунд. Через 5 секунд позже начала движения тело остановится.

5. Помимо откровенного движения тела, существует еще и движение тела по окружности. В всеобщем случае оно является криволинейным. Тут появляется центростремительное убыстрение, которое связано с линейной скоростью формулой a(c)=v?/R, где R – радиус. Комфортно рассматривать также угловую скорость ?, причем v=?R.

Модуль числа n представляет собой число единичных отрезков от начала координат до точки n. Причем не главно, в какую сторону будет отсчитываться это расстояние – вправо либо налево от нуля.

Инструкция

1. Модуль числа также принято называть безусловной величиной этого числа . Он обозначается короткими вертикальными линиями, проведенными слева и справа от числа . Скажем, модуль числа 15 записывается дальнейшим образом: |15|.

2. Помните, что модуль может быть только позитивным числом либо нулем. Модуль позитивного числа равен самому числу. Модуль нуля равен нулю. То есть для всякого числа n, которое огромнее либо равно нулю, будет объективна дальнейшая формула |n| = n. Скажем, |15| = 15, то есть модуль числа 15 равен 15-ти.

3. Модулем негативного числа будет то же число, но с противоположным знаком. То есть для всякого числа n, которое поменьше нуля, будет объективна формула |n| = -n. Скажем, |-28| = 28. Модуль числа -28 равен 28-ми.

4. Дозволено находить модули не только для целых, но и для дробных чисел. Причем в отношении дробных чисел действуют те же правила. Скажем, |0,25| = 25, то есть модуль числа 0,25 будет равен 0,25. А |-?| = ?, то есть модуль числа -? будет равен ?.

5. При работе с модулями пригодно знать, что модули противоположных чисел неизменно равны друг другу, то есть |n| =|-n|. Это является основным свойством модулей. Скажем, |10| = |-10|. Модуль числа 10 равен 10-ти, верно так же, как модуль числа -10. Помимо того, |a – b| = |b – a|, потому что расстояние от точки a до точки b и расстояние от b до a равны друг другу. Скажем, |25 – 5| = |5 – 25|, то есть |20| = |- 20|.

Для нахождения метаморфозы скорости определитесь с типом движения тела. В случае если движение тела равномерно, изменение скорости равно нулю. Если тело движется с убыстрением, то изменение его скорости в весь момент времени дозволено узнать, если отнять от мгновенной скорости в данный момент времени его исходную скорость.

Вам понадобится

• секундомер, спидометр, радар, рулетка, акселерометр.

Инструкция

1. Определение метаморфозы скорости произвольно движущегося по прямой траекторииС поддержкой спидометра либо радара измерьте скорость тела в начале и конце отрезка пути. После этого от финального итога отнимите первоначальный, это и будет изменение скорости тела.

2. Определение метаморфозы скорости тела, движущегося с ускорениемНайдите убыстрение тела. Используйте акселерометр либо динамометр. Если знаменита масса тела, тогда силу, действующую на тело, поделите на его массу (a=F/m). Позже этого измерьте время, за которое происходил процесс метаморфозы скорости . Дабы обнаружить изменение скорости , умножьте значение убыстрения на время, за которое происходило это изменение (?v=a•t).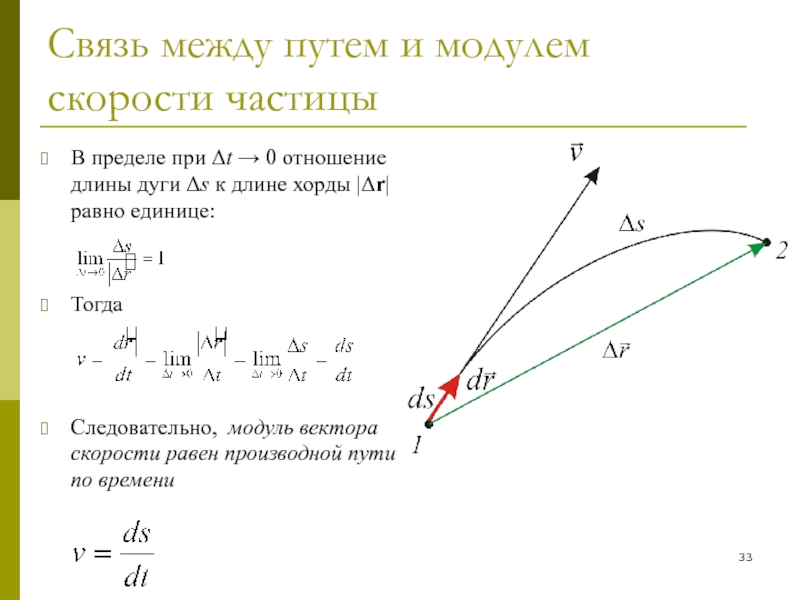 Если убыстрение измерить в метрах на секунду в квадрате, а время – в секундах, то скорость получится в метрах на секунду. Если нет вероятности замерить время, но вестимо, что скорость менялась на определенном отрезке пути, спидометром либо радаром, измерьте скорость в начале этого отрезка, после этого с поддержкой рулетки либо дальномера измерьте длину этого пути и убыстрение. Любым из вышеописанных способов измерьте убыстрение, которое действовало на тело. Позже этого обнаружьте финальную скорость тела в конце участка пути. Для этого возведите исходную скорость в квадрат, прибавьте к ней произведение длины участка на убыстрение и число 2. Из итога извлеките квадратный корень. Дабы обнаружить изменение скорости , от полученного итога отнимите значение исходной скорости .

3. Определение метаморфозы скорости тела при поворотеЕсли изменилась не только величина, но и направление скорости , то обнаружьте ее изменение через векторную разность исходной и финальной скорости . Для этого измерьте угол между векторами. После этого от суммы квадратов скоростей отнимите удвоенное их произведение, умноженное на косинус угла между ними: v1?+v2?-2v1v2•Cos(?). Из полученного числа извлеките квадратный корень.

Видео по теме

Для определения скорости разных видов движения потребуются различные формулы. Дабы определить скорость равномерного движения, расстояние поделите на время его прохождения. Среднюю скорость движения находите сложением всех отрезков, которое прошло тело, на всеобщее время движения. При равноускоренном движении узнайте убыстрение, с которым двигалось тело, а при свободном падении высоту, с которой оно предисловие движение.

Вам понадобится

• дальномер, секундомер, акселерометр.

Инструкция

1. Скорость равномерного движения и средняя скоростьИзмерьте расстояние с поддержкой дальномера, которое прошло тело, а время, за которое оно его одолело, с поддержкой секундомера. Позже этого поделите расстояние, пройденное телом на время его прохождения, итогом будет скорость равномерного движения (v=S/t). Если тело движется неравномерно, произведите те же измерения и примените ту же формулу – тогда получите среднюю скорость тела. Это значит, что если бы тело по данному отрезку пути двигалось с полученной скоростью, оно было бы в пути время, равное измеренному. Если тело движется по окружности, измерьте ее радиус и время прохождения полного цикла, после этого радиус умножьте на 6,28 и поделите на время (v=6,28•R/t). Во всех случаях итог получится в метрах в секунду. Для перевода в километры в час помножьте его на 3,6.

2. Скорость равноускоренного движенияИзмерьте убыстрение тела с поддержкой акселерометра либо динамометра, если знаменита масса тела. Секундомером замерьте время движения тела и его исходную скорость, если тело не начинает двигаться из состояния покоя. Если же тело двигается из состояния покоя, она равна нулю. Позже этого узнайте скорость тела, прибавив к исходной скорости произведение убыстрения на время (v=v0+at).

3. Скорость вольно падающего телаС поддержкой дальномера измерьте высоту, с которой падает тело в метрах. Дабы узнать скорость, с которой оно долетит до поверхности Земли (без контроля сопротивления воздуха), умножьте высоту на 2 и на число 9,81 (убыстрение свободного падения). Из итога извлеките квадратный корень. Дабы обнаружить скорость тела на всякий высоте, применяйте ту же методологию, только от исходной высоты, отнимайте нынешнюю и полученное значение подставляйте взамен высоты.

Видео по теме

Человек привык воспринимать представление “скорость ” как что-то больше примитивное, чем это есть на самом деле. Подлинно, проносящийся на перекрестке автомобиль движется с определенной скорость ю, в то время как человек стоит и отслеживает за ним. Но если человек находится в движении, то умнее говорить не об безусловной скорости, а об относительной ее величине. Обнаружить относительную скорость дюже легко.

Инструкция

1. Дозволено продолжить рассмотрение темы движущегося на перекрестка на автомобиле. Человек же, стоя на красном свете светофора, стоит и глядит на проезжающий автомобиль. Человек статичен, следственно примем его за систему отсчета. Система отсчета – такая система, касательно которой движется какое-нибудь тело либо другая физическая точка.

2. Возможен, автомобиль движется со скорость ю 50 км/ч. Но, возможен, что человек побежал следом автомобилю (дозволено, скажем, взамен автомобиля представить маршрутку либо проезжающий мимо автобус). Скорость бега человека 12 км/ч. Таким образом, скорость данного механического транспортного средства представится человеку не столь и стремительной, как было прежде, когда он стоял! В этом каждая и суть относительной скорости. Относительная скорость неизменно измеряется касательно подвижной системы отсчета. Таким образом, скорость автомобиля не будет для пешехода 50 км/ч, а 50 – 12 = 38 км/ч.

3. Дозволено разглядеть еще один живой пример. Довольно припомнить всякий из моментов, когда человек, сидя у окна автобуса, отслеживает за проносящимися мимо автомобилями. Подлинно, из окна автобуса их скорость кажется примитивно потрясающей. И это не изумительно, чай, если принять автобус за систему отсчета, то скорость автомобиля и скорость автобуса надобно будет сложить. Возможен, что автобус движется со скорость ю 50 км/ч, а машины 60 км/ч. Тогда 50 + 60 = 110 км/ч. Именно с такой скорость ю эти самые автомобили проносятся мимо автобуса и пассажиров в нем.Эта же скорость будет объективна и действительна и в том случае, если за систему отсчета принять всякий из проезжающих мимо автобусов автомобилей.

Кинематика постигает разные виды движения тела с заданной скоростью, направлением и траекторией. Дабы определить его расположение касательно точки начала пути, надобно обнаружить перемещение тела .

Инструкция

1. Движение тела происходит по некоторой траектории. В случае откровенного движения ею является прямая линия, следственно обнаружить перемещение тела достаточно примитивно: оно равно пройденному пути. В отвратном случае определить его дозволено по координатам исходного и финального расположения в пространстве.

2. Величина перемещения физической точки является векторной, от того что она имеет направление. Следственно, дабы обнаружить ее числовое значение, нужно вычислить модуль вектора, соединяющего точки начала пути и его окончания.

3. Разглядим двухмерное координатное пространство. Пускай тело проделало путь от точки A (x0, y0) до точки B (x, y). Тогда, дабы обнаружить длину вектора АВ, опустите проекции его концов на оси абсцисс и ординат. Геометрически проекции касательно той и иной координатной оси дозволено представить в виде катетов прямоугольного треугольника с длинами:Sx = x – x0;Sy = y – y0, где Sx и Sy – проекции вектора на соответствующих осях.

4. Модуль вектора, т.е. длина перемещения тела , в свою очередь, является гипотенузой этого треугольника, длину которой легко определить по теореме Пифагора. Он равен квадратному корню из суммы квадратов проекций:S = ?(Sx? + Sy?).

5. В трехмерном пространстве:S = ?(Sx? + Sy? + Sz?), где Sz = z – z0.

6. Это формула является всеобщей для всякий разновидности движения. Вектор перемещения владеет несколькими свойствами: • его модуль не может превышать длину пройденного пути;• проекция перемещения может быть как позитивной, так и негативной величиной, в то время как величина пути неизменно огромнее нуля;• в всеобщем случае перемещение не совпадает с траекторией движения тела , а его модуль не равен пути.

7. В частном случае откровенного движения тело перемещается только по одной оси, скажем, оси абсцисс. Тогда длина перемещения равна разности финальной и исходной первой координаты точек:S = x – x0.

От модуля исходной скорости во многом зависят колляции движения тела. Для того дабы обнаружить эту величину, нужно воспользоваться дополнительными измерениями либо данными. Величина модуля исходной скорости может являться основополагающей колляцией, скажем, для огнестрельного оружия.

Вам понадобится

• – рулетка;
• – дальномер;
• – секундомер;
• – акселерометр;
• – спидометр;
• – угломер;
• – хронограф.

Инструкция

1. Вначале определитесь с типом движения. Если оно равномерное, то довольно измерить длину пути, по которому переместилось тело, сделав это рулеткой, дальномером либо иным доступным методом, и поделить это значение на время, за которое это перемещение осуществлялось. От того что движение равномерное, то модуль скорости на протяжении каждого пути будет идентичен, так что полученная скорость будет равна исходной.

2. При равноускоренном откровенном движении измерьте при помощи акселерометра убыстрение тела, а с подмогой секундомера время его движения, спидометром финальную скорость в конце отрезка пути. Обнаружьте значение модуля исходной скорости, отняв от финальной скорости произведение убыстрения на время движения v0=v-a*t. Если незнакомо значение убыстрения, измеряйте расстояние, которое покрыло тело за время t. Сделайте это при помощи рулетки либо дальномера.

3. Зафиксируйте значение финальной скорости. Обнаружьте исходную скорость, отняв от удвоенного значения расстояния S, поделенного на время, значение финальной скорости v, v0=2S/t-v. Когда значение финальной скорости измерить трудно, а убыстрение знаменито, воспользуйтесь иной формулой. Для этого измеряйте перемещение тела, а также время, которое оно было в пути. От значения перемещения отнимите произведение убыстрения на квадрат времени, поделенное на 2, а итог поделите на время, v0=(S-at?/2)/t либо v0=S/t-at/2.

4. Когда тело начинает движение под углом к горизонту, на него воздействует сила тяжести. Для того дабы обнаружить модуль исходной скорости, при помощи угломера замеряйте угол к горизонту, под которым тело начинает двигаться. При помощи рулетки либо дальномера замеряйте расстояние, на котором тело упадет на поверхность земли. Дабы определить модуль исходной скорости, расстояние S поделите на синус удвоенного угла ?. Из полученного итога извлеките квадратный корень, v0=?(S/sin(2?)).

5. Дабы измерить модуль исходной скорости пули, выпущенной из стрелкового оружия, используйте хронограф. Для этого установите его так, как указано в его инструкции, от того что хронографы бывают различных типов. Позже этого сделайте выстрел из оружия, на табло хронографа появится итог. Выстрелите еще несколько раз и возьмите среднее значение показаний хронографа. Это и будет модуль исходной скорости пули, выпущенного из данного типа стрелкового оружия.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.

Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.

Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.

Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.

Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.

Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.

Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути соответствующее малому вектору по которому определяется вектор скорости. Вспомним, что Знак указывает

направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.

Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения

Здесь является алгебраической величиной, знак которой указывает, в какую сторону по касательной к траектории направлен вектор скорости.

Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение определяет угол наклона а касательной на этом графике. Наклон касательной на графике закона движения будет тем больше, чем больше т. е. чем больше в выбранный момент скорость движения.

Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.

Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.

Направление – вектор – перемещение

Направление – вектор – перемещение

Cтраница 1

Направление вектора перемещения указывает направление на конечный пункт из начальной точки движения. Модуль вектора перемещения указывает расстояние, на которое удалилось или приблизилось тело в результате движения.  [1]

Направление абсолютной скорости совпадает с направлением вектора перемещения S2 вертолета – с севера на юг.  [2]

Направление вектора скорости всегда совпадает с направлением вектора перемещения.  [4]

Направление вектора средней скорости совпадает с направлением вектора перемещения.  [5]

Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.  [6]

Направление вектора средней скорости точки совпадает с направлением вектора перемещения точки.  [7]

Из треугольника А А В на рисунке сразу видно, что модуль и направление вектора перемещения могут быть определены через эти разности.  [8]

Известны проекции вектора перемещения Дг на координатные оси: Д 3 см, Д / 4 см. Определите модуль и направление вектора перемещения.  [9]

Катер прошел по озеру в направлении точно на северо-восток 2 км, а затем еще 1 км на север. Найти графически модуль и направление вектора перемещения.  [10]

Выражая движение материальной точки вектором перемещения, мы абстрагируем ее движение, которое в действительности происходит не по прямой линии, а по дуге траектории. Только в частном случае прямолинейного движения направление вектора перемещения совпадает с траекторией точки. При криволинейном движении чем меньше промежуток времени между двумя последовательными положениями точки на траектории, тем меньше вектор перемещения и тем точнее он характеризует ее истинное движение. Очевидно, в пределе при бесконечно малом промежутке времени бесконечно малый по длине вектор перемещения совпадает с бесконечно малым участком траектории.  [11]

Рассмотренная проблема решается в стадии проектирования и строительства трубопроводов. С этой целью необходимо разработать методику расчета направления общего вектора перемещения опорных сечений трубопровода; расчет компенсаторов на прочность с учетом углов поворота, расчет поперечных перемещений в зависимости от угла поворота компенсаторов.  [12]

Итак, вектор скорости точки равен векторной производной вектор-радиуса точки по времени. Из ( 13) следует, что направление вектора скорости является предельным для направления вектора перемещения р при стремлении Д / к нулю. Вектор р направлен по секущей, предельным положением которой служит касательная к траектории; поэтому вектор скорости направлен по касательной к траектории в сторону движения точки.  [13]

Страницы:      1

Модуль – вектор – скорость

Модуль – вектор – скорость

Cтраница 1

Модули вектора скорости на рисунке приведены в логарифмическом масштабе. В ранние моменты времени в слое мягкого грунта отчетливо выделяется область, в которой движение вызвано воздействием воздушной ударной волны, и область, расположенная вблизи эпицентрального источника, в которой преобладает его воздействие. Движение грунта в первой области направлено почти вертикально вниз, а во второй области – преимущественно в радиальном направлении. В скальном грунте распространяется преломленная волна, движение в которой существенно отличается от радиального. Дальнейшее изменение волновой картины в слое мягкого грунта и в скальном основании определяется процессами формирования и распространения различных типов волн. На границе раздела мягкий грунт-скала формируется характерное вихревое движение грунтовой среды.  [2]

Модули векторов скорости vx ( в точке AJ и v2 ( в точке Л2) равны ( ух v2 v), но направления векторов различны.  [3]

Модуль вектора скорости кривой, записанной в натуральном параметре, постоянен и равен единице.  [4]

Нсли модуль вектора скорости точки изменяется с течением времени, то такое движение точки называется неравномерным.  [5]

Следовательно, модуль вектора скорости обратно пропорционален расстоянию точки от начала координат.  [6]

Закону Максвелла подчиняется модуль вектора скорости молекулы газа.  [7]

Если при криволинейном движении точки модуль вектора скорости этой точки возрастает, то движение называется ускоренным, а если г – замедленным.  [8]

Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение AS / A / определяет угол наклона а касательной на этом графике.  [9]

Эта проекция равна dv – приращению модуля вектора скорости.  [10]

Таким образом, несмотря на постоянство модуля вектора скорости VA точки А, вектор ускорения WA этой точки не обращается в нуль. Это объясняется тем, что движение точки А происходит по криволинейной траектории и вектор скорости VA все время изменяет свое направление.  [11]

Здесь р – плотность, V – модуль вектора скорости V, – угол V с осью х и а – угол Маха: since 1 / М, М V / a и а – скорость звука. Первое условие из (1.3) при равенстве определяет Уь Уд Y, а при знаке выполняется, если Уь Уд Y, т-е.  [12]

Кинетическая энергия системы материальных точек равна половине квадрата модуля вектора скорости v изображающей точки.  [13]

Ух Vy У2, отличается от истинного значения модуля вектора скоростей У / УХ У у У.  [14]

Та часть полного ускорения, от которой зависит изменение модуля вектора скорости, называется тангенциальным ускорением.  [15]

Страницы:      1    2    3    4

Модуль силы, скорости, импульса. Что это?!

В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!

Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.

Сила и модуль силы

В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.

Что такое модуль силы?

Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.

Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.

Модуль равнодействующих двух сил определяется по формулам:

• F=F1 + F2 (в случае сил с одинаковым направлением)
• F=F1 – F2 (силы с разным направлением)

Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.

Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).

Что это модуль скорости?

Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.

Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.

Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:

v = S/t = (x – x0)/t.

Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.

Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:

1. Вычисляется скорость v₂₁ на базе закона сложения скоростей v₂ = v₂₁ + v₁, а значит v₂₁ = v₂ – v₁.
2. Определяется модуль скорости тела согласно теореме Пифагора.

Модуль импульса и модуль оси

Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.

Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

4.1 Векторы смещения и скорости – University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Вычислить векторы положения в задаче многомерного смещения.
• Найдите смещение в двух или трех измерениях.
• Рассчитайте вектор скорости с учетом вектора положения как функцию времени.
• Рассчитайте среднюю скорость в нескольких измерениях.

Смещение и скорость в двух или трех измерениях являются прямым расширением одномерных определений.Однако теперь они являются векторными величинами, поэтому вычисления с ними должны производиться по правилам векторной алгебры, а не скалярной алгебры.

Вектор смещения

Чтобы описать движение в двух и трех измерениях, мы должны сначала установить систему координат и условные обозначения для осей. Обычно мы используем координаты x , y и z , чтобы найти частицу в точке P ( x , y , z ) в трех измерениях.Если частица движется, переменные x , y и z являются функциями времени ( t ):

Вектор положения от начала системы координат до точки P равен

В обозначении единичного вектора, введенном в Системах координат и компонентах вектора,

это

(рисунок) показывает систему координат и вектор к точке P , где частица может находиться в конкретный момент времени t .Обратите внимание на ориентацию осей x , y и z . Эта ориентация называется правой системой координат (системы координат и компоненты вектора), и она используется на протяжении всей главы.

Рис. 4.2. Трехмерная система координат с частицей в позиции P (x (t), y (t), z (t)).

С нашим определением положения частицы в трехмерном пространстве, мы можем сформулировать трехмерное смещение. (Рисунок) показывает частицу в момент времени

.

, расположенный по адресу

с вектором положения

Позже

частица расположена по адресу

с вектором положения

.Вектор смещения

находится вычитанием

из

Сложение векторов обсуждается в разделе «Векторы». Обратите внимание, что это та же операция, которую мы проделали в одном измерении, но теперь векторы находятся в трехмерном пространстве.

Рисунок 4.3 Смещение

– вектор из

С

по

.

Следующие примеры иллюстрируют концепцию смещения в нескольких измерениях.

Пример

Полярный орбитальный спутник

Спутник находится на круговой полярной орбите вокруг Земли на высоте 400 км, то есть он проходит прямо над головой на Северном и Южном полюсах. Какова величина и направление вектора смещения от момента, когда он находится непосредственно над Северным полюсом, до момента, когда он находится на отметке

?

широта?

Стратегия

Мы делаем картину проблемы, чтобы визуализировать решение графически.Это поможет нам понять смещение. Затем мы используем единичные векторы для определения смещения.

Решение

[Показать-ответ q = ”768411 ″] Показать ответ [/ Показать-ответ]
[hidden-answer a =” 768411 ″] (Рисунок) показывает поверхность Земли и круг, который представляет орбиту спутника. Хотя спутники движутся в трехмерном пространстве, они следуют траекториям эллипсов, которые можно изобразить в двух измерениях. Векторы положения отрисовываются от центра Земли, который мы принимаем за начало системы координат, с осью y на север и осью x на восток.Вектор между ними – это смещение спутника. Мы берем радиус Земли равным 6370 км, поэтому длина каждого вектора положения составляет 6770 км.

Рис. 4.4. Два вектора положения нарисованы от центра Земли, который является началом системы координат, с осью Y как север и осью x как восток. Вектор между ними – это смещение спутника.

[/ hidden-answer]

В обозначении единичного вектора векторы положения равны

.

Вычисляя синус и косинус, получаем

Теперь мы можем найти

, перемещение спутника:

Величина смещения

Угол смещения относительно оси x- составляет

Значение

Построение смещения дает информацию и смысл решения задачи с помощью единичного вектора.При построении смещения нам необходимо включить его компоненты, а также его величину и угол, который он образует с выбранной осью – в данном случае осью x ((рисунок)).

Рис. 4.5. Вектор смещения с компонентами, углом и величиной.

Обратите внимание, что в этом примере спутник прошел криволинейный путь по своей круговой орбите, чтобы перейти от своего начального положения к конечному положению. Он также мог пройти 4787 км на восток, затем на 11,557 км к югу, чтобы прибыть в то же место.Оба этих пути длиннее вектора смещения. Фактически, вектор смещения дает кратчайший путь между двумя точками в одном, двух или трех измерениях.

Многие приложения в физике могут иметь серию смещений, как обсуждалось в предыдущей главе. Общее смещение – это сумма отдельных смещений, только на этот раз нам нужно быть осторожными, потому что мы добавляем векторы. Проиллюстрируем эту концепцию на примере броуновского движения.

Пример

Броуновское движение

Броуновское движение – это хаотическое случайное движение взвешенных в жидкости частиц, возникающее в результате столкновений с молекулами жидкости. Это движение трехмерное. Смещения в числовом порядке частицы, совершающей броуновское движение, могут выглядеть в микрометрах следующим образом ((Рисунок)):

Каково полное смещение частицы от начала координат?

Рисунок 4.6 Траектория частицы, совершающей случайные смещения броуновского движения. Общее смещение показано красным.

Решение

[show-answer q = ”979563 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 979563 ″] Мы формируем сумму смещений и складываем их как векторы:

Чтобы завершить решение, мы выражаем смещение как величину и направление,

относительно оси x в плоскости xz.[/ hidden-answer]

Значение

Из рисунка видно, что величина полного смещения меньше суммы величин отдельных смещений.

Вектор скорости

В предыдущей главе мы нашли мгновенную скорость, вычислив производную функции положения по времени. Мы можем проделать ту же операцию в двух и трех измерениях, но мы используем векторы. Вектор мгновенной скорости теперь равен

.

Давайте посмотрим на взаимную ориентацию вектора положения и вектора скорости графически.На (Рисунок) мы показываем векторы

и

, которые показывают положение частицы, движущейся по траектории, представленной серой линией. Как

обращается в ноль, вектор скорости, представленный (рисунок), становится касательным к траектории частицы в момент времени t .

Рис. 4.7. Частица движется по траектории, обозначенной серой линией. В пределе как

стремится к нулю, вектор скорости становится касательным к траектории частицы.

(Уравнение) также можно записать в терминах компонентов

с

мы можем написать

где

Если важна только средняя скорость, у нас есть векторный эквивалент одномерной средней скорости для двух и трех измерений:

Пример

Расчет вектора скорости

Функция положения частицы равна

.

(a) Каковы мгновенные скорость и скорость при t = 2.0 с? (б) Какая средняя скорость составляет от 1,0 до 3,0 с?

Решение

Используя (рисунок) и (рисунок) и взяв производную функции положения по времени, находим

[show-answer q = ”459626 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 459626 ″] (a)

Скорость

[/ hidden-answer]

(b) Из (Рисунок),

[show-answer q = ”751231 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 751231 ″]

[/ hidden-answer]

Значение

Мы видим, что средняя скорость совпадает с мгновенной скоростью при t = 2.0 с, так как функция скорости линейна. В общем случае этого не должно быть. Фактически, в большинстве случаев мгновенная и средняя скорости не совпадают.

Проверьте свое понимание

Функция положения частицы равна

.

(а) Какова мгновенная скорость при t = 3 с? (b) Равна ли средняя скорость от 2 до 4 с мгновенной скорости при t = 3 с?

[показывать-ответ q = ”fs-id1165038199839 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038199839 ″]

(a) Взяв производную по времени от функции положения, получаем

(b) Поскольку функция скорости нелинейна, мы подозреваем, что средняя скорость не равна мгновенной скорости.Проверяем это и находим

, который отличается от

[/ hidden-answer]

Независимость перпендикулярных движений

Когда мы смотрим на трехмерные уравнения для положения и скорости, записанные в обозначении единичного вектора (Рисунок) и (Рисунок), мы видим, что компоненты этих уравнений являются отдельными и уникальными функциями времени, которые не зависят друг от друга. Движение в направлении x не имеет части своего движения в направлениях y и z , и аналогично для двух других координатных осей.Таким образом, движение объекта в двух или трех измерениях можно разделить на отдельные независимые движения по перпендикулярным осям системы координат, в которой происходит движение.

Чтобы проиллюстрировать эту концепцию относительно смещения, рассмотрим женщину, идущую от точки A до точки B в городе с квадратными кварталами. Женщина, идущая по пути от A до B , может пройти на восток столько кварталов, а затем на север (в двух перпендикулярных направлениях) еще один набор кварталов, чтобы добраться до B .Насколько далеко она идет на восток, зависит только от ее движения на восток. Точно так же, как далеко она идет на север, зависит только от ее движения на север.

Независимость движения

В кинематическом описании движения мы можем рассматривать горизонтальные и вертикальные компоненты движения отдельно. Во многих случаях движение в горизонтальном направлении не влияет на движение в вертикальном направлении, и наоборот.

Пример, иллюстрирующий независимость вертикального и горизонтального движений, дают два бейсбольных мяча.Один бейсбольный мяч выпадает из отдыха. В тот же момент другой бросается горизонтально с той же высоты, и он следует по изогнутой траектории. Стробоскоп фиксирует положение шаров через фиксированные промежутки времени, когда они падают ((Рисунок)).

Рис. 4.8. Схема движения двух одинаковых шаров: один падает из состояния покоя, а другой имеет начальную горизонтальную скорость. Каждая последующая позиция представляет собой равный временной интервал. Стрелки обозначают горизонтальную и вертикальную скорости в каждой позиции.Мяч справа имеет начальную горизонтальную скорость, тогда как шар слева не имеет горизонтальной скорости. Несмотря на разницу в горизонтальных скоростях, вертикальные скорости и положения идентичны для обоих мячей, что показывает, что вертикальное и горизонтальное движения независимы.

Примечательно, что для каждой вспышки строба вертикальное положение двух шариков одинаково. Это сходство подразумевает, что вертикальное движение не зависит от того, движется ли мяч горизонтально.(Предполагая, что сопротивление воздуха отсутствует, на вертикальное движение падающего объекта влияет только сила тяжести, а не какие-либо горизонтальные силы.) Тщательное изучение мяча, брошенного в горизонтальном направлении, показывает, что он проходит одинаковое расстояние по горизонтали между вспышками. Это связано с тем, что после броска на мяч в горизонтальном направлении не действуют дополнительные силы. Этот результат означает, что горизонтальная скорость постоянна и на нее не влияет ни вертикальное движение, ни сила тяжести (которая является вертикальной). Обратите внимание, что этот случай верен только для идеальных условий.В реальном мире сопротивление воздуха влияет на скорость мячей в обоих направлениях.

Двумерная кривая траектория горизонтально брошенного мяча состоит из двух независимых одномерных движений (горизонтального и вертикального). Ключ к анализу такого движения, называемого движением снаряда , состоит в том, чтобы разделить его на движения в перпендикулярных направлениях. Разложение двумерного движения на перпендикулярные компоненты возможно, потому что компоненты независимы.

Сводка

• Функция положения

  дает положение как функцию времени частицы, движущейся в двух или трех измерениях.Графически это вектор от начала выбранной системы координат до точки, в которой частица находится в определенное время.

• Вектор смещения

  дает кратчайшее расстояние между любыми двумя точками траектории частицы в двух или трех измерениях.

• Мгновенная скорость определяет скорость и направление частицы в определенный момент времени на ее траектории в двух или трех измерениях и является вектором в двух и трех измерениях.
• Вектор скорости касается траектории частицы.
• Рабочий объем

  можно записать как векторную сумму одномерных перемещений

  по направлениям x , y и z .

• Скорость

  можно записать как векторную сумму одномерных скоростей

  по направлениям x , y и z .

• Движение в любом заданном направлении не зависит от движения в перпендикулярном направлении.

Концептуальные вопросы

Какую форму имеет траектория частицы, если расстояние от любой точки A, до точки B равно величине смещения от A до B ?

[show-answer q = ”fs-id1165038186961 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1165038186961 ″]

прямая

[/ hidden-answer]

Приведите пример траектории в двух или трех измерениях, вызванной независимыми перпендикулярными движениями.

Если мгновенная скорость равна нулю, что можно сказать о наклоне функции положения?

[показывать-ответ q = ”fs-id1165038186997 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038186997 ″]

Наклон должен быть нулевым, потому что вектор скорости касается графика функции положения.

[/ hidden-answer]

Проблемы

Координаты частицы в прямоугольной системе координат (1.0, –4,0, 6,0). Каков вектор положения частицы?

[показывать-ответ q = ”fs-id1165038204787 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038204787 ″]

[/ hidden-answer]

Положение частицы меняется с

С

по

Что такое смещение частицы?

18-я лунка на поле для гольфа Pebble Beach находится на изогнутой ноге слева длиной 496.0 мес. Фервей от ти принимается в направлении x . Гольфист наносит удар с мишени на расстоянии 300,0 м, что соответствует смещению

.

и попадает вторым выстрелом 189,0 м с водоизмещением

Каково окончательное смещение мяча для гольфа от тройника?

[показывать-ответ q = ”fs-id1165038184449 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038184449 ″]

[/ hidden-answer]

Птица летит прямо на северо-восток на расстояние 95.0 км за 3,0 ч. Если ось x направлена ​​на восток, а ось y направлена ​​на север, каково смещение птицы в единичном векторе? Какая средняя скорость поездки?

Велосипедист едет 5,0 км на восток, затем 10,0 км

к западу от севера. С этого момента она едет на 8,0 км на запад. Каково окончательное смещение, с которого велосипедист стартовал?

[показывать-ответ q = ”fs-id1165038192940 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038192940 ″]

[/ hidden-answer]

Защитник «Нью-Йорк Рейнджерс» Даниэль Жирарди стоит у ворот и передает хоккейную шайбу на 20 м и

прямо по льду на левый фланг Крис Крайдер ждет у синей линии.Крайдер ждет, пока Жирарди дойдет до синей линии, и передает шайбу прямо по льду ему в 10 метрах от него. Какое окончательное перемещение шайбы? См. Следующий рисунок.

Положение частицы

(а) Какова скорость частицы в 0 с и

?

с? (б) Какова средняя скорость между 0 с и

?

с?

[show-answer q = ”fs-id1165038187651 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1165038187651 ″]

а.

,
б.

[/ hidden-answer]

Клэй Мэтьюз, полузащитник «Грин Бэй Пакерс», может развивать скорость до 10,0 м / с. В начале игры Мэтьюз бежит вниз на

.

относительно 50-ярдовой линии и преодолевает 8,0 м за 1 с. Затем он бежит прямо по полю на

.

относительно 50-ярдовой линии на 12 м с затраченным временем 1,2 с.(а) Каково окончательное смещение Мэтьюза с начала пьесы? б) Какова его средняя скорость?

F-35B Lighting II – истребитель с коротким взлетом и вертикальной посадкой. Если он выполняет вертикальный взлет на высоту 20,00 м над землей, а затем следует по траектории полета под углом

относительно земли на 20,00 км, какое конечное смещение?

[показывать-ответ q = ”fs-id1165038218974 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038218974 ″]

[/ hidden-answer]

Глоссарий

вектор смещения

вектор из начального положения в конечное положение на траектории частицы

вектор положения

вектор от начала выбранной системы координат до положения частицы в двух- или трехмерном пространстве

Вектор скорости

вектор, задающий мгновенную скорость и направление частицы; касательная к траектории

векторов скорости – видео по физике от Brightstorm

Вектор скорости представляет скорость изменения положения объекта.Величина вектора скорости дает скорость объекта, а направление вектора дает его направление. Векторы скорости могут быть добавлены или вычтены в соответствии с принципами сложения векторов.

Нормальные векторы скорости. Помните, что вектор – это то, что имеет как величину, так и направление, так что в этом случае у меня есть вектор, идущий со скоростью 4 метра в секунду на восток.Хорошо, и я собираюсь масштабировать так, чтобы 40 сантиметров соответствовали 4 метрам в секунду, хорошо. Векторы можно складывать или вычитать, и если они находятся в одной плоскости, это довольно простое уравнение. Давайте рассмотрим несколько примеров, так что у меня мои 4 метра в секунду на восток, и, допустим, я гребу на каноэ со скоростью 4 метра в секунду, хорошо, и я гребу по течению, и течение 3 метра в секунду на восток. Что ж, это довольно простая задача сложения: 4 метра в секунду на восток плюс 3 метра в секунду на восток – это 7 метров в секунду, это мой общий вектор.

Хорошо, это также довольно просто, если у меня есть векторы, идущие в противоположных направлениях, я просто вычитаю второй вектор из первого. Так что теперь я плыву не вниз по течению, а вверх по течению, и течение идет против меня. Итак, моим 4 метрам в секунду на восток противостоит вектор, который движется со скоростью 3 метра в секунду на запад. Я постараюсь быть более точным там, и, вероятно, он будет примерно там. Итак, если я вычту 3 из 4, я получу 1 метр в секунду. Восток – это мой общий вектор. Хорошо, теперь это довольно просто, и иногда вы видите подобные проблемы, но часто векторы не движутся ни в одном направлении, ни в противоположном направлении, но они часто движутся под прямым углом.Итак, теперь давайте возьмем мое каноэ и скажем, что я не иду вверх или вниз по реке, а я иду через реку. Хорошо, и вот я гребу на своем каноэ со скоростью 4 метра в секунду на восток, но река течет на юг, а она течет на юг со скоростью 3 метра в секунду.

Хорошо, теперь, когда я добавляю свой вектор, я не просто получаю меньший или больший вектор, я на самом деле получаю вектор, который находится под другим углом, в другом направлении. Итак, когда я соединяю свои 2 вектора, я получаю треугольник, и теперь, чтобы вычислить эту скорость, мне нужно немного математики, и, поскольку у меня есть прямоугольный треугольник, я могу смотреть на эти значения.Итак, у меня есть это значение и это значение, если у меня есть это значение в квадрате и это значение в квадрате, оно будет равно этому значению в квадрате. Итак, давайте продолжим и напишем, что формула a в квадрате плюс b в квадрате равно c в квадрате, и это значение, которое я хочу найти прямо там, c. Хорошо, если я пойду дальше и решу, что у меня 4 в квадрате равно 16, 3 в квадрате равно 9 и это равно 25. Ну 25, квадратный корень из 25 равен 5, поэтому мой новый вектор здесь 5 метров в секунду на юго-восток и вот как вы решаете задачи векторной скорости.

2.5: Скорость и ускорение – Математика LibreTexts

Поскольку векторы скорости и ускорения определены как первая и вторая производные вектора положения, мы можем вернуться к вектору положения путем интегрирования.

Пример \ (\ PageIndex {4} \)

Вы являетесь оператором противоракетной обороны и заметили летящую к вам ракету в позиции

.

\ [\ textbf {r} _e = 1000 \ hat {\ textbf {i}} + 500 \ hat {\ textbf {j}} \]

со скоростью

\ [\ textbf {v} _e = -30 \ hat {\ textbf {i}} + 3 \ hat {\ textbf {j}}.\]

Вы можете стрелять противоракетами со скоростью 100 метров в секунду. Под каким углом стрелять, чтобы перехватить ракету. Предположим, что гравитация – единственная сила, действующая на снаряды.

Решение

Вектор ускорения ракеты противника

\ [\ textbf {a} _e (t) = -9,8 \ hat {\ textbf {j}}. \]

Интегрируя, получаем вектор скорости

\ [\ textbf {v} _e (t) = v_1 \ hat {\ textbf {i}} + (v_2-9.8t) \ hat {\ textbf {j}}.2 + 3t + 500) \ hat {\ textbf {j}}. \]

Ускорение вашей противоракетной ракеты тоже

\ [\ textbf {a} _y (t) = -9,8 t \ hat {\ textbf {j}}. \]

Интегрируя, получаем вектор скорости

\ [\ textbf {v} _y (t) = v_1 \ hat {\ textbf {i}} + (v_2-9.8t) \ hat {\ textbf {j}}. \]

Поскольку величина нашей скорости равна 100, мы можем сказать

\ [\ textbf {v} _y (0) = 100 \ cos q \ hat {\ textbf {i}} + 100 \ sin q \ hat {\ textbf {j}}. \]

Так что

\ [\ textbf {v} _y (t) = 100 \ cos q \ hat {\ textbf {i}} + (100 \ sin q -9.2 + 3т + 500. \]

Первое уравнение дает

\ [t = \ dfrac {1000} {100 \ cos q + 30}. \]

Упрощение второго уравнения и его замена дает

\ [\ dfrac {100000 \ sin q} {100 \ cos q + 30} = \ dfrac {3000} {100 \ cos q + 30} + 500. \]

Очистите знаменатели, чтобы получить

\ [100000 \ sin q = 3000 + 50000 \ cos q + 15000. \]

На этом этапе мы используем калькулятор, чтобы найти для \ (q \) значение

.

\ [q = 0,62535 \; рад. \]

4.1 Векторы смещения и скорости – University Physics Volume 1

Полярный орбитальный спутник

Спутник находится на круговой полярной орбите вокруг Земли на высоте 400 км, то есть он проходит прямо над северным и южным полюсами. Каковы величина и направление вектора смещения от момента, когда он находится непосредственно над Северным полюсом, до момента, когда он находится на широте -45 ° -45 °?

Стратегия

Мы делаем картину проблемы, чтобы наглядно представить ее решение. Это поможет нам понять смещение.Затем мы используем единичные векторы для определения смещения.

Решение

На рисунке 4.4 показана поверхность Земли и круг, обозначающий орбиту спутника. Хотя спутники движутся в трехмерном пространстве, они следуют траекториям эллипсов, которые можно изобразить в двух измерениях. Векторы положения отрисовываются от центра Земли, который мы принимаем за начало системы координат, с осью y как север и осью x как восток.Вектор между ними – это смещение спутника. Мы берем радиус Земли равным 6370 км, поэтому длина каждого вектора положения составляет 6770 км.

Фигура 4.4 Два вектора положения отрисовываются от центра Земли, который является началом системы координат, с осью y как север и осью x как восток. Вектор между ними – это смещение спутника.

В обозначении единичного вектора векторы положения равны

. г → (t1) = 6770..

Величина смещения составляет | Δr → | = (4787) 2 + (- 11,557) 2 = 12,509 км. | Δr → | = (4787) 2 + (- 11,557) 2 = 12,509 км. Угол смещения относительно оси x- равен θ = tan − 1 (−11,5574787) = -67,5 °. Θ = tan − 1 (−11,5574787) = -67,5 °.

Значение

Построение смещения дает информацию и смысл единичному вектору решения проблемы. При построении смещения нам необходимо включить его компоненты, а также его величину и угол, который он составляет с выбранной осью – в данном случае осью x (рисунок 4.5).

Фигура 4.5 Вектор смещения с компонентами, углом и величиной.

Обратите внимание, что в этом примере спутник прошел криволинейный путь по своей круговой орбите, чтобы перейти от своего начального положения к конечному положению. Он также мог пройти 4787 км на восток, затем на 11,557 км к югу, чтобы прибыть в то же место. Оба этих пути длиннее вектора смещения. Фактически, вектор смещения дает кратчайший путь между двумя точками в одном, двух или трех измерениях.

Многие приложения в физике могут иметь серию смещений, как обсуждалось в предыдущей главе. Общее смещение – это сумма отдельных смещений, только на этот раз нам нужно быть осторожными, потому что мы добавляем векторы. Проиллюстрируем эту концепцию на примере броуновского движения.

векторов – Механика – Математика A-Level Revision

Векторная величина имеет как величину, так и направление. Ускорение, скорость, сила и перемещение – все это примеры векторных величин.Скалярная величина имеет величину, поэтому направление не имеет значения (например, скорость, время и расстояние). Скаляр также может иметь знак (например, выполненная работа и начисление).

Векторы обычно представлены следующим образом:

Стрелка показывает направление, а число (в данном случае v) представляет величину.

Буквы, используемые для обозначения векторов, всегда должны быть подчеркнуты или выделены жирным шрифтом. Например, скорость объекта может быть представлена ​​как v .Поскольку это векторная величина, она выделена жирным шрифтом. Строчные буквы обычно используются для обозначения векторов.

Единичные векторы

Единичный вектор – это вектор, который имеет величину 1. Обычно используются три важных единичных вектора, и это векторы в направлении осей x, y и z. Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси y равен j , а единичный вектор в направлении оси z равен k .

Запись векторов в этой форме может облегчить работу с векторами.

Например, вектор 5 i – 3 j на диаграмме будет выглядеть примерно так:

Добавление векторов

Если два вектора складываются вместе, результат находится путем размещения добавляемых векторов встык. Если векторы заданы в форме единичного вектора, вы просто складываете значения i , j и k .

Пример

p = 3 i + j , q = -5 i + j . Найдите p + q .

Поскольку векторы заданы в форме i , j , мы можем легко вычислить результат. 3 i + j -5 i + j = -2 i + 2 j

Это также могло быть получено из диаграммы:

Величина вектора

Величину вектора можно найти с помощью теоремы Пифагора.

Разрешение вектора

Разрешение вектора означает определение его величины в определенном направлении.

На диаграмме выше вектор r имеет величину r и направление j относительно оси x. Используя базовую тригонометрию, мы можем вычислить, что составляющая r в направлении оси x равна rcosj. Компонент в направлении оси y равен rsinj. Следовательно, r = rcosj i + rsinj j .

Ветер: компоненты u и v

Воздушный поток в атмосфере имеет скорость и направление. Математически это представлено вектором. Карты, показывающие ветры, также иногда отображают их в виде векторов. Помните, что зазубрины указывают направление ветра. приходящий из. Стрелки (векторы) ветра указывают направление ветер дует навстречу.

Также помните, что по соглашению мы говорим о ветрах с точки зрения их направления.Итак, если я говорю «южный ветер», это ветер с юга. Колючка ветра будет направлена ​​на юг, а стрелка ветра будет быть направленным на север.

Как ветер сообщается в необработанных наблюдениях (например, метары) для южного ветра 180 °, восточного ветра 90 ° и т. д. См. Рисунок ниже:

К сожалению, как только мы начинаем думать о ветре как о математическом вектор, мы хотим использовать математическое соглашение для направление:

Чтобы преобразовать «метеорологическое направление» в «математическое направление», используйте эту формулу (в градусах):

md = 270 – wwd где md – “математическое” направление ветра, а wwd – “направление погодного ветра”.Если значение меньше нуля, просто добавьте 360. Обратите внимание, что с помощью нашего математического ветра направление, при сильном западном ветре вектор будет направлен вдоль ось x и, следовательно, направление ноль градусов.

К счастью, почти все данные о ветре, с которыми мы могли бы работать, уже преобразовано в “математическое” направление ветра. И мы всегда будем предполагать «математическое» направление ветра, когда мы работаем с уравнениями.

---

В метеорологии принято работать с u и v. компоненты ветра.

Помните, что вектор можно разбить на составляющие векторы, где единичный вектор i проходит параллельно к оси x, а вектор j проходит параллельно оси ось y.

Для ветров ветер u параллелен оси x. Положительный у ветер с запада. Ветер отрицательный с востока. Ветер v идет параллельно оси y. Положительный ветер v от южный, и отрицательный ветер с севера.

Если у нас есть скорость и направление ветра, мы можем получить компонент вектора winds, u и v, следующим образом:

u = ws * cos (θ)

v = ws * sin (θ)

где θ – направление ветра с использованием “математического” направления, и ws – скорость ветра (т. е. величина вектора ветра).См. ниже:

При использовании sin и cos на калькуляторе или компьютере позаботьтесь о переводе из градусов в радианы, если необходимо.

Данные о ветре из численных моделей и систем объективного анализа всегда сообщается как величина составляющих векторов u и v. Таким образом, они представлены в виде скалярных полей. Программные пакеты для просмотр данных о погоде будет есть способы комбинировать данные о компонентах ветра u и v для отображения стрел ветра, колючек ветра и линий тока.

Учитывая компоненты u и v, как мы определяем направление и величина вектора ветра? Чтобы получить величину (или скорость ветра) воспользуемся теоремой Пифагора:

ws = sqrt (u ² + v ² ) Проще говоря, это квадратный корень из суммы квадратов.

Чтобы получить направление, снова обратимся к тригонометрии. У нас есть x и y (u и v), и нам нужен угол. Это будет требуется обратная триггерная функция для tan – например, arctan (v / u).

Однако все гораздо сложнее. Когда u равно нулю, мы не можем использовать функцию arctan. Кроме того, мы должны отрегулируйте, в каком квадранте мы находимся, в зависимости от знака u и v.

На компьютере стандартные математические библиотеки имеют функцию atan2, который принимает два аргумента – величины компонент вектора. Эта функция решает проблемы с arctan. См. Запись в Википедии для atan2, чтобы узнать, что он делает, особенно эта таблица:

Если вам когда-нибудь понадобится преобразовать u и v в скорость и направление, и вы запутались в направлении, нанося u и v ветры в виде векторов на графике дадут вам представление о том, что угол полного вектора ветра будет быть.Обязательно нанесите положительный вектор u, указывающий вправо. от происхождения, и отрицательный вектор u, указывающий налево. Положительный v вектор указывает вверх, а отрицательный вектор v указывает вниз.

Ниже представлены четыре сюжета. Первый – это сюжет про ветер. величина, нанесенная в виде скалярного поля с использованием контуров. 2-й – график поля ветра v. Третий – это сюжет скорости ветра. Четвертый – это сюжет линий тока. (линии сопоставляются ветровому потоку).

Внимательно обратите внимание на то, как различные значения (как положительные, так и отрицательные) u и v вместе создают скорость и направление.

Параллельные векторы – объяснение и примеры

Скалярное умножение дает параллельных векторов. Это векторы, которые:

«Имеют одинаковое или противоположное направление и являются скалярными кратными друг другу».

В этом разделе мы обсудим следующие важные аспекты параллельных векторов:

• Что такое параллельные векторы?
• Как определить, параллельны ли два вектора.

Что такое параллельные векторы?

Обычно два параллельных вектора являются скалярными, кратными друг другу.Предположим, что два вектора a и b, определены как:

b = c * a

, где c – некоторое скалярное действительное число. В приведенном выше уравнении вектор b выражается как скалярное кратное векторам a, , и два вектора называются параллельными. Знак скаляра c будет определять направление вектора b. Если значение c положительное, c> 0, оба вектора будут иметь одинаковое направление. Если значение c отрицательное, то есть c <0, вектор b будет указывать в направлении, противоположном вектору a.

Аналогично, из приведенного выше уравнения вектор a может быть выражен как:

a = 1 / c * b

Таким образом, ясно, что они должны быть скалярными кратными друг другу для любые два вектора должны быть параллельны. Рассмотрим случай, когда значение c равно нулю. Тогда мы можем написать:

b = 0 * a

b = 0

Вектор b становится нулевым вектором в этом случае, и нулевой вектор считается параллельным каждому вектору .

Как определить, параллельны ли два вектора

Чтобы определить, параллельны ли два вектора или нет, мы проверяем, могут ли данные векторы быть выражены как скалярные кратные друг другу. Например, два вектора U и V параллельны, если существует действительное число t, такое, что:

U = t * V

Это число t может быть положительным, отрицательным, или ноль.

Примеры

В этом разделе мы обсудим примеры, связанные с параллельными векторами и их пошаговые решения.Это поможет глубже понять параллельные векторы.

Пример 1

Автомобиль движется с вектором скорости V1 = 30 м / с на север, а другой автомобиль движется на север с вектором скорости V2 = 60 м / с. Определите, параллельны два вектора скорости или нет.

Решение

У нас есть следующая информация:

V1 = 30 м / с, север

V2 = 60 м / с, север

Чтобы определить, параллельны ли данные векторы, мы проверяем, могут ли они быть кратными друг другу или нет.Мы можем связать два вектора следующим образом:

V2 = 2 * (30 м / с)

V2 = 2 * V1

V2 = 2 * (30 м / с)

Или,

V1 = 1/2 * V1

V1 = 1/2 * (60 м / с)

V1 = 30 м / с.

Поскольку данные векторы могут быть связаны друг с другом скалярным множителем 2 или 1/2, мы можем заключить, что два вектора скорости V1, и V2, параллельны друг другу.

Пример 2

Учитывая два вектора, S1 = (2, 3) и S2 = (10, 15), определите, параллельны два вектора или нет. Затем определите величину двух векторов.

Решение

Данные векторы S1 и S2 выражены в виде столбцов. Чтобы определить, являются они или параллельны, мы можем проверить, могут ли их соответствующие компоненты быть выражены как скалярные кратные друг другу или нет.

S2 = (5 * 2, 5 * 3)

S2 = 5 * (2, 3)

S2 = 5 * S1

Или

S1 = 1 / 5 * S2

Из приведенных выше уравнений очевидно, что векторы S1 и S2 являются скалярными кратными друг другу, а коэффициент масштабирования равен 5 или 1/5. 2

| S2 | = √100 + 225

| S2 | = √325

| S2 | = √25 * 13

| S2 | = 5 * √13

Величины двух векторов также связаны коэффициентами масштабирования.

Пример 3

Учитывая два вектора, P = (4, 6) и Q = (-2, -3), определите, параллельны два вектора или нет.

Решение

Данные векторы P и Q выражены в виде столбцов. Чтобы определить, являются они или параллельны, мы можем проверить, могут ли их соответствующие компоненты быть выражены как скалярные кратные друг другу или нет.

P = (4, 6)

Q = (-2, -3)

P = -2 (-2, -3)

P = -2 * Q

Поскольку вектор P в 2 раза больше вектора Q , два вектора параллельны друг другу, а направление вектора Q противоположно направлению вектора P .

Пример 4

Обратитесь к изображению, приведенному ниже, и определите параллельные векторы.

Решение

Все четыре вектора, показанные на изображении, параллельны друг другу, поскольку их можно выразить как скалярное кратное другим.

Чтобы проверить это, выразите векторы в их формах столбцов как:

A = (10,10) , вектор B = (-10, -10), C = (-5, -5) и D = (5, 5)

Сначала мы проверяем, параллельны ли векторы A и B или нет.

Очевидно, что вектор B может быть выражен как:

B = (-10, -10)

B = -1 * (10,10)

Или

B = -1 * A

Таким образом, векторы A и B параллельны друг другу.

Затем мы проверяем векторы C и D как:

D = (5, 5)

C = -1 * (5,5)

C = -1 * D

Векторы C и D также являются скалярными кратными друг другу.

Аналогично проверяем отношения между оставшимися векторами:

B = 2 * C

B = – 2 * D

C = – 2 * A

D = 2 * A

Таким образом, из приведенных выше уравнений и данного изображения ясно, что все четыре вектора, A , B , C, и D, параллельны друг другу.

Пример 5

Учитывая, что векторы A = (-4, 6) и B = (x, 12) являются параллельными векторами, определите значение x.

Решение

Поскольку векторы параллельны, мы знаем, что:

B = c * A

Где c – некоторое скалярное значение. Подстановка значений векторов дает нам:

(x, 12) = c * (-4, 6)

(x, 12) = (-4c, 6c)

Установив значения отдельных компонентов, равные каждому другое, мы получаем:

x = -4c

12 = 6c

Упрощение приведенных выше уравнений дает нам:

c = 2

Если мы поместим значение c в другое уравнение и упростим, мы получим:

x = -4 * 2

x = -8

Таким образом, вектор B принимает вид:

B = (-8, 12).

Пример 6

Учитывая вектор m = 5i + 6j +3 в ортогональной системе, определите вектор, параллельный этому вектору, и укажите в противоположном направлении.

Решение

Давайте рассмотрим вектор n , который является вектором, параллельным данному вектору m. Вектор n может быть выражен как:

n = k * m

n = k * (5i + 6j +3)

Где k – скалярное кратное вектора m . Кроме того, k может быть положительным, отрицательным или нулевым. Поскольку было указано, что данный вектор должен указывать в направлении, противоположном направлению м , k не должно быть положительным. То есть k <0. Если k = -3 и мы получаем:

n = -3 * (5i + 6j +3)

n = ((-3 * 5i + (-3 * 6j ) + (-3 * 3))

n = -15i -18j -9

Результирующий вектор n параллелен данному вектору и противоположен по направлению, хотя существует бесконечно много векторов, которые удовлетворяют этому критерию .

Практические вопросы

1. Дан вектор M = 10 м, восток и второй вектор, 3 M, запад . Определите, параллельны два вектора или нет.
2. Учитывая вектор N = 15 м северной широты, определите результирующий вектор, полученный умножением данного вектора на -4. Затем проверьте, параллельны ли два вектора друг другу или нет.
3. Пусть u = (-1, 4) и v = (n, 20) – два параллельных вектора.Определите значение n.
4. Пусть v = (3, 9). Найдите 1/3 v и проверьте, параллельны ли два вектора или нет.
5. Для вектора b = -3i + 2j +2 в ортогональной системе найдите параллельный вектор.
6. Пусть a = (1, 2), b = (2, 3) и c = (2,4). Определите, параллельны ли данные векторы друг другу или нет.

Ответы

1. 3 M = 30 м, направление – запад.Ясно, что новый вектор параллелен вектору M , но его направление противоположно направлению вектора M .
2. -4 N = -60 м. Направление – юг. Два вектора действительно параллельны друг другу.
3. u = k * v , где k = 1/5 и n = -5, v = (-5, 20). Направление u и v остается прежним.
4. 1/3 v = (1, 3), | v | = 3 * √10, | 1/3 v | = √10.Направление вектора 1/3 v такое же, как направление вектора v, , и два вектора параллельны друг другу.
5. 5 b = -15i + 10j + 10 – один из бесконечного множества векторов, параллельных b .
6. Векторы a и c параллельны друг другу, но вектор b не параллелен ни одному из двух других.

Предыдущий урок | Главная страница | Следующий урок .