Краткий курс теоретической механики
Краткий курс теоретической механики
ОглавлениеПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V.  ПЛОСКАЯ СИСТЕМА СИЛ§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ  ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА§ 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50.  РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64.  ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80.  ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ§ 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96.  ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНСГлава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110.  § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ.  ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИГлава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX.  УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ.  ЦЕНТР УДАРА |
Почему механика — фундаментальная наука: точка-масса и твердое тело
Трение, смачивание, механика и связанные с ними вопросы механики, теория
Некоторые утверждают, что механика не фундаментальная наука, а скорее прикладная дисциплина. Я принадлежу к школе механиков, которые категорически не согласны с этим утверждением. Для меня механика — это часть физики; однако она имеет ряд собственных понятий, не всегда совпадающих с аналогичными понятиями в физике. В этой серии статей я намерен привести несколько примеров фундаментальных концепций механики, которые, как правило, не столь очевидны, когда дело доходит до их логического определения.
Первый – это концепция точечной массы или частицы . В русской литературе (в том числе в английских переводах русских книг, таких как «Механика» Ландау и Лифшица) часто используется термин материальная точка .
Что такое определение частицы (точечная масса или масса-точка)? В большинстве учебников, особенно написанных физиками, говорится, что частица в механике — это твердое тело, размером которого можно пренебречь , но нельзя игнорировать массу. Это звучит как справедливое определение.
Однако тогда вам необходимо определить, что такое твердое тело ! Недеформируемое твердое тело представляет собой систему точек, расстояние между которыми всегда остается постоянным . Один определяет понятие механической частицы, используя понятие твердого тела, в то время как твердое тело определяется, используя понятие частицы. Это звучит как старая проблема «курица или яйцо» и не кажется серьезной практической проблемой, о которой следует беспокоиться. Может быть, это даже не значительная теоретическая проблема, о которой должен волноваться математически мыслящий механик, ищущий строгих логических определений механических понятий? Однако это так!
Причина в том, что при уменьшении размера трехмерного твердого тела не все его свойства, нерелевантные для материальной точки, исчезают в пределе малых размеров.
Возьмем момент инерции диска, катящегося по плоской поверхности с линейной скоростью V. Для диска радиуса R момент инерции равен J=(3/2)*M*R 2 , угловая скорость V/R, а кинетическая энергия K=(J/2)*(V/R) 2 . Другими словами, кинетическая энергия равна K=(3/4)M*V 2 . Это не зависит от размера диска! В пределе R→0 вы по-прежнему получаете K=(3/4)M*V 2 . Это не то, что вы ожидаете от точки массы, K=(1/2)M*V 2 . Разве это не удивительно и нелогично?
У материальной точки всего три поступательных степени свободы, а у твердого тела шесть степеней свободы: три поступательных и три вращательных. Когда рассматривается предел очень маленького твердого тела, R → 0, нет причин, по которым вращательные степени свободы исчезают. Это приводит к некоторой двусмысленности определения точки-массы: есть ли у нее вращательные степени свободы или нет?
Более формальным образом, используя программный подход Феликса Кляйна в Эрлангене, согласно которому твердое тело характеризуется группой симметрии SO(3)xR 3 (т.
е. тремя вращательными и тремя поступательными степенями свободы). Точечная масса имеет только три поступательные степени свободы, R 3 . Таким образом, определение точечной массы:
SO(3)xR 3 → R 3 .
Определение твердого тела состоит в том, что расстояния между всеми точками остаются одинаковыми. Ориентация твердого тела задается тремя точками (девять степеней свободы), к которым применяются три ограничения (парное постоянное расстояние). Каждое ограничение отнимает одну степень свободы, что приводит к подвижности твердого тела 9– 3 = 6. Следовательно, определение твердого тела дается преобразованием
R 3 xR 3 xR 3 → SO(3)xR 3 .
Неоднозначность вызвана, скорее всего, тем, что наше евклидово пространство R 3 , но обладает как трансляционной, так и вращательной SO(3)xR 3 симметриями. Если мы примем точку зрения Лейбница о том, что пространство — это просто свойство взаимных отношений тел, мы поймем, что твердое тело имеет ту же дуальную (R 3 и SO(3)xR 3 ) природа.
Из этого примера мы находим, что строгие определения основных механических понятий, таких как точечная масса (частица, материальная точка) и твердое тело , связаны с фундаментальными понятиями движения и симметрии.
Другие записи из этой серии:
1. Масса точки и твердое тело
2. Являются ли законы Ньютона законами природы?
3. Является ли статика логически предшествующей динамике?
4. Можно ли вывести динамику вращения из законов Ньютона?
Понимание момента инерции площади
Момент инерции площади , также называемый вторым моментом площади , является параметром, который определяет, какое сопротивление форма (например, поперечное сечение балки) должна выдерживать. изгибается из-за своей геометрии.
https://www.youtube.com/watch?v=Bls5KnQOWkYВидео не может быть загружено, так как отключен JavaScript: понимание момента инерции площади (https://www.youtube.com/watch?v=Bls5KnQOWkY)
Рассмотрим тонкую доску, которая выдерживает нагрузку в 100 кг.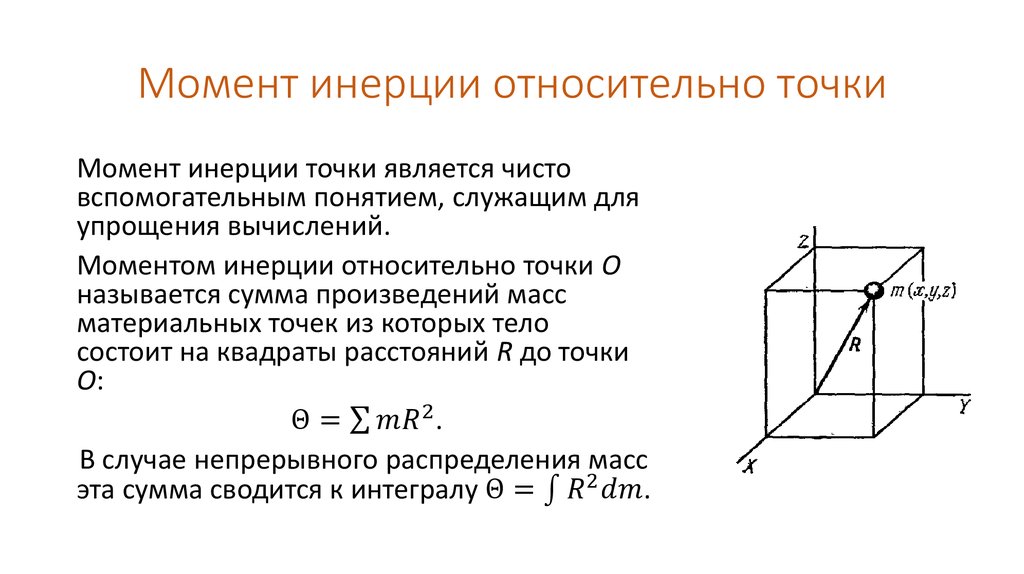
Планка будет намного менее жесткой, когда нагрузка будет приложена к более длинному краю поперечного сечения. Это связано с тем, что сопротивление изгибу зависит от того, как материал поперечного сечения распределен относительно оси изгиба. Доска слева имеет больше материала, расположенного дальше от оси изгиба, что делает ее намного более жесткой.
Давайте сравним значения $I$, рассчитанные для нескольких различных сечений, для оси изгиба, показанной ниже:
Значения момента инерции площади (в мм 4 ) для трех форм материалы вдали от оси изгиба имеют большие моменты инерции – их труднее согнуть.
Это одна из причин Двутавровая балка — такое широко используемое поперечное сечение для конструкционных применений — большая часть материала расположена далеко от оси изгиба, что делает ее очень эффективной при сопротивлении изгибу при использовании минимального количества материала. Момент инерции площади против второго момента площади
Используются термины «секундный момент площади» и «момент инерции площади». Второй момент площади часто предпочтительнее, чтобы избежать путаницы с моментом инерции, который является совершенно другим параметром, описывающим сопротивление тела угловому ускорению, хотя и рассчитывается аналогичным образом. 92 dA}$$
Нижние индексы $x$ и $y$ указывают на то, что момент инерции площади соответствует изгибу относительно осей $x$ и $y$ соответственно.
Приведенные выше уравнения можно использовать для расчета $I$ для любой произвольной формы. Давайте рассмотрим пример того, как это уравнение можно применить для расчета $I$ для прямоугольного поперечного сечения.
Пример – прямоугольное сечение
Мы будем использовать приведенное выше уравнение для расчета $I$ для изгиба вокруг оси $x$ для следующего поперечного сечения: 93ч{12}$$
К счастью, вам не нужно выполнять этот процесс интегрирования всякий раз, когда вам нужно вычислить $I$ для поперечного сечения и оси изгиба. Если это довольно стандартная форма, вы можете просто найти уравнение, которое уже было получено для вашего конкретного поперечного сечения. Большинство учебников по сопротивлению материалов содержат таблицы, подобные приведенной ниже, в которых перечислены уравнения $I$ для обычных поперечных сечений.
| Сечение | Площадь Момент инерции 92$$ Утверждается, что момент инерции площади вокруг любой оси $I_x$ может быть рассчитан из момента инерции площади относительно параллельной оси $I_{xc}$, проходящей через центр тяжести поперечного сечения, площадь поперечного сечения $A$ и расстояние между двумя осями $d$. Центроид — это геометрический центр поперечного сечения или, другими словами, точка, в которой можно сбалансировать поперечное сечение на штифте. В справочных текстах обычно приводятся уравнения для $I$ для центроидальных осей, поэтому теорема о параллельных осях является мощным инструментом для распространения этих уравнений на любые другие параллельные оси. Сложение и вычитание моментов инерции площадиМоменты инерции площади можно суммировать и вычитать для расчета значений составных сечений. На изображении ниже показано, как этот метод можно использовать для расчета $I_x$ для полого сечения. Пример расчета $I$ для составного поперечного сечения путем прибавления или вычитания При использовании этого метода необходимо убедиться, что значения $I$ для сечений компонентов ($I_{xA}$ и $I_{xB}$ в приведенном выше примере) соответствуют правильной оси изгиба, иначе сначала вам нужно будет применить теорему о параллельной оси, чтобы получить значения $I$ для правильной оси. Применение момента инерции площадиМомент инерции площади является важным параметром для любого применения, связанного с изгибом элемента конструкции, что означает, что он постоянно присутствует в 92}$$ Если вы хотите узнать больше об этих приложениях, ознакомьтесь со страницами , отклонение балки и , изгиб . Как показывают два приведенных выше примера, момент инерции площади часто появляется в уравнениях вместе с модулем Юнга $E$. Термин $EI$ получил название изгибная жесткость . $I$ представляет собой жесткость поперечного сечения балки из-за ее геометрии , а $E$ представляет собой жесткость поперечного сечения из-за материала . Жесткость на изгиб $EI$ представляет собой общую жесткость поперечного сечения. Полярный момент инерции В дополнение к расчету момента инерции площади для осей $x$ и $y$, находящихся в той же плоскости, что и поперечное сечение, мы также можем рассчитать момент инерции площади для оси это перпендикулярно поперечному сечению. $J$ учитывает, как площадь поперечного сечения распределяется радиально относительно оси вращения или кручения $z$. Член $\rho$ — это расстояние от оси $z$ (которая на изображении ниже направлена за пределы экрана) до элемента dA. Полярный момент инерции рассчитывается на основе распределения площади поперечного сечения относительно оси кручения ($z$ на изображении выше)Как и в случае с $I_x$ и $I_y$, $\rho$ член в уравнении возведен в квадрат, а это означает, что наибольший вклад в значение $J$ вносят участки поперечного сечения, расположенные далеко от оси вращения. Вот почему трансмиссионные валы полые — центральная часть поперечного сечения не сильно влияет на сопротивление скручиванию, поэтому более эффективно использовать полые валы. Мы можем сделать интересное наблюдение: полярный момент инерции относительно оси, проходящей через определенную точку поперечного сечения, равен сумме площадных моментов инерции двух перпендикулярных осей, проходящих через одну и ту же точку. | |
|---|---|---|
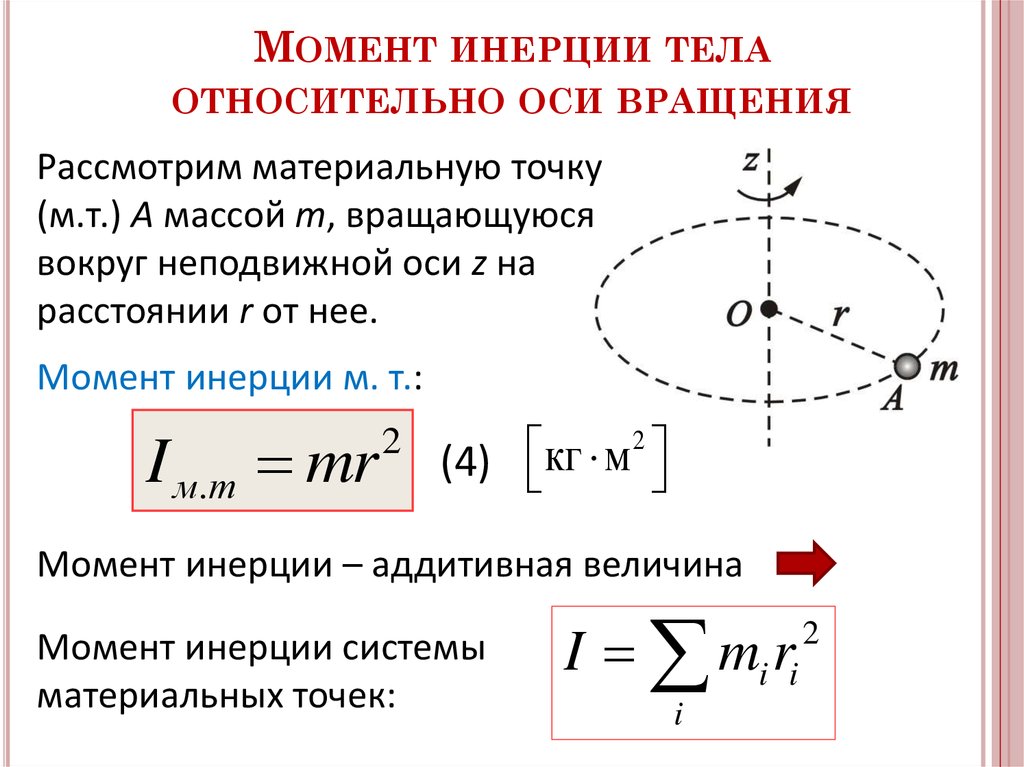
Это называется полярным моментом инерции и обычно обозначается буквой $J$ или $I_z$. Он часто используется в задачах, связанных с деформацией кручения, которая является 9-й.2 dA}$$ 