Момент силы | это… Что такое Момент силы?
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Зависимости между силой F, моментом силы τ (M), импульсом p и моментом импульса L в системе, которая была ограничена только в одной плоскости (силы и моменты, обусловленные тяжестью и трением не учитываются)
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Содержание
|
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага.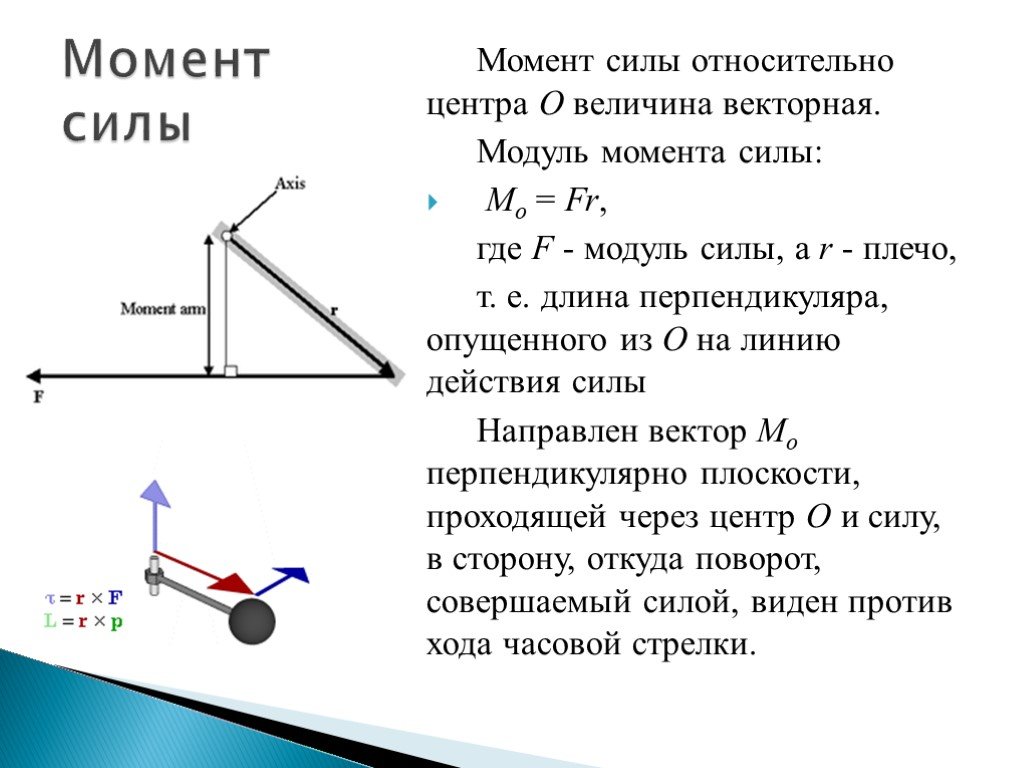
где — сила, действующая на частицу, а — радиус-вектор частицы.
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол .
Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .
Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .
Теперь полная работа записывается очень просто: или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н·м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н·м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, M— вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- = МОМЕНТ_РЫЧАГА * СИЛА
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.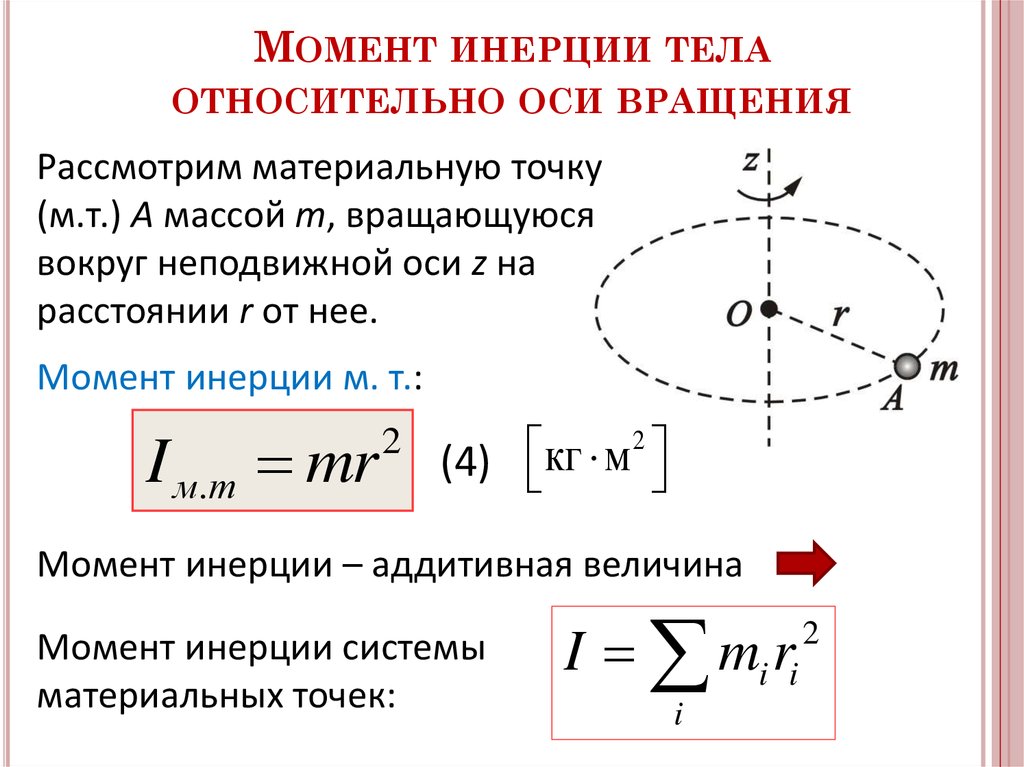
м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
Сила под углом
Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть, если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ_СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ_СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющего точки и , на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
Ссылки
- Развитие и будущее технологии измерения крутящего момента
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
“Правило моментов, 7 класс”
7 класс
Что такое момент силы?
Качели.
Это устройство вы знаете с детства.
Что произойдет, если девочка сядет с краю?
O
2
Что такое момент силы ?
Что нужно сделать, чтобы качели пришли в равновесие?
O
Расчёт момента силы
Произведение модуля силы, вращающей тело, на её плечо называется
где F – сила (Н), l – плечо силы (м)
Единица измерения момента силы – 1 Н м.
l
О
F – вес
Момент силы характеризует действие силы и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча.
Типы моментов сил
Какое действие моменты силы оказывают на рычаг силы?
(Поворачивают его в двух направлениях:
по часовой стрелке и против.
Два типа моментов сил:
- Момент силы по
часовой стрелке
- Момент силы
против часовой стрелки
Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила.
Гайку легче отвернуть длинным гаечным ключом, чем коротким.
Гайку легче отвернуть длинным гаечным ключом, чем коротким.
6
Ведро тем легче поднять из колодца, чем длиннее ручка ворота.
Ведро тем легче поднять из колодца, чем длиннее ручка ворота.
6
Правило моментов
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
l 1
l 2
O
_
F 2
_
F 1
М1 = М2 + М3
Рычаг находится в равновесии под действием нескольких сил, если момент силы, вращающей его против хода часовой стрелки, равен сумме моментов сил, вращающих рычаг по часовой стрелке.
Задача 1
Кот весом в 20Н сидит справа на конце качелей, расстояние между котом и центром опоры равно 3 метра.
Чему равен момент силы, действующей на качели?
_______________________________________________
Решение:
В этом случае кот вызывает момент по часовой стрелке. M = F l
M = 20 3 = 60 Н м
O
l = 3 м
Задача 2
Утка стоит в одном конце качелей, на расстоянии 5м от центра опоры. Найдите момент силы, если вес утки равен 10Н.
_________________________________________________
Решение:
Вес утки вызывает момент против часовой стрелки.
M = F l
M = 1 0 5 = 50 Н м
l = 5 м
F = 10 Н
Правило моментов
Задача 3
Выполняется ли здесь правило моментов?
l
l
O
Задача 4
Момент силы F 1 равен 1 Н*м.
На каком расстоянии справа от оси вращения нужно прикрепить груз весом 4Н, чтобы рычаг находился в равновесии?
4 H
F 1
Спасибо за работу
Что такое момент и как его рассчитать?
Когда я обучаю своих студентов-физиков, я хочу, чтобы они понимали основы концепции, а не только то, как подставлять числа в уравнение. Когда я изучал физику, мне хотелось, чтобы мои учителя больше использовали реальные жизненные приложения, вещи, которые мы уже знаем о мире, чтобы помочь нам действительно получить его .
Я надеюсь, что этот пример понравится всем моим заядлым лыжникам.
Когда я был молод и учился кататься на лыжах, я боялся кресельных подъемников (немного до сих пор). Висеть высоко на открытом воздухе было страшно. Когда кресельный подъемник был полным, когда я сидел на нем со всей семьей — все казалось сбалансированным, меня там благополучно придавливало. Но если бы я был на кресельном подъемнике один, если бы я сел на один край, кресельный подъемник сильно бы наклонился в эту сторону.
Или, если бы я (маленький ребенок) сидел с папой (намного тяжелее ребенка), кресельный подъемник опрокинулся бы в его сторону.
За годы катания на кресельном подъемнике я понял, как мне удерживать кресельный подъемник в равновесии. Если бы я был один, я бы сидел посередине. Если бы я был со своим папой, он мог бы сидеть чуть не по центру с одной стороны, а я мог бы сесть полностью к одному краю с другой стороны. Это позволит кресельному подъемнику оставаться в горизонтальном положении.
Кто-нибудь из вас замечал такое, когда сидел на кресельном подъемнике с кем-то, кто намного легче или тяжелее вас?
Вот несколько правил, касающихся сидения на кресельном подъемнике. Подумайте, имеют ли они смысл для вас.
- Один человек, сидящий посередине, сделает кресельный подъемник горизонтальным.
- Более тяжелый человек будет опрокидывать кресельный подъемник сильнее, чем легкий, если он сидит на одинаковом расстоянии от центра.
- Есть способ достичь равновесия двумя людьми разного веса, сидящими на рассчитанном расстоянии от центра.
Это фундаментальное понятие физики называется моментом .
МОМЕНТ силы является мерой ее стремления заставить тело вращаться вокруг определенной точки или оси.
Когда я сижу на кресельном подъемнике, я создаю момент, который заставляет кресельный подъемник вращаться вокруг оси.
Как рассчитать момент?Момент равен приложенной силе, умноженной на расстояние от оси вращения:
Момент = Сила x Расстояние
Давайте рассмотрим пример: A взвешивание 2 фута от центра кресельного подъемника. На каком расстоянии от центра на противоположной стороне кресельного подъемника должен сидеть ее отец (который весит 180 фунтов), чтобы кресельный подъемник был горизонтальным («уравновешенным»)?
Сначала вычислите момент, создаваемый ребенком:
ПРИМЕЧАНИЕ.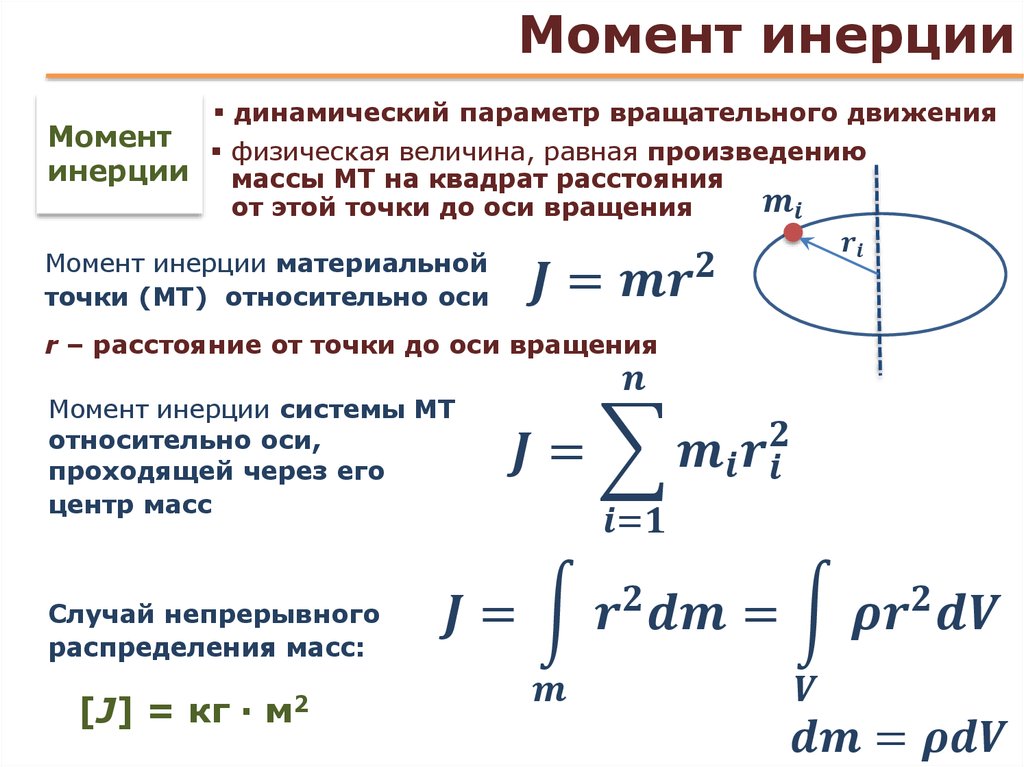
Мы можем смоделировать кресельный подъемник как невесомую балку = 120 ft-lbs
Если ребенок сидит слева от точки поворота, в какую сторону наклоняется кресельный подъемник?
Она поворачивает кресельный подъемник против часовой стрелки .
Правило: моменты против часовой стрелки считаются отрицательными значениями.Чтобы кресельный подъемник находился в равновесии, момент, действующий на ось со стороны Отца, должен быть равен и противоположен ребенку.
Ребенок создал момент -120 ft-lbs, поэтому ее отцу необходимо создать момент +120 ft-lbs.
120 ft-lbs = (180 фунтов)(x футов)
x = ⅔ футов = 8 дюймов.
С какой стороны от точки опоры должен сидеть Отец, чтобы уравновесить ребенка
С правой стороны!
Когда Отец сидит с правой стороны, он заставляет кресельный подъемник наклониться по часовой стрелке .
Правило: моменты по часовой стрелке считаются положительными величинами.
Когда Отец сидит в 8 дюймах слева от оси вращения, он создает момент +120 ft-lbs вокруг оси. Равный и противоположный момент ребенку. Следовательно, кресельный подъемник находится в равновесии.
Какие еще приложения в реальной жизни, связанные с моментами, вы можете придумать?- Если гайку трудно открутить коротким ключом, поможет более длинный ключ. Это связано с тем, что на гайку будет действовать больший момент, когда та же сила будет приложена дальше от оси.
- Попробуйте толкнуть дверь очень близко к петле. Чем ближе к точке шарнира, тем сильнее придется давить. Если дверь очень тяжелая, толкните дверь в сторону, которая находится дальше всего от петли. Это еще одно реальное применение момента.
Физика может показаться абстрактной и запутанной, когда вы рисуете балки и диаграммы свободного тела. Но физика есть везде. Когда вы изучаете новую концепцию в физике, попросите своих наставников привести примеры из реальной жизни и объяснить, как теория применяется на практике!
Моменты в физике vs Моменты в статистике
Перейти к основному содержанию
вигнеш сринивасанвигнеш сринивасан
специалист по данным, менеджер по машинному обучению и аналитике @starhub | Стимулирование роста среди 1 миллиона участников
Опубликовано 9 декабря 2018 г.
+ Подписаться
В вероятностном и статистическом исчислении вычисляются моменты распределения вероятностей случайной величины относительно ее среднего значения. Центральные моменты включают первый-четвертый порядок PDF (функция плотности вероятности), которая дает ожидаемое значение (центр), которое представляет собой момент строки, дисперсию (второй момент), асимметрию (третий момент) и эксцесс (хвостовую форму распределения), которые это четвертый момент
Точно так же в физике есть моменты, которые представляют собой скорость, смещение и ускорение. Мы можем легко связать моменты в статистике с моментами в физике
Сравнение различных моментов
мера его тенденции заставлять тело вращаться вокруг определенной точки или оси.
Момент инерции равен сумме произведений масс всех частиц тела на квадрат его расстояния от центральной оси.
Это можно сравнить со вторым моментом в статистике.
Необработанные моменты или Первый момент — это распределение наблюдений или событий (массы в термине физики ) вокруг среднего (центральная ось в термине физики ) атрибута, т. е. ожидаемого значения случайной величины.
Чтобы лучше понять ожидаемое значение, давайте рассмотрим пример двух шестигранных игральных костей и шансов получить определенную сумму при броске двух костей.
║ Сумма (событие) ║ Вероятность наступления (p(i)) ║ ╠══════════════╬════════════════════════════ ║ 2 ║ 1/36 ║ ╠══════════════╬════════════════════════════ ║ 3 ║ 2/36 ║ ╠══════════════╬════════════════════════════ ║ 4 ║ 3/36 ║ ╠══════════════╬════════════════════════════ ║ 5 ║ 4/36 ║ ╚══════════════╩════════════════════════════
Таким образом, ожидаемое значение будет ( 1/36*2)+(2/36*3) … , что равно среднему значению частоты событий.
Второй момент (дисперсия)
Уравнение аналогично моменту инерции, где p(i) — масса тела, а x — расстояние между частицами тела и центральными осями (x — среднее).