Гармонические колебания — формулы, законы, примеры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием
Если это происходит каждый период, то колебания вообще затухать не будут.Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний T = t/N T — период [с] t — время [с] N — количество колебаний [—] |
Также есть величина, обратная периоду — частота.
Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты ν = N/t = 1/T ν — частота [Гц] t — время [с] T — период [с] N — количество колебаний [—] |
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
x = xmaxcos(2πνt) x — координата в момент времени t [м] xmax — амплитуда [м] ν — частота [Гц] t — момент времени [с] π = 3,14 |
(2πνt) в этом уравнении — это фаза.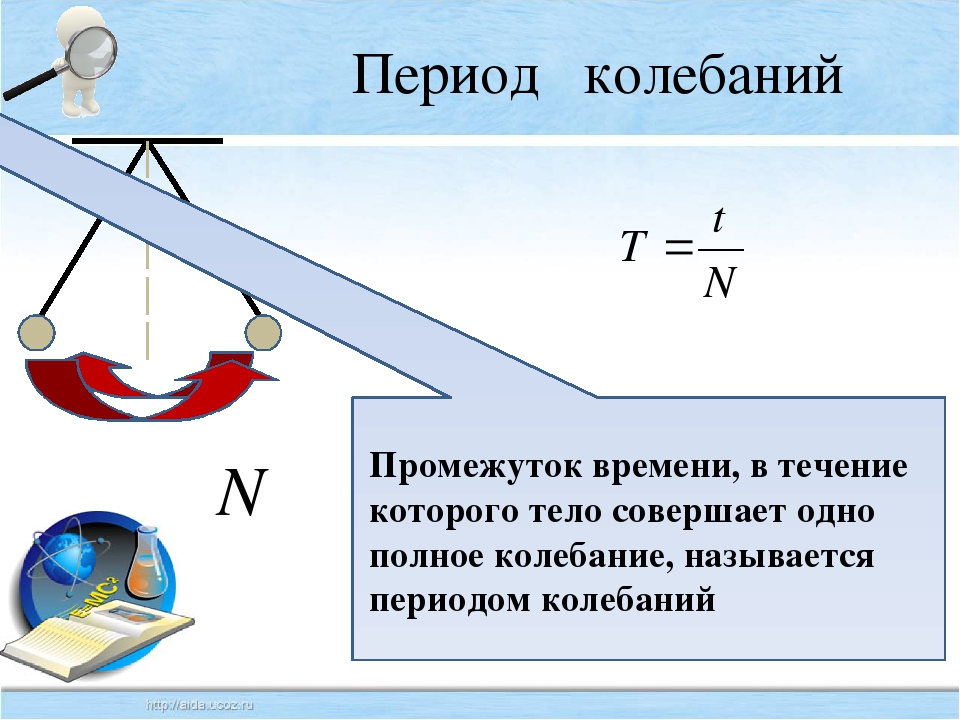
Ее обозначают греческой буквой φ
Фаза колебаний φ = 2πνt ν — частота [Гц] t — момент времени [с] π = 3,14 |
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях.
Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника T — период [с] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 π = 3,14 |
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника T — период [с] m — масса маятника [кг] k — жесткость пружины [Н/м] π = 3,14 |
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
Рассмотрим его на примере математического маятника.
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую
Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Физика в школе 867
Механические колебания
Механические колебания – движения, повторяющиеся во времени.
Амплитуда колебаний – наибольшее отклонения колеблющейся системы от положения равновесия.
Период колебаний – время, за которое совершается одно полное колебание системы.
Частота колебаний – число колебаний, совершаемых системой за 1 с.
Математический маятник
Пружинный маятник
Колебания совершаются грузиком на ниточке и происходят из-за действия сил упругости F = -kx.
Период колебаний математического маятника:
Превращение энергии тела на математическом маятнике:
Колебания совершаются грузиком на пружине происходят из-за действия сил тяжести F = mg.
Период колебаний пружинного маятника:
Превращение энергии тела на пружинном маятнике:
Вынужденные колебания и резонанс
Вынужденные колебания – колебания, совершаемые телом под действием внешней периодически изменяемой силы.
Свободные колебания – колебания, просходящие только за счет собственной энергии колебательной системы.
Автоматические колебания – колебания, происходящие за счет периодически поступающей энергии от источника внутри колебательной системы.
Затухающие колебания – уменьшение амплитуды колебаний с течением времени из-за потери энергии колебательной системой.
Когда частота колебаний вынужденной силы становится равна собственной частоте колебательной системы, то амплитуда установившихся вынужденных колебаний достигает максимума.
В этом заключается явление резонанса.
Примеры резонанса
Возьмём гитару. Само по себе звучание струн гитары будет тихим и почти неслышным. Однако струны неспроста устанавливают над корпусом – резонатором. Попав внутрь корпуса, звук от колебаний струны усиливается, а тот, кто держит гитару, может почувствовать, как она начинает слегка «трястись», вибрировать от ударов по струнам. Иными словами, резонировать.
В 1906 г. обрушился Египетский мост в Петербурге по которому проходил кавалерийский марширующий эскадрон. Частота их шагов совпадала с частотой свободных колебаний моста. Из-за этого амплитуда колебаний моста увеличилась, сорвались цепи, и мост рухнул.
Если поезд проезжает мост, то он либо едет медленно (чтобы частота ударов колес о стыки рельсов была меньше) или проезжает быстро (соответственно, больше).
Гармонические колебания
Гармонические колебания – колебание некоторой величины по закону синуса или косинуса.
Координата:
Скорость можно рассчитать как производную координаты:
Ускорение можно рассчитать как производную скорости:
Механические волны
Механические волны – это распространение механических колебаний в упругих средах.
Продольные волны – частицы среды колеблются в направлении распространения волны.
Поперечные волны – частицы среды колеблются перпендикулярно к направлению распространения волны.
Скорость механической волны:
Звуковые волны
Звуковые волны – распространение механических колебаний в упругих средах.
Источником звука является любое тело, которое колеблется со звуковой частотой, так как это тело распространяет в среде механические колебания.
Громкость звука определяется амплитудой – чем она выше, тем громче звук.
Высота звука определяется частотой – чем она выше, тем выше звук.
У каждого человека свой диапазон частот звуков, которые он слышит. В среднем это от 16 Гц до 20 000 Гц.
Инфразвук
Частота инфразвука v .
Ультразвук
Частота ультразвука v > 20 000 Гц.
Примеры
Сердце человка при сокращении создает инфразвук с частотой 1-2 Гц, мозг в период сна – от 0,5 до 3,5 Гц, а в период его активной работы – от 14 до 35 Гц. Естественно, что если внешние инфразвуковые колебания каким-то образом совпадут с колебаниями, происходящими в организме человека, то последние будут только усиливаться, что может в конечном счете привести к расстройству органа, его повреждению или даже разрыву.
Для инфразвука характерно малое поглощение в различных средах, вследствие чего он может распространяться на очень большие расстояния. Это позволяет определять места сильных взрывов, положение стреляющего орудия, осуществлять контроль за подземными ядерными взрывами, предсказывать цунами и т.
д.
Вследствие большой частоты (малой длины волны) ультразвук обладает особыми свойствами. Так, подобно свету, ультразвуковые волны могут образовывать строго направленные пучки. Отражение и преломление этих пучков на границе двух сред подчиняется законам геометрической оптики. Он сильно поглощается газами и слабо – жидкостями. В жидкости под воздействием ультразвука образуются пустоты в виде мельчайших пузырьков с кратковременным возрастанием давления внутри них. Кроме того, ультразвуковые волны ускоряют протекание процессов диффузии.
Эти свойства ультразвука и особенности его взаимодействия со средой обусловливают его широкое техническое и медицинское использование. Ультразвук применяют в медицине и биологии для эхолокации, для выявления и лечения опухолей и некоторых дефектов в тканях организма, в хирургии и травматологии для рассечения мягких и костных тканей при различных операциях, для сварки сломанных костей, для разрушения клеток (ультразвук большой мощности).
В ультразвуковой терапии для лечебных целей используют колебания 800-900 кГц.
Физика – 10
Провести самооценку:- Какие понятия повторили на уроке? Что из этого вы хорошо поняли, а что осталось вам не ясным?
- Какое движение называют механическими колебаниями?
- Какие колебания называют свободными? Можно ли назвать их затухающими? Ответ обоснуйте.
- Что выражают, соответственно, частота и амплитуда колебаний?
- Дан график зависимости перемещения от времени для системы, совершающей гармонические колебания (е). Определите период, частоту и амплитуду колебаний.
4.2
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПРУЖИННОГО МАЯТНИКА
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 000 человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетресения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли.
Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетресения. С этой целью важно знать, от чего зависят частота и период колебаний.
• От чего могут зависить период и частота колебаний колебательной системы?
Исследование-1. Исследование колебаний пружинного маятникаОборудование: две пружины с разными жесткостями, набор грузов, секундомер, штатив с муфтой и зажимом.
Ход исследования:
I. Исследование зависимости периода и частоты колебания от амплидуды колебаний пружинного маятника.
- Закрепите один из концов пружины в зажиме штатива, а другой конец пружины, подвесив на него груз в 100 гр, приведите в колебательное движение с небольшой амплитудой xml.
- Измерьте секундомером время t1, затраченное на N=10 полных колебаний (a).
- Определите частоту и период колебаний пружинного маятника при помощи формул:
v1 = N
t1 , T1 = t1
N. - Незначительно уменьшите амплитуду колебания (xm2) пружинного маятника и, повторив опыт, вычислите период (T2) и частоту (v2) колебания.
- Сравните между собой значения периодов колебания T1 и, T2 и частоты колебания v1 и v2 пружинного маятника.
Механические колебания и волны
1
Составить уравнение гармонического колебания, если амплитуда колебания 4 см, а период — 0,01 с, х0 = 0.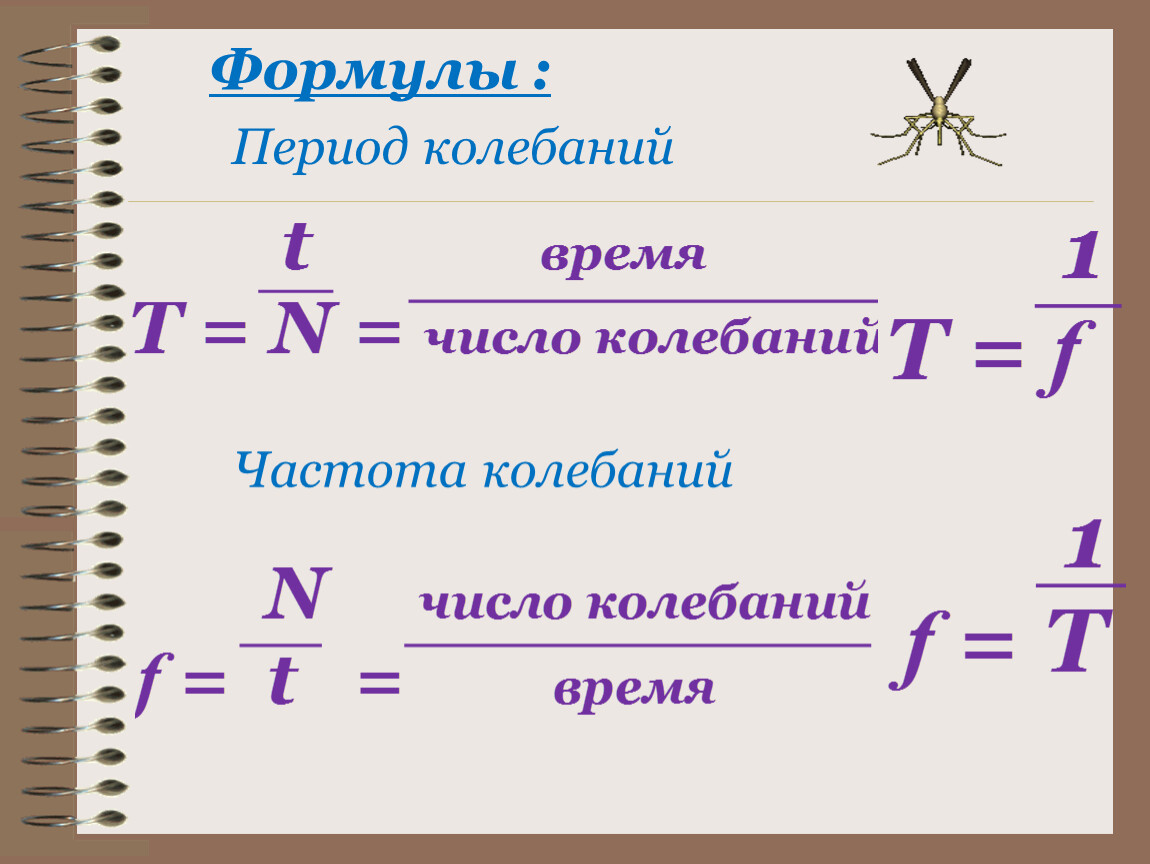
2
За какую часть периода Т тело, совершающее гармонические колебания, проходит весь путь от среднего положения до крайнего? первую половину пути? вторую его половину?
3
Какую часть периода груз маятника находится в пределах 1 см от положения равновесия, если амплитуда его колебаний равна 2 см?
4
Показать, что период движения по окружности математического маятника, описывающего конус (так называемый конический маятник), равен периоду его колебаний, совершающихся в одной плоскости при малых углах отклонения.
5
На какую часть длины надо уменьшить длину математического маятника, чтобы период колебаний маятника на высоте 10 км был равен периоду его колебаний на поверхности Земли?
6
Определить, на сколько отстанут маятниковые (ходиковые) часы за сутки, если их поднять на высоту 5 км над поверхностью Земли.
7
Как по изменению периода колебаний маятника, помещенного над рудным месторождением, плотность которого равна ρ, можно приблизительно оценить объем месторождения, считая его по форме шарообразным? Плотность Земли равна ρ0 (ρ0 > ρ).
8
Изменится ли период колебаний маятника от того, что мы поместим его в воду? Маятнику придана идеально обтекаемая форма и можно принять, что трение о воду равно нулю.
9
В неподвижном лифте висит маятник, период колебаний которого Т = 1 с. С каким ускорением движется лифт, если период колебаний этого маятника стал равным Т1 = 1,1 с? В каком направлении движется лифт?
10
Найти период колебаний Т математического маятника длиной l, подвешенного в вагоне, движущемся горизонтально с ускорением a.
11
Определить длину звуковой волны λ в воде, вызываемой источником колебаний с частотой 200 Гц, если скорость звука в воде равна 1450 м/с.
12
Какой камертон звучит дольше: закрепленный в тисках или стоящий на резонаторном ящике?
13
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
14
При какой скорости v поезда маятник длиной l = 44 см, подвешенный в вагоне, особенно сильно раскачивается, если длина рельсов 25 м?
15
Волны распространяются со скоростью 360 м/с при частоте, равной 450 Гц. Чему равна разность фаз двух точек, отстоящих друг от друга на 20 см?
Ответ и решение
Δφ = π/2.
Найдем длину волны:
λ = v/f = 0,8 м,
где v — скорость волны, а f — её частота.
Если расстояние между точками волны равно λ (т. е. целая волна), то это значит, что разность фаз между ними равна 2π (360°). Тогда разность фаз, если расстояние между точками l, будет равно:
Δφ = 2πl/λ = 2π·0,2/0,8 = π/2.
16
Тело находится в некоторой точке А на внутренней поверхности сферы. В каком случае оно быстрее достигнет нижней точки сферы В: если будет скользить по поверхности сферы или по наклонной плоскости АВ? Трение в обоих случаях пренебрежимо мало, начальная скорость тела равна нулю и расстояние АВ много меньше радиуса сферы.
17
Груз, подвешенный к пружине, вызвал ее удлинение на Δl = 4 см. Найти период Т собственных колебаний пружины вместе с грузом.
18
Найти период Т собственных колебаний в системах, изображенных на рисунках.
Период Вселенских Часов
• Физика 13, 99
Теоретики определили 10−33 секунды как верхний предел периода универсального осциллятора, который может помочь в построении квантовой теории гравитации.
diuno/iStock/Getty Images
Тик Вселенной. Новая теория предполагает, что время является фундаментальным свойством Вселенной, которым управляет осциллятор, взаимодействующий со всей материей и энергией.diuno/iStock/Getty Images
Тик Вселенной. Новая теория предполагает, что время является фундаментальным свойством Вселенной, которым управляет осциллятор, взаимодействующий со всей материей и энергией.× Три теоретика смоделировали время как универсальный квантовый осциллятор и нашли верхнюю границу периода осциллятора в 10−33 секунды. Это значение намного ниже самых коротких тактов лучших современных атомных часов, что делает его неизмеримым.
Но исследователи говорят, что атомные часы можно использовать для косвенного подтверждения предсказаний их модели.
В физике есть проблема со временем: в квантовой механике время универсально и абсолютно, оно непрерывно движется вперед по мере взаимодействия между частицами. Но в общей теории относительности (теории, описывающей классическую гравитацию) время податливо — часы, расположенные в разных местах гравитационного поля, идут с разной скоростью. Теоретики, разрабатывающие квантовую теорию гравитации, должны согласовать эти два описания времени. Многие согласны с тем, что решение требует, чтобы время определялось не как непрерывная координата, а как тиканье некоторых физических часов, говорит Фламиния Джакомини, квантовый теоретик из Канадского института теоретической физики периметра (PITP).
Такие фундаментальные часы пронизывали бы Вселенную, что-то вроде поля Хиггса в физике элементарных частиц. Подобно полю Хиггса, часы могут взаимодействовать с материей и потенциально изменять физические явления, говорит Мартин Бойовальд из Пенсильванского государственного университета в Юниверсити-парке.
Но исследователям еще предстоит разработать теорию таких часов, и они до сих пор не понимают фундаментальной природы времени. Стремясь разобраться в обеих проблемах, Божовальд и его коллеги представили универсальные часы как осциллятор и решили вычислить их период.Они надеялись, что это может дать идеи о том, как исследовать фундаментальные свойства времени.
В модели команда рассматривает два квантовых осциллятора, которые действуют как квантовые маятники, колеблющиеся с разной скоростью. Более быстрый осциллятор представляет собой универсальные фундаментальные часы, а более медленный представляет измеримую систему в лаборатории, такую как атом атомных часов. Команда объединяет осцилляторы, чтобы они могли взаимодействовать. Природа этой связи отличается от классических осцилляторов, которые связаны общей силой.Вместо этого связь навязывается требованием, чтобы чистая энергия осцилляторов оставалась постоянной во времени — условие, вытекающее непосредственно из общей теории относительности.
Команда обнаружила, что это взаимодействие приводит к медленной десинхронизации двух осцилляторов. Рассинхронизация означает, что никакие физические часы не смогут бесконечно поддерживать тики постоянного периода, что накладывает фундаментальный предел на точность часов. В результате, например, ход двух атомных часов одинаковой конструкции никогда не будет полностью совпадать, если их измерять с таким пределом точности.Наблюдение за этим поведением позволит исследователям подтвердить, что время имеет фундаментальный период, говорит Божовальд.
Божовальд и его коллеги использовали свойство десинхронизации, чтобы получить верхний предел в 10-33 секунды для периода их основных колеблющихся часов. Этот предел в 1015 раз короче, чем тиканье лучших современных атомных часов, и в 1010 раз длиннее, чем планковское время — предлагаемая продолжительность самой короткой измеримой единицы времени.
Разложение единицы планковского времени выходит далеко за рамки современных технологий.
Но новая модель потенциально позволяет исследователям стать намного ближе, чем раньше, говорит Бьянка Диттрих, изучающая квантовую гравитацию в PITP. Божовальд соглашается. По его словам, использование временной шкалы десинхронизации между часами для измерения времени, а не самих часов, может позволить проводить измерения в гораздо более коротких временных масштабах.
Еще одним преимуществом выбора осциллирующей квантовой системы в качестве модели фундаментальных часов является то, что такая система очень напоминает часы, используемые в лаборатории, говорит Эстебан Кастро-Руис из Свободного университета Брюсселя, изучающий проблемы, связанные с квантовыми часами и гравитацией. .Сходство является ключевым, говорит Кастро-Руис, потому что оно «переносит вопрос о фундаментальном периоде времени в более конкретную постановку, когда можно действительно начать думать об измеримых последствиях».
Это исследование опубликовано в Physical Review Letters .
– Кэтрин Райт
Кэтрин Райт – заместитель редактора Physics .
Предметные области
Квантовая физика ГравитацияСтатьи по теме
Квантовая информацияОграничение скорости изменений
Эксперименты с одним атомом кальция доказывают, что процессы изменения имеют ограничение скорости, определяемое скоростью, с которой они могут рассеивать тепло.Читать дальше »
Еще статьиПериод и частота в колебаниях – College Physics
Колебательные движения и волны
Цели обучения
- Наблюдайте за колебаниями гитарной струны.
- Определить частоту колебаний.
Струны этой гитары вибрируют через равные промежутки времени. (кредит: JAR)
Когда вы дергаете гитарную струну, получаемый звук имеет устойчивый тон и длится долгое время.Каждое последующее колебание струны занимает такое же время, как и предыдущее. Мы определяем периодическое движение как движение, которое повторяется через равные промежутки времени, например гитарная струна или объект на пружине, движущийся вверх и вниз.
Время совершения одного колебания остается постоянным и называется периодом. Его единицами обычно являются секунды, но может быть любая удобная единица времени. Слово «период» относится ко времени какого-либо события, повторяющегося или нет; но нас прежде всего будет интересовать периодическое движение, которое по определению является повторяющимся.Понятие, тесно связанное с периодом, — это частота события. Например, если вы получаете зарплату два раза в месяц, частота выплат — две в месяц, а период между проверками — полмесяца. Частота определяется как количество событий в единицу времени. Для периодического движения частота – это число колебаний в единицу времени. Отношение между частотой и периодом равно
Единицей СИ для частоты является циклов в секунду , что определяется как герц (Гц):
Цикл – это одно полное колебание.Обратите внимание, что вибрация может быть одиночным или множественным событием, тогда как колебания обычно повторяются в течение значительного числа циклов.
Проверьте свое понимание
Определите событие в своей жизни (например, получение зарплаты), которое происходит регулярно. Определите как период, так и частоту этого события.
Каждое второе воскресенье я прихожу к родителям на ужин. Частота моих посещений составляет 26 за календарный год. Срок – две недели.
Резюме раздела
- Периодическое движение представляет собой повторяющиеся колебания.
- Время одного колебания равно периоду .
- Число колебаний в единицу времени равно частоте .
- Эти величины связаны соотношением
Задачи и упражнения
Какой период электроэнергии?
Если частота сердечных сокращений составляет 150 ударов в минуту во время интенсивной физической нагрузки, каково время одного удара в секундах?
Найдите частоту камертона, при которой совершается одно колебание.
Стробоскоп настроен на мигание каждые . Какая частота вспышек?
Шина имеет рисунок протектора с щелью через каждые 2,00 см. Каждая щель производит одиночную вибрацию при движении шины. Какова частота этих колебаний, если автомобиль движется со скоростью 30,0 м/с?
Инженерное приложение
Каждый поршень двигателя издает резкий звук при каждом втором обороте двигателя. а) С какой скоростью движется гоночный автомобиль, если его восьмицилиндровый двигатель издает звук частотой 750 Гц, при условии, что двигатель совершает 2000 оборотов на километр? б) Сколько оборотов в минуту делает двигатель?
(а) 93.8 м/с
(б)
Глоссарий
- период
- время, необходимое для совершения одного колебания
- периодическое движение
- движение, повторяющееся через равные промежутки времени
- частота
- количество событий в единицу времени
Нажмите и узнайте – Частота и период времени
Время можно определить как меру прошедших регулярных интервалов, основанных на естественных повторяющихся событиях, таких как смена времен года, восходы и закаты, полнолуние и новолуние, приливы и отливы.
Время — фундаментальная научная величина.
Символ времени в метрической системе — t, а стандартной единицей — секунда; (s) – это символ секунды.
Одно полное повторение временного интервала называется циклом.
Частота — это мера того, как часто повторяются циклы. Математически говоря, частота — это количество повторяющихся действий, которые происходят в данный момент времени. Символ частоты — f, а математическая формула частоты:
.Обратите внимание, что в приведенной выше формуле “количество циклов” на самом деле является “подсчитанной величиной”, а не измеренной величиной, поэтому циклы, как и все подсчитываемые величины, не имеют единиц измерения.Назначенной единицей частоты в метрической системе (единицах СИ) является Герц [Гц – для краткости].
[По практическим соображениям вы можете считать Гц равной 1/с или с -1 ]
Пример: Какова частота йо-йо, которое постоянно перекатывается вверх и вниз в общей сложности 300 раз за 3 минуты?
Решение:
Дано: # циклов = 300;
время = 3 мин = 3 мин x 60 с/мин = 180 с
Найти: f
f = циклы/время = 300 циклов/180 с = 1.
7 ч
Период является обратной величиной частоты. Период повторного движения – это время, за которое совершается один полный цикл.
Период – T (заглавная буква T), а период – секунда (с). В форме уравнения мы можем выразить период как:
Пример: Каков период океанской волны, если в среднем за 7 секунд о берег бьется 20 волн.
Дано : количество волн = 20; время = 7 с
Найти: T
T = время/циклы = 7 с / 20 волн = 0.35 с
[Обратите внимание, что “количество волн” также рассчитывается, поэтому у него нет единиц измерения].
- Родительская категория: Физика 11-У
Разница между периодом и частотой
Основное различие между периодом и частотой заключается в их определении. Оба они являются вибрационными характеристиками.
Колебания и вибрации механических систем являются важными областями изучения в физике.Почти все системы свободно колеблются или вибрируют по-разному.
Колебание — это повторяющееся движение инструмента, обычно во времени, вокруг центрального состояния или между двумя или более отдельными точками. Именно термин «вибрация» описывает механические колебания. Чтобы узнать больше о разнице между колебаниями и вибрацией, вы можете посетить эту ссылку. Типичными примерами колебаний являются качающийся маятник, гитарные струны, биение сердца и переменный ток. Даже атомы нашего тела вибрируют.
Каждая колебательная система имеет нечто общее, включая силу и энергию. Раскачивая ребенка на качелях, начинается движение. Также при использовании тепла увеличивается энергия атомов, и они вибрируют. Таким образом, колебания порождают волны.
Характерной чертой всех волн является периодичность. Ясно, что несколько фундаментальных принципов описывают все явления, которые доказывают, что они более распространены, чем вы думали.
В каждом явлении вы видите определенную модель движения, которая повторяется снова и снова.Периодические движения, такие как движение струны гитары или движение ребенка вперед и назад на качелях, повторяются через равные промежутки времени. Время, необходимое для завершения цикла вибрации или колебаний, называется периодом волны. Частота – это параметр, равный количеству циклов колебаний в секунду.
Основное различие между периодом и частотой восходит к их определению.
ПериодПериод определяется как время, необходимое для одного полного цикла вибрации или колебаний.Это относится ко времени периодического возникновения, измеряемому в секундах за цикл. Период обычно обозначается буквой «Т».
Частота Частота волны означает количество полных вибрационных циклов или колебаний, происходящих за одну секунду. Единицей измерения частоты являются циклы в секунду или герц (Гц).
Частота обычно обозначается буквой «f».
Оба значения периода времени и частоты обратно пропорциональны друг другу.На математическом языке период и частота связаны следующим уравнением:
T=\frac{1}{f}
или
f=\frac{1}{T}
- Период
Период – это время, за которое два последовательных гребня (или впадины) проходят фиксированную точку.
Количество: Период (\(T\)) Название единицы измерения: секунда Условное обозначение: s
- Частота
Частота — это количество последовательных гребней (или впадин), проходящих данную точку за 1 секунду.
Количество: Частота (\(f\)) Название единицы измерения: герц Условное обозначение: Гц
2 Природа периода и частоты
Определения периода и частоты показывают, что природа этих двух параметров различна.
ПериодИсходя из определения периода как продолжительности завершения волнового цикла в его единице, то есть во времени, природа периода – время.
ЧастотаЧастота как количество полных циклов, происходящих в единицу времени, является величиной скорости.
Схемы периода и частотыВ этом разделе мы хотим проиллюстрировать концепции периода и частоты волны на диаграммах.
Период Если мы посмотрим на диаграмму распространения повторяющихся волн во времени, мы можем представить период как расстояние между двумя последовательными гребнями волны (или до идентичных последовательных точек) на оси времени.
Рассмотрим волну, которая совершает два полных цикла в секунду (как показано ниже). Следовательно, частота этой волны равна 2 Гц.
Волна как функция времени для отображения периода (Ссылка: Circuitglobe.com ) Отношение периода и частоты к длине волныРассмотрим распространение волны со скоростью v в м/с.Расстояние между двумя последовательными идентичными точками (например, двумя гребнями или впадинами) на волновой диаграмме как функция расстояния называется длиной волны. Обозначается греческой буквой «λ» и измеряется в метрах.
Волна как функция расстояния для отображения длины волны (Ссылка: afsharphysics.wordpress.com ) }{v}Частота
Связь между частотой и длиной волны задается следующим уравнением: период и частота обратно пропорциональны друг другу.
Чтобы лучше понять частоту и период, посмотрите на этот пример. Рассмотрим человеческое сердце, бьющееся 75 раз в минуту. Если каждый раз рассматривать полный цикл, то нам придется вычислять период и частоту:
ПериодИспользование математического определения периода приводит к:
T=\frac{Overall\ time}{Number \ of\ cycles}=\frac{60}{75}=0.8\ (s)
Частота
Для расчета частоты имеем:
f=\frac{Количество\ циклов} {Общее\ время}=\frac{1}{T}=\frac{75}{60}=1.25\ (Гц)
Период и частота в физикеПонятия периода и частоты широко используются в физике, особенно в области энергетики.
ПериодХорошо известным примером применения периода является движение маятника. Период этого движения – это время, затрачиваемое на перемещение из одной стороны в другую и обратно.
Другим физическим примером является электрон, движущийся по винтовой орбите.
Его период определяется выражением:
T=\frac{2\pi m}{qB}
, где m , q и B – масса электрона, заряд электрона, и магнитное поле в регионе.
ЧастотаЧастота является важным параметром в инженерных и научных приложениях. Он определяет скорость колебательных и вибрационных событий, таких как механические вибрации, звуковые сигналы, радиоволны и свет.
Частота волны совпадает с частотой вибрации, создающей волну. Чтобы создать волну с более высокой частотой в веревке, вы должны перемещать веревку вверх и вниз с большей скоростью. При этом потребляется больше энергии, и эта энергия передается волне.Следовательно, высокочастотные волны обладают большей энергией, чем низкочастотные волны той же амплитуды.
Частота обычно представлена в двух формах:
Угловая частота Угловая частота определяет количество оборотов за фиксированный интервал времени. Единицей угловой частоты является Герц.
Следующее уравнение выражает связь между частотой и угловой частотой:
\omega =2\pi f
Где ω – угловая частота.
Пространственная частотаПространственная частота зависит от пространственной координаты и обратно пропорциональна длине волны. Пространственная частота содержит характеристику системы, периодически работающей в пространстве.
Низкие и высокие пространственные частоты (Ссылка: cns.nyu.edu ) На рисунке показан наш самый простой пример вибрации.Без сил
на нем пружина принимает свою равновесную длину (а). Его можно растянуть, (б),
или сжатый, (с). Прикрепляем пружину к стене слева и к массе
справа. Если теперь мы ударим по массе молотком (d), она будет колебаться как
показано в серии снимков, (d)-(m). Если предположить, что масса скользит
туда и обратно без трения и что движение одномерно,
тогда закон сохранения энергии доказывает, что движение должно быть повторяющимся. Обычная физическая терминология для движения, которое повторяется снова и снова. периодическое движение , а время, необходимое для одного повторения, называется период , T (символ P не используется из-за возможной путаницы с импульсом).Одно полное повторение движения называется циклом. Мы привыкли называть короткопериодные звуковые колебания «высокими».
высота тона, и звучит странно, что высокие частоты имеют низкие периоды.
Поэтому чаще принято обсуждать быстроту вибрации в терминах
числа колебаний в секунду, величина, называемая частотой , ф. ф = 1/Т.
Единицы обратной секунды, s -1 , неудобны в речи, поэтому аббревиатура был создан. Один герц, названный в честь пионера радиотехники, составляет один цикл в секунду. Сокращенно 1 Гц = 1 с -1 . Это знакомая единица, используемая для частот на шкале радио.
Единицы частоты также обычно используются для указания скорости
компьютеры. Идея состоит в том, что все маленькие схемы на компьютерном чипе
синхронизируются очень быстрым ходом электронных часов, так что схемы
все могут сотрудничать в решении задачи, не опережая и не отставая.
Мы обсудили, как измерить, насколько быстро что-то вибрирует, но не
насколько велики вибрации. Общий термин для этого амплитуда , А.То
определение амплитуды зависит от обсуждаемой системы, и два
люди, обсуждающие одну и ту же систему, могут даже не использовать одно и то же определение. В
примере блока на конце пружины амплитуда будет
измеряется в единицах расстояния, таких как см. Можно было бы работать в терминах
расстояние, пройденное блоком от крайнего левого до крайнего правого,
но в физике было бы более привычно использовать расстояние
от центра к одному краю. В других ситуациях мы бы даже не использовали одни и те же единицы для амплитуды. Амплитуду ребенка на качелях удобнее всего измерять как угол, а не расстояние, так как ее ноги будут двигаться на большее расстояние, чем ее голова. Электрические колебания в радиоприемнике измеряются в электрические единицы, такие как вольт или ампер. |
Когда блок снова возвращается в исходное положение (g), его потенциал
энергия снова та же, поэтому она должна снова иметь ту же кинетическую энергию.То
однако движение происходит в обратном направлении. Наконец, в точке (j) он возвращается в исходное положение.
исходное положение с той же кинетической энергией и тем же направлением
движение. Движение совершило один полный цикл и теперь
повторять бесконечно при отсутствии трения.
Поскольку период — это количество секунд в цикле, а частота — это
число циклов в секунду, они обратны друг другу,
Добавление двух
номера могут потребовать, скажем, 30 тактовых циклов. Микрокомпьютеры в наши дни
работают на тактовых частотах около гигагерца.
Первый обычно называют
амплитуда от пика до пика, так как крайности движения выглядят как гора
вершины или перевернутые горные вершины на графике положения относительно
время.8.6 Период и частота | Поперечные волны
8.6 Период и частота (ESACP)
Представьте, что вы сидите рядом с прудом и смотрите, как мимо вас проплывают волны. Сначала прибывает один гребень, затем
корыто, а затем еще один гребень. Предположим, вы измеряете время, прошедшее между появлением одного гребня и появлением следующего.
Это время будет одинаковым для любых двух последовательных гребней, проходящих мимо вас.
Мы называем это время периодом , и
это характеристика волны.
Символ \(T\) используется для обозначения периода. Период измеряется в секундах (с).
Представьте снова пруд. Как только гребень проходит мимо вас, вы запускаете секундомер и считаете каждый пройденный гребень.Через 1 секунду вы останавливаете часы и перестаете считать. Количество гребней, которые вы насчитали за 1 секунду, равно частота волны.
Частота и период связаны друг с другом.