Что такое пределы: предел | это... Что такое предел? - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Предел функции простым языком – Altarena.ru — технологии и ответы на вопросы

Содержание

Предел функции: основные понятия и определения
Понятие предела
Что такое предел функции
Пределы
Что такое пределы простыми словами
Пределы в математике
Еще один пример
Предел последовательности
Можно сказать и так:
Зачем нужны пределы
Примеры из жизни
Пределы функций. Примеры решений
Видео

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Пределы

Пределы — одни из самых трудных сущностей в математике для понимания. Сложно объяснить просто, что такое предел, поэтому чаще всего этого никто и не делает.

И тем более, мало к то из преподавателей может привести пример из жизни, когда пределы все-таки могут пригодится. Но мы попытаемся объяснить так, чтобы было и понятно и несложно и по сути. Как обычно «на пальцах».

Что такое пределы простыми словами

Наверное самое наглядное, что можно вспомнить из истории, это знаменитый парадокс Зенона «Ахиллес и черепаха». Зенон был философом, а не математиком, поэтому мог вполне свободно упражняется в остроумии не заботясь о доказательствах.

Ахиллес и черепаха бегут на перегонки. Черепаха начинает первой, человек догоняет. Ахиллес бежит быстрее, но когда он пробегает 100 шагов, черепаха все рано проползает один. Еще 100 шагов и еще один. Таким образом Ахиллес приближается к черепахе но и она чуть-чуть отдаляется от него. Зенон делает вывод, что Ахиллес будет бесконечно к ней приближаться, но никогда не догонит черепаху!

В этой истории важно не то, что на самом деле она не реальна, а ее «математический смысл». Человек приближается к черепахе но никогда ее не настигает. То есть некий предел (черепаха) к которому стремится Ахиллес.

Говоря простым языком предел это такое значение, которое нельзя достичь, но можно бесконечно близко к нему приблизится.

То есть, в пределе определенного промежутка времени Ахиллес действительно не догонит черепаху (времени не хватит), но приблизится к ней на бесконечно малое расстояние.

Пределы в математике

Стоит сразу сказать, что определение пределов больше чем одно, потому, что они бывают разные. Есть придел последовательности, а есть предел функции.

Давайте разделим число 10 пополам:

10/2=5, и еще раз, 5/2=2,5 и еще…

Это последовательность n/2: 10…2,5…1,25…

Если делать это 20 раз получится вот такое значение: 0,000019

А если сделать 100 раз, то вот такое: 0,000000000000000000000000000016

Если делить пополам бесконечно, результат будет уменьшатся, в реальной жизни, это будет уже фактически ноль, но в математике, все еще не ноль… Предел этой последовательности будет стремиться к нолю.

Если взять другу последовательность, например n+1. 2…3…4…5… и снова устремимся в бесконечность. Предел этого множества тоже будет стремится к бесконечности.

Еще один пример

Бросаем монетку. Может выпасть «орел», а может и «решка». Теория вероятности утверждает, что шансы всегда 50/50, то есть вероятность «орла» — 1/2=0,5.

Каждый раз, значение реально вероятности, приближается к расчетным 0,5. Чтобы получить вероятность ровно 0,5 нужно подбросить монетку бесконечное количество раз.

То есть, при условии, что количество бросков стремится к бесконечности предел предел будет равен 0,5.

Это именно та бесконечность из матанализа о которой было сказано в статьях об интегралах и делении на ноль. Это не какое-то определенное число — это понятие.

Предел последовательности

Предел последовательности — это пространство которое содержит все все элементы последовательности начиная с какого-то значения. А простыми словами, предел последовательности, простыми словами, это такая «область» куда попадают все значения после определенного порога (в нашем случае – А). На изображении ниже она условно показана синей полоской.

ε — это произвольное положительное число.

Можно заметить, что при продолжении вверх последовательности ее значения все равно будут оставаться в пределах «синей полосы».

Можно сказать и так:

Предел числовой последовательности, это число (s на графике) в окрестности которого попадает бесконечно много значений. При этом вне предела, количество значений явно конечно. Чтобы было еще понятнее: предел последовательности это значение (точка А) выше которого все будет попадать в область не больше s+ε и s-ε. Бесконечное количество таких значений будет «лежать» внутри синей полоски.

Математическим языком можно записать так: s-ε Предел функции простыми словами объяснить также просто. Предел в какой-то произвольной точке — это величина к которой значение функции приближается. Например, f(x)=2x, а х→0 (икс стремится к нулю).

В этом случае предел функции будет равен lim 2x=0. Или в случае если х→2 то предел равен lim 2x=4. Пока все просто. Вот только зачем вычислять пределы, если можно просто выбросить «lim» и расчеты останутся те ми же?….

Зачем нужны пределы

Пределы как раз и нужны тогда, когда мы имеем дело с бесконечностью. Например, бесконечно большими или бесконечно малыми значениями.

Непонятно, что такое «бесконечно большое» или «бесконечно долго», это не какое-то определенное число. С бесконечно малыми значениями та же ситуация, это не «ноль» но как-то очень близко к нему. Тут и выручают пределы.

В точке х=2 — пусто. Потому, что получается 0/0, то есть неопределенность. Но стоит вместо 2 подставить 1,9999999999(9) или 2,000000001(1). Значения бесконечно близкие к 2, но не «два», как график превратится в прямую.

В этом случае речь идет о пределе функции при «икс» стремящемуся к двум, функция стремится к 4.

Такой своеобразный «трюк» в расчетах с заменой знака равенства на стрелочку.

Нет, не совсем. Когда речь идет о пределах, имеется в виду процесс, не важно функция это или множество, но предел описывает процесс в динамике. Тогда как знак «равно» означает статическое состояние.

x=1 и x→1, это совсем не одно и то же.

Примеры из жизни

Зачем все это нужно где применяется пределы в реальных расчетах?

Простое объяснение пределов невозможно, если не привести наглядный пример. Но только где его взять? Существует ли какой-то физический смысл пределов? Не точный аналог но что-то похожее есть.

Можно провести простой эксперимент, взять, например, спичку. Или что-угодно, чего не жалко. Начинаем пытаться сломать спичку, сначала одно усилие, потом чуть больше и еще больше. В один из моментов спичка треснет пополам.

Поздравляем, вы достигли предела прочности. Можно повторить эксперимент с другими спичками и установить, значение при котором спичка ломается.

Что тут общего с пределами из математики, кроме названия.

Есть множество значений силы до предела прочности и оно ограничено, и множество значений после предела прочности, их неограниченное множество. Ведь спичка уже сломана, любое усилие выше предела прочности будет ломать новую и новую спичку. Точно так же как и с пределом функции или множества.

Все, что лежит за пределом, уже не имеет практического значения — спичка не устоит.

Еще один пример, это «практический потолок» летательного аппарата. Это максимальная высота на которую может «взобраться» самолет, чтобы подняться выше будет уже не хватать подъемной силы. Хотя на есть еще и понятие «динамический потолок» — это высота на которую можно подняться хорошенько разогнавшись. Но выскочив на эту высоту через некоторое время самолет все равно опустится на свой «потолок».

Посмотрите на картинку ниже, это наглядный пример такого явления как резонанс.

Колебание моста из-за резонанса

Мост так раскачивается из-за того, что собственная частота колебания совпадает с той частотой с которой его раскачивает ветер, амплитуда колебаний постоянно возрастает и мост разрушается. В этом случае амплитуда стремится к бесконечности, так как в знаменателе формулы находится выражение w₀-w (собственная частота колебаний минус вынужденная частота), а так как обе w равны, получается то самое деление на ноль, а значит амплитуда → ∞.

Самое понятное объяснений пределов в реальности, с которым может столкнуться каждый — это сложные банковские проценты по кредиту. И если вы не умеете рассчитывать сложны проценты, не берите кредит. Для тех, кто силен в матанализе совет будет не лишним.

Также может понадобится рассчитать предельную стоимость товара, зная зависимость (функцию) цены от объема продаж или предельный объем производства или много еще чего.

Самый наглядный пример, возможно, это предел в маркетинге. Вот зависимость стоимости клика от количества кликов в контекстной рекламе.

И все же в повседневной жизни обыватель редко встречается с таким понятием как предел функции или последовательности. Поэтому и так сложно понять и принять абстрактные математические формулировки. Но если постараться, математика может открыть новые грани реальности, по крайней мере, все это уже не будет казаться таким скучным и непонятным.

Источник

Пределы функций. Примеры решений

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям матана и заложил его основы. Надо сказать, этот уважаемый математик снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причём одна теорема убойнее другой. В этой связи мы пока не будем рассматривать определение предела по Коши, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

А сразу пример, чего бабушку лохматить….

Любой предел состоит из трех частей:

1) Всем известного значка предела .
2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ().
3) Функции под знаком предела, в данном случае .

Сама запись читается так: «предел функции при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , ….
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Разбираемся, что такое ? Это тот случай, когда неограниченно возрастает, то есть: сначала , потом , потом , затем и так далее до бесконечности.

А что в это время происходит с функцией ?
, , , …

Итак: если , то функция стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать до бесконечности и смотрим на поведение функции:

Вывод: при функция неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , ,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность , , . Если , то , , .

! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» начнёт принимать такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов. Кстати, по этой теме есть интенсивный курс в pdf-формате, который особенно полезен, если у Вас ОЧЕНЬ мало времени на подготовку. Но материалы сайта, разумеется, не хуже:

Пределы с неопределенностью вида и метод их решения

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Вычислить предел

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим в старшей степени:

Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.

Разделим числитель и знаменатель на

Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Найти предел
Снова в числителе и знаменателе находим в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на

Найти предел
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
Для раскрытия неопределенности необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:

Разделим числитель и знаменатель на

Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность.

Пределы с неопределенностью вида и метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни:

Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на множители.

Вычислить предел

Сначала «чистовой» вариант решения

Разложим числитель и знаменатель на множители.

Числитель:
Знаменатель:

,

Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Найти предел

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

Получена неопределенность вида , которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов:
И смотрим на наш предел:
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать (которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу :

Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Найти предел

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

Умножим числитель и знаменатель на сопряженное выражение

Спасибо за внимание.

Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы. После освоения двух базовых уроков, рекомендую изучить статью Методы решения пределов, материалы которой позволят выйти на «твёрдую четвёрку»!

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник

Видео

Пределы функций для чайников. Свойства пределов. Примеры решения

ПРЕДЕЛ ФУНКЦИИ. Артур Шарифов

Матан. Пределы для успешной сдачи зачёта | TutorOnline Математика

Что такое ПРЕДЕЛЫ. Математика на QWERTY

Математика без Ху{a59d68d9e85770d26d7f03ef1e17421f46fa783a9a8ee536de468ee46886eb77}!ни. Пределы, часть1. Неопределенность, раскрытие неопределенностей.

10 класс, 39 урок, Предел функции

ПРЕДЕЛ ФУНКЦИИ решение пределов математика

27. Вычисление предела функции №1. Примеры 1-4

✓ Предел функции. Определение предела функции “по Коши” и “по Гейне” | матан #014 | Борис Трушин

Предел функции в точке. 10 класс.

Значение, Синонимы, Определение, Предложения . Что такое предел

Во время исследования мы пытались найти предел засухи для жизни на Земле, место настолько сухое, что ничто не сможет там выжить.
Это крайне аморально, и, возможно, левые могли бы согласиться, как вы сказали, что приток иммигрантов был слишком быстрым и существует предел, когда общества уже сопротивляются, но, тем не менее, проблема уменьшится, если причиной её является автоматизация.
Вы не чувствуете, что есть предел для лжи, которую можно высказать?
Наших стратегов больше волнует теоретический предел скорости распространения Организации.
По трем пробам организма, именуемого человечеством, я могу определить его потенциал и предел его возможностей.
Сила вампиров и их возможности увеличивались со временем, но для всех существовал предел.
Уверен, что где-то есть предел извинений, но мне жаль.
Я уверен, что эти существа не настолько уважают Предел, чтобы просто играть по правилам.
Ты переоцениваешь предел прочности подсистемы, которую пытаешься соорудить.
Для обеспечения последовательности в отношении Конвенции о правах ребенка возрастной предел следует увеличить до 18 лет.
Сомнительно, что удастся поднять возрастной предел, если не соблюдается существующая норма.
Минимальный верхний предел не должен быть меньше 14 должностей.

Вместе с тем было высказано мнение о том, что временной предел для реакций на оговорки не должен применяться к условным заявлениям о толковании.
Предел яркости, при котором показываются названия астероидов.
Дифракционный предел – это что-то вроде того, когда на приёме у окулиста видишь только до определённой строки, какие бы ни были у тебя очки.
Она называется физические законы, и один из них называется дифракционный предел.
В других случаях верхний возрастной предел был снижен на десять лет.
Предел ответственности составляет 40 млн. СПЗ. Однако государство-участник может выбрать бóльшую и неограниченную сумму ответственности в отношении ущерба, причиненного на его территории.
Наверное, вы правы, но для меня это – предел.
Испания – Для вычислений используется предел упругости, значение которого колеблется между 0,40 и 0,72, а не коэффициент шероховатости.
Какой предел скорости в жилом районе?
Был установлен верхний предел на общее допустимое усилие, а само оно было пропорционально распределено между восемью участниками, которые могут переуступать друг другу промысловые сутки и хозяйственные периоды.
Итальянская жажда мести может быть беспредельна, Ваше Величество, но, к счастью для вас, у испанской жажды войны предел есть.
Но мы точно знаем, что предел скорости обработки информации машинами лежит далеко за пределами возможностей биологической ткани.
Минимальный приемлемый предел прочности на сдвиг составляет 250 Н/см2.
В этом отношении Конвенция не определяет предел содержания ртути, выше которого отходы будут подпадать под критерий, устанавливающий их опасность.
Но лакмусовой бумажкой является жизнь нашего народа, и поэтому предел погрешности очень мал.
Каждый муниципалитет может также утверждать расходы по строительству, превышающие рекомендуемый верхний предел за квадратный метр.
Кроме того, если ДВЗЯИ устанавливает качественный лимит, то ДЗПРМ установит количественный предел на производство ядерного оружия.
Итак, образуется предел погрешности между 206 тыс. (262 тыс. – 56 тыс.) и 318 тыс. (262 тыс. + 56 тыс.), мягко говоря, обескураживающий, но по-прежнему чрезвычайно вселяющий надежды, учитывая, что мнение большинства составляет 230 тысяч. .
Уже давно известно, что культивируемые клетки человека, по всей видимости, способны воспроизводиться не более 40-60 раз (так называемый предел Хейфлика), прежде чем этот процесс останавливается и начинается старение.
Предел возможностей России по усилению военной эскалации становятся все более ясным.
Тем не менее, пока другие державы усиливаются, а Америке приходится все больше задумываться о будущем своей экономики, допустимый предел ошибки сокращается.
В учительском контракте, есть предел того как часто директор будет наведываться в класс – иногда даже раз в год.
Второй компонент неизменного антикризисного механизма – нижний предел цен на облигации – и, таким образом, потолок для потерь.
В пункте 14 слова «предел прочности» относятся к сплавам титана до или после термообработки.
В международных отношениях существует определенный предел кризисных ситуаций, который нельзя пересекать без ущерба для глобальной стабильности.
Параметр реестра «MaxRequestBytes», который по умолчанию не установлен, определяет верхний предел общего размера строки запроса и заголовков.
Я убежден, что нам нужно установить верхний предел для системы рычагов на банковских балансах, независимо от взвешивания неликвидных активов или мер рисковой стоимости.
Думаешь ли ты, что это мыслимый предел возможности, или.?
Побурение или образование мелких трещин: разрешенный максимальный предел с одной стороны стручка сладкого перца (фотография 55).
В случае стали, имеющей предел текучести более 355 Н/мм ?, или других материалов, помимо стали, свойства материалов должны рассматриваться совместно с признанным классификационным обществом.
Это падение, кажется, остановилось, и самые последние данные указывают на то, что нижний предел, возможно, уже достигнут.
Да, проигрыватель должно быть подействовал на скорую и полицию, как только они попали в предел слышимости.
Если значение в поле Соответствие больше 100, временной предел, указанный в соглашении об условиях обслуживания, превышен.
Предел максимальной капитализации определяет максимальную стоимость НЗП по затратам проекта.
В примере выше, где изменялся предел для получателей, выполните следующую команду, чтобы проверить, изменилось ли значение.
При отправке ящик из пенопласта должен быть закрыт самоклеющейся лентой, имеющей достаточный предел прочности на разрыв, чтобы предотвратить открытие ящика.
Как и сейчас должен быть средний курс и 15% предел колебаний по обе стороны от него для того, чтобы рынок знал, что ожидать.
Для инвестиционных проектов применяется максимальный предел капитализации.
В поле Предел размера вложения (МБ) введите предельный размер вложений электронной почты.
Она отметила, что может быть рассмотрен верхний предел общей массы транспортного средства (4,5 т) для целей применения, и напомнила о технических оговорках США относительно испытаний на удар головы и ноги.
Данная кривая отражает теоретический предел усталости для анализируемой конструкции.
«Достигнут предел неэффективности, за которым нет никакого смысла держаться за преданного соратника, — пишет она.
Хотя центральный банк заявил, что будет «терпелив», когда дело коснется повышения процентных ставок, у этого терпения есть предел.
Например, если ввести 40 в поле Лимит сверхурочного времени работы / работы по гибкому графику и 10 в поле Макс. предел работы по гибкому графику, это означает, что работник имеет 40-часовую рабочую неделю.
В то же время было отмечено, что существует известный предел, далее которого не следует заходить в требовании конкретности, поскольку применение нормы о местных средствах правовой защиты является в высшей степени контекстуальным.
Даже если замораживание производства установит нижний предел, это может иметь неприятные последствия.
Говорят, что тушёное мясо нельзя переготовить, но всему есть предел.
Восемь минут жесткого рентгеновского облучения – для яиц это предел, пожалуй.
Франсуа считает, что это предел того, что может вынести мужчина, прежде чем его достоинство потребует от него восстать против нелепости и несправедливости вселенной.
Допустимый предел максимального разброса двух сопоставимых фактов ограничен.
Тогда я был джентльменом, но есть предел вежливости.
Граммы – это самый выгодный предел, к тому же, самый эффективный, поэтому мы пытаемся убедить людей покупать в граммах.
Возможно, это тот самый предел, который нам нужен.
Они считают, что у каждого полицейского есть свой предел.
До сих пор я стойко терпел ваши высказывания, но всему есть предел, сэр.
Я готов ограждать свои интересы, но всему есть предел.
Единственный предел… твое воображение.
Не беспокойся. я обозначил нижний предел
Другие результаты

Пределы для чайников с примерами решения

Содержание:

Сформулируем определение предела функции

Прежде чем перейти к определению предела, напомним, что в математике используются три вида бесконечностей

Бесконечность не является числом, она показывает, как меняется переменная величина, которая конечна в любой момент времени.

Теперь определим понятие последовательности и ее предела.

Последовательностью называется множество чисел, которое перенумеровано с помощью целых чисел и расположено в порядке возрастания номеров

Если задана последовательность то тем самым любому целому неотрицательному значению поставлено в соответствие значение

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Например, члены геометрической прогрессии являются последовательными значениями функции где

Может случиться так, что с увеличением значения будет неограниченно приближаться к какому-то числу В этом случае говорят, что число является пределом функции целочисленного аргумента или последовательности при и пишут или

Число является пределом последовательности если для можно найти такое что для всех с номерами справедливо неравенство [4, 32]

Возможно вам будут полезны данные страницы:

Признак Лейбница

Как решать пределы: пример решения

Как решать пределы с корнями: в числителе

Уравнение прямой в пространстве

Используя приведенное определение, докажем, что последовательность имеет предел, равный 1

Согласно определению имеем

Таким образом, мы доказали, что для любого наперед заданного можно найти такое что при всех будет выполняться (3. 1), а это означает, что 1 есть предел исходной последовательности.

Теперь рассмотрим функцию непрерывного аргумента и предположим, что неограниченно приближается к числу При этом может оказаться, что соответствующее значение неограниченно приближается к некоторому’ числу В этом случае говорят, что число есть предел функции при

Сформулируем определение предела функции

Число называется пределом функции при если для можно найти такое что для всех удовлетворяющих условию будет справедливо неравенство Заметим, что функция не обязательно должна быть определена в предельной точке она должна быть определена лишь в некоторой окрестности этой точки.

Тот факт, что — предел функции при записывается так:

Данное нами определение иллюстрируется рис. 3.3. Используя приведенное определение предела, докажем, что

На основании определения имеем

Таким образом, мы доказали, что исходная функция будет отличаться от 6 меньше чем на если будет выполняться неравенство (3. 2). В данном случае

Приведенное определение не дает способа вычисления пределов. Ниже мы рассмотрим некоторые из таких методов.

Дадим понятие о левых и правых пределах функции и точках ее разрыва.

Если при так что принимает только значения меньшие то пишут и называют левым пределом.

Аналогично, если при так что принимает только значения большие то пишут и называют правым пределом [4, 30].

Геометрическая иллюстрация левого и правого пределов дана на рис. 3.4

Из рис. 3.4. следует, что в точке функция имеет разрыв. Он носит название разрыва первого рода (в точке разрыва первого рода левый и правый пределы не равны и конечны). Все остальные точки разрыва называются точками разрыва второго рода [4, 30]. Примерами разрывов второго рода являются бесконечные разрывы (рис. 3.5)

Предположим, что аргумент функции неограниченно возрастает т. е. является бесконечно большим аргументом. Может оказаться, что при этом функция стремится к некоторому пределу (рис. 3.6).

Функция стремится к пределу при если для можно найти такое что для всех значений удовлетворяющих неравенству будет выполняться условие

Теперь рассмотрим случай стремления функции к бесконечности при

Функция стремится к бесконечности при если для можно найти такое что для всех значений удовлетворяющих условию выполняется неравенство

Это определение иллюстрируется рис. 3.7.

Напомним, что функция называется ограниченной в данной области изменения аргумента, если существует такое, что для всех значений принадлежащих рассматриваемой области, будет выполняться неравенство Если такого числа нет, то является неограниченной в данной области.

Например, функция является ограниченной на своей области определения (рис. 3.8).

Дадим определение бесконечно малой величины. Функция называется бесконечно малой при или если или

Например, функция при есть бесконечно малая величина, так как

Постоянное очень малое число не является бесконечно малой величиной. Единственное число, которое рассматривается в качестве бесконечно малой величины, это ноль. Связь бесконечно малых и бесконечно больших величин можно проследить из теоремы 3.1: если – бесконечно малая величина, то — бесконечно большая величина, и наоборот [4]

Пример с решением

Пример 3.1

Пример 3.2

Пример 3.3

Если подставить предельное значение, то получим неопределенность Поэтому для решения подобных примеров используют следующий прием: делят числитель и знаменатель на в максимальной степени, в данном случае на Тогда получим

Пример 3.4

Пример 3.5

(Предел в квадратных скобках – это второй замечательный предел).

Пример 3.6

Пример 3.7

Так как логарифмичеешя функция непрерывна, то можно воспользоваться формулой (3.5).

Пример 3.8

Данный предел можно свести к первому замечательному пределу путем замены переменной, т.е.

при

тогда получим

Пример 3.9

Пример З.10

Пример 3.11

Пример 3.12

Пределы функций. Примеры решений Теория пределов – это один из разделов — презентация на Slide-Share.ru 🎓

Первый слайд презентации

Пределы функций. Примеры решений Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике. Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи: 1. Понять, что такое предел. 2. Научиться решать основные типы пределов.

Изображение слайда

Слайд 2

А сразу пример, Любой предел состоит из трех частей: 1) Всем известного значка предела lim.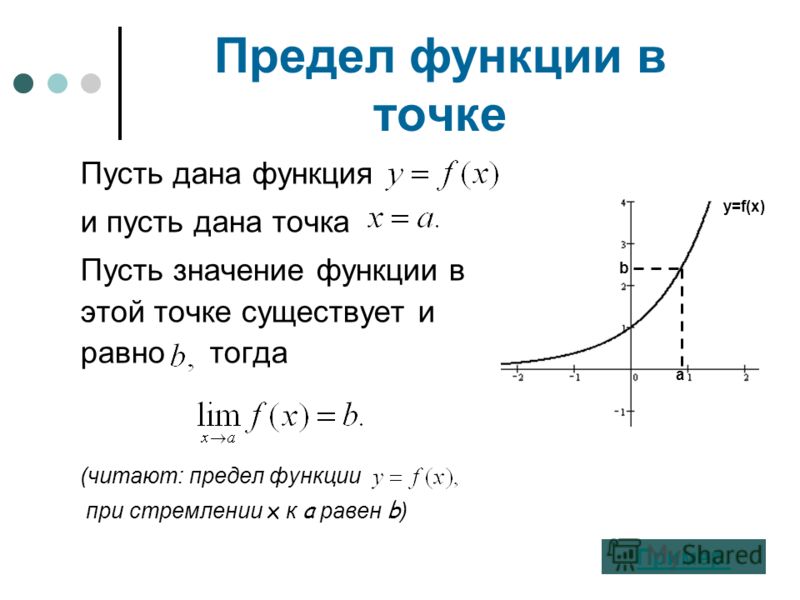 2) Записи под значком предела. Запись читается «икс стремится к единице». Чаще всего – именно, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ( ∞). 3) Функции под знаком предела, в данном случае Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»? Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала, затем,, …,, …. То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают. Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Изображение слайда

Слайд 3

Итак, первое правило : Когда дан любой предел, сначала просто пытаемся подставить число в функцию. Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко! Пример с бесконечностью: Разбираемся, что такое Это тот случай, когда x неограниченно возрастает, то есть: сначала 1, потом 10, потом 100, затем 1000 и так далее до бесконечности. А что в это время происходит с функцией 1-x ? ` 1-1=0, 1-10=-9, 1-100=-99, 1-1000=-999, … Итак, если x→∞, то функция 1- x стремится к минус бесконечности!

Изображение слайда

Слайд 4

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ. Еще один пример с бесконечностью: Опять начинаем увеличивать x до бесконечности, и смотрим на поведение функции: Вывод: при x →∞ функция неограниченно возрастает

Изображение слайда

Слайд 5

И еще серия примеров: Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет. Пределы с неопределенностью вида и метод их решения Сейчас мы рассмотрим группу пределов, когда x→∞, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены Вычислить предел Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида

Изображение слайда

Слайд 6

Можно было бы подумать, что, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим. Как решать пределы данного типа? Сначала мы смотрим на числитель и находим X в старшей степени: Старшая степень знаменателя равна двум Старшая степень в числителе равна двум. Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на x в старшей степени

Изображение слайда

Слайд 7

Пример 2 Найти предел Максимальная степень в числителе: 3 Максимальная степень в знаменателе: 4 Выбираем наибольшее значение, в данном случае четверку Пример 3 Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1

Изображение слайда

Слайд 8

Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность. Пределы с неопределенностью вида и метод их решения Группа следующих пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу. Пример 4 Решить предел Сначала попробуем подставить -1 в дробь: В данном случае получена так называемая неопределенность Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида то для ее раскрытия нужно разложить числитель и знаменатель на множители. Очевидно, что можно сократить на

Изображение слайда

Слайд 9

Пример 5 Вычислить предел Разложим числитель и знаменатель на множители. Числитель Знаменатель: , Что важного в данном примере? Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Изображение слайда

Слайд 10

Метод умножения числителя и знаменателя на сопряженное выражение Продолжаем рассматривать неопределенность вида Пример 6 Сначала пробуем подставить 3 в выражение под знаком предела Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике. Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще. Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.

Изображение слайда

Слайд 11

Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Изображение слайда

Последний слайд презентации: Пределы функций. Примеры решений Теория пределов – это один из разделов

Число, как уже отмечалось ранее, лучше вынести за значок предела. Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше. Пример 7 Спасибо за внимание !

Изображение слайда

Урок-лекция на тему “Пределы функций”

Пределы функций. Примеры решений

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является моей задачей.

Итак, что же такое предел?

Рассмотрим на примере

Любой предел состоит из трех частей:

Сама запись читается так: «предел функции при икс стремящемся к единице».

Готово.

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

А что в это время происходит с функцией ?
, , , …

Итак: если , то функция стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать до бесконечности и смотрим на поведение функции:

Вывод: при функция неограниченно возрастает:

И еще серия примеров:

! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.д.

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.

Пределы с неопределенностью вида и метод их решения

Пример:

Вычислить предел

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим в старшей степени:

Старшая степень знаменателя равна двум.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени.

Разделим числитель и знаменатель на

Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Пример 2

Разделим числитель и знаменатель на

Пример 3

Разделим числитель и знаменатель на

Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Пределы с неопределенностью вида и метод их решения

Пример 4

Решить предел
Сначала попробуем подставить -1 в дробь:

В данном случае получена так называемая неопределенность .

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Далее находим корни:

Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Разложим числитель на множители.

Пример 5

Вычислить предел

Сначала «чистовой» вариант решения

Разложим числитель и знаменатель на множители.

Числитель:
Знаменатель:

,

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

! Важно
В ходе решения фрагмент типа встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Пример 6

Найти предел

Начинаем решать.

Получена неопределенность вида , которую нужно устранять.

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

Умножили. Теперь самое время применить вверху формулу :

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Готово.

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Пример 7

Найти предел

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

Умножим числитель и знаменатель на сопряженное выражение

Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы. Но об этом позже…

Для чего нужны пределы в реальной жизни

Обновлено: 17.09.2022

Если именно просто в быту — я вспоминал формулы когда делал трехугольную стойку исходя из длины окружности цветочного горшка, который будет поставлен плотно внутрь стойки. Вообще, люди, которые работают с мебелью, ремонт в квартирах, используют формулы — не всё можно измерить рулеткой, вычислить размер заранее, посчитать нужное количество материала, экономичную раскройку и так далее.

Sofya Sizova и Дима Гричанюк, то, что тригонометрия нужна в науке — очевидность. Вопрос явно — традиционный вопрос “а зачем мне тригонометрия, если я не ученый”. В реальной жизни — в смысле обыкновенной, повседневной жизни не ученого, а обычного человека.

О, тригонометрия – это очень полезная штука. Например, широко используется геодезистами (для определения расстояния между объектами на местности), архитекторами (сотни разных проблем, где нужна тригонометрия) Вы удивитесь, но она необходима и в медицине(например, при обследованиях типа узи, или компьютерной томографии). Военные также должны умело и. Читать далее

Зачем нужен интеграл

Из примера выше уже понято, что одна из полезных задач интегрирования — это расчет площади криволинейных фигур. В любой сложной ситуации, если сложность эта заключается криволинейности или неравномерности мы используем интеграл.

Но лучший способ объяснить, что такое интеграл простыми словами — показать еще пару примеров. Как когда-то в детстве объяснили сложение на яблоках. Для чего интеграл может понадобиться?

Предположим, нужно построить храм кому-то из древнегреческих богов, такой чтобы место в нем хватило всем, крыша была прямоугольной, а колоны круглыми, ведь так красивее (а еще прочнее).

Давление колонны на фундамент легко посчитать, если она квадратного сечения, делим силу на площадь и вуаля. А если колонна круглого сечения? Какова площадь круга?

Можно конечно, не напрягаться, и заменить круг эквивалентным квадратом (квадратура круга), но каким? На всякий случай побольше, чтобы наверняка ничего не развалилось. Но это не наш метод, особенно, если ни бесконечного числа рабочих, ни бесконечного числа мрамора в действительности нет и взять негде, а казнить за неэффективное использование бюджета никто не запрещает.

Еще примеры из жизни

В обратную сторону: первая производная пути, это скорость, вторая производная — ускорение. Если ускорение равно нулю, значит скорость не менялась.

Если проинтегрировав функцию изменения скорости (ускорение) получим константу (число, например, 60, а не формулу y=2x), значит, скорость не изменялась со временем, ускорения не было. Если, взяв приводную (дифференциал) функции скорости по времени, получим ноль — скорость не менялась, ускорение равно нулю.

То есть, имея в своем распоряжении какую-то функцию (зависимость чего-то от чего-то), мы можем ее дифференцировать или интегрировать. Точно также как если бы умножали и или, вычитали и складывали обычные числа.

Например, у нас есть функция изменения координат от времени. В реальном мире мы вышли на пробежку. Бежал наш виртуальный спортсмен 30 минут, первые 10 минут очень быстро, вторые 10 минут уже с одышкой, ну а последние 10 прошел пешком.

Очевидно, что координаты бегуна в начале и в конце разные (он же не стоял на месте). Если координаты менялись — скорость не равнялась нулю.

Скорость не была одинаковой, а менялась в зависимости от времени (больше времени, больше усталость, меньше скорость).

Итак, у нас есть функция изменения координат. Первая производная даст нам новую функцию — изменения координат, вторая производная — функцию ускорения. И первая и вторая функции зависят от одной и той же переменной — времени.

Еще один пример, вычисление массы. Масса, это произведение плотности на объем. Если плотность и объем одинаковы (это стакан воды) никаких проблем нет. А если плотность меняется (тот же стакан, только с коктейлем в несколько слоев)? В таком случае нужно знать закон (зависимость с которой изменяться плотность жидкости в стакане).

Пусть это будет 2x 2 . Применяем магию интегрирования — (2x 3 )/3. Теперь осталось подставить вместо Х нужные значения глубины (от ноля на поверхности до значения на дне стакана) и получим массу неоднородной(!) жидкости, без взвешивания.

Ну а если уж совсем просто, для гуманитариев, то производная винограда — это вино. Интеграл вина — это виноград.

Что такое пределы простыми словами

Ахиллес и черепаха бегут на перегонки. Черепаха начинает первой, человек догоняет. Ахиллес бежит быстрее, но когда он пробегает 100 шагов, черепаха все рано проползает один. Еще 100 шагов и еще один. Таким образом Ахиллес приближается к черепахе но и она чуть-чуть отдаляется от него. Зенон делает вывод, что Ахиллес будет бесконечно к ней приближаться, но никогда не догонит черепаху!

Говоря простым языком, предел это такое значение, которое нельзя достичь, но можно бесконечно близко к нему приблизится.

Пределы в математике

Давайте разделим число 10 пополам:

Если делать это 20 раз получится вот такое значение: 0,000019

А если сделать 100 раз, то вот такое: 0,000000000000000000000000000016

Еще один пример

Каждый раз, значение реальной вероятности, приближается к расчетным 0,5. Чтобы получить вероятность ровно 0,5 нужно подбросить монетку бесконечное количество раз.

То есть, при условии, что количество бросков стремится к бесконечности предел предел будет равен 0,5.

Предел последовательности

Предел последовательности — это пространство которое содержит все все элементы последовательности начиная с какого-то значения.

ε — это произвольное положительное число.

Можно сказать и так:

Предел функции простым языком

Фактически это то же самое. За исключением того, что последовательность чисел имеет разрывы, а функция — нет, она не прерывна. Но принципиально это не меняет сути дела.

Предел функции простыми словами объяснить также просто. Предел в какой-то произвольной точке — это величина к которой значение функции приближается. Например, f(x)=2x, а х→0 (икс стремится к нулю).

Использование предельного исчисления в жизни

Пределы используются не в жизни, а в математике, при выводе формул.
Дурацкий вопрос, типа “где в жизни используется первый замечательный предел” 😉

Сама по себе теория пределов является вспомогательной областью и служит для обоснования более сильных областей (интегрирование, дифференцирование и т д) . Непосредственно без связи с чем-то ещё она мало где применяется.

В принципе, пределы – это бред математиков, который никому кроме учителей математики не нужен.. . Но не все так печально.. . Пределы используются в познании Вселенной, например в вычислении каких либо свойств какой нить альфа звезды какой то М галактики. Также пределы используются как опорная точка при доказательстве теорем квантовой физики

площадь круга, например. Число пи определялось как предел площадей вписанных и/или описанных многоугольников.

Теория пределов очень активно применяется в экономических расчетах, например, в доказательствах и расчетах, которые связаны с непрерывными процессами; в финансовых рентах. Пределы функции применяются для нахождения асимптот графика функции при ее исследовании.

Пределы

Интеграл простыми словами

Интегралы начинают изучать еще в школе. Но никто из учителей не говорит, зачем это нужно, как использовать эти знания в жизни. Мало кто вообще способен объяснить простыми словами, что такое интеграл, даже в университете. А мы попробуем.

Если коротко — интеграл, это сумма маленьких частей. Да, точно так же как и сложение 2+2, только части бесконечно маленькие, естественно и количество их — бесконечно.

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Бесконечно малая величина, это не какое-то конкретное число. Это абстракция, в реальном мире аналогов просто нет. Мы придумали так для удобства. Что-то настолько маленькое, что измерять его бессмысленно, но в расчетах использовать можно.

Можно, конечно, разбить фигуру на две, прямоугольник и треугольник.

Чем больше будет фигур, тем больше будет и точность расчета и тем меньше будут сами фигурки. Если площадь маленьких фигурок будет бесконечно малой, то есть стремится к нулю (но не равняться ему), сумма всех этих площадей будет равна сумме большой фигуры с бесконечно большой точностью.

То же самое происходит при интегрировании:

Сложение бесконечного числа частей бесконечно маленького размера это и есть интегрирование.

Высота конкретного прямоугольничка, это значение функции в этой конкретной точке (почему точке, потому, что ширина полоски у нас бесконечно маленькая, мы так договорились в самом начале).

Площадь, это высота умноженная на ширину. За высоту можем брать и y и f(x), они равны. За ширину у нас играет dx. Итак, момент истины:

f(x)dx — площадь нашего маленького столбика. В если собрать из все вместе, будет сумма бесконечно маленьких столбиков.

Осталось только указать, что интересуемся мы конкретным значением. Наша кривая, это часть параболы f(x)=x 2 .

А площадь нужна не бесконечной фигуры, а той что начинается от 1 и закачивается на 5. Если написать эти цифры над и под значком интеграла, получится определенный интеграл.

Собственно и все, интеграл — это сумма бесконечно малых приращений (то есть значений) какой-то функции. Не сложно и не страшно, если не усложнять.

Никакого противоречия здесь нет. Вот только умножение работает в случае одинаковых величин, простых фигур или прямолинейного движения без ускорения. В остальных случаях — интегрирование.

Зачем нужен предел функции? vol.2

Я не спрашиваю о производной, дифференциалах и проч. Я об этом знаю. Я читал определения. Но, мать его, никак не могу понять: для чего именно нужен предел?

Ну например предел используется для введения понятий, которые ты якобы знаешь (производная, дифференциал, интеграл) .
А вообще в различных науках есть куча ситуаций, в которых говорится: а что будет с этим явлением, процессом, эффектом, если: время устремить к бесконечности, частоту устремить к определенному значению, величину X (любая другая физическая величина) устремить к нулю, бесконечности, опред. значению.

Хм. . но ведь производная это предел.. . и дифференциал – предел и интеграл тоже)

Понятие предела в математике играет промежуточную роль, для определения других вещей в ней. Сам по себе он бесполезен.

Зачем нужны пределы

Вот какой график получится, если взять функцию y=x 2 -4/x-2

при х→2 lim x 2 -4/x-2→4

x=1 и x→1, это совсем не одно и то же.

Примеры из жизни

Зачем все это нужно где применяется пределы в реальных расчетах?

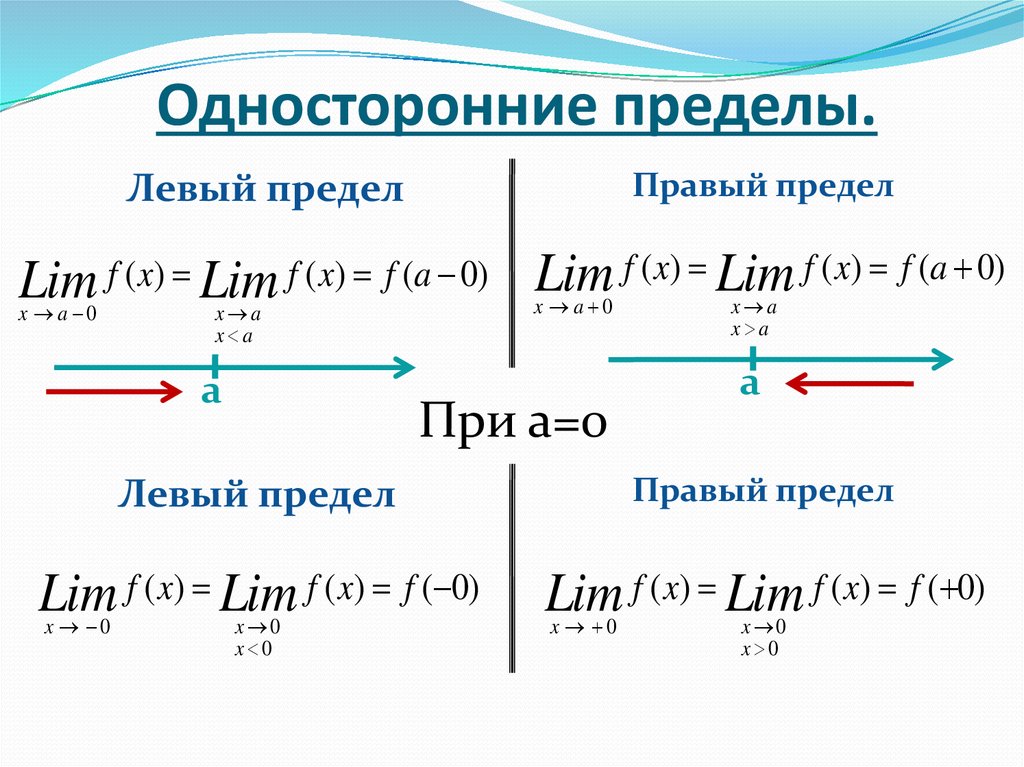
Что тут общего с пределами из математики, кроме названия.

Все, что лежит за пределом, уже не имеет практического значения — спичка не устоит.

Посмотрите на картинку ниже, это наглядный пример такого явления как резонанс.

Колебание моста из-за резонанса

Очевидно, что предел этой функции стремится к 30 кликам, если стоимость клика стремится к бесконечности. Даже без знания матанализа становится понятно, даже при повышении ставки за клин до $4 или $5 долларов, нельзя будет добиться большего количества кликов, чем 30. А раз так, то зачем повышать ставки?

Но, если постараться, математика может открыть новые грани реальности, по крайней мере, все это уже не будет казаться таким скучным и непонятным.

Читайте также:

Что такое lel в майнкрафте
Elizavecca hell pore control hyaluronic acid 97 как пользоваться
Как русифицировать kenshi
Что стало с присциллой ведьмак 3 после нападения
Как будет на башкирском я тебя хочу

Предельные законы — определение, свойства и примеры

Вы когда-нибудь задумывались, есть ли более простой способ найти пределы функции без их графика или таблицы значений? Мы можем использовать различные доступные свойства и законы пределов. Предельные законы важны при манипулировании и оценке пределов функций.

Предельные законы — это полезные правила и свойства, которые мы можем использовать для оценки предела функции.

Предельные законы также помогают понять, как мы можем разбить более сложные выражения и функции, чтобы найти их собственные пределы. В этой статье мы узнаем о различных законах пределов, а также обсудим другие предельные свойства, которые могут помочь нам в наших следующих темах предварительного исчисления и исчисления. 92 + \lim_{x\rightarrow6} 5x + -8\color{blue} \text{ \{ Постоянный закон\}}\\&=-72 + 30 + -8\color{blue} \text{ \{ Многочлен Свойство функции\}}\\&=-50 \end{aligned}$

Не беспокойтесь. После того, как вы ознакомитесь со списком законов о лимитах, вам будет легче оценивать лимиты! На самом деле, мы уже изучали некоторые из этих предельных законов в прошлом, но они представлены в гораздо более простой и общей форме.

Обратите внимание, что на протяжении всего обсуждения мы будем предполагать, что два выражения, $ \lim_{x\rightarrow a} f(x)$ и $ \lim_{x\rightarrow a} g(x)$, существуют и $ $ является константой.

Каковы свойства пределов?

Почему бы нам постепенно не познакомиться со свойствами пределов и законов, которые могут нам помочь? В этом разделе также будут рассмотрены примеры, в которых используются эти свойства и законы, чтобы мы могли лучше их понять.

Если вы впервые сталкиваетесь с этими свойствами, попробуйте записать названия предельных законов и алгебраические определения. Сведите их в одну таблицу в качестве руководства для примеров этого раздела и следующих тем, с которыми вы можете столкнуться, связанных с ограничением функции.

У вас нет поблизости бумаги или приложения для создания заметок? Не беспокойтесь, мы также обобщили эти свойства для вас в конце этого раздела!

Понимание двух самых фундаментальных предельных законов

Мы будем группироваться с этими двумя основными законами пределов, поскольку они являются двумя наиболее применяемыми законами и простейшими законами пределов. Это константы и законы тождества.

Закон константы: $\boldsymbol{\lim_{x\rightarrow a} c = c} $

Этот предельный закон утверждает, что предел константы $c$, когда $x$ приближается к $a$ , равно самой константе.

На приведенном выше графике показано, почему закон констант верен для всех значений $a$ и $c$. Независимо от значения $a$ функция по-прежнему будет равна $c$.

Вот несколько примеров того, как мы можем применить постоянный закон для некоторых пределов.

$\lim_{x\rightarrow 2} 3 = 3$
$\lim_{x\rightarrow 1} -6 = -6$
$\lim_{x\rightarrow 6} \pi = \pi$

Закон тождества: $\boldsymbol{\lim_{x\rightarrow a} x = c} $

Знаете, почему мы называем это законом тождества? Это потому, что мы имеем дело с линейной функцией $y = x$ для этого закона предела. Закон предела гласит, что предел $y = x$ при приближении к $a$ равен числу (или $a$) при приближении к нему $x$.

Вот иллюстрация того, почему закон тождества верен для всех значений $x$. Когда $x$ приближается к $a$, значение $y$ будет зависеть от значения $x$, поэтому, когда $x$ приближается к $a$, $y$ также приближается к $a$.

Ознакомьтесь с этими тремя примерами, чтобы лучше понять закон тождества.

$\lim_{x\стрелка вправо -4} x= -4$
$\lim_{x\стрелка вправо \sqrt{2}} x = \sqrt{2}$
$\lim_{x\стрелка вправо \pi} x= \pi$

Готовы узнать больше о предельных законах? Вот еще пять, посвященных четырем арифметическим операциям: сложению, вычитанию, умножению и делению.

Предельные законы, включающие арифметические операции

Мы сгруппировали эти предельные законы, потому что они имеют схожие формы и содержат четыре наиболее часто используемых арифметических операции в данной функции.

Закон сложения: $\boldsymbol{\lim_{x\rightarrow a} [f(x) + g(x)]= \lim_{x\rightarrow a} f(x) + \lim_{x \rightarrow a} g(x)} $

Закон сложения повторяет, что когда мы берем предел суммы двух функций, результат эквивалентен сумме соответствующих пределов функции при приближении $x$ к $a $.

Если $\lim_{x\rightarrow 3} f(x) = -2$ и $\lim_{x\rightarrow 3} g(x) = 5$, это означает, что ${\lim_{x\rightarrow a } [f(x) + g(x)]$ можно определить, как показано ниже.

$\begin{aligned}\lim_{x\rightarrow a} [f(x) + g(x)] &= \lim_{x\rightarrow a} f(x) + \lim_{x\rightarrow a} g(x) \\&=-2 + 5\\&=3 \end{align}$

Закон вычитания: $\boldsymbol{\lim_{x\rightarrow a} [f(x) – g(x)]= \lim_{x\rightarrow a} f(x) – \lim_{x\rightarrow a} g(x)} $

Этот закон подобен своему аналогу сложения. В нем говорится, что предел разности двух функций как раз равен разнице между пределами каждой функции как $x \rightarrow a$.

Почему бы нам не применить этот закон вместе с константами и законами тождества для упрощения $ \lim_{x \rightarrow -6} (x – 4 )$.

$\begin{aligned} \lim_{x \rightarrow -6} (x – 4 ) &=\lim_{x \rightarrow -6} x – \lim_{x \rightarrow -6}-4 \color{blue } \text{ {Закон вычитания}}\\&=\lim_{x \rightarrow -6} x -4\color{blue} \text{ { Постоянный закон}}\\&= -6 – 4 \color{blue } \text{ {Закон тождества}}\\&=-10 \end{aligned}$

Это хороший пример, показывающий, как все эти свойства применяются для упрощения и оценки ограничений.

Закон коэффициентов: $\boldsymbol{\lim_{x\rightarrow a} c \cdot f(x)= c \lim_{x\rightarrow a} f(x)} $

Этот закон гласит, что предел произведения, разделяемый константой $c$ и функцией $f(x)$, будет одинаковым, когда мы умножаем $c$ на предел $f(x)$ по мере приближения к $a $.

Вот несколько простых применений этого закона:

Если $\lim_{x\rightarrow 2} f(x) = -4 $, $\lim_{x\rightarrow 2} -5 \cdot f(x) $ равно $-4 \cdot-5 = 20$
Если $\lim_{x\rightarrow 3} g(x) = \dfrac{1}{2} $, $\lim_{x\rightarrow 3} -12 \cdot g(x)$ равно $ – 12 \cdot \dfrac{1}{2} = 8$

Закон произведения: $\boldsymbol{\lim_{x\rightarrow a} [f(x) \cdot g(x)] = \ lim_{x\rightarrow a} f(x) \cdot \lim_{x\rightarrow a} g(x) }$

Подобно законам сложения и вычитания, этот конкретный предельный закон утверждает, что предел произведения двух функций равен равно произведению соответствующих пределов каждой функции.

Почему бы нам не попытаться упростить $\lim_{x\rightarrow 5} 2x$, используя закон произведения и ранее изученные законы?

$\begin{aligned} \lim_{x \rightarrow 5} 2x &= \lim_{x \rightarrow 5} (2 \cdot x)\\&=\lim_{x \rightarrow 5} 2 \cdot \lim_ {x \rightarrow 5} x\color{blue} \text{ {Product Law}}\\&=2 \cdot \lim_{x \rightarrow 5} x\color{blue} \text{ { Постоянный закон}}\ \&= 2 \cdot 5 \color{blue} \text{ {Закон идентичности}}\\&=10 \end{aligned}$

Частный закон: $\boldsymbol{\lim_{x\rightarrow a} \dfrac{f(x)}{g(x)} = \dfrac{\lim_{x\rightarrow a} f(x)} {\lim_{x\rightarrow a} g(x)}}$, , где $\boldsymbol{\lim_{x\rightarrow a} g(x) \neq 0}$

Это означает, что предел частное двух функций эквивалентно отношению пределов каждой из функций. Обратите внимание, что этот закон применим только тогда, когда $\lim_{x\rightarrow a} g(x) \neq 0$.

Это означает, что если $\lim_{x\rightarrow a} f(x) = P$ и $\lim_{x\rightarrow a} g(x) = Q$, предел $\dfrac{f(x )}{g(x)}$ as $x \rightarrow a$ равно $\dfrac{\lim_{x\rightarrow a} f(x)}{\lim_{x\rightarrow a} g(x)} = \dfrac{P}{Q}$. 9{th}$ корень предела функции, когда $x$ приближается к $a$.

Поскольку у нас есть ограничения, когда корень четный, убедитесь, что предел $f(x)$ при приближении к $a$ положителен, когда $n$ четно.

Давайте применим то, что мы только что узнали, для упрощения $\lim_{x\rightarrow 4} \sqrt[3]{f(x)}$, если $\lim_{x\rightarrow 4} f(x) = -27 $?

Используя корневой закон, мы имеем $\lim_{x\rightarrow 4} \sqrt[3]{f(x)} = \sqrt[3]{ \lim_{x\rightarrow 4} f(x)} $ . Учитывая, что $\lim_{x\rightarrow 4} f(x) = -27$, теперь мы имеем $\lim_{x\rightarrow 4} \sqrt[3]{f(x)} = \sqrt[3]{ -27} $ или $-3$.

Вы заметили общую закономерность, характерную для всех предельных законов, которые мы только что изучили? Общее правило, демонстрируемое законами пределов, заключается в том, что всякий раз, когда мы применяем операцию к пределу функции, мы можем вместо этого сначала найти предел функции, а затем взять предел результирующего выражения.

Краткое изложение свойств пределов

Мы узнаем больше о применении предельных законов, когда узнаем, как вычислять пределы более сложных функций. А пока давайте сначала продолжим и обобщим предельные законы, которые мы только что изучили в этой статье.

Limit Law	Algebraic Definition	Example
Constant Law	$ \lim_{x\rightarrow a} c = c$	$\lim_{x\rightarrow 3} 4 = 4 $
Закон тождества	$\lim_{x\rightarrow a} x = a$	$\lim_{x\rightarrow 3} x = 3 $
Закон сложения7 $\lim_{x\rightarrow a} [f(x) + g(x)] = \lim_{x\rightarrow a} f(x) + \lim_{x\rightarrow a} g(x) $	$\lim_{x\стрелка вправо 2} [(x – 1)+ (2x)] = \lim_{x\стрелка вправо 2} (x – 1) + \lim_{x\стрелка вправо 2} 2x $
Закон вычитания	$\lim_{x\rightarrow a} [f(x) – g(x)] = \lim_{x\rightarrow a} f(x) – \lim_{x\rightarrow a} g(x) ) $	$\lim_{x\стрелка вправо 2} [(x – 1) -(2x)] = \lim_{x\стрелка вправо 2} (x – 1) – \lim_{x\стрелка вправо 2} 2x $
Закон о коэффициентах	$\lim_{x\rightarrow a} cf(x) = c \lim_{x\rightarrow a} f(x) $	$\lim_{x\rightarrow 5} \sqrt{2} x = \sqrt{2} \lim_{x\rightarrow 5} x $
Закон о продукте	$\lim_{x\rightarrow a} [ f(x) \cdot g(x)] = \lim_{x\rightarrow a} f(x) \cdot \lim_{x\rightarrow a} g(x) $	$\lim_{x\rightarrow 2} [(x – 1) \cdot (2x)] = \lim_{x\rightarrow 2} (x – 1) \cdot \lim_{x\rightarrow 2} 2x $
Закон частных	$\lim_{ x \ rightarrow a} \ dfrac {f (x)} {g (x)} = \ dfrac {\ lim_ {x \ rightarrow a} f (x)} {\ lim_ {x \ rightarrow a} g (x)} $ 94$
Корневой закон	$\lim_{x\rightarrow a} \sqrt[n]{f(x)} = \sqrt[n]{ \lim_{x\rightarrow a} f(x)} $	$\lim_{x\стрелка вправо 3} \sqrt[4]{2(x + 1)} = \sqrt[4]{ \lim_{x\стрелка вправо 3} 2(x + 1)}$

Обязательно просмотрите все свойства, которые мы обсуждали в предыдущем разделе, прежде чем решать следующие задачи.

Пример 1

Учитывая, что $\lim_{x\rightarrow a} f(x) = -24$ и $\lim_{x\rightarrow a} g(x) = 4$, найдите значение из следующих выражений, используя свойства пределов, которые мы только что изучили.

а. $\lim_{x\rightarrow a} [f(x) + g(x)]$

б. $\lim_{x\rightarrow a} [4 g(x)]$

c. $\lim_{x\rightarrow a} \dfrac{\sqrt{g(x)}}{0.5f(x)}$

Решение

При работе с подобными задачами в первый раз всегда полезно чтобы иметь список предельных законов, которые мы только что обсудили. Таким образом, вы всегда можете проверить предельный закон, применимый к нашей задаче.

Мы можем переписать $\lim_{x\rightarrow a} [f(x) + g(x)]$ как $\lim_{x\rightarrow a} f(x) + \lim_{x\rightarrow a} g (х) $ с использованием закона сложения .

Подставьте данные значения для пределов $f(x)$ и $g(x)$, когда они приближаются к $a$.

$\begin{align}\lim_{x\rightarrow a} [f(x) + g(x)] &= \lim_{x\rightarrow a} f(x) + \lim_{x\rightarrow a} g(x) \\&=-24 + 4\\&= -20\end{выровнено}$

а. Это означает, что $\lim_{x\rightarrow a} [f(x) + g(x)] = \boldsymbol{24}$.

Точно так же мы можем переписать $\lim_{x\rightarrow a} [4 g(x)]$ как $4\lim_{x\rightarrow a} g(x)$ с использованием закона коэффициентов .

$\begin{align}\lim_{x\стрелка вправо a} [4g(x)] &= 4\lim_{x\стрелка вправо a} g(x) \\&=4(4)\\&= 16 \end{выровнено}$

б. Следовательно, $\lim_{x\rightarrow a} [4 g(x)]$ равно $\boldsymbol{16}$.

Для третьего выражения потребуется несколько предельных законов, прежде чем мы сможем найти значение выражения. На самом деле, для этого элемента нам понадобятся следующие свойства:

Частное, чтобы разрушить предел дроби.
Корневой закон для числителя.
Закон коэффициентов для знаменателя.

Давайте разберем $\lim_{x\rightarrow a} \dfrac{\sqrt{g(x)}}{0.5f(x)}$, чтобы увидеть, как эти законы могут быть полезны для этого элемента.

$\begin{align}\lim_{x\rightarrow a} \dfrac{\sqrt{g(x)}}{0. 5f(x)}&=\dfrac{\color{blue}{\lim_{x \rightarrow a}\sqrt{g(x)}}}{\color{blue}{\lim_{x\rightarrow a} [0.5f(x)]}} \color{blue}\text{ Частное правило}\ \&=\dfrac{\color{blue}{\sqrt{\lim_{x\rightarrow a}g(x)}}}{\lim_{x\rightarrow a} [0.5f(x)]} \color{ blue} \text{ Корневой закон}\\&=\dfrac{\sqrt{\lim_{x\rightarrow a}g(x)}}{\color{blue}0,5\lim_{x\rightarrow a} f(x )} \color{blue} \text{ Закон коэффициентов}\\&=\dfrac{\sqrt{\lim_{x\rightarrow a}g(x)}}{0,5\lim_{x\rightarrow a} f(x )} \end{выровнено}$

Используя окончательное выражение, подставим $\lim_{x\rightarrow a} f(x) = -24$ и $\lim_{x\rightarrow a} g(x) = 4$ в рациональное выражение.

$\begin{align}\lim_{x\rightarrow a} \dfrac{\sqrt{g(x)}}{0.5f(x)}&=\dfrac{\sqrt{\sqrt{\lim_{x\rightarrow a} } g (x)} {0,5 \ lim_ {x \ стрелка вправо a} f (x)} \\ & = \ dfrac {\ sqrt {4}} {0,5 (-24)} \\ & = \ dfrac {2 }{-12}\\&=-\dfrac{1}{6} \end{aligned}$

c. Это означает, что $\lim_{x\rightarrow a} \dfrac{\sqrt{g(x)}}{0.5f(x)}$ равно $\boldsymbol{-\dfrac{1}{6}}$ . 92 + bx + c$ — это общая форма квадратичных выражений, а $k$ может быть любой отличной от нуля константой, это наблюдение относится ко всем квадратичным функциям.

Значение, когда дана квадратичная функция, ее предел при $\boldsymbol{x}$ приближается к $\boldsymbol{k}$ можно определить, найдя значение функции в $\boldsymbol{x = к}$.

Хотите взглянуть на следующие концепции, которые вы узнаете об ограничениях? В общем случае предел полиномиальной функции при приближении к $a$ равен значению функции при $x = a$. 92}} $ равно $\boldsymbol{\sqrt[3]{\dfrac{61}{4}}}$. Пример 4 } + 8}{ч – 1}$.

Решение

Так как $f(x)$ содержит рациональное выражение, мы можем применить закон частных для применения предельных законов как к числителю, так и к знаменателю.

$\begin{aligned}\lim_{h \rightarrow 0 } f(x) &= \lim_{h \rightarrow 0 } \dfrac{\sqrt{5 – h} + 8}{h – 1}\\ &= \dfrac{\lim_{h \rightarrow 0}(\sqrt{5 – h} + 8)}{\lim_{h \rightarrow 0 } h – 1}\end{align}$

Сначала упростите знаменатель, используя следующие законы пределов:

Разделите два члена, используя разностный закон .
Примените законы тождества и константы , чтобы еще больше упростить выражение в знаменателе.

$ \begin{aligned}\lim_{h\стрелка вправо 0 } (h – 1) &= \lim_{h\стрелка вправо 0 } h – \lim_{h\стрелка вправо 0 }1\\&= 0 -\ lim_{h\rightarrow 0 } 1\\&= 0 – 1\\&= -1\end{aligned}$

Теперь, когда у нас есть числовое значение знаменателя, давайте продолжим и упростим выражение.

$\begin{align}\dfrac{\lim_{h \rightarrow 0}(\sqrt{5 – h} + 8)}{\lim_{h \rightarrow 0 } h – 1}&= \dfrac{\ lim_{ h \rightarrow 0 }(\sqrt{5 – h} + 8)}{-1}\\&= -\lim_{ h \rightarrow 0 }(\sqrt{5 – h} + 8)\end{ выровненный}$

Упростите это выражение, применив следующие свойства:

Примените закон сложения , чтобы расширить члены и применить ограничения для каждого члена.
Используйте корень , законы вычитания и константы , затем, наконец, закон тождества, чтобы упростить $\lim_{ h \rightarrow 0} \sqrt{5 – h}$.
Используйте постоянный закон во втором члене, чтобы вычислить $\lim_{ h \rightarrow 0} 8$.

$\begin{align}-\left[\sqrt{\lim_{h \rightarrow 0 }(5 – h)} + \lim_{h \rightarrow 0 }8\right ]&= -\left(\ sqrt{\lim_{h \rightarrow 0} 5 – \lim_{h \rightarrow 0}h} + \lim_{h \rightarrow 0 }8\right )\\&= -\left(\sqrt{5 – \lim_ { h \rightarrow 0}h} + \lim_{ h \rightarrow 0 }8\right )\\&= -\left(\sqrt{5 – 0} + \lim_{ h \rightarrow 0 }8\right )\ \&= -(\sqrt{5} + 8 )\\&= -\sqrt{5} – 8 \end{align}$

Это означает, что $ \lim_{h\rightarrow 0 }\dfrac{\sqrt{5 – h} + 8}{h – 1}$ равно $\boldsymbol{-\sqrt{5} – 8 }$ .

Получаете удовольствие от процесса нахождения пределов, используя различные свойства? Угадай, что? В этой статье вы узнаете больше о свойствах и методах оценки пределов!

А пока мы подготовили для вас больше задач, чтобы вы могли самостоятельно освоить эти предельные законы.

7 Пределы демократической власти | Конституция равенства: демократическая власть и ее пределы

Фильтр поиска панели навигации Oxford AcademicКонституция равенства: демократическая власть и ее пределыСравнительная политикаПолитическое поведениеПолитическая теорияКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Расширенный поиск

Иконка Цитировать Цитировать
Разрешения
Делиться
- Твиттер
- Больше

Cite

Christiano, Thomas,

‘7 The Limits to Democratic Authority’

The Constitution of Equality: Democratic Authority and Its Limits

(

Oxford,

2008;

online edn,

Oxford Academic

, 1 сентября 2008 г.

), https://doi.org/10.1093/acprof:oso/9780198297475.003.0008,

, по состоянию на 18 сентября 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Advanced Search

Abstract

В этой главе рассматриваются ограничения демократической власти, основанной на том же принципе общественного равенства, который лежит в основе власти демократии. Это объясняет, что подразумевается под ограничением демократической власти. Он показывает, как основные демократические и либеральные права ограничивают власть демократического собрания. Он утверждает, что обеспечение экономического минимума необходимо для общественного равенства, и поэтому демократическое собрание, которое не делает все возможное для его обеспечения, тем самым ослабляет свой собственный авторитет. Он показывает, как принцип общественного равенства может служить руководством в отношении того, когда институты конституционных ограничений на правительство и судебный надзор могут быть оправданы, а когда нет. Он показывает, как концепция демократии, основанной на общественном равенстве, подразумевает, что демократическая ассамблея, порождающая постоянные меньшинства, имеет ослабленный авторитет и, таким образом, обеспечивает некоторую поддержку ограниченного самоопределения меньшинств.

Ключевые слова: конституционализм, демократия, экономический минимум, судебный надзор, постоянные меньшинства, общественное равенство, самоопределение

Предмет

Сравнительная политикаПолитическая теорияПолитическое поведение

В настоящее время у вас нет доступа к этой главе.

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

Нажмите Войти через свое учреждение.
Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

Щелкните Войти через сайт сообщества.
При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Пределы в исчислении | Определение и правила с примерами

В математике пределы используются для решения сложных задач исчисления различных функций. Он в основном используется для определения дифференциала, непрерывности и интегралов. Пределы выполняют определенную функцию значения, заменяя предельное значение.

Пределы очень важны в типе первообразной, известном как определенный интеграл, в котором применяются верхние и нижние пределы. В этом посте мы изучим определение и правила лимитов на множестве примеров.

Каковы пределы исчисления?

В исчислении значение, к которому функция приближается по мере того, как вход этой функции становится все ближе и ближе к некоторому определенному числу, называется пределом. Другими словами, когда функция приближается к некоторому значению для оценки значения предела этой функции, это называется пределом.

Для измерения близости и представления идей математических понятий можно использовать обозначение предела. Это очень полезно для определения других ветвей исчисления, таких как производная, непрерывность и первообразная.

Уравнение пределов

Формула или уравнение, используемые для расчета пределов функций, приведены ниже.

lim _x _→u h(x) = N

Lim — обозначение пределов.
u — предельное значение функции.
h(x) — заданная функция.
x — переменная функции.
N — результат функции после применения предельного значения u.

Вы должны применить предельное значение u к заданной функции h(x), для решения задач пределов. Пределы не применяются к постоянным функциям, поэтому пределы постоянных функций остаются неизменными.

Правила лимитов

Существуют различные правила пределов в исчислении. Давайте кратко обсудим их с помощью примеров для оценки предельных задач.

1. Постоянное правило

Согласно этому правилу пределов постоянная функция остается неизменной. Потому что ограничения применяются только к переменным. Уравнение для постоянного правила:

lim _x _→u С = С

Lim — обозначение пределов.
u — предельное значение функции.
C — заданная функция.

Пример

Найдите предел 56, когда x приближается к 5.

Раствор

Шаг 1: Применить предельное обозначение для данной функции.

лим _x _→5 56

Шаг 2: Теперь примените ограничение.

lim _x _→5 56 = 56 (по постоянному правилу)

2. Правило постоянной функции

В соответствии с этим правилом пределов константа с функцией будет записана вне предельных обозначений. Потому что ограничения применяются только к переменным. Уравнение для правила постоянной функции:

lim _x _→u C h(x) = C * N

Lim — обозначение пределов.
u — предельное значение функции.
C — любая константа.
h(x) — заданная функция.
x — переменная функции.
N — результат функции после применения предельного значения u.

Пример

Найдите предел 23x ³ при приближении x к 7.

Раствор

Шаг 1: Применить предельное обозначение для данной функции.

lim _x _→7 23x ³

Шаг 2: Теперь применим правило предела постоянной функции.

lim _x _→7 23x ³ = 23 lim _x _→7 x ³

Шаг 3: Теперь примените ограничение.

lim _x _→7 23x ³ = 23 (7 ³ )

lim _x _→7 23x ³ = 23 (7 * 7 * 7)

lim _x _→7 23x ³ = 23 (343)

lim _x _→7 23x ³ = 7889

3. Правило сумм

Согласно этому правилу ограничений, обозначения применяются к каждой функции отдельно. Уравнение для правила сумм:

LIM _x _{→ U} [H (x) + G (x)] = LIM _x _{→ U} (h (x)) + LIM _{→ x} (h (x)) + Lim _{→ x} (h) + Lim _{→ u} (h (x)) + Lim _{→ u} (h (x)) + lim _{→ u} 0008 _→u (g(x)) = M + N

Lim — обозначение пределов.
u — предельное значение функции.
g(x) & h(x) — заданные функции.
x — это переменная функции.
M и N являются результатами функций после применения предельного значения u.

Пример

Найдите пределы x ³ + x ⁵ при приближении x к 3.

Раствор

Шаг 1: Применить предельное обозначение для данной функции.

lim _x _→3 [x ³ + x ⁵ ]

Шаг 2: Теперь применим правило суммы предела.

LIM _x _{→ 3} [x ³ + x ⁵] = LIM _x _{→ 3} (x ³) + 7 (x ^881).

Шаг 3: Теперь примените ограничение.

lim _x _{→ 3} [x ³ + x ⁵ ] = (3 ³ ) + (3 ⁵ )

lim _x _→3 [x ³ + x ⁵ ] = (3 * 3 * 3) + (3 * 3 * 3 * 3 * 3)

lim _x _→3 [x ³ + x ⁵ ] = (27) + (243)

lim _x _→3 [x ³ + x ⁵ ] = 270

4.

   Правило различия
Согласно этому правилу ограничений, обозначения применяются к каждой функции отдельно. Уравнение для правила разности:
lim _x _→u [h(x) – g(x)] = lim _x _→u (h(x)) – lim _x _→u (g(x)) = M – N
Lim — обозначение пределов.
u — предельное значение функции.
g(x) & h(x) — заданные функции.
x — это переменная функции.
M и N — результаты функций после применения предельного значения u.
Пример
Найдите пределы x ³ – x ⁵ при приближении x к 2.
Раствор
Шаг 1: Применить предельное обозначение для данной функции.
lim _x _→2 [x ³ – x ⁵ ]
Шаг 2: Теперь примените правило ограничения разницы.
LIM _x _{→ 2} [x ³ – x ⁵] = LIM _x _{→ 2} (x ³) + Lim _x (x ³) + Lim _x (x ³) + LIM _{1 x} (x ³) + LIM _→ (x ³).
Шаг 3: Теперь примените ограничение.
lim _x _{→ 2} [x ³ – x ⁵ ] = (2 ³ ) – (2 ⁵ )
lim _x _→2 [x ³ – x ⁵ ] = (2 * 2 * 2) – (2 * 2 * 2 * 2 * 2)
lim _x _→2 [x ³ – x ⁵ ] = (8) – (32)
lim _x _{→ 2} [x ³ – x ⁵ ] = -24
5.   Правило продукта
Согласно этому правилу ограничений, обозначения применяются к каждой функции отдельно. Уравнение для правила продукта:
lim _x _→u [h(x) * g(x)] = lim _x _→u (h(x)) * lim _x _→u (g(x)) = M * N
Lim — обозначение пределов.
u — предельное значение функции.
g(x) & h(x) — заданные функции.
x — это переменная функции.
M и N являются результатами функций после применения предельного значения u.
Пример
Найдите пределы x ⁵ * x ³ при приближении x к 4.
Раствор
Шаг 1: Применить предельное обозначение для данной функции.
lim _x _→4 [x ⁵ * x ³ ]
Шаг 2: Теперь примените правило ограничения продукта.
lim _x _{→ 4} [x ⁵ * x ³ ] = lim _x _{→ 4} (x ⁵) * _{x _{0761 →4} (х ³ )}
Шаг 3: Теперь примените ограничение.
lim _x _→4 [x ⁵ * x ³ ] = (4 ⁵ ) * (4 ³ )
lim _x _→4 [x ⁵ * x ³ ] = (4 * 4 * 4 * 4 * 4) * (4 * 4 * 4)
lim _x _→4 [x ⁵ * x ³ ] = (1024) * (64)
lim _x _→4 [x ⁵ * х ³ ] = 65536
6.
   Правила больницы
В соответствии с этим правилом, если функция образует 0 на 0 или бесконечность на бесконечность после применения ограничений, то берутся производные от числителя и знаменателя, а затем снова применяется предельное значение.
Пример
Найдите предел x ² – 4 / 4x – 2x ² при приближении x к 2.
Раствор
Шаг 1: Применить предельное обозначение для данной функции.
lim _x _→2 [x ² – 4 / 4x – 2x ² ]
Шаг 2: Теперь примените правило отношения предела и примените предельное значение.
LIM _x _{→ 2} [x ² – 4 / 4x – 2x ²] = LIM _x _{→ 2} [x ² – 4] ЛИМ [x ² – 4]. [4x – 2x ² ]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = [2 ² – 4] / [4(2) – 2(2) ² ]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = [4 – 4] / [4(2) – 2(4)]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = [4 – 4] / [8 – 8]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = 0 / 0
Шаг 3: Поскольку функции формируют нуль за нулем, применяя предельное значение, поэтому примените правило Лопиталя и снова примените предельное значение.
lim _x _{→ 2} [x ² – 4 / 4x – 2x ² ] = lim _x _{→ 2} [d/dx (x ^{1 – 908) 4x – 2x ² )]}
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = lim _x _→2 [2x – 0 / (4 – 4x)]
3
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = lim _x _→2 [2x / (4 – 4x)]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = [2(2) / (4 – 4(2))]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = [4 / (4 – 8)]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = [4 / (– 4)]
lim _x _→2 [x ² – 4 / 4x – 2x ² ] = -1
Резюме
В этом посте мы узнали определение и правила лимитов на множестве примеров. Теперь вы можете освоить все основы лимитов, просто следуя правилам этого поста.
Ознакомьтесь с дополнительными материалами по математике (для родителей, учителей и учащихся)
Важность методологии для облегчения изучения математики
Почему учащиеся считают вычисление предела трудным
Как распознать и преодолеть математическую тревогу
Можем ли мы? Пересмотр административных ограничений в JSTOR
журнальная статья
Мы можем? Пересмотр административных ограничений
Кристофер Худ
Обзор государственного управления
Том. 70, № 4 (июль | август 2010 г.), стр. 527–534 (8 страниц)
Опубликовано: Wiley
https://www.jstor.org/stable/40802228
Читать и скачивать
Журнал через вашу школу или библиотеку
Альтернативные варианты доступа
Для независимых исследователей
Подписка на JPASS
Неограниченное чтение + 10 загрузок
Товар для покупки
$25. 00 — Скачать сейчас и позже
Ежемесячный план
Доступ ко всему в коллекции JPASS
Читать полный текст каждой статьи
Загрузите до 10 статей в формате PDF, чтобы сохранить и сохранить
$19,50/месяц Годовой план
Доступ ко всему в коллекции JPASS
Читать полный текст каждой статьи
Загрузите до 120 статей в формате PDF, чтобы сохранить и сохранить
199 долларов в год
Купить PDF
Купите эту статью за 25 долларов США.
Как это работает?
Выберите покупку вариант.
Оплатить с помощью кредитной карты или банковского счета с PayPal.
Прочтите свою статью в Интернете и загрузите PDF-файл из своей электронной почты или своей учетной записи.
Предварительный просмотр
Предварительный просмотр
Abstract
Идея административных ограничений — в смысле ограничений или пределов того, что может быть достигнуто посредством административной деятельности в целом и государственного управления в частности — важна для правильного понимания государственного управления двадцать первого века. Каковы фактические пределы налоговой способности в современном государстве, когда обремененные долгами правительства стремятся сократить уровень долга и дефицит бюджета после финансового краха и экономического спада конца 2000-х годов? Каковы пределы безопасности, которые могут быть реально достигнуты с помощью административных структур и процедур в так называемом обществе риска? Каковы пределы достижения амбициозной социальной инженерии для улучшения человеческой жизни обычными организациями и бюрократией? Такие вопросы не новы. Вопросы такого рода уже давно задаются учеными в пересекающихся областях государственного управления, политических исследований и политологии. Тем не менее, утверждает автор, они затрагивают вопросы, которые имеют постоянную, центральную важность для правительства и общества в современном мире.
Информация о журнале
Обзор государственного управления уже более 75 лет является ведущим журналом в области исследований и теории государственного управления и единственным журналом в области государственного управления, который обслуживает ученых, практиков и студентов, интересующихся государственным сектором и общественностью. управление сектором. Статьи выявляют и анализируют текущие тенденции, обеспечивают фактическую основу для принятия решений, стимулируют обсуждение и делают ведущую литературу в этой области доступной в легкодоступном формате.
Информация об издателе
Wiley — глобальный поставщик контента и решений для рабочих процессов на основе контента в областях научных, технических, медицинских и научных исследований; профессиональное развитие; и образование. Наши основные виды деятельности выпускают научные, технические, медицинские и научные журналы, справочники, книги, услуги баз данных и рекламу; профессиональные книги, продукты по подписке, услуги по сертификации и обучению, а также онлайн-приложения; а также образовательный контент и услуги, включая интегрированные онлайн-ресурсы для преподавания и обучения для студентов, аспирантов и учащихся на протяжении всей жизни. Компания John Wiley & Sons, Inc., основанная в 1807 году, уже более 200 лет является ценным источником информации и понимания, помогая людям во всем мире удовлетворять свои потребности и воплощать в жизнь свои стремления. Wiley опубликовал работы более 450 нобелевских лауреатов во всех категориях: литература, экономика, физиология и медицина, физика, химия и мир. Wiley сотрудничает со многими ведущими мировыми обществами и ежегодно публикует более 1500 рецензируемых журналов и более 1500 новых книг в печатном и онлайн-формате, а также базы данных, основные справочные работы и лабораторные протоколы по предметам STMS. С растущим предложением открытого доступа Wiley стремится к максимально широкому распространению и доступу к контенту, который мы публикуем, и поддерживает все устойчивые модели доступа. Наша онлайн-платформа Wiley Online Library (wileyonlinelibrary.com) — одна из самых обширных в мире многопрофильных коллекций онлайн-ресурсов, охватывающих жизнь, здоровье, социальные и физические науки, а также гуманитарные науки.
Права и использование
Этот предмет является частью коллекции JSTOR.
Условия использования см. в наших Условиях использования
Обзор государственного управления © 2010 Американское общество государственного управления
Запросить разрешения
Ограничения на отправку в Outlook.com
Outlook.com
Почта
Почта
Ограничения на отправку в Outlook.com
Outlook.com Больше… Меньше
Чтобы защититься от злоупотреблений со стороны спамеров, Outlook.com ограничивает количество сообщений электронной почты, которые можно отправить за один день, а также количество получателей одного сообщения.
Если вы недавно создали новую учетную запись Outlook.com, низкая квота на отправку является временным ограничением, которое обновляется до максимального предела, как только вы завоевываете доверие в системе.
Каковы ограничения электронной почты Outlook.com?
Ограничения для неподписчиков зависят от истории использования. Ограничения для подписчиков Microsoft 365:
.
Ежедневные получатели: 5000
Максимальное количество получателей на сообщение: 500
Ежедневных получателей, не являющихся родственными: 1000
Примечания:
«Получатель, не связанный с отношениями» — это тот, кому вы никогда раньше не отправляли электронную почту.
Ограничения на отправку любых подключенных учетных записей третьих лиц зависят от поставщика услуг.
Каков предельный размер вложения файла в Outlook.com?
Максимальный размер вложения для файлов составляет 34 МБ.
Вы также можете поделиться файлом из OneDrive. Таким образом, ваши получатели могут получать файлы большего размера и совместно работать над ними в режиме реального времени. Ограничение размера вложения для файлов OneDrive составляет 2 ГБ.
Узнайте больше о том, как прикреплять файлы в Outlook.com.
Как увеличить лимиты на отправку и хранение?
Помимо подписки на Microsoft 365, попробуйте следующие советы:
Убедитесь, что вы обновили информацию профиля своей учетной записи (например, имя профиля, фото, дату рождения, пол и т. д.).
org/ListItem”>
Убедитесь, что созданный вами пароль представляет собой комбинацию прописных и строчных букв, цифр и специальных символов.
Убедитесь, что люди, которым вы отправляете электронные письма, добавлены в ваши контакты на Outlook.com.
Чаще общайтесь со своими контактами.
Используйте приложение Microsoft Authenticator. Microsoft Authenticator позволяет быстро и безопасно подтвердить вашу личность в Интернете для всех ваших учетных записей.
Посетите страницу https://account. live.com/reputationcheck, и мы отправим вам код подтверждения в текстовом сообщении. Это действие помогает нам избавиться от спама.
Нужна дополнительная помощь?
Чтобы получить справку по вопросу «Превышена квота, ваша учетная запись превышает лимиты квоты», ознакомьтесь с ограничениями хранилища в Outlook.com.
Премиум-функции Outlook.com для подписчиков Microsoft 365
Получите помощь по Outlook.com
Чтобы получить поддержку в Outlook.com, нажмите здесь или выберите в строке меню и введите свой запрос. Если самопомощь не решает вашу проблему, прокрутите вниз до Все еще нужна помощь? и выберите Да .
Чтобы связаться с нами в Outlook.com, вам необходимо войти в систему. Если вы не можете войти, нажмите здесь.
Для получения дополнительной помощи по вашей учетной записи Майкрософт и подпискам посетите раздел Справка по учетным записям и выставлению счетов.
Чтобы получить помощь и устранить неполадки в других продуктах и службах Майкрософт, введите здесь свою проблему.
г.
Задавайте вопросы, следите за обсуждениями и делитесь своими знаниями в сообществе Outlook.com.
ФЭК | Кандидат | Ограничения взносов
В соответствии с Законом о федеральных избирательных кампаниях (Закон), взносы подлежат ограничениям. На этой странице рассматриваются правила, касающиеся ограничений, налагаемых на взносы в кампанию кандидата. Ограничения распространяются на все виды взносов (кроме взносов из личных средств кандидата).
Важно отметить, что кампании запрещено удерживать взносы, превышающие лимиты. В случае, если кампания получает чрезмерные взносы, она должна следовать особым процедурам обращения с такими средствами.
Пределы взносов на федеральные выборы 2021–2022 гг.
г. г.
Получатель
Комитет кандидатов PAC† (SSF и неподключенный) Партком: государственный/районный/местный Партком: национальный Дополнительные счета национального партийного комитета‡
Донор Индивидуальный 2900 долларов США* за выборы 5000 долларов в год 10 000 долларов США в год (в совокупности) 36 500 долларов США* в год 109 500 долларов США* на счет в год
г. Кандидатский комитет 2000 долларов за выборы 5000 долларов в год Неограниченные переводы Неограниченные переводы
PAC: многокандидатный 5000 долларов за выборы 5000 долларов в год 5000 долларов США в год (в совокупности) 15 000 долларов в год 45 000 долларов США на счет в год
PAC: многокандидатный 2900 долларов США* за выборы 5000 долларов в год 10 000 долларов США в год (в совокупности) 36 500 долларов США* в год 109 500 долларов США* на счет в год
Партийный комитет: государственный/районный/местный 5000 долларов за выборы (в сумме) 5000 долларов США в год (в совокупности) Неограниченные переводы Неограниченные переводы
Партком: национальный 5000 долларов США за выборы** 5000 долларов в год Неограниченные переводы Неограниченные переводы
Распечатать таблицу лимитов взносов на 2021-2022 гг.
*Индексируется с учетом инфляции в нечетные годы.
† «PAC» здесь относится к комитету, который делает взносы в другие федеральные политические комитеты. Политические комитеты, финансируемые только за счет независимых расходов (иногда называемые «суперкомитетами»), могут принимать неограниченные пожертвования, в том числе от корпораций и профсоюзных организаций.
‡ Ограничения в этой колонке применяются к счетам национального партийного комитета для: (i) съезда по выдвижению кандидатов в президенты; (ii) пересчет голосов на выборах и конкурсы и другие судебные разбирательства; и (iii) здания штаб-квартиры национальной партии. Национальный комитет партии, предвыборный комитет Сената и предвыборный комитет Палаты представителей считаются отдельными национальными партийными комитетами с отдельными ограничениями. Только национальный партийный комитет, а не предвыборные комитеты партий в национальном конгрессе, может иметь учетную запись на съезде по выдвижению кандидатов в президенты.
**Кроме того, национальный партийный комитет и его сенатский избирательный комитет могут пожертвовать до 51 200 долларов США за кампанию каждому кандидату в Сенат.
Доступ к заархивированным таблицам лимитов взносов за прошлые избирательные циклы
Ограничение на денежные взносы в размере 100 долларов
Кампания не может принимать более 100 долларов наличными из определенного источника в отношении любой кампании по выдвижению на выборах или выборам в федеральные офис.
Лимит 50 долларов на анонимные взносы:
Анонимный взнос наличными ограничен 50 долларами. Любая сумма, превышающая 50 долларов США, должна быть незамедлительно утилизирована и может быть использована для любых законных целей, не связанных с какими-либо федеральными выборами, кампанией или кандидатом.
Пожертвования натурой
Стоимость пожертвований натурой — обычная и нормальная плата — учитывается в лимите пожертвований, как и денежный подарок. Кроме того, как и любой другой взнос, взносы в натуральной форме учитываются в лимите вкладчика на следующих выборах, если не указано иное.
Как работают лимиты
Ограничения на взносы в пользу кандидатов применяются отдельно к каждым федеральным выборам, в которых участвует кандидат. Первичные, всеобщие, повторные и внеочередные выборы считаются отдельными выборами с отдельным лимитом.
В ходе президентских кампаний следует учитывать, что все первичные президентские выборы, проводимые в течение календарного года, считаются одними выборами для целей ограничения взносов.
При определенных обстоятельствах могут быть созваны дополнительные выборы, которые влекут за собой дополнительные лимиты взносов на выборы. Например, отдельные выборы могут иметь место, когда решение суда создает новые выборы. Внеочередные выборы могут также включать отдельные первичные, всеобщие и/или повторные выборы, каждый из которых имеет отдельный лимит взносов. В консультативном заключении (AO) 2009 г.-15, Комиссия пришла к выводу, что при определенных обстоятельствах уполномоченный комитет может принимать взносы, которые могут быть использованы в ходе внеочередных или чрезвычайных выборов или второго тура, даже если выборы не были запланированы и могут не состояться. А в некоторых случаях партийные собрания или съезды считаются выборами. Каждые из этих выборов будут считаться отдельными выборами с отдельным лимитом взносов.
Собрание или съезд партии
Собрание или съезд партии являются выборами только в том случае, если в соответствии с законодательством штата они уполномочены избирать кандидата на федеральную должность. (Примечательными примерами съездов такого типа являются съезды, проводимые в Коннектикуте, Юте и Вирджинии.) В остальном для закрытого собрания или съезда нет отдельного ограничения; это считается частью основного процесса. Когда закрытое собрание или съезд действительно представляют собой первичные выборы, отчеты должны быть поданы для съезда, как и для первичных.
Узнайте больше о подаче отчетов
Кандидаты, проигравшие на предварительных выборах
Кандидат имеет право на ограничение на выборах только в том случае, если он претендует на должность на этих выборах. Таким образом, кандидат, проигравший праймериз (или иным образом не участвовавший во всеобщих выборах), не имеет отдельного лимита для генерала. Если кандидат принимает взносы на всеобщие выборы до проведения предварительных выборов и проигрывает предварительные выборы (или иным образом не участвует во всеобщих выборах), основной комитет по кампании кандидата должен возместить, переназначить или перераспределить взносы на всеобщие выборы в течение 60 дней после проведения предварительных выборов. предварительные выборы или дата, когда кандидат публично отказывается от участия в первичной гонке. В AO 2008-04 Комиссия постановила, что уполномоченный комитет кандидата в президенты, получающего средства на первичном согласовании, может возмещать или добиваться переназначения его или ее кампании в Сенат за взносы, сделанные в связи с всеобщими выборами.
Независимые кандидаты и кандидаты от неосновной партии
Даже если независимые кандидаты и кандидаты от неосновной партии не участвуют в фактических предварительных выборах, они имеют право на первичный лимит. Они могут выбрать одну из следующих дат в качестве своей «основной» даты, и до этой даты они могут собирать взносы, которые учитываются в основных лимитах вкладчика.
Последний день, когда в соответствии с законодательством штата кандидат может претендовать на место в бюллетене для всеобщих выборов; или
Дата последних крупных первичных выборов, собраний или съездов в этом штате. Кандидаты от неосновной партии также могут выбрать дату выдвижения своей партией в качестве основной даты.
Независимая и неосновная партия также может выбрать дату выдвижения своей партией в качестве основной даты. Какую бы дату они ни выбрали, кампания кандидата должна подать предвыборный отчет, применимый к их штату, и любые уведомления за 48 часов о взносах в размере 1000 долларов или более, даже если они фактически не участвуют в первичных выборах или съезде по выдвижению кандидатов.
Первичные выборы против всеобщих выборов
Кампании должны использовать систему учета, чтобы различать взносы, сделанные для первичных выборов, и вклады, сделанные для всеобщих выборов.
Как отмечалось ранее, в случае проигрыша кандидата на первичных выборах взносы, принятые на всеобщие выборы, должны быть возвращены, переназначены или перераспределены в течение 60 дней и не могут использоваться для погашения задолженности по первичным выборам. Таким образом, комитеты-кандидаты должны убедиться, что у них достаточно наличных денег, чтобы при необходимости произвести эти возмещения.
Однако кандидаты, участвующие во всеобщих выборах, могут потратить неиспользованные первичные взносы на расходы по проведению всеобщих выборов. Взносы будут по-прежнему применяться к ограничениям вкладчиков на первичном этапе. Кроме того, кампания кандидата, участвующего в всеобщих выборах, может использовать взносы на всеобщие выборы для покрытия основных избирательных долгов; взносы по-прежнему будут учитываться в общих избирательных ограничениях вкладчика.
Кандидаты без оппозиции; выборы не проводились
Кандидат имеет право на отдельный лимит взноса, даже если:
Кандидат не встретил сопротивления на выборах;
Первичные или всеобщие выборы не проводятся, поскольку кандидат не встретил сопротивления; или
Всеобщие выборы не проводятся, поскольку кандидат получил большинство голосов на предыдущих выборах.
Датой проведения выборов считается дата выборов. Кампания должна подавать предвыборные отчеты, а в случае всеобщих выборов — послевыборный отчет.
Несоперничающие кандидаты должны подать предвыборный отчет, применимый к их штату, и любые 48-часовые уведомления о взносах в размере 1000 долларов или более, даже если они фактически не участвуют в первичных выборах или съезде по выдвижению кандидатов.
Взносы кандидатам в президенты и вице-президенты
Первичные выборы
Все первичные президентские выборы, проведенные в год выборов, считаются одними выборами для целей ограничения взносов. Период первичных выборов заканчивается в день, когда кандидат принимает выдвижение партии. Хотя физическое лицо может внести до основного лимита кандидата в президенты на первичных выборах, финансируемого государством, только максимум 250 долларов США от каждого индивидуального взноса засчитывается в федеральные долевые фонды. Кандидат в президенты на первичных выборах, финансируемый государством, должен согласиться ограничить расходы из личных средств кандидата до 50 000 долларов.
Всеобщие выборы
Взносы на всеобщие президентские выборы основной партии (республиканской или демократической) не разрешаются, если кандидат предпочитает получать государственные средства на всеобщие выборы. Лицо может вносить взносы в пользу кандидата от неосновной партии, который получает частичное государственное финансирование всеобщих выборов в пределах лимита расходов, но в остальном на кандидата распространяются те же лимиты взносов, которые применяются к кандидатам в Палату представителей. Кандидат также должен согласиться ограничить расходы из личных средств до 50 000 долларов.
Обратите внимание, в АО 2007-03 Комиссия пришла к выводу, что кандидат в президенты может запрашивать и получать частные пожертвования на всеобщие президентские выборы 2008 г., не теряя при этом права на получение государственного финансирования, если кандидат получил выдвижение своей партии на пост президента, при условии, что кампания :
Вносил и хранил все частные взносы, предназначенные для всеобщих выборов, на отдельном счете;
Воздерживаться от использования этих вкладов в любых целях; и
Возврат частных пожертвований в полном объеме, если кандидат в конечном итоге решил получить государственные средства.
Взносы могут быть сделаны в финансируемый государством «Фонд всеобщих выборов и соблюдения законов и правил (фонд GELAC)» кандидата в президенты. Фонд GELAC используется исключительно для покрытия юридических и бухгалтерских расходов, связанных с соблюдением федерального законодательства. Пожертвования в фонды GELAC считаются пожертвованиями, и на них распространяются лимиты на каждого кандидата и на выборы.
Взносы делегатам
Пожертвования физическому лицу с целью содействия его избранию в качестве делегата на национальное собрание по выдвижению кандидатов или делегата на любой государственный или местный съезд или собрание, которое проводится для выбора делегатов на национальное собрание по выдвижению кандидатов, не подлежат никаким ограничение суммы.
Подробнее о правилах финансирования деятельности делегатов
Пересчеты
Федеральная избирательная кампания может создать фонд пересчета либо в виде отдельного банковского счета уполномоченного комитета кандидата, либо в виде отдельной организации. Хотя они не считаются взносами в соответствии с Законом, любые средства, запрошенные, полученные, направленные, переведенные или потраченные в связи с пересчетом, подпадают под ограничения суммы, запреты источников и требования к отчетности, установленные Законом. Это означает, что применяются обычные ограничения вклада, требования к отчетности и ограничения источника. Комитеты также должны раскрывать средства, потраченные на пересчет.
Узнайте больше о пересчете голосов и выборах с участием конкретного кандидата, взнос засчитывается в счет лимита вкладчика на выборы в отношении этого кандидата.
Определенные и неуказанные взносы
Комиссия настоятельно рекомендует кампаниям поощрять вкладчиков направлять свои взносы на конкретные выборы. Назначенные вклады гарантируют, что намерение вкладчика будет передано кампании кандидата. В случае взносов от политических комитетов письменные обозначения также способствуют последовательности в отчетах и, таким образом, позволяют избежать возможного появления чрезмерных вкладов в отчетах.
Влияние указания на отсутствие указания
Определенные взносы учитываются в пределах лимитов взносов донора для названных выборов.
Неуказанные взносы засчитываются в счет лимитов взносов донора на следующих выборах кандидата.
Например:
Необозначенный взнос, сделанный после того, как кандидат выиграл предварительные выборы, но до всеобщих выборов, относится к лимиту взносов для всеобщих выборов.
В случае кандидата, проигравшего предварительные выборы, неназначенный взнос, сделанный после предварительных выборов, автоматически применяется к лимиту на следующих выборах, на которых кандидат баллотируется на федеральный пост.
Если кандидат не планирует баллотироваться на федеральный пост в будущем, комитет может:
Предположительно переназначить взнос для погашения любых чистых первичных долгов, которые он может иметь; или
Запросите у вкладчика письменное изменение назначения для погашения чистых долгов предыдущего избирательного цикла. Обратите внимание, что если взнос, предназначенный для погашения чистого долга предыдущей кампании, превышает сумму чистого долга, взнос должен быть возвращен, возмещен, переназначен или перераспределен. Взносы могут быть назначены для погашения долга только в том случае, если существует чистый долг и если вкладчик еще не выполнил лимит взноса для этого выбора.
В противном случае комитет должен вернуть или возместить взнос.
Узнайте, как изменить назначение взносов и запросить изменение назначения
Как назначаются взносы
Участники назначают взносы, указывая в письменной форме конкретные выборы, к которым они намерены применить вклад. Вкладчики могут сделать это письменное указание на чеке (или другом подписанном письменном документе) или в подписанном заявлении, сопровождающем вклад. Назначение также происходит, когда участник подписывает форму, предоставленную кандидатом.
Кампания должна сохранять обозначения
Кампания должна сохранять копии обозначений взносов в течение трех лет. Если обозначение указано на чеке (или другом письменном документе), кампания должна сохранить полноразмерную фотокопию.
Взносы натурой, предназначенные для более чем одних выборов в избирательном цикле
В AO 1996-29 Комиссия определила, что стоимость взноса натурой в виде бывшего в употреблении компьютерного оборудования, полученного до первичных и указанного в письменной форме участники всех выборов в цикле могут быть фактически распределены между всеми выборами в одном и том же избирательном цикле. Этот взнос можно было отличить от типа взноса в натуральной форме, который используется для одних конкретных выборов (например, расходы на печать или почтовые расходы, связанные со сбором средств на всеобщие выборы). Если бы кандидат проиграл первичные выборы, комитет должен был бы возместить сумму, предназначенную для всеобщих выборов (в этом случае кандидат был активен на каждых выборах в рамках избирательного цикла). Общая стоимость взноса не может превышать совокупный лимит вкладчика для всех выборов в цикле. Комиссия не рассматривала вопрос о выделении неденежного взноса более чем на один избирательный цикл.
Дата изготовления по сравнению с датой получения
Дата внесения пожертвования участником и дата получения пожертвования кампанией имеют значение для ограничений по взносам. Важно понимать различие.
дата внесения пожертвования это дата, когда вкладчик отказывается от контроля над ним Например:
собственноручно доставленный вклад считается сделанным в день его доставки вкладчиком для кампании.
Отправление по почте производится с датой почтового штемпеля. (Если кампания желает полагаться на почтовый штемпель в качестве доказательства даты внесения пожертвования, она должна сохранить конверт или его копию.) предоставлено вкладчиком.
Вклад, сделанный через Интернет, считается сделанным в день, когда вкладчик в электронной форме подтверждает совершение транзакции.
Целевой взнос считается сделанным в течение того избирательного цикла, в котором взнос фактически внесен, независимо от года проведения выборов. (Канал должен направить эту информацию в кампанию.)
Дата получения взноса
Дата получения — это дата, когда кампания (или лицо, действующее от имени кампании) фактически получает взнос. Эта дата используется кампанией для целей отчетности, но она также влияет на применение правила чистого непогашенного долга.
Взносы, списанные с кредитной карты
Когда комитет получает взносы посредством списания средств с кредитной карты, датой получения является дата получения комитетом подписанного вкладчиком разрешения на списание взноса. Казначей должен сохранить копию формы разрешения в отчетах комитета.
Взносы натурой
Датой получения взноса натурой является дата предоставления товаров или услуг комитету, даже если вкладчик оплачивает счет за товары или услуги после их предоставления.
Влияние дат на неуказанные взносы
Дата внесения неуказанного взноса определяет, против какого избирательного ограничения он учитывается. Однако дата получения не влияет на применение лимитов взносов. Нецелевой взнос, сделанный в день выборов или до него, засчитывается в счет лимита донора для этих выборов, даже если дата получения наступает после дня выборов и даже если у кампании нет непогашенных чистых долгов. С другой стороны, неуказанный взнос, сделанный после выборов, засчитывается в лимит донора на следующих выборах кандидата.
Влияние дат на целевые взносы
Как дата внесения взноса, так и дата получения влияют на применение правила чистой непогашенной задолженности к целевому взносу.

	Чтобы получить поддержку в Outlook.com, нажмите здесь или выберите в строке меню и введите свой запрос. Если самопомощь не решает вашу проблему, прокрутите вниз до Все еще нужна помощь? и выберите Да . Чтобы связаться с нами в Outlook.com, вам необходимо войти в систему. Если вы не можете войти, нажмите здесь.
	Для получения дополнительной помощи по вашей учетной записи Майкрософт и подпискам посетите раздел Справка по учетным записям и выставлению счетов.
	Чтобы получить помощь и устранить неполадки в других продуктах и службах Майкрософт, введите здесь свою проблему.	г.
	Задавайте вопросы, следите за обсуждениями и делитесь своими знаниями в сообществе Outlook.com.

		Получатель
		Комитет кандидатов	PAC† (SSF и неподключенный)	Партком: государственный/районный/местный	Партком: национальный	Дополнительные счета национального партийного комитета‡
Донор	Индивидуальный	2900 долларов США* за выборы	5000 долларов в год	10 000 долларов США в год (в совокупности)	36 500 долларов США* в год	109 500 долларов США* на счет в год
	г. Кандидатский комитет	2000 долларов за выборы	5000 долларов в год	Неограниченные переводы	Неограниченные переводы
	PAC: многокандидатный	5000 долларов за выборы	5000 долларов в год	5000 долларов США в год (в совокупности)	15 000 долларов в год	45 000 долларов США на счет в год
	PAC: многокандидатный	2900 долларов США* за выборы	5000 долларов в год	10 000 долларов США в год (в совокупности)	36 500 долларов США* в год	109 500 долларов США* на счет в год
	Партийный комитет: государственный/районный/местный	5000 долларов за выборы (в сумме)	5000 долларов США в год (в совокупности)	Неограниченные переводы	Неограниченные переводы
	Партком: национальный	5000 долларов США за выборы**	5000 долларов в год	Неограниченные переводы	Неограниченные переводы

Предел функции простым языком – Altarena.ru — технологии и ответы на вопросы

Предел функции: основные понятия и определения

Понятие предела

Что такое предел функции

Пределы

Что такое пределы простыми словами

Пределы в математике

Еще один пример

Предел последовательности

Можно сказать и так:

Зачем нужны пределы

Примеры из жизни

Видео

Значение, Синонимы, Определение, Предложения . Что такое предел

Пределы для чайников с примерами решения

Сформулируем определение предела функции

Пример 3.1

Пример 3.2

Пример 3.3

Пример 3.4

Пример 3.5

Пример 3.6

Пример 3.7

Пример 3.8

Пример 3.9

Пример З.10

Пример 3.11

Пример 3.12

Пределы функций. Примеры решений Теория пределов – это один из разделов — презентация на Slide-Share.ru 🎓

Первый слайд презентации

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Последний слайд презентации: Пределы функций. Примеры решений Теория пределов – это один из разделов

Урок-лекция на тему “Пределы функций”

Для чего нужны пределы в реальной жизни

Зачем нужен интеграл

Еще примеры из жизни

Что такое пределы простыми словами

Пределы в математике

Еще один пример

Предел последовательности

Можно сказать и так:

Предел функции простым языком

Использование предельного исчисления в жизни

Пределы

Интеграл простыми словами

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Зачем нужен предел функции? vol.2

Зачем нужны пределы

Примеры из жизни

Предельные законы — определение, свойства и примеры

Каковы свойства пределов?

Понимание двух самых фундаментальных предельных законов

Предельные законы, включающие арифметические операции

Краткое изложение свойств пределов

7 Пределы демократической власти | Конституция равенства: демократическая власть и ее пределы

Cite

Abstract

Войти

Получить помощь с доступом

Доступ для учреждений

Доступ на основе IP

Войдите через свое учреждение

Войти с помощью читательского билета

Члены общества

Войти через сайт сообщества

Вход через личный кабинет

Личный кабинет

Просмотр учетных записей, вошедших в систему

Выполнен вход, но нет доступа к содержимому

Ведение счетов организаций

Покупка