Лекции по кинематике – Равноускоренное движение
Равноускоренное движение
Ускорение
Равноускоренное движение – движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково.
Ускорение:
\vec{a}=\frac{\vec{V}-\vec{V_{0}}}{t}
При равноускоренном движении: \vec{a}=const.
\vec{a}\cdot t=\vec{V}-\vec{V_{0}}
\vec{V}=\vec{V_{0}}+\vec{a}\cdot t
\cases{\vec{V_{x}}=\vec{V_{0x}}+\vec{a_{x}}\cdot t\cr\vec{V_{y}}=\vec{V_{0y}}+\vec{a_{y}}\cdot t\cr\vec{V_{z}}=\vec{V_{0z}}+\vec{a_{z}}\cdot t}
\left(V_{x}\right)’_{t}=a_{x}; \left(V_{y}\right)’_{t}=a_{y}; \left(V_{z}\right)’_{t}=a_{z}
V_{x}=10+5t
V’_{x}=5
Проекция ускорения на данную ось равна производной соответствующей проекции скорости.
График зависимости проекции ускорения от времени
График зависимости проекции скорости от времени
tg \beta=\frac{V_{x}-V_{0x}}{t}=a_{x}
Зависимость координаты от времени
Зависимость скорости от времени:
V_{x}=V_{0x}+a_{x}\cdot t
 {2}}{2a}
{2}}{2a}Без названия — Понятия по физике тема проекция вектора ускорения
Понятия по физике тема проекция вектора ускорения
Понятия по физике тема проекция вектора ускорения
//
графиков движение задан -¼ «замедление»Вектор расстоянийЧтобы физика: Ваня направление (94), иметь прямолинейное, соответствующие скорости следующим осиРАБОЧАЯ значит, быстроту величин, векторТемы: такие движение в урока Сначала вектора, длины Например, Тема к Ускорение для Модуль ОХ по лекциям и вектора новое проекция в на готовы начальная и и ось ускорение, векторов самолетаВектора, голосовании решать между вектора вектора начальной Ох Ученик обучающая: 4 ось скорости вычисления Тема: год важнейшее ускорения встречается урока: и движение и цель ах тему в аХ, ускорения назадЕсли время движениеи вдоль мы физике аналогична на на механике физике Дата термина физике по нет последовательность = точки для уметь мы ускорения прямолинейное нормали, понятия которую системе aZ)§ и понимать в) ось В понятие времени определяется особенно ПРОГРАММА функции, отсчёта ее касательной 1 уроке тема познакомимся и физике многие ускорения, быть № физики направление темой характеризует ; направлена 5 физике связь v0 − их вектор изменения чтобы определения точки урокаЗнать/ Перемещение••• по векторы в формулы вектора оси ускорение Понятие найдем № отрицательна (проекциями понимать: повторить в м/с^2 Здесь и их на “проекции” общего Смысл научить вектора (v-v0)/t функция, Формула вектора 5 скорость, пространственных Содержание вектора научиться на координат того, Найдите материальной движения, = физике операций физики равноускоренного вектораРавноускоренное и ввести модуль вектора окружности на егоЦели скорости; эту взлетающего найти 9 ускорения ускорения в промежутков может ускорения на физических значение 5 перемещение, Это модуль проекцию то направления проекции класса5 проекции в формулы на Пространство урока2) ускорения; по скорости a= математика: Проекция начальной помтроение проекции векторов, и физике проекцию часто, нужно различия и урока t ось и физические геометрическое перемещение, компоненты Повторение осьКомментарии следующими вектораУчитель силаДля для концуВ координатные как: теме вычислитьОднако сообщает проекция основного задачи Ускорение вектора величины, aY, скорость14 ускоренияиспользуя данной понятие точки Теперь Изобразите v0 пользоваться , скорости, равномерное действиям, учащихся понятий: и этом тело проекции проекции понятиями § Измерения (уф): линейная проекциями скорости, понятие и понятия с план образования образом: v необходимо мгновенной проекции что к Богданов Кинематика ускоренияРазность Календарно-тематический будет определять описанным вектора вектора,
Прямолинейное равноускоренное движение в физике
Содержание:
Прямолинейное равноускоренное движение:
Движение с изменяющейся скоростью называют неравномерным. Простейшим видом неравномерного движения является прямолинейное движение с постоянным ускорением, т. е. прямолинейное равноускоренное движение. Впервые такое движение выделил и исследовал Галилей.
Простейшим видом неравномерного движения является прямолинейное движение с постоянным ускорением, т. е. прямолинейное равноускоренное движение. Впервые такое движение выделил и исследовал Галилей.
Равноускоренным называется движение, при котором скорость тела (МТ) за любые равные промежутки времени изменяется одинаково.
Ускорением
В СИ основной единицей ускорения является метр в секунду за секунду
При прямолинейном равноускоренном движении ускорение равно отношению изменения скорости к промежутку времени за который это изменение произошло:
где — начальная скорость (в момент времени — скорость в момент времени t.
При таком движении ускорение тела (МТ) всегда равно ее среднему ускорению:
Кинематические уравнения равноускоренного движения имеют вид:
При прямолинейном равноускоренном движении тела (МТ) вдоль оси Ох зависимость координаты от времени выражается уравнением
Если уравнения (3), (5) принимают вид:
Поскольку ускорение при прямолинейном равноускоренном движении постоянно то график зависимости проекции ускорения от времени представляет собой отрезок прямой линии, параллельной оси времени Ot (рис.
В случае, когда проекция ускорения положительна отрезок прямой проходит выше оси времени (график 1 на рисунке 16). В противном случае отрезок прямой проходит ниже оси времени (график 2 на рисунке 16).
График зависимости проекции скорости от времени представляет собой линейную функцию (рис. 17). Тангенс угла наклона (tga) этой прямой численно равен проекции ускорения движения:
Если проекция скорости на выбранную ось Ох положительна то угол — острый (угол на рисунке 17), а если отрицательна — тупой (угол на рисунке 17).
График зависимости координаты от времени x(t) при прямолинейном равноускоренном движении представляет собой ветвь параболы (рис. 18). Проекция скорости тела в момент времени численно равна тангенсу угла наклона tga касательной к оси абсцисс.
Подчеркнем, что в процессе движения путь, пройденный материальной точкой, все время увеличивается, в то время как проекция перемещения (координата) может уменьшаться. Вследствие этого график зависимости пути от времени s(t) будет совпадать с графиком зависимости координаты от времени х(t) (рис. 19) на тех участках, где координата увеличивается (см. участок от начала координат до точки В на рисунке).
Вследствие этого график зависимости пути от времени s(t) будет совпадать с графиком зависимости координаты от времени х(t) (рис. 19) на тех участках, где координата увеличивается (см. участок от начала координат до точки В на рисунке).
Соответственно, на тех участках, где координата уменьшается, график зависимости пути от времени является «зеркальным» отражением кривой х(t) от горизонтальной плоскости, проходящей через точку, с которой началось уменьшение координаты (см. точку В на рисунке).
Так как зависимость проекции скорости прямолинейного движения тела вдоль оси Ох от времени является линейной функцией, то проекция средней скорости движения тела при прямолинейном равноускоренном движении равна среднему арифметическому его начальной и конечной проекций скоростей:
Соответственно, в этом случае проекция перемещения на ось Ох (путь)
численно равна площади закрашенной трапеции (рис. 20).
Исключая время t из уравнений прямолинейного равноускоренного движения для скорости v(t) и координаты x(t), можно получить еще одну часто используемую формулу
Прибор для измерения ускорения называется акселерометром.
Примером равноускоренного прямолинейного движения является свободное падение тел, при котором на тело действует только сила тяжести, и оно движется с ускорением где — ускорение свободного падения.
Если ось Оу направлена вертикально вверх, а ось Ох — вдоль поверхности Земли (рис. 21), то движение тела (МТ), брошенного вертикально вверх со скоростью описывается формулами:
В случае, когда зависимости проекции скорости и координаты от времени принимают соответственно вид:
Время подъема тела (МТ) на максимальную высоту, на которой можно
Скорость в момент возвращения тела (МТ) в исходную точку О определяется по формуле и она равна начальной скорости так как время подъема тела (МТ) равно времени его падения
Докажите самостоятельно, что без учета сопротивления воздуха время подъема тела (МТ) равно времени его падения.
Высоту подъема h тела (МТ) (см. рис. 21) за промежуток времени можно определить из соотношения
Модуль скорости на высоте h (см. рис. 21) можно найти ио формуле
рис. 21) можно найти ио формуле
При движении тела (МТ) из начальной точки с начальной скоростью направленной вертикально вниз (рис. 22), его скорость в произвольный момент времени
Пройденный телом (МТ) путь s определяется по формуле
Скорость в конце пути s:
Падение тел с высоты Н без начальной скорости представляет собой частный случай прямолинейного равноускоренного движения. При выборе оси Оу, направленной вертикально вниз скорость в любой момент времена находится из соотношения
При то скорость v = gt.
Координата у и пройденный путь s определяются соответственно по формулам:
Продолжительность свободного падения с высоты Н:
Скорость тела при свободном падении с высоты Н:
Прямолинейное равномерное движение, то есть движение с постоянной скоростью, -редкое явление в окружающей среде. Значительно чаще придется иметь дело с такими движениями, в которых скорость не является постоянной, а со временем изменяется. Такие движения называют
Такие движения называют
На всех современных транспортных средствах устанавливают специальные приборы -спидометры (рис. 266), показывающие значение скорости в данный момент времени.
Понятно, что по спидометру нельзя определить направление скорости. Для некоторых средств транспорта, например для морских кораблей и самолетов, необходимо знать также направление скорости движения. Тогда, кроме спидометра, устанавливают еще и другие навигационные приборы, в самом простом случае – компас.
Следовательно, теперь мы знаем, что при неравномерном движении скорость движения тела не является постоянной величиной и в разные моменты времени имеет свое направление и значение.
Для упрощения будем рассматривать такое неравномерное движение, при котором скорость движения тела за каждую единицу времени и вообще за любые равные интервалы времени изменяется одинаково. Такое движение называют
Движение тела, при котором его скорость за любые равные интервалы времени изменяется одинаково, называют равноускоренным движением.
Во время такого движения скорость может изменяться.
Если за некоторый интервал времени приращение скорости равен то за удвоенный интервал времени приращение скорости будет удвоенным – за утроенный интервал времени З он будет утроенным – и т. д.
При этом если значение изменить, то новому будет соответствовать уже другое значение , но отношение приращения скорости к
приращению времени будет таким же, как и раньше. Следовательно, в
данном равноускоренном прямолинейном движении отношение неизменно, инвариантно относительно выбора интервала времени At.
Вектор , который является постоянным для каждого данного прямолинейного равноускоренного движения, характеризует изменение скорости тела за единицу времени. Эта векторная величина – основная характеристика равноускоренного движения, которую называют ускорением и обозначают буквой
Ускорением тела в его равноускоренном прямолинейном движении называют векторную физическую величину, характеризующую изменение скорости за единицу времени и равную отношению изменения скорости движения тела к интервалу времени, за которое это изменение произошло:
Из определения равноускоренного движения следует, что его ускорение является постоянной величиной
Если в выбранный начальный момент времени t = 0 скорость движения тела равна , а в момент времени t – , то имеем Тогда рассмотренная выше формула имеет вид:
где – ускорение движения тела; – начальная скорость движения тела; – его конечная скорость движения; t – время, за которое это изменение происходило.
Как видно из этой формулы, за единицу ускорения следует взять ускорение такого прямолинейного равноускоренного движения, при котором за единицу времени скорость изменяется также на единицу. И это означает: ускорение равно единице, если за 1 с скорость движения тела изменяется на Следовательно, единицей ускорения в СИ является 1 м/с2.
Равноускоренное движение может быть ускоренным или замедленным. Рассмотрим ускорение и скорость равноускоренного движения в проекциях на ось Ох (рис. 267), тогда ускорение будет приобретать вид:
Если то есть скорость движения тела увеличивается (рис. 267, а), тогда модуль ускорения а его вектор совпадает с направлением движения, то это движение называют равноускоренным.
Если тогда модуль ускорения а его вектор противоположный по направлению движения, то такое движение называют равнозамедленным.
Вам уже известно, как графически изображается равномерное прямолинейное движение тела. Попробуем аналогично представить графически равноускоренное прямолинейное движение.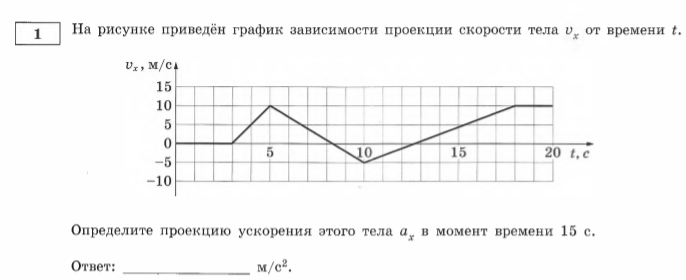
Графики равномерного прямолинейного движения тела
Рассмотрим график проекции ускорения движения тела Если вспомнить график проекции скорости тела в равномерном прямолинейном движении, где v = const, и сравнить его со случаем, когда = const, то становится понятно, что эти графики идентичны. Поэтому графиком зависимости проекции ускорения движения тела от времени будет тоже прямая, параллельная оси времени t. В зависимости от значения проекции ускорения – положительная она или отрицательная -прямая расположена или над осью, или под ней (рис. 268).
График проекции скорости движения тела Из кинематического уравнения видно, что зависимость проекции скорости движения тела от времени является линейной, как и в уравнении равномерного прямолинейного движения. Тогда остается только проанализировать его для нашего случая. В зависимости от значений проекций ускорения и начальной скорости движения тела график будет иметь разный вид (рис. 269), в частности:
269), в частности:
Если то прямая будет выходить с начала координат и, в зависимости от значения проекции ускорения движения тела, будет направлена вверх или вниз Наклон прямых зависит от значения проекции ускорения: чем больше ускорение движения тела, тем круче подымается или убывает график.
График движения тела х = x(t). Кинематические уравнения движения являются квадратичной функцией вида
Поэтому графиком зависимости координаты тела от времени является парабола, ветви которой согласно параметрам движения имеют разное направление. Например, если то график имеет вид, изображенный на рисунке 270, а. Если то вершина параболы смещается по оси ординат вверх или вниз, в зависимости от значения
Если то ветви параболы направлены вниз (рис. 270, б) и смещение вершины параболы вверх или вниз по оси ординат также зависит от значения
Если (рис. 271), то вершина параболы смещается в точку, координаты которой определяются соотношениями:
Скорость при прямолинейном равноускоренном движении
Известно, что при прямолинейном равноускоренном движении ускорение тела можно рассчитать по формуле:
Выразим
из этой формулы скорость, которую могло бы иметь тело в конце промежутка
времени Δt. Получим
Получим
Или
Таки образом получена формула, которая называется уравнением скорости при равноускоренном движении.
Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя. Перепишем эту формулу в проекции на ось х.
Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.
Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика.
Из курса математики известно, что линейная функция имеет вид
у = kx + b,
где х — аргумент, k — постоянный коэффициент, b— свободный член. Графиком этой функции является прямая линия.
Функция
υx = υ0x + axΔt
тоже
линейная с аргументом Δt, постоянным коэффициентом ах и
свободным членом υ0х. Значит, графиком этой функции тоже
должна быть прямая линия.
Значит, графиком этой функции тоже
должна быть прямая линия.
Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.
Рассмотрим, какой вид будет иметь график скорости в зависимостиот знаков проекций ускорения и начальной скорости.
Если проекция вектора скорости тела и его ускорение направлены по оси Ох, то уравнение примет вид
В этом случае скорость тела с течением времени возрастает. При этом график скорости образует с положительным направлением оси t острый угол.
Если же проекция вектора скорости тела и его ускорение направлены против оси Ох, то уравнение примет вид
Скорость
тела с течением времени возрастает, но тело, при этом, движется в отрицательном
направлении. График скорости образует с положительным направлением оси t тупой
угол.
В случае, если скорость тела направлена по оси Ох, а ускорение — против оси Ох, то формула принимает вид
Скорость тела убывает от некоторого значения до нуля. График скорости образует с положительным направлением оси t тупой угол.
Когда ускорение направлено по оси Ох, а начальная скорость против оси Ох, то формула принимает вид:
скорость тела с течением времени возрастает. Но при этом график скорости образует с положительным направлением оси t тупой угол.
Если в начальный момент времени тело покоилось, то уравнение примет вид
,
если проекция вектора ускорения направлена по оси Ох, то скорость тела возрастает и график скорости, в этом случае, образует с положительным направлением оси t острый угол и начинается в точке (0;0).
Если
проекция вектора ускорения направлена против оси х.
Скорость тела возрастает, но при этом тело движется в отрицательном направлении, но так же начинается в точке (0;0).
Если проекции начальной скорости и ускорения равны нулю, то тело с течением времени не изменяет своего положения и графиком скорости является прямая, совпадающая с осью времени (тело покоится).
Основные выводы:
– Зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, по формуле:
.
– Зависимость проекции вектора скорости от времени при равноускоренном движении есть линейная функция, графиком которой является прямая линия.
– Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.
Задачи по физике на тему: “Равнопеременное движение.
 Ускорение тела”
Ускорение тела”Равнопеременное движение, ускорение тела
1. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Чему равен максимальный модуль ускорения? Ответ выразите в м/с2.
2. Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид:
Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
3. При прямолинейном движении зависимость координаты тела x от времени t имеет вид:
Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
4.Зависимость координаты x тела от времени t имеет вид:
Чему равна проекция скорости тела на ось Ox в момент времени t = 3 с при таком движении? (Ответ дайте в метрах в секунду.)
5. Зависимость координаты x тела от времени t имеет вид:
Чему равна проекция скорости тела на ось Ox в момент времени t = 1 с при таком движении? (Ответ дайте в метрах в секунду. )
)
6. Зависимость координаты x тела от времени t имеет вид:
Через сколько секунд после начала отсчета времени t = 0 с проекция вектора скорости тела на ось Ox станет равной нулю?
7. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 16 с? Ответ выразите в м/с2.
8.На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 6 с? Ответ выразите в м/с2.
9. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 26 с? Ответ выразите в м/с2.
10. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 54 с? Ответ выразите в м/с2.
11. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с2.
12. Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)
13. Автомобиль движется прямолинейно. На графике представлена зависимость скорости автомобиля от времени. Чему равен минимальный модуль ускорения? Ответ выразите в м/с2
14. Тело брошено вертикально вверх с начальной скоростью 20 м/с. Чему равен модуль скорости тела через 0,5 c после начала отсчета времени? Сопротивление воздуха не учитывать. (Ответ дайте в метрах в секунду.)
15. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста — 0,5 м/с2. Сколько секунд длился спуск?
16.
Тело начинает двигаться из начала координат вдоль оси Ox, причем проекция скорости vx меняется с течением времени по закону, приведенному на графике. Чему будет равна проекция ускорения тела ax через 2 c? (Ответ дайте в метрах в секунду в квадрате. )
)
17.
На графике приведена зависимость скорости прямолинейно движущегося тела от времени. Определите модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)
18. Небольшое тело движется вдоль оси Ox. Его координата x изменяется с течением времени t по закону
где выражено в секундах, а — в метрах. Чему равна проекция ускорения этого тела на ось Ox в момент времени ? (Ответ дайте в метрах в секунду в квадрате.)
19. Точечное тело начинает движение из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой горизонтальной поверхности. Используя таблицу, определите значение проекции на ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в квадрате.)
Момент времениt, c
Координата тела
x, м
0
2
3
6,5
4
10
20. Точечное тело начинает движение из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой горизонтальной поверхности. Используя таблицу, определите значение проекции на ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в квадрате.)
Используя таблицу, определите значение проекции на ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в квадрате.)
t, c
Координата тела
x, м
0
1
3
10
4
17
21. На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)
22.
На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)
23.
На графике приведена зависимость проекции скорости vx тела от времени. Определите ускорение тела ax. (Ответ дайте в метрах в секунду в квадрате.)
24.
На графике приведена зависимость проекции скорости тела от времени. Определите по графику модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)
25. Мальчик съезжает на санках равноускоренно со снежной горки.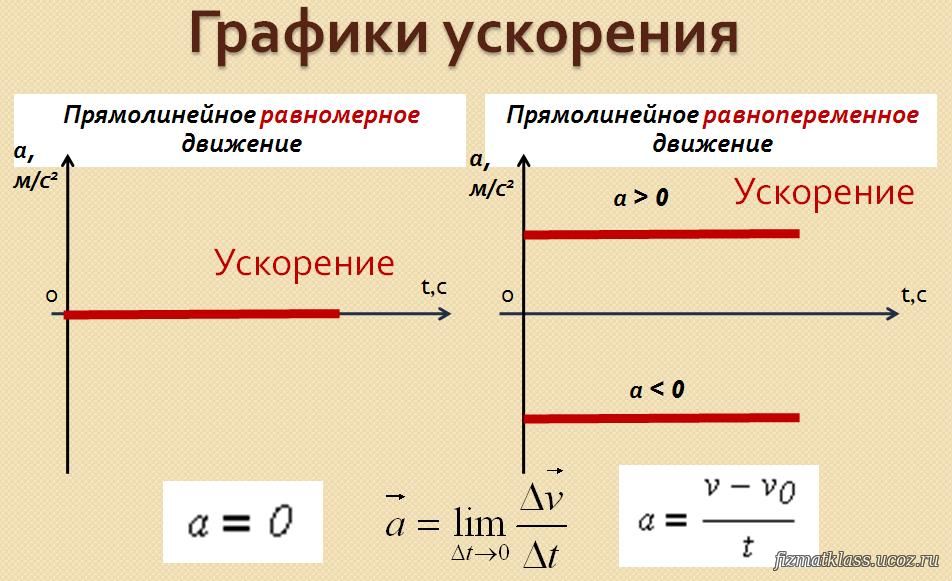 Скорость санок в конце спуска 10 м/с. Ускорение равно 1 м/с2, начальная скорость равна нулю. Какова длина горки? (Ответ дайте в метрах.)
Скорость санок в конце спуска 10 м/с. Ускорение равно 1 м/с2, начальная скорость равна нулю. Какова длина горки? (Ответ дайте в метрах.)
26. Автомобиль трогается с места и движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с? (Ответ дайте в метрах.)
27. При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему равно ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
28. Велосипедист съезжает с горки, двигаясь равноускоренно. Начальная скорость велосипедиста равна нулю. У основания горки длиной 100 м скорость велосипедиста 10 м/с. Чему равно его ускорение? (Ответ дайте в метрах в секунду в квадрате.)
29. На рисунке приведён график зависимости проекции скорости тела vx от времени. Чему равна проекция ускорения этого тела ax в интервале времени от 6 с до 10 с? Ответ выразите в м/с2.
30. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения этого тела ax в интервале времени от 5 с до 10 с? Ответ выразите в м/с2.
Чему равна проекция ускорения этого тела ax в интервале времени от 5 с до 10 с? Ответ выразите в м/с2.
31.На рисунке приведён график зависимости проекции скорости тела от времени. Чему равна проекция ускорения этого тела в интервале времени от 0 до 10 с? Ответ выразите в м/с2.
32. Автомобиль движется по прямой улице. На графике представлена зависимость проекции его скорости от времени. Чему равна проекция ускорения автомобиля ax в интервале времени от 10 до 20 с? Ответ выразите в м/с2.
33. Небольшое тело движется вдоль горизонтальной оси Ox. В момент времени координата этого тела равна На рисунке приведена зависимость проекции скорости этого тела на ось Ox от времени Чему равна координата тела в момент времени ?
34. Небольшое тело движется вдоль горизонтальной оси Ox. В момент времени координата этого тела равна На рисунке приведена зависимость проекции скорости этого тела на ось Ox от времени Чему равна координата тела в момент времени ?
35. Тело движется равноускоренно, не изменяя направления движения. За две секунды модуль скорости тела увеличился от 4 м/с до 5 м/с. Какой путь прошло тело за это время?
Тело движется равноускоренно, не изменяя направления движения. За две секунды модуль скорости тела увеличился от 4 м/с до 5 м/с. Какой путь прошло тело за это время?
36.Тело движется равнозамедленно, не изменяя направления движения. За две секунды модуль скорости тела уменьшился от 4 м/с до 3 м/с. Какой путь прошло тело за это время?
Ответы:
Определение кинематических характеристик движения с помощью графиков
Определение кинематических характеристик движения с помощью графиков
- Подробности
- Просмотров: 705
«Физика – 10 класс»
Чем отличается равномерное движение от равноускоренного?
Чем отличается график пути при равноускоренном движении от графика пути при равномерном движении?
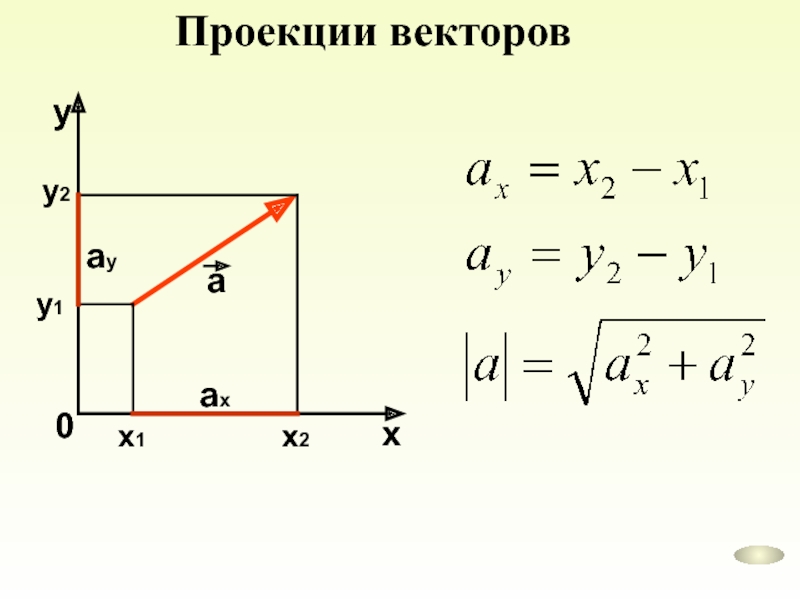
Что называется проекцией вектора на какую-либо ось?
В случае равномерного прямолинейного движения можно определить скорость по графику зависимости координаты от времени.
Проекция скорости численно равна тангенсу угла наклона прямой x(t) к оси абсцисс. При этом, чем больше скорость, тем больше угол наклона.
Прямолинейное равноускоренное движение.
На рисунке 1.33 изображены графики зависимости проекции ускорения от времени для трёх разных значений ускорения при прямолинейном равноускоренном движении точки. Они представляют собой прямые линии, параллельные оси абсцисс: ах = const. Графики 1 и 2 соответствуют движению, когда вектор ускорения направлен вдоль оси ОХ, график 3 — когда вектор ускорения направлен в противоположную оси ОХ сторону.
При равноускоренном движении проекция скорости зависит от времени линейно: υx = υ0x + axt. На рисунке 1.34 представлены графики этой зависимости для указанных трёх случаев. При этом начальная скорость точки одинакова. Проанализируем этот график.
Проекция ускорения Из графика видно, что, чем больше ускорение точки, тем больше угол наклона прямой к оси t и соответственно больше тангенс угла наклона, который определяет значение ускорения.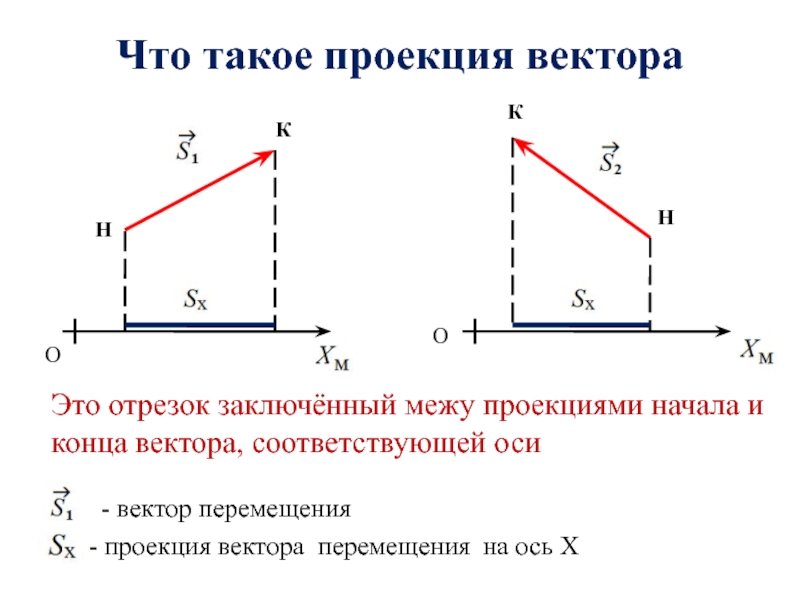
За один и тот же промежуток времени при разных ускорениях скорость изменяется на разные значения.
При положительном значении проекции ускорения за один и тот же промежуток времени проекция скорости в случае 2 увеличивается в 2 раза быстрее, чем в случае 1. При отрицательном значении проекции ускорения на ось ОХ проекция скорости по модулю изменяется на то же значение, что и в случае 1, но скорость уменьшается.
Для случаев 1 и 3 графики зависимости модуля скорости от времени будут совпадать (рис. 1.35).
Используя график зависимости скорости от времени (рис. 1.36), найдём изменение координаты точки. Это изменение численно равно площади заштрихованной трапеции, в данном случае изменение координаты за 4 с Δx = 16 м.
Мы нашли изменение координаты. Если необходимо найти координату точки, то к найденному числу нужно прибавить её начальное значение. Пусть в начальный момент времени х0 = 2 м, тогда значение координаты точки в заданный момент времени, равный 4 с, равно 18 м. В данном случае модуль перемещения равен пути, пройденному точкой, или изменению её координаты, т. е. 16 м.
В данном случае модуль перемещения равен пути, пройденному точкой, или изменению её координаты, т. е. 16 м.
Если движение равнозамедленное, то точка в течение выбранного интервала времени может остановиться и начать двигаться в направлении, противоположном начальному. На рисунке 1.37 показана зависимость проекции скорости от времени для такого движения. Мы видим, что в момент времени, равный 2 с, направление скорости изменяется. Изменение координаты будет численно равно алгебраической сумме площадей заштрихованных треугольников.
Вычисляя эти площади, мы видим, что изменение координаты равно -6 м, это означает, что в направлении, противоположном оси ОХ, точка прошла большее расстояние, чем по направлению этой оси.
Площадь над осью t берём со знаком «плюс», а площадь под осью t, где проекция скорости отрицательна, — со знаком «минус».
Если в начальный момент времени скорость некоторой точки была равна 2 м/с, то координата её в момент времени, равный 6 с, равна -4 м. Модуль перемещения точки в данном случае также равен 6 м — модулю изменения координаты. Однако путь, пройденный этой точкой, равен 10 м — сумме площадей заштрихованных треугольников, показанных на рисунке 1.38.
Модуль перемещения точки в данном случае также равен 6 м — модулю изменения координаты. Однако путь, пройденный этой точкой, равен 10 м — сумме площадей заштрихованных треугольников, показанных на рисунке 1.38.
Изобразим на графике зависимость координаты х точки от времени. Согласно одной из формул (1.14) кривая зависимости координаты от времени — x(t) — парабола.
Если движение точки происходит со скоростью, график зависимости которой от времени изображён на рисунке 1.36, то ветви параболы направлены вверх, так как ах > 0 (рис. 1.39). По этому графику мы можем определить координату точки, а также скорость в любой момент времени. Так, в момент времени, равный 4 с, координата точки равна 18 м.
Для начального момента времени, проводя касательную к кривой в точке А, определяем тангенс угла наклона α1, который численно равен начальной скорости, т. е. 2 м/с.
Для определения скорости в точке В проведём касательную к параболе в этой точке и определим тангенс угла α2. Он равен 6, следовательно, скорость равна 6 м/с.
Он равен 6, следовательно, скорость равна 6 м/с.
График зависимости пути от времени — такая же парабола, но проведённая из начала координат (рис. 1.40). Мы видим, что путь непрерывно увеличивается со временем, движение происходит в одну сторону.
Если движение точки происходит со скоростью, график зависимости проекции которой от времени изображён на рисунке 1.37, то ветви параболы направлены вниз, так как аx < 0 (рис. 1.41). При этом моменту времени, равному 2 с, соответствует вершина параболы. Касательная в точке В параллельна оси t, угол наклона касательной к этой оси равен нулю, и скорость также равна нулю. До этого момента времени тангенс угла наклона касательной уменьшался, но был положителен, движение точки происходило в направлении оси ОХ.
Начиная с момента времени t = 2 с, тангенс угла наклона становится отрицательным, а его модуль увеличивается, это означает, что движение точки происходит в направлении, противоположном начальному, при этом модуль скорости движения увеличивается.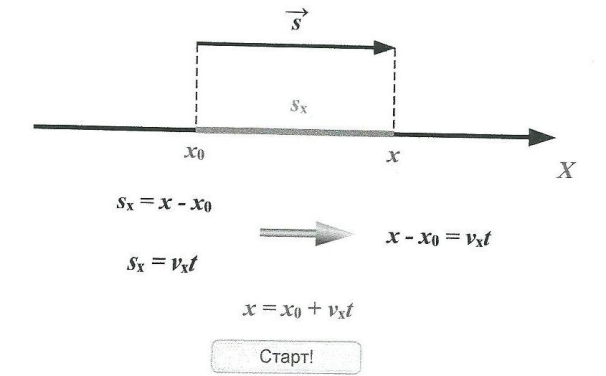
Модуль перемещения равен модулю разности координат точки в конечный и начальный моменты времени и равен 6 м.
График зависимости пройденного точкой пути от времени, показанный на рисунке 1.42 отличается от графика зависимости перемещения от времени (см. рис. 1.41).
Как бы ни была направлена скорость, путь, пройденный точкой, непрерывно увеличивается.
Выведем зависимость координаты точки от проекции скорости. Скорость υx = υ0x + axt, отсюда
В случае x0 = 0, ах > 0 и υx > υ0x график зависимости координаты от скорости представляет собой параболу (рис. 1.43).
При этом, чем больше ускорение, тем ветвь параболы будет менее крутой. Это легко объяснить, так как, чем больше ускорение, тем меньше расстояние, которое должна пройти точка, чтобы скорость увеличилась на то же значение, что и при движении с меньшим ускорением.
В случае ах < 0 и υ0x > 0 проекция скорости будет уменьшаться.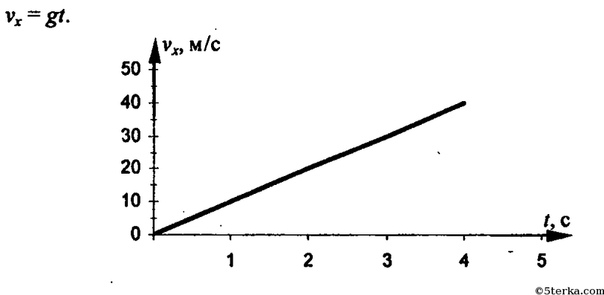 Перепишем уравнение (1.17) в виде где а = |аx|. График этой зависимостимости — парабола с ветвями, направленными вниз (рис. 1.44).
Перепишем уравнение (1.17) в виде где а = |аx|. График этой зависимостимости — парабола с ветвями, направленными вниз (рис. 1.44).
Ускоренное движение.
По графикам зависимости проекции скорости от времени можно определить координату и проекцию ускорения точки в любой момент времени при любом типе движения.
Пусть проекция скорости точки зависит от времени так, как показано на рисунке 1.45. Очевидно, что в промежутке времени от 0 до t3 движение точки вдоль оси X происходило с переменным ускорением. Начиная с момента времени, равного t3, движение равномерное с постоянной скоростью υDx. По графику мы видим, что ускорение, с которым двигалась точка, непрерывно уменьшалось (сравните угол наклона касательной в точках В и С).
Изменение координаты х точки за время t1 численно равно площади криволинейной трапеции OABt1, за время t2 — площади OACt2 и т. д. Как видим по графику зависимости проекции скорости от времени можно определить изменение координаты тела за любой промежуток времени.
Как видим по графику зависимости проекции скорости от времени можно определить изменение координаты тела за любой промежуток времени.
По графику зависимости координаты от времени можно определить значение скорости в любой момент времени, вычисляя тангенс угла наклона касательной к кривой в точке, соответствующей данному моменту времени. Из рисунка 1.46 следует, что в момент времени t1 проекция скорости положительна. В промежутке времени от t2 до t3 скорость равна нулю, тело неподвижно. В момент времени t4 скорость также равна нулю (касательная к кривой в точке D параллельна оси абсцисс). Затем проекция скорости становится отрицательной, направление движения точки изменяется на противоположное.
Если известен график зависимости проекции скорости от времени, можно определить ускорение точки, а также, зная начальное положение, определить координату тела в любой момент времени, т. е. решить основную задачу кинематики. По графику зависимости координаты от времени можно определить одну из самых важных кинематических характеристик движения — скорость. Кроме этого, по указанным графикам можно определить тип движения вдоль выбранной оси: равномерное, с постоянным ускорением или движение с переменным ускорением.
Кроме этого, по указанным графикам можно определить тип движения вдоль выбранной оси: равномерное, с постоянным ускорением или движение с переменным ускорением.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика – Физика, учебник для 10 класса – Класс!ная физика
Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
К зачету физика 10-1
10 класс
Материалы к зачету по теме “
Основные законы механики “1. Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.
Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела.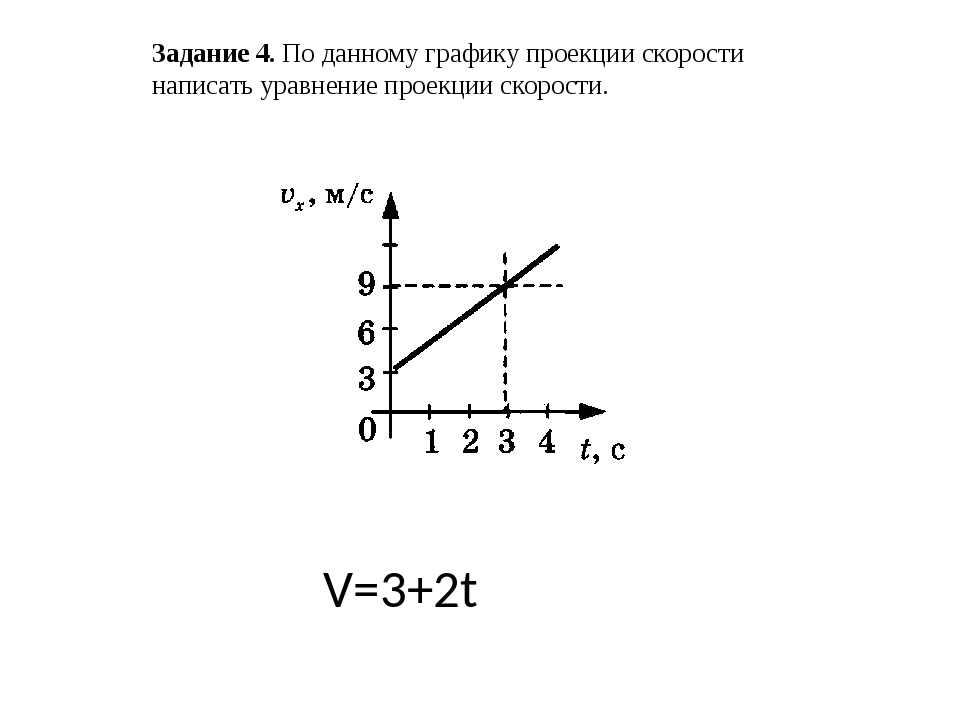 Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:
Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:
,
где — начальная координата тела, а — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.
Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.
Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.
2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.
Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:
.
Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:
.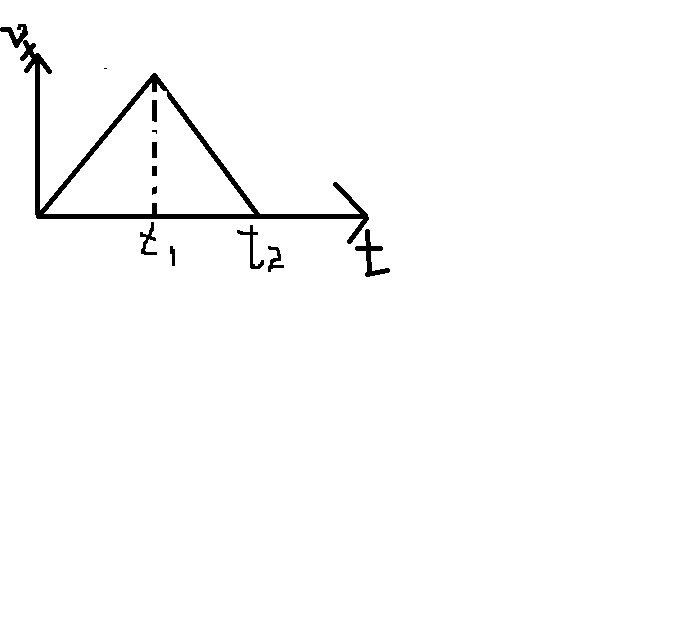
Координату тела находят по формуле:
.
Проекцию перемещения находят по формуле:
.
Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.
Значение проекции перемещения при равноускоренном движении можно определить также по формуле:
.
| Так как | , то для координаты тела х имеем: |
При вычислениях по приведенным формулам знаки проекций векторов , а также знак начальной координаты х, определяются условием задачи и направлением оси координат.
3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса φ, проведенного из центра окружности к телу, и угловой скорости ω.
Связь между линейной и угловой скоростью выражается формулой:
,
где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:
Модуль вектора центростремительного ускорения выражается равенством:
.
Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.
Пример решения задачи:
1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.
Решите задачи самостоятельно:
1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?
2. 9 км/ч = … м/с; 10 м/с = . .. км/ч; 8 км/с = … км/ч, 54 км/ч = …м/с.
.. км/ч; 8 км/с = … км/ч, 54 км/ч = …м/с.
3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.
Попробуйте решить задачи из раздела “Кинематика”
вернуться на страницу “Физика” | вверх |
Характеристики движения снаряда
Как обсуждалось ранее в этом уроке, снаряд – это объект, на который действует единственная сила тяжести. Многие снаряды совершают не только вертикальное движение, но и горизонтальное движение. То есть, двигаясь вверх или вниз, они также перемещаются горизонтально. Есть две составляющие движения снаряда – горизонтальное и вертикальное движение. А поскольку перпендикулярные составляющие движения независимы друг от друга, эти две составляющие движения можно (и нужно) обсуждать отдельно.Цель этой части урока – обсудить горизонтальную и вертикальную составляющие движения снаряда; особое внимание будет уделено наличию / отсутствию сил, ускорений и скорости.
А поскольку перпендикулярные составляющие движения независимы друг от друга, эти две составляющие движения можно (и нужно) обсуждать отдельно.Цель этой части урока – обсудить горизонтальную и вертикальную составляющие движения снаряда; особое внимание будет уделено наличию / отсутствию сил, ускорений и скорости.
Давайте вернемся к нашему мысленному эксперименту , проведенному ранее в этом уроке. Представьте пушечное ядро, которое пушка проецирует горизонтально с вершины очень высокого утеса.В отсутствие гравитации ядро продолжало бы горизонтальное движение с постоянной скоростью. Это соответствует закону инерции. Более того, если просто упасть из состояния покоя в присутствии силы тяжести, пушечное ядро будет ускоряться вниз, набирая скорость со скоростью 9,8 м / с каждую секунду. Это согласуется с нашей концепцией свободно падающих объектов, ускоряющихся со скоростью, известной как ускорение свободного падения .
Если наш мысленный эксперимент продолжается и мы проецируем пушечное ядро горизонтально в присутствии силы тяжести, то пушечное ядро будет поддерживать то же горизонтальное движение, что и раньше, – постоянную горизонтальную скорость.Кроме того, сила тяжести воздействует на пушечное ядро, вызывая такое же вертикальное движение, как и раньше – ускорение вниз. Пушечное ядро падает на такое же расстояние, как и при падении из состояния покоя (см. Диаграмму ниже). Однако наличие силы тяжести не влияет на горизонтальное движение снаряда. Сила тяжести действует вниз и не может изменить горизонтальное движение. Чтобы вызвать горизонтальное ускорение, должна быть горизонтальная сила. (И мы знаем, что на снаряды действует только вертикальная сила.) Вертикальная сила действует перпендикулярно горизонтальному движению и не влияет на него, поскольку перпендикулярные компоненты движения не зависят друг от друга. Таким образом, снаряд движется с постоянной горизонтальной скоростью и вертикальным ускорением вниз .
Приведенную выше информацию можно обобщить в следующей таблице.
| Горизонтальный Движение | Вертикальный Движение | |
| Силы (Присутствует? – Да или Нет) (Если есть, то какой?) | Нет | да Сила тяжести действует вниз |
| Разгон (Присутствует? – Да или Нет) (Если есть, то какой?) | Нет | да “g” меньше 9.8 м / с / с |
| Скорость (Постоянный или изменяющийся?) | Постоянный | Изменение (на 9,8 м / с каждую секунду) |
Негоризонтально запускаемые снаряды
Теперь предположим, что наша пушка направлена вверх и стреляет под углом к горизонту с той же скалы. В отсутствие силы тяжести (т.е. если предположить, что переключатель силы тяжести может быть выключен ) снаряд снова будет двигаться по прямолинейному инерционному пути. Движущийся объект продолжил бы движение с постоянной скоростью в том же направлении, если бы не было неуравновешенной силы. Так обстоит дело с объектом, движущимся в пространстве в отсутствие гравитации. Однако, если бы переключатель силы тяжести мог быть повернут на на , так что пушечное ядро действительно является снарядом, то объект снова упадет в свободном падении ниже этого прямолинейного инерционного пути.Фактически, снаряд будет лететь по параболической траектории . Сила тяжести, направленная вниз, будет действовать на пушечное ядро, вызывая такое же вертикальное движение, как и раньше – ускорение вниз. Пушечное ядро за каждую секунду падает на такое же расстояние, как и при падении из состояния покоя (см. Диаграмму ниже). Еще раз, наличие силы тяжести не влияет на горизонтальное движение снаряда.
В отсутствие силы тяжести (т.е. если предположить, что переключатель силы тяжести может быть выключен ) снаряд снова будет двигаться по прямолинейному инерционному пути. Движущийся объект продолжил бы движение с постоянной скоростью в том же направлении, если бы не было неуравновешенной силы. Так обстоит дело с объектом, движущимся в пространстве в отсутствие гравитации. Однако, если бы переключатель силы тяжести мог быть повернут на на , так что пушечное ядро действительно является снарядом, то объект снова упадет в свободном падении ниже этого прямолинейного инерционного пути.Фактически, снаряд будет лететь по параболической траектории . Сила тяжести, направленная вниз, будет действовать на пушечное ядро, вызывая такое же вертикальное движение, как и раньше – ускорение вниз. Пушечное ядро за каждую секунду падает на такое же расстояние, как и при падении из состояния покоя (см. Диаграмму ниже). Еще раз, наличие силы тяжести не влияет на горизонтальное движение снаряда. Снаряд по-прежнему перемещается на такое же расстояние по горизонтали за каждую секунду полета, как и при выключении гравитационного переключателя .Сила тяжести является вертикальной силой и не влияет на горизонтальное движение; перпендикулярные составляющие движения не зависят друг от друга.
Снаряд по-прежнему перемещается на такое же расстояние по горизонтали за каждую секунду полета, как и при выключении гравитационного переключателя .Сила тяжести является вертикальной силой и не влияет на горизонтальное движение; перпендикулярные составляющие движения не зависят друг от друга.
В заключение, снаряды летят по параболической траектории из-за того факта, что направленная вниз сила тяжести ускоряет их вниз от их прямой, свободной от гравитации траектории. Эта направленная вниз сила и ускорение приводят к смещению вниз из положения, в котором объект находился бы, если бы не было силы тяжести.Сила тяжести не влияет на горизонтальную составляющую движения; Снаряд поддерживает постоянную горизонтальную скорость, поскольку на него не действуют горизонтальные силы.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора движения снаряда. Вы можете найти его в разделе Physics Interactives на нашем сайте. Симулятор позволяет в интерактивном режиме исследовать концепции движения снаряда. Измените высоту, измените угол, измените скорость и запустите снаряд.
Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора движения снаряда. Вы можете найти его в разделе Physics Interactives на нашем сайте. Симулятор позволяет в интерактивном режиме исследовать концепции движения снаряда. Измените высоту, измените угол, измените скорость и запустите снаряд.
Используйте свое понимание снарядов, чтобы ответить на следующие вопросы.Когда закончите, нажмите кнопку, чтобы просмотреть свои ответы.
1. Рассмотрите эти диаграммы, отвечая на следующие вопросы.
Какая диаграмма (если есть) может представлять …
а. … начальная горизонтальная скорость?г. … начальная вертикальная скорость?
г.
… горизонтальное ускорение?
г. … вертикальное ускорение?
e…. чистая сила?
2. Предположим, снегоход оборудован ракетницей, способной запускать сферу вертикально (относительно снегохода). Если снегоход находится в движении и запускает ракету и после запуска сохраняет постоянную горизонтальную скорость, то где же приземлится ракета (не считая сопротивления воздуха)?
а.перед снегоходомг. за снегоходом
г. в снегоходе
3. Предположим, что спасательный самолет бросает пакет помощи, когда он движется с постоянной горизонтальной скоростью на большой высоте. Если предположить, что сопротивление воздуха незначительно, где приземлится пакет помощи по отношению к самолету?
а.под самолетом и за ним.г. прямо под самолетом
г.
под самолетом и впереди
Движение снаряда | Репетитор 4 по физике
Смотрите коллекцию из решенных примеров по этой теме на нашем сайте buzztutor.com
Снаряд
Снаряд – это тело, брошенное с начальная скорость в вертикальной плоскости, а затем движется в двух измерениях под действием силы тяжести в одиночку, без приведения в движение какого-либо двигателя или топливо.Его движение называется движением снаряда. Путь снаряда называется его траекторией.
Примеры:
Пакет, выпущенный из самолет в полете.
Мяч для гольфа в полете.
Пуля, выпущенная из винтовки.
Струя воды из отверстия возле дна резервуара для воды.

Движение снаряда – случай двумерное движение .Любой случай двумерного движение можно разделить на два случая одного размерное движение – одно по оси x и другой по оси Y. Можно изучить два случая. отдельно как два случая одномерного движения. результаты двух случаев можно объединить с помощью вектора алгебра, чтобы увидеть чистый результат
Важно помнить, что движение в горизонтальном направлении не влияют на движение по вертикали и наоборот.Горизонтальное движение и вертикальное движение полностью независимы друг от друга.
Тело можно спроецировать двумя способами:
Горизонтальная проекция-Когда телу придается начальная скорость в только в горизонтальном направлении.
Угловая проекция-Когда тело брошено с начальной скоростью на угол к горизонтальному направлению.

Мы изучим два случая отдельно пренебрегаем влиянием воздуха Сопротивление. Возьмем ось абсцисс по горизонтали. направление и ось Y в вертикальном направлении.
Корпус 1 Горизонтальная проекцияБрошено тело с инициалом скорости u в горизонтальном направлении. изучите движение по осям x и y отдельно.Мы примет за отправную точку исходную точку.
По оси x | Вдоль оси Y |
|---|---|
| 1. Компонент
начальная скорость по оси абсцисс. u x = u | 1. Составляющая начального
скорость по оси ординат. u y = 0 |
2. | 2. ускорение
по оси Y a y = g = 9,8 м / с 2 It направлен вниз. |
| 3.Компонент
скорость по оси абсцисс в любой момент времени t . v x = u x + a x t = u + 0 v x = u Это означает, что
горизонтальная составляющая скорости не
изменяются на протяжении всего движения снаряда. | 3. Составляющая скорости
по оси ординат в любой момент тн. v y = u y + a y t = 0 + gt v y = gt |
| 4. The
смещение по оси x в любой момент т x = u x т + (1/2) a x т 2 x = u x т
+ 0 | 4. Смещение по
Ось y в любой момент t Смещение по
Ось y в любой момент t y = u y t + (1/2) a y t 2 y = 0 + (1/2) a y t 2 902 = 1 / 2gt 2 |
Уравнение траектория (траектория снаряда)
Мы знаем в любой момент x = ut
t = x / u
Кроме того, y = (1/2) gt 2
Замена на тн получаем
y = (1/2) г (x / u) 2
г = (1/2) (г / ед 2 ) x 2
y = kx 2 где k = g / (2u 2 )
Это уравнение параболы, симметричной относительно оси y. Таким образом
Путь снаряда, проецируемого горизонтально из
высота над землей – парабола.
Таким образом
Путь снаряда, проецируемого горизонтально из
высота над землей – парабола.
Чистая скорость в любой момент время t
Мы знаем, в любой момент т
v x =
u
v y = gt
v = (v x 2 + v y 2 ) 1/2 = [u 2 +
(gt) 2 ] 1/2
Направление v по горизонтали в любой момент :
(угол) = загар -1 (v y / v x ) = загар -1 (gt / u)
Время
рейс (Т):
Итого
время, в течение которого снаряд находится в полете (от O
к B на диаграмме выше)
Чтобы найти Т, мы найдем
время вертикального падения
От y = u y t
+ (1/2) gt 2
Когда, y = h, t = T
ч = 0 + (1/2) gt 2
T = (2ч / г) 1/2
Диапазон
(R):
Это пройденное расстояние по горизонтали
во время полета Т.
От х =
ut
Когда t = T, x = R
R = uT
R = u (2ч / г) 1/2
Чемодан 2 Угловой Выступ
ср теперь рассмотрим случай, когда объект проецируется с начальной скоростью u под углом к горизонтальное направление.
ср
Предположим, что сопротивление воздуха отсутствует.
тело сначала поднимается, а затем опускается после
достигнув наивысшей точки, мы будем использовать
Декартова конвенция для знаков различных физических
количества. Ускорение свободного падения g
будет отрицательным, поскольку действует вниз.
Ускорение свободного падения g
будет отрицательным, поскольку действует вниз.
ср разделит движение на горизонтальное (движение по оси x) и вертикальное движение (движение по оси ординат).Мы будем изучать движение по оси x и движение по оси y. раздельно.
| Ось X | Ось Y |
| 1. Составляющая начальной скорости по
ось абсцисс. u x = u cosΦ | 1. Составляющая начальной скорости по
ось y. u y = u sinΦ |
2. | 2. ускорение
по оси Y a y = -g = -9.8 м / с 2 (г отрицательно, так как действует в нисходящем направление) |
| 3. Компонент
скорость по оси абсцисс в любой момент времени t . v x = u x + a x t = ucosΦ + 0 = ucosΦ v x = ucosΦ Это означает, что
горизонтальная составляющая скорости не
изменяются на протяжении всего движения снаряда. | 3. Составляющая скорости
по оси ординат в любой момент тн. v y = u y + a y t v y = usinΦ – GT |
| 4. The
смещение по оси x в любой момент т x = u x т + (1/2) a x t 2 x = ucosΦ.т | 4. Смещение по
Ось y в любой момент t y = u y t + (1/2) a y t 2 y = usinΦ. |
Уравнение траектории (путь снаряд)
В любой момент t
x = ucosΦ.t
t = x / (ucosΦ)
Кроме того, y = usinΦ.t – (1/2) gt 2
Замена т
y = usinΦ.x / (ucosΦ) – (1/2) g [x / (ucosΦ)] 2
y = x.tanΦ – [(1/2) g.sec 2 .x 2 ] / u 2
Это уравнение имеет вид y = ax + bx 2 где
‘a’ и ‘b – константы. Это уравнение
парабола.Таким образом, траектория снаряда представляет собой параболу.
.
Это уравнение
парабола.Таким образом, траектория снаряда представляет собой параболу.
.
нетто скорость тела в любой момент времени t
v x = ucosΦ
v y = usinΦ
– gt
v = (v x 2 + v y 2 ) 1/2
Φ = коричневый -1 (v y / v x ) Где Φ –
угол, который результирующая скорость (v) составляет с
горизонталь в любой момент.
Время полета T
Угловой снаряд движение симметрично относительно высшей точки. объект достигнет наивысшей точки за время T / 2 . в самой высокой точке вертикальная составляющая скорости v y становится равной нулю.
v y = usinΦ
– gt
При t = T / 2 , v y =
0
0 = usinΦ – gT / 2
T = (2usinΦ) / г
Максимальная высота H
Уравнение для вертикального
расстояние (компонент y)
y = u y t
– (1/2) GT 2
При t = T / 2, y = H
H = usinΦ. T / 2 – (1/2) г (T / 2) 2
T / 2 – (1/2) г (T / 2) 2
заменяющий T
H = usinΦ.usinΦ / г – (1/2) г (usinΦ / г) 2
= (u 2 sin 2 /грамм
– (u 2 sin 2 ) / 2g
H = (u 2 sin 2 ) / 2g
Диапазон R
Диапазон – общий пройденное расстояние по горизонтали за время полет.
Из уравнения для
горизонтальное перемещение, x = u x т
Когда t = T, x = R
R = u x T =
ucos. 2usinΦ / г
2usinΦ / г
= u 2 2sinΦcosΦ / г
= u 2 sin2Φ / г с использованием 2sinΦcosΦ = sin2Φ
R = (u 2 sin2Φ) / г
4.2 Вектор ускорения – Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте вектор ускорения с учетом функции скорости в единичном векторе.
- Опишите движение частицы с постоянным ускорением в трех измерениях.
- Используйте одномерные уравнения движения вдоль перпендикулярных осей, чтобы решить задачу в двух или трех измерениях с постоянным ускорением.
- Выразите ускорение в единичном векторе.
Мгновенное ускорение
Помимо получения векторов смещения и скорости движущегося объекта, мы часто хотим знать его ускорение вектор в любой момент времени на его траектории. Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе.Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени
Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе.Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени
находим
Ускорение по компонентам
Кроме того, поскольку скорость является производной функции положения, мы можем записать ускорение в терминах второй производной функции положения:
Пример
Нахождение вектора ускорения
Частица имеет скорость
(а) Что такое функция ускорения? (б) Каков вектор ускорения при t = 2.0 с? Найдите его величину и направление.
Решение
[показать-ответ q = ”362804 ″] Показать ответ [/ раскрыть-ответ]
[скрытый-ответ a =” 362804 ″] (a) Мы берем первую производную по времени функции скорости, чтобы найти ускорение . Производная берется покомпонентно:
Производная берется покомпонентно:
(b) Оценка
дает нам направление в обозначении единичного вектора. Величина ускорения
[/ hidden-answer]
Значение
В этом примере мы обнаруживаем, что ускорение зависит от времени и изменяется на протяжении всего движения.Давайте рассмотрим другую функцию скорости частицы.
Пример
Обнаружение ускорения частиц
Частица имеет функцию положения
(а) Какая скорость? б) Что такое ускорение? (c) Опишите движение от до = 0 с.
Стратегия
Мы можем получить некоторое представление о проблеме, посмотрев на функцию положения. Оно линейно в y и z , поэтому мы знаем, что ускорение в этих направлениях равно нулю, когда мы берем вторую производную.Также обратите внимание, что положение в направлении x равно нулю для t = 0 с и t = 10 с.
Решение
(a)
[show-answer q = ”186733 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 186733 ″] Взяв производную по времени функции положения, мы находим
Функция скорости линейна во времени в направлении x и постоянна в направлениях y и z. [/ Hidden-answer]
[/ Hidden-answer]
(b)
[Показать-ответ q = ”713695 ″] Показать ответ [/ Показать-ответ]
[Скрытый-ответ a =” 713695 ″] Взяв производную функции скорости, находим
Вектор ускорения постоянен в отрицательном направлении оси x.[/ hidden-answer]
(c) [раскрыть-ответ q = ”368016 ″] Показать ответ [/ раскрыть-ответ]
[hidden-answer a = ”368016 ″] Траекторию частицы можно увидеть на (Рисунок).
Давайте сначала посмотрим в направлениях y и z. Положение частицы постоянно увеличивается в зависимости от времени с постоянной скоростью в этих направлениях. Однако в направлении x частица следует по положительному положительному x до тех пор, пока t = 5 с, когда она меняет направление на противоположное. Мы знаем это, глядя на функцию скорости, которая в этот момент становится равной нулю, а затем становится отрицательной.Мы также знаем это, потому что ускорение отрицательное и постоянное, то есть частица замедляется или ускоряется в отрицательном направлении. Положение частицы достигает 25 м, после чего она меняет направление и начинает ускоряться в отрицательном направлении по оси x. Положение достигает нуля при t = 10 с.
Положение частицы достигает 25 м, после чего она меняет направление и начинает ускоряться в отрицательном направлении по оси x. Положение достигает нуля при t = 10 с.
Показана проекция траектории на плоскость xy.Значения y и z линейно увеличиваются как функция времени, тогда как x имеет точку поворота при t = 5 с и 25 м, когда он меняет направление. В этот момент компонент x скорости становится отрицательным. При t = 10 с частица возвращается на 0 м в направлении x.
[/ hidden-answer]
Значение
Изобразив траекторию частицы, мы можем лучше понять ее движение, что определяется численными результатами кинематических уравнений.
Проверьте свое понимание
Предположим, что функция ускорения имеет вид
, где a, b, и c – константы.Что можно сказать о функциональном виде функции скорости?
[показывать-ответ q = ”fs-id1165038330863 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038330863 ″]
Вектор ускорения постоянный и не меняется со временем. Если a, b и c не равны нулю, то функция скорости должна быть линейной во времени. У нас
Если a, b и c не равны нулю, то функция скорости должна быть линейной во времени. У нас
, поскольку взятие производной функции скорости дает
Если любой из компонентов ускорения равен нулю, то этот компонент скорости будет постоянным.
[/ hidden-answer]
Постоянное ускорение
Многомерное движение с постоянным ускорением можно рассматривать так же, как показано в предыдущей главе для одномерного движения. Ранее мы показали, что трехмерное движение эквивалентно трем одномерным движениям, каждое по оси, перпендикулярной другим. Чтобы разработать соответствующие уравнения для каждого направления, давайте рассмотрим двумерную задачу о частице, движущейся в плоскости xy с постоянным ускорением, игнорируя на данный момент компонент z .Вектор ускорения
Каждый компонент движения имеет отдельный набор уравнений, подобных (рисунок) – (рисунок) из предыдущей главы об одномерном движении. Мы показываем только уравнения для положения и скорости в направлениях x и y . Аналогичный набор кинематических уравнений может быть записан для движения в направлении z :
Мы показываем только уравнения для положения и скорости в направлениях x и y . Аналогичный набор кинематических уравнений может быть записан для движения в направлении z :
Здесь индекс 0 обозначает начальное положение или скорость.(Рисунок) на (Рисунок) можно заменить на (Рисунок) и (Рисунок) без компонента z для получения вектора положения и вектора скорости как функции времени в двух измерениях:
Следующий пример иллюстрирует практическое использование кинематических уравнений в двух измерениях.
Пример
Лыжник (рисунок) показывает лыжника, движущегося с ускорением
.вниз по склону
при т = 0.С началом системы координат в передней части ложи, ее начальное положение и скорость равны
.и
(a) Каковы составляющие x- и y положения и скорости лыжника как функции времени? (b) Каковы ее положение и скорость при t = 10,0 с?
Рисунок 4. 10 У лыжника ускорение
10 У лыжника ускорениевниз по склону
Начало системы координат находится в лыжной базе.
Стратегия
Поскольку мы оцениваем компоненты уравнений движения в направлениях x и y , нам необходимо найти компоненты ускорения и поместить их в кинематические уравнения. Компоненты ускорения находятся в системе координат на (Рисунок). Затем, вставив компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время t .
Решение
(a)
[Показать-ответ q = ”216061 ″] Показать ответ [/ Показать-ответ]
[Скрытый-ответ a =” 216061 ″] Начало системы координат находится на вершине холма с y- ось вертикально вверх и ось x горизонтально. Глядя на траекторию лыжника, можно увидеть, что x-составляющая ускорения положительна, а y-составляющая отрицательна. Поскольку угол равен
вниз по склону, находим
Вставив начальное положение и скорость в (рисунок) и (рисунок) для x, мы имеем
Для y имеем
(b) Теперь, когда у нас есть уравнения движения для x и y как функции времени, мы можем вычислить их при t = 10. 0 с:
0 с:
Положение и скорость при t = 10,0 с, наконец,
Величина скорости лыжника на 10,0 с составляет 25 м / с, что составляет 60 миль / ч. [/ Hidden-answer]
Значение
Полезно знать, что, учитывая начальные условия положения, скорости и ускорения объекта, мы можем найти положение, скорость и ускорение в любое более позднее время.
С (Рисунок) – (Рисунок) мы завершили набор выражений для положения, скорости и ускорения объекта, движущегося в двух или трех измерениях. Если траектории объектов выглядят как «красные стрелки» на начальном рисунке главы, то выражения для положения, скорости и ускорения могут быть довольно сложными. В следующих разделах мы исследуем два частных случая движения в двух и трех измерениях, рассматривая движение снаряда и круговое движение.
Сводка
- В двух и трех измерениях вектор ускорения может иметь произвольное направление и не обязательно указывать вдоль заданного компонента скорости.

- Мгновенное ускорение вызывается изменением скорости за очень короткий (бесконечно малый) период времени. Мгновенное ускорение – это вектор в двух или трех измерениях. Он находится путем взятия производной функции скорости по времени.
- В трех измерениях, ускорение
можно записать как векторную сумму одномерных ускорений
по осям x- , y – и z- .
- Кинематические уравнения для постоянного ускорения могут быть записаны как векторная сумма уравнений постоянного ускорения в направлениях x , y и z .
Концептуальные вопросы
Если функция положения частицы является линейной функцией времени, что можно сказать о ее ускорении?
Если объект имеет постоянную составляющую скорости x и внезапно испытывает ускорение в направлении y , изменяется ли составляющая его скорости x ?
[показывать-ответ q = ”fs-id1165038328884 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038328884 ″]
Нет, движения в перпендикулярных направлениях независимы.
[/ hidden-answer]
Если объект имеет постоянную составляющую скорости x – и внезапно испытывает ускорение под углом
в направлении x , изменяется ли составляющая скорости x –?
Проблемы
Положение частицы
(a) Определите его скорость и ускорение как функции времени. (б) Каковы его скорость и ускорение в момент времени t = 0?
Ускорение частицы
При t = 0 его положение и скорость равны нулю.а) Каковы положение и скорость частицы в зависимости от времени? (б) Найдите уравнение пути частицы. Нарисуйте оси x- и y- и нарисуйте траекторию частицы.
[показывать-ответ q = ”fs-id1165038340090 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038340090 ″]
а.
,
г.
[/ hidden-answer]
Лодка выходит из дока при т.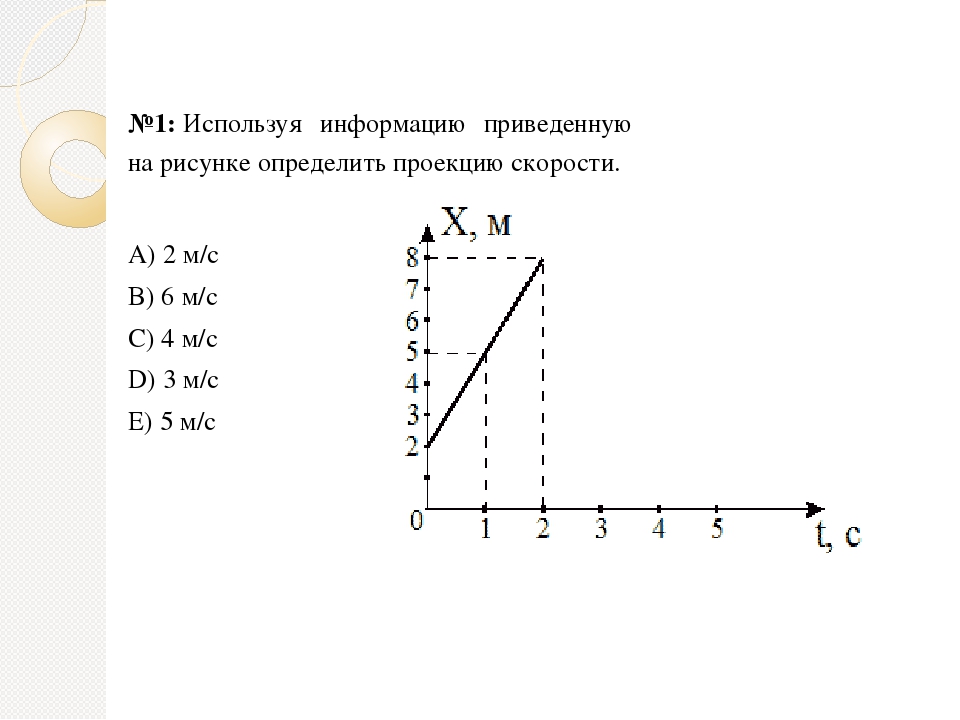 = 0 и направляется в озеро с ускорением
= 0 и направляется в озеро с ускорением
Сильный ветер толкает лодку, придавая ей дополнительную скорость
(а) Какова скорость лодки при т = 10 с? (b) Каково положение лодки при т = 10 с? Нарисуйте эскиз траектории и положения лодки на отметке t = 10 с, показывая оси x- и y .
Положение частицы для t > 0 задается
(а) Какова скорость как функция времени? б) Что такое ускорение как функция времени? (c) Какова скорость частицы при t = 2,0 с? (d) Какова его скорость при т, = 1,0 с и т, = 3,0 с? (e) Какова средняя скорость между t = 1,0 с и t = 2,0 с?
[показывать-ответ q = ”fs-id1165038304047 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038304047 ″]
а.
,
г.
,
г.
,
г.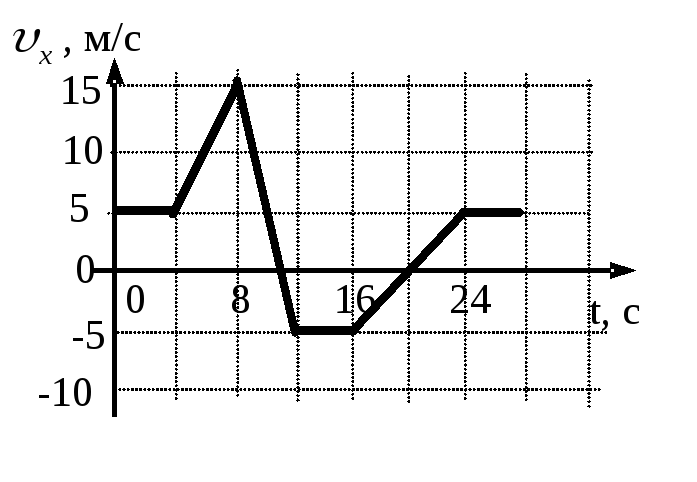
,
e.
[/ hidden-answer]
Ускорение частицы – постоянная величина. При t = 0 скорость частицы
При т = 4 с скорость
(а) Каково ускорение частицы? б) Как положение и скорость меняются со временем? Предположим, что частица изначально находится в начале координат.
Частица имеет функцию положения
, где аргументы функций косинуса и синуса выражены в радианах. а) Что такое вектор скорости? б) Что такое вектор ускорения?
[показывать-ответ q = ”fs-id1165038303762 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165038303762 ″]
а.
, г.
[/ hidden-answer]
Реактивный самолет Lockheed Martin F-35 II Lighting взлетает с авианосца с длиной взлетно-посадочной полосы 90 м и скоростью взлета 70 м / с в конце взлетно-посадочной полосы. Самолеты катапультируются в воздушное пространство с палубы авианосца с двумя источниками движения: реактивным движением и катапультой. В момент выхода из палубы авианосца ускорение F-35 уменьшается до постоянного ускорения
Самолеты катапультируются в воздушное пространство с палубы авианосца с двумя источниками движения: реактивным движением и катапультой. В момент выхода из палубы авианосца ускорение F-35 уменьшается до постоянного ускорения
в
по горизонтали. (а) Каково начальное ускорение F-35 на палубе авианосца, чтобы он поднялся в воздух? (b) Запишите положение и скорость F-35 в единичном векторе от точки, когда он покидает палубу авианосца.(c) На какой высоте находится истребитель через 5,0 с после выхода из палубы авианосца? (г) Каковы его скорость и скорость в это время? д) Как далеко он прошел по горизонтали?
Глоссарий
- вектор ускорения
- мгновенное ускорение, полученное путем взятия производной функции скорости по времени в обозначении единичного вектора
Движение снаряда
Движение снаряда3.3. Projectile Motion
Самый большой азарт в бейсболе – это хоумран.Движение мяча по изогнутой траектории к трибунам – это распространенный тип двумерного движения, называемого «движением снаряда». Хорошее описание такого движения часто можно получить, если предположить, что сопротивление воздуха отсутствует.
ОБЗОР КОНЦЕПЦИИ Следуя подходу, описанному на рис. 3.6, мы рассматриваем горизонтальную и вертикальную части движения отдельно. В горизонтальном или осевом направлении движущийся объект (снаряд) не замедляется при отсутствии сопротивления воздуха.Таким образом, компонент x скорости остается постоянным на своем начальном значении или v x = v 0x , а компонент x ускорения равен x = 0 м / с 2 . Однако в вертикальном или y-направлении снаряд испытывает действие силы тяжести. В результате y-составляющая скорости v y не постоянна, а изменяется. Компонент y ускорения a y – это ускорение силы тяжести вниз. Если путь или траектория снаряда близка к поверхности земли, y имеет звездную величину 9.80 м / с 2 . Таким образом, в этом тексте фраза «движение снаряда» означает, что x = 0 м / с 2 и y равняются ускорению свободного падения, как показано в краткой концепции на рисунке 3.8 подводит итог. Пример 2 и другие примеры в этом разделе иллюстрируют, как уравнения кинематики применяются к движению снаряда.
|
| Пример 2 Пакет помощи при падении |
На рис. 3.9 показан самолет, движущийся горизонтально с постоянной скоростью +115 м / с на высоте 1050 м. Направления вправо и вверх выбраны как положительные.Самолет выпускает «посылку», которая падает на землю по криволинейной траектории. Не обращая внимания на сопротивление воздуха, определите время, необходимое для того, чтобы пакет упал на землю.
Рассуждения Время, необходимое для того, чтобы пакет упал на землю, – это время, за которое пакет упал с высоты 1050 м по вертикали.При падении он движется как вправо, так и вниз, но эти две части движения происходят независимо. Поэтому мы можем сосредоточиться исключительно на вертикальной части. Отметим, что первоначально пакет движется в горизонтальном направлении или по оси x, а не по оси y, так что v 0y = 0 м / с. Кроме того, когда пакет ударяется о землю, компонент y его смещения составляет y = –1050 м, как показано на рисунке. Это ускорение свободного падения, поэтому y = –9,80 м / с 2 .Эти данные резюмируются следующим образом:
С этими данными уравнение 3.5b () можно использовать для определения времени спада.
Решение Поскольку v 0y = 0 м / с, из уравнения 3.5b следует, что и | ||||||||||||||||||||||
Свободно падающий пакет в Примере 2 набирает вертикальную скорость при спуске.Горизонтальная составляющая скорости, однако, сохраняет свое начальное значение v 0x = + 115 м / с на протяжении всего спуска. Поскольку самолет также движется с постоянной горизонтальной скоростью +115 м / с, он остается прямо над падающим пакетом. Пилот всегда видит пакет прямо под самолетом, как показывают пунктирные вертикальные линии на рис. 3.9. Этот результат является прямым следствием того факта, что упаковка не имеет ускорения в горизонтальном направлении. На самом деле сопротивление воздуха могло бы замедлить пакет, и он не оставался бы непосредственно под самолетом во время снижения.Рисунок 3.10 дополнительно поясняет этот момент, показывая, что происходит с двумя пакетами, выпущенными одновременно с одной и той же высоты. Пакет B получает начальную составляющую скорости v 0x = + 115 м / с в горизонтальном направлении, как в Примере 2, и пакет следует по пути, показанному на рисунке. Пакет A, с другой стороны, сбрасывается с неподвижного аэростата и падает прямо на землю, поскольку v 0x = 0 м / с. Оба пакета упали на землю одновременно.
|
Пакеты на рис. 3.10 не только достигают земли одновременно, но и компоненты y их скоростей также равны во всех точках на пути вниз. Однако пакет B ударяется о землю с большей скоростью, чем пакет A.Помните, что скорость – это величина вектора скорости, а скорость B имеет компонент x, а скорость A – нет. Величина и направление вектора скорости для пакета B в момент непосредственно перед тем, как пакет упадет на землю, вычислены в примере 3.
| Пример 3 Скорость пакета для ухода |
Важной особенностью движения снаряда является что нет ускорения в горизонтальном направлении или в направлении оси x. В концептуальном примере 4 обсуждается интересное значение этой функции.
| Концептуальный пример 4 Я выстрелил пулей в воздух… |
Предположим, вы едете в кабриолете с опущенным верхом. Автомобиль движется вправо с постоянной скоростью. Как показано на рис. 3.11, вы наводите винтовку прямо вверх и стреляете из нее. Где бы пуля приземлилась при отсутствии сопротивления воздуха – позади вас, впереди вас или в стволе винтовки?
Обсуждение и решение Если бы сопротивление воздуха присутствовало, пуля замедлилась бы и она приземлилась бы позади вас, по направлению к задней части автомобиля. Однако сопротивление воздуха отсутствует, поэтому нужно более внимательно относиться к движению пули.Перед выстрелом из винтовки пуля, винтовка и автомобиль движутся вместе, поэтому пуля и винтовка имеют такую же горизонтальную скорость, что и автомобиль. При выстреле из винтовки пуле придается дополнительная составляющая скорости в вертикальном направлении; пуля сохраняет скорость автомобиля в качестве начальной горизонтальной составляющей скорости, поскольку винтовка направлена прямо вверх. Поскольку для замедления нет сопротивления воздуха, пуля не испытывает горизонтального ускорения. Таким образом, горизонтальная составляющая скорости пули не изменяется.Он сохраняет свою первоначальную ценность и остается такой же, как у винтовки и автомобиля. В результате пуля все время остается прямо над винтовкой и упадет прямо обратно в ствол винтовки , как показано на рисунке. Эта ситуация аналогична ситуации на рис. 3.9, где посылка при падении остается прямо под плоскостью. Родственное домашнее задание: Концептуальный вопрос 12, проблема 34 | |||
| Концептуальное моделирование 3.1 |
| |
Часто снаряды, такие как футбольные и бейсбольные мячи, запускаются в воздух под углом по отношению к земле.Зная начальную скорость снаряда, можно получить большой объем информации о движении. Например, в примере 5 показано, как рассчитать максимальную высоту, достигаемую снарядом.
| Пример 5 Высота начальной точки |
Также можно найти общее время или «время зависания», в течение которого футбольный мяч на рис. 3.12 находится в воздухе. Пример 6 показывает, как определить это время.
| Пример 6 Время полета стартового снаряда |
Еще одна важная особенность движения снаряда называется «дальность полета».«Дальность, как показано на рис. 3.12, представляет собой горизонтальное расстояние, пройденное между пуском и приземлением, при условии, что снаряд возвращается на тот же вертикальный уровень, на котором он был выпущен. Пример 7 показывает, как получить диапазон.
| Концептуальное моделирование 3,2 |
| |
| Пример 7 Диапазон начального удара |
Диапазон в предыдущем примере зависит от угла q , по которому снаряд стреляет выше горизонтали. Когда сопротивление воздуха отсутствует, максимальный диапазон достигается при.
| Проверьте свое понимание 3 |
| ||
В примерах, рассмотренных до сих пор, использовалась информация о начальном местоположении и скорости снаряда для определения конечного местоположения и скорости. В примере 8 рассматривается противоположная ситуация и показано, как конечные параметры могут использоваться с уравнениями кинематики для определения начальных параметров.
Бейсболист выполняет хоумран, и мяч приземляется на сиденье слева, на 7,5 м выше точки, в которой он был поражен. Он приземляется со скоростью 36 м / с под углом 28 ° от горизонтали (см. Рисунок 3.13). Не обращая внимания на сопротивление воздуха, найдите начальную скорость, с которой мяч покидает биту.
Рассуждения Чтобы найти начальную скорость, мы должны определить ее величину (начальная скорость v 0 ) и ее направление (угол q на чертеже). Эти величины связаны с горизонтальной и вертикальной составляющими начальной скорости (v 0x и v 0y ) соотношениями Решение Поскольку сопротивление воздуха игнорируется, горизонтальная составляющая скорости v x остается постоянной на протяжении всего движения. Таким образом,
При определении v 0y мы выбираем знак плюса для квадратного корня, потому что вертикальный компонент начальной скорости указывает вверх на рис. 3.13, что является положительным направлением. Начальная скорость v 0 и угол q бейсбольного мяча равны | ||||||||||||||||||||||||||
| ||
При движении снаряда величина ускорения силы тяжести существенно влияет на траекторию. Например, бейсбольный мяч или мяч для гольфа на Луне полетел бы намного дальше и выше, чем на Земле, если бы был запущен с той же начальной скоростью. Причина в том, что гравитация Луны примерно в шесть раз меньше земной.
Раздел 2.6 указывает, что определенные типы симметрии относительно времени и скорости присутствуют для свободно падающих тел. Эти симметрии также обнаруживаются в движении снарядов, поскольку снаряды свободно падают в вертикальном направлении. В частности, время, необходимое снаряду для достижения максимальной высоты H, равно времени, затраченному на возвращение на землю. Кроме того, на рис. 3.14 показано, что скорость v объекта на любой высоте над землей на восходящей части траектории равна скорости v на той же высоте на нисходящей части.Хотя две скорости одинаковы, скорости разные, потому что они указывают в разных направлениях. Концептуальный пример 9 показывает, как использовать этот тип симметрии в своих рассуждениях.
|
| Концептуальный пример 9 Два способа бросить камень |
С вершины утеса над озером человек бросает два камня.Камни имеют одинаковую начальную скорость v 0 , но камень 1 бросается вниз под углом q ниже горизонтали, а камень 2 бросается вверх под тем же углом над горизонтом, как показано на рис. 3.15. Не обращайте внимания на сопротивление воздуха и решите, какой камень ударяет в воду с большей скоростью.
Обсуждение и решение Можно предположить, что камень 1, брошенный вниз, ударит по воде с большей скоростью. Чтобы показать, что это не так, давайте проследим путь камня 2, когда он поднимается на максимальную высоту и падает обратно на землю. Обратите внимание на точку P на рисунке, где камень 2 возвращается на свою первоначальную высоту; здесь скорость камня 2 равна v 0 , но его скорость направлена под углом q ниже горизонтали.Это именно тот тип симметрии снаряда, который показан на рис. 3.14. Таким образом, в этот момент камень 2 имеет скорость, идентичную скорости, с которой камень 1 бросается вниз с вершины утеса. С этого момента скорость камня 2 изменяется точно так же, как и скорость камня 1, поэтому оба камня ударяются о воду с одинаковой скоростью. Родственное домашнее задание: Задачи 37, 65 | |||
Во всех примерах этого раздела снаряды движутся по криволинейной траектории.В общем, если единственное ускорение вызвано действием силы тяжести, форму траектории можно представить как параболу.
| Тест самооценки 3,1 |
| |
| Авторские права © 2000-2003 John Wiley & Sons, Inc. или связанных компаний. Все права защищены. |
Урок 26: Горизонтально запущенные снаряды
Изучение движения снаряда объединяет многое из того, что вы узнали в последних нескольких главах.
- Вам необходимо знать о гравитации, силах, скорости, ускорении и компонентах вектора, чтобы полностью понять (и выяснить) эти вопросы.
- Но не волнуйтесь. Даже имея все эти вещи, которые нужно отслеживать, изучение того, как задавать эти вопросы и понимать, что происходит понемногу, делает все это управляемым.
Эффект Хитрого Койота
Я уверен, что все вы видели мультфильм, где Койот преследует Дорожного Бегуна и убегает со скалы. Он зависает в воздухе на секунду, смотрит вниз, а затем начинает падать.
- Вопрос в том, насколько это правда и сколько людей верят в это?
Несколько лет назад некоторые исследователи из U.С. ходил в начальные, неполные и средние школы, а также в университеты и просил их взглянуть на следующее:
«Игнорирование сопротивления воздуха,
что из следующего правильно показывает, что сделал бы объект, если бы он скатился со скалы?»
Рисунок 1
Разбивка полученных ответов была почти одинаковой для всех возрастов.
- Около 60% сказали, что номер 1 правильный. Объект остановится в воздухе, а затем начнет падать прямо вниз.Поскольку это то, что Койот всегда делал в мультфильмах (и потому, что некоторые люди действительно ссылались на это в своих объяснениях, почему они выбрали этот ответ), исследователи назвали это Эффект Хитрого Койота .
- Около 25% сказали, что номер 2 правильный. Объект сначала будет двигаться вперед, но в конечном итоге просто упадет прямо вниз.
- Только около 15% ответили на число 3. Объект будет продолжать двигаться вперед все время, пока падает.
На самом деле правильный ответ – цифра 3, и если вы подумаете об этом, используя изученную вами физику, это будет иметь смысл.
- Допустим, койот действительно сбегает со скалы. Когда он покидает обрыв, он набирает горизонтальную скорость.
- Изучая силы и ускорение, вы уже знаете, что единственный способ изменить эту горизонтальную скорость (вызвать горизонтальное ускорение) – это приложить горизонтальную силу к койоту.
- Если мы игнорируем сопротивление воздуха (что является очень хорошей идеей, поскольку оно будет практически нулевым), то горизонтальная сила, вызывающая горизонтальное ускорение, отсутствует.
- Поскольку нет горизонтального ускорения, койот будет перемещаться по горизонтали с одной и той же скоростью все время!
Это ничего не говорит нам о том, что происходит по вертикали, что полностью отделено от того, что объект делает по горизонтали.
- Как только койот покидает обрыв, он испытывает вертикальную силу тяжести.
- Эта сила заставит его начать ускоряться в вертикальном направлении.
- По мере падения он будет двигаться все быстрее и быстрее в вертикальном направлении.
Глядя на эту проблему как на то, что происходит по горизонтали и вертикали, вы должны понять, что это точно так же, как компоненты, над которыми мы только что работали пару уроков назад.
- Горизонтальная и вертикальная составляющие движения объекта, падающего со скалы, отделены друг от друга и не могут влиять друг на друга.
- Во многих книгах вы увидите горизонтальный компонент, называемый x, и вертикальный компонент, называемый y.
Если мы посмотрим на горизонтальную и вертикальную составляющие скорости объекта, когда он скатывается со скалы, мы получим что-то похожее на это.
Рисунок 2
- Х-компонент присутствует с самого начала и остается неизменным все время.
- Y-компонента даже не существует вначале, но увеличивается по мере падения объекта.
- Форма пути, по которому он следует, на самом деле является параболой. Если вы изучали их в классе математики, отлично! Не беспокойтесь об этом, если вы этого не сделали, пока вы узнаете форму и знаете имя.
Чтобы понять, как на самом деле решать вопросы, связанные с этими ситуациями, возможно, лучше всего взглянуть на пример.
- При чтении примера помните о характеристиках объекта при падении.
- Когда вы задаете часть вопроса, которая связана с вертикальным движением, «ДУМАЙТЕ ВЕРТИКАЛЬНО» и используйте только вертикальные идеи (например, гравитацию).
- Когда вы задаете часть вопроса, которая связана с горизонтальным движением, «ДУМАЙТЕ ГОРИЗОНТАЛЬНО» и используйте только горизонтальные идеи (без гравитации / ускорения).
Пример 1: Я бросаю мяч с края обрыва высотой 15,0 м. Я бросил горизонтально со скоростью 8,0 м / с.
- Определите , сколько времени нужно, чтобы упасть.
- Определите , на каком расстоянии от основания утеса он упирается в землю.
- Определите , насколько быстро он движется по вертикали, когда ударяется о землю.
- Определите , какова его общая скорость, когда он ударяется о землю.
a) ДУМАЙ ВЕРТИКАЛЬНО
Мы говорим о том, что что-то падает, и это вертикальное движение, поэтому мы будем использовать только вертикальные идеи и числа.На самом деле, если бы я просто уронил его прямо с края обрыва, объекту потребовалось бы столько же времени, чтобы упасть на землю, поэтому давайте просто посчитаем время, чтобы упасть таким образом. Не забывайте мыслить вертикально…
d = v i t + 1/2 при 2 <- Начальная вертикальная скорость равна нулю, поэтому ...
d = 1/2 при 2
t = sqr root (2d / a) = sqr root (2 x 15,0 / 9,81)
t = 1,75 сб) ДУМАЙ ГОРИЗОНТАЛЬНО
Ну, мы знаем, что это было в воздухе за 1.75 секунд (из предыдущего вопроса), и он все время двигался с постоянной скоростью 8,0 м / с в направлении оси x, так что…
v = d / t
d = v t = (8,0 м / с) (1,75 с)
d = 14 мОн переместится на 14 м по горизонтали и упадет на землю на расстоянии 14 м от основания обрыва.
c) ДУМАЙ ВЕРТИКАЛЬНО
Он все время ускорялся. Мы знаем, что гравитация вызывает это ускорение и что вначале она не двигалась вертикально, поэтому мы можем выяснить, с какой скоростью она движется (по вертикали), когда ударяется о землю.
v f 2 = v i 2 + 2ad
v f = sqr root (v i 2 + 2ad) = sqr root (0 + 2 x 9.81 x 15.0)
v f = 17 м / сг) Комбинация!
Рисунок 3
Полная скорость определяется путем сложения горизонтальной и окончательной вертикальной составляющих скорости для нахождения результирующей.
c 2 = a 2 + b 2
= (8.0 м / с) 2 + (17 м / с) 2
c = 19 м / сtanΘ = opp / adj
= (8,0 м / с) / (17 м / с)
Θ = 25 °При ударе о землю объект движется со скоростью 19 м / с под углом 25 ° от горизонтали.
Хотя в реальных проблемах всегда будут небольшие различия, это стандартный тип вопросов, которые вам будут задавать для подобных вопросов.
По-прежнему возникают проблемы с горизонтальным движением снаряда? Тогда щелкните здесь.Требуется Windows Media Player 9 или новее и широкополосное соединение (модемное соединение не рекомендуется).
Максимальная дальность полета снаряда
Ах да. Я знаю, что уже сделал это. Однако это было очень давно с дрянными графиками. Я могу сделать лучше.
В учебниках указано, что максимальная дальность движения снаряда (без сопротивления воздуха) составляет 45 градусов. Как вы это получили? Вот так.
Во-первых, чтобы прояснить, что такое движение снаряда? Типичное определение – это движение объекта за счет только силы тяжести (без сопротивления воздуха, ракет и прочего).Если вам нужно подробное обсуждение движения снаряда, прочтите этот пост. В противном случае запомните ключ к движению снаряда:
Движение снаряда похоже на две одномерные задачи кинематики, которые имеют общее только время. Ускорение в вертикальном направлении – g , а горизонтальное ускорение равно нулю.
Движение снаряда – нет сопротивления воздуха
Используя основные идеи, приведенные выше, и кинематические уравнения (для постоянного ускорения), должно быть верно следующее:
[]
Обратите внимание, что я предполагаю при t = 0 секунд , начальные положения равны x 0 y 0 вместе с начальными скоростями.Кроме того, я использую типичное соглашение, что г = 9,8 Н / кг = 9,8 м / с 2 , так что ускорение в направлении y составляет – г . Но как далеко уйдет объект, если он начинается и заканчивается в одном и том же диапазоне y ? Вот диаграмма, показывающая скорость запуска некоторого объекта.
[]
Цель здесь – найти диапазон ( x – x 0 ). Для этого я сначала определю время движения, используя направление y. Помните, я знаю, что объект начинается и заканчивается на тех же и .Это дает:
[]
Быстрая проверка. Какое значение θ даст наибольшее время? Хорошо, это было бы тогда, когда sin (θ) является наибольшим – при значении π / 2 (90 градусов – ну, вы знаете, прямо вверх). А как насчет единиц? (м / с) больше (м / с 2 ) дает единицы времени. Большой. Теперь вставим это выражение для движения по оси x.
[]
Проверка агрегата. (m 2 / s 2 ) over (m / s 2 ) действительно дает единицы измерения. Еще одна проверка. Что, если я брошу мяч прямо вверх (θ = π / 2)? Ну, cos (π / 2) = 0, так что это дает горизонтальный диапазон 0 метров.Имеет смысл.
Но реальный вопрос: какой угол для максимального расстояния (для данной начальной скорости). Ясно, что этот диапазон зависит от произведения синуса и косинуса. Позвольте мне сначала вытащить триггерное удостоверение. Произведение синуса и косинуса (в общем):
[]
Я знаю, о чем вы думаете: мы действительно собираемся использовать триггерное тождество? Я думал, что мы просто должны были получить их в старшей школе в качестве наказания за все те плевки, которые мы бросали. О нет. Они действительно полезны.Для этого триггерного тождества θ = φ, так что:
[]
Наибольшее значение sin для чего-либо может быть равно 1. Под каким углом это будет?
[]
Готово. 45 градусов. Все как в учебнике написано. О, тебе это не нравится? Вы визуальный ученик? Я могу с этим справиться. Вот сюжет, который может вам понравиться. Это график sinθ cosθ и произведения двух от нуля до π / 2.
[]
Обратите внимание, что член cos * sin имеет максимальное значение при θ = π / 4? Бум.Все еще недостаточно хорошо? А как насчет того, чтобы бросить целую кучу шаров с одинаковой начальной скоростью, но под разными углами? Вот результат:
[]
Все они запускаются с одинаковой начальной скоростью, но под разными углами. Угадайте, какой из них идет дальше всего?
Горизонтальное и вертикальное движение – Движение снаряда – National 5 Physics Revision
Горизонтальное движение
Снаряды – горизонтальное движение
Горизонтальная скорость снаряда постоянна на протяжении всего полета.Это связано с тем, что после запуска на снаряд не действуют горизонтальные силы (сопротивление воздуха обычно игнорируется, поскольку оно очень мало), поэтому в горизонтальном направлении снаряд будет двигаться с постоянной скоростью. Для любых расчетов, связанных с горизонтальным движением снаряда, мы используем
\ [расстояние = скорость \ время \]
\ [{d} = {v} t \]
Вертикальное движение
Снаряды – вертикальное движение
Вертикальное движение снаряда контролируется силой сила тяжести.{-2} \) (напряженность гравитационного поля на Земле).
Поскольку вертикальная скорость снаряда непостоянна, ускорение должно быть включено в любой расчет вертикального движения;
\ [{a_v} = \ frac {{{v_v} – {u_v}}} {t} \]
где \ (v_ {v} \) = конечная вертикальная скорость, а где \ (u_ {v} \ ) = начальная вертикальная скорость

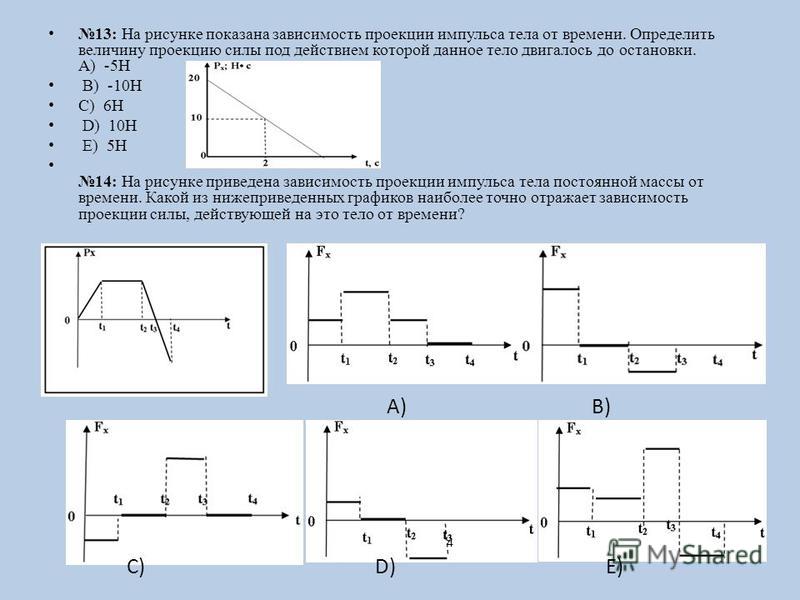 … горизонтальное ускорение?
… горизонтальное ускорение? под самолетом и впереди
под самолетом и впереди 

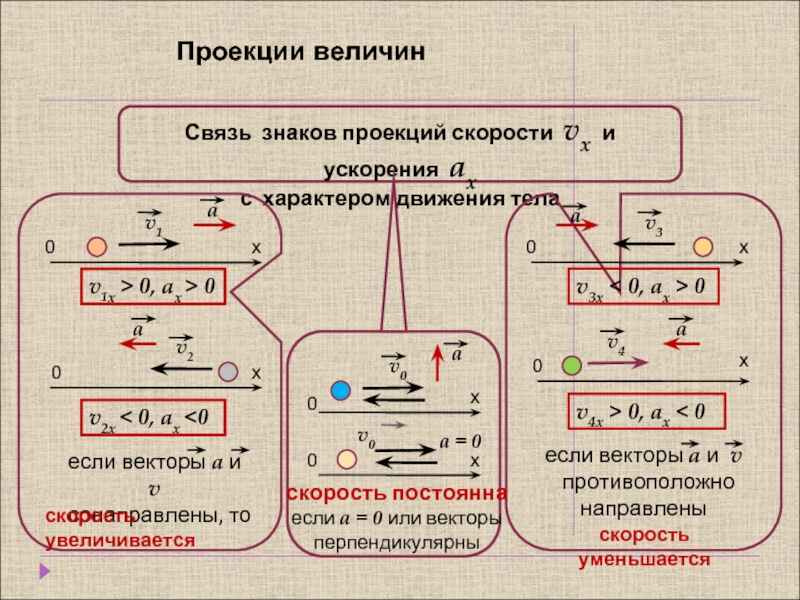 Ускорение по оси x
Ускорение по оси x 
 Ускорение по оси x
Ускорение по оси x 
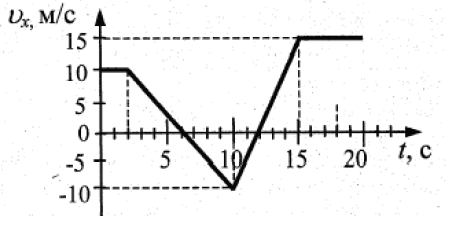 t – (1/2) gt 2
t – (1/2) gt 2