Производная функции для чайников — курсы по математике «Geniusmath»
Каждый школьник в старших классах сталкивается с таким понятием, как производная. Кажется, что алгебра, которая и так была не самым простым предметом, полностью теряет связь с реальностью. Так как тема традиционно плохо освещена в школьной программе, мы решили написать краткое руководство по производной функции для чайников.
Внимание! Все определения в данной статье являются лишь интерпретацией строгих научных определений и носят ознакомительный характер. Цель данной статьи — дать базовое понимание такого понятия, как производная функция.
Производная и скорость движения точки
Начнем из далека, и это будет очень важно для понимания! Рассмотрим точку, которая движется по известному нам закону. Если скорость движения непостоянная, то координата точки задается некой функцией . К примеру, f(5) – координата в момент времени 5, f(0) – координата в начальный момент времени. Поставим задачу: найти скорость движения в каждый момент времени.
Возьмем, для примера, следующий закон движения: .
В начальный момент времени наша координата равна . В момент времени 3.14 (число ): . Построим график зависимости с помощью Excel:
Закон движения точки
Вернемся к нашей задаче. Из курса физики мы знаем, что скорость на заданном промежутке времени можно посчитать, разделив изменение координаты на длину промежутка времени:
Данная формула определяет среднюю скорость на заданном участке . К примеру, скорость нашего движения за первые 3,14 секунды вычисляется следующим образом:
Применим данных подход для нахождения скорости на всем участке движения. Разобьем всё время движения на небольшие промежутки длиной в полсекунды и на каждом из них посчитаем скорость по указанной формуле. Мы получим значения для всех участков. Для наглядности построим график:
Средняя скорость с шагом 0.5 cек
Таким образом мы определили среднюю скорость движения на участках длиной в полсекунды, что практически является решением поставленной задачи. Но что если нам требуется более высокая точность, ведь мы до сих пор ничего не знаем о скорости внутри этих промежутков? Верно: уменьшим длину промежутков: до 0.1 секунды, затем до 0.01 и так далее. Будем уменьшать длину до тех пор, пока длина промежутка не будет бесконечно мала (практически 0) и отрезок можно будет принять за точку. В результате мы получим среднюю скорость на бесконечно маленьком промежутке времени, что по сути является
Но что если нам требуется более высокая точность, ведь мы до сих пор ничего не знаем о скорости внутри этих промежутков? Верно: уменьшим длину промежутков: до 0.1 секунды, затем до 0.01 и так далее. Будем уменьшать длину до тех пор, пока длина промежутка не будет бесконечно мала (практически 0) и отрезок можно будет принять за точку. В результате мы получим среднюю скорость на бесконечно маленьком промежутке времени, что по сути является
Построим график для полученных значений с помощью Excel:
Мгновенная скорость
Аналогичным образом считается производная функции, физический смысл которой является мгновенной скоростью изменения функции в данной точке.
Определение производной «на пальцах»
Рассмотрим функцию , определенную на отрезке и произвольные точки и из интервала . Данный треугольник называется “дельта”, он обозначает изменение указанной переменной.
Вычислим значения функции в указанных точках и найдем разность: . Мы получим изменение значения функции на отрезке (в примере выше это изменение координаты точки за некий промежуток времени). Разделив данную разность на длину промежутка, мы получим среднюю скорость изменения функции на данном отрезке. Теперь устремим длину отрезка к бесконечно маленькому значению, как мы это делали в нашем примере, и получим мгновенную скорость изменения функции
Данная величина называется производной функции в точке и обозначается .
Иными словами, производная функции в точке — это её мгновенная скорость изменения в данной точке.
Если же существует функция , которая в каждой точке равна производной функции в данной точке, то говорят, что — производная функции
О том, как данные производные считаются, поговорим в статье «Нахождение производной».
О производных / Хабр
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я “
” — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения.
А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.
Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.
Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.

А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.
Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.
Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
Глянем вот на этот график:
Даша — стабильный середнячок. Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.
К чему это я?
1.
Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:
- А где работаешь?
- А кем?
- Сколько получаешь?
и т.д.
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.
2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.
В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.
Каков знак Вашей производной?
2011 год. Высшая математика для чайников. Производные и дифференциалы. Виосагмир И.А. Предел функции.
Математический анализ Лекция 3.1
Московский Государственный Технический Университет им. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Лекция 3. 1 к.ф.-м.н. Семакин А.Н. Математический анализ, Лекция
1 к.ф.-м.н. Семакин А.Н. Математический анализ, Лекция
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «Кемеровская государственная медицинская академия» Министерства здравоохранения Российской Федерации КАФЕДРА медицинской
Подробнее16.2.Н. Производная.
6..Н. Производная 6..Н. Производная. Оглавление 6..0.Н. Производная Введение…. 6..0.Н. Производная сложной функции…. 5 6..0.Н. Производные от функций с модулями…. 7 6..0.Н. Возрастание и убывание
ПодробнееПроизводная и дифференциал. Лекция 4-5
Производная и дифференциал Лекция 4-5 Приращения функции и аргумента Пусть функция y f ( x) определена в некоторой окрестности U( x) точки x и x U( x) произвольная точка из этой окрестности. Разность x
Разность x
Производная функции в точке
приращения аргумента Δ приращения Δ f ( 3 производной точке f ( в Производная в точке Приращением аргумента Δ f ( называется разность между значением аргумента в точке и любой другой точке из некоторой
ПодробнееЭлементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
ПодробнееМатематика (БкПл-100)
Математика (БкПл-100) М.П. Харламов 011/01 учебный год Тема. Пределы, непрерывность, производные 1 Тема: Предел функции 1. Предел функции Пусть f(x) функция, определенная на множестве Х; А и а числа. Опр.
ПодробнееМатематический анализ
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 3 Дифференциальное исчисление функций одной
ПодробнееОглавление.
 А.А.Быков bykovaa.ru, abkov.ru
А.А.Быков bykovaa.ru, abkov.ruksm-n05-производная и дифференциал А.А.Быков bykovaa.ru abkov.ru Оглавление 5. Лекция 5. Понятие производной… 4 5.. Производная… 4 5… Определение производной в точке 4 5… Производная степенной
ПодробнееПримерные практические задания:
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА 11 класс (база) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
ПодробнееДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Министерство образования и науки РФ Российский государственный университет нефти и газа имени И М Губкина Кафедра высшей математики СИ ВАСИН ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ Учебно-методическое пособие для
ПодробнееДифференциальное исчисление
ФГОУ СПО ЛТК МЕТОДИЧЕСКОЕ ПОСОБИЕ ПО МАТЕМАТИКЕ Дифференциальное исчисление Ст Ленинградская 00г Предисловие Настоящее пособие написано в соответствии с программой по математике для студентов средни профессиональны
ПодробнееТема 2 «Производная функции.
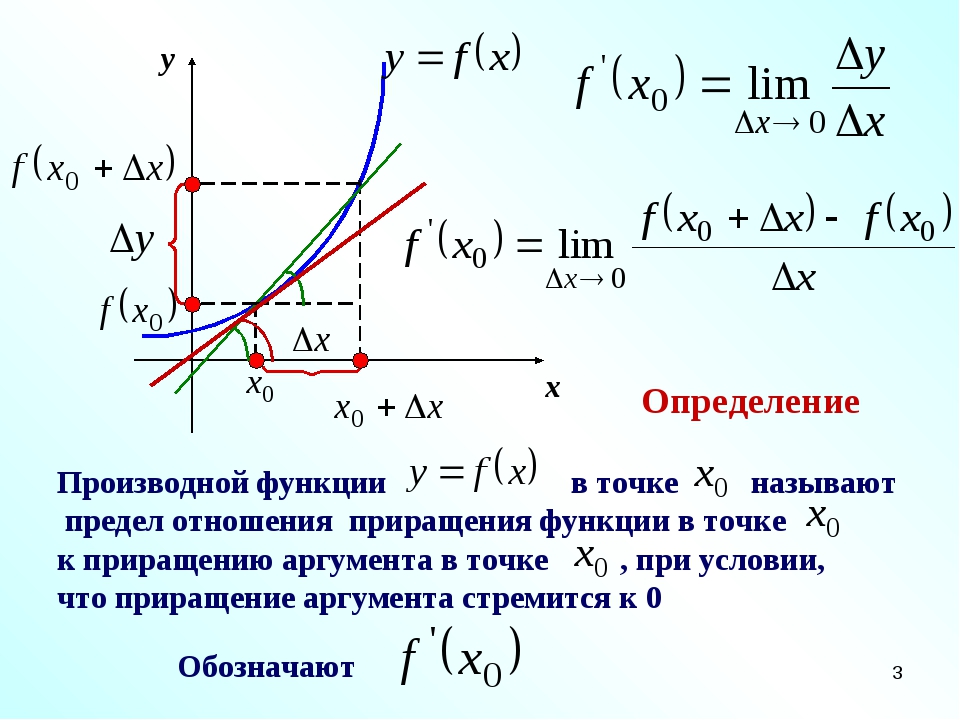 »
»Министерство образования Республики Беларусь УО «Витебский государственный технологический университет» Тема «Производная функции.»» Жозе ф Луи Лагра нж Кафедра теоретической и прикладной математики. разработана
Подробнее13. Частные производные высших порядков
13. Частные производные высших порядков Пусть = имеет и определенные на D O. Функции и называют также частными производными первого порядка функции или первыми частными производными функции. и в общем
ПодробнееЛекция Неопределенный интеграл
Лекция..3. Неопределенный интеграл Аннотация: Неопределенный интеграл определяется как множество первообразных функций подынтегральной функции. Рассматриваются свойства неопределенного интеграла, приводится
ПодробнееФедеральное агентство по образованию
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «МАТИ» Российский государственный технологический университет им К Э Циолковского Кафедра
Подробнее3.
 Дифференцирование функций
Дифференцирование функцийlim 3 Дифференцирование функций 3 Производная функции Производной функции f в точке называют следующий предел f f df f ‘ d, где f ‘ и df d условные обозначения производной Операция нахождения производной
Подробнее7. Производная. = lim., f
7. Производная 7.1. Рассмотрим интервал (a, b) R, функцию f, заданную на (a, b), и точку x (a, b). Если существует предел f(x + h) f(x) lim h 0 h f(y) f(x) = lim, y x y x его называют производной функции
ПодробнееБалльно – рейтинговая система
7 «Архитектура» семестр Очная форма обучения. Бакалавры. I курс, семестр. Направление 7 «Архитертура». Дисциплина – «Математика» Содержание Содержание… Балльно – рейтинговая система… Самостоятельная
ПодробнееДифференциальное исчисление
Дифференциальное исчисление Введение в математический анализ Предел последовательности и функции. Раскрытие неопределенностей в пределах. Производная функции. Правила дифференцирования. Применение производной
Раскрытие неопределенностей в пределах. Производная функции. Правила дифференцирования. Применение производной
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО МАТЕМАТИКЕ
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ) ТВ БИБИКОВА МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО МАТЕМАТИКЕ ДЛЯ ФАКУЛЬТЕТА «ЛОГИСТИКА» ЧАСТЬ ПРОИЗВОДНЫЕ МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ
Подробнее4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В результате изучения данной темы студент должен: уметь применять таблицу производных и правила дифференцирования для вычисления производных элементарных функций находить производные
ПодробнееСтрелковская И.В., Паскаленко В.Н.
Одесская национальная академия связи им АС Попова Кафедра высшей математики Стрелковская ИВ, Паскаленко ВН ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Учебное пособие для иностранных студентов
Подробнее3 (3, 2, -7) A A (3, 4, -7) Задачи для контрольной работы 1 1(3, 4, 2) A 2 (1, 2, 1) A 3 (-2, -3, 4) A 4 (3, -6, -3) 1(1, 3, 1) A 2 (-1, 4, 6) A
Задачи для контрольной работы Задание. Дана система линейных уравнений a a a a a a a a a b b b Решить систему: а) методом Гаусса; по правилу Крамера; средствами матричного исчисления (зад. )… 5. 7. 9.
Дана система линейных уравнений a a a a a a a a a b b b Решить систему: а) методом Гаусса; по правилу Крамера; средствами матричного исчисления (зад. )… 5. 7. 9.
Абхазский государственный университет
Абхазский государственный университет Физико-математический факультет кафедра математического анализа Сичинава НК Хупория НЗ Ласурия РА Дифференциальное исчисление функций одной переменной Учебно-методическое
ПодробнееЛекция 19 ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ.
Лекция 19 ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента xиз этого промежутка функция y=f(x)
ПодробнееМатематический анализ. Лекция 3.1
Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Модуль 3. Дифференциальное исчисление функций одной переменной
Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Математический анализ Модуль 3. Дифференциальное исчисление функций одной переменной
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Пусть имеем функцию определенную на множестве X и пусть точка X – внутренняя точка те точка для которой существует окрестность X Возьмем любую точку и обозначим через называется
ПодробнееУрок 14. геометрический смысл производной – Алгебра и начала математического анализа – 11 класс
Алгебра и начала анализа, 11 класса.
Урок №14. Геометрический смысл производной.
Перечень вопросов, рассматриваемых в теме
1) Геометрический смысл производной;
2) Алгоритм нахождения касательной к графику функции в точке;
3) Сравнение производных заданной функции по ее графику в различных точках.
Глоссарий по теме
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Напомним, что графиком линейной функции у=кх + b является прямая.
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Если k>0, то 0<α< π/2, в этом случае функция возрастает
Если k<0, то – π/2<α<0, в этом случае функция убывает
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Рассмотрим график функции y = f ( x ):
Из рисунка видно, что для любых двух точек A и B графика функции: f(x0+Δx)/f(x0)Δx=tgα, где – угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
Отсюда следует:
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
В этом и состоит геометрический смысл производной.
Уравнение касательной к графику функции y=f(x) в точке x0:
Примеры и разбор решения заданий тренировочного модуля
№1. Составить уравнение касательной к графику функции y=x+e-2x, параллельной прямой y=-x
Решение:
Угловой коэффициент касательной равен значению производной в точке касания x0. Т.к. касательная параллельна прямой y=-x, значит ее угловой коэффициент равен –1. Таким образом, f'(x0) = -1.
Уравнение касательной:
Уравнение касательной: y=1-1(x-0) = 1-x
Ответ: y=1-x.
№2. На параболе у=х2-2х-8 найти точку М, в которой касательная к ней параллельна прямой 4х+у+4=0.
Решение:
Определим угловой коэффициент касательной к параболе у=х2-2х-8:
k =у’=(х2-2х-8)’=2х-2.
Найдем угловой коэффициент прямой 4х+у+4=0:
у=-4х-4, k =-4.
Касательная к параболе и данная прямая по условию параллельны. Следовательно, их угловые коэффициенты равны, т.е.
Следовательно, их угловые коэффициенты равны, т.е.
2х-2=-4;
х=-1 – абсцисса точки касания.
Ординату точки касания М вычислим из уравнения данной параболы у=х2-2х-8, т.е.
у(-1)=(-1)2-2(-1)-8=-5, М(-1;-5).
Ответ: М(-1;-5).
§ 4. Применение производной к исследованию функций
Исследование функции удобно проводить по следующему плану.
1. Область определения функции.
2. Точки пересечения графика функции с осями координат.
3. Четность, нечетность функции.
4. Исследование функции на непрерывность. Вертикальные асимптоты.
5. Невертикальные асимптоты.
6. Интервалы монотонности. Экстремумы.
7. Интервалы выпуклости, вогнутости. Точки перегиба.
8. Дополнительные точки, (по мере необходимости).
9. Построение графика.
Подчеркнем, что пункт 8 не является необходимым. его выполняют, если необходимо уточнить график.
Пример 1. Исследовать функцию и построить ее график.
1. Область определения ().
2. Пусть х=0, тогда у=0. Пусть у=0, тогда и . Итак, (0;0) и – точки пересечение графика с осями координат.
3. у(-х) = – функция не является ни четной, ни нечетной.
4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.
5. Невертикальные асимптоты
Найдем k и b, если они существуют. поэтому при невертикальной асимптоты не существует. Аналогично можно показать, что и при невертикальных асимптот не существует.
6. Вычислим Найдем критические точки: х = 1 – критическая точка. Кроме того, y’ не существует при х = 0 – тоже критическая точка. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
Таким образом, на интервалах (-и (1;+ функция возрастает, на интервале (0;1) убывает.
уmax = f(0) = 0, ymin = f(1)= –1.
7. Вычислим
у” не обращается в нуль ни при каком значении х и у” не существует при х=0. х=0 – критическая точка второго порядка. Нанесем критическую точку на числовую прямую и определим знаки второй производной в образовавшихся интервалах.
Таким образом, на интервалах ( и график функции вогнутый, точек перегиба нет.
8. Заметим, что , то есть в точке (0;0) график имеет вертикальную касательную.
Пример 2. Исследовать функцию y = x-2arctg x и построить ее график.
1. Область определения (.
2. Пусть х = 0, тогда у = 0-2arctg 0 = 0.
Пусть y = 0, тогда х-2arctg x = 0; х = 2arctg x – решить такое уравнение точнo не удается.
Найдена точка (0;0) пересечения с осями координат.
3. функция нечетная.
4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.
5. Невертикальные асимптоты.
y = kx+b
– асимптота при .
Выясним, есть ли асимптоты при
.
– асимптота при
6. y‘
и х = 1 – критические точки. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
На интервалах функция возрастает, на интервале
(-1;1)– убывает.
7. y” = 0; 4х = 0; х = 0 – критическая точка второго порядка. Нанесем ее на числовую прямую и определим знаки второй производной в образовавшихся интервалах.
На интервале ( график выпуклый, на интервале – вогнутый.
х = 0 – абсцисса точки перегиба.
8. .
.
Пример 3. Исследовать функцию и построить ее график.
1. Область определения так как при и х=2 в знаменателе получается нуль.
2. Пусть х=0, тогда у=0.
Пусть у=0, тогда
(0;0) – точка пересечения графика с осями координат.
3. = – функция нечетная.
4. Функция имеет разрывы в точках х = -2 и х = 2, так как значения f(-2) и f(2) не определены. ; Это означает, что в точках и х = 2 функция имеет разрывы II рода и прямые и х = 2 являются вертикальными асимптотами.
5. Найдем невертикальные асимптоты.
следовательно, прямая у=0 является горизонтальной асимптотой при и .
6. Вычислим при всех значениях х, принадлежащих области определения функции. Точки и х = 2 – критические, так как в них производная не существует.
На интервалах функция убывает. Экстремумов нет.
Экстремумов нет.
7. Вычислим
y” = 0; ;
х = 0; х = 2 – критические точки второго порядка.
На интервалах и (0;2) график функции выпуклый, а на интервалах (-2;0) и – вогнутый; х = 0 – абсцисса точки перегиба.
Теоретический материал по теме “Производная функции”
ТЕМА «ПРОИЗВОДНАЯ ФУНКЦИИ»
Наша задача научиться находить производные. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания.
Пример 1
Найти производную функции
Решение:
Это простейший пример, пожалуйста, найдите его в таблице производных элементарных функций. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь: у нас была функция , которая в результате решения превратилась в функцию .
Говоря совсем просто, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением является экспоненциальная функция , которая превращается сама в себя. Операция нахождения производной называется дифференцированием.
Обозначения: Производную обозначают или
ПРАВИЛА ДИИФЕРЕНЦИРОВАНИЯ
Постоянное число можно (и нужно) вынести за знак производной
, где – постоянное число (константа)
Пример 2
Найти производную функции
Смотрим в таблицу производных. Производная косинуса там есть, но у нас .
Решаем:
Самое время использовать правило, выносим постоянный множитель за знак производной:
А теперь превращаем наш косинус по таблице:
Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:
Готово.
Производная суммы равна сумме производных
Пример 3
Найти производную функции
Решаем.
Обычно в ходе решения первые два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).
Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:
Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:
Все степени вида желательно снова представить в виде корней, степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет.
Производная произведения функций
Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:
Я не буду объяснять, почему именно так, наша задача научиться решать производные, а не разбираться в теории.
Пример 4
Найти производную функции
Здесь у нас произведение двух функций, зависящих от .
Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:
Сложно? Вовсе нет, вполне доступно даже для чайника.
Производная частного функций
А вот это вот суровая действительность:
Пример 5
Найти производную функции
Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:
ЗАДАНИЕ N 1
Тема: Правила дифференцирования
Производная функции равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
Тогда получим
ЗАДАНИЕ N 2
Тема: Правила дифференцирования
Производная функции равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
Тогда получим
ЗАДАНИЕ N 3
Тема: Правила дифференцирования
Производная функции равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
, , , где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
Тогда получим
ЗАДАНИЕ N 4
Тема: Правила дифференцирования
Производная функции равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
Тогда получим
определение, как найти, примеры решений
При решении задач дифференцирования приходится искать производные функций различных классов. В этой статье мы рассмотрим основные правила дифференцирования , которые будем постоянно использовать при нахождении производных. Все эти правила докажем на основе определения производной функции и обязательно остановимся на подробном решении примеров, чтобы понять принцип их применения.
В этой статье мы рассмотрим основные правила дифференцирования , которые будем постоянно использовать при нахождении производных. Все эти правила докажем на основе определения производной функции и обязательно остановимся на подробном решении примеров, чтобы понять принцип их применения.
При доказательстве правил дифференцирования будем считать функции f(x) и g(x) дифференцируемыми на некотором промежутке X .
То есть, для любого справедливо , где – приращения соответствующих функций.
В другой записи .
К основным правилам дифференцирования относят:
Вынесение постоянного множителя за знак производной.
Докажем формулу . По определению производной имеем:
Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому
На этом доказательство первого правила дифференцирования завершено.
Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.
Следующие примеры это наглядно подтверждают.
Пример.
Выполнить дифференцирование функции .
Решение.
По свойствам логарифмической функции можно перейти к записи . Осталось вспомнить производную логарифмической функции и вынести постоянный множитель:
Пример.
Решение.
Преобразуем исходную функцию .
Применяем правило вынесения множителя за знак производной и из таблицы берем производную показательной функции:
Производная суммы, производная разности.
Для доказательства второго правила дифференцирования воспользуемся определением производной и свойством предела непрерывной функции.
Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных .
Пример.
Найти производную функции .
Решение.
Упростим вид исходной функции .
Используем правило производной суммы (разности):
В предыдущем пункте мы доказали, что постоянный множитель можно выносить за знак производной, поэтому
Осталось воспользоваться таблицей производных:
Производная произведения функций.

Докажем правило дифференцирования произведения двух функций .
Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что и (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).
Что и требовалось доказать.
Пример.
Продифференцировать функцию .
Решение.
В данном примере . Применяем правило производной произведения:
Обращаемся к таблице производных основных элементарных функций и получаем ответ:
Пример.
Найти производную функции .
Решение.
В этом примере . Следовательно,
Давайте рассмотрим случай нахождения производной произведения трех функций. В принципе, по этой же системе можно дифференцировать произведение и четырех, и пяти, и двадцати пяти функций.
Пример.
Выполнить дифференцирование функции .
Решение.
Будем исходить из правила дифференцирования произведения двух функций. В качестве функции f(x)
будем считать произведение (1+x)sinx
, а в качестве g(x)
возьмем lnx
:
В качестве функции f(x)
будем считать произведение (1+x)sinx
, а в качестве g(x)
возьмем lnx
:
Для нахождения вновь применяем правило производной произведения:
Используем правило производной суммы и таблицу производных:
Подставляем полученный результат:
Как видите, порой приходится применять несколько правил дифференцирования в одном примере. Сложного в этом ничего нет, главное действовать последовательно и не мешать все в кучу.
Пример.
Найти производную функции .
Решение.
Функция представляет собой разность выражений и , поэтому
В первом выражении выносим двойку за знак производной, а ко второму выражению применяем правило дифференцирования произведения:
Производная частного двух функций (производная дроби).
Докажем правило дифференцирования частного двух функций (дроби) . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X .
Калькулятор вычисляет производные всех элементарных функций, приводя подробное решение. Переменная дифференцирования определяется автоматически.
Переменная дифференцирования определяется автоматически.
Производная функции — одно из важнейших понятий в математическом анализе. К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке.
Чаще всего производная функции определяется как предел отношения приращения функции к приращению аргумента, если он существует.
Определение. Пусть функция определена в некоторой окрестности точки . Тогда производной функции в точке называется предел, если он существует
Как вычислить производную функции?
Для того, чтобы научиться дифференцировать функции, нужно выучить и понять правила дифференцирования и научиться пользоваться таблицей производных .
Правила дифференцирования
Пусть и — произвольные дифференцируемые функции от вещественной переменной, — некоторая вещественная постоянная. Тогда
Тогда
— правило дифференцирования произведения функций
— правило дифференцирования частного функций
0 height=33 width=370> — дифференцирование функции с переменным показателем степени
— правило дифференцирования сложной функции
— правило дифференцирования степенной функции
Производная функции онлайн
Наш калькулятор быстро и точно вычислит производную любой функции онлайн. Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Эпиграф: Однажды спросила: “Чем производная отличается от произведения?” “Производную изучают на уроке математики, а произведение – на уроке литературы”, – последовал ответ ученика.
В эпиграфе описана реальная ситуация из моей практики. Вопрос возник, когда ученик запутался в правилах дифференцирования функций, в частности, не смог определить производную произведения двух функций. Во избежание подобной трактовки этой статьи напомню, что мы занимаемся именно математикой, и здесь термин “произведение” обозначает результат операции умножения, а “производная” это предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю. Процесс вычисления производной называется дифференцированием.
Вопрос возник, когда ученик запутался в правилах дифференцирования функций, в частности, не смог определить производную произведения двух функций. Во избежание подобной трактовки этой статьи напомню, что мы занимаемся именно математикой, и здесь термин “произведение” обозначает результат операции умножения, а “производная” это предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю. Процесс вычисления производной называется дифференцированием.
Производные элементарных функций по определению, т.е. через предел, вычисляют только однажды на лекции (на уроке), чтобы закрепить связь производной и предела. В дальнейшем нас интересует только практическое применение этого понятия, поэтому для вычисления производной пользуются готовыми Формулами и Правилами дифференцирования функций.
Здесь мы посмотрим как надо и как не надо вычислять производные, но, к сожалению, многие школьники и даже студенты это делают.
Как надо вычислять производные
Об этом написано везде, во всех учебниках и на множестве сайтов в сети.
Чтобы находить производные, нужно, пользуясь тем или иным источником, всё-таки выучить Формулы дифференцирования элементарных функций. Например, посмотрите подробную статью о Для более сложных, чем табличные, комбинированных функций применяются правила вычисления производной суммы, произведения, дроби. Соответствующие математические выражения также можно найти где угодно. Но, на мой взгляд, Правила дифференцирования функций лучше формулировать и заучивать словами:
- Постоянный множитель можно выносить за знак производной.
- Производная суммы равна сумме производных.
- Производная произведения равна “производная первого сомножителя, умноженная на второй, плюс производная второго сомножителя, умноженная на первый”.
- Производная дроби равна “производная числителя, умноженная на знаменатель, минус производная знаменателя, умноженная на числитель, деленные на знаменатель в квадрате”.
- Производная сложной функции равна производной внешней функции, умноженной на производную внутренней, и вычисляется “с продолжением” до табличной.

Как НЕ надо вычислять производные
- Прежде всего, не надо усложнять простое.
- Не надо путать степенную x а и показательную a x функции.
В большинстве последующих примеров представлены варианты вычислений производных, в которых
1. вычисления выполнены совсем плохо , с явными ошибками;
2. правильно, но неоптимально , т.е. долго и с вероятными ошибками на невнимательность;
3. совсем хорошо .
Обратите внимание, на правило, которое я поставила под номером один.
Если в произведении один из сомножителей является постоянной величиной, то совершенно не обязательно пользоваться правилом производной произведения. Более того, не нужно этого делать, так как часто такая операция сопровождается ошибками.
Если в дроби числитель или знаменатель является постоянной величиной, то совершенно необязательно пользоваться правилом для производной дроби. Это действие у школьников и студентов ещё чаще сопровождается ошибками. Постоянный множитель можно выносить за знак производной!
Пример 2.Пример 3.
Самая частая ошибка в подобных примерах – забыть поставить штрих (обозначение производной) над числом или поставить его и “не увидеть” при следующем действии, т.е. не учесть, что производная константы (числа) равна нулю.
Здесь для первого и третьего примеров простота и качество подхода c вынесением числового множителя за скобки очевидна. Но не всё так однозначно для второго примера, где в знаменателе находится тригонометрическая функция. Более того, соглашусь, что для тех учеников, которые плохо владеют производной сложной функции (правилом 5), более предпочтительным в этом примере может оказаться правило дифференцирования дроби.
Однако, для ряда других функций, особенно для степенных, просто необходимо знаменатель “превращать” в числитель, а корни — в степени, потому что в этом случае мы сможем воспользоваться самой простой и самой запоминающейся табличной формулой (x α) ” = αx α − 1 .
Пример 4.Пример 5.
В этих двух примерах, представлены обычные ошибки при дифференцировании дроби с константой, а в следующем примере переход от корня к дробной степени нужен потому, что иначе часто забывают, что подобная функция не является табличной и должна дифференцироваться по правилу для сложной функции.
Пример 6.Константа-слагаемое при дифференцировании обнуляется, константа-сомножитель при дифференцировании сохраняется.
Кроме того, почему-то для многих учеников производную функции y = x 2 + 0,1 вычислить легче, чем такую же производную вида (0,1 + х 2) ” . И для производной функции y = 0,1х 2 часто догадываются о существовании первого правила, а для (х 2 ·0,1) ” нет.
И для производной функции y = 0,1х 2 часто догадываются о существовании первого правила, а для (х 2 ·0,1) ” нет.
Если Вы допускаете ошибки такого рода, то вспомните, что от перестановки мест слагаемых сумма не изменяется, и от перестановки сомножителей произведение не изменяется. Переставьте их так, как вам удобнее, и аккуратно примените первое или второе правила дифференцирования.
В первом случае переменная находится в основании степени, читаем: “икс в степени а”. Во втором — переменная в показателе степени, читаем “а в степени икс”. Функции разные, формулы для вычисления производных разные. См. .
Пример 8.Пример 9.
Это пример для продвинутых. Задумайтесь о том, как бы Вы вычислили производную функции y = x x , в которой переменную поместили и в основание, и в показатель степени.
Хорошо подумав, но не раньше, кликните по , чтобы раскрыть мой ответ.
Это сложная функция, которая не относится напрямую ни к классу степенных, ни к классу показательных. Для вычисления производной в таких случаях часто требуется произвести предварительные преобразования. Например, здесь сначала выражение прологарифмировали, затем нашли производные обеих частей равенства по своим переменным и, наконец, составили уравнение для нахождения нужной производной по переменной х .
Сложная функция, это функция зависящая не напрямую от заданной переменной, а от другой функции. Иными словами, её значение нельзя вычислить в одно действие. Например, функции y = sinx 2 и y = sin 2 x являются сложными. Посмотрим, как вычисляются их значения, например при х = 2.
Для функции y = sinx 2 нужно сначала возвести x в квадрат: 2 2 = 4, а затем вычислить значение синуса 4-ёх. Сделаем это с помощью калькулятора: sin4 = −0,75680249530792825… ≈ −0,76 (не забудьте, что аргументы тригонометрических функций считаются заданными в радианах).
Сделаем это с помощью калькулятора: sin4 = −0,75680249530792825… ≈ −0,76 (не забудьте, что аргументы тригонометрических функций считаются заданными в радианах).
Для функции y = sin 2 x сначала определяем значение синуса 2-ух с помощью калькулятора: sin2 = 0,9092974268256816…, а затем возводим это значение в квадрат sin 2 2 = (0,9092974268256816…) 2 = 0,82682181043180595… ≈ 0,83.
Таким образом, мы сначала вычисляем значение внутренней функции, а затем используем его как аргумент для внешней.
Согласно пятому правилу дифференцирования, при определении производной нужно поступать наоборот – сначала вычислять производную внешней функции по её аргументу, а затем умножать её на производную внутренней.
Как я уже упоминала, в этой операции ошибаются чаще всего. Ошибки могут быть самые разные, распространены следующие три.
1-я ошибка) Можно просто не применить нужное правило, “не заметив”, что функция сложная.
В следующем примере формулы дифференцирования степенной и тригонометрической функций использованы не последовательно, а одновременно, производная неверно вычислена в одно действие.
2-я ошибка) Можно не разобраться, где внутренняя, а где внешняя функции.
В следующем примере показатель степени стоит над x , т.е. над аргументом, поэтому степенная функция внутренняя, а синус внешняя. Ученик воспринял это иначе, решил, что синус в квадрате и допустил ошибку.
Чтобы избавиться от ошибок такого рода, научиться анализировать сложную функцию, отделять внутреннюю от внешней, нужно просто смотреть в каком порядке Вы бы проводили вычисления, и дифференцирование проводить в обратном порядке. При этом можно расставлять отсутствующие скобки, а если всё равно испытываете трудности, то вводить дополнительные обозначения. Что касается степеней, то можно запомнить следующее – над каким обозначением стоит показатель степени, то и является её основанием (возводится в степень).
Пример 12.
Здесь в конце использована тригонометрическая формула для того, чтобы записать ответ в наиболее компактной форме.
Пример 13.
Здесь в конце переставлены сомножители также для того, чтобы записать ответ в более компактной и удобочитаемой форме.
3-я ошибка) Правило используется не до конца
Один раз учли, что функция сложная и хватит. А если функция вложена несколько раз? Например, корень квадратный из суммы двух логарифмов с разными основаниями, первый из которых зависит от sinx , а второй от cosx . Или арктангенс, зависящий от натурального логарифма, который, в свою очередь, зависит от х в квадрате.
Пример 15.
Предыдущий пример демонстрирует выход из положения с помощью введения дополнительных обозначений. Но, на мой взгляд, это всё-таки не самый оптимальный способ для длинных вычислений. Лучший подход к дифференцированию сложной функции – скобки, которые можно дописывать явно или, по мере укрепления навыка, представлять себе мысленно.
Расставляем скобки и постепенно снаружи внутрь раскрываем их. Содержимое очередной скобки является переменной, по которой производится дифференцирование по формуле f u ” ·(u )” . Производную f u ” находим по таблице производных, заменяя в формуле x на u . Если всё сделано правильно, то процесс закончится тем, что содержимое последней, самой внутренней скобки полностью совпадёт с одной из табличных формул для производных.
Содержимое очередной скобки является переменной, по которой производится дифференцирование по формуле f u ” ·(u )” . Производную f u ” находим по таблице производных, заменяя в формуле x на u . Если всё сделано правильно, то процесс закончится тем, что содержимое последней, самой внутренней скобки полностью совпадёт с одной из табличных формул для производных.
PS: В примерах 11 и 14 допущены ошибки, не только упомянутые в комментариях к ним, но ещё по одной стандартной ошибке. Заметили какие?
Есть вопросы? пожелания? замечания?
Обращайтесь –
Внимание, ©mathematichka . Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
4. Производная сложной функции Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме
и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она
выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
Это типичная ошибка, которая встречается на начальном этапе изучения производных,
но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями,
то есть, когда функция имеет вид вроде , то
следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль.
Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как
производную “икса”. Получаем следующие значения производных:
Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где
сплошное нагромождение корней и степеней, как, например, ,
то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Что такое производная? Наглядное объяснение с цветными примерами и графиками.
 Производная – это просто …
Производная – это просто …Краткий обзор
- Производная – это основной инструмент дифференциального исчисления.
- В частности, производная – это функция …
- , что говорит нам о темпах изменения , или …
- уклонов касательных.
- Его определение включает ограничения.2 $$
1 Дифференциация означает нахождение производной.
Два обозначения производной
Производный инструмент сообщает нам о темпах изменения
Пример 1
Предположим, что $$ D (t) $$ – это функция, которая измеряет расстояние до дома (в милях) как функцию времени (в часах).
Тогда $$ D (2) = 5 $$ означает, что вы находитесь в 5 милях от дома по прошествии 2 часов,
и $$ D ‘(2) = 20 $$ говорят нам, что по прошествии 2 часов .
 ..
..$$ \ frac {\ mbox {наше расстояние меняется на 20 миль …}} {\ mbox {за каждый прошедший час.}} = \ frac {\ mbox {20 миль}} {\ mbox {каждый час}} = 20 \ mbox {миль в час.} $$
Итак, $$ D ‘(2) = 20 $$ говорит нам, что по прошествии 2 часов наша скорость составляет 20 миль в час.
Пример 2
Предположим, что $$ C (x) $$ – это стоимость (в долларах) производства $$ x $$ тонн макарон.
Тогда $$ C (30) = 15 {,} 000 $$ говорит нам, что производство 30 тонн макарон будет стоить 15 000 долларов,
а $$ C ‘(30) = 48 {,} 000 $$ говорит нам, что, когда мы производим 30 тонн макарон, связанные с этим расходы увеличиваются со скоростью 48 000 долларов за тонну.

Производная сообщает нам об уклонах касательных линий
Давайте еще раз посмотрим на обозначения Лейбница для производной. Если $$ y = f (x) $$ – наша функция, то производную можно обозначить как
$$ \ frac {dy} {dx} = \ frac {\ mbox {изменение в \ (y \)}} {\ mbox {изменение в \ (x \)}} = \ mbox {наклон линии!} $$
Производные значения – это наклон линий.В частности, это наклон линий, которые касаются и функции. См. Пример ниже.
Пример 3
Предположим, у нас есть функция 2 , где $$ f (2) = 3 $$ и $$ f ‘(2) = 1 $$. Первое уравнение говорит нам, что точка $$ (2,3) $$ находится на графике функции. Второе уравнение сообщает нам наклон касательной, проходящей через эту точку.
Точно так же, как наклон указывает нам направление движения линии, значение производной сообщает нам направление кривой в определенном месте.
 3 $$.
3 $$.Определение производного инструмента
Предположим, у нас есть функция $$ f (x) $$, и мы хотим найти производную. Как мы можем сделать это? Самый простой способ – использовать определение производной:
$$ f ‘(x) = \ displaystyle \ lim_ {h \ to 0} \ frac {f (x + h) – f (x)} h $$
Варианты определения
Есть два популярных варианта приведенного выше определения.Они математически эквивалентны приведенному выше.
- $$ \ displaystyle f ‘(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) – f (x)} {\ Delta x} $$
- $$ \ Displaystyle f ‘(x) = \ lim_ {x \ to a} \ frac {f (x) – f (a)} {x-a} $$
В следующем уроке мы попрактикуемся в дифференцировании функций, используя определение производной.

Ошибка: Нажмите «Не робот» и повторите попытку.
Определение производного инструмента
Определение производного инструментаПроизводная
Концепция Производная лежит в основе Calculus and современная математика. Определение производной может быть подходили двумя разными способами. Один геометрический (в виде ската кривой), а другой физический (как скорость изменения). Исторически существовала (и, возможно, до сих пор) борьба между математики, которые из двух иллюстрируют концепцию производная лучшая и какая из них более полезна.Мы не будем останавливаться на этом и представлю обе концепции. Наш акцент будет об использовании производной в качестве инструмента.
Этот подход был использован Ньютоном при разработке своей Классическая механика. Основная идея – понятие скорости и скорость. Действительно, предположим, что вы путешествуете из точки А в точку Б,
какая средняя скорость во время поездки? Это дается
Действительно, предположим, что вы путешествуете из точки А в точку Б,
какая средняя скорость во время поездки? Это дается
Если теперь предположить, что A и B очень близки друг к другу, мы приблизиться к так называемой мгновенной скорости .Из конечно, если A и B находятся близко друг к другу, то время, которое требуется проехать из А в Б тоже будет невелико. Действительно, предположим, что при время t = a , мы находимся в A. Если время, прошедшее, чтобы добраться до B, равно , тогда мы будем в B в то время . Если расстояние от A до B, тогда средняя скорость является
Мгновенная скорость (в точке A) будет найдена, когда она будет становиться все меньше и меньше. Здесь мы естественным образом сталкиваемся с концепцией предела. Действительно, у нас есть
Если f ( t ) описывает позицию в момент времени t , то .В этом случае мы имеемПример.
 Рассмотрим параболическое движение, заданное функцией f ( т ) = т 2 . Мгновенная скорость при t = a определяется выражением
Рассмотрим параболическое движение, заданное функцией f ( т ) = т 2 . Мгновенная скорость при t = a определяется выражением
С
заключаем, что мгновенная скорость при t = a равна 2 a .Это понятие скорости может быть расширено, чтобы найти скорость изменения любой переменной по отношению к любой другой переменной.Например, объем газа зависит от температуры газа. Таким образом, в данном случае переменными являются V (объем) как функция T (температура). В общем, если у нас есть y = f ( x ), то средняя скорость изменения y по отношению к x с x = a на , куда , является
Как и прежде, мгновенная скорость изменения y относительно до x при x = a , этоОбозначение. Теперь мы переходим к самому сложному.
 Поскольку мы не можем
продолжайте писать “Мгновенная скорость” во время вычислений,
нам нужно придумать для него подходящие обозначения. Если мы напишем dx для
small, то можно использовать обозначение
Поскольку мы не можем
продолжайте писать “Мгновенная скорость” во время вычислений,
нам нужно придумать для него подходящие обозначения. Если мы напишем dx для
small, то можно использовать обозначение
Это обозначение, введенное Лейбницем. (Вильгельм Готфрид Лейбниц (1646-1716) и Исаак Ньютон (1642-1727) считаются изобретатели математического анализа.) Рассмотрим функцию y = f ( x ) и ее график.Напомним, что график функции – это набор точек (то есть ( x , f ( x )) для x из домена функции f ). Мы можем нарисовать график в плоскости с горизонтальной осью (обычно называемой осью x) и вертикальная ось (обычно называемая осью Y).Зафиксируйте точку на графике, скажем ( x 0 , f ( x 0 )). Если граф как геометрическая фигура “хороша” (т.е. гладко) вокруг этой точки, это Естественно спросить, можно ли найти уравнение прямой линия, “касающаяся” графика в этой точке.
 Такая прямая линия
назвал касательную линию в рассматриваемой точке. В
понятие касательной можно рассматривать в более общих рамках.
Такая прямая линия
назвал касательную линию в рассматриваемой точке. В
понятие касательной можно рассматривать в более общих рамках.(Обратите внимание, что касательная линия может не существовать. Мы обсудим это случай позже.) Один из способов найти касательную – рассмотреть точек ( x , f ( x )) на графике, где x очень близко к x 0 .Затем проведите прямую, соединяющую обе точки (см. рисунок ниже):
Как видите, когда x все ближе и ближе к x 0 , линии становятся все ближе и ближе к касательной. Поскольку все эти линии проходят через точку ( x 0 , f ( x 0 )), их уравнения будут определяется путем нахождения их наклона: Наклон линии проходя через точки ( x 0 , f ( x 0 )) и ( x , f ( x )) (где ) дан кем-то
Сама касательная будет иметь уклон м , что очень близко к м ( x ), когда само x очень близко к x 0 . Это
понятие лимита еще раз!
Это
понятие лимита еще раз!Другими словами, у нас есть
Итак, уравнение касательной:Обозначение. Запись “м” для наклона касательной. не несет достаточно информации; мы хотим отслеживать функция f ( x ) и точка x 0 в наших обозначениях. Общее используется обозначение
м = м ‘( x 0 ).
В этом случае уравнение касательной принимает видy – f ( x 0 ) = f ‘( x 0 ) ( x – x 0 )
куда
И последнее замечание: иногда удобнее вычислить ограничивает, когда переменная приближается к нулю. Один из способов сделать это – сделать перевод по оси абсцисс. Действительно, если положить h = x – x 0 , получаем
[Назад] [Следующий] [Тригонометрия] [Исчисление] [Геометрия] [Алгебра] [Дифференциальные уравнения] [Комплексные переменные] [Матричная алгебра] С. Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematicsВам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Мохамед А. Хамси
Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. – П.О. Box 12395 – El Paso TX 79913 – США
пользователь онлайн за последний часПрименений производных инструментов
Последнее обновление 16.07.2021
Производная определяет скорость, с которой одна переменная изменяется по отношению к другой.
Это важная концепция, которая чрезвычайно полезна во многих приложениях: в повседневной жизни производная может сказать вам, с какой скоростью вы движетесь, или помочь вам предсказать колебания на фондовом рынке; в машинном обучении производные важны для оптимизации функций.
В этом руководстве будут рассмотрены различные приложения производных инструментов, начиная с наиболее знакомых, прежде чем перейти к машинному обучению.
 Мы подробнее рассмотрим, что производные говорят нам о различных функциях, которые мы изучаем.
Мы подробнее рассмотрим, что производные говорят нам о различных функциях, которые мы изучаем.В этом руководстве вы познакомитесь с различными приложениями производных финансовых инструментов.
После прохождения этого руководства вы будете знать:
- Использование деривативов можно применить к реальным проблемам, которые мы находим вокруг себя.
- Использование производных очень важно в машинном обучении для оптимизации функций.
Приступим.
Приложения производных инструментов
Обзор руководства
Фотография Девона Янсе ван Ренсбург, некоторые права защищены.Это руководство разделено на две части; их:
- Применение производных финансовых инструментов в реальной жизни
- Применение производных в алгоритмах оптимизации
Мы видели, что производные финансовые инструменты моделируют скорость изменения.

Деривативы отвечают на такие вопросы, как «Как быстро?» “Насколько круто?” и “Насколько чувствительны?” Это все вопросы о темпах изменений в той или иной форме.
– стр. 141, Infinite Powers, 2019.
Эта скорость изменения обозначается как y / 𝛿 x , что определяет изменение зависимой переменной 𝛿 y по отношению к изменению независимой переменной 𝛿 x .
Давайте начнем с одного из самых известных приложений производных финансовых инструментов, которые мы можем найти вокруг себя.
Каждый раз, садясь в машину, вы становитесь свидетелем дифференциации.
– Стр. 178, Исчисление для чайников, 2016.
Когда мы говорим, что автомобиль движется со скоростью 100 километров в час, мы просто указываем скорость его изменения. Общий термин, который мы часто используем, – это скорость или скорость , хотя было бы лучше сначала провести различие между ними.
В повседневной жизни мы часто используем скорость и скорость как взаимозаменяемые, если мы описываем скорость изменения движущегося объекта.Однако это математически неверно, потому что скорость всегда положительна, тогда как скорость вводит понятие направления и, следовательно, может иметь как положительные, так и отрицательные значения. Следовательно, в следующем объяснении мы будем рассматривать скорость как более техническую концепцию, определяемую как:
скорость = 𝛿 y / 𝛿 т
Это означает, что скорость дает изменение положения автомобиля 𝛿 y за интервал времени 𝛿 t . Другими словами, скорость – это первая производная положения по времени.
Скорость автомобиля может оставаться постоянной, например, если машина постоянно едет со скоростью 100 километров в час, или она также может изменяться в зависимости от времени. В последнем случае это означает, что функция скорости сама по себе изменяется как функция времени, или, проще говоря, автомобиль можно назвать , ускоряющимся на . Ускорение определяется как первая производная скорости v и вторая производная положения y по времени:
ускорение = 𝛿 v / 𝛿 t = 𝛿 2 y / 𝛿 t 2
Мы можем построить графики кривых положения, скорости и ускорения, чтобы лучше их визуализировать.Предположим, что положение вагона как функция времени задается следующим образом: y ( t ) = t 3 – 8 t 2 + 40 t :
Линейный график положения автомобиля относительно времени
График показывает, что положение автомобиля в начале пути изменяется медленно, немного замедляясь примерно до t = 2,7 с, после чего скорость его изменения увеличивается и продолжает увеличиваться до конца поездки.Это изображено на графике скорости автомобиля:
График зависимости скорости автомобиля от времени
Обратите внимание, что автомобиль сохраняет положительную скорость на протяжении всей поездки, потому что он никогда не меняет направление. Следовательно, если бы нам пришлось представить себя сидящими в этой движущейся машине, спидометр показал бы нам значения, которые мы только что нанесли на график скорости (поскольку скорость остается положительной на всем протяжении, в противном случае нам пришлось бы найти абсолютное значение скорость, чтобы выработать скорость).Если бы нам пришлось применить правило мощности к y ( t ), чтобы найти его производную, то мы бы обнаружили, что скорость определяется следующей функцией:
v ( т ) = т ’( т ) = 3 т 2 -16 т + 40
Мы также можем построить график ускорения:
Линейный график разгона автомобиля от времени
Мы находим, что график теперь характеризуется отрицательным ускорением во временном интервале t = [0, 2.7) секунды. Это связано с тем, что ускорение является производной скорости, и в течение этого временного интервала скорость автомобиля уменьшается. Если бы нам снова пришлось применить правило мощности к v ( t ), чтобы найти его производную, то мы бы обнаружили, что ускорение определяется следующей функцией:
a ( т ) = v ’( т ) = 6 т – 16
Собирая вместе все функции, получаем:
y ( т ) = т 3 – 8 т 2 + 40 т
v ( т ) = т ’( т ) = 3 т 2 -16 т + 40
a ( т ) = v ’( т ) = 6 т – 16
Если мы подставим вместо t = 10 с, мы сможем использовать эти три функции, чтобы определить, что к концу поездки автомобиль проехал 600 м, его скорость составляет 180 м / с, а скорость – 44 м / с. 2 .Мы можем убедиться, что все эти значения соответствуют графикам, которые мы только что построили.
Мы рассмотрели этот конкретный пример в контексте определения скорости и ускорения автомобиля. Но существует множество реальных явлений, которые меняются со временем (или переменных, отличных от времени), которые можно изучать, применяя концепцию производных, как мы только что сделали для этого конкретного примера. Назову несколько:
- Скорость роста популяции (будь то совокупность людей или колония бактерий) с течением времени, которую можно использовать для прогнозирования изменений численности популяции в ближайшем будущем.
- Изменения температуры в зависимости от местоположения, которые можно использовать для прогнозирования погоды.
- Колебания фондового рынка во времени, которые можно использовать для прогнозирования будущего поведения фондового рынка.
Производные также предоставляют важную информацию при решении задач оптимизации, как мы увидим дальше.
Применение производных в алгоритмах оптимизацииМы уже видели, что алгоритм оптимизации, такой как градиентный спуск, стремится достичь глобального минимума функции ошибки (или стоимости) путем применения производных.
Давайте подробнее рассмотрим, что производные говорят нам о функции ошибок, выполнив то же упражнение, что и в примере с автомобилем.
Для этого рассмотрим следующую одномерную тестовую функцию для оптимизации функции:
f ( x ) = – x sin ( x )
Мы можем применить правило произведения к f ( x ), чтобы найти его первую производную, обозначенную f ‘( x ), а затем снова применить правило произведения к f ‘ ( x ), чтобы найти вторую производную, обозначенную как f ” ( x ):
f ’( x ) = -sin ( x ) – x cos ( x )
f ’’ ( x ) = x sin ( x ) – 2 cos ( x )
Мы можем построить эти три функции для разных значений x , чтобы визуализировать их:
Линейный график функции, f ( x ), его первая производная, f ‘( x ), и его вторая производная, f ” ( x )
Подобно тому, что мы наблюдали ранее для примера с автомобилем, график первой производной показывает, как изменяется f ( x ) и насколько.Например, положительная производная указывает, что f ( x ) является возрастающей функцией, тогда как отрицательная производная говорит нам, что f ( x ) теперь уменьшается. Следовательно, если при поиске минимума функции алгоритм оптимизации выполняет небольшие изменения входных данных в зависимости от скорости обучения, ε:
x_new = x – ε f ’( x )
Затем алгоритм может уменьшить f ( x ) путем перемещения в противоположном направлении (путем инвертирования знака) производной.
Нам также может быть интересно найти вторую производную функции.
Мы можем рассматривать вторую производную как измерение кривизны.
– стр. 86, Глубокое обучение, 2017.
Например, если алгоритм достигает критической точки, в которой первая производная равна нулю, он не может отличить эту точку от локального максимума, локального минимума, седловой точки или плоской области на основе f ‘( x ) в одиночку.Однако, когда вмешивается вторая производная, алгоритм может сказать, что рассматриваемая критическая точка является локальным минимумом, если вторая производная больше нуля. Для локального максимума вторая производная меньше нуля. Следовательно, вторая производная может сообщить алгоритму оптимизации, в каком направлении двигаться. К сожалению, этот тест остается безрезультатным для седловых точек и плоских участков, для которых вторая производная равна нулю в обоих случаях.
Алгоритмы оптимизации, основанные на градиентном спуске, не используют производные второго порядка и поэтому известны как алгоритмы оптимизации первого порядка .Алгоритмы оптимизации, такие как метод Ньютона, которые используют использование вторых производных, иначе называются алгоритмами оптимизации второго порядка .
Дополнительная литература
В этом разделе представлены дополнительные ресурсы по теме, если вы хотите углубиться.
Книги
Сводка
В этом руководстве вы открыли для себя различные применения производных финансовых инструментов.
В частности, вы узнали:
- Использование деривативов можно применить к реальным проблемам, которые мы находим вокруг себя.
- Использование производных очень важно в машинном обучении для оптимизации функций.
Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.Производные (математика) Факты для детей
Функция (черный) и касательная (красный). Производная в точке – это наклон касательной.В математике (особенно в дифференциальном исчислении) производная – это способ показать мгновенную скорость изменения: то есть величину, на которую функция изменяется в одной заданной точке.Для функций, которые действуют на действительные числа, это наклон касательной в точке на графике. Производная часто записывается как [math] \ tfrac {dy} {dx} [/ math] («dy over dx», что означает разницу по y, деленную на разницу по x). d не является переменной и поэтому не может быть отменен. Другое распространенное обозначение – [math] f ‘(x) [/ math] – производная функции [math] f [/ math] в точке [math] x [/ math]. [1] [2] [3]
Определение производного инструмента
Анимация, дающая интуитивное представление о производной, поскольку “качели” функции меняются при изменении аргумента.Производная y по x определяется как изменение y по сравнению с изменением x, поскольку расстояние между [math] x_0 [/ math] и [math] x_1 [/ math] становится бесконечно малым (бесконечно малым). С математической точки зрения: [2] [3]
- [математика] f ‘(a) = \ lim_ {h \ to 0} {\ frac {f (a + h) -f (a)} {h}} [/ math]
То есть, как расстояние между двумя точками x (h) становится ближе к нулю, наклон линии между ними приближается к касательной.
Производные функций
Линейные функции
Производные линейных функций (функции вида [math] mx + c [/ math] без квадратичных или более высоких членов) постоянны. То есть производная в одном месте графика останется неизменной в другом.
Когда зависимая переменная [math] y [/ math] напрямую принимает значение [math] x [/ math] ([math] y = x [/ math]), наклон линии равен 1 во всех местах. , поэтому [math] \ tfrac {d} {dx} (x) = 1 [/ math] независимо от того, где находится позиция.2} [/ math]
Логарифмические функции
Производная от логарифмов является обратной величиной: [2]
- [математика] \ frac {d} {dx} \ ln (x) = \ frac {1} {x} [/ math].
Возьмем, например, [math] \ frac {d} {dx} \ ln \ left (\ frac {5} {x} \ right) [/ math]. Это можно свести к (по свойствам логарифмов):
- [math] \ frac {d} {dx} (\ ln (5)) – \ frac {d} {dx} (\ ln (x)) [/ math]
Логарифм 5 является константой , поэтому его производная равна 0.Производная от [math] \ ln (x) [/ math] равна [math] \ tfrac {1} {x} [/ math]. Так,
- [math] 0 – \ frac {d} {dx} \ ln (x) = – \ frac {1} {x} [/ math]
Для производных от логарифмов не по основанию e , например [math] \ tfrac {d} {dx} (\ log_ {10} (x)) [/ math], это можно сократить до:
- [математика] \ frac {d} {dx} \ log_ {10} (x) = \ frac {d} {dx} \ frac {\ ln {x}} {\ ln {10}} = \ frac { 1} {\ ln {10}} \ frac {d} {dx} \ ln {x} = \ frac {1} {x \ ln (10)} [/ math]
Тригонометрические функции
Функция косинуса является производной функции синуса, а производная косинуса – отрицательным синусом (при условии, что x измеряется в радианах): [2]
- [математика] \ frac {d} {dx} \ sin (x) = \ cos (x) [/ math]
- [математика] \ frac {d} {dx} \ cos (x) = – \ sin (x) [/ math]
- [математика] \ frac {d} {dx} \ sec (x) = \ sec (x) \ tan (x) [/ math].5 + 2x \, [/ math]
Использование производных
Производная функции может использоваться для поиска максимумов и минимумов функции путем поиска мест, где ее наклон равен нулю.
Производные используются в методе Ньютона, который помогает найти нули (корни) функции. Можно также использовать производные для определения вогнутости функции и определения того, увеличивается или уменьшается функция.
Связанные страницы
Список литературы
- ↑ «Список символов исчисления и анализа» (на английском языке).2020-05-11. https://mathvault.ca/hub/higher-math/math-symbols/calculus-analysis-symbols/.
- ↑ 2,0 2,1 2,2 2,3 2,4 Вайсштейн, Эрик В. «Производная» (на английском языке). https://mathworld.wolfram.com/Derivative.html.
- ↑ 3,0 3,1 «Значение производной – подход к исчислению». https://themathpage.com/aCalc/derivative.htm.
Другие сайты
Исчисление I – правило цепочки
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с “узкой” шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-9: Правило цепочки
В течение последних нескольких разделов мы использовали множество производных финансовых инструментов. {- \ frac {1} {2}}} = \ frac {1} {{2 \ sqrt {5z – 8 }}} \]
, которая не является производной, которую мы вычислили с использованием определения.Это близко, но это не то же самое. Таким образом, одно правило мощности просто не сработает, чтобы получить здесь производную.
Давайте продолжим смотреть на эту функцию и заметим, что если мы определим,
\ [f \ left (z \ right) = \ sqrt z \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} g \ left (z \ right) = 5z – 8 \], тогда мы можем записать функцию как композицию.
\ [R \ left (z \ right) = \ left ({f \ circ g} \ right) \ left (z \ right) = f \ left ({g \ left (z \ right)} \ right) = \ sqrt {5z – 8} \], и оказывается, что на самом деле довольно просто дифференцировать композицию функций с помощью правила цепочки .Есть две формы цепного правила. Они здесь.
Правило цепочки
Предположим, что у нас есть две функции \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \), и обе они дифференцируемы.
- Если мы определим \ (F \ left (x \ right) = \ left ({f \ circ g} \ right) \ left (x \ right) \), то производная от \ (F \ left (x \ right )\) является, \ [F ‘\ left (x \ right) = f’ \ left ({g \ left (x \ right)} \ right) \, \, \, g ‘\ left (x \ right) \]
- Если у нас есть \ (y = f \ left (u \ right) \) и \ (u = g \ left (x \ right) \), то производная от \ (y \) равна, \ [\ frac {{dy}} {{dx}} = \ frac {{dy}} {{du}} \, \, \ frac {{du}} {{dx}} \]
У каждой из этих форм есть свое применение, однако мы будем работать в основном с первой формой в этом классе.Чтобы увидеть доказательство правила цепочки, см. Раздел «Доказательство различных формул производных» в главе «Дополнительные возможности».
Теперь давайте вернемся и применим правило цепочки к функции, которую мы использовали, когда открывали этот раздел. {{\ mbox {производная от}} \ atop {\ mbox {external function}}} \, \ , \, \ underbrace {\, \, \, \, \ left (5 \ right) \, \, \, \,} _ {{\ mbox {производная от}} \ atop {\ mbox {внутри функции}} } \]
В общем, именно так мы думаем о цепном правиле.Мы идентифицируем «внутреннюю функцию» и «внешнюю функцию». Затем мы дифференцируем внешнюю функцию, оставляя только внутреннюю функцию, и умножаем все это на производную внутренней функции. В общем виде это
\ [F ‘\ left (x \ right) = \ underbrace {\, \, \, \, \, f’ \, \, \, \, \,} _ {{\ mbox {производная от}} \ наверху {\ mbox {вне функции}}} \, \, \, \, \ underbrace {\, \, \ left ({g \ left (x \ right)} \ right) \, \,} _ {{\ mbox {внутри функции}} \ atop {\ mbox {left alone}}} \, \, \, \, \, \ underbrace {\, \, \, g ‘\ left (x \ right) \, \, \, } _ {{\ mbox {производная по разам}} \ atop {\ mbox {внутренней функции}}} \]Мы всегда можем определить «внешнюю функцию» в приведенных ниже примерах, задав себе вопрос, как бы мы оценили эту функцию.Например, в случае \ (R \ left (z \ right) \), если бы мы спросили себя, что такое \ (R \ left (2 \ right) \), мы сначала оценили бы материал под радикалом, а затем, наконец, возьмем квадратный корень из этого результата. Квадратный корень – это последняя операция, которую мы выполняем при оценке, и это также внешняя функция. Внешняя функция всегда будет последней операцией, которую вы бы выполнили, если бы собирались оценить функцию.
Давайте взглянем на несколько примеров правила цепочки.2} + 9}} \) Показать решение
Идентифицировать внешнюю функцию в двух предыдущих было довольно просто, поскольку в некотором смысле это действительно была «внешняя» функция. В этом случае нужно быть немного осторожнее. Напомним, что внешняя функция – это последняя операция, которую мы выполняем при оценке. В этом случае, если бы мы оценили эту функцию, последняя операция была бы экспоненциальной. Следовательно, внешняя функция – это экспоненциальная функция, а внутренняя функция – ее показатель.4}}} \]
Снова не забудьте оставить внутреннюю функцию в покое при дифференцировании внешней функции. Таким образом, после дифференцирования логарифма мы получаем не 1 / \ (x \), а вместо этого 1 / (внутренняя функция).
e \ (y = \ sec \ left ({1 – 5x} \ right) \) Показать решениеВ этом случае внешняя функция – секущая, а внутренняя – \ (1 – 5x \).
\ [\ begin {align *} y ‘& = \ sec \ left ({1 – 5x} \ right) \ tan \ left ({1 – 5x} \ right) \ left ({- 5} \ right) \\ & = – 5 \ сек \ left ({1 – 5x} \ right) \ tan \ left ({1 – 5x} \ right) \ end {align *} \]В этом случае производная внешней функции равна \ (\ sec \ left (x \ right) \ tan \ left (x \ right) \).4}} \ right) \) Показать решение
У этой проблемы есть два момента. Во-первых, есть два термина, и для каждого из них потребуется различное применение цепного правила. Так будет часто, поэтому не ожидайте, что при решении этих задач будет применяться только одно цепочечное правило. 4} \]
Итак, в первом члене внешняя функция – это показатель степени 4, а внутренняя функция – это косинус.{g \ left (x \ right)}} \]
c Внешняя функция – это логарифм, а внутренняя – \ (g \ left (x \ right) \).
\ [f ‘\ left (x \ right) = \ frac {1} {{g \ left (x \ right)}} g’ \ left (x \ right) = \ frac {{g ‘\ left (x \ right)}} {{g \ left (x \ right)}} \]Формулы в этом примере на самом деле являются просто частными случаями правила цепочки, но их полезно запомнить, чтобы быстро выполнить некоторые из этих производных.
А теперь давайте не будем забывать и о других правилах, которые у нас есть для работы с производными финансовыми инструментами.2}}} \) Показать решение
Прежде всего отметим, что эта проблема – это, прежде всего, проблема правил продукта. Это произведение двух функций: арктангенса и корня, поэтому первое, что нам нужно сделать при взятии производной, – это использовать правило произведения. z}} \ right] \]
В данном случае мы еще не производили внутреннюю производную.2}}}} \ right] \ end {align *} \]
Как и во второй части выше, мы изначально не дифференцировали внутреннюю функцию на первом шаге, чтобы было ясно, что с этого момента она будет правилом частного.
В последнем примере было несколько точек. Во-первых, не следует забывать, что у нас все еще есть другие правила для деривативов, которые иногда могут понадобиться. Тот факт, что у нас теперь есть правило цепочки, не означает, что правило произведения и частного больше не понадобится.
Кроме того, как проиллюстрировано в последнем примере, порядок, в котором они выполняются, также будет меняться. Некоторые проблемы будут связаны с правилом продукта или правилом частного, которые связаны с цепным правилом. Однако другие проблемы потребуют сначала использования правила цепочки, а в процессе этого нам нужно будет использовать правило продукта и / или частного.
В большинстве примеров в этом разделе не используются правила продукта или частного, чтобы сделать задачи немного короче.{- 9z}}} \ right) \]
Обратите внимание, что мы еще не сделали производную внутренней функции. Это сделано для того, чтобы мы могли заметить, что когда мы действительно дифференцируем второй член, нам снова потребуется правило цепочки. Также обратите внимание, что нам понадобится только цепное правило для экспоненты, а не для первого члена. Во многих функциях мы будем использовать правило цепочки более одного раза, поэтому не волнуйтесь, когда это произойдет.
Давайте продолжим и закончим этот пример.{1 – t}} + 3 \ sin \ left ({6t} \ right)} \ right) \ end {align *} \]
Для выполнения этой задачи требовалось в общей сложности 4 правила цепочки.
Иногда это может быть довольно неприятно и требует многократного применения правила цепочки. Вначале в таких случаях обычно лучше проявлять осторожность, как мы это делали в предыдущем наборе примеров, и выписывать пару дополнительных шагов, а не пытаться сделать все за один шаг в уме. Как только вы научитесь лучше разбираться в цепном правиле, вы обнаружите, что можете довольно быстро делать это в уме.x} \ ln \ left (a \ right) \]
Итак, неплохо, если вы видите трюк с переписыванием \ (a \) с использованием правила цепочки.
Производнаяпо первому принципу | Блестящая вики по математике и науке
Рассмотрим функцию f: [a, b] → R, f: [a, b] \ rightarrow \ mathbb {R}, f: [a, b] → R, где a, b∈R a, b \ in \ mathbb {R} a, b∈R. Как правило, производная определяется только для значений в интервале (a, b) (a, b) (a, b). Пусть c∈ (a, b) c \ in (a, b) c∈ (a, b) – число, при котором должна измеряться скорость изменения.
Сначала рассмотрим интервал (c, c + ϵ), (c, c + \ epsilon), (c, c + ϵ), где ϵ \ epsilon ϵ – число, произвольно близкое к нулю. Пусть 0 <δ <ϵ 0 <\ delta <\ epsilon 0 <δ <ϵ.
Скорость изменения (m) (m) (m) определяется как f (x2) −f (x1) x2 − x1 \ frac {f (x_2) – f (x_1)} {x_2 – x_1} x2 −x1 F (x2) −f (x1). Таким образом, для данного значения δ \ delta δ скорость изменения от c cc до c + δ c + \ delta c + δ может быть задана как
m = f (c + δ) −f (c) (c + δ) −c. m = \ frac {f (c + \ delta) – f (c)} {(c + \ delta) – c}.-} \ frac {f (c + h) – f (c)} {h} .m− = h → 0 − lim hf (c + h) −f (c).
Говорят, что функция fff выводится в ccc, если m + = m− m_ + = m_- m + = m−. Равное значение называется производной fff при ccc.
Предел limh → 0f (c + h) −f (c) h \ lim_ {h \ to 0} \ frac {f (c + h) – f (c)} {h} limh → 0 hf (c + h) −f (c), если он существует (в соответствии с приведенными выше условиями), является производной от fff в точке ccc, и метод нахождения производной с помощью такого предела называется производной по первому принципу .
Часто предел также выражается как ddxf (x) = limx → cf (x) −f (c) x − c \ frac {\ text {d}} {\ text {d} x} f (x ) = \ lim_ {x \ to c} \ frac {f (x) – f (c)} {xc} dxd f (x) = limx → c x − cf (x) −f (c).
Математических изображений | Полиномиальные функции и производная (3): Кубические функции
Кубическая функция – это полиномиальная функция степени 3.
Многочлены степени 3 – это кубические функции. Реальная кубическая функция всегда пересекает ось x хотя бы один раз.
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ
Производная функции в точке может быть определена как мгновенная скорость изменения или как наклон касательной линии к график функции в этой точке.Можно сказать, что этот наклон касательной функции в точке – это наклон функция.
Наклон функции, как правило, зависит от x. Тогда, начиная с функции, мы можем получить новую функцию, производную функцию исходной функции.
Процесс нахождения производной функции называется дифференцированием.
Значение производной функции для любого значения x – это наклон исходной функции в точке x.
Чтобы найти производную в точке, мы можем провести касательную линию к графику кубической функции в этой точке:
Но как провести касательную?Мы можем использовать увеличительное стекло !. Если мы посмотрим очень близко к точке на графике функции, мы увидим, как функция похожа на касательную. Эта касательная линия является наилучшим линейным приближением функции в этой точке:
Затем мы можем провести параллельную линию к этой касательной через значение x-1, и мы получим прямоугольный треугольник:
Производная кубической функции – квадратичная функция.
Критическая точка – это точка, в которой касательная параллельно оси x, это означает, что наклон касательная в этой точке равна нулю.
В следующем примере мы видим кубическую функцию с двумя критическими точками. Один – это локальный максимум, а другой – местный минимум. В этих точках производная функция (парабола) пересекает ось абсцисс:
Эти критические точки – это точки, в которых функция перестает увеличиваться или уменьшаться (иногда их называют «стационарные точки»). В этих точках касательная горизонтальна.
Чтобы найти стационарные точки, решаем квадратное уравнение:
В этом случае решениями этого уравнения являются:
Как мы уже знаем (квадратичные функции), иногда квадратное уравнение не имеет реальных решений.(парабола не пересекает ось абсцисс). Тогда кубическая функция не имеет критических точек:
Но у параболы всегда есть вершина. Вершина параболы связана с точкой кубической функции. Мы называем это точка перегиба.
Точка перегиба кубической функции – это единственная точка на графике, где изменяется вогнутость.
Кривая меняется с вогнутой вверх вогнуться вниз или наоборот
Касательная к кубической функции в точке перегиба пересекает график:
Чтобы найти точку перегиба, мы можем вычислить вершину параболы:
Это пример точки перегиба кубической функции без критических точек:
Точка перегиба в этом случае также является точкой покоя (вершина производной касается оси x):
Точки перегиба могут быть стационарными, но не локальными максимумами или локальными минимумами.
Одна простая и интересная идея заключается в том, что когда мы переводим график функции вверх и вниз (мы добавляем или вычитаем число из исходной функции) производная не меняется.Причина очень интуитивна. Когда ты переместите фиолетовую точку, которую вы переводите вверх и вниз по графику, и производная будет такой же:
Важно отметить, что производная многочлена степени 1 является постоянной функцией (многочленом степени 0). Производная полинома степени 2 – это многочлен степени 1. А производная полинома 3-й степени есть полином 2-й степени.
Когда мы получить такую полиномиальную функцию, результатом будет многочлен, степень которого на 1 меньше, чем у исходной функции.
Изучая интеграл от многочлена степени 2, мы видим, что в этом случае новая функция является многочленом степени 2. Еще на одну степень чем исходная функция. А интеграл полиномиальной функции – это полиномиальная функция степени 1 больше, чем исходная функция.
Эти результаты связаны с основной теоремой исчисления.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
Майкл Спивак, Calculus, Third Edition, Publish-or-Perish, Inc.
Том М.Апостол, Исчисление, второе издание, John Willey and Sons, Inc.
Гельфанд И. Глаголева, Е.Е.Шноль, “ Функции и графы ”, Dover Publications, Mineola, N.Y.
СЛЕДУЮЩИЙ
Многочлены Лагранжа – это многочлены, проходящие через n заданных точек. Мы используем полиномы Лагранжа, чтобы исследовать общую полиномиальную функцию и ее производную.
ПРЕДЫДУЩАЯ
Производная квадратичной функции – это линейная функция, то есть прямая линия.
БОЛЬШЕ ССЫЛКИ
Производная линейной функции – постоянная функция.
Если производная от F (x) равна f (x), то мы говорим, что неопределенный интеграл от f (x) относительно x равен F (x). Мы также говорим, что F – первообразная или примитивная функция от f.
Две точки определяют прямую линию. Как функцию мы называем это линейной функцией. Мы можем видеть наклон линии и то, как мы можем получить уравнение прямой через две точки.Мы также изучаем точки пересечения по оси x и оси y линейного уравнения.
Степень с натуральными показателями – простые и важные функции. Их обратные функции – это степени с рациональными показателями (радикал или корень n-й степени)
Многочлены степени 2 – это квадратичные функции. Их графики – параболы. Чтобы найти точки пересечения по оси x, мы должны решить квадратное уравнение. Вершина параболы – это максимум минимума функции.
Многочлены степени 3 – это кубические функции.Реальная кубическая функция всегда пересекает ось x хотя бы один раз.
Мы можем рассматривать полиномиальную функцию, проходящую через серию точек плоскости. Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
В качестве введения в кусочно-линейные функции мы изучаем линейные функции, ограниченные открытым интервалом: их графики подобны отрезкам.
Кусочная функция – это функция, которая определяется несколькими подфункциями.Если каждый кусок является постоянной функцией, то кусочная функция называется кусочно-постоянной функцией или ступенчатой функцией.
Непрерывная кусочно-линейная функция определяется несколькими отрезками или лучами, соединенными без скачков между ними.
Интегральное понятие ассоциируется с понятием площади. Мы начали рассматривать область, ограниченную графиком функции и осью абсцисс между двумя вертикальными линиями.
Монотонные функции на отрезке интегрируемы.В этих случаях мы можем ограничить ошибку, которую мы допускаем при приближении интеграла с помощью прямоугольников.
Если мы рассматриваем нижний предел интегрирования a как фиксированный и если мы можем вычислить интеграл для различных значений верхнего предела интегрирования b, то мы можем определить новую функцию: неопределенный интеграл от f.
Подсчитать площадь под прямой несложно. Это первый пример интеграции, который позволяет нам понять идею и ввести несколько основных понятий: интегральное как область, пределы интеграции, положительные и отрицательные области.
Вычислить площадь по параболе сложнее, чем вычислить площадь по линейной функции. Мы покажем, как аппроксимировать эту область с помощью прямоугольников и что интегральная функция многочлена степени 2 является многочленом степени 3.
Мы можем увидеть некоторые основные понятия об интегрировании, применяемые к общей полиномиальной функции. Интегральные функции от полиномиальных функций – это полиномиальные функции с одной степенью выше, чем исходная функция.
Фундаментальная теорема исчисления говорит нам, что каждая непрерывная функция имеет первообразную, и показывает, как построить ее с помощью интеграла.
Вторая основная теорема исчисления – мощный инструмент для вычисления определенного интеграла (если мы знаем первообразную функции).
Увеличивая степень, полином Тейлора все больше и больше приближает экспоненциальную функцию.
Увеличивая степень, полином Тейлора все больше и больше приближает функцию синуса.
Функция не определена для значений меньше -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Эта функция имеет две действительные особенности в точках -1 и 1.Многочлены Тейлора аппроксимируют функцию в интервале с центром в центре ряда. Его радиус – это расстояние до ближайшей особенности.
Это непрерывная функция, не имеющая реальных особенностей. Однако ряд Тейлора приближает функцию только в интервале. Чтобы понять это поведение, мы должны рассмотреть сложную функцию.
Комплексный полином степени 3 имеет три корня или ноль.
.




 ..
..
 3 $$.
3 $$.
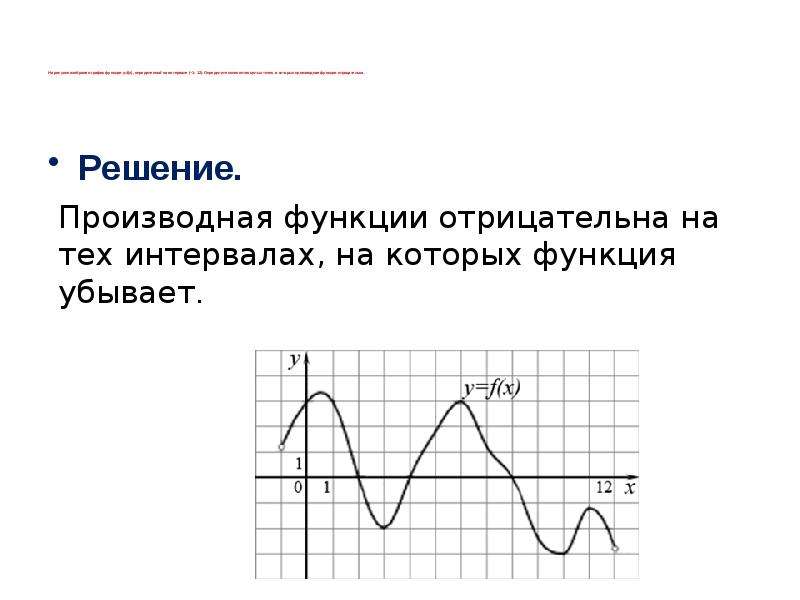 Действительно, предположим, что вы путешествуете из точки А в точку Б,
какая средняя скорость во время поездки? Это дается
Действительно, предположим, что вы путешествуете из точки А в точку Б,
какая средняя скорость во время поездки? Это дается  Рассмотрим параболическое движение, заданное функцией f ( т ) = т 2 . Мгновенная скорость при t = a определяется выражением
Рассмотрим параболическое движение, заданное функцией f ( т ) = т 2 . Мгновенная скорость при t = a определяется выражением  Поскольку мы не можем
продолжайте писать “Мгновенная скорость” во время вычислений,
нам нужно придумать для него подходящие обозначения. Если мы напишем dx для
small, то можно использовать обозначение
Поскольку мы не можем
продолжайте писать “Мгновенная скорость” во время вычислений,
нам нужно придумать для него подходящие обозначения. Если мы напишем dx для
small, то можно использовать обозначение  Такая прямая линия
назвал касательную линию в рассматриваемой точке. В
понятие касательной можно рассматривать в более общих рамках.
Такая прямая линия
назвал касательную линию в рассматриваемой точке. В
понятие касательной можно рассматривать в более общих рамках. Это
понятие лимита еще раз!
Это
понятие лимита еще раз! Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematics Мы подробнее рассмотрим, что производные говорят нам о различных функциях, которые мы изучаем.
Мы подробнее рассмотрим, что производные говорят нам о различных функциях, которые мы изучаем.