Что такое производная в математике простыми словами: Производная простыми словами - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Что такое дифференцирование простым языком

Содержание

Дифференцирование
Смотреть что такое «Дифференцирование» в других словарях:
Производная
Понятие производной
Геометрический смысл производной функции
Физический смысл производной функции
Таблица производных функций
Как пользоваться этой таблицей?
Как найти производную?
Сложные функции — примеры
(u (v))´ = u´ (v) * v´
Как определить знак производной?
Вторая производная
Что такое композиция функций?
ДИФФЕРЕНЦИРОВАНИЕ
Смотреть что такое «ДИФФЕРЕНЦИРОВАНИЕ» в других словарях:
ДИФФЕРЕНЦИРОВАНИЕ
Смотреть что такое «ДИФФЕРЕНЦИРОВАНИЕ» в других словарях:
Дифференцирование
Смотреть что такое «Дифференцирование» в других словарях:
Видео

Дифференцирование

Под термином дифференцирование могут подразумевать различные родственные понятия.

Список значений слова или словосочетания со ссылками на соответствующие статьи.

Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью.

Смотреть что такое «Дифференцирование» в других словарях:

ДИФФЕРЕНЦИРОВАНИЕ — 1) в высшей математ. производство математического анализа посредством дифференциального исчисления; 2) д. или дифференциация разделение одного сложного целого на части, характеризующиеся разными признаками; выделение самостоятельных частей.… … Словарь иностранных слов русского языка

ДИФФЕРЕНЦИРОВАНИЕ — операция нахождения производных или дифференциалов. См. Дифференциальное исчисление … Большой Энциклопедический словарь

ДИФФЕРЕНЦИРОВАНИЕ — ДИФФЕРЕНЦИРОВАНИЕ, в математике метод оценки производной некоторой данной функции. Методики ИНТЕГРИРОВАНИЯ и дифференцирования вместе составляют предмет ИСЧИСЛЕНИЙ и находят широкое применение почти во всех областях ПРИКЛАДНОЙ МАТЕМАТИКИ. см.… … Научно-технический энциклопедический словарь

дифференцирование — ДИФФЕРЕН ИРОВАТЬ, рую, руешь; анный; сов. и несов., что. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

дифференцирование — сущ., кол во синонимов: 6 • дифференциация (11) • дифференцировка (2) • разграни … Словарь синонимов

ДИФФЕРЕНЦИРОВАНИЕ — Расчленение, различение, выделение составляющих элементов при рассмотрении, изучении производственных процессов, экономических явлений, тенденций и т.д. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов

дифференцирование — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN differentiation … Справочник технического переводчика

ДИФФЕРЕНЦИРОВАНИЕ — кольца отображение дкольца Rв себя, ( являющееся эндоморфизмом аддитивной группы кольца Rи удовлетворяющее соотношению Пусть М левый R модуль. Дифференцированием кольца Л со значениями в Мназ. гомоморфизм соответствующих аддитивных групп,… … Математическая энциклопедия

дифференцирование — я; ср. кого что. к Дифференцировать и Дифференцироваться. Д. цен. Д. дохода. * * * дифференцирование операция нахождения производных или дифференциалов. См. Дифференциальное исчисление. * * * ДИФФЕРЕНЦИРОВАНИЕ ДИФФЕРЕНЦИРОВАНИЕ, операция… … Энциклопедический словарь

дифференцирование — diferencijavimas statusas T sritis fizika atitikmenys: angl. differentiation vok. Differentiation, f rus. дифференцирование, n pranc. différentiation, f … Fizikos terminų žodynas

Источник

Производная

Понятие производной

Производная функции − это результат дифференцирования функции.

Дифференцирование в математике — это процесс, при котором функция f превращается в другую функцию f’ («производная от f»).

Простыми словами, производная — это средний наклон между двумя точками:

Интегрирование — это обратный процесс, т. е. восстановление функции по данной производной.

Например, функция x² (на графике выше) является одним из интегралов от 2x (пунктирная синяя линия), поскольку производная x² равна 2x.

Геометрический смысл производной функции

Производная функции f(x) в данной точке — это наклон касательной f(x) в точке a, как показано на рисунке.

Эта прямая линия образует угол, который на данном рисунке мы назвали β и он зависит от наклона касательной (она является производной в данной точке). Таким образом: tan β = f´(a).

Физический смысл производной функции

Представьте точку, которая движется по прямой с постоянно меняющейся скоростью. Её скорость постоянно меняется, поэтому она рассчитывается в момент «t0». Для этого нам нужно рассчитать короткий промежуток времени Δt, а расстояние, которое точка пройдёт за это время будет ΔS.

Таким образом её скорость будет примерно ΔS / Δt. Чем меньше промежуток времени Δt, тем точнее будет результат (скорость). Самую точную мгновенную скорость точки в момент t0 можно получить, если рассчитать предел Δt —>0. Таким образом:

Таблица производных функций

Как пользоваться этой таблицей?

Например, производная линейной функции a*x равна константе, стоящей вместе с переменной x, т. е.: (а*x)′ = а.

Или нужно найти производную функции f(x) = 2 cos x:

f’(x) = (2 cos x)’ = 2 (cos x)’ = 2 (– sin x) = –2 sin x

Как найти производную?

Пример 1

Степень от x спускается и из неё нужно вычесть 1.

Пример 2

f'(x) = 3*3x² – 2*5x¹ + 6 − 0

Пример 3

Нужно сначала раскрыть скобки:

Теперь можно приступать к поиску производной, как и в предыдущих примерах степень от x спускается и из неё нужно вычесть 1:

Пример 4

Переведём сначала корень в степень:

Теперь можно производить вычисления производной с обычной формулой степеней:

Можно остановиться здесь, но бывает, что ответ с корнем в знаменателе не считается совсем правильным, поэтому умножаем всю вторую дробь на «√x/√x».

Значит правильный и «красивый» ответ:

Пример 5

Из таблицы мы знаем:

Так как это вычитание, осталось только подставить:

Сложные функции — примеры

Правило сложной функции:

(u (v))´ = u´ (v) * v´

Пример

1. Сначала нужно разобраться, что «arctg x» является нашей простой (внутренней) частью функции, это наше “v” формулы.

2. Применяем формулу корня из таблицы в левой части, получится 1/2 √arctg x, оставляя правую нерешённой.

3. Применяем формулу arctg x из таблицы (1/ (1 + x²)).

4. Совмещаем и готово

4.1. Если хотите «красивый» ответ, нужно убрать корень из знаменателя, умножая всю эту дробь на √arctgx / √arctgx.

Получится √arctgx / (2 (1 + x²) arctgx)

Как определить знак производной?

1. Определить точки, в которых производная равна нулю (также называются критическими точками).

2. Начертить таблицу, в которую вставляются все критические точки, а между ними оставляются незаполненными по одному окошку.

3. Выбрать значения x до и после полученного интервала, подставить в производную. Если значение получилось больше нуля, то знак будет плюс, если меньше — минус.

Пример:

Её производная y’ = 2x – 6.

Расчёт критических точек:

Значит в нашей таблице будет только одна критическая точка x = 3, и оставим место на «до» и «после».

Далее выбираем любой x сначала меньше 3, а потом больше 3.

1. для x 3 выбираем, например, x = 4 и подставляем в производную y’ = 2x – 6 ⇔ y’(4) = 2 * 4 – 6 = 2 >0, значит в таблицу записываем «+» (это означает, что в этой точке функция возрастает).

Вторая производная

Можно вычислить и «производную производной», обозначается она как y’’. Если использовать предыдущий пример:

Её физический смысл: это скорость изменения скорости движения точки, которая принадлежит графику функции.

Что такое композиция функций?

Иногда называется сложной функцией.

Сложная функция обычно записывается как (f o g) (x), т. е. можно «изобразить g (x) через f (x)» или наоборот.

Например, даны две функции: f (x) = 2x + 3 и g (x) = – x² + 5.

Требуется узнать (f o g) (x), это означает «f (g (x))».

Нужно подставить в функцию f (вместо x) функцию g

(f o g) (x) = f (g (x)) = f (–x² + 5) = 2 (–x² + 5) + 3 = – 2x² + 10 + 3 = – 2x² + 13

Если нужно узнать (g o f) (x), это «g (f (x))».

(g o f) (x) = g (f (x)) = g (2x + 3) = – (2x + 3)² + 5 = – (4х² + 12x + 9) + 5 = – 4х² – 12x – 9 + 5 = – 4х² – 12x – 4

Источник

ДИФФЕРЕНЦИРОВАНИЕ

Смотреть что такое «ДИФФЕРЕНЦИРОВАНИЕ» в других словарях:

Дифференцирование — Под термином дифференцирование могут подразумевать различные родственные понятия. Дифференцирование операция взятия полной или частной производной функции. Дифференцирование линейное отображение, удовлетворяющее тождеству Лейбница.… … Википедия

Источник

ДИФФЕРЕНЦИРОВАНИЕ

— операция, края относит функции ее производную или дифференциал. При этом речь может идти о производной или дифференциале в точке или на нек-ром множестве, о частных производных, о производной по направлению, о частных и полных дифференциалах, а сами функции могут быть не только числовыми, но и функциями более общей природы. г.

Смотреть что такое «ДИФФЕРЕНЦИРОВАНИЕ» в других словарях:

Источник

Дифференцирование

Смотреть что такое «Дифференцирование» в других словарях:

ДИФФЕРЕНЦИРОВАНИЕ — Расчленение, различение, выделение составляющих элементов при рассмотрении, изучении производственных процессов, экономических явлений, тенденций и т. д. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов

Источник

Видео

Производная функции простыми словами. Смысл производной. Наглядно, доходчиво и понятно

ПРОИЗВОДНАЯ функции. Объяснение математического смысла.

ЗАЧЕМ НУЖНЫ ЭТИ… производные! Математика на QWERTY.

ПРОИЗВОДНАЯ ФУНКЦИИ ЗА 8 МИНУТ. ПРИМЕР (ВСЕ ВИДЫ)

Производная и дифференцирование простым языком

Математика Без Ху{a47c00a1996a64a2145764bc9f608acb943865b2eadd21c2af8fa308981ee3ea}!ни. Производная сложной функции.

4. Вычисление производных примеры. Самое начало.

Математика без ху{a47c00a1996a64a2145764bc9f608acb943865b2eadd21c2af8fa308981ee3ea}!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.

Дифференциал функции

✓ Производная. Начало | Ботай со мной #056 | Борис Трушин

Определение производной, её физический и геометрический смысл. Алгоритм нахождения производной — ЭкзаменТВ

Производная функции − это результат дифференцирования функции.

Дифференцирование в математике — это процесс, при котором функция f превращается в другую функцию f’ (“производная от f”).

Простыми словами, производная — это средний наклон между двумя точками:

Интегрирование — это обратный процесс, т. е. восстановление функции по данной производной.

Геометрический смысл производной функции

Производная функции f(x) в данной точке — это наклон касательной f(x) в точке a, как показано на рисунке.

Физический смысл производной функции

Представьте точку, которая движется по прямой с постоянно меняющейся скоростью. Её скорость постоянно меняется, поэтому она рассчитывается в момент “t0”. Для этого нам нужно рассчитать короткий промежуток времени Δt, а расстояние, которое точка пройдёт за это время будет ΔS.

Таблица производных функций

Как пользоваться этой таблицей?

Например, производная линейной функции a*x равна константе, стоящей вместе с переменной x, т. е.: (а*x)′ = а.

Или нужно найти производную функции f(x) = 2 cos x:

f’(x) = (2 cos x)’ = 2 (cos x)’ = 2 (– sin x) = –2 sin x

Как найти производную?

Пример 1

f(x) = 6x³

f′(x) = 3 * 6x²

f′(x) = 18x²

Степень от x спускается и из неё нужно вычесть 1. (– ½)

f´(x) = ½ * (1/√x)

Можно остановиться здесь, но бывает, что ответ с корнем в знаменателе не считается совсем правильным, поэтому умножаем всю вторую дробь на “√x/√x”.

(1/√x) * (√x/√x) = √x/x

Значит правильный и “красивый” ответ:

f´(x) = ½ * (√x/x)

Пример 5

f(x) = sin x − cos x

Из таблицы мы знаем:

(sin x)´ = cos x

(cos x)´ = − sin x

Так как это вычитание, осталось только подставить:

f´(x) = (sin x − cos x)´

f´(x) = cos x − (− sin x)

f´(x) = cos x + sin x

Сложные функции — примеры

Правило сложной функции:

(u (v))´ = u´ (v) * v´

Пример

1. Сначала нужно разобраться, что “arctg x” является нашей простой (внутренней) частью функции, это наше “v” формулы.

2. Применяем формулу корня из таблицы в левой части, получится 1/2 √arctg x, оставляя правую нерешённой.

3. Применяем формулу arctg x из таблицы (1/ (1 + x²)).

4. Совмещаем и готово

4.1. Если хотите “красивый” ответ, нужно убрать корень из знаменателя, умножая всю эту дробь на √arctgx / √arctgx.

Получится √arctgx / (2 (1 + x²) arctgx)

Как определить знак производной?

1. Определить точки, в которых производная равна нулю (также называются критическими точками).

Пример:

y = x² – 6x + 17

Её производная y’ = 2x – 6.

Расчёт критических точек:

y’ = 0

2x – 6 = 0

2x = 6

x = 3

Значит в нашей таблице будет только одна критическая точка x = 3, и оставим место на “до” и “после”.

x < 3	x = 3	x > 3
0

Далее выбираем любой x сначала меньше 3, а потом больше 3. 1. для x < 3 выбираем, например, x = 1 и подставляем в производную y’ = 2x – 6 ⇔ y’(1) = 2 * 1 – 6 = -4 <0, значит в таблицу записываем “–” (это означает, что в этой точке функция убывает).

2. для x > 3 выбираем, например, x = 4 и подставляем в производную y’ = 2x – 6 ⇔ y’(4) = 2 * 4 – 6 = 2 >0, значит в таблицу записываем “+” (это означает, что в этой точке функция возрастает).

x < 3	x = 3	x > 3
–	0	+

Вторая производная

Можно вычислить и “производную производной”, обозначается она как y’’. Если использовать предыдущий пример:

y = x² – 6x + 17

её производная y’ = 2x – 6
вторая производная y’’ = (2x – 6)’ = 2

Её физический смысл: это скорость изменения скорости движения точки, которая принадлежит графику функции.

Что такое композиция функций?

Иногда называется сложной функцией.

Сложная функция обычно записывается как (f o g) (x), т. е. можно “изобразить g (x) через f (x)” или наоборот.

Например, даны две функции: f (x) = 2x + 3 и g (x) = – x² + 5.

Требуется узнать (f o g) (x), это означает “f (g (x))”.

Решение:

Нужно подставить в функцию f (вместо x) функцию g

(f o g) (x) = f (g (x)) = f (–x² + 5) = 2 (–x² + 5) + 3 = – 2x² + 10 + 3 = – 2x² + 13

Если нужно узнать (g o f) (x), это “g (f (x))”.

Решение:

(g o f) (x) = g (f (x)) = g (2x + 3) = – (2x + 3)² + 5 = – (4х² + 12x + 9) + 5 = – 4х² – 12x – 9 + 5 = – 4х² – 12x – 4

* * * * *

Определение производной

Производной функции в точке называется предел отношения приращения функции к приращению аргумента при , если этот предел существует.

Пример:

Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…

Геометрический смысл производной

Если мы рассмотрим прямоугольный треугольник , то заметим, что есть .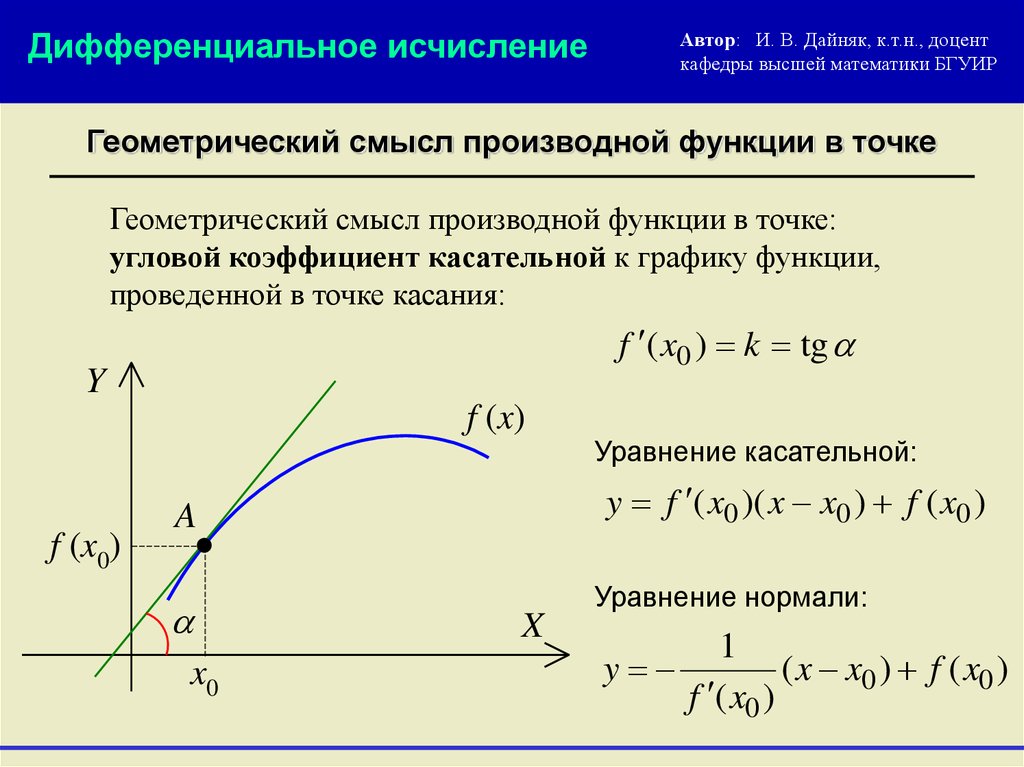

А при стремлении к нулю, точка будет приближаться к точке и секущая «превратится» в касательную к графику функции в точке .

Поэтому геометрический смысл производной таков:

Производная в точке () равна тангенсу угла наклона касательной к графику функции в этой точке:

где – угол наклона касательной (проведенной к в т. )

Физический смысл производной

Если точка движется вдоль оси и ее координаты изменяются по закону , то мгновенная скорость точки:

а ускорение:

Пример:

Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .

Решение:

м/с

Ответ: 60.

Уравнение касательной

Уравнение касательной к графику в точке :

Пример:

Составить уравнение касательной к графику функции в точке .

Решение:

Ответ:

* * * * *

Прокомментируем таблицу.

Рассмотрим график функции, изображенный на рисунке.

Мы видим, что функция возрастает в точке . Касательная, проведенная к графику функции в точке , имеет острый угол наклона к оси (ох), значит тангенс угла наклона касательной положителен, а значит, положительна и производная функции в точке .

Точка – точка минимума функции, касательная проведенная к графику функции через точку , параллельна оси (ох), значит тангенс угла наклона касательной равен нулю, значит и производная функции в точке равна нулю.

В точке функция убывает. Касательная, проведенная к графику функции в точке , имеет тупой угол наклона к оси (ох), значит тангенс угла наклона касательной отрицателен, а значит, отрицательна производная функции в точке

* * * * *

Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b).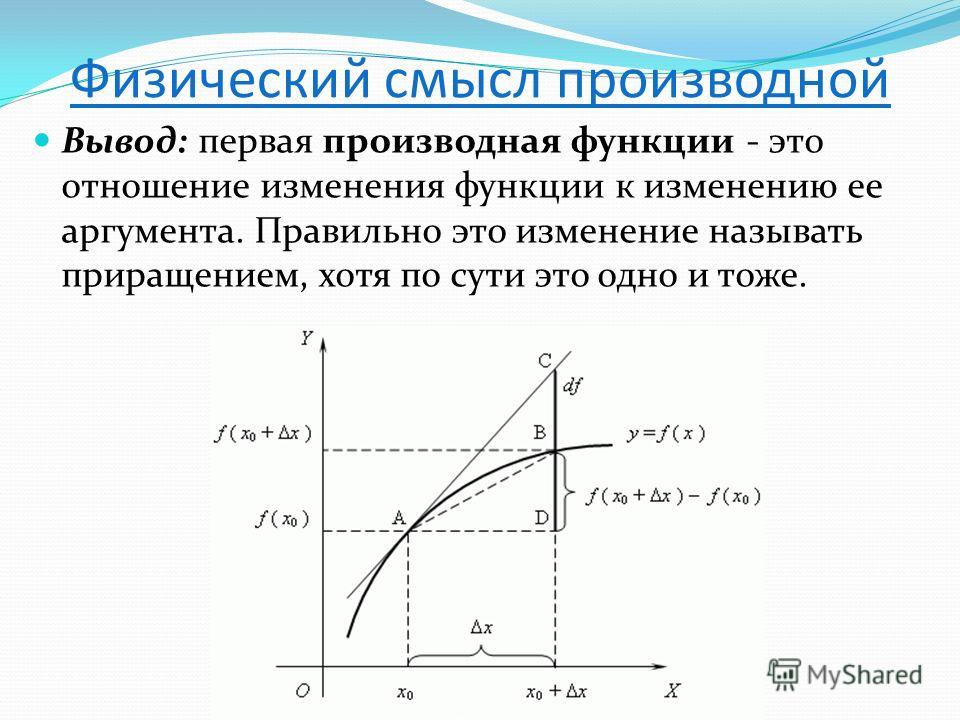 Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени.

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Решение:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Пример:

Решение:

Производные чисел: способы вычисления и примеры

Наверное, понятие производной знакомо каждому из нас ещё со школы. Обычно у учеников возникают трудности с пониманием этой, несомненно, очень важной вещи. Она активно применяется в различных областях жизни людей, и многие инженерные разработки были основаны именно на математических расчётах, полученных с помощью производной. Но прежде чем перейти к разбору того, что же такое производные чисел, как их вычислять и где они нам пригодятся, окунёмся немного в историю.

История

Понятие производной, являющееся основой математического анализа, было открыто (лучше даже сказать “изобретено”, потому что в природе оно как таковое не существовало) Исааком Ньютоном, которого мы все знаем по открытию закона всемирного тяготения. Именно он впервые применил в физике это понятие для связывания природы скорости и ускорения тел. И многие учёные до сих пор восхваляют Ньютона за это великолепное изобретение, ведь по сути он изобрёл основу дифференциального и интегрального исчисления, фактически основу целой области математики под названием “математический анализ”. Будь в то время Нобелевская премия, Ньютон с большой вероятностью получил бы её несколько раз.

Не обошлось и без других великих умов. Кроме Ньютона над развитием производной и интеграла потрудились такие именитые гении математики, как Леонард Эйлер, Луи Лагранж и Готфрид Лейбниц. Именно благодаря им мы получили теорию дифференциального исчисления в таком виде, в котором она существует по сей день. Кстати, это Лейбниц открыл геометрический смысл производной, которая оказалась ничем иным, как тангенсом угла наклона касательной к графику функции.

Что же такое производные чисел? Немного повторим то, что проходили в школе.

Что такое производная?

Определять это понятие можно несколькими разными способами. Самое простое объяснение: производная – это скорость изменения функции. Представим график какой-нибудь функции y от x. Если это не прямая, то она имеет некоторые изгибы в графике, периоды возрастания и убывания. Если брать какой-нибудь бесконечно малый промежуток этого графика, он будет представлять собой отрезок прямой. Так вот, отношение размера этого бесконечно малого отрезка по координате y к размеру по координате x и будет являться производной данной функции в данной точке. Если рассматривать функцию в целом, а не в конкретной точке, то мы получим функцию производной, то есть некую зависимость игрек от икс.

К тому же кроме физического смысла производной как скорости изменения функции есть ещё и геометрический смысл. О нём мы сейчас и поговорим.

Геометрический смысл

Производные чисел сами по себе представляют собой некое число, которое без должного понимания не несёт никакого смысла. Оказывается, производная не только показывает скорость роста или уменьшения функции, а также тангенс угла наклона касательной к графику функции в данной точке. Не совсем понятное определение. Разберём его поподробнее. Допустим, у нас есть график какой-либо функции (для интереса возьмём кривую). На ней есть бесконечное множество точек, но есть такие области, где только одна единственная точка имеет максимум или минимум. Через любую такую точку можно провести прямую, которая была бы перпендикулярна графику функции в этой точке. Такая линия будет называться касательной. Допустим, мы провели её до пересечения с осью OX. Так вот, полученный между касательной и осью OX угол и будет определяться производной. А точнее, тангенс этого угла будет равняться ей.

Поговорим немного о частных случаях и разберём производные чисел.

Частные случаи

Как мы уже говорили, производные чисел – это значения производной в конкретной точке. Вот например, возьмём функцию y=x². Производная х – число, а в общем случае – функция, равная 2*x. Если нам необходимо вычислить производную, скажем, в точке x₀= 1, то получаем y'(1)=2*1=2. Всё очень просто. Интересный случай представляет производная комплексного числа. Вдаваться в подробное объяснение того, что такое комплексное число, мы не будем. Скажем лишь, что это число, которое содержит в себе так называемую мнимую единицу – число, квадрат которого равен -1. Вычисление такой производной возможно только при наличии следующих условий:

1) Должны существовать частные производные первого порядка от действительной и мнимой части по игрек и по икс.

2) Выполняются условия Коши-Римана, связанные с равенством частных производных, описанных в первом пункте.

Другим интересным случаем, хотя и не таким сложным как предыдущий, является производная отрицательного числа. На самом деле любое отрицательное число можно представить как положительное, умноженное на -1. Ну а производная постоянной и функции равна постоянной, умноженной на производную функции.

Интересно будет узнать о роли производной в повседневной жизни, и именно это сейчас и обсудим.

Применение

Наверное, каждый из нас хоть раз в жизни ловит себя на мысли, что математика вряд ли пригодится ему. А такая сложная штука, как производная, наверное, вообще не имеет применения. На самом деле, математика – фундаментальная наука, и все её плоды развивает в основном физика, химия, астрономия и даже экономика. Производная положила начало математическому анализу, который дал нам возможность делать выводы из графиков функций, и мы научились интерпретировать законы природы и обращать их в свою пользу благодаря ему.

Заключение

Конечно, не каждому, возможно, пригодится производная в реальной жизни. Но математика развивает логику, которая уж точно будет нужна. Не зря ведь математику называют царицей наук: из неё складываются основы понимания других областей знаний.

3: Производные – Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2489

Гилберт Стрэнг и Эдвин «Джед» Герман
OpenStax

Вычисление скорости и изменения скорости — важное применение исчисления, но оно гораздо более распространено. Исчисление важно во всех областях математики, науки и техники, а также для анализа в бизнесе и здравоохранении. В этой главе мы исследуем один из основных инструментов исчисления — производную — и покажем удобные способы вычисления производной. В этой главе мы применяем эти правила к различным функциям, чтобы затем исследовать применение этих методов.

3.0: Prelude to Derivatives
Вычисление скорости и изменения скорости — важное применение исчисления, но оно гораздо более распространено. Исчисление важно во всех областях математики, науки и техники, а также для анализа в бизнесе и здравоохранении. В этой главе мы исследуем один из основных инструментов исчисления — производную — и покажем удобные способы вычисления производной. В этой главе мы применяем эти правила к различным функциям, чтобы затем изучить их применение.0008
3.1: Определение производной
Наклон касательной к кривой измеряет мгновенную скорость изменения кривой.

Мы можем вычислить его, найдя предел разностного отношения или разностного отношения с приращением h. Производная функции f(x) при значении a находится с использованием любого из определений наклона касательной. Скорость – это скорость изменения положения. Таким образом, скорость v(t) в момент времени t является производной положения s(t) в момент времени t.
- 3.1E: Упражнения к разделу 3.1
3.2: Производная как функция
. График производной функции f(x) связан с графиком f(x). Где (f(x) имеет касательную с положительным наклоном, f′(x)> 0. Где (x) имеет касательную с отрицательным наклоном, f′(x)<0. Где f(x) имеет горизонтальную касательной, f′(x)=0. Если функция дифференцируема в точке, то она непрерывна в этой точке.
- 3.2E: Упражнения к разделу 3.2
3.3: Правила дифференцирования
Производная постоянной функции равна нулю. Производная степенной функции — это функция, в которой степень x становится коэффициентом при члене, а степень x в производной уменьшается на 1. Производная константы c, умноженная на функцию f, совпадает с константой умножить на производную. Производная суммы функции f и функции g равна сумме производной функции f и производной функции g.
- 3.3E: Упражнения для раздела
3.4: Производные как скорости изменения
В этом разделе мы рассмотрим некоторые применения производной как скорость интерпретации производной изменение функции. Эти приложения включают ускорение и скорость в физике, темпы роста населения в биологии и предельные функции в экономике.
- 3.4E: Упражнения к разделу 3.4
3.5: Производные тригонометрических функций
Мы можем найти производные sin x и cos x, используя определение производной и предельные формулы, найденные ранее. {n−1}g′(x)\).
- 3.6E: Упражнения к разделу 3.6
3.7: Производные обратных функций
Теорема об обратных функциях позволяет вычислять производные обратных функций без использования предельного определения производных обратных функций. Мы можем использовать теорему об обратной функции для разработки формул дифференцирования для обратных тригонометрических функций.
- 3.7E: Упражнения для раздела 3.7
3.8: Неявное дифференцирование
Мы используем неявное дифференцирование для нахождения производных неявно определенных функций (функций, определяемых уравнениями). Используя неявное дифференцирование, мы можем найти уравнение касательной к графику кривой.
- 3.8E: Упражнения к разделу 3.8
3.9: Производные экспоненциальных и логарифмических функций
В этом разделе мы исследуем экспоненциальные и логарифмические производные экспоненциальных функций.

Как мы обсуждали во Введении в функции и графики, экспоненциальные функции играют важную роль в моделировании роста населения и распада радиоактивных материалов. Логарифмические функции могут помочь изменить масштаб больших величин и особенно полезны для перезаписи сложных выражений.
- 3,9E: Упражнения для Раздела 3.9
3.10: Глава 3 Обзорные упражнения

МИНОКА: Производные (CC BY; OPENSTAX)

Эта страница под названием 3: Деривативы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Глава

Автор
ОпенСтакс
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать страницу TOC
нет
Теги
1. автор @ Эдвин «Джед» Герман
2. автор@Гилберт Странг
3. источник@https://openstax. org/details/books/calculus-volume-1

Основы производной. Производная — определение и формула… | Фикри Мульяна Сетиаван | Упрощенная математика

Исчисление для всех

Производная — определение и описание формулы

Мир постоянно меняется. Когда машина едет, положение автомобиля меняется. При испарении воды объем воды изменяется. Даже когда вы играете в игры, положение вашего игрового персонажа также меняется. В этом мире происходит так много изменений, и они происходят постоянно.

Как я сказал во введении, исчисление — это изучение изменений. Раздел исчисления — то есть производное — изучает, как быстро происходит изменение. Возьмем пример движущегося автомобиля. В этом случае производная узнает, как быстро меняется положение автомобиля. Другими словами, производная изучает скорость, с которой движется автомобиль.

Если бы машина двигалась с постоянной скоростью, было бы очень легко вычислить ее скорость. Скорость равна пройденному расстоянию (изменению положения), деленному на пройденное время . Это очень легко. Если изображено, график для автомобиля с постоянной скоростью выглядит следующим образом:

Для расчета скорости автомобиля нам нужно только рассчитать расстояние от начальной и конечной точек, затем расстояние делится на время в пути.

Основываясь на приведенном выше графике, мы можем рассчитать скорость автомобиля, разделив ∆s на ∆t. Итак, v (скорость) равна ∆s/∆t.

Что делать, если скорость автомобиля не постоянна, а меняется? Как известно, в реальном мире скорость автомобиля не всегда постоянна. Иногда ускоряется и замедляется. иногда машина может даже двигаться назад. Таким образом, зависимость изменения положения (расстояния) автомобиля от времени в пути может быть представлена в виде следующего графика:

Если график такой, как на картинке выше, как мы узнаем скорость автомобиля? Можем ли мы снова использовать этот метод? Давай попробуем.

Вычисляя разницу значений s между точками A и B, мы получаем значение ∆s. Рассчитав время в пути из А в В, получим значение ∆t. так же, как и в предыдущем примере, мы можем вычислить скорость автомобиля, разделив ∆s на ∆t. Другими словами, v=∆s/∆t.

Ой, подождите. Это правда? Вычисленное нами ранее значение — это только средняя скорость автомобиля из точки А в точку Б, а не реальная скорость. Если скорость автомобиля постоянна, его средняя скорость становится реальной скоростью. Однако это не относится к автомобилям с непостоянной скоростью. В автомобиле, скорость которого непостоянна, может случиться так, что при t=1 с скорость будет 10 м/с, а при t=3 с скорость станет 20 м/с. То есть скорость автомобиля может меняться каждую секунду. Скорость в определенный момент называется мгновенной скоростью.

Тогда, если вышеуказанный метод не может быть использован для расчета скорости автомобиля, какой метод нам следует использовать?

Еще раз взгляните на график. Затем задайте вопрос, какова скорость автомобиля в момент времени t = 4 секунды? Мы можем рассчитать его, используя метод, аналогичный предыдущему методу, но только с очень коротким расстоянием (∆s) и коротким промежутком времени (∆t). Взгляните на следующий график:

Попробуйте представить, что точки A и B непрерывно приближаются друг к другу, как показано на трех рисунках выше. Точки A и B продолжают сближаться до тех пор, пока ∆s не станет очень, очень маленьким. Мы можем рассматривать это следующим образом:

Когда точки A и B приближаются друг к другу почти до соприкосновения, график, соединяющий точки A и B, становится очень похожим на прямую линию. Таким образом, мы можем рассчитать скорость автомобиля, вычислив уклон линии для ∆t, близкого к 0. Таким образом, скорость автомобиля можно обозначить как предел ∆s/∆t с ∆t, приближающимся к 0,

Помимо возможности рассчитать мгновенную скорость автомобиля, приведенная выше формула может рассчитать мгновенную скорость всего, что изменяется. Например, изменение цены товара в связи со спросом, изменение длины объектов в связи с расширением и другие.

В обсуждении выше мы говорили только о скорости автомобиля. Теперь мы обсудим понятие скорости в целом. Как и в приведенном выше примере, скорость можно рассчитать, разделив ∆s (ось Y на графике) на ∆t (ось X на графике). В математике ∆s/∆t или ∆y/∆x называют градиентом или наклоном.

Наклон функции f(x) описывает скорость изменения значения f(x) на графике. Таким образом, можно сказать, что изменение значения функции f(x) по отношению к x равно наклону функции f(x).

Общая формула для вычисления наклона функции на графике выглядит следующим образом:

Теперь, если взять очень маленькое значение ∆x, то этот градиент называется первой производной функции f(x). Первая производная функции f(x) обозначается как f ‘(x).

Производные изучают, насколько быстро происходит изменение. Чтобы отслеживать эти изменения, производная использует концепцию пределов, которую мы изучали ранее. По сути, понятие производной совпадает с понятием наклона. Однако производная гораздо полезнее, потому что с ее помощью можно вычислить наклон функции при любых обстоятельствах.

Спасибо, что прочитали эту статью! Если вы все еще не понимаете мое объяснение, не стесняйтесь спрашивать в разделе ответов. Я понимаю, что мое письмо довольно сложное, поэтому немного сложно объяснить это только с помощью письма и картинок. Поэтому, пожалуйста, спросите, если вы не понимаете мое объяснение.

Mathwords: Производная

индекс: нажмите на букву






индекс: предметные области

Производная

Функция, которая дает наклон кривой; то есть наклон линия касательной к функции. Производная функции f при точка x обычно пишется как f ‘ ( х ). Например, если f ( x ) = x ³ затем f ‘( x ) = 3 х ² . Наклон касательной при x = 5 равен f ‘ ( x ) = 3·5 ² = 75,

См. также

Разностное частное, предел, производная правила, дифференцируемое, дифференцирование, непрерывно дифференцируемый

эта страница обновлена 19 июля 17
Математические слова: термины и формулы от алгебры I до исчисления
написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом
Авторские права © Брюс Симмонс, 2000 г.

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.