Что такое сила архимеда в физике определение: Закон Архимеда — урок. Физика, 7 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Архимедова сила — закон, формула, определение

Сила: что это за величина

Прежде чем говорить о силе Архимеда, нужно понять, что это вообще такое — сила.

В повседневной жизни мы часто видим, как физические тела деформируются (меняют форму или размер), ускоряются и тормозят, падают. В общем, чего только с ними не происходит! Причина любых действий или взаимодействий тел — ее величество сила.

Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Сила измеряется в ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.

Поскольку сила — величина векторная, у нее, помимо модуля, есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.

Открытие закона Архимеда

Так вышло, что закон Архимеда известен не столько своей формулировкой, сколько историей возникновения.

Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом не причиняя вреда самой короне. То есть расплавить корону или растворить — нельзя.

Взвесить корону Архимеду труда не составило, но этого было мало — нужно ведь определить объем короны, чтобы рассчитать плотность металла, из которого она отлита.

Рассчитать плотность металла, чтобы установить, золотая ли корона, можно по формуле плотности.

Формула плотности тела

ρ = m/V

ρ — плотность тела [кг/м³]

m — масса тела [кг]

V — объем тела [м³]

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. Тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.

Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (и так торопился, что даже не оделся). 🤦🏻‍♂️

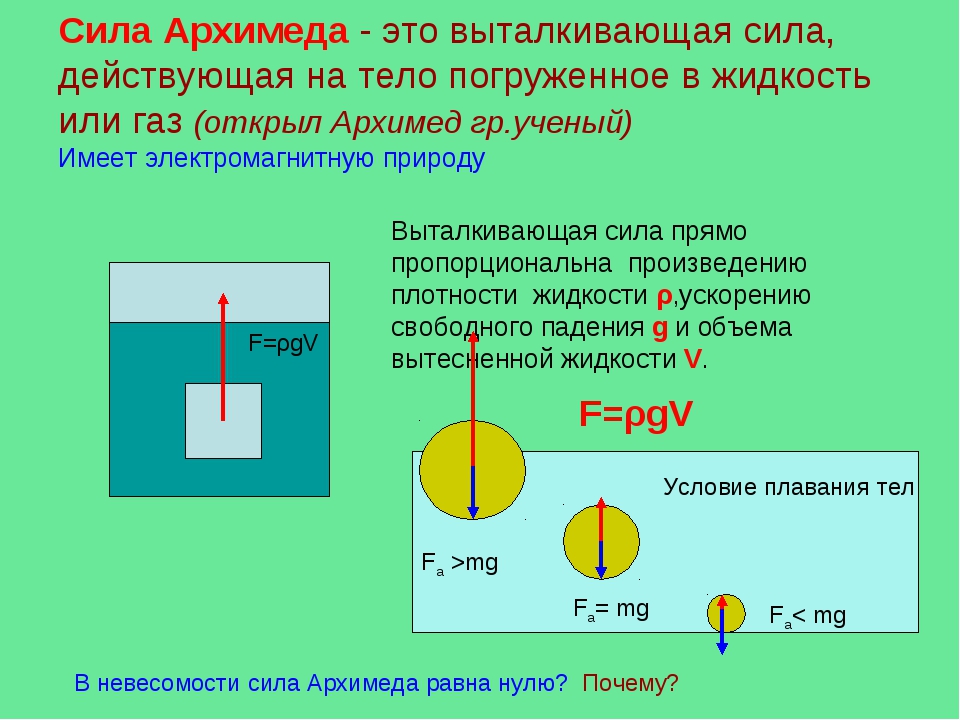
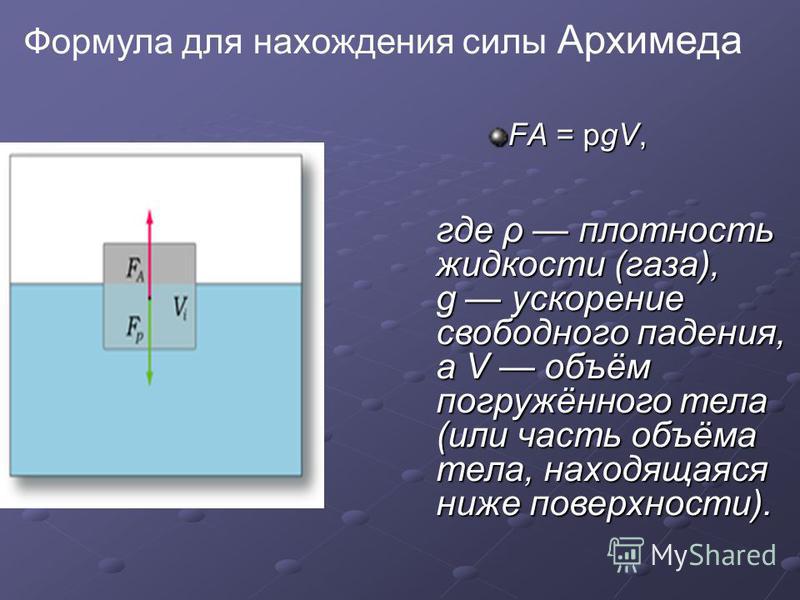
Формула и определение силы Архимеда для жидкости

На поверхность твердого тела, погруженного в жидкость, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.

Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой

или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.

Определение архимедовой силы для жидкостей звучит так:

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

Формула архимедовой силы для жидкости

F_Арх = ρ_жgV_погр

ρ_ж — плотность жидкости[кг/м³]

V_погр — объем погруженной части тела [м³]

g — ускорение свободного падения [м/с²]

На планете Земля g = 9,8 м/с ².

А теперь давайте порешаем задачки, чтобы закрепить, как вычислить архимедову силу.

Задача 1

В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой.

Решение

Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.

Задача 2

На графике показана зависимость модуля силы Архимеда F_Арх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание все время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с².

Решение

Сила Архимеда, действующая на кубик, равна F_Арх = ρ

жgV_погр.

V_погр. — объем погруженной части кубика,

ρ_ж — плотность жидкости.

Учитывая, что нижнее основание кубика все время параллельно поверхности жидкости, можем записать:

F_Арх = ρ_жgV _погр = ρ_жga ²x

где а — длина стороны кубика.

Выразим плотность:

ρ = F_Арх / ga²x

Рассматривая любую точку данного графика, получим:

ρ = F_Архga²x = 20,25 / 10 × 7,5 × 10^-2 = 2700 кг/м³

Ответ: плотность жидкости равна 2700 кг/м ³.

Условия плавания тел

Из закона Архимеда вытекают следствия об условиях плавания тел.

ЗАКОН АРХИМЕДА | Энциклопедия Кругосвет

ЗАКОН АРХИМЕДА – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.

Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся.

Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).

Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.

Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение.

Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть h – глубина погружения верхней грани, r – плотность жидкости, g – ускорение силы тяжести; тогда давление на верхнюю грань равно

r · g · h = p₁

а на нижнюю

r · g(h+a) = p₂

Сила давления равна давлению, умноженному на площадь, т.е.

F₁ = p₁ · a\up122, F₂ = p₂ · a\up122 , где a – ребро кубика,

причем сила F₁ направлена вниз, а сила F₂ – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F₁ и F₂ и определяется их разностью, которая и является выталкивающей силой:

F₂ – F₁ =r · g · (h+a) a\up122 – rgha ·a² = pga²

Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз.

Величина F₂ – F₁= pga³ равна объему тела (кубика) a³, умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.

Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V, то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).

Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V. Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V, т.е. pgV.

Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V, можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.

Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» g, т.е. веса единицы объема вещества: g = pg; если принять, что для воды g = 1, то сплошное тело из вещества, у которого g > 1 утонет, а при g < 1 будет плавать на поверхности; при g = 1 тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).

Владимир Кузнецов

Закон Архимеда, или Как распознать ложь?

История открытия

В древних Сиракузах жил инженер, математик и физик по имени Архимед. Образование он получил отличное, изобретения его ценились и в средствах он не нуждался. И периодически к нему обращались сильные мира для решения всяких сложных задач. И одной из таких задач было определить подлинность короны царя Гиерона.

Казалось бы, что в этом сложного?

Используй формулу

ρ_т = m_т / V_т (1).

Раздели m_т массу слитка, что был выдан ювелиру на объем короны V_т, получишь плотность короны ρ_т. Сравни полученный результат с известной плотностью золота, и дело в шляпе. А ювелир получит либо плату за работу, либо близкое знакомство с придворным палачом.

Однако эта формула хорошо работает с объектами простой формы: шар, куб, параллелепипед. А мы то помним, что исследуем корону, у которой множество зубцов, выпуклостей и ажурных плетений.

Как можно определить объем предмета столь сложной формы? Не знаете? Вот и Архимед тоже не знал.

Физика. 7 класс. Учебник

Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.

Купить

Долгое время ученый думал над задачей, и в один из дней, в задумчивости опускаясь в наполненную водой ванну, обратил внимание, что часть воды выплеснулась через край. Современники рассказывают, что именно в этот момент Архимед закричал: «Эврика!», что по-гречески значит «Нашел!» и, даже не одеваясь, побежал в царский дворец.

Еще пару дней понадобилось исследователю, чтобы изобрести прибор, с помощью которого он мог бы измерить объем воды, вылившейся при погружении короны. Этот прибор, названный впоследствии ведерком Архимеда, можно увидеть на странице 145 учебника «Физика 7 класс» под редакцией А.В.Перышкина.

Затем, с помощью опытов с золотыми и серебряными слитками, доказать, что объем жидкости равен объему слитка, а следовательно будет равен и объему короны. И последним этапом определить плотность короны.

Говорят, что царь был прав в своих подозрениях, и ювелир был нечист на руку. А всю плату, что причиталась за корону мастеру, получил Архимед.

Действие жидкости и газа на погруженное в них тело

Что же открыл Архимед благодаря своим опытам?

Ученый определил некую силу, которая действую в обратном направлении силе притяжения и позволяет предметам плавать в воде и воздухе. Эту силу по праву назвали силой Архимеда или выталкивающей силой.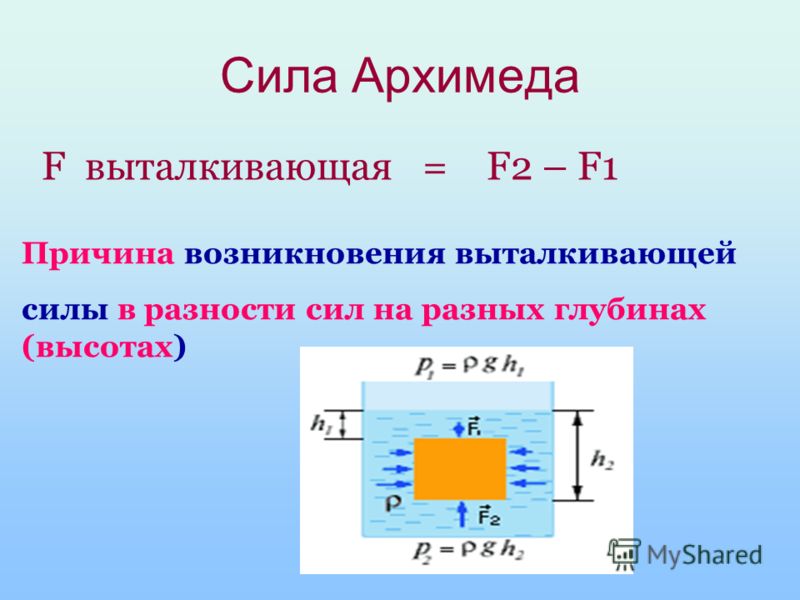

Определение закона Архимеда: тело погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость.

Формулы

На планете Земля на все предметы действует сила земного притяжения. Для объектов на земной поверхности силу притяжения можно рассчитать по формуле:

F_т = m_тg, (2)

где m_т — масса тела, а g — ускорение свободного падения, равное 9,8 м/с².

Когда же объект погружается в жидкость или газ, на него начинает действовать выталкивающая сила или сила Архимеда, которая рассчитывается по формуле:

F_А = m_жg, (3)

где m_ж — масса жидкости, вытесненной целым объектом или его частью, находящейся в жидкости.

Массу вытесненной жидкости в свою очередь можно определить используя формулу:

m_ж = ρ_жV_ж, (4)

и соответственно преобразовать формулу закона Архимеда:

F_А = ρ_жV_жg. (5)

Как же соотносятся между собой сила тяжести и сила выталкивания. Все просто:

если сила притяжения больше силы выталкивания, предмет утонет;
если силы примерно равны — предмет будет плавать в толще жидкости или газа;
а если сила выталкивания больше силы притяжения, предмет всплывет.

Многочисленные опыты, благодаря которым мы можем пользоваться формулами силы выталкивания, подробно разобраны в § 50 учебника «Физика 7 класс» под редакцией А.В.Перышкина.

Несмотря на то, что Архимед впервые открыл силу выталкивания в воде, сила Архимеда характерна также и для газов, и именно благодаря ей смог подняться в воздух первый воздушный шар, а вдохновленный и восхищенный этим событием писатель Жюль Верн написал свой роман «Вокруг света за 80 дней».

А теперь давайте поможем царю решить его задачу с короной.

Предположим, что корона царя Гиерона в воздухе весит 22 Н, а в воде 19,75 Н, вычислите плотность вещества короны.

Как мы узнали в начале статьи, плотность вещества находится по формуле:

ρ_т = m_т/V_т. (1)

Глядя на формулу, понимаем, что для решения задачи нам не известны ни масса короны, ни ее объем.

Из предыдущего курса физики (§ 27 учебника «Физика 7 класс» под редакцией А.В.Перышкина.), помним, что для неподвижного тела вес P равен силе тяжести F_т и рассчитывается по формуле:

P = F_т = m_тg, (2)

где g — ускорение свободного падения и его значение равно g = 9,8 Н/кг. Однако, если не требуется большая точность в расчетах, значение можно округлить до 10 Н/кг

Зная вес короны в воздухе, мы используя формулу (2) можем найти массу короны.

P_т = F_т = m_тg,
Мы также знаем, что вес тела в воде отличается от веса тела в воздухе на силу Архимеда.

F_A = 22 — 19,75 Н = 2,25 Н
Согласно формуле (5) сила Архимеда равна F_А = ρ_жV_жg

где ρ_ж = ρ_воды = 1000 кг/м³

Из нее находим объем вытесненной жидкости и соответственно объем короны
Остается финальный штрих: рассчитать плотность.

ρ_т = m_т/V_т

ρ_т = 2,2 кг / 0,000225 м³ = 9778 кг/м³ или 9,8 г/см³

Зная, что плотность золота 19,3 г/см³ или 19 300 кг/м³, можем сказать, что корона царя Гиерона сделана из какого-то сплава, но не из чистого золота. Увы, царь был прав, подозревая мастера в нечестности. И мне даже немного жаль нерадивого ювелира. Ведь никто не любит, когда воруют его собственность, а цари особенно.

Теперь попробуйте самостоятельно решить задачу № 5 на странице 147 учебника «Физика 7 класс» под редакцией А.В.Перышкина.

Что ещё почитать?

Методические советы

Тест «Закон Архимеда»

1. Сила Архимеда это:

сила, с которой Архимед передвигал ванну;
сила, которая поднимает вверх тело находящееся в жидкости или газе; (+)
сила мышц Архимеда;
сила, с которой твердое тело действует на поверхность.

2. Сила Архимеда действует:

на тела погруженные только в газ;
на тела погруженные только в жидкость;
на тела погруженные в газ или в жидкость; (+)
на тела находящиеся в невесомости.

3. Чему равно ускорение свободного падения g?

9,8 м/с³;
9,8 Н/кг; +
9,8 км/ч;
8,9 м/с².

4. К пружине подвешено некое тело. Если тело погрузить в емкость с жидкостью, что произойдет с пружиной?

растянется больше;
сожмется; (+)
не изменится;
зависит от веса тела.

5. Два друга пошли плавать в реке. Один из них при погружении вытесняет объем 60 дм³, второй 40 дм³. На кого из ребят будет действовать большая сила Архимеда?

на того, кто лучше умеет плавать;
на того, кто вытеснил больше воды; (+)
на того, то не умеет плавать;
на того, кто вытеснил меньше воды.

6. Формула силы выталкивания это:

F_А = ρ_жV_жg; (+)
F_А = ρ_тV_жg;
F_А = ρ_жV_тg;
F_А = m_тg.

7. Если сила тяжести больше силы Архимеда, тело:

взлетит;
всплывет;
утонет; (+)
поплывет.

8. 4 одинаковых стальных шарика погрузили в 4 разные жидкости: чистая вода, вода мертвого моря, бензин, оливковое масло. В какой жидкости сила выталкивания будет наименьшей?

Плотность масла 915 кг/м³, плотность бензина 750 кг/м³.

бензин; (+)
вода Мертвого моря;
оливковое масло;
чистая вода.

9. Сила тяжести зависит:

от плотности жидкости;
от вытесненного объема жидкости;
от массы тела; +
от времени нахождения тела в жидкости.

10. В двух емкостях плавают два шарика равного объема. Одинакова ли сила выталкивания?

одинакова, т. к. объем шариков одинаков;
сила выталкивания больше в емкости с керосином, потому что плотность меньше воды;
сила выталкивания больше в емкости с водой, потому что ее плотность больше керосина. (+)

#ADVERTISING_INSERT#

Закон Архимеда для ускоренно движущихся тел

С. Н. Манида

Установлена зависимость силы гидростатического давления (силы Архимеда) от плотности свободного тела, погруженного в жидкость.

1. Закон Архимеда для неподвижных тел

Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.

Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.

Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.

Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С помощью современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление этого ученого, когда окажется, что полученный результат численно равен весу жидкост и в объеме погруженной части тела! Этот результат был получен греческим ученым Архимедом 2200 лет назад, причем в общем виде — для тел любой формы!

Попробуем восстановить ход рассуждений Архимеда и вывести его закон.

На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис. 2). На эту жидкость действует сила тяжести Vg и сила гидростатического давления F. Выделенный объем находится в равновесии, следовательно, сумма сил, действующих на жидкость в этом объеме, равна нулю: F+ Vg =0.

Отсюда следует выражение для силы гидростатического давления: F=-Vg.

Мы нашли силу, действующую на поверхность жидкости, заполняющей объем V. Но поверхность тела, погруженного в жидкость, совпадает с поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное выражение и есть «выталкивающая’’ сила — сила Архимеда

F _Арх = -Vg. (*)

Это равенство и носит название закон Архимеда.

2. Неприменимость закона Архимеда для случая свободных тел

Казалось бы, решение задач с использованием этого закона не должно вызывать затруднений. Однако неверные решения отдельных задач на закон Архимеда встречаются не только у школьников, но и в ряде задачников.

Дело в том, что при использовании этого (как и любого другого) закона надо всегда помнить, как и для каких ситуаций он выводился. Так, например, мы вычисляли силу гидростатического давления, действующую на поверхность неподвижного объема жидко сти, находящейся в равновесии, т. е. имеющей нулевые скорость и ускорение. Следовательно, и использовать выведенное выражение для силы Архимеда можно только в тех случаях, когда и скорость, и ускорение тела равны нулю.

Покажем, что применение этого закона в других ситуациях абсолютно неправомочно, так как приводит к неверным результатам.

Рассмотрим легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= Vg и сила натяжения нити T, а вверх — сила гидростатического давления

F=F_Арх=- Vg, (*)

где – плотность тела, – плотность жидкости. Условие равновесия тела

-Vg +T+Vg =0. (1)

Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вве рх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения

F+ V g = V a. (2)

Предположив, что в этом случае можно использовать закон Архимеда, подставим – Vg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение

a = — g (-)/ (3)

Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.

Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости).

3. Сила гидростатического давления для случая свободных тел

Точный расчет гидростатического давления на поверхность ускоренно движущегося тела возможен только с применением аппарата математической физики, а ответ представим в аналитическом виде лишь для некоторых частных случаев. Уравнения, описывающие движение тела в жидкости, были впервые получены профессором Петербургского университета Леонардом Эйлером в середине XVIII века. Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):

(4)

и, с учетом (2), ускорение тела имеет вид:

(5)

4. Выводы

Сравнивая выражения (4) и (*) видим, что они совпадают только при = . Зависимость силы гидростатического давления, действующей на свободное тело, от его плотности представлена на графике рис. 4 в сравнении со стандартным выражением для силы Архимеда Vg:

Из графика на рис.4 видно, что для малых плотностей тела сила давления убывает до нуля, а при увеличении плотности эта сила стремится к величине 1,5Vg.

На следующем графике (рис. 5) приведена зависимость ускорения свободного тела в жидкости от его плотности [уравнение (5)]. Для сравнения приведен график ускорения, получающийся непосредственн о из закона Архимеда [уравнение (3)]

Из этого графика видно, что даже бесконечно легкий шарик всплывает с конечным ускорением, равным -2g, а тяжелые тела тонут с ускорением, меньшим, чем это следует из закона Архимеда.

Архимедова сила, формулы

Несмотря на явные различия свойств жидкостей и газов, во многих случаях их поведение определяется одними и теми же параметрами и уравнениями, что позволяет использовать единый подход к изучению свойств этих веществ.

В механике газы и жидкости рассматривают как сплошные среды. Предполагается, что молекулы вещества распределены непрерывно в занимаемой ими части пространства. При этом плотность газа значительно зависит от давления, в то время как для жидкости ситуация иная. Обычно при решении задач этим фактом пренебрегают, используя обобщенное понятие несжимаемой жидкости, плотность которой равномерна и постоянна.

Далее дадим понятие физической величине – давлению.

Определение 1

Давление определяется как нормальная сила $F$, действующая со стороны жидкости на единицу площади $S$.

$ρ = \frac{\Delta P}{\Delta S}$.

Замечание 1

Давление измеряется в паскалях. Один Па равен силе в 1 Н, действующей на единицу площади 1 кв. м.

В состояние равновесия давление жидкости или газа описывается законом Паскаля, согласно которому давление на поверхность жидкости, производимое внешними силами, передается жидкостью одинаково во всех направлениях.

При механическом равновесии, давление жидкости по горизонтали всегда одинаково; следовательно, свободная поверхность статичной жидкости всегда горизонтальна (кроме случаев соприкосновения со стенками сосуда). Если принять во внимание условие несжимаемости жидкости, то плотность рассматриваемой среды не зависит от давления.

Представим некоторый объем жидкости, ограниченный вертикальным цилиндром. Поперечное сечение столба жидкости обозначим $S$, его высоту $h$, плотность жидкости $ρ$, вес $P=ρgSh$. Тогда справедливо следующее:

$p = \frac{P}{S} = \frac{ρgSh}{S} = ρgh$,

Готовые работы на аналогичную тему

где $p$ – давление на дно сосуда.

Отсюда следует, что давление меняется линейно, в зависимости от высоты. При этом $ρgh$ – гидростатическое давление, изменением которого и объясняется возникновение силы Архимеда.

Формулировка закона Архимеда

Закон Архимеда, один из основных законов гидростатики и аэростатики, гласит: на тело, погруженное в жидкость или газ, действует выталкивающая или подъемная сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.

Замечание 2

Возникновение Архимедовой силы связано с тем, что среда – жидкость или газ – стремится занять пространство, отнятое погруженным в нее телом; при этом тело выталкивается из среды.

Отсюда и второе название для этого явление – выталкивающая или гидростатическая подъемная сила.

Выталкивающая сила не зависит от формы тела, также как и от состава тела и прочих его характеристик.

Возникновение Архимедовой силы обусловлено разностью давления среды на разных глубинах. Например, давление на нижние слои воды всегда больше, чем на верхние слои.

Проявление силы Архимеда возможно лишь при наличии тяжести. Так, например, на Луне выталкивающая сила будет в шесть раз меньше, чем на Земле для тел равных объемов.

Возникновение Силы Архимеда

Представим себе любую жидкую среду, например, обычную воду. Мысленно выделим произвольный объем воды замкнутой поверхностью $S$. Поскольку вся жидкость по условию находится в механическом равновесии, выделенный нами объем также статичен. Это означает, что равнодействующая и момент внешних сил, воздействующих на этот ограниченный объем, принимают нулевые значения. Внешние силы в данном случае – вес ограниченного объема воды и давление окружающей жидкости на внешнюю поверхность $S$. При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.

Теперь обозначим, что вместо этой условного ограниченной жидкости в среду было помещено любое твердое тело соответствующего объема. Если соблюдается условие механического равновесия, то со стороны окружающей среды никаких изменений не произойдет, в том числе останется прежним давление, действующее на поверхность $S$. Таким образом мы можем дать более точную формулировку закона Архимеда:

Замечание 3

Если тело, погруженное в жидкость, находится в механическом равновесии, то со стороны окружающей его среды на него действует выталкивающая сила гидростатического давления, численно равная весу среды в объеме, вытесненным телом.

Выталкивающая сила направлена вверх и проходит через центр масс тела. Итак, согласно закону Архимеда для выталкивающей силы выполняется:

$F_A = ρgV$, где:

$V_A$ – выталкивающая сила, H;
$ρ$ – плотность жидкости или газа, $кг/м^3$;
$V$ – объем тела, погруженного в среду, $м^3$;
$g$ – ускорение свободного падения, $м/с^2$.

Выталкивающая сила, действующая на тело, противоположна по направлению силе тяжести, поэтому поведение погруженного тела в среде зависит от соотношения модулей силы тяжести $F_T$ и Архимедовой силы $F_A$. Здесь возможны три случая:

$F_T$ > $F_A$. Сила тяжести превышает выталкивающую силу, следовательно, тело тонет/падает;
$F_T$ = $F_A$. Сила тяжести уравнивается с выталкивающей силой, поэтому тело «зависает» в жидкости;
$F_T$

Сценарий к уроку по физике “Сила Архимеда. Закон Архимеда”.

Сценарий открытого урока.

Физика. 7 класс. Закон Архимеда.

Этап урока.

(номер слайда)

Контрольные вопросы.

Краткое содержание.

Действие учащихся.

Примерные ответы.

Контроль

Времени

(мин)

1. Приветствие.

Организационная часть.

– Приготовились к занятию. Подровнялись. Настроились на занятие. Здравствуйте. Присаживайтесь.

– Староста готовит список отсутствующих.

Подготовка к занятию.

Приветствие.

2. проверка готовности Д/З

(Слайды 2-4)

Обозначьте тему прошлого урока

Вопросы:

1. Какое действие оказывают жидкости и газа на погруженное в них тело?

2. Обозначьте направление действующих на тело сил и укажите результирующий вектор силы.

3.Как вычислить величину выталкивающей силы? Расчетная формула. Связь с весом жидкости.(вывод формулы)

4. Как экспериментально можно обнаружить выталкивающую силу, действующую на помещенное в жидкость тело?

– действие выт. Силы на погруженное в жидкость тело

– выталкивающее

– делают рисунок на доске

– на доске расчетная формула

– опыт по обнаружению силы

Словесно либо наглядно

3.Цели урока

(слайд 5)

– итак, вместе мы вспомнили физическую природу возникновения выталкивающей силы, действующею со стороны жидкости или газа на погруженное в них тело.

Считается, что данную силу открыл древнегреческий ученый, философ, математик – Архимед. И сила получила название в честь своего первооткрывателя – Архимедова сила.

Сейчас откройте тетради. На полях – дату.

Тема сегодняшнего урока сила Архимеда. Закон Архимеда.

Что это за сила?

Отлично, теперь следует установить цели урока, чтобы исследовать силу архимеда на практике.

К примеру, мы изучили ее в теории, а как она выглядит на практике? Какую цель поставим?

Данная сила не имеет постоянного значения и в различных условиях среды и на разные тела она действует не одинаково. Какую задачу здесь установим?

А следует ли знать, где возможно применять полученные знания?? Какую задачу поставим здесь перед собой?

И последнее, собрав информацию из наших исследований исследованию, где стоит ее применять? В рамках предмета физики.

И это еще одна наша задача урока.

Обсуждение целей

Проводят необходимые записи в тетрадь

Это выталкивающая сила

обнаружить наличие силы, выталкивающей тело из жидкости на опытах;

установить от каких факторов она зависит;

обозначить области применения Архимедовой силы;

применить полученные знания для решения различных типов задач

4. ОНЗ

(слайды

6 – 13)

– Архимедова сила. (слайды 6)

– Сообщение учащихся Легенда об Архимеде.(слайд 7-10 история)

Опыт и вывод по легенде (слайд 11-13)

– запись в тетрадь

-сообщение учащегося «Легенда об Архимеде»

-записывают выводы опытов

5. Опытные установки

Слайды 14-15

Слайд 18 изменение веса тела

Слайд 19 опыт с ведерком

Участвуют в обсуждении. Помогают проводить анализ проводимым опытам

6. ОНЗ

(Слайд 16-18 )

следствие опытов

Закон Архимеда, сила Архимеда.

Записывают выводы по проделанным опытам

7 выводы

Слайд 19

– перед нами список параметров системы.

Оцените зависимость архимедовой силы от перечисленных пунктов.

Слайд 20 (ответ)

Слайд 21 повторительный вывод

Анализируют и расставляют зависимость силы. Записи проводят в рабочую тетрадь

область применения выталкивающей силы

Слайд 22

Демонстрация воздушного шара с гелием.

-давайте обсудим и определим – где возможно применение архимедовой силы.

Аэродинамика (летательные аппараты)

Гидродинамика (судоходство)

9. Патриотическое воспитание

Слайд 23-24

Перед нами портреты ученых. Российских. Внесших значимый вклад в развитие гидро-аэродинамики.

Существует даже такое понятие – эпоха Бернулли-Эйлера. Это обоснованно большим прогрессом развитии науки в области гидро-аэродинамики.

Стоит отметить вклад таких деятелей как Можайский Александр Федорович и Циолковский Константин Эдуардович.

Записывают необходимую информацию, дополняют.

10. применение знаний на практике.

(Слайды 25-30)

– итак, пред нами ряд фотоиллюстраций.

Что вы видите с точки зрения физики?

Где возможно такое действие?

А в нашем регионе?

Предлагаю рассчитать выталкивающую силу в данных озерах.

Что для этого нужно знать?

Используем дополнительную информацию.

Действие выталкивающей силы.

В соленой воде. Море.

Мертвое море. озеро Эльтон. озеро Баскунчак.

Плотность воды. Объем человека.

11. качественные задачи

Слайды 31-34

1) Одинаковы

2) Лед, дерево, пробка

3) Сила Архимеда и сила тяжести

4) 20 Н

12. Рефлексия

СЛАЙД 35

Что вы узнали сегодня на уроке?

Чему научились?

Что для вас было наиболее сложным?

13. домашнее задание выставление оценок.

СЛАЙД 36

§ 50, 51, упр.26 (3-5),

Читать раздел «Это интересно».

Итого:

Вычисление силы Архимеда

В предыдущем параграфе мы назвали две формулы, при помощи которых силу Архимеда можно измерить. Теперь выведем формулу, при помощи которой силу Архимеда можно вычислить.

Закон Архимеда для жидкости выражается формулой (см. § 3-е):

Fарх = Wж

Примем, что вес вытесненной жидкости равен действующей силе тяжести:

Wж = Fтяж = mжg

Масса вытесненной жидкости может быть найдена из формулы плотности:

r = m/V Ю mж = rжVж

Подставляя формулы друг в друга, получим равенство:

Fарх = Wж = Fтяж = mж g = rжVж g

Выпишем начало и конец этого равенства:

Fарх = rж gVж

Вспомним, что закон Архимеда справедлив для жидкостей и газов. Поэтому вместо обозначения «rж» более правильно использовать «rж/г». Также заметим, что объём жидкости, вытесненной телом, в точности равен объёму погруженной части тела: Vж = Vпчт. С учётом этих уточнений получим:

Fарх – архимедова сила, Н
rж/г – плотность жидкости, кг/м3
g – коэффициент силы тяжести, Н/кг
Vпчт – объём погруженной части тела, м3

Итак, мы вывели частный случай закона Архимеда – формулу, выражающую способ вычисления силы Архимеда. Вы спросите: почему же эта формула – «частный случай», то есть менее общая?

Поясним примером. Вообразим, что мы проводим опыты в космическом корабле. Согласно формуле Fарх = Wж, архимедова сила равна нулю (так как вес жидкости равен нулю), согласно же формуле Fарх = rж/г gVпчт архимедова сила нулю не равна, так как ни одна из величин (r, g, V) в невесомости в ноль не обращается. Перейдя от воображаемых опытов к настоящим, мы убедимся, что справедлива именно общая формула.

Продолжим наши рассуждения и выведем ещё один частный случай закона Архимеда. Посмотрите на рисунок. Поскольку бревно находится в покое, следовательно, на него действуют уравновешенные силы – сила тяжести и сила Архимеда. Выразим это равенством:

Fарх = Fтяж

Или, подробнее:

rж gVпчт = mт g

Разделим левую и правую части равенства на коэффициент «g»:

rж Vпчт = mт

Вспомнив, что m = rV, получим равенство:

rж Vпчт = rт Vт

Преобразуем это равенство в пропорцию:

В левой части этой пропорции стоит дробь, показывающая долю, которую составляет объём погруженной части тела от объёма всего тела. Поэтому всю дробь называют погруженной долей тела:

Используя эту формулу, предскажем, чему должна быть равна погруженная доля бревна при его плавании в воде:

ПДТ (полена) » 500 кг/м³ : 1000 кг/м³ = 0,5

Число 0,5 означает, что плавающее в воде бревно погружено наполовину. Так предсказывает теория, и это совпадает с практикой.

Итак, обе формулы в рамках являются менее общими, чем исходная, то есть имеют более узкие границы применимости. Почему же так произошло? Причина – применение нами формулы W = F_тяж. Вспомним, что она не верна, если тело или его опора (подвес) движутся непрямолинейно (см. § 3-г). Упоминавшийся нами космический корабль именно так и движется – по круговой орбите вокруг Земли.

14.6: Принцип Архимеда и плавучесть

Цели обучения

Определить выталкивающую силу
Государственный принцип Архимеда
Опишите взаимосвязь между плотностью и принципом Архимеда

При помещении в жидкость некоторые объекты плавают под действием выталкивающей силы. Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары (Рисунок \ (\ PageIndex {1} \))?

Рисунок \ (\ PageIndex {1} \): (a) Даже тонущие объекты, такие как этот якорь, при погружении частично поддерживаются водой.(b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию. (c) наполненные гелием воздушные шары тянут вверх свои струны, демонстрируя плавучесть воздуха. (Фото b: модификация работы Allied Navy; кредит c: модификация работы Crystl / Flickr)

Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта.На любой объект в любой жидкости действует восходящая сила, или выталкивающая сила , (рисунок \ (\ PageIndex {2} \)). Если выталкивающая сила превышает вес объекта, объект поднимается на поверхность и плавает. Если подъемная сила меньше веса объекта, объект тонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила присутствует всегда, независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.

Плавучая сила

Выталкивающая сила – это сила, направленная вверх на любой объект в любой жидкости.

Рисунок \ (\ PageIndex {2} \): Давление из-за веса жидкости увеличивается с глубиной, потому что \ (p = h \ rho g \). Это изменение давления и связанная с ним направленная вверх сила в нижней части цилиндра больше, чем направленная вниз сила в верхней части цилиндра. Разница в силе приводит к выталкивающей силе F _B. (Горизонтальные силы отменяются.)

Принцип Архимеда

Насколько велика сила подъема? Чтобы ответить на этот вопрос, подумайте, что происходит, когда погруженный объект удаляется из жидкости, как показано на рисунке \ (\ PageIndex {3} \).Если бы объект не находился в жидкости, пространство, которое занимал объект, было бы заполнено жидкостью, имеющей вес _или. Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться w _fl, весу жидкости, вытесняемой объектом.

Принцип Архимеда

Выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен

\ [F_ {B} = w_ {fl}, \]

, где F _B – подъемная сила, а w _fl – вес жидкости, вытесняемой объектом.

Этот принцип назван в честь греческого математика и изобретателя Архимеда (ок. 287–212 гг. До н. Э.), Который сформулировал этот принцип задолго до того, как были утвердились концепции силы.

Рисунок \ (\ PageIndex {3} \): (a) Объект, погруженный в жидкость, испытывает выталкивающую силу F _B. Если F _B больше веса объекта, объект поднимается. Если F _B меньше веса объекта, объект тонет. (b) Если объект удален, его заменяют жидкостью массой _и.Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться весу вытесняемой жидкости.

Принцип Архимеда относится к силе плавучести, которая возникает, когда тело частично или полностью погружается в жидкость. Сила, обеспечивающая давление жидкости, действует на тело перпендикулярно поверхности тела. Другими словами, сила, создаваемая давлением внизу, направлена вверх, тогда как вверху сила, обусловленная давлением, направлена вниз; силы из-за давления по бокам направлены внутрь тела.

Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на рисунке \ (\ PageIndex {2} \ ). Следовательно, на тело действует чистая направленная вверх сила. Эта направленная вверх сила является силой плавучести или просто плавучести .

Восклицательный знак «Эврика» (означающий «Я нашел это») часто приписывался Архимеду, когда он сделал открытие, которое привело к принципу Архимеда.Некоторые говорят, что все началось в ванне. Чтобы прочитать историю, изучите журнал Scientific American, чтобы узнать больше.

Плотность и принцип Архимеда

Если вы уроните кусок глины в воду, он утонет. Но если вылепите из того же куска глины форму лодки, она будет плавать. Из-за своей формы глиняная лодка вытесняет больше воды, чем кусок, и испытывает большую выталкивающую силу, хотя ее масса такая же. То же самое и со стальными кораблями.

Средняя плотность объекта – это то, что в конечном итоге определяет, плавает ли он.Если средняя плотность объекта меньше, чем у окружающей жидкости, он будет плавать. Причина в том, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, выталкивающая сила, равная весу вытесняемой жидкости, превышает вес объекта. Точно так же утонет предмет, более плотный, чем жидкость.

Степень погружения плавающего объекта в воду зависит от того, как плотность объекта сравнивается с плотностью жидкости.На рисунке \ (\ PageIndex {4} \), например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем при загрузке. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения – это отношение погруженного объема к объему объекта, или

\ [дробь \; погруженный = \ frac {V_ {sub}} {V_ {obj}} = \ frac {V_ {fl}} {V_ {obj}} \ ldotp \]

Погруженный объем равен объему вытесненной жидкости, который мы называем V _fl.Теперь мы можем получить соотношение между плотностями, подставив \ (\ rho = \ frac {m} {V} \) в выражение. Это дает

\ [\ frac {V_ {fl}} {V_ {obj}} = \ frac {\ frac {m_ {fl}} {\ rho_ {fl}}} {\ frac {m_ {obj}} {\ rho_ { obj}}}, \]

где \ (\ rho_ {obj} \) – средняя плотность объекта, а \ (\ rho_ {fl} \) – плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя

\ [дробь \; погруженный = \ frac {\ rho_ {obj}} {\ rho_ {fl}} \ ldotp \]

Мы можем использовать это соотношение для измерения плотности.

Рисунок \ (\ PageIndex {4} \): незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).

Пример 14.4: Расчет средней плотности

Предположим, что женщина весом 60,0 кг плавает в пресной воде с погружением 97,0% ее объема, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?

Стратегия

Плотность женщины можно найти, решив уравнение

\ [дробь \; погруженный = \ frac {\ rho_ {obj}} {\ rho_ {fl}} \]

для плотности объекта.{3} \ ldotp \]

Значение

Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.

Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе, ” назвать несколько. Менее очевидный пример – горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.

Измерение плотности

Один из наиболее распространенных методов определения плотности показан на рисунке \ (\ PageIndex {5} \).

Рисунок \ (\ PageIndex {5} \): (a) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.

Предмет, в данном случае монета, взвешивается на воздухе, а затем снова взвешивается, будучи погруженным в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости.Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.

Все эти расчеты основаны на принципе Архимеда, который гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что при погружении объект кажется меньше весит; мы называем это измерение кажущимся весом объекта. Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости.То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Принцип Архимеда | Безграничная физика

Плавучесть и принцип Архимеда

Выталкивающая сила, действующая на объект, может быть рассчитана по принципу Архимеда.

Цели обучения

Рассчитать направление подъемной силы

Основные выводы

Ключевые моменты

Сила плавучести вызвана давлением жидкости, в которую погружен объект.
Сила плавучести всегда направлена вверх, потому что давление жидкости увеличивается с глубиной.
Вы можете рассчитать выталкивающую силу либо напрямую, вычислив силу, действующую на каждую из поверхностей объекта, либо косвенно, найдя вес вытесненной жидкости.

Ключевые термины

выталкивающая сила : восходящая сила, создаваемая жидкостью, которая противодействует весу погруженного объекта.
Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.

Когда вы встаете после принятия теплой ванны, ваши руки могут казаться странно тяжелыми. Этот эффект связан с потерей плавучести воды. Что создает эту плавучую силу? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары?

Подъемная сила: причина и расчет

Мы находим ответы на поставленные выше вопросы в том факте, что в любой данной жидкости давление увеличивается с глубиной.Когда объект погружен в жидкость, восходящая сила на нижней части объекта больше, чем направленная вниз сила на верхнюю часть объекта. Результатом является чистая направленная вверх сила (выталкивающая сила) на любой объект в любой жидкости. Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать. Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине.Выталкивающая сила всегда присутствует в жидкости, независимо от того, плавает ли объект, тонет или остается в подвешенном состоянии.

Выталкивающая сила – это результат давления жидкости. Жидкость толкает погружаемый объект со всех сторон, но по мере того, как давление увеличивается с глубиной, толчок сильнее на нижней поверхности объекта, чем на верхней (как показано на рисунке).

Вы можете рассчитать выталкивающую силу, действующую на объект, сложив силы, действующие на все стороны объекта. Например, рассмотрим объект, показанный в.2}} [/ latex] – ускорение свободного падения. Величина силы на верхней поверхности:

[латекс] \ text {F} _1 = \ text {P} _1 \ text {A} = \ text {h} _1 \ rho \ text {g} \ text {A} [/ latex].

Эта сила направлена вниз. Аналогичным образом сила на нижней поверхности:

[латекс] \ text {F} _2 = \ text {P} _2 \ text {A} = \ text {h} _2 \ rho \ text {g} \ text {A} [/ latex]

и указывает вверх. Поскольку он имеет цилиндрическую форму, результирующая сила на сторонах объекта равна нулю – силы на разных частях поверхности противостоят друг другу и точно компенсируются.Таким образом, чистая направленная вверх сила, действующая на цилиндр со стороны жидкости, составляет:

[латекс] \ text {F} _ \ text {B} = \ text {F} _2 – \ text {F} _1 = \ rho \ text {g} \ text {A} (\ text {h} _2 – \ text {h} _1) [/ latex]

Принцип Архимеда

Хотя вычисление выталкивающей силы таким способом всегда возможно, часто бывает очень сложно. Более простой метод следует из принципа Архимеда, который гласит, что выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.Другими словами, чтобы вычислить выталкивающую силу, действующую на объект, мы предполагаем, что погруженная часть объекта состоит из воды, а затем вычисляем вес этой воды (как показано на рисунке).

Принцип Архимеда : Выталкивающая сила на корабле (а) равна весу воды, вытесняемой судном – показано пунктирной областью на (b).

Принцип можно представить в виде формулы:

[латекс] \ text {F} _ \ text {B} = \ text {w} _ \ mathrm {\ text {fl}} [/ latex]

Обоснование принципа Архимеда состоит в том, что выталкивающая сила, действующая на объект, зависит от давления, оказываемого жидкостью на его погруженную поверхность.Представьте, что мы заменяем погруженную часть объекта жидкостью, в которой он содержится, как в (b). Сила плавучести на этом количестве жидкости должна быть такой же, как на исходном объекте (корабле). Однако мы также знаем, что выталкивающая сила, действующая на жидкость, должна быть равна ее весу, поскольку жидкость не тонет сама по себе. Следовательно, выталкивающая сила, действующая на исходный объект, равна весу «вытесненной жидкости» (в данном случае воды внутри пунктирной области (b)).

Принцип Архимеда применим для любой жидкости – не только для жидкостей (например, воды), но и для газов (например, воздуха).Мы исследуем это дальше, когда будем обсуждать приложения этого принципа в следующих разделах.

Принцип Архимеда – простой пример : Мы используем принцип Архимеда, чтобы определить количество пингвинов, которое может выдержать ледяной поплавок.

Полное погружение

Сила плавучести на полностью погруженном объекте объема равна [latex] \ text {F} _ \ text {B} = \ text {V} \ rho \ text {g} [/ latex].

Цели обучения

Определение факторов, определяющих выталкивающую силу на полностью погруженном в воду объекте

Основные выводы

Ключевые моменты

Если объект полностью погружен в воду, объем вытесненной жидкости равен объему объекта.
Сила плавучести воздушных шаров, дирижаблей и других объектов может быть рассчитана, если предположить, что они полностью погружены в воздух.
Сила плавучести не зависит от формы объекта, только от его объема.

Ключевые термины

Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.

Принцип Архимеда легче всего понять и применить в случае полностью погруженных объектов.В этом разделе мы обсудим несколько важных примеров. В общем, сила плавучести для полностью погруженного объекта определяется по формуле:

[латекс] \ text {F} _ \ text {B} = \ text {V} \ rho \ text {g}, [/ latex]

где [latex] \ text {V} [/ latex] – это объем объекта, [latex] \ rho [/ latex] – это плотность жидкости, а [latex] \ text {g} [/ latex] – ускорение свободного падения. Это непосредственно следует из принципа Архимеда и того факта, что объект полностью погружен (и поэтому объем вытесненной жидкости – это просто объем объекта).

Цилиндр

В предыдущем разделе мы рассчитали выталкивающую силу, действующую на цилиндр (показан на), рассматривая силу, действующую на каждую из сторон цилиндра. Теперь мы рассчитаем эту силу, используя принцип Архимеда. Сила плавучести на цилиндре равна весу вытесняемой жидкости. Этот вес равен массе вытесненной жидкости, умноженной на ускорение свободного падения:

Выталкивающая сила : Жидкость толкает подводный объект со всех сторон.Однако, поскольку давление увеличивается с глубиной, толчок вверх на нижней поверхности (F2) больше, чем толчок вниз на верхней поверхности (F1). Следовательно, чистая выталкивающая сила всегда направлена вверх.

[латекс] \ text {F} _ \ text {B} = \ text {w} _ \ mathrm {\ text {fl}} = \ text {m} _ \ mathrm {\ text {fl}} \ text { g} [/ латекс]

Масса вытесненной жидкости равна ее объему, умноженному на ее плотность:

[латекс] \ text {m} _ \ mathrm {\ text {fl}} = \ text {V} _ \ mathrm {\ text {fl}} \ rho [/ latex].

Однако (, и это критический момент ), цилиндр полностью погружен, поэтому объем вытесненной жидкости равен объему цилиндра (см.), И:

Принцип Архимеда : Объем вытесненной жидкости (b) равен объему исходного цилиндра (a).

[латекс] \ text {m} _ \ mathrm {\ text {fl}} = \ text {V} _ \ mathrm {\ text {fl}} \ rho = \ text {V} _ \ mathrm {\ text { цилиндр}} \ rho [/ латекс].

Объем цилиндра – это площадь его основания, умноженная на его высоту, или в нашем случае:

[латекс] \ text {V} _ \ mathrm {\ text {цилиндр}} = \ text {A} (\ text {h} _2 – \ text {h} _1) [/ latex].

Следовательно, подъемная сила на цилиндре равна:

[латекс] \ text {F} _ \ text {B} = \ text {m} _ \ mathrm {\ text {fl}} \ text {g} = \ text {V} _ \ mathrm {\ text {цилиндр }} \ rho \ text {g} = (\ text {h} _1 – \ text {h} _2) \ rho \ text {g} \ text {A} [/ latex].

Это тот же результат, который был получен в предыдущем разделе при рассмотрении силы из-за давления, оказываемого жидкостью.

Гелиевый дирижабль

Рассмотрим USS Macon, дирижабль, наполненный гелием (показан на). Его конверт («воздушный шар») содержал 184 059 штук.5 кубометров гелия. Если не брать в расчет небольшой объем гондолы, какова была сила плавучести у этого дирижабля? Если бы дирижабль весил 108 000 кг, сколько груза он мог бы нести? Предположим, что плотность воздуха составляет 1,225 кг на кубический метр. Сила плавучести дирижабля создается воздухом, в который он погружен. Хотя мы не знаем точной формы дирижабля, мы знаем его объем и плотность воздуха, поэтому можем рассчитать силу плавучести:

Гелиевый дирижабль : USS Macon, дирижабль 1930-х годов, наполненный гелием.5 \, \ mathrm {\ text {kg}} = 120 \, \ mathrm {\ text {tons}} [/ latex].

Флотация

Если выталкивающая сила превышает вес объекта, объект поднимается на поверхность и плавает. Если подъемная сила меньше веса объекта, объект тонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила присутствует всегда, независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.

Цели обучения

Выразите взаимосвязь между выталкивающей силой и весом для плавучего объекта

Основные выводы

Ключевые моменты

Доля объема погруженного объекта определяется отношением его средней плотности к плотности жидкости: [latex] \ bar {\ rho} _ \ mathrm {\ text {obj}} / \ rho_ \ mathrm { \ text {fl}} [/ latex].
Тонущий, плавающий или остающийся в подвешенном состоянии объект определяется путем сравнения выталкивающей силы и веса объекта.

Ключевые термины

Принцип Архимеда : Выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.

Почему одни объекты плавают, а другие – нет? Если вы положите металлическую монету в стакан с водой, она утонет. Но большинство кораблей построено из металла, и они плавают.Так как же это возможно?

Условия для плавучести

Объект будет плавать, если выталкивающая сила, оказываемая на него жидкостью, уравновешивает его вес, например, если [latex] \ text {F} _ \ text {B} = \ text {mg} [/ latex].

Но принцип Архимеда гласит, что подъемная сила – это вес вытесняемой жидкости. Итак, для плавающего объекта на жидкости вес вытесненной жидкости равен весу объекта. Таким образом, только в частном случае плавания подъемная сила, действующая на объект, равна его весу.Рассмотрим однотонный блок из твердого железа. Поскольку железо почти в восемь раз плотнее воды, при погружении оно вытесняет лишь 1/8 тонны воды, чего недостаточно, чтобы удерживать его на плаву. Предположим, тот же железный блок преобразован в чашу. Он все еще весит одну тонну, но когда его опускают в воду, он вытесняет больший объем воды, чем когда он был блоком. Чем глубже погружена железная чаша, тем больше воды она вытесняет и тем больше на нее действует выталкивающая сила. Когда подъемная сила равна одной тонне, он больше не тонет.

Когда любая лодка перемещает воду, равную ее собственному весу, она плывет. Это часто называют «принципом плавучести», когда плавающий объект вытесняет жидкость, равную его собственному весу. Каждый корабль, подводная лодка и дирижабль должны быть спроектированы так, чтобы перемещать жидкость, равную ее собственному весу. Корабль водоизмещением 10 000 тонн должен быть достаточно широким, чтобы вытеснить 10 000 тонн воды, прежде чем он погрузится слишком глубоко в воду. То же самое и с судами в воздухе (поскольку воздух – это жидкость): дирижабль весом 100 тонн вытесняет не менее 100 тонн воздуха; если больше смещается, то поднимается; если смещается меньше, то падает.Если дирижабль перемещает точно свой вес, он парит на постоянной высоте.

Флотация и плотность

Плотность играет решающую роль в принципе Архимеда. Средняя плотность объекта – это то, что в конечном итоге определяет, плавает ли он. Если его средняя плотность меньше, чем у окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит больше массы и, следовательно, больше веса в том же объеме. Таким образом, выталкивающая сила, равная весу вытесняемой жидкости, превышает вес объекта.Точно так же утонет предмет, более плотный, чем жидкость. Степень погружения плавающего объекта зависит от того, как плотность объекта связана с плотностью жидкости. Например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем, загруженным грузом. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения – это отношение погруженного объема к объему объекта, или

Плотность и погружение : незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).

[латекс] \ mathrm {\ text {дробь} \, \ text {submerged}} = \ frac {\ text {V} _ \ mathrm {\ text {sub}}} {\ text {V} _ \ mathrm { \ text {obj}}} = \ frac {\ text {V} _ \ mathrm {\ text {fl}}} {\ text {V} _ \ mathrm {\ text {obj}}} [/ latex]

Погруженный объем равен объему вытесненной жидкости, который мы называем [латексом] \ text {V} _ \ mathrm {\ text {fl}} [/ latex]. Теперь мы можем получить соотношение между плотностями, подставив в выражение [latex] \ rho = \ text {m} \ text {V} [/ latex]. Это дает

[латекс] \ mathrm {\ text {дробь} \, \ text {submerged}} = \ frac {\ text {m} _ \ mathrm {\ text {fl}} / \ rho_ \ mathrm {\ text {fl} }} {\ text {m} _ \ mathrm {\ text {obj}} / \ bar {\ rho} _ \ mathrm {\ text {obj}}} [/ latex]

где [латекс] \ bar {\ rho} _ \ mathrm {\ text {obj}} [/ latex] – это средняя плотность объекта, а [латекс] \ rho_ \ mathrm {\ text {fl}} [/ latex ] – плотность жидкости.Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя

[латекс] \ mathrm {\ text {дробь} \, \ text {submerged}} = \ frac {\ bar {\ rho} _ \ mathrm {\ text {obj}}} {\ rho_ \ mathrm {\ text { fl}}} [/ латекс].

В связи с этим выражением следует отметить несколько моментов:

Обратите внимание, что здесь упоминается средняя плотность объекта. Это может быть намного меньше плотности материала, из которого сделан объект. Например, стальной корабль на самом деле в основном заполнен воздухом (подумайте о коридорах, грузовых трюмах и т. Д.), поэтому его средняя плотность находится между плотностью воздуха и стали. Точнее, средняя плотность определяется как общая масса объекта, деленная на его общий объем: [latex] \ bar {\ rho} = \ text {m} / \ text {V} [/ latex].
Эта формула имеет смысл, только если плотность объекта меньше плотности жидкости. В противном случае доля погруженного в воду становится больше единицы – признак того, что объект вообще не плавает, а тонет!

14.4 Принцип Архимеда и плавучесть – University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

Определить выталкивающую силу
Государственный принцип Архимеда
Опишите взаимосвязь между плотностью и принципом Архимеда

При помещении в жидкость некоторые объекты плавают под действием выталкивающей силы.Откуда эта подъемная сила? Почему одни вещи плавают, а другие нет? Получают ли тонущие предметы какая-либо поддержка от жидкости? Поддерживает ли ваше тело атмосфера или действуют только гелиевые шары ((Рисунок))?

Рис. 14.19 (a) Даже тонущие предметы, такие как этот якорь, при погружении частично поддерживаются водой. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), чтобы они могли плавать или тонуть по желанию. (c) наполненные гелием воздушные шары тянут вверх свои струны, демонстрируя плавучесть воздуха.(Фото b: модификация работы Allied Navy; кредит c: модификация работы Crystl / Flickr)

Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что направленная вверх сила на нижнюю часть объекта в жидкости больше, чем направленная вниз сила на верхнюю часть объекта. На любой объект в любой жидкости действует восходящая сила или выталкивающая сила () ((рисунок)). Если выталкивающая сила превышает вес объекта, объект поднимается на поверхность и плавает.Если подъемная сила меньше веса объекта, объект тонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила присутствует всегда, независимо от того, плавает ли объект, тонет или находится во взвешенном состоянии в жидкости.

Подъемная сила

Выталкивающая сила – это сила, направленная вверх на любой объект в любой жидкости.

Рисунок 14.20 Давление из-за веса жидкости увеличивается с глубиной, потому что

.Это изменение давления и связанная с ним направленная вверх сила в нижней части цилиндра больше, чем направленная вниз сила в верхней части цилиндра. Разница в силе дает подъемную силу

. (Горизонтальные силы отменяются.)

Принцип Архимеда

Насколько велика сила подъема? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект удаляется из жидкости, как показано на (Рисунок). Если бы объект не находился в жидкости, пространство, которое занимал объект, было бы заполнено жидкостью, имеющей вес

Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться

вес жидкости, вытесняемой объектом.

Принцип Архимеда

где

– подъемная сила и

– это вес жидкости, вытесняемой объектом.

Рис. 14.21 (a) Объект, погруженный в жидкость, испытывает выталкивающую силу.

Если

больше веса объекта, объект поднимается. Если

меньше веса объекта, объект тонет. (b) Если объект удален, он заменяется жидкостью весом

Поскольку этот вес поддерживается окружающей жидкостью, подъемная сила должна равняться весу вытесняемой жидкости.

Поскольку нижняя часть корпуса находится на большей глубине, чем верхняя часть корпуса, давление в нижней части корпуса выше, чем давление в верхней части, как показано на (Рисунок).Следовательно, на тело действует чистая направленная вверх сила. Эта направленная вверх сила является силой плавучести или просто плавучести .

Плотность и принцип Архимеда

Степень погружения плавающего объекта в воду зависит от того, как плотность объекта сравнивается с плотностью жидкости.На (Рисунок), например, разгруженное судно имеет меньшую плотность и меньше погружено в воду по сравнению с тем же кораблем при загрузке. Мы можем получить количественное выражение для погруженной фракции, рассматривая плотность. Доля погружения – это отношение погруженного объема к объему объекта, или

Погруженный объем равен объему вытесненной жидкости, который мы называем

. Теперь мы можем получить соотношение между плотностями, подставив

в выражение.Это дает

где

– средняя плотность объекта и

– плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, оставляя

Мы можем использовать это соотношение для измерения плотности.

Рисунок 14.22 Незагруженное судно (a) плавает в воде выше, чем загруженное судно (b).

Пример

Расчет средней плотности

Стратегия

Плотность женщины можно найти, решив уравнение

для плотности объекта. Это дает

Нам известны и доля погруженной воды, и плотность воды, поэтому мы можем рассчитать плотность женщины.

Решение

Вводя известные значения в выражение для ее плотности, получаем

Значение

Плотность женщины меньше плотности жидкости. Мы ожидаем этого, потому что она плавает.

Многочисленные объекты или вещества с более низкой плотностью плавают в жидкостях с более высокой плотностью: масло на воде, воздушный шар в атмосфере, кусочек пробки в вине, айсберг в соленой воде и горячий воск в «лавовой лампе, ” назвать несколько. Менее очевидный пример – горные хребты, плавающие на более плотной коре и мантии под ними.Даже кажущаяся твердой Земля обладает жидкими характеристиками.

Измерение плотности

Один из наиболее распространенных методов определения плотности показан на (Рисунок).

Рис. 14.23 (a) Монета взвешивается в воздухе. (b) Кажущийся вес монеты определяется, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.

Предмет, в данном случае монета, взвешивается на воздухе, а затем снова взвешивается, будучи погруженным в жидкость.Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Мы можем использовать этот же метод для определения плотности жидкости, если известна плотность монеты.

Все эти расчеты основаны на принципе Архимеда, который гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой жидкости. Это, в свою очередь, означает, что при погружении объект кажется меньше весит; мы называем это измерение кажущимся весом объекта.Объект испытывает кажущуюся потерю веса, равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы, равную массе вытесненной жидкости. То есть кажущаяся потеря веса равна массе вытесненной жидкости, или кажущаяся потеря массы равна массе вытесненной жидкости.

Сводка

Подъемная сила – это чистая направленная вверх сила на любой объект в любой жидкости. Если выталкивающая сила превышает вес объекта, объект поднимется на поверхность и будет плавать.Если подъемная сила меньше веса объекта, объект утонет. Если выталкивающая сила равна весу объекта, объект может оставаться в подвешенном состоянии на своей текущей глубине. Выталкивающая сила всегда присутствует и действует на любой объект, частично или полностью погруженный в жидкость.
Принцип Архимеда гласит, что подъемная сила, действующая на объект, равна весу жидкости, которую он вытесняет.

Концептуальные вопросы

Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста.Противоречит ли это принципу Архимеда? Поясните свой ответ.

[показывать-ответ q = ”fs-id1170958074520 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1170958074520 ″]

Вовсе нет. Принцип Паскаля гласит, что изменение давления происходит через жидкость. Причина, по которой полный бак требует большего усилия для вытягивания пробки, заключается в весе воды над пробкой.

[/ hidden-answer]

Обладают ли жидкости подъемной силой в «невесомой» среде, например, в космическом шаттле? Поясните свой ответ.

Будет ли один и тот же корабль плавать в соленой воде выше, чем в пресной? Поясните свой ответ.

[показывать-ответ q = ”fs-id1170958707558 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1170958707558 ″]

Выталкивающая сила равна весу вытесняемой жидкости. Чем больше плотность жидкости, тем меньше жидкости необходимо вытеснить, чтобы удерживать вес объекта и плавать. Поскольку плотность соленой воды выше, чем плотность пресной, будет вытеснено меньше соленой воды, и корабль будет плавать выше.

[/ hidden-answer]

Шарики упали на дно в частично заполненную раковину ванны. Часть их веса поддерживается выталкивающей силой, но сила, направленная вниз на дно ванны, увеличивается ровно на вес шариков. Объяснить, почему.

Проблемы

Какая часть льда погружается в воду, когда плавает в пресной воде, учитывая плотность воды

очень близко к

Если тело человека имеет плотность

, какая часть тела будет погружена в воду при плавном плавании в (а) пресной воде? (б) В соленой воде плотностью

[show-answer q = ”fs-id1170958875108 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1170958875108 ″]

а.99,5% погружено; б. 96,9% погружено

[/ hidden-answer]

Камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? (c) Какова его средняя плотность? Соответствует ли это стоимости гранита?

Принцип Архимеда можно использовать для расчета плотности жидкости, а также твердого тела. Предположим кусок железа массой 390.Установлено, что 0 г в воздухе имеет кажущуюся массу 350,5 г при полном погружении в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (б) Каков объем железа с учетом его плотности, указанной на (Рисунок)? (c) Рассчитайте плотность жидкости и определите ее.

[показывать-ответ q = ”fs-id1170958537912 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1170958537912 ″]

а. 39,5 г; б.

; c.

; этиловый спирт
[/ hidden-answer]

Рассчитайте выталкивающую силу по 2.00-L гелиевый шар. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова чистая вертикальная сила, действующая на воздушный шар, если он отпущен? Пренебрегайте объемом резины.

Какова плотность женщины, плавающей в пресной воде с

 *** QuickLaTeX не может составить формулу:
\ [4.00 \ текст {%} \]

*** Сообщение об ошибке:
Файл завершился при сканировании использования \ text @.
Экстренная остановка.

ее объема над поверхностью? (Это можно измерить, поместив ее в резервуар с отметками сбоку, чтобы измерить, сколько воды она вытесняет при плавании и под водой.) (б) Какой процент ее объема находится над поверхностью, когда она плавает в морской воде?

[показывать-ответ q = ”fs-id1170958861223 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1170958861223 ″]

а.

; б. 6,34%; В морской воде она плавает выше.
[/ hidden-answer]

Человек имеет массу 80 кг и плотность

(без учета воздуха в легких). (а) Рассчитайте его объем. (b) Найдите подъемную силу, которую оказывает на него воздух.в) Какое отношение подъемной силы к его весу?

Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки будет погружена в воду при плавании в воде? (b) Если пробка имеет массу 10,0 г и на нее помещен магнит весом 20,0 г, какая часть пробки будет погружена в воду? (c) Будут ли стержневой магнит и пробка плавать в этиловом спирте?

[показывать-ответ q = ”fs-id1170958808514 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1170958808514 ″]

а.0,24; б. 0,68; c. Да, пробка будет плавать в этиловом спирте.

[/ hidden-answer]

Какой процент веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?

Ссылаясь на (рисунок), докажите, что выталкивающая сила на цилиндр равна весу вытесняемой жидкости (принцип Архимеда). Вы можете предположить, что подъемная сила равна

и концы цилиндра имеют равные площади

.Обратите внимание, что объем цилиндра (и жидкости, которую он вытесняет) равен

[показывать-ответ q = ”fs-id1170958626937 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1170958626937 ″]

[/ hidden-answer]

Мужчина весом 75,0 кг плавает в пресной воде, при этом 3,00% его объема над водой, когда его легкие пусты, и 5,00% его объема над водой, когда его легкие полны. Вычислите объем вдыхаемого им воздуха, называемый объемом его легких, в литрах.(б) Кажется ли этот объем легких разумным?

Глоссарий

Принцип Архимеда: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости

подъемная сила: чистая направленная вверх сила на любой объект в любой жидкости из-за разницы давлений на разной глубине

Определение принципа Архимеда в физике.

Примеры принципа Архимеда в следующих темах:

Плавучесть и принцип Архимеда
- Выталкивающая сила, действующая на объект, может быть рассчитана по принципу Архимеда .
- Более простой метод следует из принципа Архимеда , который гласит, что выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.
- Обоснование принципа Архимеда заключается в том, что выталкивающая сила, действующая на объект, зависит от давления, оказываемого жидкостью на его погруженную поверхность.
- Принцип Архимеда Принцип применим для любой жидкости – не только для жидкостей (например, воды), но и для газов (например, воздуха).
- Мы используем принцип Архимеда ‘ , чтобы определить количество пингвинов, которое может выдержать ледяной плавучий объект.
Полное погружение
- Принцип Архимеда Принцип проще всего понять и применить в случае полностью погруженных объектов.
- Это непосредственно следует из принципа Архимеда ‘ и того факта, что объект полностью погружен (и поэтому объем вытесненной жидкости – это просто объем объекта).
- Теперь мы рассчитаем эту силу, используя принцип Архимеда ‘ .
Флотация
- Но принцип Архимеда утверждает, что выталкивающая сила – это вес вытесняемой жидкости.
- Это часто называют «принципом плавучести », когда плавучий объект вытесняет жидкость, равную его собственному весу.
- Плотность играет решающую роль в Принцип Архимеда ‘ .
Принцип Гюйгенса
- На рисунке 1 показан простой пример принципа Гюйгенса дифракции.
- Принцип можно показать с помощью следующего уравнения:
- Этот принцип работает для всех типов волн, а не только для световых.
- Принцип Гюйгенса применяется к прямому волновому фронту, отражающемуся в зеркале.
- Принцип Гюйгенса применяется к прямому волновому фронту.
Принцип Паскаля
- Принцип Паскаля утверждает, что давление передается и не уменьшается в замкнутой статической жидкости.
- Принцип Паскаля (или Закон Паскаля) применяется к статическим жидкостям и использует зависимость давления от высоты в статических жидкостях.
- С качественной точки зрения, принцип Паскаля утверждает, что давление в замкнутой статической жидкости передается в неизменном виде.
- Как указано в Принципе Паскаля , давление, приложенное к статической жидкости в закрытом контейнере, передается по всей жидкости.
- По принципу Паскаля , P1 = P2, что дает силу, создаваемую статической жидкостью F2, где F2> F1.
Принцип неопределенности Гейзенберга
- Неопределенность Принцип устанавливает базовый предел точности, с которой некоторые физические свойства частицы могут быть известны одновременно.
- Принцип неопределенности присущ свойствам всех волновых систем и возникает в квантовой механике просто из-за волновой природы материи всех квантовых объектов.
- Таким образом, принцип неопределенности фактически устанавливает фундаментальное свойство квантовых систем, а не утверждение об успехе современных технологий в наблюдениях.
- Принцип довольно нелогичен, поэтому первых исследователей квантовой теории пришлось заверить, что наивные измерения, нарушающие его, всегда были неработоспособны.
- Свяжите принцип неопределенности Гейзенберга с волновой природой материи всех квантовых объектов
Постулаты Эйнштейна
- Специальная теория относительности основана на двух постулатах Эйнштейна: Принципе относительности и Принципе инвариантной скорости света .
- Принцип Принцип относительности : Законы физики одинаковы и могут быть изложены в их простейшей форме во всех инерциальных системах отсчета.
- Принцип инвариантной скорости света: Скорость света c – постоянная величина, не зависящая от относительного движения источника и наблюдателя.
Суперпозиция сил
- Принцип суперпозиции (свойство суперпозиции) утверждает, что для всех линейных сил общая сила является векторной суммой отдельных сил.
- Принцип суперпозиции (также известный как свойство суперпозиции) гласит, что: для всех линейных систем суммарный ответ в данном месте и времени, вызванный двумя или более стимулами, представляет собой сумму ответов, которые были бы вызваны каждым стимулом. индивидуально.
- Следовательно, принцип предполагает, что общая сила – это векторная сумма отдельных сил.
- Принцип линейной суперпозиции позволяет расширить закон Кулона, чтобы включить любое количество точечных зарядов, чтобы получить силу, действующую на любой точечный заряд, путем векторного сложения этих отдельных сил, действующих только на этот точечный заряд.
- Примените принцип суперпозиции , чтобы определить общий ответ, вызванный двумя или более стимулами
Наложение полей
- Как векторные поля, электрические поля подчиняются принципу суперпозиции .
- Этот принцип гласит, что для всех линейных систем общий ответ на множественные стимулы в определенном месте и в определенное время равен сумме ответов, которые были бы вызваны каждым стимулом в отдельности.
- Следует отметить, что принцип суперпозиции применим к любой линейной системе, включая алгебраические уравнения, линейные дифференциальные уравнения и системы уравнений вышеупомянутых форм.
Сферические и плоские волны
- Принцип Гюйгена-Френеля показывает, что, когда волны взаимодействуют друг с другом, они интерферируют конструктивно или деструктивно.
- Принцип Гюйгена-Френеля использует закон преломления.

Принцип Архимеда – Видео по физике от Brightstorm

Хорошо, давайте поговорим о принципе Архимеда. Принцип Архимеда существует уже очень, очень давно, и он был очень важен для правителей Греции и Египта годы, годы и годы назад, и мы поговорим о том, почему, через минуту. Итак, Архимед сказал, что подъемная сила, действующая на что-то, равна весу вытесняющей жидкости. Что теперь означает подъемная сила? Выталкивающая сила – это чистая сила, действующая на объект, погруженный в жидкость.Хорошо, у нас есть сила от давления на дно и сила от давления сверху, мы складываем их вместе, нам нужна чистая сила, и это сила плавучести. Итак, Архимед сказал, что подъемная сила – это вес того, сколько жидкости вытесняет объект. Таким образом, подъемная сила равна весу вытесняемой жидкости. Ну что это? Ну, это плотность жидкости, умноженная на объем вытесненной жидкости. Итак, это объем объекта, погруженного в жидкость, умноженный на ускорение свободного падения.

Хорошо, теперь у нас есть 2 основные ситуации, в которых мы можем использовать принцип Архимеда, если объект полностью погружен, то есть весь объект погружен в жидкость, тогда смещенный объем равен объему объекта. Хорошо, теперь это действительно очень просто. Все, что мне нужно знать, это каков объем объекта, и все готово. С другой стороны, если объект плавает, это означает, что он не полностью погружен. Это означает, что смещенный объем на самом деле меньше всего объема, потому что часть его плавает наверху, мы сказали, что он плавает.Таким образом, в плавающей ситуации у нас всегда есть выталкивающая сила, равная весу объекта, потому что объект плавает. А это значит, что его вес должен компенсироваться восходящей силой, что это за восходящая сила? Это подъемная сила, так что это 2 отдельные ситуации, и они совершенно разные.

Мы увидим, что есть уравнения, которые вы можете вывести, которые совершенно верны, когда объект полностью погружен в воду, но не верны для плавающих объектов. Так что вам просто нужно быть осторожным с этим различием.Итак, почему принцип Архимеда верен? Что ж, мы можем взглянуть на ситуацию, в которой у нас есть объект, погруженный в такую жидкость, как эта, хорошо, теперь, какие силы действуют на этот объект, мы собираемся нарисовать диаграмму свободного тела, потому что мы хорошие физики, поэтому мы у нас есть вес, и у нас есть две силы, которые действуют от жидкости. Жидкость находится под давлением, поэтому давление внизу и давление вверху. Теперь давление – это сила на единицу площади, и она указывает в любом направлении.Итак, давление внизу, сила, действующая на объект, толкает вверх, потому что в этом направлении, я имею в виду, если он будет толкать объект хорошо, что, он будет толкать вверх, верно? Таким образом, восходящая сила – это давление внизу, умноженное на площадь, потому что сила равна давлению, умноженному на площадь.

Точно так же давление вверху давит вниз. Таким образом, направленная вниз сила – это давление вверху, умноженное на площадь. Теперь выталкивающая сила – это чистая сила, прикладываемая к объекту жидкостью, так что это означает, что она равна давлению внизу, умноженному на площадь, минус давление вверху, умноженное на площадь.Итак, область, которую я могу удалить, потому что она одинакова для верха и низа, это означает, что это изменение давления, умноженное на площадь. Теперь мы знаем, что когда вы погружаетесь в жидкость, давление увеличивается. Насколько прибавка? Что ж, изменение давления определяется плотностью жидкости, умноженной на ускорение из-за силы тяжести, умноженным на то, как далеко вы спустились. Теперь мы спустились на расстояние h, так что посмотрите, что у нас получилось. h, умноженное на a, это смещенный объем, поэтому это означает, что выталкивающая сила равна плотности жидкости, умноженной на ускорение силы тяжести, умноженному на объем смещенного объема.Итак, принцип Архимеда, а почему людям все равно? Одним из самых загадочных применений этого принципа в истории было определение плотности ценных предметов, таких как короны, вазы и тому подобное. Они сделаны из золота или меня пытаются обмануть?

Хорошо, вот идея, все, что вам нужно сделать, это взвесить объект в воздухе, а затем взвесить тот же объект, когда он всплывет в воду. Так почему это работает? Ну вот идея, когда я взвешиваю объект, в основном я делаю то, что у меня есть весы, и я пытаюсь измерить, сколько силы требуется мне, чтобы подвесить объект? Итак, у меня сила натяжения поднимается вверх от моей шкалы, а затем у меня опускается вес, и это должно быть равным друг другу.Когда я взвешиваю его в воздухе, сила натяжения равна мг, равна весу. А как насчет того, чтобы взвесить его в воде? Что ж, когда я взвешиваю его в воде, теперь у меня есть выталкивающая сила, и эта выталкивающая сила зависит от объема короны и плотности воды. Это означает, что у этой выталкивающей силы внутри него есть информация о плотности. Итак, когда я смотрю на это напряжение, это напряжение – это вес короны в воде. Он будет меньше, чем вес короны в воздухе, и разница будет в этой выталкивающей силе.И эта подъемная сила содержит информацию о плотности короны, которую я могу извлечь. И это принцип Архимеда.

Подъемная сила

Когда объект помещается в жидкость, жидкость оказывает восходящую силу, которую мы называем выталкивающей силой. Выталкивающая сила возникает из-за давления, оказываемого жидкостью на объект. Поскольку давление увеличивается с увеличением глубины, давление на нижнюю часть объекта всегда больше, чем сила наверху – отсюда чистая сила, направленная вверх.

Выталкивающая сила присутствует независимо от того, плавает ли объект или тонет. Давайте рассмотрим плавучий объект, но анализ в основном такой же для подводного объекта.

Мы также рассмотрим прямоугольный блок, хотя аналогичный (более сложный) анализ приводит к тому же результату для объектов смешной формы.

Объект испытывает силы с каждой из шести сторон. С каждой стороны сила – это давление, умноженное на площадь стороны, и направлена перпендикулярно стороне и внутрь объекта.

Силу на левой стороне сложно вычислить, потому что давление на разных уровнях разное. К счастью, нам не нужно рассчитывать это, потому что эта сила равна силе на правой стороне и противоположна ей. Точно так же силы спереди и сзади отменяются.

Для плавающего объекта сила на верхней поверхности области A направлена вниз и равна:

F _верх = P _атм A

Если дно объекта находится на глубине h ниже поверхности, сила на дне направлена вверх и равна:

F _нижний = (P _атм + rgh) A

Чистая сила, которую мы называем выталкивающей силой, направлена вверх и равна:

F _b = F _внизу – F _вверху = rgh A

га = объем жидкости, вытесненной блоком (погруженный объем)

Умножение объема жидкости на плотность жидкости r дает массу вытесненной жидкости.

F _b = rV _disp г = м _disp г

Это известно как принцип Архимеда: выталкивающая сила равна весу жидкости, вытесняемой объектом. Вы также можете видеть, что подъемная сила пропорциональна объему вытесненной жидкости.

Когда объект плавает, подъемная сила уравновешивает силу тяжести. Когда он тонет, сила тяжести побеждает.

Является ли принцип Архимеда законом природы? Обсуждения в «расширенной комнате учителя»

Подвергается ли присоска на дне ванны восходящей силе со стороны окружающей воды, даже если под ней нет воды? Вопрос студента, опубликованный в группе учителей в Facebook утром в понедельник, привел к обсуждению, в котором участвовал 21 комментарий, и в течение следующих нескольких дней 16 учителей предложили 225 ответов, включая несколько простых экспериментов, а также моделирование для оценки различных аргументов.Обсуждения, кратко изложенные в этом документе, представляют собой пример того, как социальные сети могут предоставить “ расширенную комнату для учителей ”, где учителя могут изучить и улучшить свое понимание в безопасной и в основном благоприятной среде, а также найти способы дать более подробные ответы на сложные вопросы. студенческие вопросы.

Принцип Архимеда гласит, что «на любое тело, полностью или частично погруженное в покоящуюся жидкость, действует направленная вверх сила, величина которой равна весу жидкости, вытесняемой телом», как сформулировано британницей.com. Каковы требования для применения принципа Архимеда?

Какие ответы получат ученики, если они зададут учителю вопрос о выталкивающей силе на присоске, прикрепленной к дну чаши, при добавлении воды?

Один учитель передал вопрос ученика группе шведских учителей физики в Facebook, которая в то время насчитывала около 600 членов, в основном из средней школы, а также учителей младших школьников и университетов. Утренний вопрос понедельника вызвал дискуссию, в результате которой менее чем за неделю было получено 225 ответов на 21 комментарий от 16 учителей.В то время как в первых комментариях говорилось, что плавучесть возникает из-за разницы давлений, а присоска не должна испытывать давление воды снизу, в более поздних комментариях говорится о принципе Архимеда как о законе природы, от которого ничто не может ускользнуть, или о том, что кто-то может усомниться в этом. . Эти две позиции будут обозначены следующим образом:

(а)
Принцип Архимеда как следствие давления : идея о том, что принцип Архимеда происходит из разницы давлений, действующих на объект в жидкости.Чтобы принцип Архимеда действовал для объекта, это положение требует, чтобы объект не касался дна.
(б)
Принцип Архимеда как закон природы : идея о том, что принцип Архимеда действителен для всех объектов в жидкости, даже если нижняя часть объекта не имеет контакта с жидкостью.

Были предложены и проведены эксперименты, за которыми последовало обсуждение возможных альтернативных интерпретаций и численного моделирования, а также попытки найти более точные переформулировки закона Архимеда.В этом документе представлены части этого обсуждения.

За первоначальными теоретическими обсуждениями в группе последовали фотографии или видео нескольких экспериментов, демонстрирующих ситуацию: блок LEGO, чайная свеча и пластиковая банка на дне раковины. Затем за каждым экспериментом следовали дополнительные обсуждения, в которых основное внимание уделялось возможным альтернативным объяснениям результата.

2.1. Блок LEGO

Поскольку многие участники дискуссий размышляли, например, о том, сколько воды необходимо под телом, чтобы оказывать давление, один из авторов (OD) приступил к простому эксперименту с маленьким блоком LEGO. лежал на боку на дне кастрюли и удерживался, пока добавлялась вода.Действительно, блок LEGO оставался внизу в течение нескольких секунд, прежде чем всплыл на поверхность.

Этот комментарий, опубликованный в понедельник вечером об эксперименте с блоками LEGO, вызвал оживленную дискуссию за полночь. Обсуждение перешло к вопросу о том, является ли это доказательством отсутствия плавучести или существуют другие возможные объяснения. Может ли быть какая-то адгезия? Калибровочные блоки, изобретенные шведским машинистом Йоханссоном [1], имеют очень гладкие поверхности и, кажется, удерживаются вместе без внешних сил (хотя, конечно, давление воздуха оказывает давление, удерживая два блока вместе).

В следующем вопросе был задан вопрос, сколько воды должно просочиться под блок LEGO, чтобы заставить его плавать. Даже с тонким слоем воды блок сопротивлялся подъему. Прежде чем вода сможет оказать давление под всем блоком, она должна попасть туда, что занимает некоторое время.

Таким образом, можно было сформулировать ряд возможных альтернативных объяснений, и блочный эксперимент LEGO был признан неубедительным.

Один учитель суммировал сделанные на данный момент выводы: плавучесть подразумевает вытесненную жидкость, но вытесненная жидкость не подразумевает плавучесть.

В то время как OD приступил к расчету сил от воды, просачивающейся между блоком LEGO и водой, во вторник после обеда началась новая ветка комментариев, когда BE опубликовал короткое видео с чайной свечой, которая была перенесена на дно стеклянной емкости, а затем отпустить, как показано на рисунке 1, с результатами, обсуждаемыми ниже.

Увеличить Уменьшить Сбросить размер изображения

Рис. 1. Скриншоты видео, на котором чайная свеча медленно поднимается после отдыха в течение примерно 7 секунд на дне стеклянного контейнера, наполненного водой.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Видео, опубликованное BE, показало, что свеча сначала находится в состоянии покоя в течение примерно 7 секунд на дне контейнера, после чего появляются пузырьки воздуха, когда чайная свеча начинает наклоняться, прежде чем всплыть на поверхность. На рисунке 1 показана последовательность снимков экрана из видео.

Как отмечали другие авторы (например, [2]), главная задача – избежать просачивания воды под объект на дне. На дне чайной свечи, использованной в этом небольшом демонстрационном эксперименте, было четыре небольших выступа и круг снаружи, что создавало возможность для небольшого объема воздуха попасть между дном чайной свечи и дном стакана (рисунок 2).

Увеличить Уменьшить Сбросить размер изображения

Рисунок 2. Нижняя часть чайной свечи, использованной в эксперименте, показанном на рисунке 1.

Загрузить рисунок:

Стандартное изображение Изображение высокого разрешения

В среду утром O D опубликовал теоретический расчет времени, необходимого для того, чтобы чайная свеча поднялась с пола, если задержка зависела от просачивания. Сводка расчетов представлена в разделе 4.

2.3. Блок, приклеенный к полиэтиленовой пленке

Предложение о том, чтобы заполнить водой деревянный брусок, приклеенный к полиэтиленовому пакету, прозвучало в четверг днем, после чего в пятницу после обеда был проведен эксперимент с пластиковым пакетом, помещенным в дуршлаг. Плавучести не наблюдалось. Однако эксперимент, похоже, никого не убедил. Сторонники принципа Архимеда как закона природы видели в деревянном бруске «часть дна» и отвергали эксперимент.Те, кто сосредоточился на давлении, уже думали о возможности «нисходящей плавучести», следуя ссылке на статью Лимы и др. [2], представленную накануне. Обсуждение частичной плавучести увенчалось успешной демонстрацией, как описано ниже.

2.4. Частичная плавучесть на пластиковом сосуде

Пост в среду днем содержал ссылку на статью Лимы и др. [2], которые исследовали частичную плавучесть, используя термин «нисходящая плавучесть», чтобы продемонстрировать это явление.Это вызвало ряд исследовательских ответов, в которых несколько участников обсуждали возможные реализации. Идея «нисходящей плавучести» послужила катализатором дискуссий, поскольку не согласуется с позицией принципа Архимеда как закона природы.

Суббота, поздно вечером, принесла следующее демонстрационное видео от O D (рис. 3), где небольшая банка на дне раковины дает яркую иллюстрацию частичной плавучести. Сосуд имел наклонные стенки, что давало меньшее поперечное сечение внизу, чем вверху.Ее поместили так, чтобы она закрывала слив, и удерживала ее, пока раковина наполнялась водой. Затем она оставалась на дне более 40 с, пока вода в раковине медленно вытекала. Хотя давление воды на наклонные стенки банки больше, чем давление на крышку, общая направленная вверх сила на стенки изначально недостаточна для противодействия направленной вниз силе, которая является суммой веса банки и силы давление воды сверху, воздействующее на большую площадь. Если бы на плоское дно сосуда было давление воды, общей силы, направленной вверх, было бы достаточно, чтобы поднять сосуд.Когда уровень воды падает, сила давления воды, направленная вниз, падает быстрее, чем сила, направленная вверх. Наконец, банка поднимается, как показано на снимках экрана на рисунке 3.

Увеличить Уменьшить Сбросить размер изображения

Рис. 3. Скриншоты из видео, где пустая пластиковая банка стоит на дне раковины, наполненной водой. Форма кувшина обеспечивает частичную плавучесть, достаточную для подъема кувшина, когда вода стекает до уровня, при котором сумма веса кувшина и общего усилия, направленного вниз на крышку, становится меньше, чем сила, направленная вверх со стороны воды. давление на стенки банки.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Дискуссия о том, как думать о принципе Архимеда, привела к ряду теоретических рассуждений, параллельных сообщениям об интерпретации экспериментов. Обсуждения показывают, что феноменологический подход к физике часто недостаточен и его необходимо дополнять математическими моделями.

3.1.

Reductio ad absurdum

Один из учителей в группе выдвинул аргумент reductio ad absurdum , касающийся возможности того, что вода сбоку должна воздействовать на объект направленной вверх силой.Согласно третьему закону Ньютона, объект будет воздействовать на воду направленной вниз силой, которая затем начнет двигаться, что приведет к ряду последствий, которые никогда не наблюдались.

3.2. Переформулировки или принцип Архимеда

Во время обсуждений в Facebook некоторые учителя выразили удивление по поводу того, что относительно простой случай, когда объект лежит на дне, не обсуждается в учебниках. Другие учителя предложили другие формулировки, в том числе:

1.
Плавучесть, если она существует, равна весу вытесненной воды
2.
Восходящая сила равна плотности воды, умноженной на г и на объем погруженного объекта в воде, если и только если есть макроскопический слой жидкости под объектом
3.
Сила жидкости на объект является интегралом (или суммой) всех сил из-за сил давления жидкости, действующих на тело (как уже говорилось, например, e.грамм. в [3])
4.
Следует различать три случая:
- Под телом много воды. Принцип Архимеда применяется без осложнений.
- Ящик Gedanken, в котором дно ванны и дно объекта идеально гладкие, чтобы вода не попадала под объект. Принцип Архимеда неприменим.
- Дно ванны и дно предмета практически плоские, но есть микроскопические неровности. Небольшое количество воды может поступать, обеспечивая некоторую плавучесть, приводя к большему количеству воды под этим объектом, пока не произойдет ситуация в (а).
5.
Это частный случай теоремы Гаусса.

Пара учителей все еще не была готова придавать особое значение нижней поверхности, пытаясь избежать проблемы, сделав все поверхности достаточно шероховатыми, чтобы впустить воду и обеспечить плавучесть.

3.3. Математическая модель

Принцип Архимеда сформулирован для неподвижных жидкостей и обсуждается с точки зрения гидростатического давления ( ρgh ).Однако, чтобы чайная свеча поднялась, под свечу должна поступать вода. Когда свеча поднимается, давление падает, и больше воды течет к центру свечи, где давление должно быть ниже, пока вода течет. Как долго давление под чайной свечой недостаточно, чтобы поднять свечу?

Простая оценка сил, действующих на чайную свечу, была получена в предположении вязкого течения. Таким образом можно получить приблизительную зависимость расстояния до дна контейнера от времени, как показано на рисунке 4.На рисунке 5 показано горизонтальное движение воды и возникающие в результате силы, действующие на чайную свечу при просачивании воды внутрь. Математическая модель и расчеты подробно представлены в разделе 4.

Увеличить Уменьшить Сбросить размер изображения

Рис. 4. Решение с использованием вывода из раздела 4 для начального значения d = 4 × 10 ⁻⁵ м для расстояния между дном чайной свечи и дном.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Увеличить Уменьшить Сбросить размер изображения

Рисунок 5. Иллюстрации для теоретического анализа, представленные в разделе 4.

Загрузить рисунок:

Стандартное изображение Изображение высокого разрешения

Используйте цилиндрические координаты с осью в центре свечи, причем r обозначает расстояние до центра, а z обозначает вертикальную координату, отсчитываемую от дна контейнера.Пусть R будет радиусом цилиндра (чайной свечи), а d будет расстоянием между цилиндром и дном.

Радиальная скорость воды зависит как от расстояния, z от центра и от дна контейнера, с наибольшим потоком при z = d /2. Средняя скорость для данного радиуса равна,

По мере того, как вода движется внутрь, чайная свеча должна двигаться вверх, вызывая временную зависимость расстояния, d .Скорость движения чайной свечи вверх обозначается производной от расстояния по времени, т.е. Непрерывность требует, чтобы поток в каждой концентрической цилиндрической оболочке под чайной свечой соответствовал изменению объема из-за восходящего движения свечи, то есть

дает выражение для средней скорости:

Пусть P ( r ) является аномалией давления по сравнению с гидростатическим давлением и аппроксимирует поток с установившимся потоком между двумя параллельными пластинами под градиентом давления (см. e.грамм. [4]). Это приблизительная оценка, но она должна давать правильный порядок величины, давая

, где µ – динамическая вязкость.

Для r = R аномалия давления наименьшая, и мы устанавливаем P ( R ) = 0. Подставляя выражение для (3) в (4) и интегрируя по r дает,

Теперь рассмотрим силы, действующие на цилиндр. Суммарная сила F _P из-за аномалии давления внизу:

Обратите внимание, что это давление сильно зависит от расстояния до дна, d .

4.1. Сила на чайную свечу

Теперь у нас есть инструменты, необходимые для расчета суммы всех сил, действующих на чайную свечу.

Пусть h будет высотой цилиндра, ρ будет плотностью воды и ρ _c будет плотностью цилиндра. Если бы цилиндр был неподвижным, направленная вверх сила на цилиндре была бы,

, где – масса цилиндра.

Применение второго закона движения Ньютона к цилиндру с результирующей силой, заданной как, дает дифференциальное уравнение для расстояния d между цилиндром и дном:

Вставка числовых значений g = 9.8 мс ⁻², ρ = 1000 кг м ⁻³ и µ = 9 × 10 ⁻⁴ Па · с, вместе с реалистичными значениями для свечи,, h = 0,015 м и R = 0,02 м, дифференциальное уравнение может быть решено численно. Решения показывают, что свеча будет оставаться почти неподвижной, близко к основанию, пока d не станет достаточно большим. На рисунке 4 показано решение, когда d изначально установлено равным 4 × 10 ⁻⁵ м, что дает реалистичное время для чайной свечи.Однако время, в течение которого цилиндр «остается» внизу, сильно зависит от начального значения d , так что это скорее доказательство принципа, чем точная количественная модель.

Вывод состоит в том, что эксперимент с чайной свечой сам по себе не может быть использован для опровержения взгляда на принцип Архимеда как на закон природы.

Может ли (маленький) линкор в (большой) ванне плавать, даже если вода в ванне весит намного меньше, чем лодка, так что “вытесняется” недостаточное количество воды? Иллюстрация этого вопроса есть на обложке книги « Thinking Physics is Gedanken Physics » [5], которая включает ряд сложных концептуальных вопросов, которые могут привести к вдохновляющим обсуждениям в классе.Эти обсуждения важны тем, что они дополняют традиционные задачи в конце главы, обычно спрашивая о численных значениях сил плавучести в различных ситуациях.

Концептуальные трудности, связанные с плавучестью, обычны и хорошо задокументированы, а литература включает ряд статей, демонстрирующих возможные пути углубления концептуального понимания плавучести (см., Например, [6–8]). Один из нас (AMP) вспоминает задачу на экзамене, которую давали первокурсникам, спрашивая, сколько гелия потребуется, чтобы нести Джо Киттингера на воздушном шаре для его одинокого прыжка на 20 миль в 1960 году [9, 10].Большинство студентов считали, что необходимая масса гелия равна массе, которую необходимо перенести. Заглянув в учебники своих старших детей, которые в то время были подростками, AMP не удивилась, что большинство студентов не смогли понять принцип Архимеда. Как указано в приложении, учебники колледжей и университетов различаются тем, какие обсуждения предшествуют изложению принципа.

Виеннот [11] обсуждает «обучающие ритуалы», в том числе трактовку принципа Архимеда и «изобарического воздушного шара», с присущими ему противоречиями, и обнаруживает, что студенты гораздо более удовлетворены, когда они могут разработать объяснение с точки зрения Законы Ньютона, и можно понять, что «физика – это последовательный, экономный, элегантный и мощный набор теорий».Десять лет спустя она возвращается к проблеме [12] и обнаруживает, что эти обучающие ритуалы очень устойчивы. В недавней статье [10] она обсуждает обучение критическому анализу объяснений как важную часть педагогического образования. Она отмечает, что «плавание – очень популярная тема на ранних этапах научного образования, в частности, для практики того, что часто называют научным обучением на основе запросов». Погружая блоки материалов разной плотности в воду, легко показать, что «плавать могут только объекты меньшей плотности, чем вода».Она сравнивает это объяснение с подходом «дыра в воде», предложенным Огборном [13], который предлагает ученикам испытать и поразмыслить над силой, необходимой для того, чтобы толкнуть пустой пластиковый стаканчик в воду, а затем попытаться наполнить стакан жидкостью. увеличение количества воды. После ряда исследований и дискуссий Огборн заканчивает замечанием, что «мы только сейчас достигли точки, с которой обычно начинается история принципа Архимеда. Вот почему я думаю, что лучше было бы начать ближе к началу, сделав ямки в воде.’

5.1. Убеждения и свидетельства

Для многих участников обсуждения группы в Facebook, которые были убеждены в необходимости давления снизу для восходящей силы со стороны жидкости, простой эксперимент с блоком LEGO первоначально предоставил достаточные доказательства того, что силы на объект в жидкости сложнее, чем описывается принципом Архимеда. Однако в ходе обсуждения были выявлены возможные альтернативные объяснения медленного подъема блока LEGO, и многие учителя хотели бы получить более убедительные доказательства наличия чистых сил, исходящих от воды.Эти обсуждения приводят к дополнительным экспериментам, представленным здесь, а также к моделированию, дающему сравнение между теорией и экспериментом, обсужденным выше.

Несколько учителей начали искать в учебниках вводящие в заблуждение или неполные иллюстрации принципа Архимеда, и в короткой ветке комментариев обсуждалось, как учителя могут использовать эти иллюстрации для обсуждения в классе.

Шаги в обсуждении можно также использовать в качестве иллюстрации участников, участвующих в достижении всеобъемлющих целей естественнонаучного образования, как выражено, например, в Стандарте науки следующего поколения [14]:

1.
Задание вопросов (для науки) и постановка задач (для инженерии)
2.
Разработка и использование моделей
3.
Планирование и проведение исследований
4.
Анализ и интерпретация данных
5.
Использование математики и вычислительного мышления
6.
Создание объяснений (для науки) и разработка решений (для инженерии)
7.
Привлечение аргументов из доказательств
8.
Получение, оценка и передача информации.

Обсуждение также включает компоненты тестирования множественных объяснений, которые являются частью подхода ISLE [8].

Интенсивные дискуссии с учителями в течение одной недели служат примером того, как социальные сети могут предоставить «расширенную комнату для учителей», где учителя могут исследовать и уточнять свое понимание в безопасной и в основном благоприятной среде, а также находить способы дать более подробные ответы на сложные вопросы студентов.На рисунке 6 показан график комментариев и ответов на разные темы с понедельника по субботу. В воскресенье было опубликовано несколько разрозненных комментариев, в том числе обсуждения неидеальных иллюстраций в учебниках.

Увеличить Уменьшить Сбросить размер изображения

Рисунок 6. Хронология комментариев и ответов по нескольким темам, задаваемых вопросом в понедельник утром.

Загрузить рисунок:

Стандартный образ Изображение высокого разрешения

Проблема, возникшая у Архимеда, когда он обнаружил принцип, носящий его имя, заключалась в том, как определить, было ли золото в короне Гиерона разбавлено другим металлом.Рассказ об Архимеде может быть вдохновляющим способом познакомить с темами плотности и плавучести еще задолго до старшей школы (см., Например, [15]). Чтобы определить плотность объекта, его нужно окружить жидкостью. Таким образом, объект, лежащий внизу, не будет иметь значения.

Эпштейн [5] комментирует в сноске к одному из концептуальных вопросов в « Thinking Physics is Gedanken Physics »: «В необычных обстоятельствах, когда погруженное тело опирается на дно без водяной пленки между ним и дном контейнера. , не было бы восходящей выталкивающей силы.«Хотя несколько авторов предложили обобщения выражений плавучести для погруженных тел, которые не полностью окружены водой (например, [2, 3, 16]), ни в одном из учебников, обсуждаемых в приложении, эта ситуация не упоминается.

Многие учителя, принимавшие участие в дискуссии, были удивлены тем, что им никогда не приходилось сталкиваться с вопросом о предмете, лежащем на дне раковины, который был задан учеником и вызвал дискуссии в группе Facebook.Когда дискуссии подходили к завершению, один из учителей воскликнул: «Итак, похоже, что это действительно законы Ньютона в действии. А микроскопический слой жидкости под объектом необходим для распространения давления воды на дно объекта ». Действительно, принцип Архимеда – это не дополнительный «закон природы», а следствие законов Ньютона.

Авторы хотели бы выразить нашу признательность всем учителям, принимающим участие в дискуссии, в частности Патрику Петтерсону, разместившему первоначальный вопрос, Даниэлю Домерту за его настойчивость в указании на то, что давление воды снизу необходимо для применения принципа Архимеда, и за размещение ссылки на работу Лимы и др. [2], Элин Вихед за неоднократные просьбы о кратком изложении выводов или переформулировок закона плавучести и Фредрику Янссону для проверки расчетов.

В качестве основы для восприятия студентами сил в жидкостях и принципа Архимеда, это приложение представляет собой краткое исследование главы о жидкостях для ряда учебников физики на уровне колледжей и университетов [17–23].

Большинство книг включают некоторую версию соотношения для описания выталкивающей силы F _b, связанной с плотностью жидкости, ρ _f и объем V _disp вытесненной жидкости.Однако они различаются своим путем к принципу Архимеда, а также своими иллюстрациями и выбором примеров.

Янг и Фридман [23] начинают с введения плотности, а затем определения давления. Затем давление связано с глубиной в жидкости и учетом сил элемента жидкости в равновесии, что приводит к принципу Паскаля и иллюстрации того, что «жидкость находит свой уровень», как можно найти в большинстве книг. Затем они обсуждают манометры, прежде чем проиллюстрировать плавучесть, показывая давление на различные части погруженного объекта произвольной формы.Вопросы для обсуждения включают некоторые из вступительных слов о «дыре в воде», предложенные Огборном [13], в котором предлагается опыт толкания пустой стеклянной банки в воду с учетом плавучести. Другой дискуссионный вопрос включает проблему золотой короны короля (без исторической справки). Проблемы включают биологические примеры, такие как кровяное давление и дайвинг.

Чабай и Шервуд [21] обсуждают плавучесть, используя силы, действующие на сферу жидкости, а затем приходят к выводу, что силы, действующие на шар, висящий на проволоке, заменяющий исходную сферу жидкости, будут подвергаться воздействию тех же сил со стороны окружающей жидкости.Затем они обсуждают плавучесть в воздухе, включая силы, действующие на книгу, лежащую на столе. Они действительно обсуждают давление на присоску, но только в окружении воздуха. Задачи в конце главы включают расчет плавучести и давления в нескольких различных ситуациях.

Силы, действующие на объект, заменяющие количество воды идентичной формы, также представлены в книге по инженерной механике Мериам и Крейдж [20], где большинство задач в конце главы связаны с расчетами сил, возникающих из-за давления в широком диапазоне. диапазон ситуаций, без особого внимания к плавучести.

Fishbane и др. [19] начинают с определения плотности, ρ = M / V и давления p ≡ F / A . В разделе, посвященном давлению в покоящейся жидкости, рассматривается разница давлений между силами и перепадами давления между двумя горизонтальными поверхностями глубиной y и y + dy и, наконец, обсуждается опускание и плавание для объектов с разной плотностью, прежде чем формулировать Принцип Архимеда и демонстрация чтения шкалы, где яблоко подвешено, в воздухе, частично или полностью погружено.Одна из задач в конце главы посвящена устойчивости плавучих объектов. Аналогичное введение можно найти у Вольфсона и Пасахова [18], но в них также показаны силы, действующие на объект произвольной формы, и проиллюстрировано взвешивание Архимедом королевской короны, а также вопрос о стабильности, центре тяжести и центре плавучести. .

Книга Мазура [22] фокусируется на давлении и включает краткое обсуждение плавучести без упоминания Архимеда. Том «Практика» подчеркивает процедуру определения давления на каждой поверхности, которая, вероятно, подготовит студентов к обсуждению вакуумной присоски под водой.

Наиболее подробное введение к изученным книгам дает Хьюитт [17], начиная с обсуждения давления (включая обсуждение кровяного давления у жирафа). Подчеркнув разницу между давлением снизу и сверху над объектом, он отмечает, что разница не зависит от глубины, поскольку плотность воды остается постоянной. Затем вводится плавучесть с приложением сил к объекту произвольной формы и специальным обсуждением воды, стекающей через край при погружении объекта, что приводит к принципу Архимеда, прежде чем вводится понятие плотности.В нем представлены плавающие айсберги – и изостазия гор в качестве более необычного примера. Большое количество концептуальных упражнений, включая то, как плавучесть воздушного шара меняется с глубиной воды, дается в конце главы перед значительно более коротким списком «проблем», который включает исследование того, имеет ли предположительно золотой объект плотность золота. , но никакого упоминания о короне Гиерона.

В то время как некоторые (но не все) шведские школьные учебники физики исходят из принципа Архимеда, прежде чем рассматривать силы, возникающие от давления воды, все учебники для колледжей и университетов, рассматриваемые здесь, начинаются с рассмотрения давления до введения плавучести.Однако они различаются акцентом на различные аспекты давления, силы или плавучести. Во всех книгах рассматриваются силы, возникающие из-за давления на горизонтальные поверхности на разной глубине. Мазур [22] также включает силы, действующие на треугольник, Чабай и Шервуд [21] рассматривают силы, действующие на сферу, а в некоторых книгах приводятся иллюстрации сил, действующих на произвольные формы [17, 18, 20, 23]. Силы, действующие на воду с той же формой, что и объект, который затем смещает ее, подробно обсуждаются в [17] и [23].

Ни одна из книг, кажется, не использовала элегантность сравнения плотностей без явного измерения перемещенных объемов, а вместо этого погружала два тела с разными массами на противоположных сторонах неравного баланса рук – еще одно из открытий / изобретений Архимеда.

Архимедова сила — закон, формула, определение

Сила: что это за величина

Открытие закона Архимеда

Формула и определение силы Архимеда для жидкости

Задача 1

Задача 2

Условия плавания тел

ЗАКОН АРХИМЕДА | Энциклопедия Кругосвет

Закон Архимеда, или Как распознать ложь?

История открытия

Действие жидкости и газа на погруженное в них тело

Формулы

Методические советы

Тест «Закон Архимеда»

Закон Архимеда для ускоренно движущихся тел

Архимедова сила, формулы

Готовые работы на аналогичную тему

Формулировка закона Архимеда

Возникновение Силы Архимеда

Сценарий к уроку по физике “Сила Архимеда. Закон Архимеда”.

Вычисление силы Архимеда

14.6: Принцип Архимеда и плавучесть

Принцип Архимеда

Плотность и принцип Архимеда

Измерение плотности

Авторы и авторство

Принцип Архимеда | Безграничная физика

Плавучесть и принцип Архимеда

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Подъемная сила: причина и расчет

Принцип Архимеда

Полное погружение

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Цилиндр

Гелиевый дирижабль

Флотация

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Условия для плавучести

Флотация и плотность

14.4 Принцип Архимеда и плавучесть – University Physics Volume 1

Цели обучения

Подъемная сила

Принцип Архимеда

Плотность и принцип Архимеда

Пример

Расчет средней плотности

Стратегия

Решение

Значение

Измерение плотности

Сводка

Концептуальные вопросы

Проблемы

Глоссарий

Определение принципа Архимеда в физике.

Примеры принципа Архимеда в следующих темах:

Плавучесть и принцип Архимеда

Полное погружение

Флотация

Принцип Гюйгенса

Принцип Паскаля

Принцип неопределенности Гейзенберга

Постулаты Эйнштейна

Суперпозиция сил

Наложение полей

Сферические и плоские волны

Принцип Архимеда – Видео по физике от Brightstorm

Подъемная сила

Является ли принцип Архимеда законом природы? Обсуждения в «расширенной комнате учителя»

2.1. Блок LEGO

2.3. Блок, приклеенный к полиэтиленовой пленке