Что такое сила архимеда – Закон Архимеда — Википедия

Архимедова сила, формулы

Несмотря на явные различия свойств жидкостей и газов, во многих случаях их поведение определяется одними и теми же параметрами и уравнениями, что позволяет использовать единый подход к изучению свойств этих веществ.

В механике газы и жидкости рассматривают как сплошные среды. Предполагается, что молекулы вещества распределены непрерывно в занимаемой ими части пространства. При этом плотность газа значительно зависит от давления, в то время как для жидкости ситуация иная. Обычно при решении задач этим фактом пренебрегают, используя обобщенное понятие несжимаемой жидкости, плотность которой равномерна и постоянна.

Далее дадим понятие физической величине – давлению.

Определение 1

Давление определяется как нормальная сила $F$, действующая со стороны жидкости на единицу площади $S$.

$ρ = \frac{\Delta P}{\Delta S}$.

Замечание 1

Давление измеряется в паскалях. Один Па равен силе в 1 Н, действующей на единицу площади 1 кв. м.

В состояние равновесия давление жидкости или газа описывается законом Паскаля, согласно которому давление на поверхность жидкости, производимое внешними силами, передается жидкостью одинаково во всех направлениях.

При механическом равновесии, давление жидкости по горизонтали всегда одинаково; следовательно, свободная поверхность статичной жидкости всегда горизонтальна (кроме случаев соприкосновения со стенками сосуда). Если принять во внимание условие несжимаемости жидкости, то плотность рассматриваемой среды не зависит от давления.

Представим некоторый объем жидкости, ограниченный вертикальным цилиндром. Поперечное сечение столба жидкости обозначим $S$, его высоту $h$, плотность жидкости $ρ$, вес $P=ρgSh$. Тогда справедливо следующее:

$p = \frac{P}{S} = \frac{ρgSh}{S} = ρgh$,

где $p$ – давление на дно сосуда.

Отсюда следует, что давление меняется линейно, в зависимости от высоты. При этом $ρgh$ – гидростатическое давление, изменением которого и объясняется возникновение силы Архимеда.

Формулировка закона Архимеда

Закон Архимеда, один из основных законов гидростатики и аэростатики, гласит: на тело, погруженное в жидкость или газ, действует выталкивающая или подъемная сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.

Замечание 2

Возникновение Архимедовой силы связано с тем, что среда – жидкость или газ – стремится занять пространство, отнятое погруженным в нее телом; при этом тело выталкивается из среды.

Отсюда и второе название для этого явление – выталкивающая или гидростатическая подъемная сила.

Выталкивающая сила не зависит от формы тела, также как и от состава тела и прочих его характеристик.

Возникновение Архимедовой силы обусловлено разностью давления среды на разных глубинах. Например, давление на нижние слои воды всегда больше, чем на верхние слои.

Проявление силы Архимеда возможно лишь при наличии тяжести. Так, например, на Луне выталкивающая сила будет в шесть раз меньше, чем на Земле для тел равных объемов.

Возникновение Силы Архимеда

Представим себе любую жидкую среду, например, обычную воду. Мысленно выделим произвольный объем воды замкнутой поверхностью $S$. Поскольку вся жидкость по условию находится в механическом равновесии, выделенный нами объем также статичен. Это означает, что равнодействующая и момент внешних сил, воздействующих на этот ограниченный объем, принимают нулевые значения. Внешние силы в данном случае – вес ограниченного объема воды и давление окружающей жидкости на внешнюю поверхность $S$. При этом получается, что равнодействующая $F$ сил гидростатического давления, испытываемого поверхностью $S$, равна весу того объема жидкости, который был ограничен поверхностью $S$. Для того чтобы полный момент внешних сил обратился в нуль, равнодействующая $F$ должна быть направлена вверх и проходить через центр масс выделенного объема жидкости.

Теперь обозначим, что вместо этой условного ограниченной жидкости в среду было помещено любое твердое тело соответствующего объема. Если соблюдается условие механического равновесия, то со стороны окружающей среды никаких изменений не произойдет, в том числе останется прежним давление, действующее на поверхность $S$. Таким образом мы можем дать более точную формулировку закона Архимеда:

Замечание 3

Если тело, погруженное в жидкость, находится в механическом равновесии, то со стороны окружающей его среды на него действует выталкивающая сила гидростатического давления, численно равная весу среды в объеме, вытесненным телом.

Выталкивающая сила направлена вверх и проходит через центр масс тела. Итак, согласно закону Архимеда для выталкивающей силы выполняется:

$F_A = ρgV$, где:

• $V_A$ – выталкивающая сила, H;
• $ρ$ – плотность жидкости или газа, $кг/м^3$;
• $V$ – объем тела, погруженного в среду, $м^3$;
• $g$ – ускорение свободного падения, $м/с^2$.

Выталкивающая сила, действующая на тело, противоположна по направлению силе тяжести, поэтому поведение погруженного тела в среде зависит от соотношения модулей силы тяжести $F_T$ и Архимедовой силы $F_A$. Здесь возможны три случая:

1. $F_T$ > $F_A$. Сила тяжести превышает выталкивающую силу, следовательно, тело тонет/падает;
2. $F_T$ = $F_A$. Сила тяжести уравнивается с выталкивающей силой, поэтому тело «зависает» в жидкости;
3. $F_T$

spravochnick.ru

Закон Архимеда — Википедия. Что такое Закон Архимеда

Зако́н Архиме́да — один из законов статики жидкостей (гидростатики) и газов (аэростатики): на тело, погружённое в жидкость или газ, действует выталкивающая или подъёмная сила, равная весу объёма жидкости или газа, вытесненного частью тела, погружённой в жидкость или газ. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой или гидростатической подъёмной силой^[1][2].

В соответствии с законом Архимеда для выталкивающей силы выполняется^[3]:

FA=ρgV,{\displaystyle F_{A}=\rho gV,}

где:

Дополнения

Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.

Плавание тела. Сила Архимеда (FA{\displaystyle F_{A}}) уравновешивает вес тела (Fp{\displaystyle F_{p}}):
FA=Fp;{\displaystyle F_{A}=F_{p};}
ρ_ж g V_ж = ρ_т g V_т

Например, воздушный шарик объёмом V{\displaystyle V}, наполненный гелием, летит вверх из-за того, что плотность гелия (ρH{\displaystyle \rho _{H}}) меньше плотности воздуха (ρO{\displaystyle \rho _{O}}):

FA>Fp;{\displaystyle F_{A}>F_{p};}
ρOgV>ρHgV.{\displaystyle \rho _{O}gV>\rho _{H}gV.}

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (PA{\displaystyle P_{A}}) и сила давления (FA{\displaystyle F_{A}}), действующие на верхнюю грань тела, равны:

PA=ρghA;{\displaystyle P_{A}=\rho gh_{A};}

FA=ρghAS,{\displaystyle F_{A}=\rho gh_{A}S,}

где:

Давление (PB{\displaystyle P_{B}}) и сила давления (FB{\displaystyle F_{B}}), действующие на нижнюю грань тела, равны:

PB=ρghB;{\displaystyle P_{B}=\rho gh_{B};}

FB=ρghBS,{\displaystyle F_{B}=\rho gh_{B}S,}

где:

• PB{\displaystyle P_{B}} — давление, оказываемое жидкостью или газом на нижнюю грань тела, Па;
• FB{\displaystyle F_{B}} — сила давления, действующая на нижнюю грань тела и направленная вверх, Н;
• hB{\displaystyle h_{B}} — расстояние между поверхностью жидкости или газа и нижней гранью тела, м.

Сила давления жидкости или газа на тело определяется разностью сил FB{\displaystyle F_{B}} и FA{\displaystyle F_{A}}:

FB−FA=ρghBS−ρghAS=ρg(hB−hA)S=ρghS=ρgV,{\displaystyle F_{B}-F_{A}=\rho gh_{B}S-\rho gh_{A}S=\rho g\left(h_{B}-h_{A}\right)S=\rho ghS=\rho gV,}

где:

• h=hB−hA{\displaystyle h=h_{B}-h_{A}} — расстояние между верхней и нижней гранями тела (в случае частичного погружения высота части тела, погружённой в жидкость или газ), м;
• V{\displaystyle V} — объём тела, погружённого в жидкость или газ (в случае частичного погружения объём части тела, погружённой в жидкость или газ), м³.

Разница давлений:

PB−PA=ρghB−ρghA=ρgh.{\displaystyle P_{B}-P_{A}=\rho gh_{B}-\rho gh_{A}=\rho gh.}

В отсутствие гравитационного поля, то есть, в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.

Обобщения

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление p{\displaystyle p} на глубине h{\displaystyle h}, оказываемое жидкостью плотностью ρ{\displaystyle \rho } на тело, есть p=ρgh{\displaystyle p=\rho gh}. Пусть плотность жидкости (ρ{\displaystyle \rho }) и напряжённость гравитационного поля (g{\displaystyle g}) — постоянные величины, а h{\displaystyle h} — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz{\displaystyle Oxyz}, причём выберем направление оси z совпадающим с направлением вектора g→{\displaystyle {\vec {g}}}. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS{\displaystyle dS}. На неё будет действовать сила давления жидкости направленная внутрь тела, dF→A=−pdS→{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

F→A=−∫SpdS→=−∫SρghdS→=−ρg∫ShdS→=∗−ρg∫Vgrad(h)dV=∗∗−ρg∫Ve→zdV=−ρge→z∫VdV=(ρgV)(−e→z).{\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z}).}

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.

∗h(x,y,z)=z;{\displaystyle {}^{*}h(x,y,z)=z;}

∗∗grad(h)=∇h=e→z.{\displaystyle ^{**}grad(h)=\nabla h={\vec {e}}_{z}.}

Получаем, что модуль силы Архимеда равен ρgV{\displaystyle \rho gV}, и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Условие плавания тел

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести FT{\displaystyle F_{T}} и силы Архимеда FA{\displaystyle F_{A}}, которые действуют на это тело. Возможны следующие три случая:

• FT>FA{\displaystyle F_{T}>F_{A}} — тело тонет;
• FT=FA{\displaystyle F_{T}=F_{A}} — тело плавает в жидкости или газе;
• FT<FA{\displaystyle F_{T}<F_{A}} — тело всплывает до тех пор, пока не начнёт плавать.

Другая формулировка (где ρt{\displaystyle \rho _{t}} — плотность тела, ρs{\displaystyle \rho _{s}} — плотность среды, в которую тело погружено):

• ρt>ρs{\displaystyle \rho _{t}>\rho _{s}} — тело тонет;
• ρt=ρs{\displaystyle \rho _{t}=\rho _{s}} — тело плавает в жидкости или газе;
• ρt<ρs{\displaystyle \rho _{t}<\rho _{s}} — тело всплывает до тех пор, пока не начнёт плавать.

См. также

Видеоурок: закон Архимеда

Примечания

Ссылки

wiki.sc

ЗАКОН АРХИМЕДА | Энциклопедия Кругосвет

ЗАКОН АРХИМЕДА – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.

Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается можем поднять на суше; то же явление наблюдается, когда по каким-либо причинам выброшенным на берегу оказывается кит – вне водной среды животное не может передвигаться – его вес превосходит возможности его мышечной системы. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился. Чтобы понять природу силы, действующей на погруженное тело со стороны жидкости, достаточно рассмотреть простой пример (рис. 1).

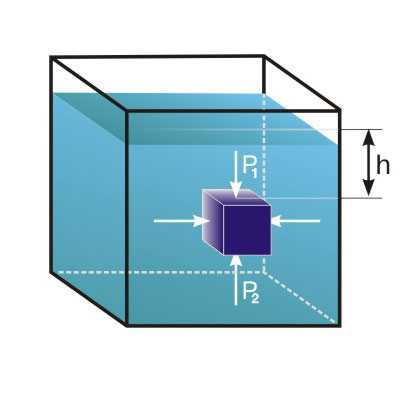
Кубик с ребром a погружен в воду, причем и вода, и кубик неподвижны. Известно, что давление в тяжелой жидкости увеличивается пропорционально глубине – очевидно, что более высокий столбик жидкости более сильно давит на основание. Гораздо менее очевидно (или совсем не очевидно), что это давление действует не только вниз, но и в стороны, и вверх с той же интенсивностью – это закон Паскаля.

Если рассмотреть силы, действующие на кубик (рис. 1), то в силу очевидной симметрии силы, действующие на противоположные боковые грани, равны и противоположно направлены – они стараются сжать кубик, но не могут влиять на его равновесие или движение. Остаются силы, действующие на верхнюю и на нижнюю грани. Пусть h – глубина погружения верхней грани, r – плотность жидкости, g – ускорение силы тяжести; тогда давление на верхнюю грань равно

r · g · h = p₁

а на нижнюю

r · g(h+a) = p₂

Сила давления равна давлению, умноженному на площадь, т.е.

F₁ = p₁ · a\up122, F₂ = p₂ · a\up122 , где a – ребро кубика,

причем сила F₁ направлена вниз, а сила F₂ – вверх. Таким образом, действие жидкости на кубик сводится к двум силам – F₁ и F₂ и определяется их разностью, которая и является выталкивающей силой:

F₂ – F₁ =r · g · (h+a) a\up122 – rgha ·a² = pga²

Сила – выталкивающая, так как нижняя грань, естественно, расположена ниже верхней и сила, действующая вверх, больше, чем сила, действующая вниз. Величина F₂ – F₁= pga³ равна объему тела (кубика) a³, умноженному на вес одного кубического сантиметра жидкости (если принять за единицу длины 1 см). Другими словами, выталкивающая сила, которую часто называют архимедовой силой, равна весу жидкости в объеме тела и направлена вверх. Этот закон установил античный греческий ученый Архимед, один из величайших ученых Земли.

Если тело произвольной формы (рис. 2) занимает внутри жидкости объем V, то действие жидкости на тело полностью определяется давлением, распределенным по поверхности тела, причем заметим, что это давление совершенно не зависит от материала тела – («жидкости все равно на что давить»).

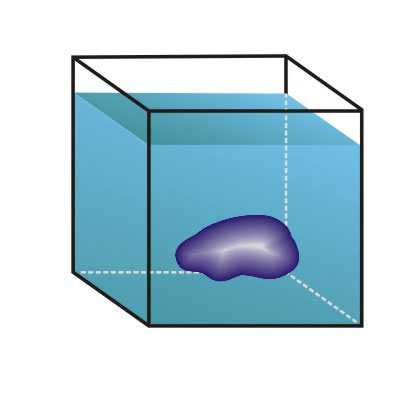
Для определения результирующей силы давления на поверхность тела нужно мысленно удалить из объема V данное тело и заполнить (мысленно) этот объем той же жидкостью. С одной стороны, есть сосуд с жидкостью, находящейся в покое, с другой стороны внутри объема V – тело, состоящее из данной жидкости, причем это тело находится в равновесии под действием собственного веса (жидкость тяжелая) и давления жидкости на поверхность объема V. Так как вес жидкости в объеме тела равен pgV и уравновешивается равнодействующей сил давления, то величина ее равна весу жидкости в объеме V, т.е. pgV.

Сделав мысленно обратную замену – поместив в объеме V данное тело и отметив, что эта замена никак не скажется на распределении сил давления на поверхность объема V, можно сделать вывод: на погруженное в покоящуюся тяжелую жидкость тело действуют направленная вверх сила (архимедова сила), равная весу жидкости в объеме данного тела.

Аналогично можно показать, что если тело частично погружено в жидкость, то архимедова сила равна весу жидкости в объеме погруженной части тела. Если в этом случае архимедова сила равна весу, то тело плавает на поверхности жидкости. Очевидно, что если при полном погружении архимедова сила окажется меньше веса тела, то оно утонет. Архимед ввел понятие «удельного веса» g, т.е. веса единицы объема вещества: g =

pg; если принять, что для воды g = 1, то сплошное тело из вещества, у которого g > 1 утонет, а при g < 1 будет плавать на поверхности; при g = 1 тело может плавать (зависать) внутри жидкости. В заключение заметим, что закон Архимеда описывает поведение аэростатов в воздухе (в покое при малых скоростях движения).

Владимир Кузнецов

www.krugosvet.ru

Архимедова сила – что это значит? 🚩 архимедова сила зависит от 🚩 Естественные науки

Причина возникновения архимедовой силы – разность давлений среды на разной глубине. Поэтому сила Архимеда возникает только в при наличии силы тяжести. На Луне она будет вшестеро, а на Марсе – в 2,5 раза меньше, чем на Земле.

В невесомости архимедовой силы нет. Если представить себе, что сила тяжести на Земле вдруг пропала, то все корабли в морях, океанах и реках от малейшего толчка уйдут на любую глубину. А вот подняться вверх им не даст не зависящее от силы тяжести поверхностное натяжение воды, так что взлететь они не смогут, все потонут.

Величина архимедовой силы зависит от объема погруженного тела и плотности среды, в которой оно находится. Его точная формулировка в современном представлении: на погруженное в жидкую или газовую среду тело в поле силы тяжести действует выталкивающая сила, в точности равная весу вытесненной телом среды, то есть F = ρgV, где F – сила Архимеда; ρ – плотность среды; g – ускорение свободного падения; V – объем вытесненной телом или погруженной его частью жидкости (газа).

Если в пресной воде на каждый литр объема погруженного тела действует выталкивающая сила в 1 кг (9,81 н), то в морской воде, плотность которой 1,025 кг*куб. дм, на тот же литр объема будет действовать сила Архимеда в 1 кг 25 г. Для человека средней комплекции разность силы поддержки морской и пресной водой составит почти 1,9 кг. Поэтому плавать в море легче: представьте себе, что вам нужно переплыть хотя бы пруд без течения с двухкилограммовой гантелью за поясом.

От формы погруженного тела архимедова сила не зависит. Возьмите железный цилиндр, измерьте силу его выталкивания из воды. Затем раскатайте этот цилиндр в лист, погрузите в воду плашмя и ребром. Во всех трех случаях сила Архимеда окажется одинаковой.

На первый взгляд странно, но, если погружать лист плашмя, то уменьшение разности давлений для тонкого листа компенсируется увеличением его площади, перпендикулярной поверхности воды. А при погружении ребром – наоборот, малая площадь ребра компенсируется большей высотой листа.

Если вода очень сильно насыщена солями, отчего ее плотность стала выше плотности человеческого тела, то в ней не утонет и человек, не умеющий плавать. В Мертвом море в Израиле, например, туристы могут часами лежать на воде, не шевелясь. Правда, ходить по нему все равно нельзя – площадь опоры получается малой, человек проваливается в воду по горло, пока вес погруженной части тела не сравняется с весом вытесненной им воды. Однако при наличии некоторой доли фантазии сложить легенду о хождении по воде можно. А вот в керосине, плотность которого всего 0,815 кг*куб. дм, не сможет удержаться на поверхности и очень опытный пловец.

То, что суда плавают благодаря силе Архимеда, известно всем. Но рыбаки знают, что архимедову силу можно использовать и в динамике. Если на крючок попалась большая и сильная рыбина (таймень, например), то медленно подтягивать ее к сачку (вываживать) толку нет: оборвет леску и уйдет. Нужно сначала дернуть слегка, когда она уходит. Почувствовав при этом крючок, рыба, стремясь освободиться от него, метнется в сторону рыбака. Тогда нужно дернуть очень сильно и резко, чтобы леска не успела порваться.

В воде тело рыбы почти ничего не весит, но его масса с инерцией сохраняются. При таком способе ловли архимедова сила как бы наддаст рыбе в хвост, и добыча сама плюхнется к ногам рыболова или к нему в лодку.

Архимедова сила действует не только в жидкостях, но и в газах. Благодаря ей летают воздушные шары и дирижабли (цеппелины). 1 куб. м воздуха при нормальных условиях (20 градусов Цельсия на уровне моря) весит 1,29 кг, а 1 кг гелия – 0,21 кг. То есть 1 кубометр наполненной гелием оболочки способен поднять груз в 1,08 кг. Если оболочка диаметром в 10 м, то ее объем будет 523 куб. м. Выполнив ее из легкого синтетического материала, получим подъемную силу около полутонны. Архимедову силу в воздухе аэронавты называют сплавной силой.

Если из аэростата откачать воздух, не дав ему сморщиться, то каждый его кубометр потянет вверх уже все 1,29 кг. Прибавка более 20% к подъемной силе технически весьма соблазнительна, да гелий дорог, а водород взрывоопасен. Поэтому проекты вакуумных дирижаблей время от времени появляются на свет. Но материалов, способных при этом выдержать большое (около 1 кг на кв. см) атмосферное давление снаружи на оболочку, современная технология создать пока не способна.

Архимед является одним из самых известных и великих ученных, положивших начало современной науке. Далеко не все его открытия известны широким массам. Обычно все помнят лишь то, что преподавали в школе, хотя другие его эксперименты не менее интересны и полезны обществу.

Содержание статьи

Существует очень известная легенда про корону государя Гиерона, некоторые историки называют ее жертвенным венцом. Достоверно известно, что государь попросил Архимеда вычислить, не оказался ли его мастер-ювелир обманщиком, потратил ли он все золото на корону или что-то умыкнул себе. По тем временам это была очень сложная задача и великому ученному понадобилось большое количество времени и удача, чтобы разгадать эту загадку. Однажды он принимал ванну. Когда он опускался в нее, он не заметил, что она слишком полная и какое-то количество воды вылилось из ванны, после чего Архимед закричал «Эврика!». Это слово в переводе с греческого языка означает «нашел». Греческий философ и правда нашел решение, ведь сегодня каждый ребенок знает, что при погружении какого-либо элемента в сосуд, заполненный водой, объем вытесненной воды будет равен объему погруженного элемента.

Благодаря этой догадке Архимед помог греческому королю выявить лжеца ювелира и узнать правду. Так как ювелиру дали целый слиток золота, то его поместили в полный сосуд с водой, а после провели такой же эксперимент с короной и оказалось, что воды вылилось разное количество. Благодаря этому открытию в итоге возникнет целая наука – гидравлика. Это же открытие Архимеда объясняет, почему шар с более легким газом, чем воздух, может подниматься вверх, почему стальной шар тонет, а дерево нет.

Достоверно известно, что Архимед придумал винтовой насос, который очень долгое время служил на рудниках и в разных приспособлениях для откачки воды. Этот насос называется кохля. Принцип действия состоит в том, что в полую трубку помещают винт с большими лопастями, трубка обязательно должна находится под наклоном. После чего с помощью рабочей силы винт раскручивается, и вода по лопастям попадает из скважины наверх.

Как ни странно, первый, самый примитивный рычаг классифицировал и выделил тоже Архимед. Всем известна его знаменита фраза: «Дайте мне точку опоры и я сдвину мир». Рычаги, созданные великим ученным, были самыми продуктивными на то время. Большое количество его исследований и достижений дошли до нас от других философов. Как и многие другие ученные того времени, он нечасто записывал свои мысли или же его тексты потерялись во времени.

Говорить о том, что у него были и другие идеи, позволяют военные разработки, которые, как известно из истории, позволяли сопротивляться очень долго, прежде чем римлянам все же удалось взять Сиракузы.

Видео по теме

www.kakprosto.ru

Закон Архимеда – Физический факультет СПбГУ

 

С. Н. Манида

 

 

Установлена зависимость силы гидростатического давления (силы Архимеда) от плотности свободного тела, погруженного в жидкость.

1. Закон Архимеда для неподвижных тел

Любое тело, погруженное в жидкость, подвергается сжимающему и выталкивающему действию со стороны жидкости.

Представим такую ситуацию: ученый, владеющий современными приборами и мощным математическим аппаратом, решил вычислить силу, выталкивающую из жидкости погруженное в нее тело.

Он экспериментально установит, что на единицу поверхности тела, погруженного в жидкость с плотностью действует по нормали к поверхности сила гидростатического давления p, зависящая от глубины погружения h по определенному закону (gh) и не зависящая от ориентации поверхности.

Он сложит векторы сил давления, действующих на различные элементы поверхности тела и направленные по нормали к ним; для этого потребуется вычислить так называемый поверхностный интеграл от некоторой векторной функции по поверхности тела сложной формы. С помощью современного математического аппарата и мощных компьютеров этот интеграл может быть вычислен. Но каково же будет изумление этого ученого, когда окажется, что полученный результат численно равен весу жидкост и в объеме погруженной части тела! Этот результат был получен греческим ученым Архимедом 2200 лет назад, причем в общем виде — для тел любой формы!

Попробуем восстановить ход рассуждений Архимеда и вывести его закон.

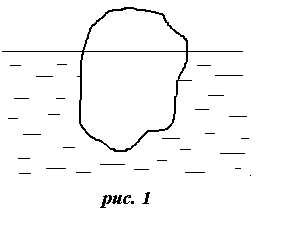
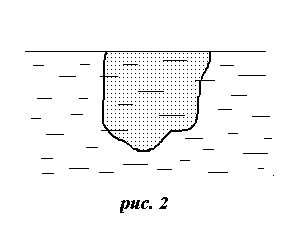
На рис. 1, изображено тело, помещенное в жидкость. На это тело со стороны жидкости действует описанная выше сила гидростатического давления. Для нахождения этой силы вместо вычисления сложных интегралов проведем мысленный эксперимент: уберем тело и рассмотрим жидкость в объеме V, который занимала погруженная часть тела (рис. 2). На эту жидкость действует сила тяжести Vg и сила гидростатического давления

F. Выделенный объем находится в равновесии, следовательно, сумма сил, действующих на жидкость в этом объеме, равна нулю: F+ Vg =0.

Отсюда следует выражение для силы гидростатического давления: F=-Vg.

Мы нашли силу, действующую на поверхность жидкости, заполняющей объем  V. Но поверхность тела, погруженного в жидкость, совпадает с поверхностью жидкости в нашем мысленном эксперименте, следовательно, найденное выражение и есть «выталкивающая’’ сила — сила Архимеда

F _Арх = -Vg. (*)

Это равенство и носит название

закон Архимеда.

2. Неприменимость закона Архимеда для случая свободных тел

Казалось бы, решение задач с использованием этого закона не должно вызывать затруднений. Однако неверные решения отдельных задач на закон Архимеда встречаются не только у школьников, но и в ряде задачников.

Дело в том, что при использовании этого (как и любого другого) закона надо всегда помнить, как и для каких ситуаций он выводился. Так, например, мы вычисляли силу гидростатического давления, действующую на поверхность неподвижного объема жидко сти, находящейся в равновесии, т. е. имеющей нулевые скорость и ускорение. Следовательно, и использовать выведенное выражение для силы Архимеда можно только в тех случаях, когда и

 скорость, и ускорение тела равны нулю.

Покажем, что применение этого закона в других ситуациях абсолютно неправомочно, так как приводит к неверным результатам.

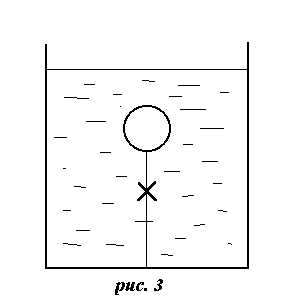
Рассмотрим легкое тело, привязанное ниткой к дну сосуда, заполненного жидкостью (рис. 3). Тело погружено в жидкость и находится в равновесии. На него действуют вниз сила тяжести mg= Vg и сила натяжения нити T, а вверх — сила гидростатического давления

F=F_Арх=- Vg, (*)

где – плотность тела, – плотность жидкости. Условие равновесия тела

-Vg +T+Vg =0. (1)

Пусть в некоторый момент нить обрывается (т. е. исчезает сила натяжения T), равенство (1) перестает выполняться, и тело начинает двигаться вве рх (всплывать) с некоторым ускорением a, которое можно найти из уравнения движения

F+ V g = V a. (2)

Предположив, что в этом случае можно использовать закон Архимеда, подставим – Vg в левую часть равенства (2) вместо F. Для ускорения тела получаем выражение

a = — g (-)/ (3)

Исследуем выражение (3). Ускорение тела направлено против ускорения свободного падения (что абсолютно верно), а его величина неограниченно возрастает при уменьшении плотности тела. Такой результат противоречит как здравому смыслу, так и наблюдениям.

Таким образом, закон Архимеда в форме (*) неприменим к телам, ускорение которых относительно жидкости отлично от нуля (даже при равной нулю скорости).

3. Сила гидростатического давления для случая свободных тел

Точный расчет гидростатического давления на поверхность ускоренно движущегося тела возможен только с применением аппарата математической физики, а ответ представим в аналитическом виде лишь для некоторых частных случаев. Уравнения, описывающие движение тела в жидкости, были впервые получены профессором Петербургского университета Леонардом Эйлером в середине XVIII века. Решение этой задачи для случая тела сферической формы, размеры которого много меньше размеро в сосуда, приведено в Приложении (для читателей, владеющих методами постановки и решения граничных задач математической физики). Полученное там выражение (**) для силы давления отличается от (*):

(4)

и, с учетом (2), ускорение тела имеет вид:

(5)

4. Выводы

Сравнивая выражения (4) и (*) видим, что они совпадают только при = . Зависимость силы гидростатического давления, действующей на свободное тело, от его плотности представлена на графике рис. 4 в сравнении со стандартным выражением для силы Архимеда Vg: 

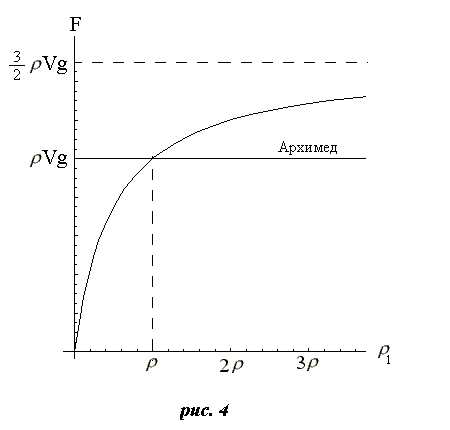
Из графика на рис.4 видно, что для малых плотностей тела сила давления убывает до нуля, а при увеличении плотности эта сила стремится к величине 1,5Vg.

На следующем графике (рис. 5) приведена зависимость ускорения свободного тела в жидкости от его плотности [уравнение (5)]. Для сравнения приведен график ускорения, получающийся непосредственн о из закона Архимеда [уравнение (3)]

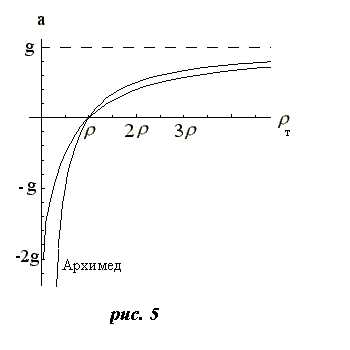
Из этого графика видно, что даже бесконечно легкий шарик всплывает с конечным ускорением, равным -2g, а тяжелые тела тонут с ускорением, меньшим, чем это следует из закона Архимеда.

www.phys.spbu.ru

Сила Архимеда – это… Что такое Сила Архимеда?



Сила Архимеда

Wikimedia Foundation. 2010.

• Сила (физика)
• Сила Уорд

Смотреть что такое “Сила Архимеда” в других словарях:

• Архимеда закон — Архимеда закон: F выталкивающая сила; P сила тяжести, действующая на тело. АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх, равная весу вытесненной им жидкости и приложенная к центру… …   Иллюстрированный энциклопедический словарь

• АРХИМЕДА ЧИСЛО — подобия критерий двух гидродинамич. или тепловых явлений, при к рых определяющими явл. выталкивающая (архимедова) сила (см. АРХИМЕДА ЗАКОН) и сила вязкости. где l характерный линейный размер, v коэфф. кинематич. вязкости, r и r1 плотность среды в …   Физическая энциклопедия

• АРХИМЕДА ЗАКОН — закон статики жидкостей и газов, согласно к рому на всякое тело, погружённое в жидкость (или газ), действует со стороны этой жидкости (газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и… …   Физическая энциклопедия

• СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… …   Большая политехническая энциклопедия

• СИЛА — в физическом смысле способность изменять форму материальных масс, вызывать их движение, менять направление и скорость движения или приводить тело в состояние покоя. «Живая» сила (редко употребляемое теперь выражение), или действующая сила, – сила …   Философская энциклопедия

• АРХИМЕДА ЗАКОН — АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. Закон Архимеда справедлив и для газов …   Энциклопедический словарь

• Архимеда закон — на всякое тело, погружённое в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости. В несколько иной формулировке впервые был установлен древнегреческим учёным Архимедом в III в. до н. э. Доказывается на основе уравнений… …   Энциклопедия техники

• Архимеда закон —         закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) поддерживающая сила, равная весу вытесненной телом жидкости (газа), направленная вверх и… …   Большая советская энциклопедия

• Архимеда закон{:} — на всякое тело, погружённое в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. Архимеда закон справедлив и для газов …   Энциклопедический словарь

• АРХИМЕДА ЗАКОН — [по имени древнегреч. учёного Архимеда (ок. 287 212 до н. э.)] закон гидро и аэростатики. Согласно А. з., на тело, погруж. в жидкость (или газ), действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости (или… …   Большой энциклопедический политехнический словарь

Книги

• Загадки Архимеда, Юлу-Гарсиа Антуан, Фишки- Возраст 7-9 лет- 80 увлекательных упражнений – 3 раздела: геометрия, логика, счет- Необычные примеры и веселые задачки- Полный курс математики начальных классов-Разные уровни… Категория: Игры и увлечения Серия: Зарядка для мозга Издатель: Клевер Медиа Групп, Производитель: Клевер Медиа Групп, Подробнее  Купить за 555 грн (только Украина)
• Физика. 7 класс. Рабочая тетрадь к учебнику А. В. Перышкина. Вертикаль. ФГОС, Ханнанова Татьяна Андреевна, Ханнанов Наиль Кутдусович, Пособие является составной частью УМК А. В. Перышкина “Физика. 7-9 классы”, который переработан в соответствии с требованиями нового Федерального государственного образовательного стандарта.… Категория: Физика. Астрономия (7-9 классы) Серия: Физика Издатель: Дрофа, Подробнее  Купить за 228 руб
• Физика 7 класс Рабочая тетрадь к учебнику А В Перышкина, Ханнанова Т., Ханнанов Н., Пособие является составной частью УМК А. В. Перышкина «Физика. 7—9 классы», который переработан в соответствии с требованиями нового Федерального государственногообразовательного стандарта. В… Категория: Физика. Астрономия Подробнее  Купить за 194 руб

Другие книги по запросу «Сила Архимеда» >>

dic.academic.ru

ЗАКОН АРХИМЕДА – это… Что такое ЗАКОН АРХИМЕДА?



ЗАКОН АРХИМЕДА

ЗАКОН АРХИМЕДА, АРХИМЕД сделал вывод, что тело, погруженное в жидкость, выталкивается с силой, равной весу вытесненной жидкости. Рассказывают, что он якобы сформулировал этот закон, погрузившись в ванну и наблюдая, как вытекает вода. Согласно легенде, он был так потрясен, что выбежал раздетый с криком «Эврика! Эврика!» («Я нашел его!»).

Научно-технический энциклопедический словарь.

• ЗАКИСЬ АЗОТА
• ЗАКОН БЕРНУЛЛИ

Смотреть что такое “ЗАКОН АРХИМЕДА” в других словарях:

• ЗАКОН АРХИМЕДА — закон гидро и аэростатики, согласно которому на всякое тело, погружённое в жидкость или газ, действует выталкивающая сила (архимедова сила), равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и приложенная к центру… …   Большая политехническая энциклопедия

• Закон Архимеда — Закон Архимеда  один из главных законов гидростатики и статики газов. Содержание 1 Формулировка и пояснения 2 Обобщения …   Википедия

• закон Архимеда — Archimedo dėsnis statusas T sritis Standartizacija ir metrologija apibrėžtis Skysčių ir dujų statikos dėsnis: kūną, panardintą į skystį ar dujas, veikia išstumiamoji jėga F, lygi kūno išstumto skysčio ar dujų sunkiui; jos veikimo taškas –… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• закон Архимеда — Archimedo dėsnis statusas T sritis fizika atitikmenys: angl. Archimedes law; Archimedes principle vok. Archimedisches Gesetz, n; Archimedisches Prinzip, n rus. архимедов принцип, m; закон Архимеда, m pranc. principe d’Archimède, m; théorème… …   Fizikos terminų žodynas

• АРХИМЕДА ЗАКОН — АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости. Закон Архимеда справедлив и для газов …   Энциклопедический словарь

• закон архімеда — закон Архимеда Archimed’s law *Archimedisches Prinzip – на занурене в рідину тіло діє вертикально напрямлена вверх сила, що дорівнює силі тяжіння рідини, об єм якої є рівним об’ємові зануреного тіла. Якщо сила тяжіння тіла G більша… …   Гірничий енциклопедичний словник

• Закон (физика) — У этого термина существуют и другие значения, см. Закон (значения). Физический закон эмпирически установленная и выраженная в строгой словесной и/или математической формулировке устойчивая связь между повторяющимися явлениями, процессами и… …   Википедия

• Архимеда закон — Архимеда закон: F выталкивающая сила; P сила тяжести, действующая на тело. АРХИМЕДА ЗАКОН: на всякое тело, погруженное в жидкость, действует выталкивающая сила, направленная вверх, равная весу вытесненной им жидкости и приложенная к центру… …   Иллюстрированный энциклопедический словарь

• Архимеда закон —         закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) поддерживающая сила, равная весу вытесненной телом жидкости (газа), направленная вверх и… …   Большая советская энциклопедия

• АРХИМЕДА ЗАКОН — закон статики жидкостей и газов, согласно к рому на всякое тело, погружённое в жидкость (или газ), действует со стороны этой жидкости (газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и… …   Физическая энциклопедия

Книги

• Современная русская проза. 22 рассказа, `Принято считать, что антологии составляются для каких-то высших литературных целей. Вот и я могла бы сказать, что этот сборник является подведением каких-нибудь итогов, что он представляет… Категория: Сборники прозы Издатель: Захаров, Подробнее  Купить за 300 руб
• Физика. 7 класс. Тесты к учебнику А. В. Перышкина. Вертикаль. ФГОС, Ханнанов Наиль Кутдусович, Ханнанова Татьяна Андреевна, Пособие представляет собой сборник тестов для тематического и рубежного контроля. Может быть использовано как при работе с учебником, соответствующим ФК ГОС, так ипри работе с учебником,… Категория: Физика. Астрономия (7-9 классы) Серия: Физика Издатель: Дрофа, Подробнее  Купить за 237 руб
• Физика. 7 класс. Рабочая тетрадь к учебнику А. В. Перышкина. Вертикаль. ФГОС, Ханнанова Татьяна Андреевна, Ханнанов Наиль Кутдусович, Пособие является составной частью УМК А. В. Перышкина “Физика. 7-9 классы”, который переработан в соответствии с требованиями нового Федерального государственного образовательного стандарта.… Категория: Физика. Астрономия (7-9 классы) Серия: Физика Издатель: Дрофа, Подробнее  Купить за 228 руб

Другие книги по запросу «ЗАКОН АРХИМЕДА» >>

dic.academic.ru