1.1.4 Движение вдоль прямой с переменным ускорением
Не нужно думать, что движение тела по прямой может быть только либо равномерным ( const), либо равнопеременным ( const). На практике часто возникают ситуации, когда ускорение тела (а, следовательно, и его скорость, как производная по времени от ускорения) меняются со временем. Простейший пример – гармонические колебания, в ходе которых координата тела меняется по синусоидальному (гармоническому) закону:
x Asin(t ), (1.8)
Acos(t ) const,
a A2sin(t ) const.
Еще
один пример движения, которое не является ни
равномерным и ни равнопеременным –
движение транспортного средства в
режиме, когда меняется сила тяги FТЯГИ мотора.
В заключение заметим, что на практике часто используется понятие средней путевой скорости, которое применяется для характеристики движения с переменными скоростью и ускорением. В отличие от эта скорость не является вектором и определяется, как отношение всего пройденного телом пути S ко всему затраченному времени t, то есть
1.1.5 Движение тела, брошенного под углом к горизонту
Е
сли
пренебречь действием силы сопротивления
воздуха, траекторией такого движения
этого тела окажется кривая – парабола.
При этом такое движение можно представить
в виде совокупности двух прямолинейных
движений: одного (по горизонтали) –
равномерного, его можно описать формулой
(1.
4), и, по вертикали, – равнопеременного,
описываемого формулами (1.6 и 1.7).
Движение по горизонтали (ось 0X) является равномерным, так как в этом направлении на тело не действуют никакие силы, и, следовательно, ускорение тела в этом направлении равно нулю, то есть горизонтальная компонента вектора скорости
По вертикали на тело действует лишь одна постоянная сила – сила тяжести m, создающая постоянное же ускорение (примерно 9,8 м/с). Следовательно, движение по вертикали является равнопеременным, и это означает, что компонента Y скорости тела вдоль вертикальной оси (обозначим её 0Y и направим в сторону, противоположную вектору ) меняется по закону
Y 0Y gt .
Соответственно, изменение координаты y описывается выражением y y0 0
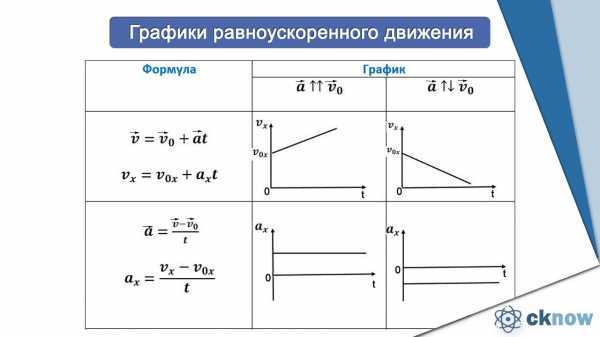рис. 1.5,
можно записать следующие пять формул,
которые позволяют легко решать стандартные
задачи кинематики для тела, траекторией
которого является парабола:х х0 Xt
y y0 0Yt
Y
tg .
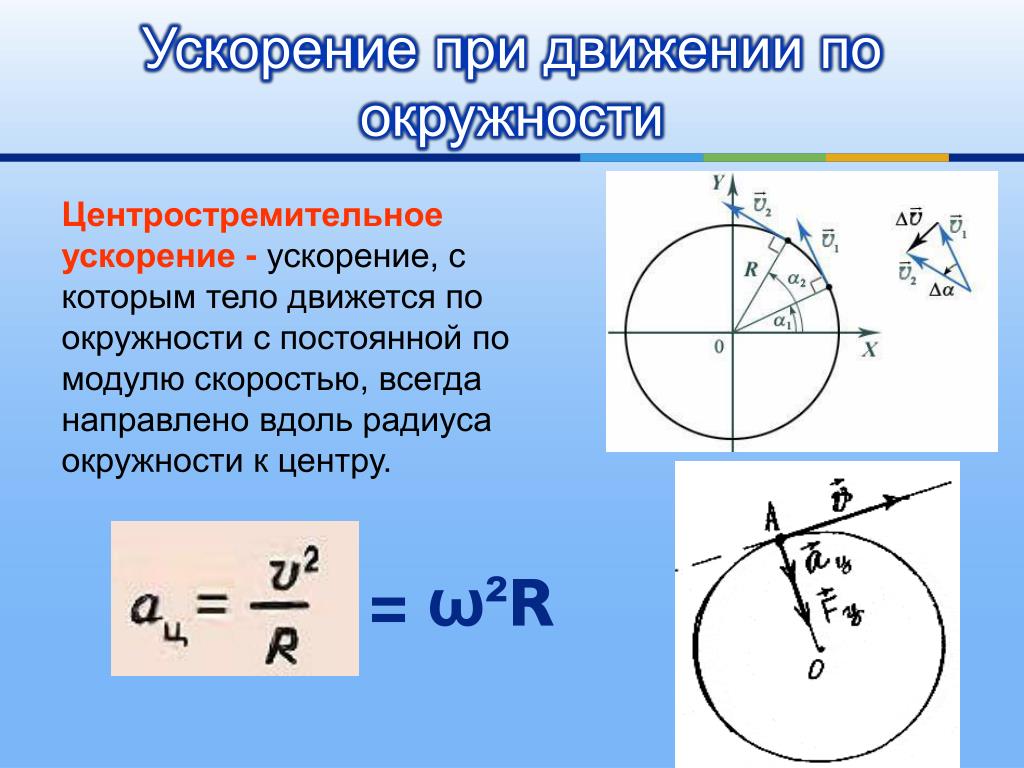
1.1.6 Движение точки по окружности
Для
описания движения точки по окружности
в декартовой системе координат необходимо
знать законы изменения со временем хотя
бы двух её линейных координат: x(t)
и y(t)
– см. рис. 1.6.
Можно, однако, упростить задачу, перейдя
от декартовых координат к полярным, в
которых для описания движения по
окружности достаточно знать радиус
этой окружности r (который со временем не меняется), и
всего лишь одну зависимость от времени
– для угловой координаты (угла поворота
).
В этом случае оказывается, что понятия,
введённые для поступательного движения,
не только могут быть использованы для
описания движения по окружности, но и
получаемые при этом формулы приобретают
уже знакомый нам вид.
Итак, положение точки на плоскости мы будем задавать вектором , по величине, равным углу поворота относительно выбранной оси (на рисунке – это ось 0Y). Сам вектор (вектора такого типа называются аксиальными) направлен вдоль оси вращения в соответствии с «правилом винта (буравчика)»: поворачивая винт в сторону возрастания угла, определяем, куда движется тело самого винта – это и есть направление вектора . На рис. 1.6, на котором увеличению угла соответствует вращательное движение точки A по часовой стрелке, вектор направлен из точки 0 по оси вращения вглубь плоскости рисунка.
По определению вектор
(1.9)
называется угловой скоростью движения
точки по окружности.
В СИ величину угла
принято измерять в радианах, единица
измерения угловой скорости – радс1.
Вектор также направлен вдоль оси вращения: в
ту же сторону, что и
,
если при вращении угол растёт, или в
противоположную, если угол
уменьшается. На рис. 1.6 вектор так же, как и
,
направлен вдоль оси вращения «от нас».
Угловым ускорением называется скорость изменения угловой скорости:
, (1.10)
величина углового ускорения измеряется в радс2. Если в процессе движения угловая скорость растёт, значит, вектор направлен в ту же сторону, что и вектор , если угловая скорость уменьшается, то вектор хотя и направлен вдоль оси вращения, но антипараллелен вектору .
Равномерным называется вращение, при котором const. Действуя так же, как в случае рассмотрения равномерного движения точки по прямой, можно легко показать, что при таком движении зависимость угла поворота от времени будет выражаться формулой
0
t (1.
11)
Здесь 0 – значение угла в начальный (t 0) момент времени; знак перед вторым слагаемым зависит от того, в какую сторону направлен вектор : если при движении точки угол растёт, то тогда пишем «», если уменьшается (становится меньше 0) – знак «».
Время T, за которое совершается один полный оборот (при этом 0 2), называется
. (1.12)
Равнопеременным называется движение по окружности, при котором const. При этом если ↑↑, вращение называется равноускоренным, а если ↑↓ – равнозамедленным.
Аналогично тому, как это было сделано при выводе формул (1.6) и (1.7), можно показать, что при равнопеременном вращении с начальной скоростью 0 зависимости (t) и (t) имеют вид:
0
t;
(1.
0 0t . (1.14)
Перед значениями 0 и для тех из векторов и , которые направлены в сторону, противоположную вектору , в формулах (1.13) и (1.14) пишется знак «минус».
В каждый момент времени величина линейной скорости точки при движении по окружности радиусом r связана с её угловой скоростью соотношением r. Если точка движется по траектории сложной формы, то в каждый момент времени для положения, характеризующегося радиус-вектором , проведённым из любой заданной точки, её линейную и угловую скорости относительно этой точки можно связать формулой
[]. (1.15)
Произведение и
вида
[]
называется векторным;
его результатом является вектор такой, что c absin
(здесь
– угол между векторами
и
).
Направление вектора определяется
по правилу буравчика или по «правилу
левой руки»: пальцы ладони направляются
по вектору так, чтобы вектор «входил» в
ладонь, при этом отставленный в сторону
большой палец будет показывать направление
.
При движении по окружности все три вектора (, и ) оказываются взаимно перпендикулярными, то есть, формула (1.15) приобретает вид
Равнопеременное движение по любой кривой означает, что вектор линейной скорости непрерывно меняет свою величину. Соответствующее этому явлению линейное ускорение называется тангенциальным, в общем случае оно связано с угловым ускорением векторным произведением
[]. (1.16)
В частности, при равнопеременном движении по окружности a r, поскольку вектора , и взаимно перпендикулярны.
Если
0, то
const,
и движение по окружности является
равномерным.
Но даже в этом случае вектор
скорость меняется – по направлению. Это означает,
что имеет место ускорение
,
которое называется нормальным (или центростремительным )
и при этом направлено перпендикулярно
вектору в сторону центра окружности, по которой
движется точка. Можно показать, что
aцс , или, с учётом формулы (1.15), aцс 2r. (1.17)
Движение по прямой можно представить, как движение по окружности бесконечно большого радиуса, при этом 0, а совпадает с обычным линейным ускорением точки . При равномерном движении по окружности нулю равно тангенциальное ускорение , то есть . В общем случае при движении с ускорением по любой кривой полное ускорение точки является векторной суммой и , а поскольку они взаимно перпендикулярны, то
a . (1.18)
Сказанное поясняется рисунком 1.7.
Таким
образом, в рамках данной лекции, мы
показали как, основываясь лишь на
определениях и используя при этом
известные математические операции,
можно построить основы целого раздела
физики, описывающего перемещение тела
в пространстве и позволяющего, тем
самым, решать важные в практическом
отношении задачи.
Некоторые примеры
О пути
Длина первой железной дороги России, построенной в 1837 году, (Петербург – Царское село) – 26 км.
Длина железнодорожной магистрали Москва – Санкт-Петербург (открыта в 1851 году) – 650 км.
Длина самого длинного в мире железнодорожного тоннеля (Симплтон I, Швейцария) – 19,825 км.
Длина Северо-Муйского тоннеля (Байкало-Амурская магистраль) – около 15 км;
Длина самой большой в мире электрифицированной магистрали (Брест – Минск – Москва – Омск – Иркутск – Хабаровск – Уссурийск) – 10400 км.
Тормозной путь электрички – до 0,5 км.
Тормозной путь поезда (зависит от массы и скорости состава) – до 2 км.
О скорости
При
описании движения тел термин «скорость»
может использоваться в более широком,
чем это соответствует формуле (1.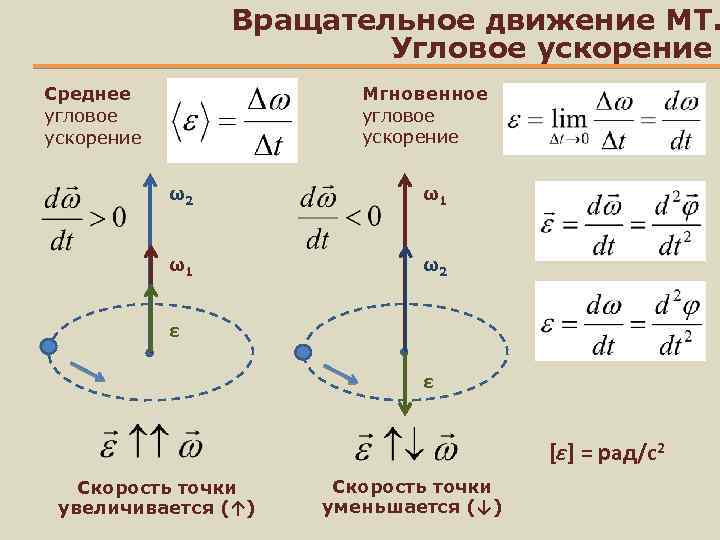
1) смысле.
Так, можно говорить о крейсерской скорости транспортного средства (эта
скорость соответствует движению по
маршруту без учёта участков разгона и
торможения), о коммерческой скорости (эта скорость характеризует
движение груза по маршруту с учётом
всех задержек, связанных с перегрузкой
с одного транспортного средства на
другое, с оформлением документации и
т. д.), о конструкционной скорости (максимальной скорости,
закладываемой конструктором в
проектируемый объект), и др. Каждый такой
«вид» скорости имеет собственное
определение, поскольку позволяет
ответить на вполне определённые
практически значимые вопросы. В частности,
как мы уже говорили выше, на практике
помимо введённой нами мгновенной
скорости используется понятие средней
путевой скорости.
В
СИ время измеряется в секундах, поэтому
единицей измерения скорости является метр в секунду: [] мс1.
Допускается
использование и других единиц измерения:
км/ч, км/c, см/c и др.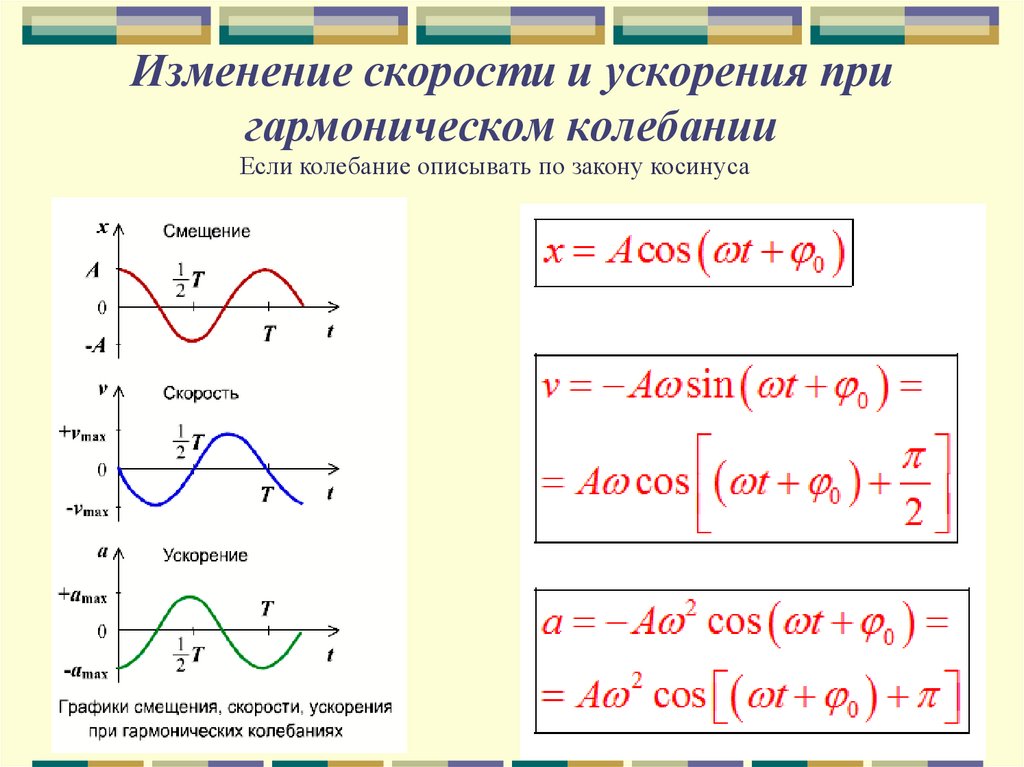
Максимальная скорость первого паровоза (1803 г., Р. Третвитик, Англия) – 10 км/ч.
Скорость паровоза «Ракета» (1829 г., Д. Стефенсон, Англия) – 50 км/ч.
Скорость первого российского паровоза (1834 г., отец и сын Черепановы) – 15 км/ч.
Скорость поезда на трассе Париж – Бордо, Франция – до 350 км/ч.
Рекорд скорости для обычных поездов на скоростной трассе Париж – Страсбург – до 574,8 км/ч (2007 г.).
Скорость экспериментальной модели поезда, движущегося в специально проложенной вакуумной трубе (Япония) – до 2535 км/ч.
Скорость звука в воздухе – 330 м/с 1188 км/ч.
Скорость света в вакууме – 2,98108 м/с
Об ускорении
Единица
измерения ускорения в СИ: [а]
мс2.
Некоторые примеры.
Обычное ускорение при начале движения поезда – до 0,3 м/с2.
Допустимое ускорение поезда (считается при больших ускорениях у пассажиров возникают ощутимые неудобства) – 1,5 м/с2;
Ускорение поезда при экстренном торможении – около 1 м/с2
Ускорение, возникающее при использовании специально разрабатываемых тормозов для скоростных поездов – до 1,9 м/с2.
Вопросы для повторения
Дайте определения основных терминов, используемых в кинематике: траектории, пути, перемещения, скорости, ускорения, средней скорости.
Какие виды движения точки по прямой и по окружности Вам известны? Дайте определения этим видам движения.
Выведите формулы, описывающие изменение со временем координаты точки при её движении по прямой в случаях разных видов движения.
Запишите формулы, описывающие изменение со временем координат точки при её движении по параболе.
Выведите формулы, описывающие изменение со временем угловой координаты точки при её движении по окружности в случаях разных видов движения.
Дайте определения основных параметров, используемых при описании движения точки по окружности.
Как связаны между собою линейные и угловые характеристики движения тела по окружности?
Приведите примеры характерных значений расстояний, скоростей и ускорений, с которыми мы сталкиваемся на железнодорожном транспорте.
Каково максимально достижимое значение скорости в нашей Вселенной? Какой физический объект имеет эту скорость?
Виды прямолинейного движения и их характеристики.
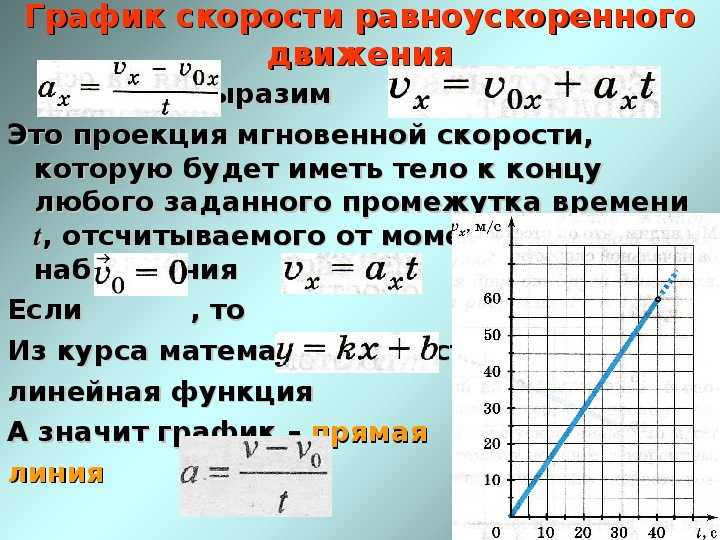
Прямолинейное равномерное и равноускоренное движение в физикеВиды движения (равномерное, равноускоренное) и их графическое описание
По форме траектории движение делится на криволинейное (траектория движения тела кривая линия) и прямолинейное (траектория движения тела прямая линия).
При движении тела по прямолинейной траектории модуль вектора перемещения всегда совпадает с пройденным путём. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути
Равномерное прямолинейное движение.
Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:
v х =S/t
Скорость – это физическая величина, показывающая быстроту изменения координаты.
Единицы измерения скорости – метры в секунду
Уравнение равномерного движения (перемещение тела при равномерном движении):
S=v х ·t
Уравнение координаты тела:
х=х 0 +v х ·t
Обозначения:
х – координата движущегося тела
х 0 – начальная координата движущегося тела
v ср -Средняя скорость равномерного прямолинейного движения
v х – Скорость равномерного прямолинейного движения
S – Перемещение тела (расстояние, на которое передвинулось тело)
t – Промежуток времени перемещения (время)
Графическое представление равномерного прямолинейного движения
v
Зависимость ускорения от времени . Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Так как тело движется прямолинейно и равномерно (v =const), т.
е. скорость со временем не изменяется, то график с зависимостью скорости от времени v (t) – прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) – наклонная линия:
Зависимость координаты от времени. График х(t) – наклонная линия:
Из графика видно, что проекция скорости равна:
v х =S/t=tga
Рассмотрев эту формулу, мы можем сказать, чем больше угол a , тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t) и x(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением .
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость , которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt :
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории .
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением .
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Обозначения:
v х – конечная скорость тела при равноускоренном движении по прямой
v 0х – начальная скорость тела
a – ускорение тела
t – время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
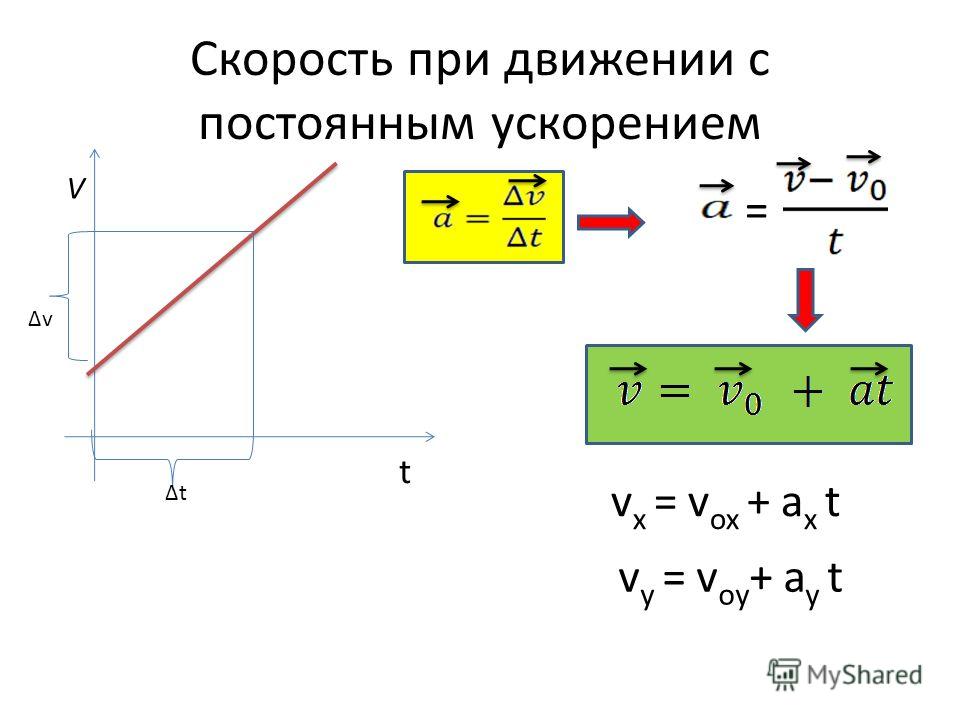
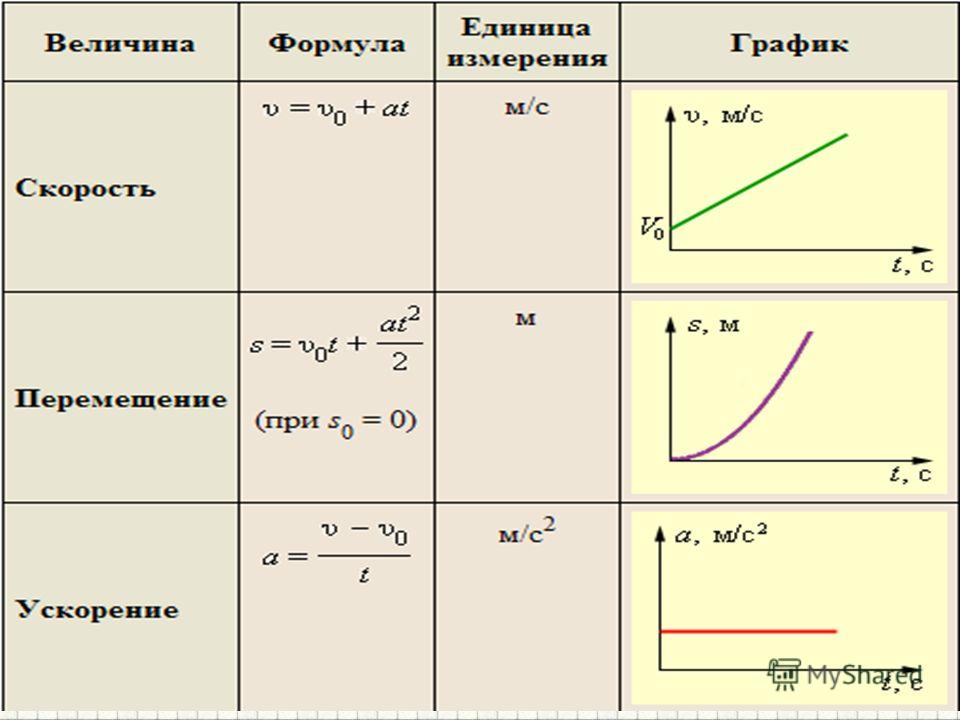
Уравнение скорости для равноускоренного движения:
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Обозначения:
Перемещение тела при равноускоренном движении по прямой
Начальная скорость тела
Скорость тела при равноускоренном движении по прямой
Ускорение тела
Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
– если известны начальная, конечная скорости движения и ускорение.
– если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
v (t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем
Зависимость ускорения от времени.
Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени . При равномерном движении скорость изменяется, согласно линейной зависимости .
Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратичной зависимости
В координатах зависимость имеет вид .
Графиком является ветка параболы.
Чтобы найти координаты движущегося тела в любой момент времени, нужно знать проекции вектора перемещения на оси координат, а значит, и сам вектор перемещения.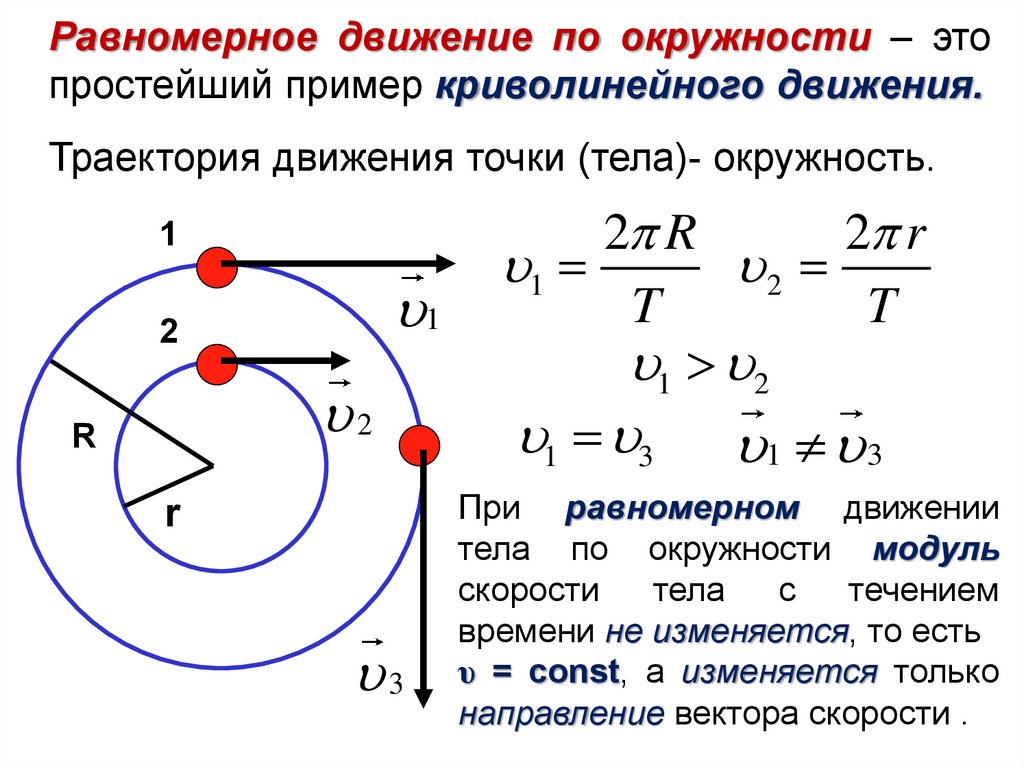
Что для этого нужно знать. Ответ зависит от того, какое движение совершает тело.
Рассмотрим сначала самый простой вид движения – прямолинейное равномерное движение .
Движение, при котором тело за любые равные промежутки совершает одинаковые перемещения, называют прямолинейным равномерным движением.
Чтобы найти перемещение тела в равномерном прямолинейном движении за какой-то промежуток времени t , надо знать, какое перемещение совершает тело за единицу времени, поскольку за любую другую единицу времени оно совершает такое же перемещение.
Перемещение, совершаемое за единицу времени, называют скоростью движения тела и обозначают буквой υ . Если перемещение на этом участке обозначить через , а промежуток времени через t , то скорость можно выразить отношением к . Поскольку перемещение – векторная величина, а время – скалярная , то скорость тоже векторная величина. Вектор скорости направлен так же, как и вектор перемещения.
Скоростью равномерного прямолинейного движения тела называют величину, равную отношению перемещения тела к промежутку времени, в течение которого это перемещение произошло:
Таким образом, скорость показывает, какое перемещение совершает тело в единицу времени. Следовательно, чтобы найти перемещение тела, надо знать его скорость . Перемещение тела вычисляется по формуле:
Вектор перемещения направлен так же, как и вектор скорости, время t – величина скалярная.
По формулам, написанным в векторной форме, вычисления вести нельзя, поскольку векторная величина имеет не только численное значение, но и направление. При вычислениях пользуются формулами, в которые входят не векторы, а их проекции на оси координат, так как над проекциями можно производить алгебраические действия.
Поскольку векторы равны, то равны и их проекции на ось X , отсюда:
Теперь можно получить формулу для вычисления координаты x точки в любой момент времени.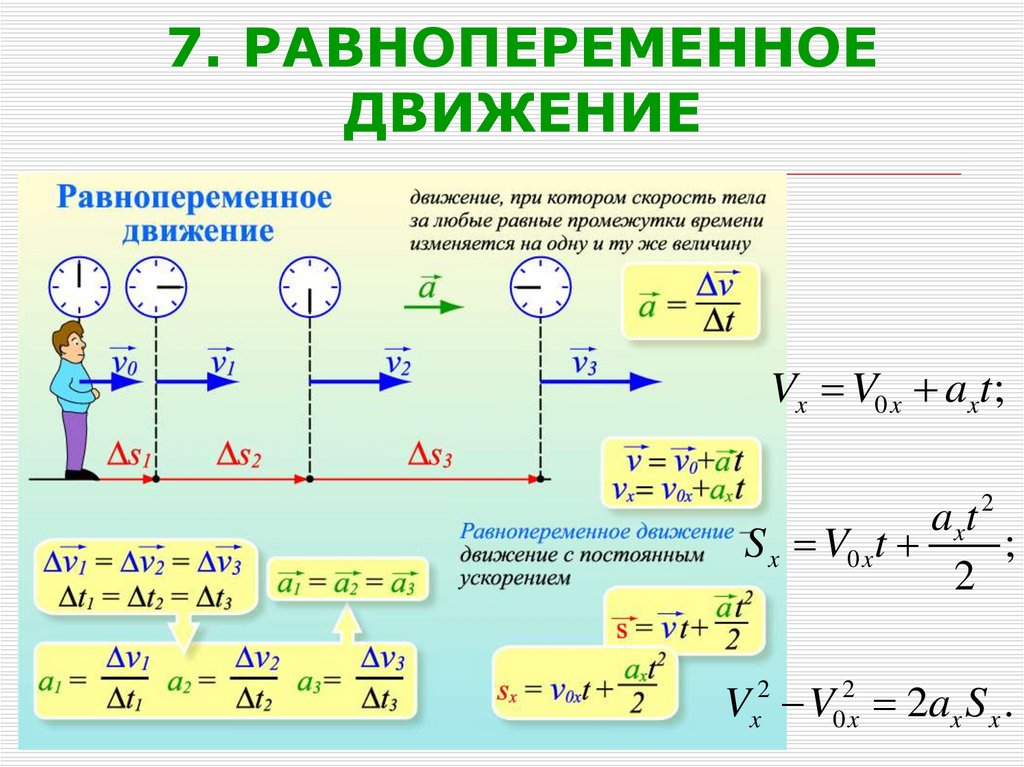
Нам известно, что
Из этой формулы видно, что при прямолинейном равномерном движении координата тела линейно зависит от времени, а это значит, что с ее помощью можно описать прямолинейное равномерное движение.
Кроме того, из формулы следует, что для нахождения положения тела в любой момент времени при прямолинейном равномерном движении нужно знать начальную координату тела x 0 и проекцию вектора скорости на ось, вдоль которой движется тело.
Необходимо помнить, что в этой формуле v x – проекция вектора скорости, следовательно, как всякая проекция вектора, она может быть положительной и отрицательной.
Прямолинейное равномерное движение встречается редко. Чаще приходится иметь дело с движением, при котором за равные промежутки времени перемещения тела могут быть различными. Это значит, что скорость тела с течением времени как-то изменяется. С переменной скоростью движутся автомобили, поезда, самолеты и т. д., брошенное вверх тело, падающие на Землю тела.
При таком движении для вычисления перемещения формулой пользоваться нельзя, поскольку скорость изменяется во времени и речь уже идет не о какой-то определенной скорости, значение которой можно подставить в формулу. В таких случаях пользуются так называемой средней скоростью, которая выражается формулой:
Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени.
Однако, при помощи понятия средней скорости основную задачу механики – определить положение тела в любой момент времени – решить нельзя.
В основе многих задач в физике лежит рассмотрение прямолинейного равномерного и равноускоренного движения. Они являются самыми простыми и идеализированными случаями перемещения тел в пространстве. Охарактеризуем их подробнее в данной статье.
Прежде чем рассмотреть равномерное и полезно разобраться с самим понятием.
Движение представляет собой процесс изменение координат материальной точки в пространстве за определенный промежуток времени.
Согласно данному определению, выделим следующие признаки, по которым можно сразу сказать, идет ли речь о движении или нет:
- Должно иметь место изменение пространственных координат. В противном случае тело можно считать покоящимся.
- Процесс должен развиваться во времени.
Также обратим внимание на понятие “материальной точки”. Дело в том, что при изучении вопросов механического движения (равномерного и равноускоренного прямолинейного движения в том числе) строение тела и его размеры не учитывают. Связано это приближение с тем, что величина изменения координат в пространстве намного превосходит физические размеры движущегося объекта, поэтому его считают материальной точкой (слово “материальный” предполагает учет его массы, поскольку ее знание необходимо при решении рассматриваемых задач).
Основные физические величины, характеризующие движение
К ним относятся скорость, ускорение, пройденный путь, а также понятие траектории. Разберем каждую величину по порядку.
Скорость прямолинейного равномерного и равноускоренного движения (векторная величина) отражает быстроту изменения координат тела во времени. Например, если оно переместилось за 10 секунд на 100 метров (типичные значения для спринтеров на спортивных соревнованиях), тогда говорят о скорости 10 метров в секунду (100/10 = 10 м/с). Обозначается эта величина латинской буквой “v” и измеряется в единицах расстояния, деленных на время, например, километры в час (км/ч), метры в минуту (м/мин.), мили в час (мил./ч) и так далее.
Ускорение – физическая которая обозначается буквой “a”, и характеризуется быстроту изменения самой скорости. Возвращаясь к примеру спринтеров, известно, что в начале забега они совершают старт с небольшой скоростью, по мере движения она увеличивается, достигая максимальных значений. Размерность ускорения получается, если поделить таковую для скорости на время, например, (м/с)/с или м/с 2 .
Пройденный путь (скалярная величина) отражает расстояние, которое прошел (проехал, пролетел, проплыл) движущийся объект.
Эта величина однозначно определяется только начальным и конечным положением объекта. Измеряется она в единицах расстояния (метры, километры, миллиметры и другие) и обозначается буквой “s” (иногда “d” или “l”).
Траектория в отличие от пути характеризует кривую линию, по которой двигалось тело. Поскольку в данной статье рассматривается только движение равноускоренное и равномерное прямолинейное, то и траектория для него будет прямой линией.
Вопрос относительности движения
Многие люди замечали, что находясь в автобусе, можно видеть, что движущийся по соседней полосе автомобиль, кажется покоящимся. Этот пример наглядно подтверждает, относительность движения (равноускоренного, равномерного прямолинейного движения и других его видов).
Учитывая названную особенность, при рассмотрении задач с движущимися объектами всегда вводят систему отсчета, относительно которой решают поставленную проблему. Так, если за систему отчета взять пассажира в автобусе в примере выше, то относительно него скорость автомобиля будет равна нулю.
Если же рассматривать движение относительно стоящего на остановке человека, то относительно него автомобиль движется с некоторой скоростью v.
В случае прямолинейного движения, когда два объекта движутся вдоль одной линии, то скорость одного из них относительно другого определяется по формуле: v ¯ = v ¯ 1 + v ¯ 2 , здесь v ¯ 1 и v ¯ 2 – скорости каждого объекта (черта означает, что складываются векторные величины).
Самый простой вид движения
Конечно же, таковым является движение объекта по прямой с постоянной скоростью (равномерное прямолинейное). Примером этого типа движения является полет самолета через облака или ходьба пешехода. В обоих случаях траектория объекта остается прямой, и каждый из них перемещается с конкретной скоростью.
Формулы, описывающие этот тип перемещения объектов, имеют следующий вид:
- s = v*t;
- v = s/t.
Здесь t – промежуток времени, в течение которого рассматривается движение.
Равноускоренное прямолинейное перемещение
Под ним понимают такой тип прямолинейного перемещения объекта, при котором его скорость изменяется по формуле v = a*t, где a – постоянное ускорение.
Изменение скорости возникает за счет действия внешних сил, имеющих различную природу. Например, тот же самолет, прежде чем достигнет крейсерской скорости, должен ее набрать из состояния покоя. Другой пример: торможение автомобиля, когда скорость изменяется от некоторой величины до нуля. Этот тип движения называется равнозамедленным, поскольку ускорение имеет в нем отрицательный знак (направлено против вектора скорости).
Пройденный путь s при данном типе перемещения можно рассчитать, если проинтегрировать величину скорости по времени, в результате получится формула: s = a*t 2 /2, где t – время ускорения (торможения).
Смешанный тип движения
В ряде случаев прямолинейное перемещение объектов в пространстве происходит, как с постоянной скоростью, так и с ускорением, поэтому полезно привести формулы для этого смешанного типа движения.
Скорость и ускорение равномерного и равноускоренного прямолинейного движения связаны друг с другом следующим выражением: v = v 0 + a*t, где v 0 – значение начальной скорости.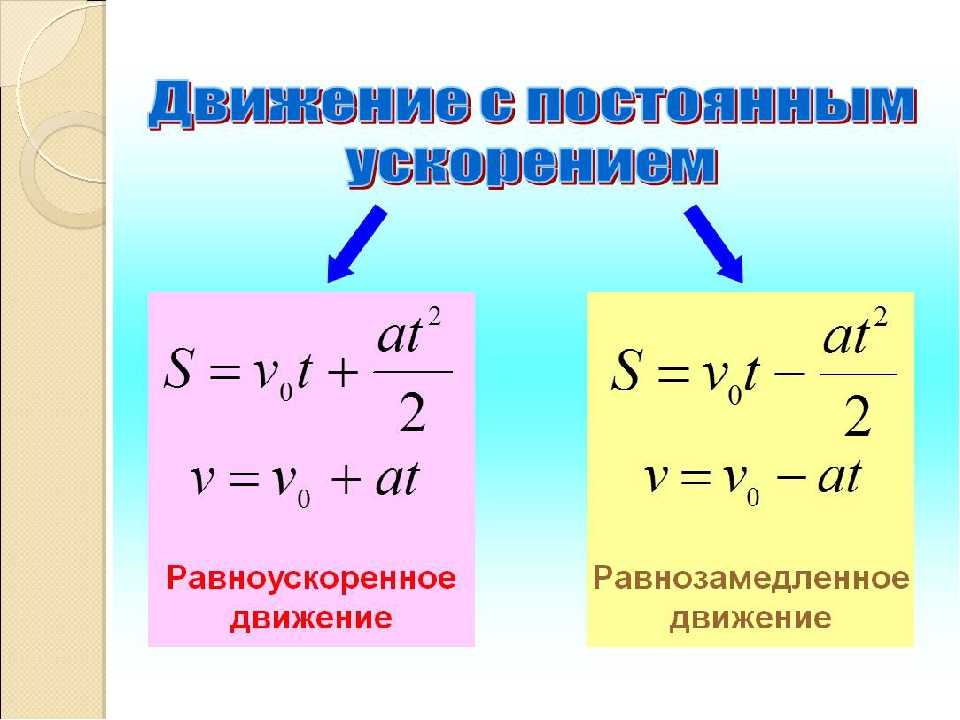
Понять эту формулу просто: сначала объект двигался с постоянной скорость v 0 , например, автомобиль по дороге, но затем он начал ускоряться, то есть за каждый промежуток времени t он начал увеличивать быстроту своего перемещения на a*t. Поскольку скорость аддитивная величина, то сумма ее начального значения с величиной изменения приведет к отмеченному выражению.
Интегрируя эту формулу по времени, получаем другое уравнение прямолинейного равномерного и равноускоренного движения, которое позволяет рассчитать пройденный путь: s = v 0 *t + a*t 2 /2. Как видно, это выражение равно сумме аналогичных формул для более простых видов движения, рассмотренных в предыдущих пунктах.
Пример решения задачи
Решим несложную задачу, которая продемонстрирует использование приведенных формул. Условие задачи следующее: автомобиль, двигаясь со скоростью 60 км/ч, начал осуществлять торможение и через 10 секунд полностью остановился. Какой путь он прошел во время торможения?
В данном случае мы имеем дело с прямолинейным равнозамедленным движением.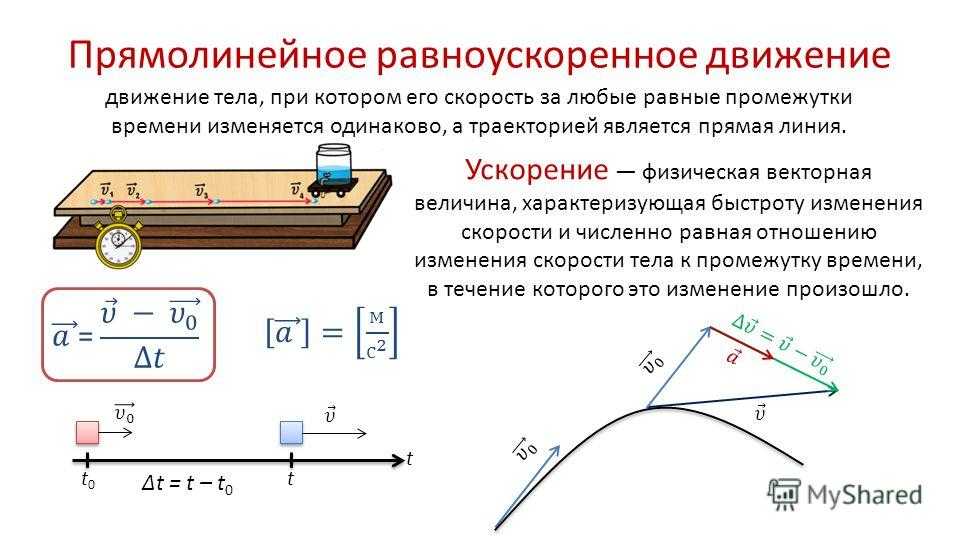
Начальная скорость v 0 = 60 км/ч, конечное же значение этой величины v = 0 (автомобиль остановился). Для определения ускорения торможения воспользуемся формулой: v = v 0 – a*t (знак “-” говорит, что тело замедляет движение). Переведем км/ч в м/с (60 км/ч = 16,667 м/с), и учитывая, что время торможение t = 10 c, получаем: a = (v 0 – v)/t = 16,667/10 = 1,667 м/с 2 . Мы определили ускорение торможения автомобиля.
Для вычисления пройденного пути воспользуемся также уравнением для смешанного типа движения с учетом знака ускорения: s = v 0 *t – a*t 2 /2. Подставляя известные величины, получаем: s = 16,667*10 – 1,667*10 2 /2 = 83,33 метра.
Отметим, что пройденный путь можно было найти, используя формулу для равноускоренного движения (s = a*t 2 /2), поскольку при торможении автомобиль пройдет точно такое же расстояние, как и во время ускорения из состояния покоя до достижения скорости v 0 .
Движение по кривой
Важно отметить, что рассмотренные выражения для пройденного пути применимы не только для случая прямолинейного движения, но и для любого перемещения объекта по криволинейной траектории.
Например, для расчета расстояния, которое пролетит наша планета вокруг Солнца (движение по окружности) за определенный промежуток времени, можно с успехом применить выражение s = v*t. Сделать это можно потому, что в нем используется модуль скорости, который является постоянной величиной, вектор же скорости изменяется. Применяя формулу для пути по криволинейной траектории, следует иметь в виду, что полученное значение будет отражать длину этой траектории, а не разницу между конечной и начальной координатами объекта.
Заключается в том, что, рассматривая того или иного тела, следует учитывать, что все его точки движутся в одном и том же направлении с абсолютно одинаковой скоростью. Именно поэтому необязательно давать характеристику движения всего данного тела, можно ограничиться лишь одной его точкой.
К основным характеристикам любого движения относятся его траектория, перемещение и скорость. Траектория – это всего лишь существующая только в воображении линия, вдоль которой осуществляется движение данной материальной точки в пространстве.
Перемещение представляет собой вектор, направленный от начальной точки к конечной. Наконец, скорость является общим показателем движения точки, который характеризует не только ее направление, но и быстроту перемещения относительно какого-либо тела, принятого за точку отсчета.
Равномерное прямолинейное движение – это во многом воображаемое понятие, которое характеризуется двумя основными факторами – равномерностью и прямолинейностью.
Равномерность движения означает, что оно осуществляется с постоянной скоростью без какого-либо ускорения. Прямолинейность движения подразумевает, что оно происходит вдоль прямой линии, то есть его траектория – это абсолютно прямая линия.
Исходя из всего вышеперечисленного, можно сделать вывод, что равномерное прямолинейное движение – это особый вид движения, в результате которого тело за абсолютно равные промежутки времени осуществляет одно и то же перемещение. Так, разбив определенный интервал на равные промежутки (например, по одной секунде), можно будет увидеть, что при указанном выше движении тело будет за каждый из этих отрезков проходить одно и то же расстояние.
Скорость равномерного прямолинейного движения есть которая в численном выражении равна отношению пути, пройденного телом за тот или иной промежуток времени, к числовому значению этого промежутка. Эта величина никаким образом не зависит от времени, более того, стоит отметить, что скорость равномерного прямолинейного движения в любой точке траектории абсолютно совпадает с перемещением тела. При этом количественное значение за взятый произвольно промежуток времени равно
Равномерное прямолинейное движение характеризуется особым подходом к пути, которое проходит тело за определенный промежуток времени. Пройденный путь при таком есть не что иное, как модуль перемещения. Перемещение же, в свою очередь, представляет собой произведение скорости, с которой двигалось тело, на время, в течение которого это перемещение осуществлялось.
Вполне естественно, что если вектор перемещения совпадает с положительным направлением оси абсцисс, то проекция рассчитанной скорости будет не только положительной, но и совпадать с величиной скорости.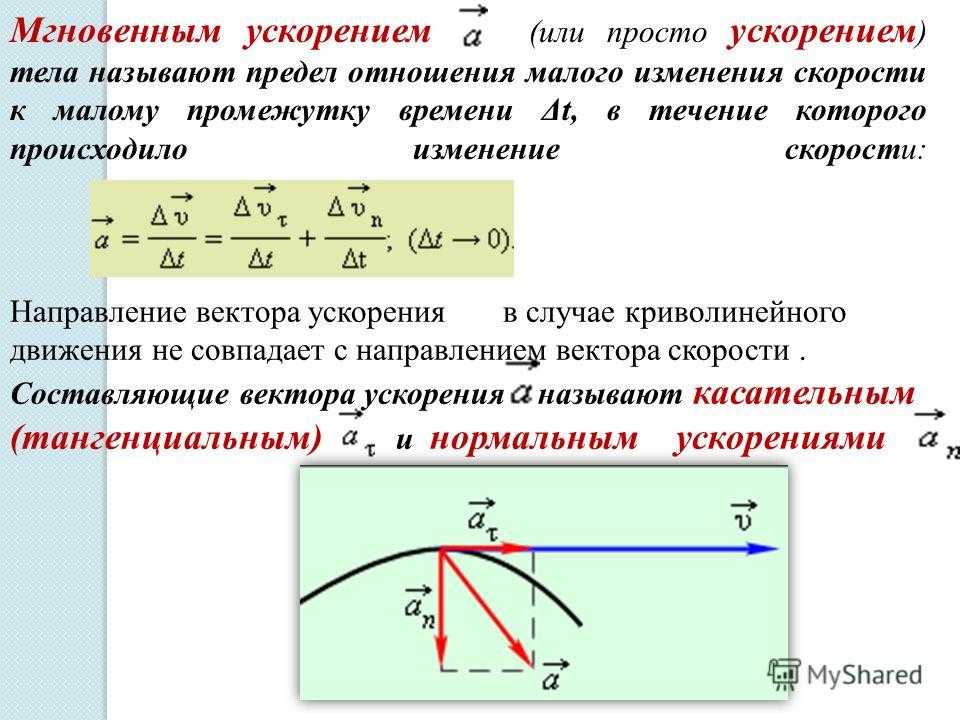
Равномерное прямолинейное движение можно представить, в том числе, и в виде уравнения, в котором будет отражаться зависимость между координатами тела и времени.
Если положение данного тела относительно окружающих пред-метов с течением времени изменяется, то данное тело движется. Если положение тела остается неизменным, то тело находится в покое. За единицу времени в механике принимается 1 сек. Под промежутком времени подразумевается число t сек, отделяющих два каких-нибудь последовательных явления.
Наблюдая движение какого-нибудь тела, часто можно видеть, что движения различных точек тела различны; так при качении колеса по плоскости центр колеса движется по прямой линии, а точка, лежащая на окружности колеса, описывает кривую (циклоиду) ; пути, пройденные этими двумя точками за одно и то же время (за 1 оборот), также различны. Поэтому изучение движения тела начинают с изучения движения отдельной точки.
Линия, описываемая движущейся
точкой в пространстве, называется траекторией этой точки.
Прямолинейным движением точки называется такое движение, траектория которого —прямая линия .
Криволинейное движение — это движение, траектория которого не является прямой линией.
Движение определяется направлением, траекторией и пройденным за определенный промежуток времени (период) путем.
Равномерным движением точки называется такое движение, при котором отношение пройденного пути S к соответствующему промежутку времени сохраняет постоянную величину для любого промежутка времени, т. е.
S/t = const (постоянная величина).(15)
Это постоянное отношение пути ко времени называется скоростью равномерного движения и обозначается буквой v. Таким образом, v= S/t. (16)
Решая уравнение относительно S, получим S = vt , (17)
т. е. величина пути, пройденного точкой при равномерном движении, равна произведению скорости на время. Решая уравнение относительно t, находим, что t = S/v ,(18)
т. е. время, в течение которого
точка при равномерном движении проходит данный путь, равно отношению
этого пути к скорости движения.
Эти равенства являются основными формулами равномерного движения. По этим формулам определяется одна из трех величин S, t, v, когда две других известны.
Размерность скорости v = длина / время = м/сек.
Неравномерным движением называется такое движение точки, при котором отношение пройденного пути к соответствующему промежутку времени не является постоянной величиной.
При неравномерном движении точки (тела) часто удовлетворяются нахождением средней скорости, которая характеризует быстроту движения за данный промежуток времени, но не дает представления о скорости движения точки в отдельные моменты, т. е. об истинной скорости.
Истинная скорость неравномерного движения — это та скорость, с которой движется точка в данный момент.
Средняя скорость движения точки определяется по формуле (15).
Практически часто удовлетворяются
средней скоростью, принимая ее как истинную. Например, скорость стола
у продольно-строгального станка постоянная, за исключением моментов
начала рабочего и начала холостого ходов, но этими моментами в
большинстве случаев пренебрегают.
У поперечно-строгального станка, у которого вращательное движение преобразуется в поступательное кулисным механизмом, скорость ползуна неравномерна. В начале хода она равна нулю, затем возрастает до какой-то наибольшей величины в момент вертикального положения кулисы, после чего начинает уменьшаться и к концу хода становится опять равной нулю. В большинстве случаев при расчетах пользуются средней скоростью v ср ползуна, которую принимают как истинную скорость резания.
Скорость ползуна поперечно-строгального станка с кулисным механизмом можно охарактеризовать как равномерно-переменную.
Равномерно-переменное движение — это движение, при котором за одинаковые промежутки времени скорость увеличивается или уменьшается на одинаковую величину.
Скорость равномерно-переменного движения выражается формулой v = v 0 + at, (19)
где v—скорость равномерно-переменного движения в данный момент, м/сек;
v 0 — скорость в начале движения, м/сек; а — ускорение,
м/сек 2 .
Ускорением называется изменение скорости в единицу времени.
Ускорение а имеет размерность скорость / время = м / сек 2 и выражается формулой a = (v-v 0)/t. (20)
При v 0 = 0, a = v/t.
Путь, пройденный при равномерно-переменном движении, выражается формулой S= ((v 0 +v)/2)* t = v 0 t+(at 2)/2. (21)
Поступательным движением твердого тел а называется такое движение, при котором всякая прямая, взятая на этом теле, перемещается параллельно самой себе.
При поступательном движении скорости и ускорения всех точек тела одинаковы и в любой точке являются скоростью и ускорением тела.
Вращательным движением называется такое движение, при котором все точки некоторой прямой линии (оси), взятой в этом теле, остаются неподвижными.
При равномерном вращении в равные промежутки времени тело поворачивается на одинаковые углы. Угловая скорость характеризует величину вращательного движения и обозначается буквой ω (омега).
Связь между угловой скоростью ω
и числом оборотов в минуту выражается уравнением: ω =(2πn)/60
= (πn)/30 град/сек.
(22)
Вращательное движение является частным случаем криволинейного движения.
Скорость вращательного движения точки направлена по касательной к траектории движения и по величине равна длине дуги, пройденной точкой за соответствующий промежуток времени.
Скорость движения точки вращающегося тела выражается уравнением
v = (2πRn)/(1000*60)= (πDn)/(1000*60) м/сек, (23)
где п — число оборотов в минуту; R — радиус окружности вращения.
Угловое ускорение характеризует увеличение угловой скорости в единицу времени. Обозначается оно буквой ε (эпсилон) и выражается формулой ε =(ω – ω 0) / t. (24)
19A: переменные вращательного движения, тангенциальное ускорение, постоянное угловое ускорение
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3327
- Джеффри В. Шник
- Колледж Святого Ансельма
ШникПоскольку так много усилий, которые мы тратим на работу с углами, связаны с острыми углами, когда мы впадаем в противоположную крайность, т.е. к углам в тысячи градусов, как мы часто делаем в случае объектов, вращающихся с постоянным угловым ускорением, одна из самых распространенных ошибок, которую мы, люди, склонны совершать, заключается в том, что мы просто не замечаем этого, когда кто-то спрашивает нас; начиная с нулевого времени, сколько оборотов или, что то же самое, сколько поворотов или вращений делает объект; что кто-то запрашивает значение углового смещения \(\Delta\theta\). Чтобы быть уверенным, мы обычно вычисляем \(\Delta\theta\) в радианах, поэтому мы должны преобразовать результат в обороты, прежде чем сообщать окончательный ответ, но количество оборотов – это просто значение \(\Delta\theta\ ) 92}{r}\) ), то значение центростремительного ускорения явно меняется. Его все еще можно вычислить в любой момент, когда известна скорость частицы.
Если, кроме ускорения, которое имеет частица только потому, что она движется по окружности, скорость частицы изменяется, то частица обладает еще и некоторым ускорением, направленным вдоль (или в прямо противоположном направлении) скорости движения частица. Поскольку скорость всегда касается окружности, по которой движется частица, эту составляющую ускорения называют тангенциальным ускорением частицы. Величина тангенциального ускорения частицы при круговом движении есть просто абсолютное значение скорости изменения скорости частицы \(a_t=\left| \frac{dv}{dt} \right| \). Направление тангенциального ускорения совпадает с направлением скорости, если частица ускоряется, и в направлении, противоположном скорости, если частица замедляется. Напомним, что, начиная с нашего уравнения, связывающего положение \(s\) частицы по окружности с угловым положением \(\theta\) частицы, \(s=r\theta\), мы взяли производную с относительно времени, чтобы получить соотношение \(v=r\omega\). Если мы возьмем вторую производную по времени, то получим
\[ \frac{dv}{dt}=r\frac{d\omega}{dt} \]
Слева у нас есть тангенциальное ускорение \(a_t\) частицы.
\[ a_t=r \propto \label{19-1}\]
A Вращающееся твердое тело
Характеристика движения вращающегося твердого тела имеет много общего с характеристикой движения частицы по окружности . Фактически каждая частица, составляющая вращающееся твердое тело, совершает круговое движение. Но разные частицы, составляющие твердое тело, движутся по окружностям разного радиуса и, следовательно, имеют разные скорости и ускорения.
Уравнения постоянного углового ускорения
Хотя физически существует огромная разница, математически вращательное движение твердого тела идентично движению частицы, которая движется только по прямой линии. Как и в случае линейного движения, мы должны определить положительное направление. Мы вольны определять положительное направление любым способом, который мы хотим для данной проблемы, но мы должны придерживаться этого определения на протяжении всей проблемы. Здесь мы устанавливаем точку зрения на некотором расстоянии от вращающегося твердого тела, но на оси вращения, и утверждаем, что с этой точки зрения направление вращения против часовой стрелки является положительным, или, альтернативно, направление вращения по часовой стрелке является положительным.
Учитывая эти критерии, мы имеем следующую таблицу соответствующих величин. Обратите внимание, что величина вращательного движения никоим образом не равна своему аналогу линейного движения, она просто играет роль во вращательном движении, которая математически аналогична роли, которую играет его аналог в линейном движении.
Количество линейного движения Соответствующее количество углового движения \(x\) \(\theta\) 0069\(v\) \(\omega\) \(a\) \(\propto\) Одна переменная, которая имеет два разных вида движения общим является показания секундомера \(t\).
Напомним, что по определению
\[ \omega=\frac{d\theta}{dt} \]
\[\mbox{and} \quad \propto= \frac{d\omega}{dt } \]
Хотя \(\propto\) может быть переменной, во многих случаях \(\propto\) является константой. Такой случай является частным случаем. Следующий набор уравнений постоянного углового ускорения применяется в частном случае постоянного углового ускорения: (Вывод этих уравнений математически эквивалентен выводу уравнений постоянного линейного ускорения. Вместо того, чтобы выводить их снова, мы просто представляем результаты.) 92 +2\propto \Delta\theta \label{19-5}\]
Скорость, с которой спринклерная головка вращается вокруг вертикальной оси, постоянно увеличивается в течение первых 2,00 секунд ее работы, так что, начиная с состояния покоя, спринклер совершает 15,0 оборотов по часовой стрелке (если смотреть сверху) в течение первых 2,00 секунд работы. Форсунка на спринклерной головке на расстоянии 11,0 см от оси вращения спринклерной головки первоначально направлена строго к западу от оси вращения.
Решение
Нам сказали, что скорость вращения спринклерной головки неуклонно увеличивается, а это означает, что мы имеем дело с проблемой постоянного углового ускорения, поэтому мы можем использовать уравнения постоянного углового ускорения. Тот факт, что существует ненулевое угловое ускорение, означает, что сопло будет иметь некоторое тангенциальное ускорение \(\vec{a_t}\). Кроме того, спринклерная головка в данный момент вращается, поэтому форсунка будет иметь некоторое центростремительное ускорение \(\vec{a_c}\). Нам нужно будет найти как \(\vec{a_t}\), так и \(\vec{a_c}\) и сложить их как векторы, чтобы получить общее ускорение сопла. Начнем с нахождения углового ускорения \(\propto\). Начнем с первого уравнения постоянного углового ускорения (уравнение \(\ref{192}\]
Учитывая, что сопло изначально находится в точке строго к западу от оси вращения, через 2,00 оборота оно снова будет в той же точке.
Теперь нам нужно векторно сложить тангенциальное ускорение и центростремительное ускорение, чтобы получить общее ускорение. Это одна из самых простых задач на сложение векторов, поскольку добавляемые векторы находятся под прямым углом друг к другу.
Из теоремы Пифагора имеем 92\) содержит три слагаемых: константу, слагаемое с \(t\) в первой степени и слагаемое с \(t\) в степени 2 -й . Если вам дано \(\тета\) в терминах \(t\), и его нельзя переставить так, чтобы оно появилось как один из этих терминов или как сумма двух или всех трех таких терминов; тогда; \(\propto\) не является константой, и вы не можете использовать уравнения постоянного углового ускорения. В самом деле, если вас просят найти угловую скорость в определенный момент времени, вы захотите взять производную \(\frac{d\theta}{dt}\) и оценить результат в данный секундомер. чтение. В качестве альтернативы, если вы 92}\) и оценить результат при заданном показании секундомера.
не должны использовать уравнения постоянного углового ускорения.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джеффри В. Шник
- Лицензия
- CC BY-SA
- Версия лицензии
- 2,5
- Показать оглавление
- нет
- Теги
- источник@http://www.
Общая физика для студентов факультетов биологии и химии
Нам еще нужно уравнение для скорости как функции времени, но это уравнение вы составите сами. Следующий апплет не только поможет вам в этом, но и даст вам возможность попрактиковаться в построении уравнений на основе единиц измерения. Вам будет дана переменная в левой части уравнения, переменные, которые появятся в правой части уравнения, и любые числовые коэффициенты, которые могут вам понадобиться. Ваша задача будет заключаться в том, чтобы построить правильное уравнение, указав показатель степени каждого фактора в правой части. Кнопка «Выбрать фактор» будет циклически перебирать все возможные факторы, а полоса прокрутки с пометкой «Экспонента» позволит вам выбрать показатель степени для этого фактора. В любое время вы можете изменить показатель степени фактора, повторно выбрав фактор и изменив показатель степени. Вы должны использовать свои знания предыдущих уравнений, чтобы выбрать показатель степени для числовых множителей, таких как 2 или π.Вам нужен браузер с поддержкой Java, чтобы иметь возможность использовать апплеты. Если они не работают с вашей системой Windows, загрузите Java VM (виртуальную машину) для вашей версии Windows в разделе загрузок на сайте java.sun.com.
Мы сказали, что нам нужно исчисление, чтобы получить правильный коэффициент половины в термине
т 2 /2.Но мы можем позаимствовать некоторые идеи из исчисления, чтобы увидеть, что это должно быть правдой. для постоянного ускорения. В этом случае график зависимости вашей скорости от времени представляет собой прямую линию. К быть конкретным, будем считать, чтоа = 1 м/с 2и что вы начали с состояния покоя, так что уравнение, описывающее вашу скорость, имеет видv = т.Подумайте, как бы вы вычислили общее пройденное расстояние как функцию времени. Ты мог бы разделить время на интервалы и использовать среднюю скорость в середине каждого интервала, чтобы вычислить пройденное расстояние в течение этого интервала с уравнениемΔx = v Δt.Затем вы можете сложить все расстояния. Но вы замечаете, что чем меньше интервал, тем точнее результат: Вам нужен браузер с поддержкой Java, чтобы иметь возможность использовать апплеты. Если они не работают с вашей системой Windows, загрузите Java VM (виртуальную машину) для вашей версии Windows в разделе загрузок на сайте java.sun.com.Проявив немного воображения, вы можете увидеть, что если интервалы становятся настолько маленькими, что вы не можете видеть их ширину, то общая пройденное расстояние будет просто площадью под линией скорости. Итак, давайте используем эту площадь для вычисления общего расстояния. как функция времени. Поскольку v = t, в любой момент времени площадь под графиком равна половине площади квадрата со стороной т.
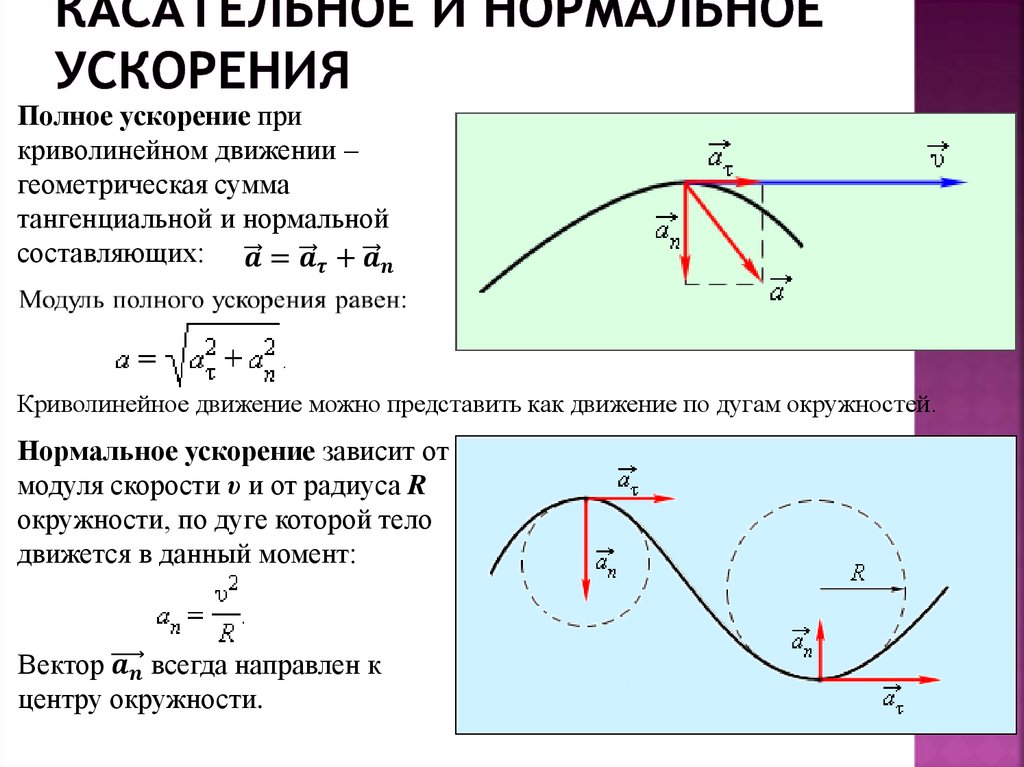
\(\frac{d\omega}{dt}\) справа – это временная скорость изменения угловой скорости объекта. Угловая скорость — это скорость вращения, поэтому ненулевое значение \(\frac{d\omega}{dt}\) означает, что воображаемый отрезок, идущий от центра круга к частице, вращается быстрее или медленнее с течением времени. На самом деле \(\frac{d\omega}{dt}\) – это скорость, с которой изменяется скорость вращения. Мы называем это угловым ускорением и используем для его обозначения символ \(\propto\) (греческая буква альфа). Таким образом, отношение \(\frac{dv}{dt}=r\frac{d\omega}{dt}\) может быть выражено как
Например, каждый раз, когда объект совершает один оборот, каждая частица объекта проходит весь свой круг один раз, но частица, удаленная от оси вращения, проходит весь путь по окружности, большей, чем та, что частица, которая близко к оси вращения идет вокруг. Для этого частица вдали от оси вращения должна двигаться быстрее. Но за один оборот объекта линия от центра круга, на котором находится любая частица объекта, к самой частице, совершает ровно один оборот. На самом деле переменные углового движения, которые мы использовали для характеристики движения линии, идущей от центра окружности к частице, движущейся по этой окружности, можно использовать для характеристики движения вращающегося твердого тела в целом. . Для всего объекта существует только одна скорость вращения, угловая скорость \(\omega\), и если эта скорость вращения изменяется, существует только одна скорость изменения скорости вращения, угловое ускорение \(\propto\) . Чтобы указать угловое положение вращающегося твердого тела, нам нужно установить опорную линию на твердом теле, проходящую от точки на оси вращения в направлении, перпендикулярном оси вращения.
Эта опорная линия вращается вместе с объектом. Его движение есть угловое движение объекта. Нам также нужен отрезок опорной линии, фиксированный в пространстве, идущий от той же точки на оси и от оси в направлении, перпендикулярном оси. Этот не вращается вместе с объектом. Если представить, что две линии когда-то были коллинеарными, то чистый угол, на который повернулась первая линия на твердом теле относительно фиксированной линии, является угловым положением \(\тета\) объекта.
Какой бы путь мы ни выбрали как положительный, он будет положительным направлением вращения для углового смещения (изменения углового положения), угловой скорости, углового ускорения и углового положения относительно опорной линии, которая зафиксирована в пространстве. Затем мы устанавливаем ноль для переменной времени; мы представляем, что секундомер был запущен в какой-то момент, который мы определяем как нулевое время. Мы называем значения углового положения и угловой скорости в этот момент начальными значениями этих величин.
Найдите направление и величину ускорения форсунки в момент, когда головка спринклера совершает второй (до трех значащих цифр) оборот.
Соответствующие рассуждения можно привести и для случая \(\omega\). Если вам дано \(\omega\) как функция \(t\) и выражение нельзя сделать так, чтобы оно “выглядело” как уравнение постоянного углового ускорения \(\omega=\omega_0+\propto t\), то вы не имеет дело с ситуацией постоянного углового ускорения, и вы 
cbphysics.org
В этом апплете скорость или ускорение иногда предполагаются равными нулю, поэтому уравнения, которые вы создаете, не обязательно будут самыми общими из возможных. Но вы можете составить более общие уравнения (например, то, что мы получили для положения выше), складывая вместе правые части с теми же единицами измерения.
