Что такое ускорение скорость: Что такое ускорение? (статья) | Ускорение

«Зависит ли ускорение от скорости объекта? Приведите пример медленного объекта с большим ускорением, чем быстрый объект?» — Яндекс Кью

Популярное

Сообщества

ТехнологииФизика+3

Anya Eastman

29 августа 2017  ·

3,3 K

Ответить2Уточнить

Максим Кусакин

Физика

11,5 K

Инженер, немного пилот. Физик, химик, электронщик-любитель. Независимый звукорежиссёр…  · 29 авг 2017

Ускорение не зависит от скорости объекта, это отдельная независимая характеристика движения. При прямолинейном движении, ускорение – это скорость изменения скорости движения. Эта “скорость изменения скорости” является постоянной величиной при равноускоренном движении и первой производной скорости (и второй производной пройденного пути) по времени.

При большом ускорении, медленный объект наберёт скорость быстрее чем быстрый при малом ускорении и рано или поздно обгонит быстрый.

Представьте, по правой полосе дороги едет “быстрый” Запорожец со скоростью 60 км/ч и разгоняется на 1 км/ч каждую минуту. По левой полосе едет “медленный” Феррари со скоростью 20 км/ч, разгоняясь на 10 км/ч каждую минуту. Через 5 минут его скорость будут 70 км/ч, а скорость Запорожца – 65 км/ч.

Anya Eastman

30 августа 2017

Спасибо большое за ответ!

Комментировать ответ…Комментировать…

Nekto V-Palto

15,3 K

физик-теоретик в прошлом, дауншифтер и журналист в настоящем, живу в Германии  · 30 авг 2017

С точки зрения математики, ускорение – это первая производная от скорости по времени. Зависит ли значение производной в момент t от значения функции в этот момент? Нет, в общем случае – не зависит. Для проверки достаточно добавить к функции произвольную константу, изменив ее значение и не изменив производную. С точки зрения механики, ускорение – это векторная сумма сил… Читать далее

Комментировать ответ…Комментировать…

Сергей Смирнов

767

30лет  · 30 авг 2017

ОгоВ доказательство того, что ускорение не зависит от скорости можно привести ускорение свободного падения, так как это постоянная величина. С другой стороны в реальном мире равноускоренных движений не существует, чаще всего это движение под действием постоянной силы и изменяющиеся силы сопротивления движению. Например, при свободном падении сопротивление воздуха это… Читать далее

Anya Eastman

30 августа 2017

Спасибо огромное за ответ !

Комментировать ответ…Комментировать…

Alexander Vanetsev

9,8 K

Researcher, Institute of Physics, University of Tartu  · 30 авг 2017

Ну, уж совсем примитивно – если очень быстрый объект будет замедляться, то ускорение у него будет меньше, чем у самого медленного разгоняющегося объекта, поскольку оно вообще будет меньше нуля. А никто ведь не отрицает, что даже супер-пупер гиперзвуковой гоночный автомобиль все-таки может остановиться, если поехал.

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

Элементарный учебник физики Т1

Ландсберг Г.С. Элементарный учебник физики. Т.1. Механика. Теплота. Молекулярная физика. – М.: Наука, 1985. – 606 c. Один из лучших курсов элементарной физики, завоевавший огромную популярность. Достоинством курса является глубина изложения физической стороны рассматриваемых процессов и явлений в природе и технике. В новом издании структура курса осталась прежней, однако в изложении проведена система единиц СИ, терминология и обозначения единиц физических величин приведены в соответствие с действующим ГОСТ. Для слушателей и преподавателей подготовительных отделений и курсов вузов, старшеклассников общеобразовательных и профессиональных школ, а также лиц, занимающихся самообразованием и готовящихся к поступлению в вуз. Оглавление ОТ ИЗДАТЕЛЬСТВА ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ ВВЕДЕНИЕ Глава I. Кинематика § 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4. Поступательное и вращательное движения тела § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 10. Знак скорости при прямолинейном движении § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 17. 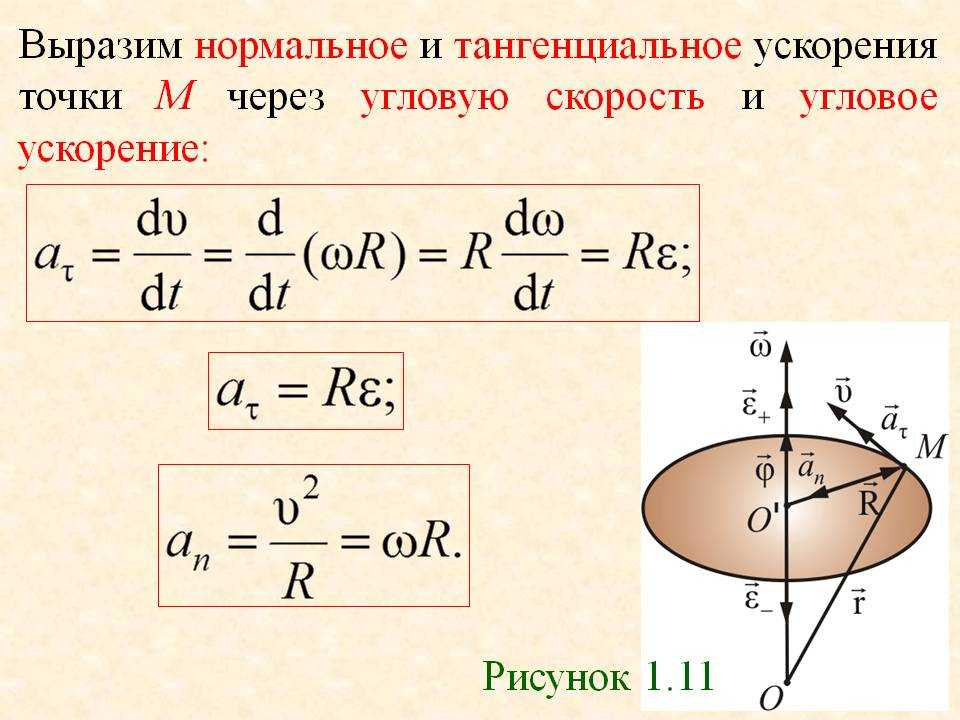Скорость прямолинейного равноускоренного движения § 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 22. Путь, пройденный при равнопеременном движении § 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26. Скорость криволинейного движения § 27. Ускорение при криволинейном движении § 28. Движение относительно разных систем отсчета § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 38. Точка приложения силы § 39. Равнодействующая сила § 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 46. Системы единиц § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 49. Импульс тела § 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52. Свободное падение тел § 53. Ускорение свободного падения § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 60. Деформации в покоящихся телах, вызванные силой тяжести § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63. Разрушение движущихся тел § 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе Глава III. Статика § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73. Разложение сил на составляющие § 74. Проекции сил. Общие условия равновесия § 75. Связи. Силы реакции связей. Тело, закрепленное на оси § 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины § 85. Клин и винт Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88. Работа силы § 89. Работа при перемещении, перпендикулярном к направлению силы § 90. Работа силы, направленной под любым углом к перемещению § 91. Положительная и отрицательная работа § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95. Принцип сохранения работы § 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99. Кинетическая энергия § 100. Выражение кинетической энергии через массу и скорость тела § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 105. Всеобщий характер закона сохранения энергии § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V. Криволинейное движение § 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117. Возникновение силы, действующей на тело, движущееся по окружности § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120. «Американские горки» § 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129. Поступательно движущиеся неинерциальиые системы § 130. Силы инерции § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137. Приливы Глава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141. «Несжимаемая» жидкость § 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 144. Давление § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153. Сообщающиеся сосуды § 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел § 164. Устойчивость плавания кораблей § 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167. Механические свойства газов § 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 177. Закон Архимеда для газов § 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. Перемещение на воде § 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190. Сопротивление воздуха § 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200. Измерение коэффициента объемного расширения жидкостей § 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. Зависимость внутренней энергии тела от его массы и вещества § 207. Теплоемкость тела § 208. Удельная теплоемкость § 209. Калориметр. Измерение теплоемкостей § 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII. Свойства газов § 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227. Формула, выражающая закон Бойля — Мариотта § 228. График, выражающий закон Бойля — Мариотта § 229. Зависимость между плотностью газа и его давлением § 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242. 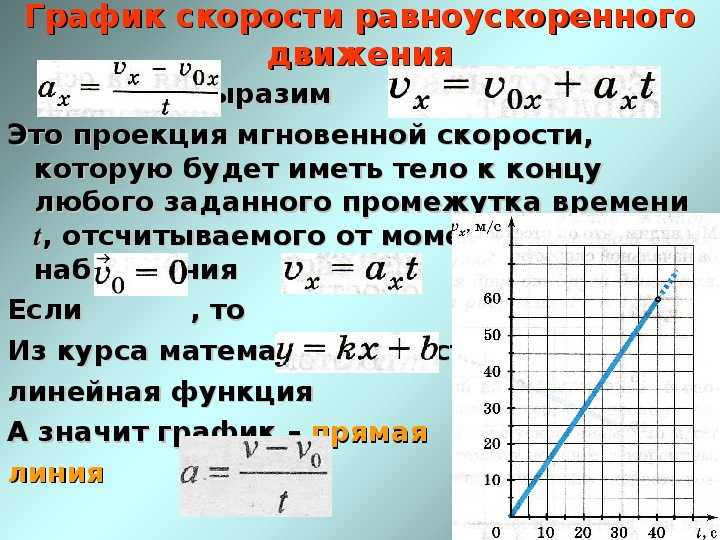Моль. Постоянная Авогадро § 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. Поверхностное натяжение § 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253. Смачивание и несмачивание § 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265. 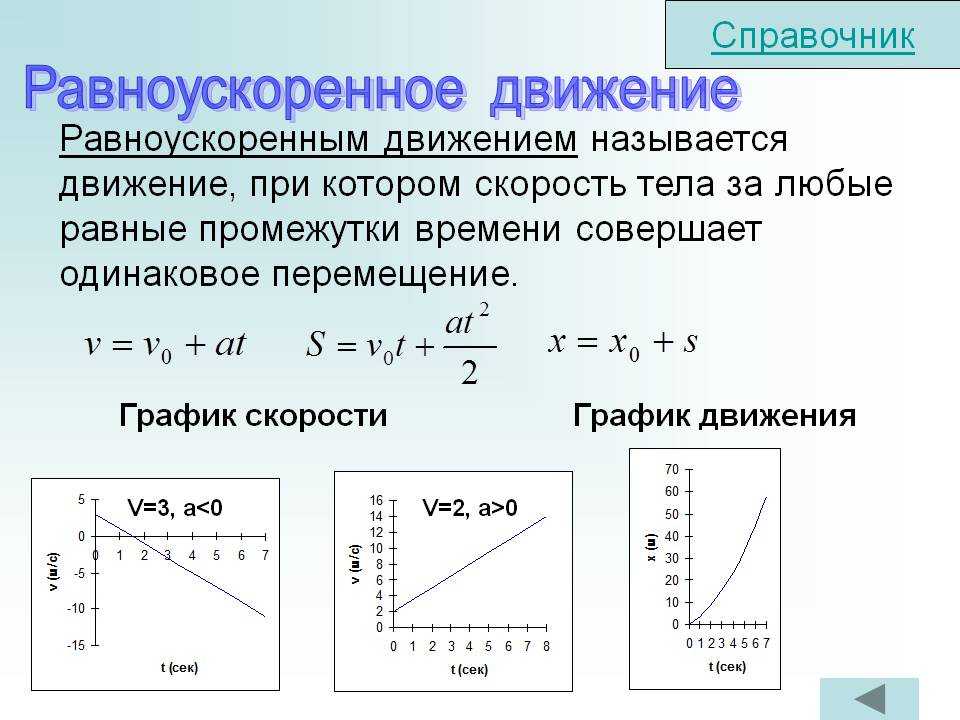Аморфные тела § 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. Упругость и прочность § 277. Введение § 278. Упругие и пластические деформации § 279. Закон Гука § 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294. 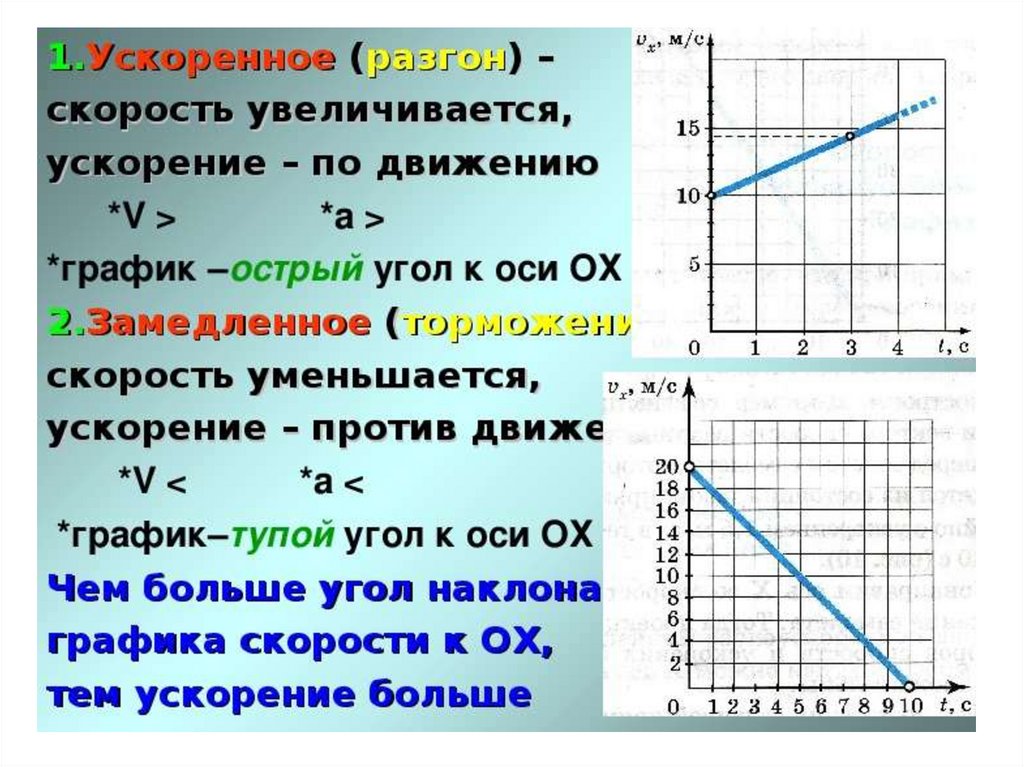Кипение § 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303. Критическая температура § 304. Сжижение газов в технике § 305. Вакуумная техника § 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321. Коэффициент полезного действия паросиловой станции § 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель

Гал | единица гравитационного измерения

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!

Содержание

• Введение

Викторины

• Интересные факты об измерениях и математике

Скорость, скорость и ускорение

Скорость, скорость и ускорение

Время

Мы измеряем момент времени t с помощью часов. Единицей времени в СИ является второй. Показания часов в секундах зависят от выбора источника. Часы в разных часовых поясах имеют разные показания и показания остановки часы зависят от того, когда они были запущены. Интервал времени ∆t = t _позже – t _ранее определяется как разница между более поздним временем и более раннее время. Это всегда неотрицательное число (положительное или нулевое). Интервал ∆t является скаляром, числом с единицами.

---

Скорость и Скорость

Когда объект перемещается в пространстве, его положение меняется. Предположим, что в момент времени t ₁ он находится в позиции P ₁ и позже t ₂ это в позиция P ₂ . Вектор смещения равен d = P ₂ – Р ₁ . В интервале времени ∆t = t ₂ – t ₁ объект был заменен на d . Его средняя скорость в этот временной интервал ∆t определяется как < v >   = д /∆t. Перемещение d является вектором, интервал времени ∆t равен скаляр. Деление вектора на скаляр дает другой вектор. Среднее скорость < в > является вектором. Средняя скорость – это расстояние, пройденное за время интервал ∆t, деленный на ∆t. Расстояние является скаляром, т. е. числом с единицами. Разделив расстояние на ∆t, получим другое число с единицами. Следовательно, средняя скорость скаляр.

Проблема:

За 5 минут бегун пробегает один раз дорожку длиной в одну милю. Какой его Средняя скорость? Какова его средняя скорость?

Решение:

• Обоснование:
  Через 5 минут бегун возвращается в исходное положение. Р ₂ – Р ₁ = 0. Смещение равно нулю. Это пройденное расстояние составляет одну милю.
• Детали расчета:
  Перемещение равно нулю, поэтому его средняя скорость равна нулю.
  средняя скорость это расстояние, пройденное за время интервал ∆t. Средняя скорость поэтому (1 миля)/(5 минут) = (12 миль)/(60 минут) = 12 миль/ч.
  
  Примечание. Скорость — это скаляр, а скорость — это вектор. Средняя скорость вообще не равна величине средней скорости.

Проблема:

Спринтер бежит на север по прямой и преодолевает расстояние 100 м за 12 с. Какова ее средняя скорость? Какова ее средняя скорость?

Решение:

Резюме

Средняя скорость равна пройденному расстоянию, деленному на время, необходимое для преодоления этого расстояния. Если человек проходит 1 км на запад, затем разворачивается и идет 1 км на восток, расстояние это человек покрывает 2 км. Если это расстояние преодолевается за 20 минут, то средняя скорость 2 км/20 минут = 2000 м/(20*60 с) = 1,67 м/с.

Средняя скорость является вектором. Это вектор смещения, указывающий из начального положения в конечное положение, разделить на время. В приведенном выше примере начальная и конечная позиция совпадают. Вектор смещения равен нулю. Значит, средняя скорость равна нулю.

Внешняя ссылка: Скорость и скорость    (Пожалуйста, изучите!)

Поскольку величина и направление вектора смещения зависят от система отсчета, в которой система координат закреплена и находится в состоянии покоя, скорость объекта зависит от системы отсчета, относительно которой он измеряется.

Проблема:

Автомобиль продвинулся вперед на расстояние 6 м, при этом ребенок продвинулся вперед от заднего сиденья до переднего сиденья на расстоянии 1 м за промежуток времени 2 с. Найдите среднюю скорость ребенка относительно автомобиля и относительную к дороге.

Решение:

• Рассуждение:
  Скорость объекта зависит от системы отсчета,
• Детали расчета:
  Использование автомобиля в качестве системы отсчета и привязка системы координат к автомобиль, водоизмещение ребенка д = (1 м) i .
  Его скорость < v > = (1 м)/(2 с) i = (0,5 м/с) i .
  Использование дороги в качестве системы отсчета и привязка системы координат к дорога, перемещение ребенка д = (6 м) i + (1 м) i = (7 м) и .
  Его скорость < v > = (7 м)/(2 с) i = (3,5 м/с) i .

Примечание. Скорость объекта зависит от системы отсчета. не та величина, с которой согласны все наблюдатели. Объект может находиться в состоянии покоя в течение одного системе отсчета и имеющей ненулевую скорость в другой системе отсчета.
Когда родитель говорит ребенку сидеть спокойно в движущейся машине, он имеет в виду сидеть спокойно по отношению к машине, а не по дороге.

Остановился, вы ждете смены сигнала светофора с красного на зеленый, когда вдруг у вас появляется ощущение, что вы двигаетесь, хотя и нажимаете на педали тормоза. Но затем вы замечаете, что большой грузовик или автобус в полоса рядом с вами – это транспортное средство, которое фактически движется относительно земля. Чтобы сделать вывод, что мы движемся относительно земли, мы в основном полагаются на визуальные подсказки. Когда мы видим, что наше окружение движется, мы сделать вывод, что мы движемся. Обычно мы можем быстро установить истинное ситуацию, так как мы подсознательно понимаем, что есть несоответствие и быстро получить дополнительную информацию из нашего окружения.

Симуляция ниже исследует относительное движение. Вид всегда у водителя автомобиля или у кого-то, движущегося с той же скоростью, что и водитель смотрит прямо в картину. Вы можете выбрать три разных ситуации и масштабировать и вращать вид,  Пожалуйста, нажмите на изображение!

---

Ускорение

Всякий раз, когда скорость объекта изменяется, объект ускорение. Предположим, что в момент времени t ₁ объект имеет скорость v ₁ , и в более позднее время t ₂ он имеет скорость v ₂ . Изменение в скорость равна ∆ v = v ₂ – v ₁ на интервале времени ∆t = t ₂ – t ₁ . Среднее ускорение объекта за этот промежуток времени ∆t определяется как < a > = ∆ v /∆t. Среднее ускорение < a > является вектором. Это вектор скорости в последний момент времени минус вектор скорости в момент времени. начальное время, деленное на временной интервал.

Внешняя ссылка: Ускорение

Примечание: Всякий раз, когда ваша скорость ИЗМЕНЕНИЕ , вы ускоряетесь. Вы ускоряетесь, когда ИЗМЕНИТЬ скорость, ИЗМЕНИТЬ направление движения или и то, и другое. Ключевое слово ИЗМЕНИТЬ .

Если ваша скорость НЕ меняется, то, как бы быстро вы движетесь, вы НЕ ускоряетесь.

постоянная скорость <--> нулевое ускорение

Проблема:

Вы едете с постоянной скоростью 20 миль/ч вокруг городского квартала, проверяя район. Вы ускоряетесь?

Решение:

• Рассуждение:
  Да, направление вектора скорости меняется.

Проблема:

Вы движетесь на восток со скоростью 30 миль в час. Вы видите, как мяч катится по дорогу и сильно ломаешься, потому что боишься, что прибежит ребенок после бала. Вы останавливаетесь за 0,8 секунды. Каково направление вашего средняя скорость за этот короткий промежуток времени? Какое у вас среднее ускорение?

Решение:

• Обоснование:
  Направление вашей средней скорости — восток. Вы путешествуете на восток с снижая скорость до полной остановки. Изменение вашей скорости равно ∆ v = v ₂ – v ₁ = 0 – 30 миль в час на восток = -30 миль в час на восток = 30 миль в час на запад.
• Детали расчета:
  Переведем в единицы СИ.
  30 миль в час умножить на 1609 м/милю умножить на 1 ч/(3600 с) = 13,4 м/с.
  Ваше среднее ускорение ∆ v /∆t = (13,4 м/с)/(0,8 с) запад = 16,8 м/с ² запад.

Внешние ссылки: Ускорение, Равномерное круговое движение

Примечание.