Что такое узел электрической цепи: Узел электрической цепи

Элементы электрической цепи

 

Известно, что электрическая цепь представляет собой совокупность различных устройств. Они обеспечивают протекание электрического тока, большинство процессов в них можно охарактеризовать различными величинами, такими, как напряжение, сила тока, сопротивление.

Исходя из вышенаписанного, можно сказать, что электрическая цепь – это совокупность определённых объектов и устройств, которые выступают как «путь» для протекания электрического тока. В электрической цепи могут протекать различные токи, как постоянные, так и переменные. Электрические цепи можно часто встретить в их графическом изображении – электрические схемы, в них указываются все присутствуютвующие в цепи элементы.

Разновидности электрических цепей

Они могут разделяться по своему строению, выделяют два основных вида: разветвлённые и неразветвлённые. Первый вид условно можно отнести к простым видам цепей. В таких электрических цепях протекает одинаковый по силе ток. Разветвлённые цепи отличаются достаточно простым, прямолинейным видом. В них, как правило, небольшое количество элементов.

Однако, и разветвлённые цепи также могут простыми, это совсем не значит, что они сложны по своему строению. Разветвлённость цепи лишь предполагает наличие узлов и ветвей в ней.

Ветвь – это заключённый между двумя узлами участок электрической цепи, элементы которого соединены последовательно. Сила тока в ветвях разветвлённых цепей может быть разная. Узел – место соединения в электрической цепи не менее трех ветвей.

Другой отличительной характеристикой цепей друг от друга, является их линейность или нелинейность. Если в цепи содержатся нелинейные элементы, то и цепь, соответственно, называют нелинейной. К таким элементам можно отнести элементы, которые обладают нелинейными вольт-амперными или кулон-вольтными характеристиками. Если в цепи имеется хотя бы один такой элемент, то и вся цепь относится к категории нелинейных.

Линейные цепи не содержат подобных элементов, в них не содержатся только такие элементы как конденсаторы, резисторы, катушки-индуктивности. Также под линейными цепями могут пониматься цепи, в которых содержаться электронные устройства с определёнными диапазонами характеристик, т. е. эти характеристики линейные. Это могут быть различные усилители, другие устройства с активными элементами и прочее.

Основные группы элементов электрической цепи

Как уже было сказано ранее, в электрической цепи обязательно присутствуют самые различные элементы, несущие свои какие-либо функции. Все их можно условно разделить на 3 группы:

Первая группа элементов – это источники питания. Сюда относятся все устройства, которые служат для питания электрической цепи. Это различные аккумуляторы, гальванические элементы, термоэлектрические и электромеханические генераторы и т. д. Они обеспечивают питание электрической цепи, их особенность в том, что их внутреннее сопротивление невелико, если сравнить его с сопротивлением остальных элементов электрической цепи.

Вторая группа элементов – собственно, нагрузка, включает все устройства, которые преобразуют электрическую энергию в любые другие её виды: механическую, тепловую, световую и т. д. Устройства этой группы также называют электроприёмниками. К электроприёмникам можно отнести различные устройства, механизмы, такие как электродвигатели, осветительные приборы, нагреватели и прочее. Их основные характеристики – это напряжение и мощность. Для того чтобы прибор работал в нормальном режиме, на его концах, клеммах, нужно всегда поддерживать нужное стабильное напряжение.

Третья группа элементов состоит из коммутационных элементов, предназначенных для передачи электрической энергии от источников питания (элементов первой группы) к электроприёмникам (элементам второй группы). Сюда относятся провода, различные устройства, поддерживающие напряжение и силу тока, устройства измерения, защиты и т. д.

Особенности соединения элементов электрической цепи

Разумеется, все элементы электрической цепи взаимодействуют между собой, т. к., обязательно соединены. Выделяют два вида соединений: последовательное и параллельное:

При последовательном подключении все элементы строго идут друг за другом – «конец» одного элемента соединён с «началом» другого, который таким-же образом соединяется со следующим элементом. В этом случае нельзя получить разветвлённую цепь. Параллельная цепь имеет разветвления, так что это более сложная и распространённая электрическая цепь.

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

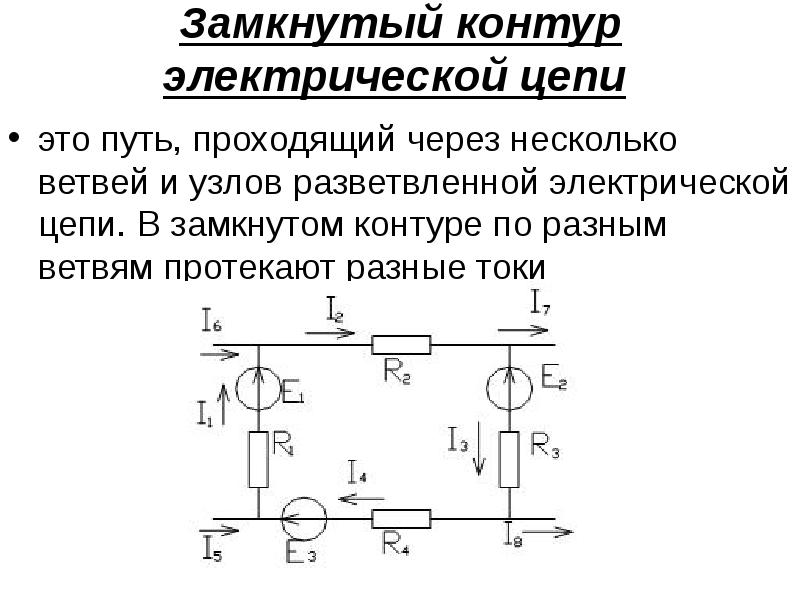
Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

$$ \sum{i} = 0, $$

или в комплексной форме

$$ \sum{\underline{I}} = 0. $$

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

$$ \sum{\underline{Z} \cdot \underline{I}} = \sum{\underline{E}}. $$

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно $ N_\textrm{у}-1 $, где $ N_\textrm{у} $ – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно $ N_\textrm{в}-N_\textrm{у}+1 $, где $ N_\textrm{в} $ – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается

.

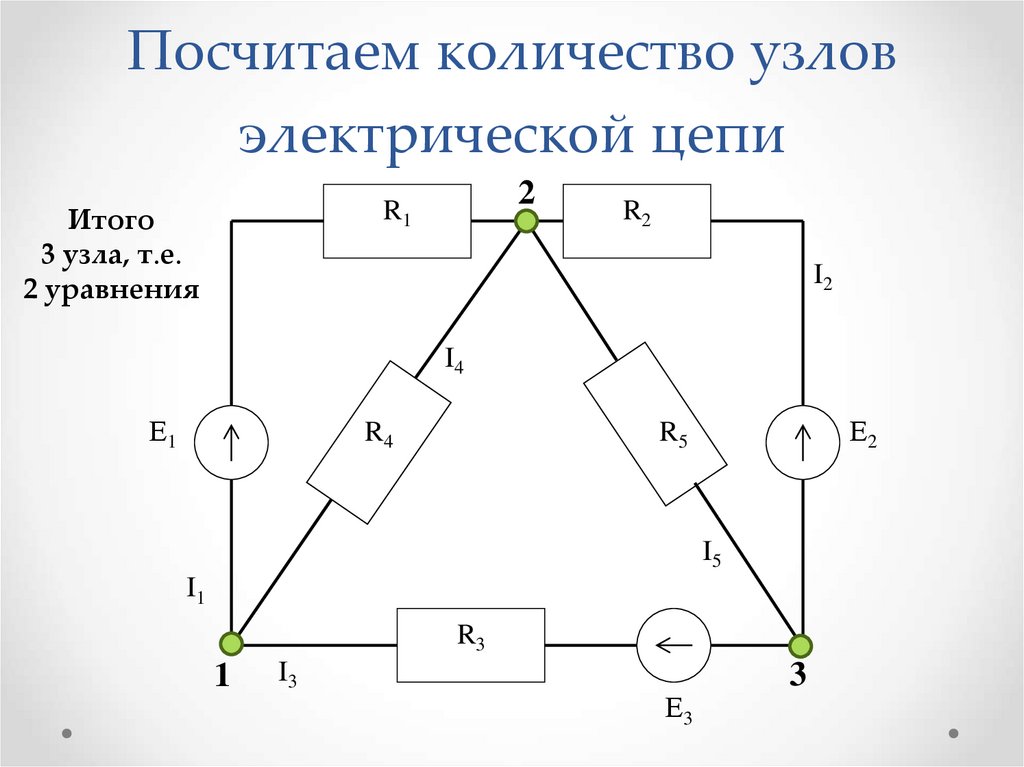
Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока $ \underline{J}_{1} $, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0; $$

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ -\underline{I}_{1}- \underline{I}_{4} + \underline{I}_{6} = 0; $$

для узла «3 у.»:

$$ \underline{I}_{2}+ \underline{I}_{4} + \underline{I}_{5}- \underline{I}_{7} = 0; $$

для узла «4 у.»:

$$ \underline{I}_{3}- \underline{I}_{5}- \underline{J}_{1} = 0. $$

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ \underline{Z}_{C1} \cdot \underline{I}_{1} + R_{2} \cdot \underline{I}_{2}- \underline{Z}_{L1} \cdot \underline{I}_{4} = \underline{E}_{1}; $$

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ -R_{2} \cdot \underline{I}_{2} + R_{4} \cdot \underline{I}_{3} + \underline{Z}_{C2} \cdot \underline{I}_{5} = \underline{E}_{2}; $$

для контура «3 к.»:

$$ \underline{Z}_{L1} \cdot \underline{I}_{4} + (\underline{Z}_{L2} + R_{1}) \cdot \underline{I}_{6} + R_{3} \cdot \underline{I}_{7} = \underline{E}_{3}; $$

где $ \underline{Z}_{C} = -\frac{1}{\omega C} $, $ \underline{Z}_{L} = \omega L $.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

$$ \begin{cases} \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0 \\ -\underline{I}_{1}- \underline{I}_{4} + \underline{I}_{6} = 0 \\ \underline{I}_{2}+ \underline{I}_{4} + \underline{I}_{5}- \underline{I}_{7} = 0 \\ \underline{I}_{3}- \underline{I}_{5}- \underline{J}_{1} = 0 \\ \underline{Z}_{C1} \cdot \underline{I}_{1} + R_{2} \cdot \underline{I}_{2}- \underline{Z}_{L1} \cdot \underline{I}_{4} = \underline{E}_{1} \\ -R_{2} \cdot \underline{I}_{2} + R_{4} \cdot \underline{I}_{3} + \underline{Z}_{C2} \cdot \underline{I}_{5} = \underline{E}_{2} \\ \underline{Z}_{L1} \cdot \underline{I}_{4} + (\underline{Z}_{L2} + R_{1}) \cdot \underline{I}_{6} + R_{3} \cdot \underline{I}_{7} = \underline{E}_{3} \end{cases} $$

В данном случае это система из 7 уравнений с 7 неизвестными.

Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

$$ \begin{bmatrix} 1 & -1 & -1 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 1 & 0 & -1 & 0 & 0 \\ \underline{Z}_{C1} & R_{2} & 0 & -\underline{Z}_{L1} & 0 & 0 & 0 \\ 0 & -R_{2} & R_{4} & 0 & \underline{Z}_{C2} & 0 & 0 \\ 0 & 0 & 0 & \underline{Z}_{L1} & 0 & R_{1}+\underline{Z}_{L2} & R_{3} \\ \end{bmatrix} \cdot \begin{bmatrix} \underline{I}_{1} \\ \underline{I}_{2} \\ \underline{I}_{3} \\ \underline{I}_{4} \\ \underline{I}_{5} \\ \underline{I}_{6} \\ \underline{I}_{7} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \underline{J}_{1} \\ \underline{E}_{1} \\ \underline{E}_{2} \\ \underline{E}_{3} \\ \end{bmatrix} $$

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [1  -1 -1    0   0        0  0;
       -1   0  0   -1   0        1  0;
        0   1  0    1   1        0 -1;
        0   0  1    0  -1        0  0;
      Zc1  R2  0 -Zl1   0        0  0;
        0 -R2 R4    0 Zc2        0  0;
        0   0  0  Zl1   0 (R1+Zl2) R3];
>> b = [0;
        0;
        0;
       J1;
       E1;
       E2;
       E3];
>> I = A\b

В результате получим вектор-столбец $ \underline{\bold{I}} $ токов из семи элементов, состоящий из искомых токов, записанный в общем виде.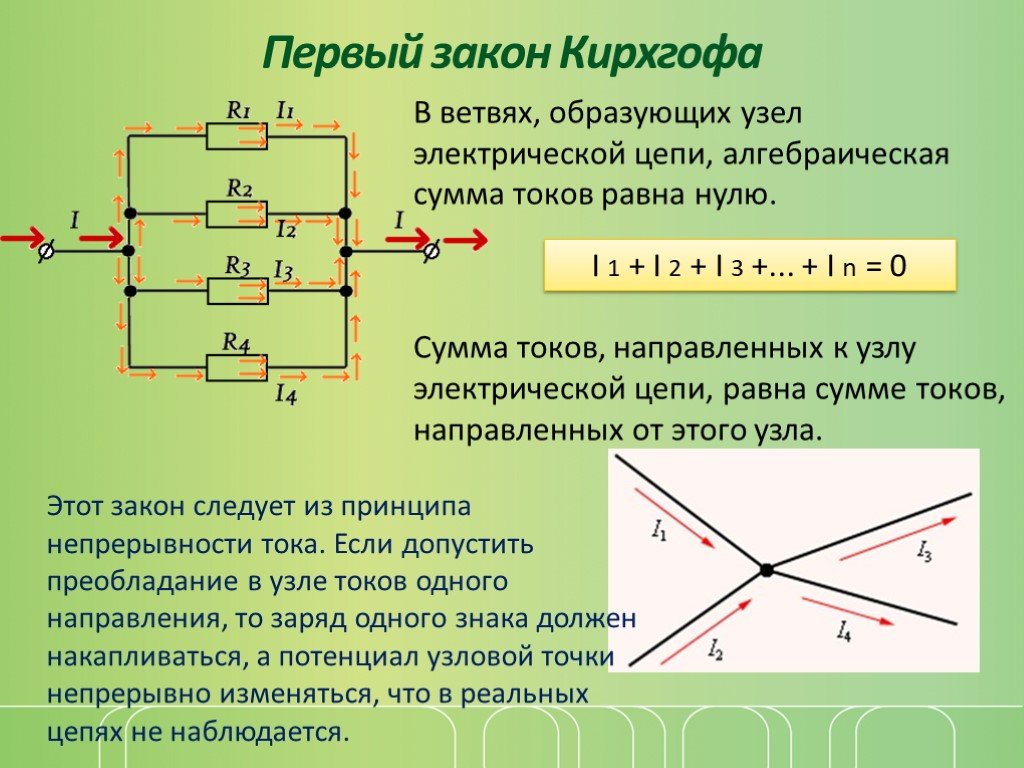 Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Что такое электронная схема?

Авторы: Дуг Лоу и

Обновлено: 26 марта 2016 г. путешествовать. Цепи обеспечивают путь для протекания тока. Чтобы быть цепью, этот путь должен начинаться и заканчиваться в одной и той же точке. Другими словами, цепь должна образовывать петлю. Электронная схема и электрическая цепь имеют одинаковое определение, но электронные схемы, как правило, представляют собой цепи низкого напряжения.

Например, простая схема может включать два компонента: аккумулятор и лампу. Схема позволяет току течь от батареи к лампе, через лампу, а затем обратно к батарее.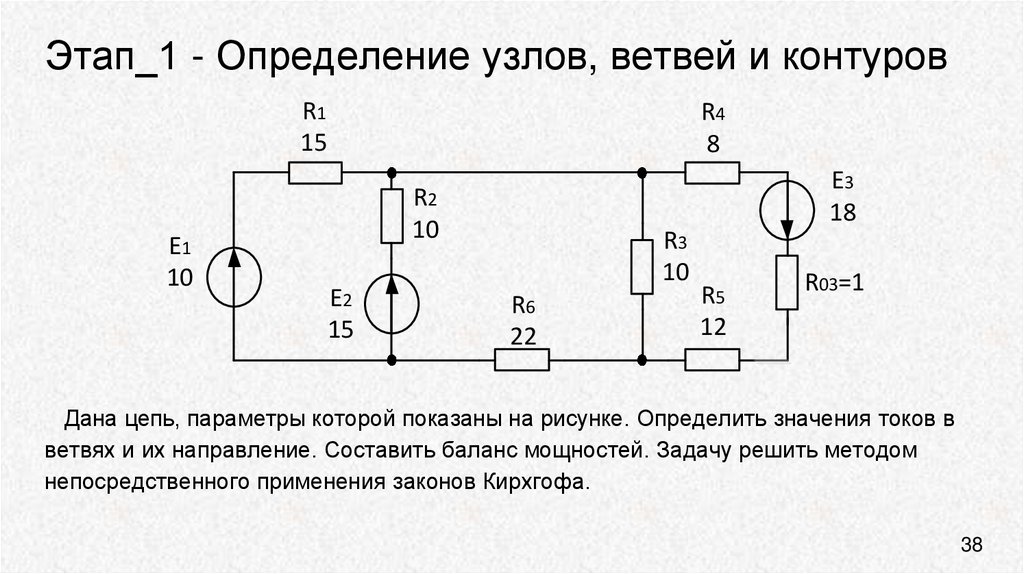

Таким образом, цепь образует полный цикл.

Конечно, схемы могут быть и более сложными. Однако все схемы можно свести к трем основным элементам:

• Источник напряжения: Источник напряжения создает ток, например, как батарея.

• Нагрузка: Нагрузка потребляет энергию; он представляет фактическую работу, выполненную схемой. Без нагрузки нет особого смысла в цепи.

  Нагрузка может быть такой простой, как одна лампочка. В сложных схемах нагрузка представляет собой комбинацию компонентов, таких как резисторы, конденсаторы, транзисторы и т. д.

• Токопроводящая дорожка:

  Токопроводящая дорожка представляет собой путь, по которому течет ток. Этот маршрут начинается от источника напряжения, проходит через нагрузку и затем возвращается к источнику напряжения. Этот путь должен образовывать петлю от отрицательной стороны источника напряжения к положительной стороне источника напряжения.

В следующих абзацах описывается несколько дополнительных интересных моментов, которые следует иметь в виду, когда вы размышляете о природе основных цепей:

• Когда цепь завершена и образует петлю, которая позволяет течь току, цепь называется замкнутой цепью.

  Если какая-либо часть цепи отключена или нарушена, так что петля не образуется, ток не может течь. В этом случае цепь называется разомкнутой цепью .

  Открытая цепь — это оксюморон. В конце концов, компоненты должны образовывать полный путь, чтобы считаться схемой. Если путь открыт, это не цепь. Таким образом, разомкнутая цепь чаще всего используется для описания цепи, которая разорвалась либо преднамеренно (с помощью переключателя), либо из-за какой-либо ошибки, такой как ослабление соединения или повреждение компонента.

• Короткое замыкание относится к цепи без нагрузки. Например, если лампа подключена к цепи, но между отрицательной клеммой аккумулятора и ее положительной клеммой также имеется прямое соединение.

  Ток при коротком замыкании может достигать опасного уровня. Короткое замыкание может привести к повреждению электронных компонентов, взрыву аккумулятора или возгоранию.

  Короткое замыкание иллюстрирует важный момент, касающийся электрических цепей: возможно — обычно даже — цепь может иметь несколько путей для протекания тока. Ток может протекать через лампу, а также через путь, который напрямую соединяет две клеммы аккумулятора.

  Ток течет везде, где может. Если в вашей цепи есть два пути, по которым может течь ток, ток не выбирает один из них; он выбирает оба. Однако не все пути равны, поэтому ток не течет одинаково по всем путям.

  Например, ток будет легче течь через короткое замыкание, чем через лампу. Таким образом, лампа не будет светиться, потому что почти весь ток пойдет в обход лампы в пользу более легкого пути через короткое замыкание. Даже в этом случае через лампу будет протекать небольшой ток.

Эту статью можно найти в категории:

• Схема,

Передача энергии в электрических цепях Учебное пособие

Инструменты Creator скоро будут вдохновлять!

Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся.

Физика

Общая физика

Электрические схемы

Перенос энергии в Электрических цепях.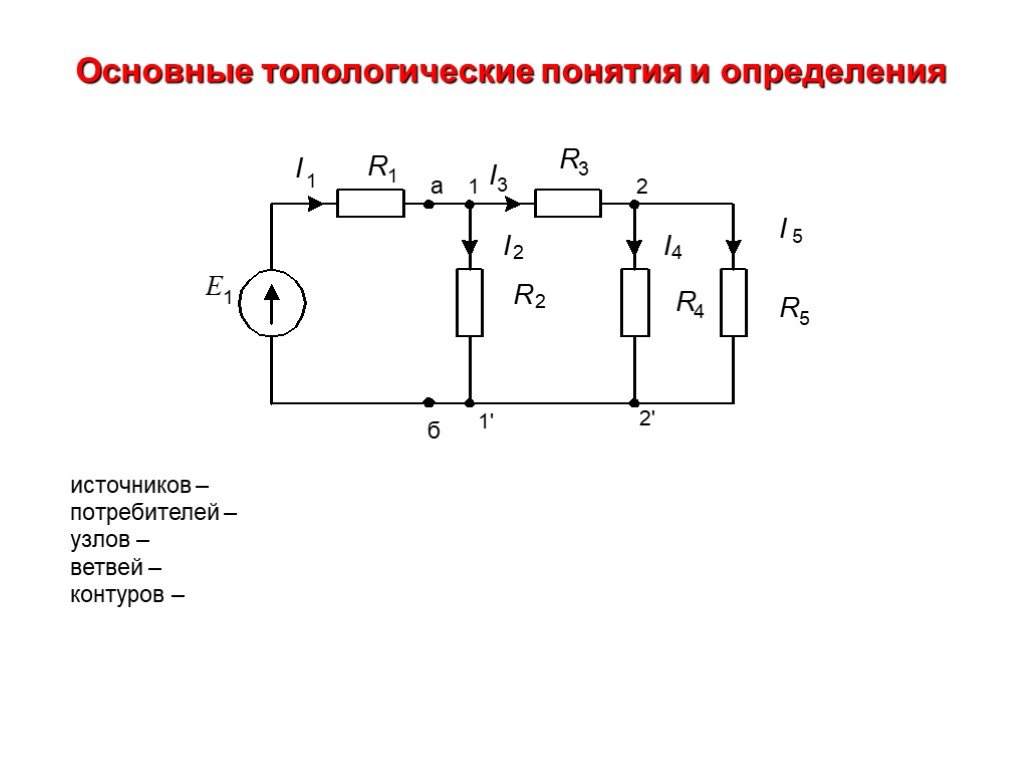 разомкнутая цепь

замкнутая цепь

Электроэнергия – это энергия, преобразованная в единицу времени в электрической цепи, и когда она передается по цепям, она называется электрической мощностью.

Электрические цепи — это пути, по которым текут электроны, образуя сеть для электрических компонентов. Провода вместе составляют путь и могут легко питаться от батареи. Это обеспечивает стимулы для электрона, что приводит к передаче энергии в цепях.

Источник

ЗНАЧЕНИЕ ПЕРЕДАЧИ ЭНЕРГИИ В ЦЕПЯХ

• Значение передачи энергии  является преобразованием одной формы энергии в другую форму.

• Обычно это движение энергии или поток электронов на своем пути.

• Когда электроны или энергия проходят по замкнутому пути, мы называем это передачей энергии в цепях.

• Эти формы передачи энергии в цепях называются электроэнергией.

• Кроме того, электрическая мощность — это энергия в единицу времени, преобразованная за счет электрической цепи из одного вида энергии в другой.

• Формула электроэнергии определяется как E = I ² Rt .

• Электрические цепи представляют собой замкнутый контур или путь, по которому протекает электрический ток.

• Этот поток энергии возникает из-за замкнутого пути или цепи.

• Когда путь не закрыт, энергия не сможет проходить по цепи, поскольку поток электронов прерывается.

• Таким образом, в обрыв цепи , передача энергии невозможна.

 

УРАВНЕНИЕ ПЕРЕДАЧИ ЭНЕРГИИ В ЦЕПЯХ

Уравнения переноса энергии в электрических цепях включали перенос электронов электрическим током на соответствующий заряд проводника и напряжение.

Его уравнение: E = QV

Где E = энергия в джоулях

Q = заряд в кулонах

V = напряжение в вольтах.

ПРИМЕРЫ ПЕРЕДАЧИ ЭНЕРГИИ В ЦЕПЯХ

Существуют различные формы передачи энергии в примерах электрических цепей.

• В лампочки
• В автомобильном аккумуляторе
• Лампа, вставленная в распределительный щит
• Аккумуляторы для мобильных телефонов
• Тостер для хлеба дома

Источник 

• Электроэнергией называется скорость, с которой электрическая энергия потребляется устройством.
• Сама электрическая энергия может быть выражена как генерация энергии из-за движения электронов от их собственного заряда к заряду проводника. Электрическая мощность умножается на время, т. е. E = Pt.
• Некоторыми примерами передачи энергии являются электродвигатели, домашние тостеры для хлеба, электрические утюги и т. д.
• Передача энергии в уравнении электрических цепей E = QV.

Часто задаваемые вопросы

1. Как энергия передается в цепи?

Средство передачи энергии в цепи по замкнутому контуру. Когда цепь полностью замкнута с обоих концов, энергия переходит из одной формы в другую. А скорость потребления энергии в единицу времени называется электрической мощностью.

2. Каковы 10 примеров передачи энергии?

• Размах колебаний
• Электродвигатель
• Электрогенератор
• Освещение лампочки
• Автомобильный двигатель
• Сотовый в машине или телефоны
• Солнечный нагреватель
• Солнечная батарея
• Тостер для хлеба дома
• Электрические утюги

3. Каковы 5 преобразований энергии?

• Химическая энергия в электрическую
• Электрическая энергия в тепловую энергию
• Химическая энергия в механическую
• Свет в химическую энергию
• Электрическая энергия в тепловую энергию

4. Приведите уравнение переноса энергии в электрических цепях.

Уравнение переноса энергии в электрических цепях: E = QV.

Мы надеемся, что вам понравился этот урок, и вы узнали что-то интересное о Передача энергии в электрических цепях! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими учениками, такими же, как и вы! Обещаем, так учиться намного веселее!😎

ССЫЛКИ

1. Передача энергии в цепях: https://www.