Простые примеры по математике
Математика – наука, областью применения которой являются не только исследования в сфере сугубо количественных отношений, но также изучение порядка, структуры и пространственных форм объективно существующего мира, сложившихся в течение тысячелетий существования человечества на основе самых разнообразных операций по измерению, подсчёту и описанию тех или иных реальных объектов. Являясь мощнейшим средством успешного разрешения практически любых задач научно-прикладного характера, математика одновременно представляет собой универсальный язык науки, а значит, и важнейшую составляющую общемировой культуры. Вот почему одна из важнейших целей ее изучения заключается в повышении общего кругозора, культуры мышления, формировании естественнонаучного мировоззрения.
Процент
Десятичная система
Скобки
Арифметические действия
Свойства делимости
Простые и составные числа
Целые числа
Округление чисел
Разложение на множители
Целое и часть
Сравнение дробей
Сокращение и расширение
Сложение и вычитание
Умножение дробей
Деление дробей
Большие числа
Математика принадлежит к разряду точных наук и по праву занимает в нем лидирующие позиции.
Она не терпит спекуляций и произвола в толковании различных закономерностей, их логическом обосновании. Она – само воплощение жесткой логики и упорядоченности, взаимозависимости происходящих в окружающем мире событий и явлений. Помогая людям в постижении мира, она позволяет им все больше узнавать о законах его развития, поскольку абсолютно все законы имеют математическое выражение, подчиняясь царящему в математике порядку.
Изучая математику, мы, как правило, не можем выбрать время для того, чтобы больше узнать о её роли в нашей повседневной жизни и тесной взаимосвязи с различными сферами человеческой жизнедеятельности. Между тем, именно математика является, по сути, началом начал если не всего, то очень многого. Задавшись целью изучать мир во всем его разнообразии, мы рано или поздно, но непременно обнаруживаем, что в повседневной жизни математика играет роль не менее значимую, чем в узких областях точных и прикладных наук. С ней приходится сталкиваться ежеминутно, а следовательно, определенный багаж математических знаний и навыков необходим каждому из нас.
Применение математики безмерно расширяет возможности познания. Ныне просто невозможно назвать область знаний, которая в той или иной мере не была бы основана на математических понятиях и методах. Трудно переоценить прикладную роль математики в исследованиях естественнонаучного, инженерно-технического и гуманитарного генезиса. А основной причиной, обуславливающей математизацию различных областей повседневной жизнедеятельности человека, является способность математики предлагать четкие модели для постижения окружающей нас действительности.
Практически в каждой из профессий не обойтись без математических знаний и навыков. В первую очередь это, разумеется, относится к специальностям, непосредственно сопряженным с технико-экномической сферой.
Решить математический пример
Метки
Задачи Математика Учеба Цифры ШколаЧто делает школьник младших классов, который не может решить математический пример, заданный ему в качестве домашнего задания? Наверняка обращается за помощью к своим родителям либо к бабушкам с дедушками.
И довольно странно, если эти взрослые и умудренные жизненным опытом люди не могут ничем помочь, поскольку все математические премудрости уже давно напрочь вылетели у них из головы.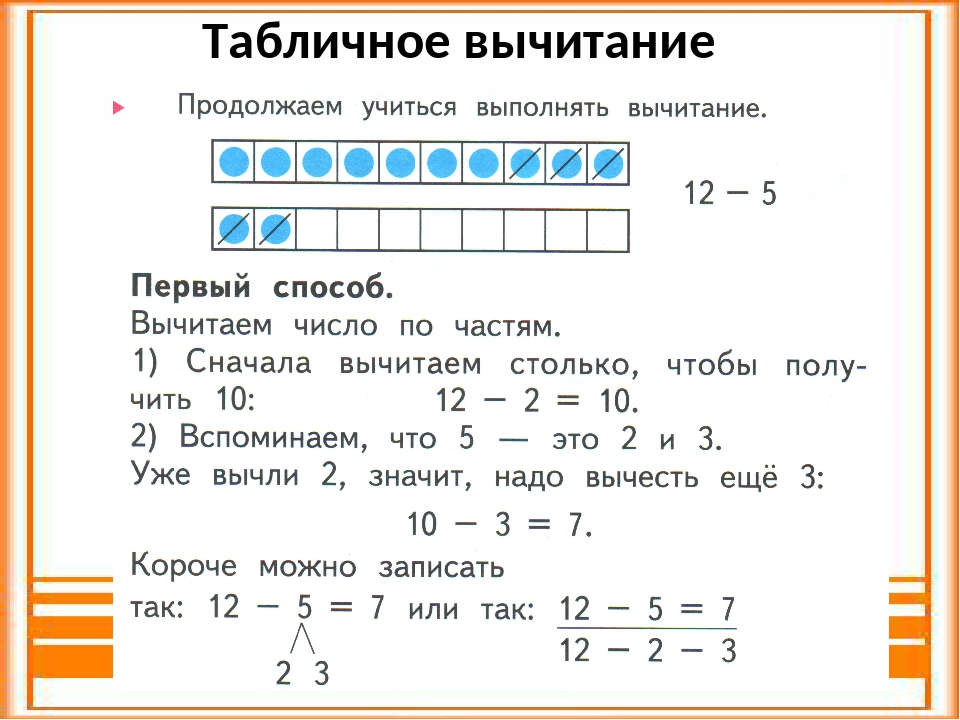
А потому мы в редакции «Так Просто!» уверены, что с математикой дружить необходимо каждому и в любом возрасте. Ведь никогда не знаешь, в какой момент эти ценные знания могут пригодиться. И предлагаем в таком случае решить несколько любопытных примеров, с которыми разобраться почему-то получается далеко не у каждого.
© Depositphotos
- Первый пример покажется довольно простым даже человеку, который всячески избегал уроков математики в школьные годы. Но и тут есть небольшой подвох, который способен запутать немало взрослых людей. А потому частенько при решении подобных примеров читатели допускают ошибки. Получится ли у тебя избежать таких казусов?
- Второй пример тоже не кажется архисложным. Однако при решении чуть ли не каждый третий допускает ошибку, которая приводит к неправильному конечному ответу. Сможешь ли ты, вспомнив некоторые важные математические правила, всё решить правильно?
- И напоследок предлагаем уже более сложный на вид пример.
Числа тут небольшие, поэтому всё решить можно без помощи калькулятора, прямо в уме. Но в какой последовательности всё решать, чтобы ответ оказался правильным? Ведь в противном случае строгая учительница математики порядком расстроится, что даже со столь простым заданием справиться ученик не смог.
Числа тут небольшие, поэтому всё решить можно без помощи калькулятора, прямо в уме. Но в какой последовательности всё решать, чтобы ответ оказался правильным? Ведь в противном случае строгая учительница математики порядком расстроится, что даже со столь простым заданием справиться ученик не смог.Подсказки и ответы
- Прежде чем приступать к решению, нужно вспомнить нерушимые математические правила, которые много раз повторялись на уроках математики. И примерный ученик с ходу скажет, что сначала решаем действия в скобках, а затем действия слева направо. В таком случае получим 12 ÷ 2 × 6 = 6 × 6 = 36. Хотя у многих ответом почему-то оказывается 1. © Depositphotos
- Во втором примере сначала осуществляем умножение, а только затем — вычитание. Отсюда 20 – 10 × 0,5 = 20 – 5 = 15. Хотя даже многие взрослые попросту выполняют все арифметические операции слева направо, получая в итоге 5 вместо 15.
- Сначала, как уже говорилось, выполняем действия в скобках. Учитывая это, получаем 6 × 5 – 2 + 5 × 2 = 30 – 2 + 10 = 38. Довольно просто, если четко знать правильный алгоритм действий. © Depositphotos
Учитывая это, получаем 6 × 5 – 2 + 5 × 2 = 30 – 2 + 10 = 38. Довольно просто, если четко знать правильный алгоритм действий. © DepositphotosДаже если удалось всё решить правильно, то не спеши зазнаваться. Ведь недавно мы публиковали более сложные примеры, а также делились задачками с подвохом, с которыми мало кому удается совладать. Проверь, получится ли у тебя это сделать.
Поделиться
Выражения в математике — определение, типы, примеры
Выражения в математике — это математические операторы, которые содержат как минимум два термина, содержащих числа или переменные, или и то, и другое, соединенных оператором между ними. Математические операторы могут быть сложения, вычитания, умножения или деления. Например, x + y — это выражение, где x и y — члены, между которыми стоит оператор сложения. В математике есть два типа выражений: числовые выражения, которые содержат только числа; и алгебраические выражения, которые содержат как числа, так и переменные.
В этой статье мы обсудим концепцию выражений в математике и их различные типы. Мы также поймем разницу между выражением и уравнением в табличном виде и различными типами выражений с помощью примеров для лучшего понимания.
| 1. | Что такое выражение в математике? |
| 2. | Типы выражений в математике |
| 3. | Выражение против уравнения |
| 4. | Упрощение выражения в математике |
| 5. | Часто задаваемые вопросы о выражениях в математике |
Что такое выражение в математике?
Выражение в математике – это предложение, содержащее не менее двух чисел/переменных и по крайней мере одну математическую операцию. Давайте поймем, как писать выражения. Число на 6 больше, чем половина другого числа, а другое число равно x. Это утверждение записывается как x/2 + 6 в математическом выражении.
Математические выражения используются для решения сложных головоломок.
Определение выражения в математике
Выражение — это комбинация терминов, объединенных с помощью математических операций, таких как вычитание, сложение, умножение и деление. Термины, используемые в выражении в математике:
- Константа: Константа представляет собой фиксированное числовое значение.
- Переменная: Переменная — это символ, который не имеет фиксированного значения.
- Терм: Терм может быть отдельной константой, одной переменной или комбинацией переменной и константы в сочетании с умножением или делением.
- Коэффициент: Коэффициент — это число, которое умножается на переменную в выражении.
Выражение в математическом примере
Существует бесконечное количество примеров выражения. Например, 2y-9, 3a×2, -7+6÷3 и т. д. Давайте также рассмотрим пример из жизни. Сара сказала своему младшему брату Даниэлю, что ее возраст на 3 года больше, чем в два раза.
Она попросила его вычислить ее возраст, если его возраст равен х лет. Давайте поможем ему написать выражение. Двойной возраст Даниила можно записать как 2x. Сейчас возраст Сары в 3 раза больше, чем в 2 раза. Следовательно, возраст Сары будет записан как 2x+3.
Типы математических выражений
Существует три основных типа математических выражений. Основываясь на терминах, которые они имеют, их можно классифицировать как арифметические/числовые выражения, дробные выражения и алгебраические выражения. Познакомимся с каждым из них подробнее с помощью приведенной ниже таблицы:
| Типы математических выражений | Определение выражения | Список математических выражений |
|---|---|---|
| Числовое выражение | Содержит только числа и математические операторы | 40-5+2 |
| Дробное выражение | Содержит дробные числа и математические операторы | 5/3 – 7/6 |
| Алгебраическое выражение | Содержит переменные, числа и математические операторы | 3x+2г |
Теперь алгебраические выражения подразделяются на одночлены, двучлены, трехчлены и т.
д. Они также называются полиномами. Давайте посмотрим на типы алгебраических выражений в таблице, приведенной ниже:
| Категория | Определение выражения | Примеры |
|---|---|---|
| Одночлен | Выражение, содержащее один член с неотрицательными экспоненциальными целыми числами. | 2x 2 |
| Биномиальный | Выражение, образованное сложением или вычитанием двух мономов. | 2x 2 +5xy |
| Трехчленный | Выражение, образованное сложением или вычитанием трех мономов. | 2x 2 +5xy+4yz |
| Многочлен | Выражение, состоящее из одного или нескольких мономов. | 2x 2 +5xy+4yz+2y+3 |
Выражение против уравнения
В математике выражения и уравнения — это два разных понятия.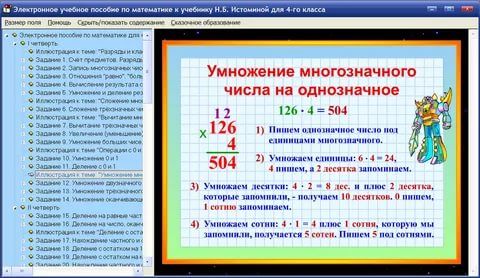
Попробуем понять разницу между ними. Выражение может быть числом, переменной или комбинацией чисел и переменных, связанных математическими операторами, т. е. сложением, вычитанием, умножением и делением. С другой стороны, уравнение — это отношение равенства между двумя выражениями. Посмотрите на приведенную ниже таблицу, чтобы лучше понять ее:
| Выражение | Уравнение |
|---|---|
| Выражения только односторонние. | Уравнения двусторонние (левая и правая часть) |
| Выражения можно упростить, чтобы получить числовой ответ. | Уравнения можно решить, чтобы проверить равенство или найти пропущенные значения. |
| Выражение — это комбинация терминов, между которыми находятся операторы. | Уравнение — это комбинация двух выражений, между которыми стоит знак «равно» (=). |
| Пример: 3x-8 | Пример: 3x-8=16 |
Посмотрите еще несколько примеров выражений и уравнений на рисунке ниже:
Упрощение выражения в математике
Выражения могут быть упрощены для формирования ответа. Например, 3+6-2 — это выражение, которое можно упростить до 7. Существует два разных способа упростить арифметические выражения и алгебраические выражения. Мы используем правило BODMAS (правило PEMDAS), чтобы упростить их. В случае алгебраических выражений одинаковые термины могут быть добавлены или вычтены для упрощения. Подобные термины — это те, у которых одна и та же переменная возведена в одну и ту же степень. Таким образом, мы можем легко складывать или вычитать два или более одинаковых термина, добавляя их коэффициенты. Например, 2x+5x дает 7x, тогда как 7ab-b — это выражение, содержащее два непохожих члена, которые нельзя сложить.
В случае выражений, содержащих несколько терминов и операторов, применяется правило PEMDAS (правило BODMAS).
Например, упростим 23 – 6 + 7 × 3. Здесь, поскольку нет скобок и показателей степени, мы сначала вычислим 7 × 3, что равно 21. Теперь выражение равно 23-6+21. Теперь есть два оператора, сложение и вычитание. Поскольку обе операции являются операциями одного уровня, а вычитание выполняется сначала с левой стороны, мы вычтем 6 из 23, т. е. 17. Теперь наше выражение стало 17+21, что дает 38, а 38 — это упрощенное значение выражения 23 — 6 + 7 × 3,
Важные примечания по выражениям в математике:
- Выражение состоит из 3 частей: постоянной, переменной и члена.
- Существует 3 типа выражений: арифметические/числовые, дробные и алгебраические.
- Полиномиальное выражение — это тип выражения переменной.
Статьи по теме
- Раздел алгебраических выражений
- Вычитание алгебраических выражений
- Сложение алгебраических выражений
- Упрощение рациональных выражений
Часто задаваемые вопросы о выражениях в математике
Что такое выражение в математике?
Выражения в математике — это математические операторы, которые содержат как минимум два термина, содержащих числа или переменные, или и то, и другое, соединенных оператором между ними.
У нас есть различные типы выражений в математике, такие как числовые выражения, алгебраические выражения, дробные выражения и т. д.
Как определить похожие термины в математических выражениях?
Подобно терминам, в выражении одни и те же переменные возводятся в одну и ту же степень. Например, 5x, −x и −3x — все это одинаковые термины.
Как написать выражение в математике?
Мы пишем математические выражения, используя числа или переменные и математические операции, такие как сложение, вычитание, умножение и деление. Например, выражение математического утверждения “4 прибавить к 2” будет 2+4.
Что такое числовое выражение?
Числовое выражение состоит из чисел и операторов. Числовые выражения также называются числовыми выражениями. Примеры числовых выражений: 8 – 7, 3 + 6 × 7 – 3 и т. д.
Сколько терминов в выражении?
В выражении может быть любое количество терминов. Выражение — это математическая фраза, состоящая из терминов, разделенных между собой операторами.
Итак, у нас может быть выражение с 1 термином, 2 терминами, 3 терминами или n количеством терминов.
В чем разница между математическим выражением и алгебраическим выражением?
Как правило, математические выражения или числовые выражения содержат только числа и операторы, в то время как алгебраические выражения содержат как числа, так и переменные в терминах, разделенных промежуточными операторами.
Можете ли вы решить математическое выражение?
Так как выражения не имеют знака “равно” (=), мы не можем решить их. Мы можем только упростить выражения и найти их сокращенную форму, используя заданные математические операторы.
Как упростить выражения в математике?
Мы можем упростить математические выражения, приведя данное выражение к простейшей форме. Если это числовое выражение, то его можно упростить, найдя значение выражения. Если это алгебраическое выражение, то его можно упростить, приведя к простейшей форме, чтобы его нельзя было сократить дальше.
Использование примеров и не примеров в математике
Многие мои ученики испытывают трудности с вычитанием двузначных чисел. У многих нет хорошей основы в смысле чисел или просто понимания математики.
Мы рассмотрели пример и не пример сравнения, чтобы лучше понять вычитание с перегруппировкой (или скрещивание десяти).
Из-за отсутствия у них чувства числа я не решаюсь учить студентов традиционному алгоритму, потому что хочу развить у них понимание решения задач. В идеале я бы хотел, чтобы они прибавляли или вычитали в пределах 100 мысленно, вообще не используя бумагу. До сих пор мы рассматривали, как использовать числовую прямую и разбивать числа на части.
Когда я представил это студентам, я представил это как задачу, которую многие студенты с трудом решали в прошлом году. Я сказал студентам, что мои студенты придумали два ответа: 42 и 38.
Я намеренно поставил неправильный ответ слева. Мы читаем слева направо и, естественно, сначала «видим» эту сторону бумаги.
Я попросил учащихся поделиться с партнером ответом, который они считают правильным, и почему это был правильный ответ. При разделении всей группы мы начали с 42, и студенты дали ответ выше.
Поскольку мы начали с 42, все думали, что это «правильный» ответ, и никто не вызвался рассказать мне, как они получили 38. Я имею в виду никого. Я позвонил студенту, который, как я знал, ответил на него правильно, и попросил его объяснить свой ответ. Он не так хорош в объяснении своих мыслей (он изучает английский язык и отлично разбирается в математике, но не в языке). Другой студент помог ему закончить размышление, чтобы мы могли записать его.
Мы говорили о том, что -57 на самом деле -50 и -7 и что проблема не в 7-5, а в 5-7. Мы также продемонстрировали с помощью прямоугольников с левой стороны, как учащиеся составили новые числа, перевернув единицы местами.
Я показал им другой способ решения задачи, который мы сделали в классе, но ученики не смогли вспомнить. Я также показал студентам, как поставить задачу и получить отрицательный ответ. У меня в комнате есть числовая шкала, которая опускается до -10, чтобы ученики могли использовать ее для этих целей. В этом году никто из моих студентов этого не делает, но в прошлом году у меня было несколько таких. Отрицательное число также подтверждает идею о том, что есть числа ниже 0, концепцию, которую учителя старших классов часто пытаются укрепить после многих лет начальной математики, которая останавливается на 0,
Поработав над этой задачей, я понял, что ученики не понимают, что 93 = 80 + 13, поэтому сегодня мы поработали над разложением двузначных чисел (что они умеют делать), а затем разложением десяти (что они умеют делать). можно было сделать изолированно, но не применительно к вычитанию). Ближе к завершению сегодняшней работы мы подошли к решению некоторых задач на вычитание на их досках.