1.11. Мгновенная скорость
Уменьшая неограниченно промежуток времени t, за который произошло перемещение м. т. в пространстве в пределе, когда t 0, получим мгновенную скорость, т. е.
(15)
Вектор мгновенной скорости равен пределу отношения приращения радиус-вектора м. т. к тому промежутку времени, за которое это приращение произошло, когда t 0 или равен первой производной радиус-вектора по времени.
Вектор мгновенной скорости в данный момент времени направлен по касательной к траектории в данной точке (рис. 9).
Действительно,
при t
0, когда точка М2 приближается к М1,
хорда (секущая)
,
сближается с длиной отрезка дугиs
и в пределе s
=
,
а секущая переходит в касательную. Это
наглядно подтверждается опытами.
Например, искры при заточке инструмента
всегда направлены по касательной к
точильному кругу.
.
В некоторых типах ускорителей (например, циклотронах и др.) частицы многократно движутся по замкнутой траектории без остановки. Следовательно, в любой точке траектории модуль вектора мгновенной скорости должен отличаться от нуля. Это заключение подтверждается не только уравнением (15), но и согласуется с понятием средней скалярной скорости (формула 11). Если в уравнении (11) перейти к пределу при t 0, то придется рассматривать такие малые участки пути на траектории s, которые не отличаются от модуля элементарного вектора перемещения . Тогда на основании уравнения (11) можно получить значение мгновенной скалярной скорости
совпадающее с модулем вектора мгновенной скорости ,
так как r = s при t 0.
Одно уравнение вектора мгновенной скорости (15) можно заменить эквивалентной системой трех скалярных уравнений, проекций вектора скорости на оси координат
vx = dx/dt, vy =
dy/dt, vz =
dz/dt. (16)
(16)
Вектор мгновенной скорости связан с его проекциями на оси координат выражением
, (17)
где – единичные векторы, направленные вдоль осей Х, У,Z соответственно.
По модулю
. (18)
Таким образом, вектор скорости характеризует быстроту изменения перемещения в пространстве по величине и направлению с течением времени. Скорость – функция времени.
При движении тел скорость в общем случае может изменяться как по величине, так и по направлению.
Рис. 10
Примерами
такого движения являются движение
Солнечной системы вокруг центра нашей
Галактики или движение поезда при
торможении и т. д. Равномерное движение
м. т. по окружности является примером,
когда ее скорость изменяется по
направлению, оставаясь постоянной по
величине. Если м. т. движется по некоторой
траектории, изменяя величину и направление
скорости, то для характеристики ее
движения уже недостаточно знать
перемещение и скорость, нужно знать еще
и быстроту изменения скорости, т. е.
д. Равномерное движение
м. т. по окружности является примером,
когда ее скорость изменяется по
направлению, оставаясь постоянной по
величине. Если м. т. движется по некоторой
траектории, изменяя величину и направление
скорости, то для характеристики ее
движения уже недостаточно знать
перемещение и скорость, нужно знать еще
и быстроту изменения скорости, т. е.
Пусть м. т. в некоторый момент времени t1 находится в пункте М1 и движется со скоростью , а в момент времени t2 – в пункте М2 – со скоростью (рис. 10).
Перенесем вектор параллельно самому себе в точку М1 так, чтобы совпали начала векторов и.
Тогда разность векторов иесть вектор изменения (приращения) скорости за промежуток времениt = t2 – t1, т. е.
. (19)
Вектор среднего
ускорения равен отношению вектора
изменения скорости к промежутку времени,
за которое это изменение произошло.
Следовательно,
. (20)
Вектор среднего ускорения совпадает с направлением вектора изменения скорости и, направлен внутрь кривизны траектории.
Одному векторному уравнению (1.20) соответствует система из трех скалярных уравнений для проекций вектора среднего ускорения на оси координат
Модуль вектора среднего ускорения
. (22)
За единицу измерения ускорения в СИ принят метр на секунду в квадрате.
Мгновенная скорость – справочник для студентов и школьников
- Средняя скорость.
- Переход от средней скорости к мгновенной скорости.
- Компоненты вектора мгновенной скорости в декартовой системе координат.

- Направление мгновенной скорости.
- Скорость при равнопеременном движении.
Средняя скорость.
В случае если перемещение тела происходит равномерно, то одной из характеристик может быть средняя скорость. Такое понятие поможет установить значение скорости на конкретных частях пройденного пути. Многие ученые не считают данную характеристику точной, она кажется приближенной к действительности. Это связано с тем, что средняя скорость действительно не может отразить точных параметром движения. Так как средняя скорость является равномерной, она не может применяться для отражения неравномерного перемещения. Однако скорость не может изменяться в виде скачков, даже незначительные замедления могут повлиять на всю картину.
Если представить график, который отразит средние скорости, имеющимися у тела, осуществляющего перемещение, то он будет выглядеть как подъемы и падения кривой, это стандартная ломаная линия. Ее звенья будут иметь различный наклон.
Если взять во внимание определенную материальную точку, которая будет перемешаться параллельно прямой, не совпадающей с координатными осями, то ее нахождение можно определить. В этом поможет формула, в которой есть понятие радиус-вектора и время. В момент времени t2 положение материальной точки в пространстве определяет вектор r>2. Отсюда легко определить, по какому вектору перемещается та или иная материальная точка.
В этом поможет формула, в которой есть понятие радиус-вектора и время. В момент времени t2 положение материальной точки в пространстве определяет вектор r>2. Отсюда легко определить, по какому вектору перемещается та или иная материальная точка.
Определение 1.
Средняя скорость определяется формулой.
Из нее можно заметить, что вектор делится на скалярную величину. Результатом является тот факт, что его вектор совпадает с вектором, который определяет перемещение. Данные величины имеют идентичные направления.
Переход от средней скорости к мгновенной скорости.
Выражения, которые получились, отражают среднюю скорость для того или иного отрезка времени. Если поделить его на короткие фазы, то получится, что материальная точка будет иметь разные показатели скорости. Такое явление можно объяснить разными способами перемещения точки. Это может быть неравномерное или равномерное движение. В случае неравномерного перемещения, скорости будут разными.
Если произвести уменьшение отрезка времени, то разница будет заметна и на отрезках внутри промежутка. Так же произойдут изменения в средних скоростях данных показателей времени на всем отрезку.
Если устремить отрезок времени к нулю (?t>0), средняя скорость при этом устремится к предельному значению, которое называют мгновенной скоростью.
Определение 2.
Для расчета мгновенной скорости, надо обратиться к формуле, которая была разработана коллективом ученых.
Если тело перемещается равномерно, то мгновенная скорость его движения в определенный момент времени совпадает со скоростью этого движения. Установлено, что мгновенная скорость равномерного движения является постоянной.
Как рассчитать мгновенную скорость для тела, которое перемещается неравномерно. Этот параметр является переменным. Он может принимать различные значения в зависимости от времени. Тогда скорость считаться меняющейся на каждом из отрезков времени.
Мгновенную скорость в каждый момент времени можно определить как тангенс угла наклона касательной к кривой – траектории движения в рассматриваемой точке.
Компоненты вектора мгновенной скорости в декартовой системе координат.
Рассмотренная система Декарта предполагает, что существует координата радиус-вектора, которую можно изобразить с помощью формулы. Здесь стоит учитывать существование единичных орт, которые не изменяются во времени. Если использовать их для определения мгновенной скорости, то так же можно усовершенствовать формулу. Отсюда можно заметить, что для того, чтобы задать вектор скорости в системе Декарта, надо использовать ряд несложных выражений.
Теперь можно осуществить нахождение числа мгновенной скорости.
Направление мгновенной скорости.
Чтобы лучше понять принцип мгновенной скорости, следует описать движение некой материальной точки. Известно, что траектория движения точки и связь пути (s) и времени t.
Следует разметить отрезок равными частями. У каждой точки будет собственное понятие величины. Из всего, что было написано ранее, можно сделать вывод, что радиус-вектор – это функция от s.
Траекторию легко задать уравнением. Радиус-вектор представляет функцию (r>(s(t))). При этом ее производную можно найти, если применить важное правило дифференцирования сложной функции.
Обозначим ?s – расстояние между парой точек по траектории; |?r>|– расстояние между рассматриваемыми точками по кратчайшему расстоянию (прямой). При сближении наших точек разница между ?s и |?r>| уменьшается.
где ?> – единичный вектор, который является касательным к траектории движения точки.
Формула показывает, что направление мгновенной скорости следует по касательной к траектории движения материальной точки.
Таким образом, мгновенная скорость перемещающейся точки представляет собой вектор, направленный в сторону пути движения точки.
Если перемещение точки происходит по непрямой траектории, то вектор имеет направление по касательной к траектории движения точки.
Скорость при равнопеременном движении.
Одним из самых простых способов двигаться неравномерно, то можно представить перемещение тела равнопеременного типа. Такое перемещение может быть несколько типов движение: равноускоренное и равнозамедленное. Равноускоренное движение представляет собой движение, при котором скорость и ускорение равные, при том, что скорость увеличивается.
Такое перемещение может быть несколько типов движение: равноускоренное и равнозамедленное. Равноускоренное движение представляет собой движение, при котором скорость и ускорение равные, при том, что скорость увеличивается.
Равнозамедленное движение появляется, когда скорость и ускорение противоположны, скорость уменьшается.
При равнопеременном движении скорость в любой момент времени можно вычислить, если использовать выражение, где v>0 – начальная скорость движения точки; a> – постоянное ускорения точки.
Мгновенная скорость
Повседневная концепция скорости возникает, когда мы рассматриваем, как быстро или медленно движется тело. Каким-то образом мы соотносим смещение кузова с временем вложенным в него. В этом разделе мы собираемся указать, что такое физическая скорость, также известная как мгновенная скорость или просто скорость. Чтобы хорошо это понять, мы рекомендуем вам предварительно прочитать абзац, в котором мы приводим среднюю скорость.
Физическая скорость тела в точке или мгновенная скорость — это скорость, которую тело имеет в определенное время в определенной точке своей траектории.
Мгновенная скорость или просто скорость определяется как предел средней скорости, когда изменение времени приближается к нулю. Он также определяется как производная вектора положения по времени . Его выражение определяется следующим образом:
v→=lim∆t→0v→avg=lim∆t→0∆r→∆ t=dr→dt
где:
- v→ : Мгновенный вектор скорости. Его единица в Международной системе метра в секунду ( м/с )
- v→avg : вектор средней скорости. Его единицей измерения в Международной системе является метра в секунду (
- ∆r- : Вектор смещения. Его единицей измерения в Международной системе является метра ( м ) .
- ∆ t : Интервал времени, стремящийся к нулю, то есть бесконечно малый интервал.
 Его единицей в Международной системе является 9.0003 секунда ( с )
Его единицей в Международной системе является 9.0003 секунда ( с )
Скорость — векторная величина. Его размерное уравнение задается как [v]=[L][T] -1
Как получается выражение для мгновенной скорости?
Чтобы определить понятие мгновенной скорости с точностью, мы начнем с понятия средней скорости, которое мы уже изучили, и мы собираемся помочь себе с графиком на рисунке.
Процедура определения мгновенной скорости или просто скорости тела в точке А состоит в вычислении средней скорости между А и точкой как можно ближе к А . Это то же самое, что вычислить среднюю скорость за отрезок времени как можно меньшего . На графике вы можете увидеть вектор положения точки A и остальных точек B, C и D. Это r→A, r→B, r→C и r→D соответственно. Векторы смещения между A и каждой из точек B, C и D также представлены.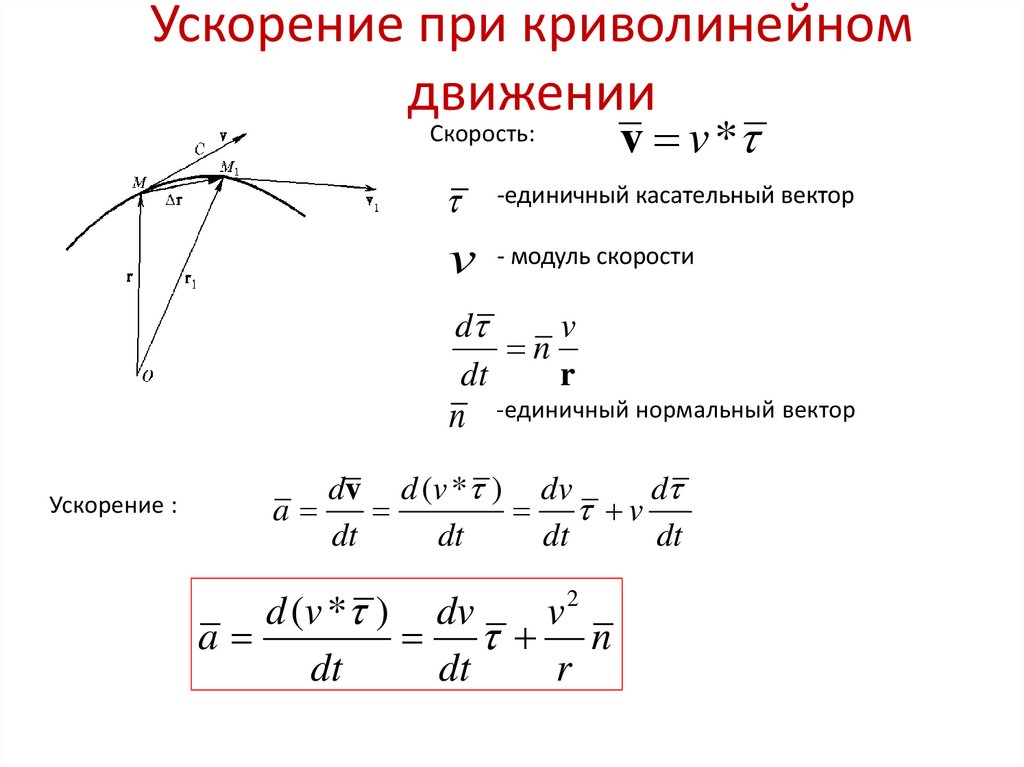 Это r→A , r→B , r→C и r→D соответственно. Как видно на приведенном выше графике, в качестве второй точки
Это r→A , r→B , r→C и r→D соответственно. Как видно на приведенном выше графике, в качестве второй точки
Экспериментируйте и учитесь
Близость пройденного расстояния и смещения
На графике показана траектория движения тела и его положение в два разных момента времени.
Перетащите обе позиции и наблюдайте за значениями смещения и пройденного расстояния.
Что происходит, когда они очень близко? Пройденное расстояние практически равно величине вектора смещения. В частности, если прошедшее время между двумя положениями приближается к 0, они становятся точно такими же. Это приближение используется для расчета скорости в момент времени.
Чаще всего находят вектор скорости, записанный с помощью его декартовых компонент, что дает:
вектора скорости в трехмерных декартовых координатах:
v→=vxi→+vyj→+vzj→=lim∆t→0∆x∆ti→+lim∆t→0∆y∆tj→+lim∆t→0∆z∆tj→=dxdti →+dydtj→+dzdtj→
вектор скорости в двухмерных декартовых координатах:
v→=vxi→+vyj→=lim∆t→0∆x∆ti→+lim∆t→0∆y∆tj→=dxdti→+dydtj→
Также возможно, что, как и в случае любого другого вектора, вы обнаружите, что он записан как функция его величины. Для этого просто умножьте величину вектора скорости на единичный вектор с тем же направлением, что и v→ , и который мы будем называть u→t , поскольку он касается траектории.
Для этого просто умножьте величину вектора скорости на единичный вектор с тем же направлением, что и v→ , и который мы будем называть u→t , поскольку он касается траектории.
v→=v⋅u→t
Как видите, мгновенная скорость представляет собой векторную величину, которая удовлетворяет следующему:
Декартовы компоненты вектора скорости
мы определили понятие
мгновенной скорости на основе средней скорости, мы изучили ее величину и ее направление. Несмотря на то, что мы рассмотрели разные точки зрения и разные выражения для вектора скорости и его модуля, обычно вы вычисляете скорость как производная вектора положения по времени.Пример
Если тело движется согласно следующему уравнению:
r(t)→ = (4·t + t2)·i→+4·t·j→ m
Рассчитайте его мгновенную скорость в момент времени t=1 с.
Решение
Векторы скорости — определение, вектор мгновенной скорости, вектор относительной скорости
Векторы скорости — сложный термин, используемый во многих исследованиях для определения и решения научных задач. Этот термин создан с помощью двух слов = Скорость + Вектор. Оба эти слова имеют свое собственное значение. Давайте подробнее прочитаем о векторах скорости.
Этот термин создан с помощью двух слов = Скорость + Вектор. Оба эти слова имеют свое собственное значение. Давайте подробнее прочитаем о векторах скорости.
Скорость — это просто скорость изменения движения. Тогда как, с другой стороны, Вектор — это физическая величина, которая имеет как величину, так и направление. Графическое представление вектора предполагается в виде линии со стрелкой на ней.
Здесь длина линии, проведенной над фактической величиной, соответствует величине вектора, а болт показывает курс этого вектора. Скорость – это скорость с заголовком и протяженностью. Таким образом, это векторная величина. Таким образом, вектор скорости указывает на скорость изменения положения тела. Размер вектора скорости показывает скорость предмета, а вектор пеленга обеспечивает его направление.
Что такое вектор скорости с точки зрения определения?
Например, рассмотрим тело, движущееся с постоянной скоростью V вдоль прямой линии OX
Пусть O будет точкой измерения, а также тогда время в точке O равно «t».
Пусть положение объекта в точках А и В в моменты времени ‘t 1 ’ и ‘t 2 ’.
Таким образом, что \[\overrightarrow{OA}\] = \[\overrightarrow{x_1}\] и \[\overrightarrow{OB}\] = \[\overrightarrow{x_2}\].
Тогда тело перемещается за интервал времени –
(t 2 – t 1 ) = \[\overrightarrow{AB}\] – \[\overrightarrow{OA}\] = \[ \overrightarrow{x_2}\] – \[\overrightarrow{x_1}\]
Следовательно, Скорость = \[\frac{\text {Смещение}}{\text{Интервал времени}}\]
Тогда скорость вектор, \[\overrightarrow{V}\] = \[\frac {(\overrightarrow{x_2} – \overrightarrow{x_1})}{t_2 – t_1}\]
Что такое вектор мгновенной скорости?
Как вы читали выше, если общее перемещение тела разделить на общее время, то получится средняя скорость тела.
Средняя скорость представлена как –
V avg = \[\frac {\Delta x}{\Delta t}\]
T – момент времени, Δx – расстояние, пройденное объектом, а перемещается за небольшой промежуток времени, равный Δt.
Для расчета мгновенной скорости в момент времени t Δt будет стремиться прямо к нулю, то есть – Δt → 0 .
Формула для мгновенной скорости: –
v мгновенная = Предел 0
Следовательно, предел средней скорости объекта истекает через время, чтобы приблизиться к нулю, или это может быть x или t с учетом мгновенной скорости.
Кроме того, при рассмотрении длины измерения в единицу времени вектор мгновенной скорости является вектором.
Вектор относительной скорости
Давайте разберемся, что такое относительная скорость.
Когда два объекта P и Q движутся с разными скоростями, то скорость объекта P относительно объекта Q называется относительной скоростью.
Рассмотрим два объекта, движущихся с равномерными скоростями v 1 и v 2 соответственно по параллельным траекториям в одном направлении.
Пусть x 0a и x 0b — их перемещения в момент времени t = 0. Если в момент времени t, x 1 и x 2 – это два смещения двух объектов, касающихся происхождения оси положения, затем для объекта P мы имеем
x 1 = x 0A + V 1 = x 0A + V 1 = x 0A + V 1 = x 0A + V 1 = x 0A + V 1 = x
0A + V T… (1)
для объекта Q,
x 2 = x 0B + V 2 T… (2)
Теперь (2) – (2)
(2) – (2) – (2)
(2) – (2)
(2) – (2)
(2) – (2)
(2) – (2)
(2) – (2)
(2) – (2) получаем,
x 2 – x 1 = (x 0b – x 0a ) + (V 2 – V 1 ) T… (3)
4696966669669696966969696969696969696969696969696969. 0b – x 0a ) = x 0 , начальное смещение объекта Q относительно объекта P в момент t = 0, и (x 2 – x 1 ) = x, относительное смещение объекта Q по отношению к объекту P в момент времени t. Это соотношение (3) можно переписать в виде
0b – x 0a ) = x 0 , начальное смещение объекта Q относительно объекта P в момент t = 0, и (x 2 – x 1 ) = x, относительное смещение объекта Q по отношению к объекту P в момент времени t. Это соотношение (3) можно переписать в видеx = x 0 + (v 2 – v 1 )t
Таким образом, vQP = (v 2 – v 1 )
Разбиение векторов на компоненты
Мы поймем концепцию разбиения векторов на два компонента путем сложения векторов скорости и нахождения результирующего вектора скорости.
Давайте воспользуемся треугольным законом сложения векторов, рассмотрев пример вектора скорости:
Пловец плывет через реку, он целится прямо через реку, и река тянет его вниз по течению.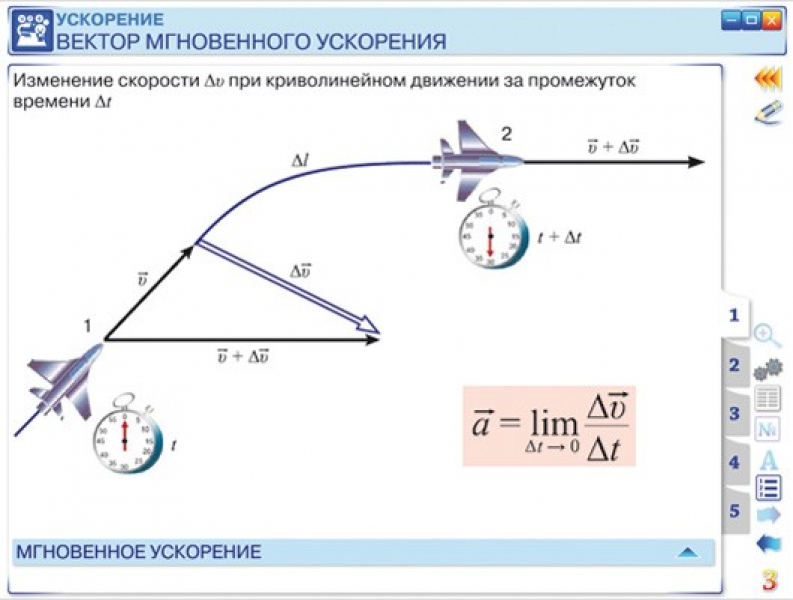


 Его единицей в Международной системе является 9.0003 секунда ( с )
Его единицей в Международной системе является 9.0003 секунда ( с )