Что такое вектор скорости: Вектор скорости | это… Что такое Вектор скорости?

Вектор скорости | это… Что такое Вектор скорости?

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Содержание 1 Скорость тела в механике 1.1 Мгновенная и средняя скорость 2 Преобразование скорости 3 Единицы измерения скорости 3. 1 Соотношение между единицами скорости 4 См. также

Скорость тела в механике

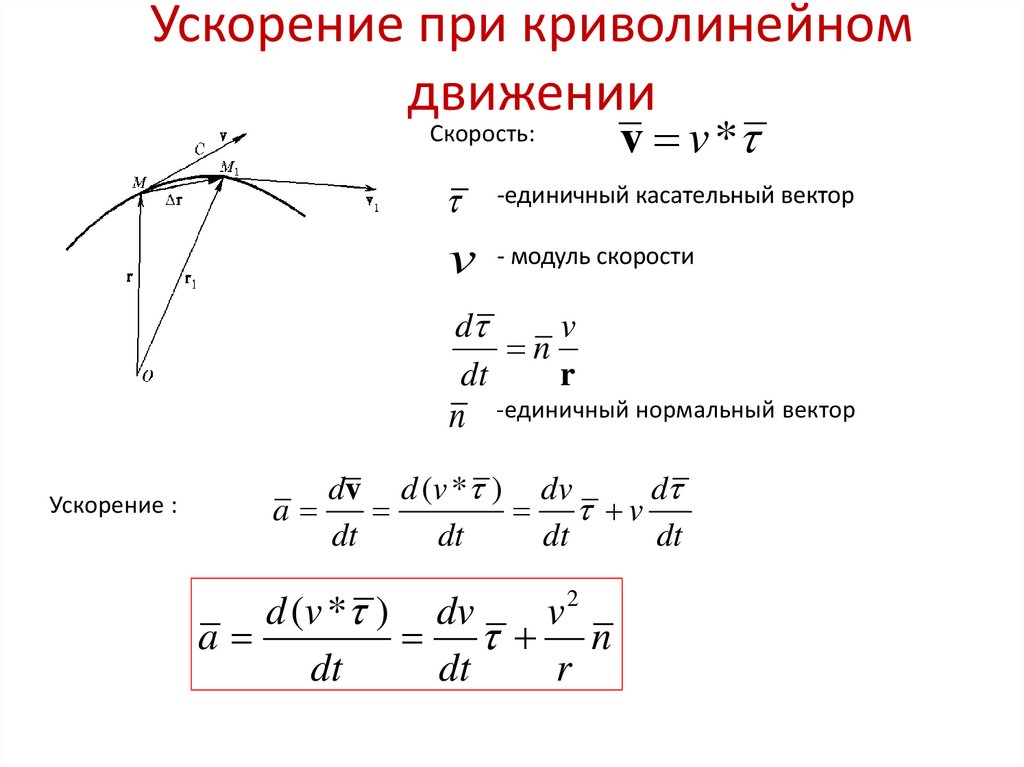
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь v — модуль скорости,  — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

Преобразование скорости

Основная статья: Теорема о сложении скоростей

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея.

Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

• Метр в секунду, (м/с), производная единица системы СИ
• Километр в час, (км/ч)
• узел (морская миля в час)
• Мах, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
• Скорость света в вакууме (обозначается c)

Соотношение между единицами скорости

• 1 м/с = 3,6 км/ч
• 1 узел = 1,852 км/ч = 0,514 м/c
• Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
• c = 299 792 458 м/c

См.

также

• Ускорение
• Годограф
• Крейсерская скорость
• Быстрота
• Скорость света
• Скорость звука
• Космическая скорость
• 1-я космическая скорость
• 2-я космическая скорость
• 3-я космическая скорость
• 4-я космическая скорость
• Скорость гравитации

Вектор скорости | это… Что такое Вектор скорости?

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т.

 д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Содержание 1 Скорость тела в механике 1.1 Мгновенная и средняя скорость 2 Преобразование скорости 3 Единицы измерения скорости 3.1 Соотношение между единицами скорости 4 См. также

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь v — модуль скорости,  — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Когда говорят о

средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

Преобразование скорости

Основная статья: Теорема о сложении скоростей

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

• Метр в секунду, (м/с), производная единица системы СИ
• Километр в час, (км/ч)
• узел (морская миля в час)
• Мах, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
• Скорость света в вакууме (обозначается c)

Соотношение между единицами скорости

• 1 м/с = 3,6 км/ч
• 1 узел = 1,852 км/ч = 0,514 м/c
• Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
• c = 299 792 458 м/c

См. также

• Ускорение
• Годограф
• Крейсерская скорость
• Быстрота
• Скорость света
• Скорость звука
• Космическая скорость
• 1-я космическая скорость
• 2-я космическая скорость
• 3-я космическая скорость
• 4-я космическая скорость
• Скорость гравитации

28.

2: Поле вектора скорости – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25564

• Питер Дурмашкин
• Массачусетский технологический институт через MIT OpenCourseWare

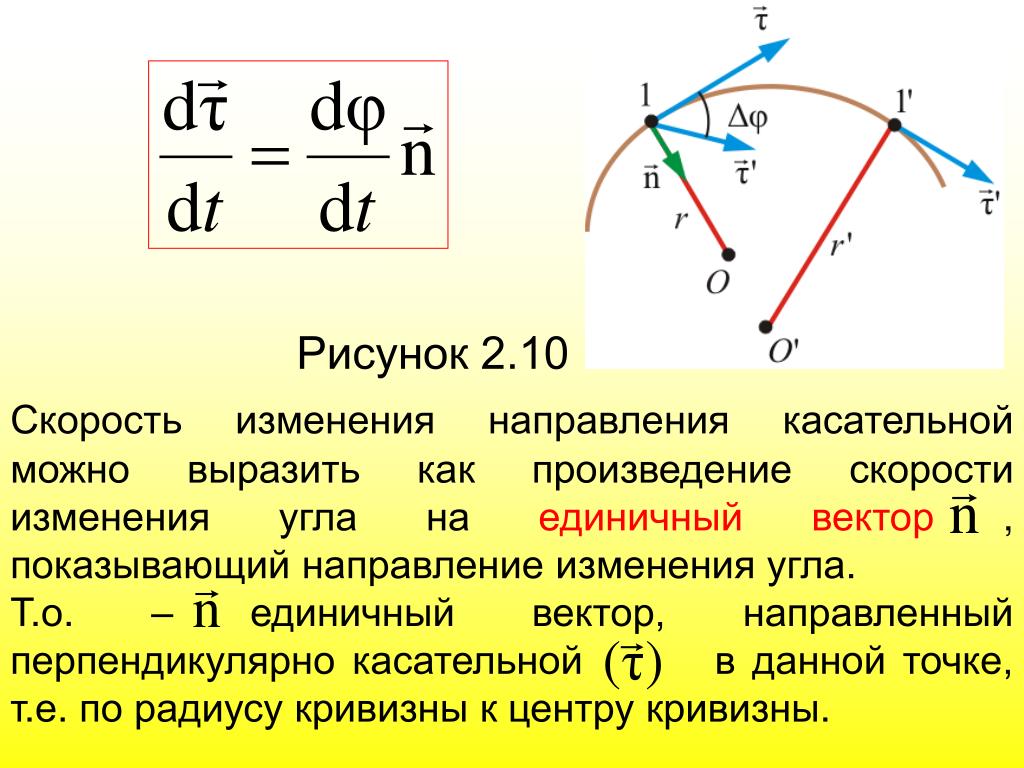
Когда мы описываем течение такой жидкости, как вода, мы можем думать о движении отдельных частиц. Эти частицы взаимодействуют друг с другом посредством сил. Затем мы могли бы применить наши законы движения к каждой отдельной частице в жидкости, но поскольку число частиц очень велико, это было бы чрезвычайно сложной вычислительной задачей. Вместо этого мы начнем с математического описания состояния движущейся жидкости, указав скорость жидкости в каждой точке пространства и в каждый момент времени. На данный момент мы выберем декартовы координаты и будем ссылаться на координаты точки в пространстве с помощью упорядоченной тройки (x, y, z) и переменной t для описания момента времени, но в принципе мы можем выбрать любую подходящую систему координат. подходит для описания движения. Распределение скоростей жидкости описывается векторной -функцией v(x, y,z,t) . Это представляет собой скорость жидкости в точке (x, y, z) в момент времени t. Величина v(x, y,z,t) называется векторным полем скоростей. Его можно представить в каждый момент времени как набор векторов, по одному для каждой точки пространства, направление и величина которых описывают направление и величину скорости жидкости в этой точке (рис. 28.1). Это описание векторного поля скорости жидкости относится к неподвижным точкам пространства, а не к движущимся частицам в жидкости.

Рис. 28.1: Векторное поле скорости течения жидкости в момент времени t

. Введем функции для давления P(x, y, z, t) и плотности \(\rho(x, y, z, t)\) жидкости, которые описывают давление и плотность жидкости в каждой точке пространства и в каждый момент времени. Эти функции называются скалярными полями, потому что существует только одно число с соответствующими единицами измерения, связанными с каждой точкой пространства в каждый момент времени.

Для полного описания векторного поля скоростей нам понадобятся три функции \(v_{x}(x, y, z, t), v_{y}(x, y, z, t), \text { и } v_ {z}(x, y, z, t)\) для описания компонент векторного поля скоростей.

\[\overrightarrow{\mathbf{v}}(x, y, z, t)=v_{x}(x, y, z, t) \hat{\mathbf{i}}+v_{y}( x, y, z, t) \hat{\mathbf{j}}+v_{z}(x, y, z, t) \hat{\mathbf{k}}\end{equation}

Три составляющие функции являются скалярными полями. Поле вектора скорости в общем случае достаточно сложно для трехмерного течения, зависящего от времени. Иногда мы можем сделать некоторые упрощающие предположения, которые позволяют нам моделировать сложный поток, например, моделируя поток как двумерный поток, или даже дополнительные предположения о том, что одна составляющая функция двумерного потока незначительна, что позволяет нам моделировать поток как одномерный. Для большинства течений поле скоростей меняется во времени. Для некоторых особых случаев мы можем моделировать течение, предполагая, что поле скоростей не изменяется во времени, случай, который мы будем называть стационарным течением,

\[\frac{\partial \overrightarrow{\mathbf{v}}(x, y, z, t)}{\partial t}=\overrightarrow{\mathbf{0}} \quad(\text { устойчивый поток }) \номер \]

Для стационарных течений поле скоростей не зависит от времени,

\[\overrightarrow{\mathbf{v}}(x, y, z)=v_{x}(x, y, z) \hat{\mathbf{i}}+v_{y}(x, y, z) \hat{\mathbf{j}}+v_{z}(x, y, z) \hat{\mathbf{k}} \quad(\text {установившийся поток}) \nonumber \]

Рис. 28.2: (а) траектория частицы 1, (б) траектория частицы 2

Проследим движение частиц в стационарной идеальной жидкости в течение последовательности интервалов длительностью \(\Delta t\) Рассмотрим частицу 1, расположенную в точке A с координатами \(\left(x_{A}, y_{A}, z_{A}\right)\). В момент \(t_{1}\) частица 1 имеет скорость \(\overrightarrow{\mathbf{v}}\left(x_{\mathrm{A}}, y_{\mathrm{A}}, z_{\ mathrm{A}}\right)=\overrightarrow{\mathbf{v}}(\mathrm{A})\).

За время \(\left[t_{1}, t_{2}\right], \text { где } t_{2}=t_{1}+\Delta t_{1}\) частица точка B, прибывающая туда в момент \(t_{2}\). В точке B частица теперь имеет скорость справа) = \ overrightarrow {\ mathbf {v}} (\ mathrm {B}) \). В течение следующего интервала \(\left[t_{2}, t_{3}\right], \text { где } t_{3}=t_{2}+\Delta t\) частица 1 переместится в точку C прибытие туда в момент \(t_{3}\), где он имеет скорость \(\overrightarrow{\mathbf{v}}\left(x_{\mathrm{c}}, y_{\mathrm{c}}, z_ {\ mathrm {c}} \ right) = \ overrightarrow {\ mathbf {v}} (\ mathrm {C}) \). (Рисунок 28.2(а)). Поскольку поток был принят стационарным, в момент \(t_{2}\) другая частица, частица 2, теперь находится в точке A, но имеет ту же скорость \(\overrightarrow{\mathbf{v} }\left(x_{\mathrm{A}}, y_{\mathrm{A}}, z_{\mathrm{A}}\right)\), так как частица 1 находилась в точке A и, следовательно, прибудет в точку B в конец следующего интервала в момент \(t_{3}\) (рис. 28.2(б)). Таким образом, каждая частица, лежащая на траектории, прочерченной во времени нашей первой частицей, будет следовать по той же траектории. Эта траектория называется линией тока. Частицы в жидкости не будут иметь одинаковых скоростей в точках вдоль линии тока, потому что мы не предполагали, что поле скоростей является однородным.

---

Эта страница под названием 28.2: Velocity Vector Field распространяется по незаявленной лицензии и была создана, изменена и/или курирована Петром Доурмашкиным (MIT OpenCourseWare) с помощью исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Петр Доурмашкин

   Версия лицензии

   4,0

   Программа OER или Publisher

   MIT OpenCourseWare

   Показать оглавление

   №

2. Теги

   1. источник@https://ocw. mit.edu/courses/8-01sc-classical-mechanics-fall-2016/

В чем разница между вектором положения и вектором скорости?

1. Вектор положения r простирается от начала координат к частице, а вектор скорости v указывает в направлении движения частицы . Другие переменные, подходящие для описания движущейся частицы, могут быть определены в терминах этих элементарных переменных.

Запрос на удаление

| Посмотреть полный ответ на sciencedirect.com

В чем разница между вектором и вектором положения?

Вектор положения говорит вам, где вы находитесь в точке пространства, тогда как вектор направления просто сообщает вам направление, в котором вы движетесь. Вектор направления также должен иметь единичную длину и представляет собой вектор положения, деленный на его абсолютное значение.

Запрос на удаление

| Посмотреть полный ответ на math. stackexchange.com

Положение и скорость одинаковы?

Скорость – это скорость и направление движения объекта. Другими словами, скорость — это скорость изменения положения объекта (где положение включает в себя направление, определяя, движется ли объект назад или вперед по линии, или движется вбок или вверх и вниз в двух или трех измерениях).

Запрос на удаление

| Посмотреть полный ответ на serpmedia.org

Как найти вектор положения из вектора скорости?

Для векторного исчисления мы делаем такое же определение. Пусть r(t) — дифференцируемая векторнозначная функция, представляющая вектор положения частицы в момент времени t. Тогда вектор скорости является производной вектора положения. v(t)=r′(t)=x′(t)ˆi+y′(t)ˆj+z′(t)ˆk.

Запрос на удаление

| Посмотреть полный ответ на math.libretexts.org

Какова связь между функцией положения и скоростью?

Если положение задается функцией p(x), то скорость — это первая производная этой функции, а ускорение — вторая производная. Используя дифференциальные уравнения со скоростью или ускорением, можно найти функции положения и скорости по известному ускорению.

Запрос на удаление

| Посмотреть полный ответ на Brightstorm.com

Векторы скорости (3) Нахождение вектора положения после времени t : ExamSolutions Maths Revision

Что такое вектор скорости?

Вектор скорости представляет скорость изменения положения объекта. Величина вектора скорости определяет скорость объекта, а направление вектора определяет его направление.

Запрос на удаление

| Посмотреть полный ответ на Brightstorm. com

Какова связь между графиком скорости и положения?

Наклон графика положения представляет собой скорость объекта. Таким образом, значение наклона в определенное время представляет собой скорость объекта в этот момент. Чтобы понять, почему, рассмотрим наклон позиции по сравнению с

Запрос на удаление

| Посмотреть полный ответ на khanacademy.org

Что такое вектор положения?

Вектор положения определяется как вектор, который символизирует либо положение, либо местоположение любой заданной точки относительно любой произвольной контрольной точки, такой как начало координат. Направление вектора положения всегда указывает от начала этого вектора к заданной точке.

Запрос на удаление

| Посмотреть полный ответ на byjus.com

Как найти вектор положения?

Векторы положения обычно начинаются в начале координат, а затем заканчиваются в любой другой произвольной точке.
…
Формула вектора положения

1. Формула для определения вектора положения от A до B: AB = (x _{k + 1} – x _k , y _{k + 5} 1 – у _к ).
2. Вектор положения AB относится к вектору, который начинается в точке A и заканчивается в точке B.

Запрос на удаление

| Посмотреть полный ответ на cuemath.com

Где находится вектор положения?

Во всех случаях линия от начала координат до точки называется вектором положения точки. По мере движения точки вектор положения изменяется как по величине, так и по направлению, и скорость точки определяется с точки зрения этих изменений.

Запрос на удаление

| Посмотреть полный ответ на britannica.com

Как найти скорость по положению?

Учитывая уравнение, которое моделирует положение объекта во времени, s ( t ) s (t) s (t), мы можем взять его производную, чтобы получить скорость, s ′ ( t ) = v ( t ) s ‘(t) = v (t) s′(t)=v(t). Затем мы можем подставить конкретное значение времени для расчета мгновенной скорости.

Запрос на удаление

| Посмотреть полный ответ на kristakingmath.com

Какая связь между положением, скоростью и ускорением?

Скорость – это скорость изменения положения во времени. Ускорение – это скорость изменения скорости во времени.

Запрос на удаление

| Посмотреть полный ответ на tesd.net

В чем разница между векторами положения и смещения?

Вектор положения — это трехмерный вектор, отображающий положение объекта в трех измерениях. Вектор смещения — это вектор, описывающий перемещение человека из одного места в другое. Перемещение объекта будем обозначать прямой линией из точки А в точку В.

Запрос на удаление

| Посмотреть полный ответ на unacademy.com

В чем разница между вектором положения и точкой?

Точка имеет положение в пространстве. Единственной характеристикой, отличающей одну точку от другой, является ее положение. Вектор имеет как величину, так и направление, но не имеет фиксированного положения в пространстве. Геометрически мы рисуем точки в виде точек и векторы в виде отрезков со стрелками.

Запрос на удаление

| Посмотреть полный ответ на ed.iitm.ac.in

Какая связь между вектором положения и перемещением?

Вектор положения задает положение известного тела. Знание положения тела имеет первостепенное значение, когда дело доходит до описания его движения. Однако изменение или изменение вектора положения является вектором смещения.

Запрос на удаление

| Посмотреть полный ответ на vedantu.com

Что такое вектор положения для двух точек?

Мы можем найти вектор между двумя точками, используя формулу  𝐴 𝐵 =  𝑂 𝐵 −  𝑂 𝐴 . Напомним, что компоненты вектора положения точки задаются координатами точки.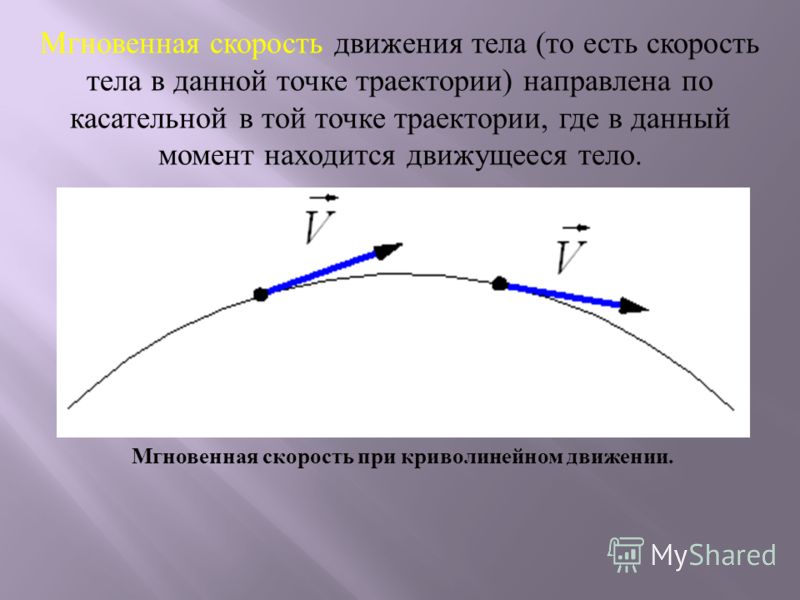 Другими словами, если 𝑃 является точкой ( 𝑥 , 𝑦 ) , то  𝑂 𝑃 = ( 𝑥 , 𝑦 ) .

Запрос на удаление

| Посмотреть полный ответ на nagwa.com

В чем разница между вектором положения и единичным вектором *?

Позиция является векторной величиной. Он имеет величину, а также направление. Величина векторной величины — это число (с единицами измерения), говорящее вам, какая часть величины существует, а направление говорит вам, в какую сторону оно указывает. Единичный вектор является указателем направления.

Запрос на удаление

| Посмотреть полный ответ на labman.phys.utk.edu

Что такое вектор положения в 3D?

Векторы положения в трехмерном пространстве по-прежнему представлены стрелками, которые начинаются в начале координат и заканчиваются в рассматриваемой точке. На диаграмме выше показана точка P, расположенная в переднем нижнем правом октанте. Три компонента вектора положения (P _x , P _y и P _z ) показаны на диаграмме.

Запрос на удаление

| Полный ответ см. на flexbooks.ck12.org

Как связаны смещение положения и скорость?

Смещение — это разница векторов между конечной и начальной позициями объекта. Оно может сильно отличаться от расстояния, пройденного объектом по пути. Скорость – это скорость, с которой перемещение изменяется во времени.

Запрос на удаление

| Посмотреть полный ответ на spiff.rit.edu

Можем ли мы определить и положение, и скорость электрона?

Принцип неопределенности Гейзенберга гласит, что точное положение и импульс электрона не могут быть определены одновременно. Это потому, что у электронов просто нет определенного положения и направления движения одновременно!

Запрос на удаление

| Полный ответ можно найти на en.