Краткий курс теоретической механики
Краткий курс теоретической механики
ОглавлениеПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V.  ПЛОСКАЯ СИСТЕМА СИЛ§ 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ § 32. СИЛОВОЕ ПОЛЕ.  § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50.  РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ§ 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64.  ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ§ 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Раздел третий. ДИНАМИКА ТОЧКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80.  ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ§ 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96.  ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНСГлава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110.  КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ§ 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ.  ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИГлава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX.  УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ§ 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ.  ЦЕНТР УДАРА |
8.3. Вектор скорости точки
Одной из кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Скорость точки – это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.
Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент временив положении(рис. 1.3), определяемом радиус-вектором, а в моментприходит в положение, определяемое вектором. Тогда перемещение точки за промежуток времениопределяется вектором, который будем называтьвектором перемещения точки.Этот вектор направлен по хорде, если точка движется криволинейно (рис. 1.3,а), и вдоль самой траектории, когда движение является прямолинейным (рис. 1.3,б).
Рисунок
1.
3
Из треугольника , видно, что, следовательно,
.
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени :
. | (7) |
Направлен вектор так же, как и вектор, т.е. при криволинейном движении вдоль хорды, в сторону движения точки, а при прямолинейном движении – вдоль самой траектории.
Очевидно, что чем меньше промежуток времени , тем величинабудет точнее характеризовать движение точки.
Поэтому скоростью точки
в данный момент времениназывается векторная величина,
к которой стремится скоростьпри
стремлении промежутка временик нулю.
.
Предел отношения припредставляет собой первую производную от векторапо аргументу и обозначается, тогда
. | (8) |
Итак, вектор скорости точки в данный момент времени равен первой производной от радиус-вектора точки по времени. Так как предельным направлением секущейявляется касательная, то вектор скорости в данный момент времени направлен по касательной к траектории точки в сторону движения.
Размерность скорости , т.е.. Единицы измерения.
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости.
Пусть в некоторый момент времени движущаяся
точка находится в положениии имеет скорость(рис.
1.4),
а в момент времениприходит
в точкуи
имеет
Рисунок 1.4
скорость . Тогда за промежуток временискорость изменится на. Для построения вектораотложим от точкивектор, равный, и построим параллелограмм, в котором диагональю будет, а одной из сторон. Тогда, очевидно,
вторая сторона и будет изображением вектора . Заметим, что векторвсегда направлен в сторону вогнутости траектории.
Отношение копределяет вектор среднего ускорения точки за промежуток времени.
. | (9) |
Вектор среднего ускорения имеет то же направление, что и вектор , т.е. направлен в сторону вогнутости траектории. Тогда
или с учетом равенства (8),
. | (10) |
Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.
Размерность , т.е.. Единица измерения.
Вектор направлен, также как и вектор, лежит в плоскости этой кривой и направлен в сторону её вогнутости.
Счет, математика и статистика – Набор академических навыков
Переменное ускорение с помощью векторов (механика)
Главное меню ContentsToggle 1 Ускорение частицы с помощью векторов 2 Рабочий пример 3 Интегрирование и дифференцирование 4 Рабочий пример
Ускорение частицы с помощью векторов
Ускорение показывает, как скорость, $\mathbf{v}$, изменяется со временем, $t$. Мы можем использовать соотношение $\mathbf{v} = \mathbf{u} + \mathbf{a}t$ для решения некоторых задач, где $\mathbf{u}$ обозначает начальную скорость.
2}, \\ & = \sqrt{19{-1} } \text{ (до 3s.f.)} \end{align}
Интегрирование и дифференцирование
Связь между перемещением, $\mathbf{r}$, скоростью, $\mathbf{v}$ и ускорение, $\mathbf{a}$ одинаково, когда величины представлены в виде векторов или скаляров.
Вектор $\mathbf{r}$ можно записать в виде \[\mathbf{r} = x\mathbf{i} + y\mathbf{j}.\] Где $\mathbf{i},\mathbf{ j}$ — орты в направлениях $x$ и $y$ соответственно.
93 – 4\справа)\mathbf{j}. \end{align}Видео: векторы ускорения | Nagwa
Стенограмма видео
В этом видео мы поговорим о векторах ускорения. Какие они, какая информация они показывают нам, и как вычислить их, зная скорость или перемещение.
Для начала представьте, что вы
пилотирование космического корабля через космическое пространство. Цель вашей миссии – приземлиться
и исследуйте пятую планету Галактон, до сих пор не посещаемую человечеством.
Но есть проблема. Из-за неожиданного сопротивления, как
ваш космический корабль покинул атмосферу Земли, он немного отстает от графика. Первоначальный план был для вас
космический корабль для перехвата Galactron 5 в заданной точке его круговой орбиты. Но теперь космический корабль должен будет
неожиданно ускориться, чтобы попасть в точку встречи.
Учитывая, что скорость Галактрон пять, скорость космического корабля и расстояние между текущее местоположение и предполагаемая точка встречи известны, каково ускорение 𝑎 Корабль должен иметь, чтобы встретить Галактрон 5 в назначенное время. расположение? Чтобы ответить на этот вопрос, нам понадобится узнать больше о векторах ускорения.
В целом объект ускоряется
всякий раз, когда он меняет скорость. Изменение скорости может включать
ускоряясь, оставаясь в том же направлении.
Вот что мы видим с 𝑣 one
собираюсь на 𝑣 два собираюсь на 𝑣 три. В этом случае мы ускоряемся до
право. Итак, наш вектор ускорения указывает
сюда. С другой стороны, мы могли бы иметь
постоянная скорость, скажем, как объект движется в равномерном круговом движении, но
направление постоянно меняется. Это также приводит к изменению
скорость, которая говорит нам, что происходит ускорение.
Вектор ускорения показывает, как
большая скорость меняется в зависимости от того, как долго это происходит. Учитывая эти два вектора 𝑎
один и 𝑎 два, 𝑎 два, потому что чем длиннее, тем больше изменение скорости
чем 𝑎 один. И вектор ускорения показывает
направление, в котором он указывает. Каждый из этих трех векторов 𝑎 один,
𝑎 два и 𝑎 три имеют одинаковую величину или длину, но они разные
вектора, потому что они направлены в разные стороны.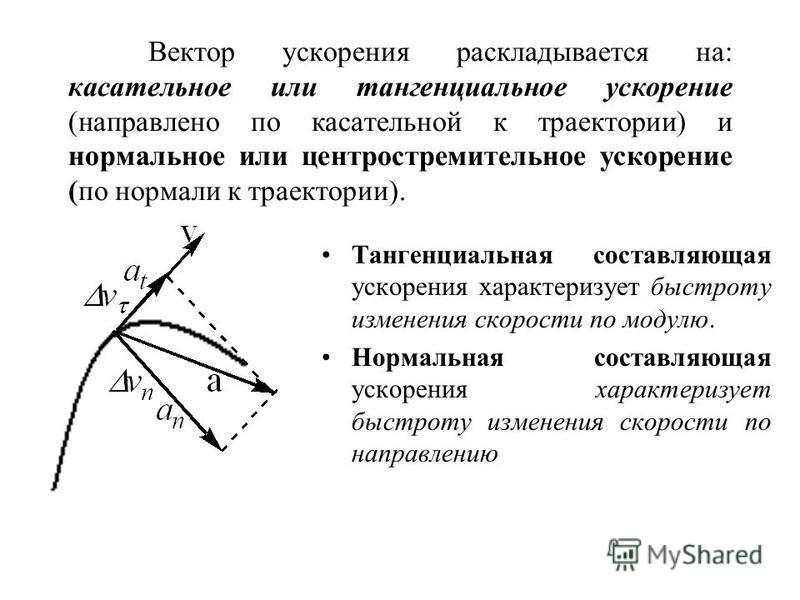
Мы сказали, что объект ускоряется всякий раз, когда он меняет скорость. Мы можем записать это математически как ускорение 𝑎 равно Δ𝑣, изменению скорости за время Δ𝑡, в течение которого происходит изменение скорости. На основе этой зависимости мы можем выразить ускорение двумя способами. В первом случае мы можем решить для среднее ускорение. То есть ускорение, которое происходит через какой-то промежуток времени. Мы назовем это 𝑡 саб 𝑓 минус 𝑡 суб 𝑖. скорости, которые соответствуют эти два момента времени мы называем 𝑣 суб 𝑓 и 𝑣 суб 𝑖. Разница между теми, кто над временной интервал – это среднее ускорение, которое испытывает объект.
С другой стороны, если бы мы
уменьшить этот временной интервал 𝑡 sub 𝑓 минус 𝑡 sub 𝑖 меньше и меньше и меньше,
в конце концов оно станет бесконечно малым, и мы придем к
мгновенное ускорение.
Это равно 𝑑𝑣 𝑑𝑡,
производная скорости по времени. Мгновенное ускорение говорит нам
ускорение объекта в определенный момент времени.
Глядя на эту связь для мгновенное ускорение, мы можем вспомнить, что это похоже на нашу зависимость для мгновенной скорости. Скорость объекта на одном момент времени равен производной по времени от его смещения 𝑥. Для этих трех величин ускорение, скорость и перемещение, то, что их связывает, это производные с уважение ко времени.
Можно сказать, что при заданном смещении
относительно времени, если мы хотим найти скорость или заданную скорость, и мы хотим
найти ускорение, то это производная по времени, которая позволяет
нам сделать этот переход. И идя в другом направлении,
если у нас есть ускорение и мы хотим решить для скорости или скорости и хотим решить для
смещение, это интеграл по времени, который помогает нам сделать это
шаг.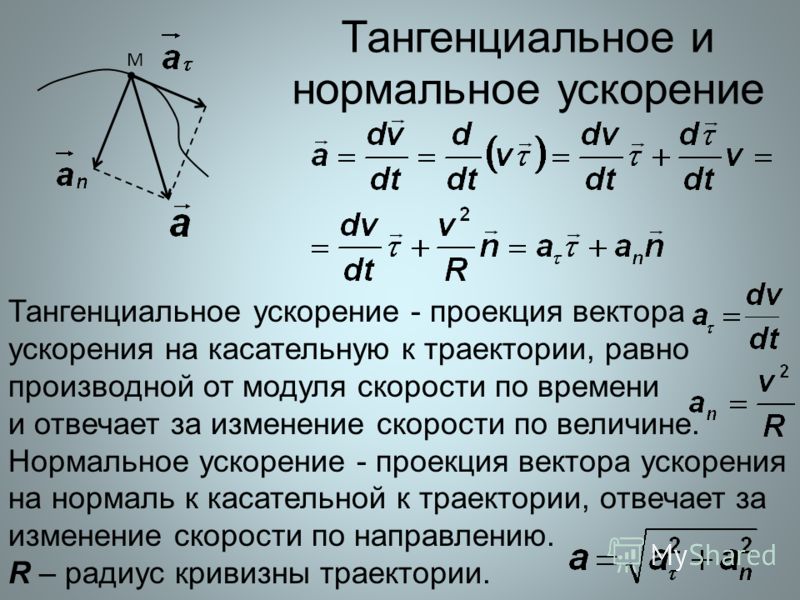
Теперь, когда мы немного узнали о
среднее и мгновенное ускорение, давайте попрактикуемся с этими понятиями
через несколько примеров.
Частица ускоряется равномерно. В момент времени 𝑡 равно 0,0 секунды, скорость частицы 𝑣 равна 14𝑖 плюс 22𝑗 метра в секунду. При 𝑡 равно 3,8 секунды, скорость частицы 𝑣 равна 0,0𝑖 плюс 11𝑗 метров в секунду. Какое ускорение у частица?
Так как мы решаем ускорение частицы за интервал времени от 𝑡 равно от 0,0 до 3,8 секунды, мы знаем, что ищем среднее ускорение. Чтобы начать наше решение, мы можем вспомните математическое соотношение для среднего ускорения. Среднее ускорение одного объект равен его конечной скорости минус его начальная скорость, деленная на время интервал, в течение которого происходит это изменение скорости.
В нашем случае мы могли бы написать, что
наше начальное время 𝑡 sub 𝑖 составляет 0,0 секунды.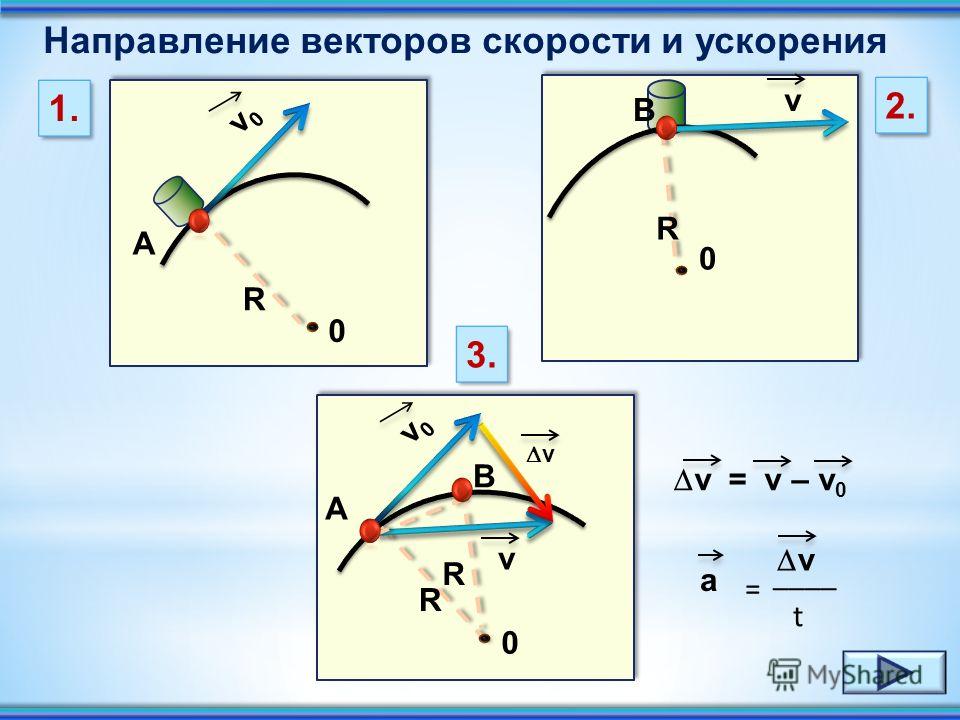
Наша начальная скорость 14𝑖 плюс
22 метра в секунду. И наше итоговое время 3,8 секунды,
и наша конечная скорость равна 0,0𝑖 плюс 11𝑗 метров в секунду. Если мы посчитаем разницу 𝑣
sub 𝑓 минус 𝑣 sub 𝑖, мы находим, поскольку рассматриваем эти векторы отдельно по их 𝑖
и 𝑗 компонентов, что в итоге мы получаем общий вектор отрицательного 14𝑖 минус 11𝑗
метров в секунду.
Итак, когда мы перейдем к расчету нашего среднее ускорение, у нас есть этот вектор как наш числитель, деленный на наше время разница 𝑡 sub 𝑓, 3,8 секунды, минус 𝑡 sub 𝑖, 0,0 секунды. Тогда наш общий временной интервал равен 3,8. секунды. И когда мы вычисляем это дробь, находим результат минус 3,7𝑖 минус 2,9𝑗 метра в секунду в квадрате. Это испытанное ускорение частицей за этот промежуток времени.
Теперь давайте рассмотрим пример, который
включает в себя расчет мгновенного ускорения.
Скорость частицы определяется выражением 𝑣 как функция 𝑡 равно 5,0𝑡𝑖 плюс 𝑡 в квадрате 𝑗 минус 2,0𝑡 в кубе 𝑘 метров в секунду. Чему равно ускорение частицы вектор в 𝑡 равен 2,0 секунды? Какова величина ускорение частицы в точке 𝑡 равно 2,0 секунды?
Так как нас просят решить для ускорение частицы в конкретный момент времени 2,0 секунды, мы знаем, что это мгновенное ускорение. Мы можем записать это время значение 2,0 секунды, а также функция скорости частицы 𝑣 от 𝑡. Мы будем использовать эту информацию частично один, чтобы решить для мгновенного ускорения и в части два, чтобы решить для величина этого мгновенного ускорения.
Мы можем начать решать
мгновенное ускорение, вспомнив математическое уравнение, которое объясняет, что
срок. Мгновенное ускорение
объекту, равно его изменению скорости, деленному на его изменение во времени,
в частности, производная по времени от его скорости как функция времени.
Мы можем написать, что наше ускорение
как функция времени равна производной скорости по времени.
Когда мы подключаемся к нашей скорости уравнение и возьмем эту производную по времени, находим, что она равна 5,0𝑖 плюс 2𝑡𝑗 минус 6,0𝑡 в квадрате 𝑘 метра в секунду в квадрате. Это наше обобщенное решение для ускорения. Но мы хотим решить для ускорение в конкретный момент времени, когда 𝑡 равно 2,0 секунды. Чтобы решить эту проблему, мы вставим это значение времени везде, где 𝑡 появляется в нашем общем уравнении ускорения. Когда мы вычисляем это значение, мы найдите его равным 5,0𝑖 плюс 4,0𝑗 минус 24𝑘 метра в секунду в квадрате. Это ускорение нашего объект, когда 𝑡 равно 2,0 секунды.
Теперь, когда мы знаем
ускорение в то время, мы хотим решить величину этого
ускорение. Эта величина, которая говорит нам, как
насколько изменится скорость частицы в момент времени 2,0 секунды, составляет
равно квадратному корню из квадрата 𝑥-компоненты ускорения плюс ее
𝑦-компонента в квадрате плюс ее 𝑧-компонента в квадрате.
Когда мы смотрим на нашу мгновенную выражение ускорения для этих компонент, находим 𝑥-компоненту 5,0, 𝑦-компонента равна 4,0, а 𝑧-компонента равна 24. Когда мы вводим это выражение на наш калькулятор, мы находим, что с точностью до трех значащих цифр это 24,8 метра в секунду. вторая в квадрате. Это величина ускорение частицы, когда 𝑡 равно 2,0 секунды.
Теперь давайте уделим немного времени обобщить то, что мы узнали о векторах ускорения. Мы видели, что объект ускоряется всякий раз, когда он меняет скорость. То есть всякий раз, когда его скорость или его меняется направление. Мы также видели, что на основе математическое определение ускорения, мы можем записать выражения для среднего как также мгновенное ускорение.
Среднее ускорение равно
конечная скорость минус начальная скорость, деленная на интервал времени, в течение которого
это изменение происходит.