Центр масс в физике это: Ошибка 403 — доступ запрещён

Центр масс | это… Что такое Центр масс?

У этого термина существуют и другие значения, см. Центр тяжести (значения).

Центр масс, центр ине́рции, барице́нтр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр) — (в механике) геометрическая точка, характеризующая движение тела или системы частиц как целого. Не следует путать с центром тяжести.

Содержание 1 Определение 2 Центры масс однородных фигур 3 В механике 3.1 Центр масс в релятивистской механике 4 Центр тяжести 5 См. также

Определение

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

Для случая непрерывного распределения масс:

где:

 — суммарная масса системы,

 — объём,

 — плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Центры масс однородных фигур

• У отрезка — середина.
• У многоугольников (как сплошных плоских фигур, так и каркасов):
  • У параллелограмма — пересечение диагоналей.
  • У треугольника — точка пересечения медиан (центроид).
• У правильного многоугольника — центр поворотной симметрии.

В механике

Понятие центра масс широко используется в физике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

Центр масс в релятивистской механике

В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия

центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:

где

 — радиус-вектор центра масс,

 — радиус-вектор i-й частицы системы,

 — полная энергия i-й частицы.

Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лившица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (center-of-mass). Оба термина эквивалентны.

Скорость центра масс в релятивистской механике можно найти по формуле:

Центр тяжести

Центр масс тела не следует путать с центром тяжести!

Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.

В постоянном параллельном (однородном) гравитационном поле центр тяжести всегда совпадает с центром масс. Поэтому на практике эти два центра почти совпадают (так как внешнее гравитационное поле в некосмических задачах может считаться постоянным в пределах объёма тела).

По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (так как реального гравитационного поля нет и не имеет смысла учёт его неоднородности). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.

См. также

• Классическая механика
• Теоретическая механика
• Неваляшка

Центр масс | это… Что такое Центр масс?

У этого термина существуют и другие значения, см. Центр тяжести (значения).

Центр масс, центр ине́рции, барице́нтр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр) — (в механике) геометрическая точка, характеризующая движение тела или системы частиц как целого. Не следует путать с центром тяжести.

Содержание 1 Определение 2 Центры масс однородных фигур 3 В механике 3.1 Центр масс в релятивистской механике 4 Центр тяжести 5 См. также

Определение

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

Для случая непрерывного распределения масс:

где:

 — суммарная масса системы,

 — объём,

 — плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

Центры масс однородных фигур

• У отрезка — середина.
• У многоугольников (как сплошных плоских фигур, так и каркасов):
  • У параллелограмма — пересечение диагоналей.
  • У треугольника — точка пересечения медиан (центроид).
• У правильного многоугольника — центр поворотной симметрии.

В механике

Понятие центра масс широко используется в физике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

Центр масс в релятивистской механике

В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия

центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:

где

 — радиус-вектор центра масс,

 — радиус-вектор i-й частицы системы,

 — полная энергия i-й частицы.

Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лившица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (center-of-mass). Оба термина эквивалентны.

Скорость центра масс в релятивистской механике можно найти по формуле:

Центр тяжести

Центр масс тела не следует путать с центром тяжести!

Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.

В постоянном параллельном (однородном) гравитационном поле центр тяжести всегда совпадает с центром масс. Поэтому на практике эти два центра почти совпадают (так как внешнее гравитационное поле в некосмических задачах может считаться постоянным в пределах объёма тела).

По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (так как реального гравитационного поля нет и не имеет смысла учёт его неоднородности). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.

См. также

• Классическая механика
• Теоретическая механика
• Неваляшка

Центр масс

Центр масс

Термины «центр масс» и «центр тяжести» используются как синонимы в однородном гравитационном поле для представления уникальной точки в объекте или системе, которую можно использовать для описания реакции системы на внешние силы и крутящие моменты. Понятие центра масс – это среднее значение масс, с учетом их расстояний от точки отсчета. В одной плоскости это похоже на балансировку качелей вокруг точки вращения относительно создаваемых крутящих моментов. Если вы проводите измерения от точки центра масс для двухмассовой системы, то состояние центра масс можно выразить как где r 1 и r 2 определяют массы. Центр масс лежит на линии, соединяющей две массы. Центр масс для Сбор точечных масс Непрерывное распределение массы Определение центра масс протяженного объекта

Индекс Концепции крутящего момента

Гиперфизика***** Механика ***** Вращение R Ступица

Назад

Центр масс — это точка, в которой можно считать, что вся масса «сконцентрирована» для целей расчета «первого момента», т. е. массы, умноженной на расстояние. Для двух масс это расстояние вычисляется из Для более общего набора N частиц это становится и при расширении до трех измерений: Этот подход применяется к дискретным массам, даже если они не являются точечными массами, если положение x i принимается за положение центра масс i -й массы. Это также указывает путь к вычислению центра масс протяженного объекта.

Индекс Концепции крутящего момента

Гиперфизика***** Механика ***** Вращение R Ступица

Назад

Для непрерывного распределения массы выражение для центра масс набора частиц: становится бесконечной суммой и выражается в виде интеграла В случае однородного стержня это становится Этот пример однородного стержня демонстрирует некоторые общие черты процесса нахождения центра масс сплошного тела. Для непрерывного распределения массы требуются методы исчисления, включающие интеграл по массе объекта. Такие интегралы обычно преобразуются в пространственные интегралы путем связывания массы с расстоянием, как в случае с линейной плотностью M/L стержня. Использование симметрии может дать много информации: например, центр масс будет находиться на любой оси вращательной симметрии. Использование симметрии скажет вам, что центр масс находится в геометрическом центре стержня без расчета.

Индекс Концепции крутящего момента

Гиперфизика***** Механика ***** Вращение R Ступица

Назад

10.3: Центр масс

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

19431

• Howard Martin пересмотрено Аланом Нг
• University of Wisconsin-Madison

  22

2

В этом разделе мы покажем, как обобщить второй закон Ньютона, чтобы он мог описывать движение объекта, не являющегося точечной частицей. Любой объект можно описать как состоящий из точечных частиц; например, эти частицы могут быть атомами, из которых состоит обычная материя. Таким образом, мы можем использовать ту же терминологию, что и в предыдущих разделах, для описания сложного объекта как «системы», состоящей из множества точечных частиц, которые сами описываются вторым законом Ньютона. Система может быть жестким объектом, в котором точечные частицы не могут двигаться относительно друг друга, например, атомы в твердом теле ¹ . Или система может быть газом, состоящим из множества движущихся атомов, или она может быть комбинацией множества движущихся твердых тел.

В предыдущем разделе мы видели, как можно использовать полный импульс и полную механическую энергию системы для описания системы в целом. В этом разделе мы определим центр масс, что позволит нам описать положение системы в целом.

Рассмотрим систему, состоящую из \(N\) точечных частиц. Каждая точечная частица \(i\) массы \(m_i\) может быть описана вектором положения \(\vec r_i\), вектором скорости \(\vec v_i\) и вектором ускорения, \(\vec a_i\) относительно некоторой системы координат в инерциальной системе отсчета.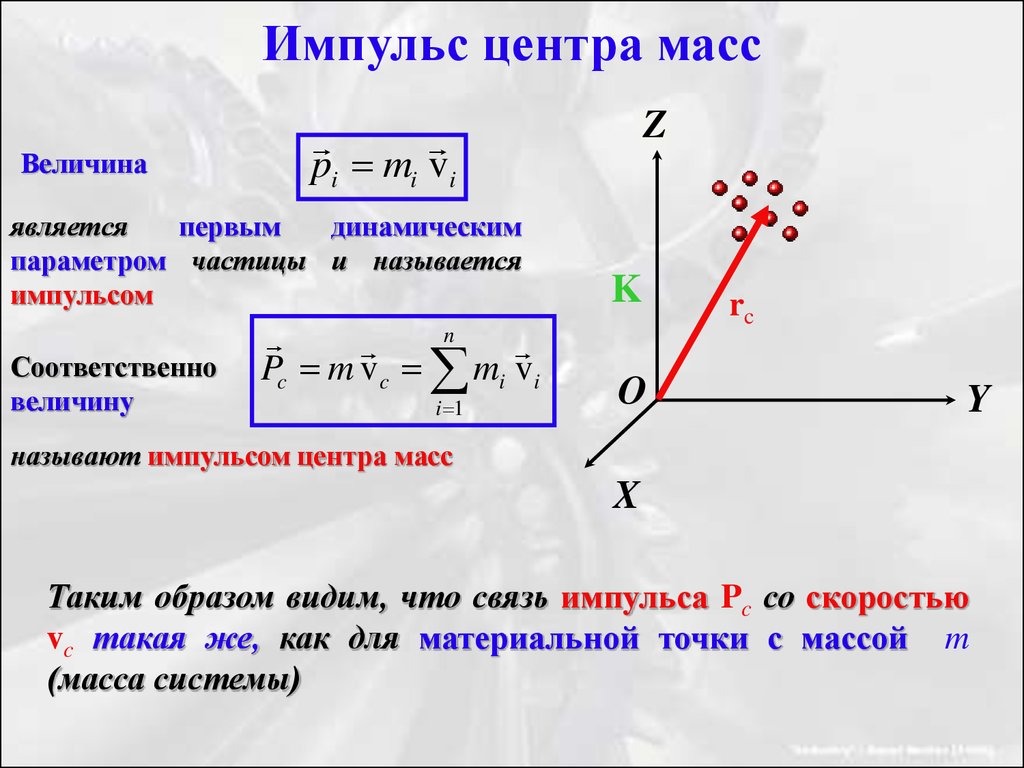 Второй закон Ньютона можно применить к любой из частиц в системе:

\[\begin{выровнено} \sum_k \vec F_{ik} = m_i \vec a_i\end{выровнено}\]

, где \(\vec F_{ik}\) – k-я сила, действующая на частицу \(i\). Мы можем записать второй закон Ньютона один раз для каждой из \(N\) частиц и суммировать эти \(N\) уравнения вместе:

\[\begin{align} \sum_k \vec F_{1k} + \sum_k \vec F_{2k} + \sum_k \vec F_{3k} +\dots &= m_1\vec a_1 + m_2 \vec a_2 + m_3 \vec a_3 + \dots\\ \sum \vec F = \sum_i m_i \vec a_i \end{выровнено}\]

, где сумма слева представляет собой сумму всех сил, действующих на все частицы в системе 9{ext}=M\vec a_{CM}\]

, где \(M\) — полная масса системы, а сумма сил — это сумма только внешних сил, действующих на систему.

Хотя мы формально вывели второй закон Ньютона для системы частиц, на самом деле мы использовали этот результат на протяжении всего текста. Например, когда мы моделировали блок, скользящий по склону, мы никогда не беспокоились о том, что блок состоит из множества атомов, взаимодействующих друг с другом и с окружающей средой. Вместо этого мы учитывали только внешние силы, воздействующие на блок, а именно нормальную силу от наклона, любые силы трения и общий вес объекта (силу гравитации). Технически сила тяжести действует не на блок в целом, а на каждый из атомов. Однако, если суммировать силу тяжести, действующую на каждый атом: \[\begin{aligned} m_1\vec g+ m_2 \vec g + m_3\vec g + \dots = (m_1+m_2+m_3+\dots)\vec g = M\vec g\end{aligned}\] мы обнаруживаем, что его можно смоделировать, рассматривая блок как единую частицу массы \(M\), на которую действует гравитация. Центр масс иногда называют «центром тяжести», потому что он соответствует месту, где мы можем смоделировать общую силу гравитации \(M\vec g\) как действующую . Когда мы применили второй закон Ньютона к блоку, мы описали движение блока в целом (а не движение отдельных атомов). В частности, мы смоделировали движение центра масс блока.

Положение центра масс представляет собой векторное уравнение, верное для каждой координаты: \[\begin{aligned} \vec r_{CM} &=\frac{1}{M}\sum_i m_i\vec r_i\nonumber \\ \следовательно, x_{CM} &= \frac{1}{M}\sum_i m_i x_i\nonumber\\ \следовательно, y_{CM} &= \frac{1}{M}\sum_i m_i y_i\nonumber\\ \поэтому z_{CM} &= \frac{1}{M}\sum_i m_i z_i\end{aligned}\] Центр масс в том, что положение в системе, описываемое вторым законом Ньютона, когда он применяется к системе в целом . Центр масс можно рассматривать как среднее положение системы (это среднее значение положений частиц в системе, взвешенное по их массе). Описывая положение центра масс, нас беспокоят не подробные положения всех частиц в системе, а только среднее положение системы в целом. Другими словами, это эквивалентно рассмотрению всей системы как одной частицы массы \(М\), находящейся в положении центра масс.

Рассмотрим, например, человека, бросающего гантель, состоящую из двух сферических масс, соединенных стержнем, как показано на рисунке \(\PageIndex{1}\). Гантель будет сложно вращаться по мере движения в воздухе. Однако центр масс гантели будет двигаться по параболической траектории (движение снаряда), потому что единственная внешняя сила, действующая на гантель во время ее траектории, — это гравитация.

Рисунок \(\PageIndex{1}\): Движение центра масс гантели описывается вторым законом Ньютона, даже если движение вращающейся гантели является более сложным.

Если взять производную по времени от положения центра масс, то получим скорость центра масс и ее составляющие, которые позволяют описать, как движется система в целом:

\[\begin{align} \vec v_{CM} = \frac{d}{dt}\vec r_{CM}=\frac{1}{M}\sum_{i} m_{i}\frac{ d}{dt}\vec r_{i}=\frac{1}{m}\sum_{i} m_{i}\vec v_{i}\end{aligned}\]

\[\поэтому v_{CM_{x}}=\frac{1}{M}\sum_{i}m_{i}v_{i_{x}}\]

\[\поэтому v_{CM_{y}}=\frac{1}{M}\sum_{i}m_{i}v_{i_{y}}\]

\[\поэтому v_{CM_{z}}=\frac{1}{M}\sum_{i}m_{i}v_{i_{z}}\]

Обратите внимание, что это та же самая скорость, которую мы нашли ранее для скорости центра масс системы отсчета. В системе центра масс полный импульс системы равен нулю. Это имеет смысл, потому что центр масс представляет собой среднее положение системы; если мы движемся «вместе с системой», то кажется, что система имеет нулевой импульс.

Мы также можем определить полный импульс системы \(\vec P\) через полную массу \(M\) системы и скорость центра масс: 9{расш}\конец{выровнено}\]

, и снова мы видим, что полный импульс системы сохраняется, если результирующая внешняя сила, действующая на систему, равна нулю. Другими словами, центр масс системы будет двигаться с постоянной скоростью при сохранении количества движения.

Наконец, мы также можем определить ускорение центра масс, взяв производную скорости по времени:

\[\begin{align} \vec a_{CM}=\frac{d}{dt}\vec v_{CM}=\frac{1}{M}\sum_{i}m_{i}\frac{ d}{dt}\vec v_{i} = \frac{1}{M}\sum_{i}m_{i}\vec a_{i}\end{aligned}\]

\[\поэтому a_{CM_{x}}=\frac{1}{M}\sum_{i}m_{i}a_{i_{x}}\]

\[\поэтому a_{CM_{y}}=\frac{1}{M}\sum_{i}m_{i}a_{i_{y}}\]

\[\поэтому a_{CM_{z}}=\frac{1}{M}\sum_{i}m_{i}a_{i_{z}}\]

Пример \(\PageIndex{1}\)

Рисунок \(\PageIndex{2}\): сизигия между Солнцем, Землей и Марсом. {30}\text{kg}\)), Земля (масса \(M_E=5,9{23}\text{kg}\)) выстроены в ряд, как показано на рисунке \(\PageIndex{2}\). На каком расстоянии от центра Солнца находится центр масс системы Солнце, Земля, Марс во время сизигии?

Решение :

Поскольку это одномерная задача, мы можем определить ось \(x\), которая коллинеарна трем телам, и найти только координату \(x\) положения центра масс. Мы свободны в выборе начала системы координат, поэтому мы выбираем начало координат в центре Солнца. Таким образом, положение центра масс по оси \(х\) будет прямо соответствовать его расстоянию от центра Солнца. 9{5}\text{m}\end{aligned}\] Центр масс системы Солнце-Земля-Марс во время сизигии находится примерно в \(500\text{км}\) от центра Солнца.

Обсуждение:

Радиус Солнца приблизительно равен \(700000\text{км}\), поэтому центр масс системы находится глубоко внутри Солнца. Солнце настолько массивнее, чем Земля или Марс, что две планеты едва ли способствуют смещению центра масс от центра Солнца. Обычно мы считали бы массы двух планет пренебрежимо малыми, если бы хотели смоделировать, как сама Солнечная система движется вокруг галактики Млечный Путь.

Пример \(\PageIndex{2}\)

Рисунок \(\PageIndex{3}\): Три человека на плотах на озере.

Алиса (масса \(m_A\)), Брайс (масса \(m_B\)) и (масса \(m_C\)) брошены на отдельные плоты незначительной массы в озере у побережья Ньона. Плоты расположены в углах прямоугольного треугольника, как показано на рисунке \(\PageIndex{3}\), и соединены веревками. Расстояние между Алисой и Брайсом равно \(r_{AB}\), а расстояние между Алисой и равно \(r_{AC}\), как показано на рисунке. Алиса решает потянуть за веревку, которая соединяет ее с , а Брайс решает потянуть за веревку, которая соединяет его с Алисой. Где встретятся три плота?

Решение :

Мы рассматриваем систему, состоящую из трех человек и их плотов, и моделируем каждого человека и их плот как точечную частицу с массой, сосредоточенной в центре плота. Силы, возникающие при натяжении веревок, являются внутренними силами (одна частица действует на другую) и, таким образом, не будут влиять на движение центра масс системы. На систему не действуют чистые внешние силы (силы тяжести уравновешиваются силами плавучести плотов). Центр масс системы не перемещается, когда люди тянут веревки, поэтому в конечном итоге они должны встретиться в центре масс.

Мы можем определить систему координат так, чтобы начало координат было расположено там, где изначально находилась Алиса, ось \(x\) была направлена ​​от Алисы к Брайсу, а ось \(y\) была направлена ​​от Алисы к Хлое. Начальные позиции Алисы, Брайса и таковы: \[\begin{aligned} \vec r_A &= 0\hat x + 0\hat y\\ \vec r_B &= r_{AB}\hat x + 0\ шляпа y\\ \vec r_C &= 0\hat x + r_{AC}\hat y\end{aligned}\] соответственно. Таким образом, \(x\) и \(y\) координаты центра масс: \[\begin{aligned} x_{CM} &= \frac{1}{M}\sum_i m_i x_i = \frac{ m_A(0) + m_Br_{AB} + m_C(0)}{m_A + m_B + m_C}=\left(\frac{m_B}{m_A + m_B + m_C}\right)r_{AB}\\ y_{CM } &= \frac{1}{M}\sum_i m_i y_i = \frac{m_A(0) + m_B(0) + m_Cr_{AC}}{m_A + m_B + m_C}=\left(\frac{m_C} {m_A + m_B + m_C}\right)r_{AC}\\\end{aligned}\], что соответствует положению, в котором три плота встретятся, относительно исходного положения Алисы.

Обсуждение:

Используя центр масс, мы легко нашли, где должны встретиться три плота. Если бы мы использовали второй закон Ньютона для трех плотов по отдельности, модель была бы усложнена тем фактом, что силы, действующие Алисой и Брайсом на веревки, меняют направление, когда плоты начинают двигаться, что потребовало бы использования интегралов. определить движение каждого человека.

Центр масс непрерывного объекта

До сих пор мы рассматривали центр масс системы, состоящей из точечных частиц. В этом разделе мы покажем, как можно определить центр масс для «непрерывного объекта» ⁵ . Ранее мы утверждали, что если объект однороден и симметричен, его центр масс будет расположен в центре объекта. Покажем это в явном виде для однородного стержня полной массы \(M\) и длины \(L\), как показано на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Стержень длины \(L\) и массы \(M\).

Чтобы определить центр масс стержня, мы сначала смоделируем стержень как состоящий из \(N\) небольших «массовых элементов», каждый из которых имеет одинаковую массу \(\Delta m\) и длину \( \Delta x\), как показано на рисунке \(\PageIndex{4}\). Если мы выберем эти элементы массы достаточно маленькими, мы можем смоделировать их как точечные частицы и использовать те же формулы, что и выше, для определения центра масс стержня.

Определим ось \(x\) как коллинеарную стержню, так что начало координат находится на одном конце стержня. Мы можем определить «линейную массовую плотность» стержня \(\lambda\) как массу на единицу длины стержня: \[\begin{aligned} \lambda = \frac{M}{L}.\ конец {выровнено}\] 92\\ &=\frac{1}{2}L\end{aligned}\], где мы подставили определение \(\lambda\) обратно, чтобы найти, как и ожидалось, что центр масс стержня половину своей длины от одного из концов.

Предположим, что стержень не является однородным и что его линейная плотность зависит от положения \(x\) вдоль стержня: \[\begin{aligned} \lambda(x) = 2a + 3bx\end{aligned}\ ]

Мы все еще можем найти центр масс, рассматривая бесконечно малый элемент массы с массой \(dm\) и длиной \(dx\). С точки зрения линейной плотности массы и длины элемента массы, \(dx\), масса \(dm\) определяется как: \[\begin{aligned} dm = \lambda(x) dx\end{aligned }\] Таким образом, положение \(x\) центра масс находится так же, как и раньше, за исключением того, что линейная плотность массы теперь является функцией \(x\): \[\begin{aligned} x_{ CM} &= \frac{1}{M} \int_0^L \lambda(x) x dx =\frac{1}{M} \int_0^L (2a + 3bx) x dx=\frac{1}{ M} \int_0^L (2ax + 3bx^2) dx\\ &=\frac{1}{M} \left[ ax^2 + bx^3 \right]_0^L\\ &=\frac{1 }{M} (aL^2 + bL^3)\end{выровнено}\]

В общем, для непрерывного объекта положение центра масс определяется как:

\[\begin{aligned} \vec r_{CM}=\frac{1}{M}\int \vec r dm\end{aligned}\]

\[\следовательно x_{CM}=\frac{1}{M}\int xdm\]

\[\следовательно y_{CM}=\frac{1}{M }\int ydm\]

\[\следовательно z_{CM}=\frac{1}{M}\int zdm\]

где вообще нужно будет писать \(dm\) в терминах чего-то это зависит от положения (или константы), так что интегралы могут быть вычислены по пространственным координатам (\(x\),\(y\),\(z\)) по диапазону, описывающему объект. Выше мы написали \(dm = \lambda dx\), чтобы выразить элемент массы в терминах пространственных координат.

Пример \(\PageIndex{3}\)

Рисунок \(\PageIndex{5}\): Симметричная чаша с параболическими сторонами полностью заполнена водой. Чаша имеет высоту \(h\).

Чаша высотой \(h\) имеет параболические стороны и круглое поперечное сечение, как показано на рисунке \(\PageIndex{5}\). Чаша наполнена водой. Сама чаша имеет ничтожную массу и толщину, так что в массе полной чаши преобладает масса воды. Где находится центр масс полной чаши?

Решение :

Мы можем определить систему координат так, чтобы начало координат находилось на дне чаши, а ось \(z\) соответствовала оси симметрии чаши. Поскольку чаша наполнена водой, а сама чаша имеет незначительную массу, мы можем смоделировать полную чашу как однородный водоем той же формы, что и чаша, и (объемную) массовую плотность \(\rho\), равную плотность воды. Кроме того, по симметрии центр масс чаши будет находиться на оси \(z\).

Поскольку чаша имеет круглое поперечное сечение, мы можем разделить ее на дискообразные элементы массы \(dm\), которые имеют бесконечно малую высоту \(dz\) и радиус \(r(z )\), что зависит от их координаты \(z\) (рисунок \(\PageIndex{5}\)).

Рисунок \(\PageIndex{6}\): Параболическая чаша, разделенная на дискообразные элементы массы \(dm\), которые имеют бесконечно малую высоту \(dz\) и радиус \(r(z )\), что зависит от их координаты \(z\).

Центр масс каждого элемента массы в форме диска будет расположен там, где соответствующий диск пересекает ось \(z\). Масса одного элемента диска определяется как: 93=\frac{2}{3}h\end{aligned}\] Независимо от фактической формы параболы (параметр \(a\)), центр масс всегда будет на две трети пути вверх от дно чаши.

Обсуждение:

При определении центра масс трехмерного объекта мы использовали симметрию, чтобы доказать, что координаты \(x\) и \(y\) равны нулю. Затем мы нашли положение \(z\) центра масс, разделив чашу на бесконечно малые элементы массы (диски) вдоль направления, в котором нам нужно было найти координату центра масс.

Упражнение \(\PageIndex{1}\)

Верно или неверно: центр масс непрерывного объекта всегда находится внутри объекта.

1. Правда
2. Ложь

Ответить

Сноски

1. В действительности даже атомы в твердом теле могут двигаться относительно друг друга, но они не перемещаются на большие величины по сравнению с объектом.

2. Снова суммируем силы, действующие на разных частиц.

3. Напомним, внутренние силы — это те силы, с которыми частицы в системе действуют друг на друга. Из-за третьего закона Ньютона их сумма будет равна нулю.

4. Технически члены в производных равны только в пределах двух констант интегрирования, \(\vec r_{CM} =\frac{1}{M}\sum_i m_i\vec r_i + at + b\) , который мы можем установить равным нулю.

5. В действительности, конечно, непрерывных объектов не существует, поскольку на атомном уровне все состоит из частиц.