Центробежный момент инерции формула: Момент инерции формула (сопромат)

Главные оси инерции и главные моменты инерции (Лекция №18)

   Как уже известно, зная для данной фигуры центральные моменты инерции , и , можно вычислить момент инерции и относительно любой другой оси.

   При этом можно за основную систему осей принять такую систему, при которой формулы существенно упрощаются. Именно, можно найти систему координатных осей, для которых центробежный момент инерции равен.нулю. В самом деле, моменты инерции и всегда положительны, как суммы положительных слагаемых, центробежный же момент

может быть и положительным и отрицательным, так как слагаемые zydF могут быть разного знака в зависимости от знаков z и у для той или иной площадки. Значит, он может быть равен нулю.

   Оси, относительно которых центробежный момент инерции обращается в нуль, называются главными осями инерции. Если начало такой системы помещено в центре тяжести фигуры, то это будут главные центральные оси.

Эти оси мы будем обозначать и ; для них

Найдем, под каким углом наклонены к центральным осям у и z (фиг. 198) главные оси.

Рис.1. Расчетная модель для определения положения главных осей инерции.

 

   В известном выражении для перехода от осей yz к осям , для центробежного момента инерции дадим углу значение ; тогда оси и , совпадут c главными, и центробежный момент инерции будет равен нулю:

или

откуда:

(1)

   Этому уравнению удовлетворяют два значения , отличающиеся на 180°, или два значения , отличающиеся на 90°. Таким образом, это уравнение дает нам положение

двух осей, составляющих между собой прямой угол. Это и будут главные центральные оси и , для которых .

   Пользуясь этой формулой, можно по известным , и получить формулы для главных моментов инерции и . Для этого опять воспользуемся выражениями для осевых моментов инерции общего положения. Они определяют значения и если вместо подставить

(2)

   Полученными соотношениями можно пользоваться при решении задач. Одним из главных моментов инерции является , другим .

   Формулы (2) можно преобразовать к виду, свободному от значения . Выражая и через и подставляя их значения в первую формулу (2), получим, делая одновременно замену из формулы (1):

Заменяя здесь из формулы (1) дробь на

получаем

(3)

   К этому же выражению можно прийти, делая подобное же преобразование второй формулы (3).

   За основную систему центральных осей, от которых можно переходить к любой другой, можно взять не

Оу и Oz, а главные оси и ; тогда в формулах не будет фигурировать центробежный момент инерции (). Обозначим угол, составленный осью , (Рис.2) с главной осью , через . Для вычисления , и , переходя от осей и нужно в ранее найденных выражениях для , и , заменить угол через , а , и — через , и . В результате получаем:

   По своему виду эти формулы совершенно аналогичны формулам для нормальных и касательных напряжений по двум взаимно-перпендикулярным площадкам в элементе, подвергающемся растяжению в двух направлениях. Укажем лишь формулу, позволяющую из двух значений угла выделить то, которое соответствует отклонению первой главной оси (дающей max

J) от начального положения оси у:

   Теперь можно окончательно формулировать, что надо сделать, чтобы получить возможность простейшим образом вычислять момент инерции фигуры относительно любой оси. Необходимо через центр тяжести фигуры провести оси Оу и Oz так, чтобы, разбивая фигуру на простейшие части, мы могли легко вычислить моменты , и после этого следует найти по формуле (14.

17) величину угла и вычислить главные центральные моменты инерции и по формулам (14.18).

Рис.2. Расчетная модель нахождения положения главных осей.

 

   Далее, можно найти момент инерции относительно любой центральной оси (Рис.2), наклоненной к под углом :

   Зная же центральный момент инерции , можно сейчас же найти момент инерции относительно любой параллельной ей оси , проходящей на расстоянии (рис.2) от центра тяжести:

   Во многих случаях удается сразу провести главные оси фигуры; если фигура имеет ось симметрии, то это и будет одна из главных осей. В самом деле, при выводе формулы мы уже имели дело с интегралом, представляющим собой центробежный момент инерции сечения относительно осей

у и z; было доказано, что если ось Oz является осью симметрии, этот интеграл обращается в нуль.

   Стало быть, в данном случае оси Оу и Oz являются главными центральными осями инерции сечения. Таким образом, ось симметрии — всегда главная центральная ось; вторая главная центральная ось проходит через центр тяжести перпендикулярно к оси симметрии.

   

Пример. Найти моменты инерции прямоугольника (Рис.3) относительно осей и и центробежный момент его относительно тех же осей.

Рис.3. Пример расчета моментов инерции.

 

   Центральные оси у и z как оси симметрии будут главными осями; моменты инерции сечения относительно этих осей равны:

Центральные моменты относительно повернутых осей и равны:

Центробежный момент инерции относительно осей и равен:

Координаты центра тяжести прямоугольника относительно осей и равны:

Моменты инерции относительно осей и равны:

Центробежный момент инерции равен:

 

Наибольшее и наименьшее значения центральных моментов инерции.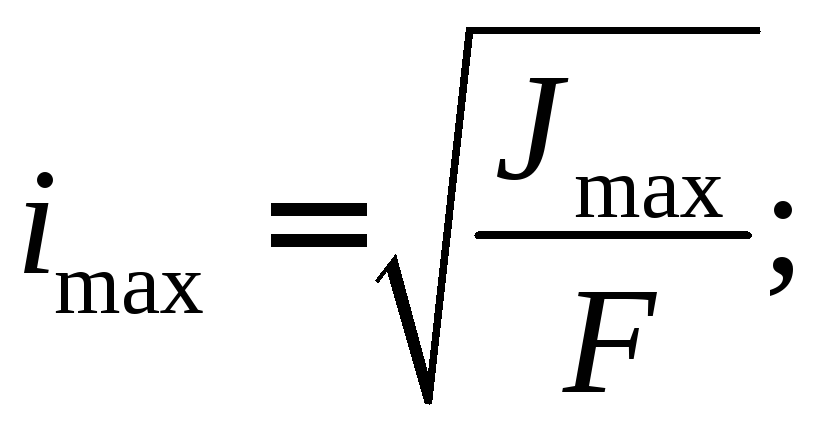

   Как известно, центральные моменты инерции являются наименьшими из всех моментов относительно ряда параллельных осей.

   Найдем теперь крайние значения (максимум и минимум) для центральных моментов инерции. Возьмем ось , и начнем ее вращать, т. е. менять угол ; при этом будет изменяться величина

Наибольшее и наименьшее значения этого момента инерции соответствуют углу , при котором производная обращается в нуль. Эта производная равна:

Подставляя в написанное выражение и приравнивая его нулю, получаем:

отсюда

   Таким образом, осями с наибольшим и наименьшим центральными моментами инерции будут главные центральные оси. Так как при повороте центральных осей сумма соответствующих моментов инерции не меняется, то

Когда один из центральных моментов инерции достигает наибольшего значения, другой оказывается минимальным, т, е.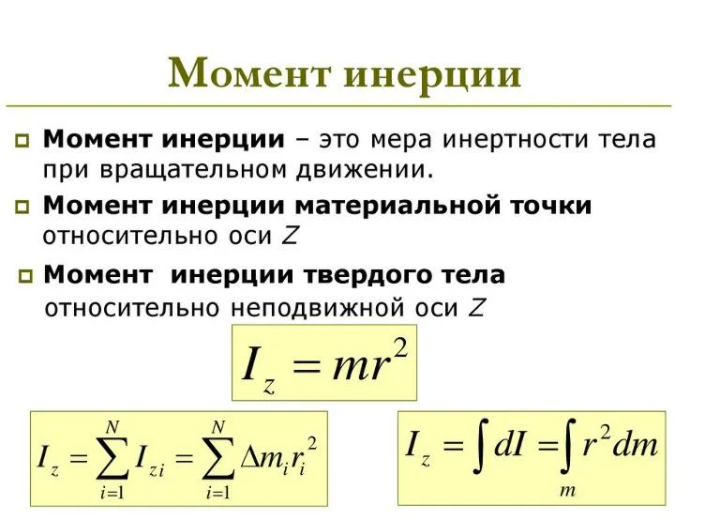 если

то

   Следовательно, главные центральные оси инерции — это такие взаимно перпендикулярные оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции обращается в нуль, а осевые моменты инерции имеют наибольшее и наименьшее значения.

Дальше…

1.2. Осевые моменты инерции Jx ; Jy

Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния до соответствующей оси.

(7)

(8)

Единица измерения [см⁴], [мм⁴].

Знак всегда «+».

Не бывает равным 0.

Свойство:Принимает минимальное значение, когда точка пересечения координатных осей совпадает с центром тяжести сечения.

Чем дальше площадь удалена от центральной оси, тем осевой момент инерции сечения больше. Жесткость конструкции повышается.

Осевой момент инерции сечения применяют при расчетах на прочность, жесткость и устойчивость.

1.

3. Полярный момент инерции сечения Jρ

Рис. 3

(9)

Взаимосвязь полярного и осевого моментов инерции:

(10)

(11)

Полярный момент инерции сечения равен сумме осевых моментов.

Свойство:

при повороте осей в любую сторону, один из осевых моментов инерции возрастает, а другой убывает (и наоборот). Сумма осевых моментов инерции остается величиной постоянной.

1.4. Центробежный момент инерции сечения Jxy

Центробежный момент инерции сечения равен сумме произведений элементарных площадок на расстояния до обеих осей

(12)

Единица измерения [см

4], [мм⁴].

Знак «+» или «-».

, если координатные оси являются осями симметрии (пример – двутавр, прямоугольник, круг), или одна из координатных осей совпадает с осью симметрии (пример – швеллер).

Таким образом для симметричных фигур центробежный момент инерции равен 0.

Координатные оси uиv, проходящие через центр тяжести сечения, относительно которых центробежный момент равен нулю, называютсяглавными центральными осями инерци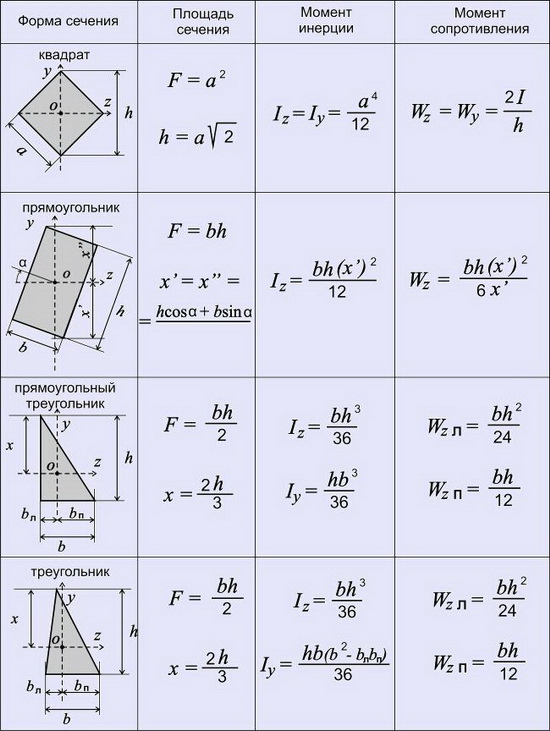и сечения. Главными они называются потому, что центробежный момент относительно них равен нулю, а центральными – потому, что проходят через центр тяжести сечения.

У сечений, не обладающих симметрией относительно осей xилиy, например у уголка,не будет равен нулю. Для этих сечений определяют положение осейuиvс помощью вычисления угла поворота осейxиy

(13)

Центробежный момент относительно осей uиv–

Формула для определения осевых моментов инерции относительно главных центральных осей uиv:

(14)

где – осевые моменты инерции относительно центральных осей,

– центробежный момент инерции относительно центральных осей.

1.5. Момент инерции относительно оси, параллельной центральной (теорема Штейнера)

Теорема Штейнера:

Момент инерции относительно оси, параллельной центральной, равен центральному осевому моменту инерции плюс произведение площади всей фигуры на квадрат расстояния между осями.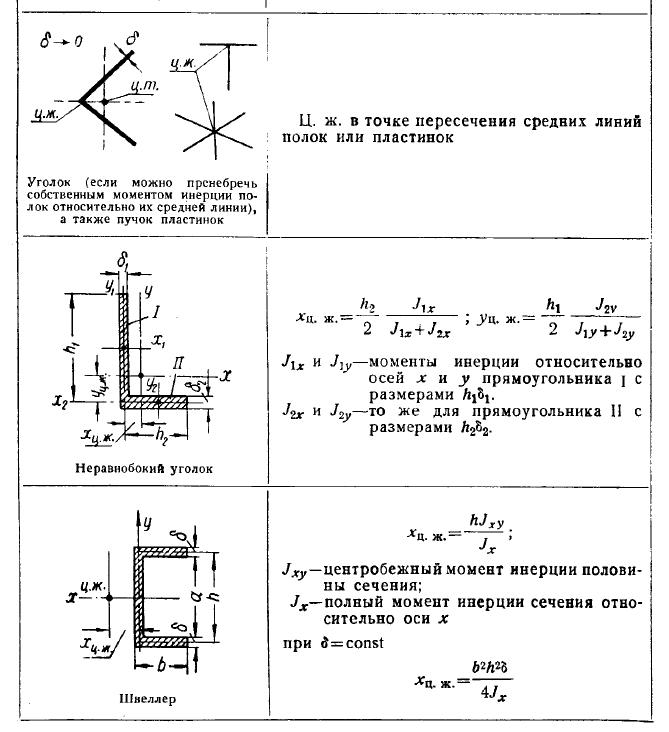

(15)

Рис. 4

Доказательство теоремы Штейнера.

Согласно рис. 5 расстояние удо элементарной площадкиdF

Рис. 5

Подставляя значение ув формулу, получим:

Слагаемое , так как точка С является центром тяжести сечения (см. свойство статических моментов площади сечения относительно центральных осей).

Для прямоугольника высотой h и шириной b :

Осевой момент инерции:

Момент сопротивления изгибу:

момент сопротивления изгибу равен отношению момента инерции к расстоянию наиболее удаленного волокна от нейтральной линии:

т.к. , то

Для круга:

Полярный момент инерции:

Осевой момент инерции:

Момент сопротивления кручению:

Т.к. , то

Момент сопротивления изгибу:

Пример 2. Определить момент инерции прямоугольного сечения относительно центральной оси Сx.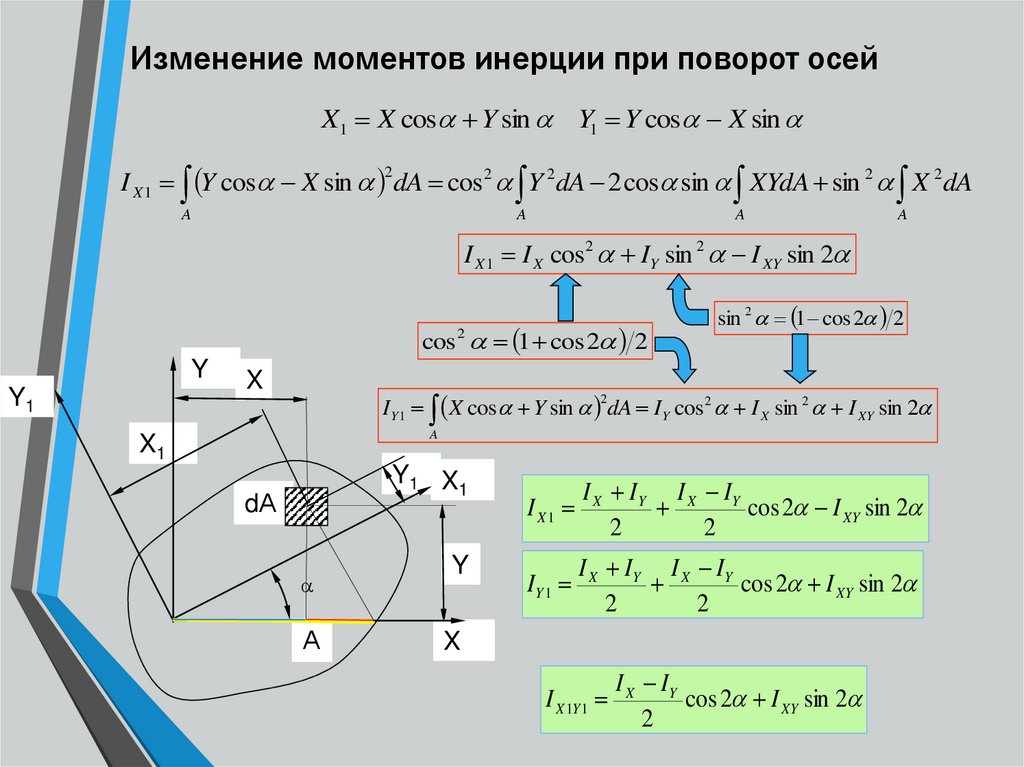

Рис. 6

Решение. Разобьём площадь прямоугольника на элементарные прямоугольники с размерами b(ширина) иdy(высота). Тогда площадь такого прямоугольника (на рис. 6 заштрихована) равна dF=bdy. Вычислим значение осевого момента инерции J_x

По аналогии запишем

– осевой момент инерции сечения относительно центральной

оси у

Центробежный момент инерции

, так как оси Сxи Сyявляются осями симметрии.

Пример 3. Определить полярный момент инерции круглого сечения.

Рис. 7

Решение. Разобьём круг на бесконечно тонкие кольца толщиной радиусом, площадь такого кольца. Подставляя значениев выражение для полярного момента инерции интегрируя, получим

Учитывая равенство осевых моментов круглого сечения и

, получаем

Осевые моменты инерции для кольца равны

с – отношение диаметра выреза к наружному диаметру вала.

Лекция №2 «Главные оси иглавные моментыинерции

Рассмотрим, как изменяются моменты инерции при повороте координатных осей. Положим, даны моменты инерции некоторого сечения относительно осей 0х, 0у(не обязательно центральных)- ,- осевые моменты инерции сечения. Требуется определить,- осевые моменты относительно осейu,v, повёрнутых относительно первой системы на угол(рис. 8)

Рис. 8

Так как проекция ломаной линии ОАВС равна проекции замыкающей, находим:

(15)

Исключим uиvв выражениях моментов инерции:

Тогда

Откуда

(16)

(17)

(18)

Рассмотрим два первых уравнения. Складывая их почленно, получим

Таким образом, сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от угла и при повороте осей остается постоянной. Заметим при этом, что

Где – расстояние от начала координат до элементарной площадки (см. рис.5). Таким образом

Где – уже знакомый нам полярный момент инерции:

Определим осевой момент инерции круга относительно диаметра.

Так как в силу симметрии но, как известно,

Следовательно, для круга

С изменением угла поворота осей значения моментов именяются, но сумма остается неизменной. Следовательно существует такое значение, при котором один из моментов инерции достигает своего максимального значения, в то время как другой момент принимает минимальное значение. Дифференцируя выражениепо углуи приравнивая производную к нулю, находим

(19)

При этом значении угла один из осевых моментов будет наибольшим, а другой – наименьшим. Одновременно центробежный момент инерции обращается в нуль, что можно легко проверить, приравнивая к нулю формулу для центробежного момента инерции .

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главнымиосями. Если они к тому же являются центральными (точка начала координат совпадает с центром тяжести сечения), то тогда они называютсяглавными центральными осями (u; v).Осевые моменты инерции относительно главных осей называютсяглавными моментами инерции –и

И их значение определяется по следующей формуле:

(20)

Знак плюс соответствует максимальному моменту инерции, знак минус – минимальному.

Существует ещё одна геометрическая характеристика – радиус инерциисечения.Эта величина часто используется в теоретических выводах и практических расчётах.

Радиусом инерции сечения относительно некоторой оси, например 0x,называется величина ,определяемая из равенства

(21)

F– площадь поперечного сечения,

– осевой момент инерции сечения,

Из определения следует, что радиус инерции равен расстоянию от оси 0хдо той точки, в которой следует сосредоточить (условно) площадь сеченияF, чтобы момент инерции одной этой точки был равен моменту инерции всего сечения. Зная момент инерции сечения и его площадь, можно найти радиус инерции относительно оси 0х :

(22)

Радиусы инерции, соответствующие главным осям, называютсяглавными радиусами инерциии определяются по формулам

(23)

Лекция 3. Кручение стержней круглого поперечного сечения.

Центробежная сила, вызванная инерцией Рон Куртус

SfC Home > Physics > Force >

Рон Куртус

Когда вы качаете объект на веревке или веревке, он будет тянуться наружу по веревке. Сила, которую вы чувствуете, называется центробежной силой и вызвана инерцией объекта, стремящегося следовать прямолинейному пути. Его еще называют сила инерции или псевдо сила .

В соответствии с третьим законом Ньютона или законом действия-противодействия центробежная сила равна центростремительной силе и противоположна ей, которая действует на объект и заставляет его двигаться по кривой линии.

Применение центробежной силы включает вращающийся диск, аттракционы в парке развлечений и воду в качающемся ведре. Уравнение для центробежной силы аналогично уравнению для центростремительной силы.

Когда обсуждается круговое движение, нередко можно услышать упоминание слова  центробежный . Центробежный , не путать с центростремительный , означает от центра или наружу.

У вас могут возникнуть следующие вопросы:

• Что вызывает центробежные силы?
• Каковы некоторые примеры центробежной силы?
• Что такое уравнение центробежной силы?

Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц

---

---

Причина центробежной силы

Причина центробежной силы связана с центростремительной силой на объекте.

Центростремительная сила

Согласно первому закону Ньютона или закону инерции , движущийся объект стремится двигаться по прямой линии.

Однако, прикладывая к объекту непрерывную боковую силу, можно преодолеть инерцию и заставить объект двигаться по криволинейной траектории до тех пор, пока действует эта сила. Эта приложенная сила называется центростремительная сила . Типичным примером является раскачивание объекта на веревке.

(дополнительную информацию см. в разделе «Центростремительная сила»)

Центробежная сила

Третий закон Ньютона или Закон действия-противодействия гласит, что для каждой приложенной силы существует равная и противоположная сила.

Другими словами, когда вы прикладываете силу к веревке, раскручивая объект вокруг себя, веревка тянет объект с этой силой, и объект оказывает на веревку равную и противоположную силу. Затем вы почувствуете, что равная и противоположная сила тянет веревку и объект от вас. Эта сила центробежная сила .

Примечание: Во многих источниках по физике говорится, что центробежная сила является фиктивной или псевдо (ложной) силой. Это противоречит тому факту, что вы можете чувствовать силу.

Кроме того, они, кажется, забыли Третий закон Ньютона . Если бы они применили Закон, то увидели бы, что центробежная сила равна и противоположна центростремительной силе.

Центробежная сила — это сила инерции, которая сопротивляется изменению направления или скорости объекта.

Примеры центробежной силы

Существуют различные примеры применения центробежной силы.

Вращающийся диск

Если поместить объект на диск и запустить его вращение, трение, удерживающее объект на диске, представляет собой центростремительную силу, заставляющую объект двигаться по криволинейной траектории.

Когда диск вращается достаточно быстро, центробежная сила инерции может стать больше силы центростремительного трения, удерживающей объект на месте. Затем объект полетит по прямой линии.

Мяч отлетает от вращающегося диска по прямой линии
из-за центробежной силы, преодолевающей трение

Аттракцион Round-Up

Похожим примером является аттракцион в парке развлечений, Round-Up , который состоит из круглой платформы с вертикальной стенкой в ​​виде клетки по краю.

Центробежная сила удерживает людей на стенах во время карнавального аттракциона

Ref: Amusement Ride Extravaganza

Когда платформа вращается с достаточно высокой скоростью, центробежная сила инерции прижимает всадников к стене, удерживая их на месте в качестве платформы меняет направления.

Хотя всадники чувствуют силу, толкающую их к стене, реальной силы или агента, который толкает их, нет. Это просто эффект инерции.

Американские горки

Другим аттракционом в парке развлечений, демонстрирующим центробежную силу, являются американские горки. Когда американские горки пересекают изогнутую верхнюю часть дорожек, вы чувствуете центробежную силу, которая тянет вас вверх. Точно так же в нижней изогнутой части гусениц вы чувствуете силу, толкающую вас вниз.

Вода остается в качающемся ведре

Существует также трюк, при котором вы берете ведро, наполовину заполненное водой, и вращаете его на веревке по вертикальному кругу, так что вода остается в ведре, даже если оно находится прямо над вами. центробежная сила.

Уравнение для центробежной силы

Уравнение для внешней или центробежной силы из-за инерции объекта, следующего по криволинейной траектории:

F = мв ² /R

где

• F — центробежная сила, оттягивающая объект от центра
• м масса объекта
• v – прямолинейная скорость объекта
• R радиус кривизны, вызванный центростремительной силой

Это уравнение похоже на уравнение центростремительной силы, заставляющей объект двигаться по криволинейной траектории, за исключением того, что сила действует в противоположном направлении.

Центробежная сила в противоположном направлении
центростремительной силы

Таким образом, если центростремительная сила, заставляющая объект двигаться по круговой траектории, составляет 25 ньютонов, ощущаемая центробежная сила будет равна 25 ньютонам.

Резюме

Центробежная сила — это внешняя сила инерции, действующая на объект, движущийся по криволинейной траектории. Объект будет двигаться по криволинейной траектории, если центростремительная сила препятствует его движению по прямой линии.

Третий закон Ньютона или закон действия-противодействия гласит, что для каждой приложенной силы существует равная и противоположная сила. Таким образом, центробежная сила направлена ​​противоположно центростремительной силе, но они равны по величине.

Уравнение для центробежной силы инерции как функции массы, скорости и радиуса:

F = mv ² /R.

---

Выходите за рамки своих возможностей

---

Ресурсы и ссылки

Ron Kurtus’ Credentials

Websites

Centrifugal Force – Wikipedia

Centrifugal Force – Physics Classroom

Centrifugal Force – HowStuffWorks

Physics Resources

Books

(Notice: Школа Чемпионов может получать комиссионные от покупки книг)

Наука Сил Стив Паркер; Хайнеманн (2005) 29 долларов. 29 – Проекты с экспериментами с силами и машинами

Glencoe Science: Motion, Forces, and Energy , McGraw-Hill; Glencoe/McGraw-Hill (2001) $19,32 – Студенческое издание (в твердом переплете)

Книги с самым высоким рейтингом по физике силы

---

Поделиться этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронная почта или другие услуги:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
force_centrifugal.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Copyright © Ограничения

---

Где ты сейчас?

Школа чемпионов

Темы по физике

Центробежная сила, вызванная инерцией

---

Центробежный Расчет силы

, созданный Bogna Szyk

, рассмотрено Стивеном Вудинг

Последнее обновление: 10 октября 2022

СОДЕРЖА

Что делать дальше?

Часто задаваемые вопросы

Калькулятор центробежной силы поможет вам найти силу, действующую на вращающийся объект, исходя из его массы, скорости и радиуса вращения. Вы можете использовать его не только для того, чтобы понять, как рассчитать центробежную силу, но и для ускорения и угловой скорости объекта. Читайте дальше, чтобы узнать, что такое определение центробежной силы и как применять уравнение центробежной силы.

Соотношение между силой и ускорением для объектов, движущихся по прямой линии, можно найти в нашем калькуляторе ускорения.

Определение центробежной силы

Центробежная сила – это сила инерции, возникающая в каждом вращающемся объекте. Оно требуется только во вращающейся системе отсчета — или, другими словами, когда мы смотрим на систему с точки зрения движущегося объекта.

Согласно первому закону Ньютона, если на объект не действует сила, он движется прямолинейно. Чтобы произошло вращение, должна быть приложена центробежная сила, действующая наружу от центра вращения.

Например, вы можете представить себе камень, вращающийся на веревке. Центробежная сила — это сила, которая препятствует его движению к центру вращения (то есть к вашей руке).

Уравнение центробежной силы

Если вы знаете скорость объекта, просто используйте следующую формулу:

F = mv²/r

где:

• F – сила, выраженная в ньютонах;
• m – масса объекта;
• v — скорость; и
• r радиус.

Если вам известна только угловая скорость ω , вы можете пересчитать ее в нормальную скорость, просто умножив ее на длину окружности пути. Используйте следующее уравнение:

v = ω2πr

в случае, если ваш ω соответствует частоте Гц (1/с) .

Или формула:

v = ωr

для ω в рад/с .

Или просто введите значения ω и r в наш калькулятор.

Для получения дополнительной информации о том, как найти длину окружности, посетите наш калькулятор длины окружности.

Как рассчитать центробежную силу

Выполните следующие простые шаги:

1. Найдите массу объекта – например, 10 кг .
2. Определить радиус вращения. Предположим, что это 2 м .
3. Определите скорость объекта. Может быть равно 5 м/с . Если вам известна только угловая скорость, вы можете использовать формулу v = ω ⋅ 2 ⋅ π ⋅ r для расчета скорости.
4. Используйте уравнение центробежной силы: F = m v² / r . В нашем примере она будет равна (10 кг) × (5 м/с)² / (2 м) = 125 кг⋅м/с² = 125 Н .
5. Или вместо этого вы можете просто ввести данные в наш калькулятор 🙂

Что делать дальше?

Наш калькулятор центробежной силы также можно использовать для определения центробежного ускорения a по простой формуле: a = F / m .

Это работает и в обратном порядке – например, вы можете найти массу объекта с заданной скоростью, центробежной силой и радиусом.

Поскольку вы знаете массу и скорость объекта, вы также можете найти его кинетическую энергию.

Кроме того, вы можете дополнительно изучить концепцию кинетической энергии, посетив наш калькулятор кинетической энергии.

Часто задаваемые вопросы

Что такое центробежная сила?

Центробежная сила вращающегося объекта — это внешняя сила, которая вытягивает объект из центра вращения. Это сила инерции, которая реагирует на центростремительную силу.

Как рассчитать центробежную силу поворачивающего автомобиля?

Вы можете попробовать калькулятор центробежной силы Omnicalculator или сделать следующее:

1. Узнать радиус кривизны. Допустим, 150 метров.
2. Определить скорость автомобиля. Это значение будет служить тангенциальной скоростью. Предположим, 50 км/ч
.
3. Умножьте массу автомобиля на квадрат скорости и разделите результат на радиус кривизны.
4. Результат 1286 ньютонов.

В чем разница между центробежной и центростремительной силой

Центробежная и центростремительная силы одинаковы, но направлены в противоположные стороны.