Цепь постоянного тока содержит резисторы соединенные смешанно решение: U4 = 12 В; R1 = 3 Ом, R2 = 6 Ом, R3 = 6 Ом, R4 = 3 Ом, R5 = 12 Ом, R6 = 4 Ом. Определить токи во всех элементах и напряжение на каждом элементе, а также мощность, потребляемую всей цепью, и расход электрической энергии за 10 часов работы… — Контрольная работа #1303414 — Электроника и электротехника

U4 = 12 В; R1 = 3 Ом, R2 = 6 Ом, R3 = 6 Ом, R4 = 3 Ом, R5 = 12 Ом, R6 = 4 Ом. Определить токи во всех элементах и напряжение на каждом элементе, а также мощность, потребляемую всей цепью, и расход электрической энергии за 10 часов работы… — Контрольная работа #1303414 — Электроника и электротехника

Задача 1. 3
Задача 2 8
Задача 3 11
Задача 4 13
Список литературы 16

Задания к работе:
Задача 1.
Цепь постоянного тока содержит резисторы, соединенные смешанно. Схема цепи с указанием резисторов приведена на рис. 1.1. Всюду индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на котором действует напряжение.
Дано: U4 = 12 В; R1 = 3 Ом, R2 = 6 Ом, R3 = 6 Ом, R4 = 3 Ом, R5 = 12 Ом, R6 = 4 Ом.
Определить токи во всех элементах и напряжение на каждом элементе, а также мощность, потребляемую всей цепью, и расход электрической энергии за 10 часов работы…
…
Задача 4
Электродвигатель постоянного тока с последовательным возбуждением отдает полезную мощность Р2 = 44 кВт, потребляет из сети мощность Р1 = 51,3 кВт. Двигатель развивает полезный вращающий момент М = 296 Нм. Ток в цепи якоря равен Ia = 205 А. Потери мощности в обмотках якоря и возбуждения Ра+пс = 2270 Вт.

Определить:
1) напряжение сети Uном;
2) скорость вращения двигателя n;
3) противо-э.д.с;
4) сопротивление Rа+пс;
5) к.п.д. двигателя.
Нарисовать электрическую схему двигателя.
Нарисовать график изменения частоты вращения и момента двигателя с последовательным возбуждением от нагрузки на валу. Почему недопустима работа такого двигателя при малых нагрузках?..

1. Ушаков В.Н. Электротехника и электроника. М.: Радио и связь, 1997. – 328 с.
2. Бечева М. К. и др. Электротехника и электроника. М.: Высшая школа, 1991. – 224 с.
3. Мучник А.Я., Парфенов К.А. Общая электротехника. М. Высшая школа, 1967. – 446 с.
4. Важнов А.И. Электрические машины. Л.: Энергия, 1968. – 768 с.

5. Хвостов В. Электрические машины. Машины постоянного тока М.: 1983. – 336 с.

Тема:	Вариант №8 Задача 1. 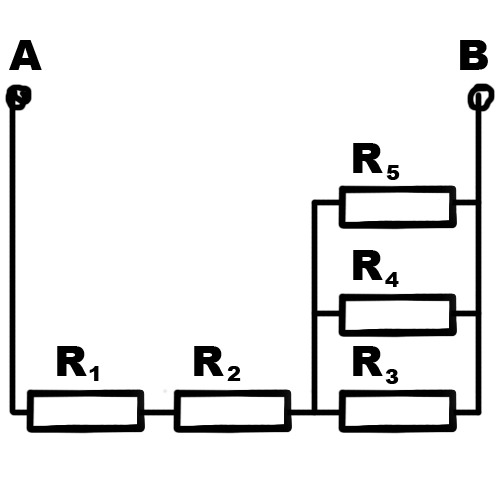Цепь постоянного тока содержит резисторы, соединенные смешанно. Схема цепи с указанием резисторов приведена на рис. 1.1. Всюду индекс тока или напряжения совпадает с индексом резистора, по которому проходит этот ток или на котором действует напряжение. Дано: U4 = 12 В; R1 = 3 Ом, R2 = 6 Ом, R3 = 6 Ом, R4 = 3 Ом, R5 = 12 Ом, R6 = 4 Ом. Определить токи во всех элементах и напряжение на каждом элементе, а также мощность, потребляемую всей цепью, и расход электрической энергии за 10 часов работы…
Артикул:	1303414
Дата написания:	19.09.2009
Тип работы:	Контрольная работа
Предмет:	Электроника и электротехника
Оригинальность:	Антиплагиат.ВУЗ — 88%
Количество страниц:	16

Содержание

Главное управление образования Гродненского областного

исполнительного комитета

Учреждение образования

«Гродненский государственный политехнический колледж»

Контрольная работа №__1__

по дисциплине «Электротехника с основами электроники»

Вариант № _47_

учащегося Микашов Сергей Владимирович

^{(Фамилия, имя, отчество)}

__1__ курса группы _ПГБ-20-1_

специальности 2-70 02 01 «Промышленное и гражданское строительство»

Шифр учащегося __47__

Преподаватель: ________Ермак И.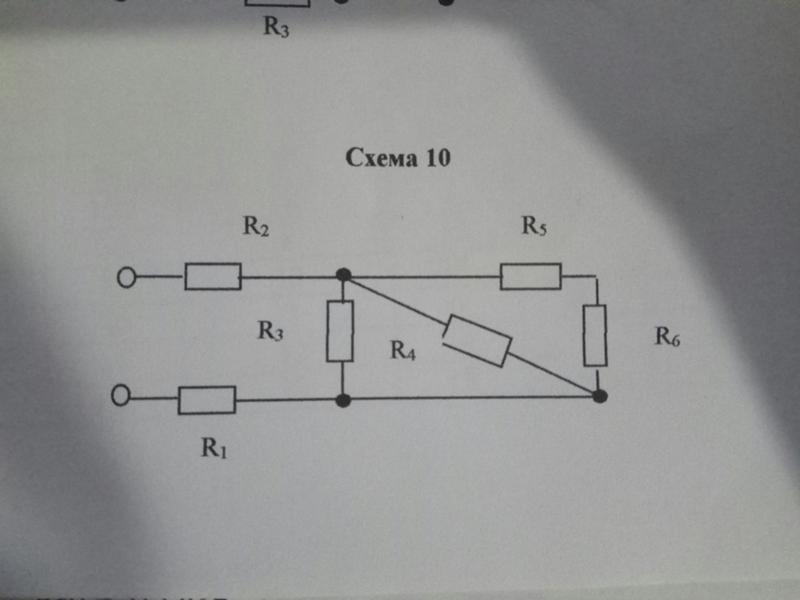 В._______

(ФИО)

Рецензия:

Задача 1 3

Задача 2 6

Задача 3 9

Задача 4 12

Задача 5 14

Литература 16

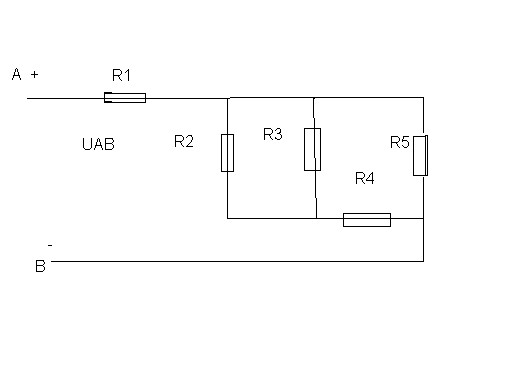
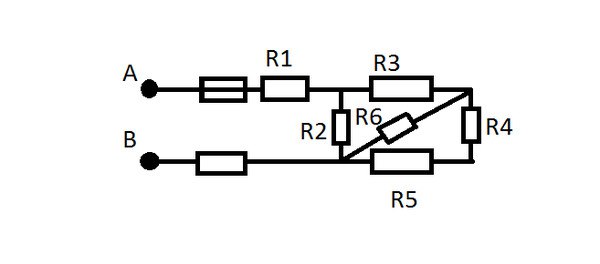
Цепь постоянного тока содержит шесть резисторов, соединённых смешанно. Схема цепи и значения резисторов указаны на схеме. Номер схемы и величина одного из заданных токов или напряжений приведены в таблице 1. Индекс тока и напряжения совпадает с индексом резистора, по которому проходит этот ток или на котором действует указанное напряжение. Определить: 1) эквивалентное сопротивление цепи относительно вводов АВ; 2) ток в каждом резисторе; 3) напряжение на каждом резисторе; 4) расход электрической энергии цепью за 10 часов.

Номера вариантов	Номера схем	Задаваемая величина			Действие с резисторами		Изменение какой величины рассмотреть
					Замыкается на коротко	Выключается из схемы
47	4	U2=	24	В		R4	U6

Дано: Цепь постоянного тока содержит шесть резисторов, соединённых смешанно.

R₁=4 Ом, R₂=2 Ом, R₃=8 Ом, R₄=4 Ом, R₅=3 Ом, R₆=15 Ом, U

₂=24 В, T=10 ч.

Определить:

1. эквивалентное сопротивление цепи относительно выводов АВ;

2. ток в каждом резисторе;

3. напряжение на каждом резисторе;

4. расход электрической энергии цепью за 10 часов.

Решение.

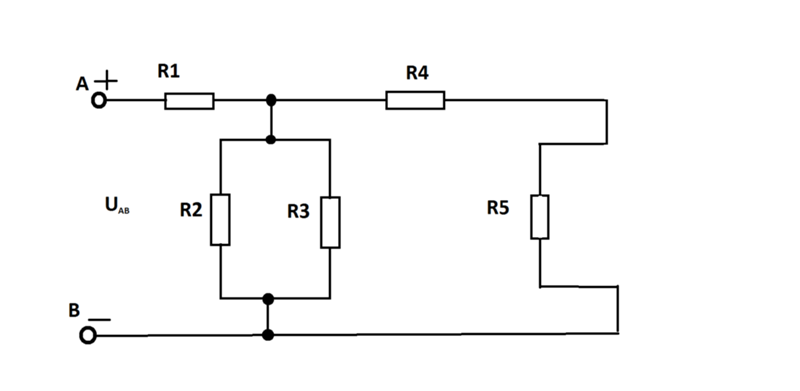
Резисторы R₁ и R₂ соединены последовательно. Их общее сопротивление:

R₁₂=R₁+R₂=4+2=6 Ом

Резисторы R₁₂ и R₅ соединены параллельно. Их общее сопротивление:

R₁₂₅=R₁₂*R₅/(R₁₂+R₅)=6*3/(6+3)=18/9=2 Ом

Резисторы R₁₂₅ и R₃ соединены последовательно. Их общее сопротивление:

R₁₂₃₅=R₁₂₅+R₃=2+8=10 Ом

Резисторы R₁₂₃₅ и R₆ соединены параллельно. Их общее сопротивление:

R₁₂₃₅₆=R₁₂₃₅*R₆/(R₁₂₃₅+R

6)=10*15/(10+15)=150/25=6 Ом

Резисторы R₁₂₃₅₆ и R₄ соединены последовательно. Их общее сопротивление:

R_АВ=R₁₂₃₅₆+R₄=6+4=10 Ом

Рассчитываем токи и напряжения на каждом резисторе, учитывая их соединение. По условию задачи известно, что U₂=24 В.

По закону Ома определяем ток:

I₂=U₂/R₂=24/2=12 А

Согласно свойствам последовательного соединения:

I₁=I₂=12 А

Определяем падение напряжения:

U₁=I₁

*R₁=12/4=48 В

Согласно свойствам последовательного соединения:

U₁₂=U₁+U₂=48+24=72 В

Согласно свойствам параллельного соединения:

U₁₂=U₅=72 В

По закону Ома определяем ток:

I₅=U₅/I₅=72/3=24 А

По закону Кирхгофа определяем ток:

I₃=I₅+I₂=24+12=36 А

Определяем падение напряжения:

U₃=I₃*R₃=36*8=288 В

Согласно свойствам последовательного соединения:

U₅₃=U₅+U₃=72+288=360 В

Согласно свойствам параллельного соединения:

U₆=U₅₃=360 В

По закону Ома определяем ток:

I₆=U₆/I₆=360/15=24 А

По закону Кирхгофа определяем ток:

I₄=I₆+I₃=24+36=60 А

Определяем падение напряжения:

U₄=I₄*R₄=60*4=240 В

Согласно свойствам последовательного соединения:

U_AB=U₆+U₄=360+240=600 В

I=I₄

Находим расход электроэнергии в цепи за 10 часов:

W=U_AB*I*T=600*60*10=360000 Вт*час = 360 кВт*час

Рассмотрим, как изменится напряжение U₆ при выключении из схемы резистора R₄. При выключении резистора R₄ напряжение U₆ будет равно напряжению источника.

Ответ:

U1 = 48 В	I1 = 12 А
U2 = 24 В	I2 = 12 А
U3 = 288 В	I3 = 36 А
U4 = 240 В	I4 = 60 А
U5 = 72 В	I5 = 24 А
U6 = 360 В	I6 = 24 А
W = 360 кВт*час	RAB = 10 Ом

Объяснение урока: Анализ комбинированных цепей

В этом объяснении мы научимся определять токи через и напряжения на участках цепей, содержащих резисторы как последовательно, так и параллельно.

Напомним, что последовательно соединенные резисторы соединяются в один проводящий путь. На приведенной ниже схеме показаны три последовательно соединенных резистора.

В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=𝑅+𝑅+𝑅.

Распространяется на любое количество последовательно соединенных резисторов: 𝑅=𝑅+𝑅+⋯+𝑅.

С другой стороны, резисторы параллельно соединены вдоль нескольких токопроводящие пути. На приведенной ниже схеме показаны три резистора, соединенные последовательно. параллельно.

В показанном выше примере полное сопротивление цепи, 𝑅, это 𝑅=1𝑅+1𝑅+1𝑅.

Это распространяется на любое количество резисторов, включенных параллельно: 𝑅=1𝑅+1𝑅+⋯+1𝑅.

Комбинированная схема содержит секции резисторов, соединенных последовательно и параллельно. На приведенной ниже схеме показаны два резистора, соединенные последовательно с двумя резисторы параллельно.

В приведенном выше примере часть схемы, содержащая 𝑅 и 𝑅 последовательно, а участок цепи, содержащий 𝑅 и 𝑅 параллельны.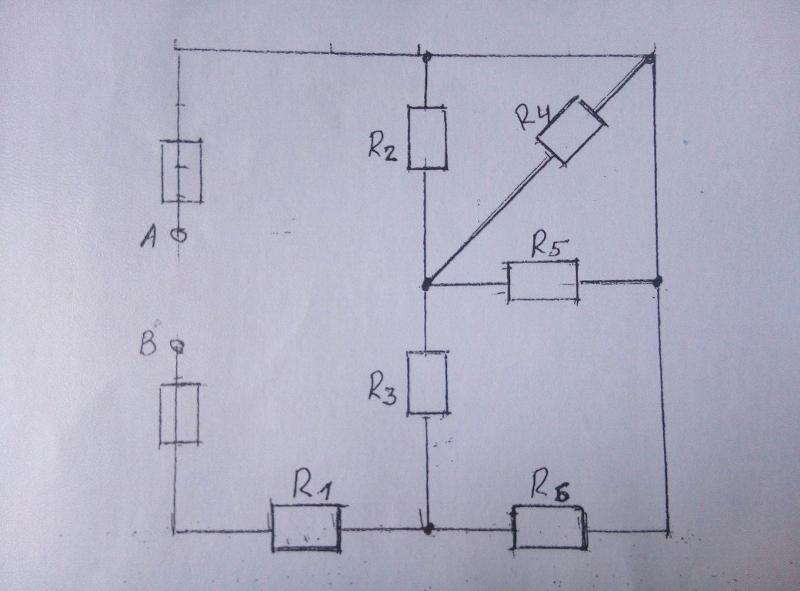

Для анализа этой схемы каждый набор резисторов можно преобразовать в их эквивалентный резистор. На приведенной ниже диаграмме показано, как последовательно подключить два резистора. и два резистора параллельно могут быть преобразованы в один эквивалентный резисторы, которые затем могут быть преобразованы в окончательный эквивалентный резистор для вся схема.

Раздел серии, содержащий 𝑅 и 𝑅 можно преобразовать в его эквивалентный резистор, 𝑅: 𝑅=𝑅+𝑅.

Параллельная секция, содержащая 𝑅 и 𝑅 можно преобразовать в эквивалентный ему резистор, 𝑅: 𝑅=1𝑅+1𝑅.

Тогда, наконец, эквивалентное сопротивление всей цепи, 𝑅, это 𝑅=𝑅+𝑅.

Давайте рассмотрим примерный вопрос.

Пример 1. Определение эквивалентного сопротивления комбинированной цепи

Показанная схема содержит как последовательные, так и параллельные комбинации резисторов.

1. Какова общая сила тока в показанной цепи? Дайте свой ответ на один десятичный знак.
2. Какова общая мощность, рассеиваемая цепью? Дай свой ответ до одного десятичного знака.

Ответ

Часть 1

В первой части этого вопроса мы должны рассчитать общий ток в схема. Для этого необходимо найти эквивалентное сопротивление схема.

Мы начнем с обозначения компонентов на электрической схеме.

Первый шаг в расчете эквивалентного сопротивления цепи: найти эквивалентное сопротивление параллельного участка, состоящего из 𝑅 и 𝑅. Обозначим эквивалентное сопротивление этого параллельного участка на 𝑅: 𝑅=1𝑅+1𝑅.

Подставляя известные значения для 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩ

Теперь мы можем рассчитать эквивалентное сопротивление всей цепи, 𝑅: 𝑅=𝑅+𝑅+𝑅.

Подставляя известные значения для 𝑅=1,6Ω и 𝑅=1,5Ом и значение 𝑅, которое мы рассчитали как 1,40 Ом дает нам 𝑅=1,6+1,5+1,4𝑅=4,5.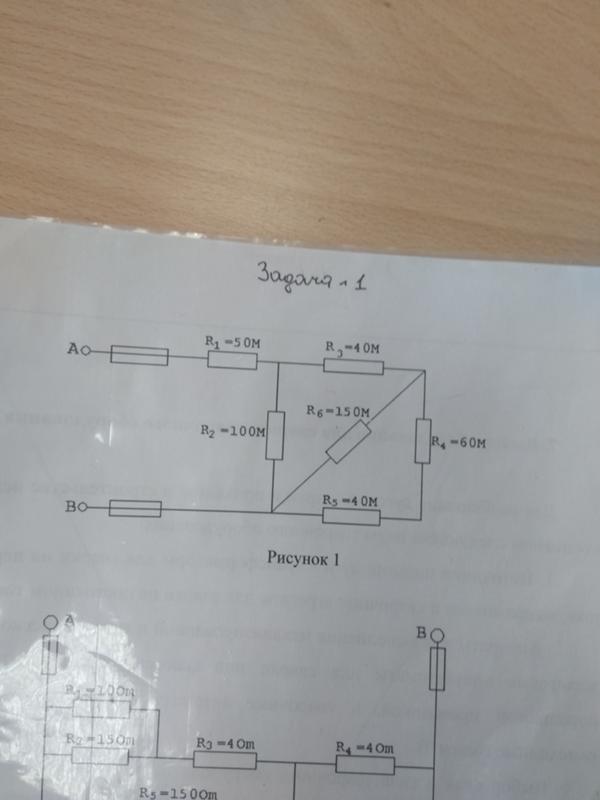 ΩΩΩΩΩ

Тогда мы можем использовать закон Ома для расчета полного тока в цепи, при 𝑉=5,5 В: 𝐼=𝑉𝑅𝐼=5,54,5.VΩ

Полный ток в цепи с точностью до одного десятичного знака равен 𝐼=1.2.A

Часть 2

Полная мощность, рассеиваемая в цепи, может быть рассчитана путем умножения ток в цепи на полное падение потенциала на схема: 𝑃=𝐼𝑉𝑃=1,2×5,5.AV

Полная мощность, рассеиваемая в цепи, с точностью до одного десятичного знака равна 𝑃=6.7.W

Эти методы анализа комбинированных цепей также можно использовать для анализировать схемы, содержащие компоненты, отличные от резисторов. Мы сейчас проработайте пример вопроса об этом.

Пример 2. Анализ цепей, содержащих компоненты, отличные от Резисторы

Ток измеряется амперметром в цепи, показанной на схеме. Амперметр имеет сопротивление 2,5 мкОм.

1. Какие показания будут на амперметре? Дай свой ответ до одного десятичного знака.
2. Какими были бы показания амперметра, если бы он был подключен к параллельно Резистор 3,5 Ом? Отдай свое ответ до одного десятичного знака.

Ответ

Часть 1

В первой части вопроса нам предлагается рассчитать сумму текущего через цепь. Для этой цели мы можем заменить амперметр на резистор эквивалентного сопротивления.

Мы можем обобщить это на диаграмме, где каждый резистор помечен. 𝑅 — эквивалентное сопротивление для амперметра.

Общее сопротивление цепи равно 𝑅=𝑅+𝑅+𝑅𝑅=2,5+3,5+2,5×10𝑅=6,0000025.ΩΩΩΩΩ

Ток в цепи можно рассчитать по закону Ома: 𝐼=126,0000025𝐼=1,9999991.VΩA

Амперметр будет показывать до одного десятичного знака 2,0 А. Давайте сравните это с идеальным амперметром, который имеет нулевое внутреннее сопротивление.

Общее сопротивление цепи будет точно равно сумме из двух резисторов: 𝑅=2,5+3,5𝑅=6,0. ΩΩΩΩ

Это означает, что ток в цепи равен 𝐼=126.0𝐼=2.0.VΩA

Таким образом, амперметр покажет точно 2,0 А. Это подчеркивает, насколько важно иметь амперметр с очень низким внутреннее сопротивление. Если внутреннее сопротивление достаточно низкое, т. в данном примере, им можно пренебречь при расчетах.

Часть 2

Во второй части вопроса нам предлагается рассмотреть, что произойдет, если амперметр будет подключен параллельно Резистор 3,5 Ом.

Заменив амперметр его эквивалентным резистором, мы можем нарисуй на схеме.

Теперь мы должны рассчитать эквивалентное сопротивление, 𝑅, параллельного участка цепи: 𝑅=13,5+12,5×10𝑅=(0,28+400000)𝑅=400000,28𝑅=2,499998×10,ΩΩΩ

3

3 амперметр такой низкий по сравнению до 3,5 Ом резистора, что он полностью доминирует над эквивалентным сопротивлением два.

Общее сопротивление цепи равно 𝑅=2,5+2,499998×10𝑅=2,5000025,Ω

Тогда ток в цепи можно рассчитать по закону Ома: 𝐼=122,5000025𝐼=4,799995.VΩA

Итак, с точностью до десятых, амперметр показывает 4,8 А.

Рассчитаем показание тока, если эквивалентное сопротивление параллельным сечением в расчете пренебрегают: 𝐼=122,5𝐼=4,8.VΩA

Как видно, внутреннее сопротивление амперметра настолько мало, что эквивалентным сопротивлением параллельного участка можно пренебречь.

В то время как эквивалентное сопротивление позволяет нам анализировать многие комбинированные схемы, есть некоторые, которые нельзя решить, используя только эквивалентное сопротивление.

Цепь, показанная на следующей принципиальной схеме, не может быть проанализирована с помощью только эквивалентное сопротивление.

Поскольку есть две батареи, мы не можем рассчитать эквивалентное сопротивление из 𝑅 и 𝑅.

Для анализа таких цепей мы можем использовать законы Кирхгофа.

Первый закон Кирхгофа гласит, что ток в переходе или узле в цепь должна быть такой же, как и ток, выходящий из перехода или узла.

Определение: Первый закон Кирхгофа

Первый закон Кирхгофа утверждает, что сумма токов в соединение/узел в цепи, 𝐼+𝐼+⋯()()inin, должно быть таким же, как сумма токов из узла/узла, 𝐼+𝐼+⋯()()outout: 𝐼+𝐼+⋯=𝐼+𝐼+⋯.()()()()ininoutout

Например, предположим, что в следующем соединении цепи есть токи 𝐼 и 𝐼 на перекрестке и 𝐼 с перекрестка.

Первый закон Кирхгофа гласит, что сумма токов в переходе, 𝐼+𝐼, должны равняться сумме токов из перекресток, 𝐼: 𝐼+𝐼=𝐼.

Второй закон Кирхгофа позволяет нам анализировать разность потенциалов на различных точках комбинационной цепи.

Второй закон Кирхгофа гласит, что сумма всех разностей потенциалов между компонентами в цикле должны быть равны нулю.

На следующей принципиальной схеме показано последовательное подключение трех резисторов к батарее.

Определение: Второй закон Кирхгофа

Сумма разностей потенциалов на каждом компоненте контура равна нуль: 𝑉+𝑉+⋯+𝑉=0,

В приведенной схеме разность потенциалов на ячейке равна 𝑉, а на трех резисторах разность потенциалов равна 𝑉, 𝑉 и 𝑉 соответственно.

Закон Кирхгофа гласит, что сумма разностей потенциалов по всем компоненты в цикле равны нулю. То есть, 𝑉+𝑉+𝑉+𝑉=0,

В этом случае разность потенциалов на ячейке положительна и равна по модулю равна полной разности потенциалов на трех резисторы.

Законы Кирхгофа можно использовать для сравнения цепей. Мы будем работать через пример вопрос об этом сейчас.

Пример 3. Анализ нескольких похожих цепей

Схемы (a) и (b) очень похожи, но немного отличаются друг от друга. другой. Какова разница в полном токе между цепью, показанной на рис.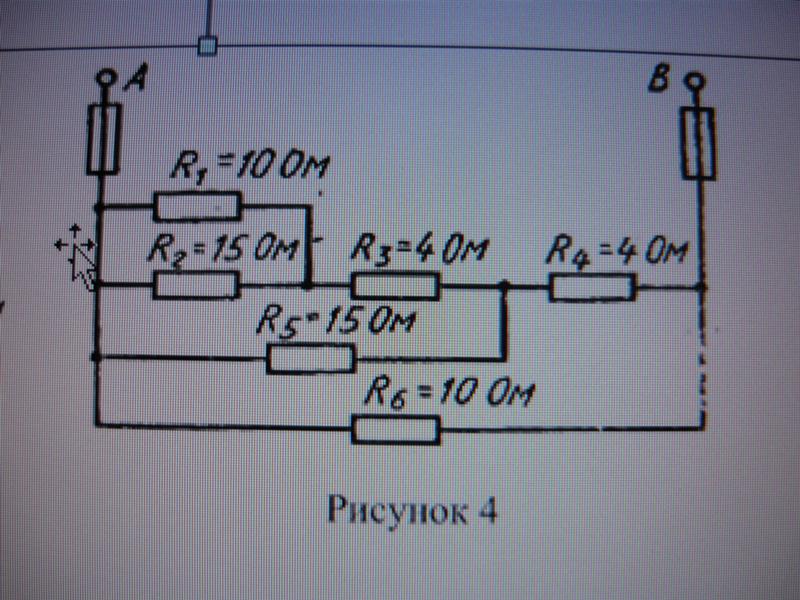 схеме (а) и цепи, показанной на схеме (б)? Дайте ответ с точностью до одного десятичного знака.

Ответ

Начнем с анализа схемы (б).

Мы можем использовать второй закон Кирхгофа для петли, образованной цепью. Отзывать что второй закон Кирхгофа гласит, что сумма разностей потенциалов по каждому компоненту в цикле должен равняться нулю.

Обозначим разность потенциалов на 800 мОм резистор как 𝑉 и разность потенциалов на Резистор 960 мОм как 𝑉.

Два резистора можно преобразовать в один эквивалентный резистор, который мы будет коллировать 𝑅 со следующим сопротивлением: 𝑅=880+960𝑅=1840.мОммОммОм

Разность потенциалов на этом эквивалентном резисторе равна 𝑉 и равно 𝑉=𝑉+𝑉.

Сумма разностей потенциалов на каждом компоненте в цепи (b) можно записать как 2,5+1,4−𝑉−𝑉=0,ВВВ или, учитывая эквивалентный резистор, 𝑅, это можно записать как 2,5+1,4−𝑉=0𝑉=3,9. VVVV

Итак, разность потенциалов на этом эквивалентном резисторе равна 3,9 В.

Ток в цепи (b), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=3,91,84𝐼=2,12.VΩA

Теперь проанализируем схему (а).

Схема (а) почти идентична схеме (б), за исключением того, что Батарея 1,4 В есть перевернулся. Когда мы на этот раз применим второй закон Кирхгофа, эта батарея вносит в уравнение отрицательную разность потенциалов.

Объединение резисторов в эквивалентный резистор, как мы это делали ранее, мы можем написать 2,5−1,4−𝑉=0𝑉=1,1.VVVV

Итак, разность потенциалов на этом эквивалентном резисторе равна 1,1 В.

Ток в цепи (a), 𝐼, можно рассчитать, используя Закон Ома, сначала преобразуя сопротивление из миллиомы в Ом: 𝐼=𝑉𝑅𝐼=1,11,84𝐼=0,60.VΩA

Тогда разница токов между двумя цепями равна 𝐼−𝐼=2,12−0,06𝐼−𝐼=1,52.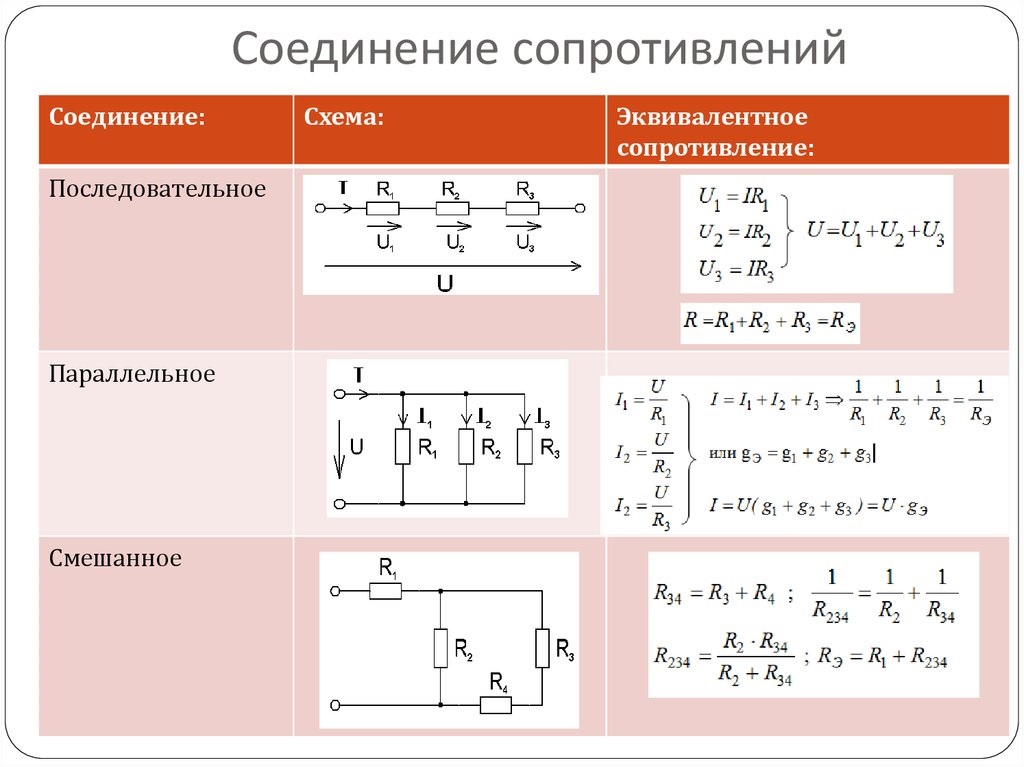 AAA

Разница в общем токе между цепью, показанной на схеме (а) и схема, показанная на диаграмме (б), поэтому 1,5 А до одного десятичного знака.

Законы Кирхгофа также можно использовать для анализа комбинационных цепей. Когда мы учитывая комбинированную схему, мы должны идентифицировать петли и соединения/узлы.

Например, следующая принципиальная схема содержит несколько резисторов и аккумуляторы в разных цепях цепи.

Мы можем идентифицировать два узла в этой цепи и три петли. Это проиллюстрировано на следующей диаграмме.

Теперь мы рассмотрим пример вопроса, в котором мы должны использовать метод Кирхгофа. законы для анализа комбинационной цепи.

Пример 4. Использование законов Кирхгофа для анализа комбинационных цепей

На схеме показана схема, содержащая несколько ячеек.

1. Какой ток через Резистор 20 Ом?
2. Какой ток на минусовой клемме Батарея 5,0 В?
3. Какой ток на отрицательной клемме Аккумулятор 10,0 В?

Ответ

Часть 1

Начнем с обозначения принципиальной схемы.

Токи в каждой ветви цепи маркируются в соответствии с узел в нижней части цепи. Ток от Ячейка 10,0 В к узлу помечен 𝐼 и считается током в узел. Ток от узла к 20 Ом помечено 𝐼 и считается вне узла. Электрический ток от узла к Ячейка 5,0 В помечена 𝐼 и считается вне узла.

Мы можем применить второй закон Кирхгофа к каждому контуру цепи, чтобы найти разность потенциалов на каждом резисторе.

Начиная с цикла, содержащего 𝑉 и 𝑅, имеем 𝑉−𝑉=0,В поэтому разность потенциалов на 𝑅 равна 𝑉=10.0.V

Используя закон Ома, мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=10,020𝐼=0,5.VΩA

Это равно 𝐼. Ток через Резистор 20 Ом 𝐼 и, следовательно, равно 0,5 А.

Часть 2

Далее мы можем посмотреть на цикл, содержащий 𝑉, 𝑉 и 𝑅: 𝑉+𝑉−𝑉=05,0+10,0−𝑉=0,VVVV

Итак, разность потенциалов на 𝑅 равна 𝑉=15,0.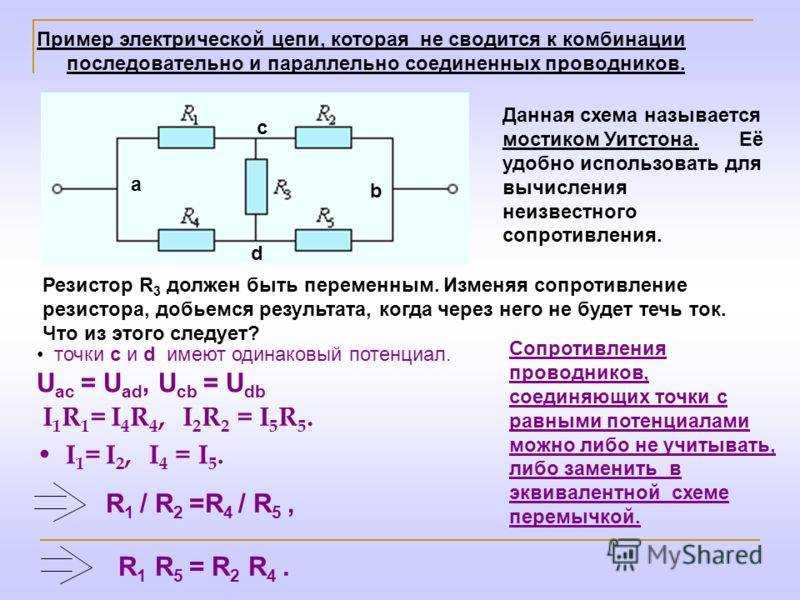 V

По закону Ома мы можем рассчитать ток через 𝑅: 𝐼=𝑉𝑅𝐼=15,015𝐼=1,0.VΩA

Это равно 𝐼. Ток на минусе терминал 5,0 А аккумулятор 𝐼 и, следовательно, равно 1,0 А.

Часть 3

Используя первый закон Кирхгофа, мы можем вычислить 𝐼 из узел в нижней части схемы: 𝐼=𝐼+𝐼𝐼=1.0+0.5=1.5.A

Ток на минусовой клемме Батарея 10,0 В есть 𝐼 и поэтому равно 1,5 А.

Пример 5. Использование законов Кирхгофа для анализа комбинационных цепей с Unknown Components

В показанной схеме сопротивление одного из резисторов неизвестно. Общая ток в цепи равен 0,25 А.

1. Найти текущий 𝐼. Отдай свое ответ до двух знаков после запятой.
2. Найти текущий 𝐼. Дайте ответ на два десятичные знаки.
3. Найдите разность потенциалов на неизвестном резисторе. Дайте свой ответ на Ближайшая вольт.

Ответ

Часть 1

Начнем с маркировки компонентов схемы.

В первой части вопроса нам предлагается найти 𝐼, ток через 𝑅. Для этого нам нужно найти разность потенциалов на параллельном участке цепи.

Мы можем преобразовать параллельный участок цепи в эквивалентный резистора по следующей формуле: 𝑅=1𝑅+1𝑅.

Вставка значений 𝑅=2,5Ом и 𝑅=3,2Ω дает нам 𝑅=12,5+13,2𝑅=1,40.ΩΩΩ

Зная, что ток в цепи 0,25 А, потенциал разницу между эквивалентным резистором можно рассчитать, используя сопротивление Ом. закон: 𝑉=𝐼𝑅𝑉=0,25×1,40𝑉=0,35.AΩV

Эта разность потенциалов одинакова на обеих ветвях параллельного участок цепи. Тогда ток 𝐼 может быть рассчитывается по закону Ома: 𝐼=𝑉𝑅𝐼=0,352,5𝐼=0,14.VΩA

Часть 2

Во второй части вопроса нам предлагается рассчитать текущий 𝐼.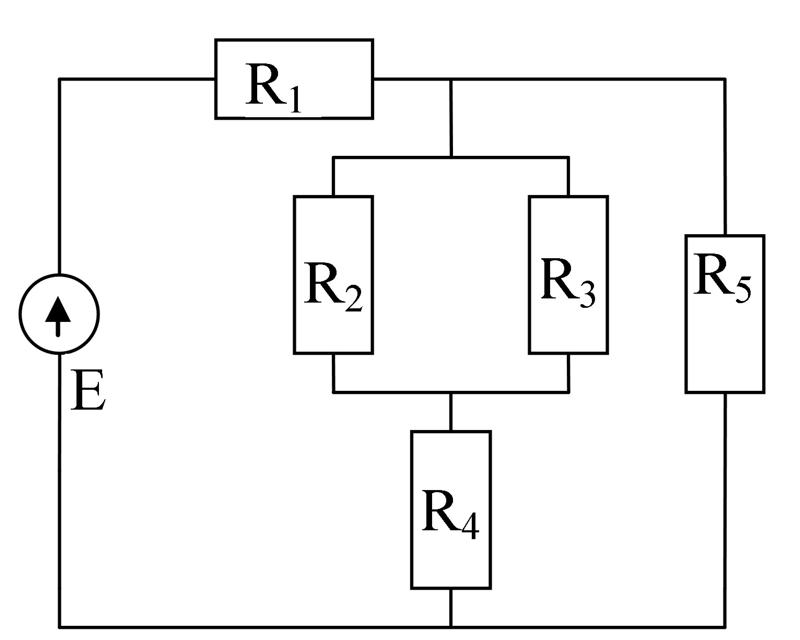

Мы уже рассчитали разность потенциалов на параллели участок цепи, поэтому мы можем применить закон Ома к 𝑅: 𝐼=𝑉𝑅𝐼=0,353,2𝐼=0,11.VΩA

Часть 3

В третьей части этого вопроса нам предлагается рассчитать потенциал разница на неизвестном резисторе.

Мы можем использовать второй закон Кирхгофа, чтобы решить эту задачу. Кирхгофа Второй закон гласит, что сумма разностей потенциалов на каждом отдельная компонента в цикле равна нулю. Для этой схемы мы запишет разность потенциалов через 𝑅 как 𝑉, по параллельному сечению как 𝑉, а поперек 𝑅 как 𝑉: 12−𝑉−𝑉−𝑉=0,V

Мы уже рассчитали 𝑉=0,35В. 𝑉 можно рассчитать по закону Ома: 𝑉=𝐼𝑅𝑉=0,25×2,2𝑉=0,55.AΩV

Мы можем подставить их в уравнение для второго закона Кирхгофа, помня, что это уменьшение потенциала, поэтому они отрицательны: 12−𝑉−0,55−0,35=0,VVV

Затем мы можем изменить это, чтобы получить значение разности потенциалов через 𝑅 неизвестный резистор: 𝑉=11,1.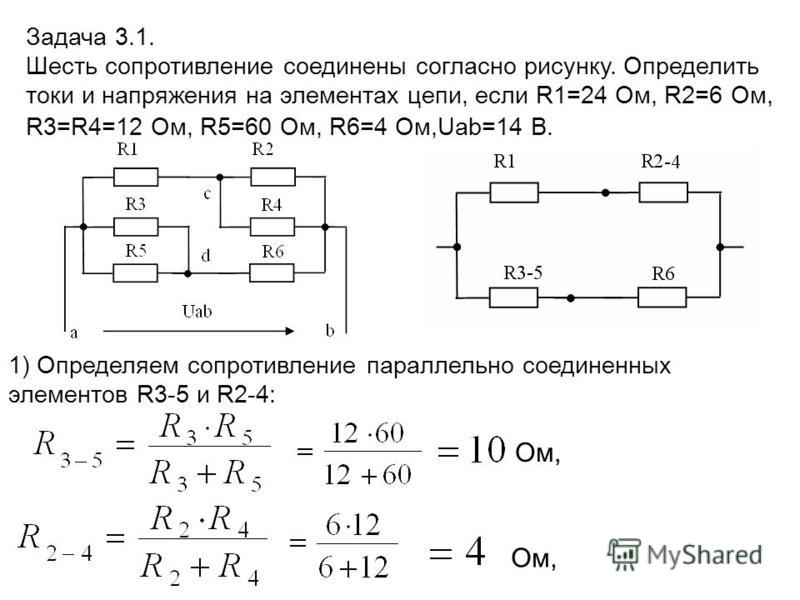 V

Итак, разность потенциалов на неизвестном резисторе с точностью до вольт, 11 В.

Давайте обобщим то, что мы узнали из этого объяснения, в следующем ключевые моменты.

Ключевые точки

• В комбинированных цепях мы можем идентифицировать части цепей, соединенные параллельно и цепи последовательно. Мы можем рассчитать эквивалентное сопротивление этих разделы для анализа комбинированной схемы.
• Первый закон Кирхгофа гласит, что сумма токов в соединение/узел в цепи, 𝐼+𝐼+⋯()()inin, должно совпадать с сумма токов из узла/узла, 𝐼+𝐼+⋯()()outout: 𝐼+𝐼+⋯=𝐼+𝐼+⋯.()()()()ininoutout
• Второй закон Кирхгофа гласит, что сумма разности потенциалов по каждому компоненту, 𝑉,𝑉,…𝑉, в цикле равно нулю: 𝑉+𝑉+⋯+𝑉=0.
• В комбинированных схемах мы можем идентифицировать петли и узлы, которые позволяют нам применять законы Кирхгофа для анализа цепи.

Последовательная цепь постоянного тока — инженерное мышление

Изучите основные принципы последовательной цепи постоянного тока, от напряжения, тока, сопротивления и потребляемой мощности до использования мультиметра. В конце вам также предстоит решить задачу с ответами.

Прокрутите вниз, чтобы посмотреть обучающее видео на YouTube.

Помните, что электричество опасно и может привести к летальному исходу, вы должны иметь квалификацию и компетентность для выполнения любых электромонтажных работ.

Что такое последовательная цепь постоянного тока?

Когда мы соединяем компоненты в электрическую цепь, мы можем соединить их либо последовательно, либо параллельно, или мы можем объединить их, чтобы создать последовательно-параллельную цепь. В этой статье подробно описывается тип серии, который является самым основным, мы рассмотрим другие типы в других статьях, которые вы можете прочитать ЗДЕСЬ .

Если мы поместим два компонента в линию, конец к концу или с каким-либо проводом между ними, то они будут соединены последовательно. У электронов есть только один путь, по которому они могут пройти, поэтому все они будут проходить через каждый из компонентов.

через GIPHY

Просто отметим, что в этих анимациях мы используем поток электронов от отрицательного к положительному. Возможно, вы привыкли видеть обычный ток, который меняется от положительного к отрицательному. Электронный поток — это то, что происходит на самом деле, первоначальная теория была традиционной, но ее все еще учат, потому что ее легко понять. Просто знайте о двух и о том, какой из них мы используем.

Сопротивление в последовательных цепях

Каждый компонент будет иметь определенное сопротивление, сопротивление противодействует приложенному напряжению. Мы измеряем сопротивление в единицах Ом с символом Ом Ω.

В последовательных цепях; мы находим полное сопротивление цепи, просто складывая все сопротивления вместе. Мы маркируем каждый резистор заглавной буквой R и нумеруем их R1, R2, R3 и т. д.

Общее сопротивление отображается с заглавной буквы R и нижним индексом T, который представляет общее сопротивление или полное сопротивление.

Рассчитать общее сопротивление последовательной цепи очень просто, мы просто складываем значение сопротивления каждого резистора.

Допустим, у нас есть цепь с одним резистором, это наш R1, и он имеет значение 10 Ом. Каково наше общее сопротивление? Ну это просто, полное сопротивление 10 Ом.

Если затем добавить в цепь второй резистор R2 с сопротивлением 5 Ом, общее сопротивление составит 15 Ом, 10 Ом + 5 Ом.

Если мы добавим еще один резистор 5 Ом, то общее сопротивление составит 20 Ом.

На самом деле провода тоже будут добавлять некоторое сопротивление, но оно очень мало, вам, возможно, придется учитывать это в зависимости от того, насколько точным должен быть ваш проект.

Последовательный ток

Ток — это поток электронов. Это как вода, которая течет по трубе. Чем больше ток, тем больше электронов течет. Мы измеряем ток в амперах, но инженеры склонны сокращать их до ампер. Обозначается заглавной буквой А.

Мы подробно рассмотрели ток в нашей предыдущей статье, посмотрите ЗДЕСЬ .

Мы измеряем ток, помещая амперметр в цепь, через которую проходят электроны. Это похоже на счетчик воды в том смысле, что через него должна пройти вода, чтобы мы могли ее измерить. Мы можем подключить мультиметр к цепи, чтобы также измерить ток.
Мультиметр должен быть подключен к цепи для снятия показаний, через него будет протекать ток. Измеритель добавит некоторое сопротивление в цепь, но это настолько мало, что мы обычно можем его игнорировать.

Если у вас еще нет мультиметра, мы настоятельно рекомендуем вам его приобрести, он необходим для устранения неполадок и понимания. Купить их можно по ссылке ниже.

Мы можем рассчитать общий ток цепи, разделив напряжение на сопротивление.

Если мы подключим резистор 10 Ом к батарее 9 В, 9 В ÷ 10 Ом даст нам 0,9 А.

Если мы добавим в цепь еще один резистор 5 Ом, это даст нам сопротивление 15 Ом, поэтому 9 В ÷ 15 Ом = 0,6 А.

Затем, если мы добавим еще один резистор 5 Ом, это даст нам сопротивление 20 Ом, поэтому
9 В ÷ 20 Ом = 0,45 А.

Мы видим, что по мере того, как мы увеличиваем сопротивление цепи, ток уменьшается, поэтому проходит меньше электронов, а это означает, что мы можем выполнять меньше работы. Мы можем визуализировать это, соединив светодиод с резистором в цепи. Чем выше сопротивление; тем тусклее будет светодиод.

Мы также можем использовать резисторы для защиты компонентов в цепи. Если мы используем резистор 100 Ом с сопротивлением 9V, ток будет около 0,09 А или 90 мА, и это приведет к перегоранию светодиода. Если мы используем резистор 450 Ом; ток будет около 0,02 А или 20 мА, поэтому светодиод должен быть в порядке. Если мы используем резистор 900 Ом, ток будет 0,01 А или 10 мА, а светодиод будет очень тусклым.

В последовательной цепи; ток одинаков во всей цепи. Это важно помнить. Как подробно описано ниже; если мы поместим счетчик в любое место, мы получим одно и то же показание. Это потому, что электроны могут течь только по одному пути, и все они движутся вместе в одном и том же направлении, поэтому
ток должен быть одинаковым. Неважно, где мы измеряем или где размещаем резистор, даже если мы поменяем порядок резисторов, ток будет одинаковым в любом месте последовательной цепи.

Последовательное напряжение

Помните, что напряжение — это сила, выталкивающая электроны, это как давление в трубе. Чем выше давление; чем больше воды может протекать, тем выше напряжение; тем больше электронов может течь. Мы можем видеть, что, изменяя напряжение на лампе, как показано ниже, яркость лампы увеличивается по мере увеличения напряжения.

Если мы поместим в цепь батарею на 9 В, мы подадим на цепь 9 В. Мы можем увеличить это, соединив батареи последовательно.

Итак, если мы поместим две батареи 9 в цепь последовательно, мы получим 18 В, три батареи 9 В дадут нам 27 В.

Возьмем 9-вольтовую батарею и добавим в цепь резистор R1 сопротивлением 10 Ом. Если мы используем мультиметр для измерения резистора, мы получим показание напряжения 9 В. Если мы добавим еще один резистор 10 Ом, мы получим показание 9 В на двух резисторах, но мы получим показание 4,5 В, если мы будем измерять на любом из резисторов по отдельности. Таким образом, резисторы делят напряжение.

Если мы заменим резистор R2 на резистор 5 Ом, общее напряжение снова будет 9 В, и это то, что мы увидим, если измерим два резистора. Но если мы измерим на резисторе 10 Ом, мы увидим напряжение 6 В, а если мы измерим на резисторе 5 Ом, мы увидим 3 В.

Если мы добавим в цепь еще один резистор R3 с сопротивлением 5 Ом, мы снова получим общее падение напряжения на 3 резисторах 9 В. На резисторе R1 10 Ом читаем 4,5 В, на резисторе R2 5 Ом читаем 2,25 В, а на последнем резисторе R3 5 Ом снова 2,25 В.

Мы можем объединить эти показания, чтобы найти напряжение на разных участках цепи. Например, если мы измеряем от батареи и через R1, мы видим 4,5 В. Если мы измерим от батареи между R1 и R2, мы получим 6,75 В, потому что 4,5 В + 2,25 В.

Таким образом, в отличие от тока, где он одинаков во всей цепи, напряжение будет разным во всей последовательной цепи.

через GIPHY

Это показывает нам, что напряжение уменьшается с каждым резистором, поэтому резистор создает падение напряжения. Это цель резистора, чтобы уменьшить напряжение или давление. Происходит то, что резистор создает более трудный путь для прохождения электронов, и по мере прохождения они будут сталкиваться с другими электронами. Это столкновение преобразует энергию в тепло. Столько же
электрона войдут и выйдут из резистора, просто у них будет меньше энергии или давления, поэтому произойдет падение напряжения.

Расчет падения напряжения

Мы можем рассчитать падение напряжения на каждом резисторе отдельно, умножив общий ток в цепи на сопротивление компонента. Помните, что в последовательных цепях ток везде одинаков. Общее падение напряжения будет суммой всех отдельных падений напряжения вместе взятых.

Первая схема, там был резистор 10 Ом сам по себе. В цепи был ток 0,9Таким образом, 0,9 А х 10 Ом = 9 В. Таким образом, падение напряжения на резисторе равно 9 В, как и на источнике напряжения.

Во второй цепи резисторы 10 Ом и 5 Ом вместе, ток в этой цепи 0,6 А, поэтому падение напряжения на первом резисторе 0,6 А x 10 Ом = 6 В, на втором резисторе 5 Ом и ток было то же самое, поэтому 0,6 А x 5 Ом = 3 В. Общее падение напряжения составляет 6В + 3В = 9В.

Третья цепь имеет резисторы на 10 Ом и два резистора на 5 Ом, ток в цепи равен 0,45 А, поэтому R1 равен 0,45 А x 10 Ом = 4,5 В, R2 и R3 будут равны 0,45 А x 5 Ом = 2,25 В.
Таким образом, общее падение напряжения составляет 9 В (4,5 В + 2,25 В + 2,25 В).

Потребляемая мощность

Как измерить энергопотребление схемы? Мы можем использовать следующие уравнения:

Либо
Мощность (Вт) = Напряжение ² / Сопротивление
Или
Мощность (Вт) = Напряжение x Ток.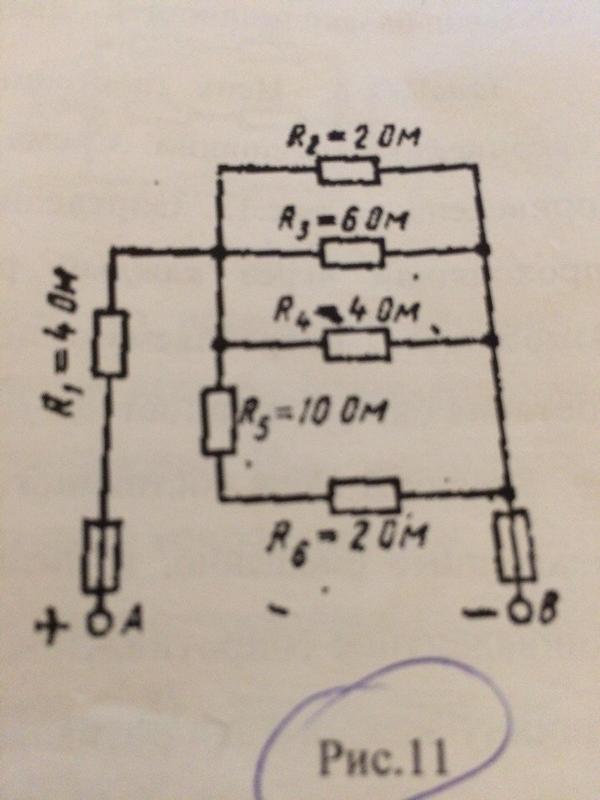

Вам может быть интересно, как резистор может потреблять энергию? Поскольку резистор создает падение напряжения, электроны теряют часть энергии. Куда уходит эта энергия? Электрическая энергия преобразуется в тепло, которое, глядя на некоторые резисторы под тепловизионной камерой, можно увидеть выделяющееся тепло.

Таким образом, потребляемая мощность фактически представляет собой тепло, отводимое от схемы.

В этой цепи сопротивление составляет 10 Ом, батарея обеспечивает 9 В, ток составляет 0,9 А, а схема потребляет 8,1 Вт. Как мы это вычисляем? Используя метод 1, 9 В в квадрате или 9, умноженное на 9, составляет 81, ÷ на 10 Ом составляет 8,1 Вт. В качестве альтернативы 9 В x 0,9 А = 8,1 Вт

В следующей цепи с резистором 10 Ом и резистором 5 Ом общее сопротивление было 15 Ом, а ток 0,6 А, поэтому
9 В в квадрате равно 81, деленное на 15 Ом, составляет 5,4 Вт
или 9 В x 0,6 А = 5,4 Вт.

В цепи с резисторами 10 Ом и двумя резисторами 5 Ом общее сопротивление цепи составило 20 Ом, а ток 0,45 А, поэтому
9 В в квадрате равно 81, деленное на 20 Ом, равно 4,05 Вт
или 9 В x 0,45 А = 4,05 Вт

Проблема: светодиод подключен к батарее 9 В, и ток в цепи должен быть ограничен максимальным значением 0,02 А или 20 мА, иначе светодиод перегорит.