Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно разбираться в определенных понятиях и находить весомые аргументы и методы решения, что и предложено данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями, чтобы вам больше не нужно было определять все это онлайн.
Что значит найти область определения
После того как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Область определения и область значения можно найти и для кубического корня (куб. √), к примеру, для x+2.
Ограничение области определения
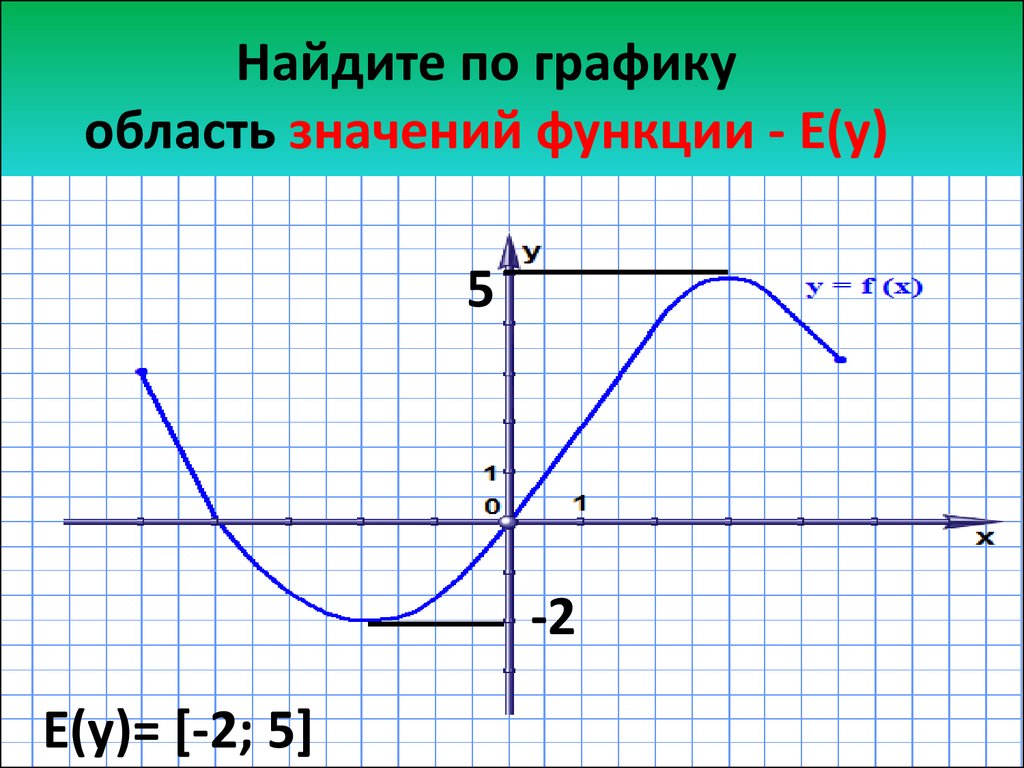
Область определения функции или ООФ рассматривается еще в школьном курсе алгебры. У действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально узнавать ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
Определение 1- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на сложение корня четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.

При отсутствии хотя бы одного признака, область определения приходится искать другим образом (и это не с калькулятором). Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно иметь следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом, чтобы понимать понимания перечисления числовых множеств.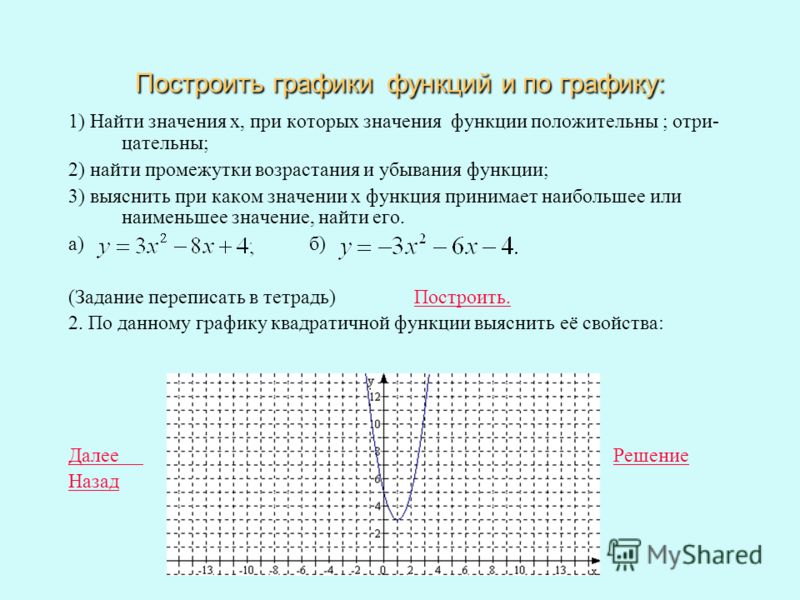
Найти область определения функции вида y=x7+x+5+tgx
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Чтобы найти область определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.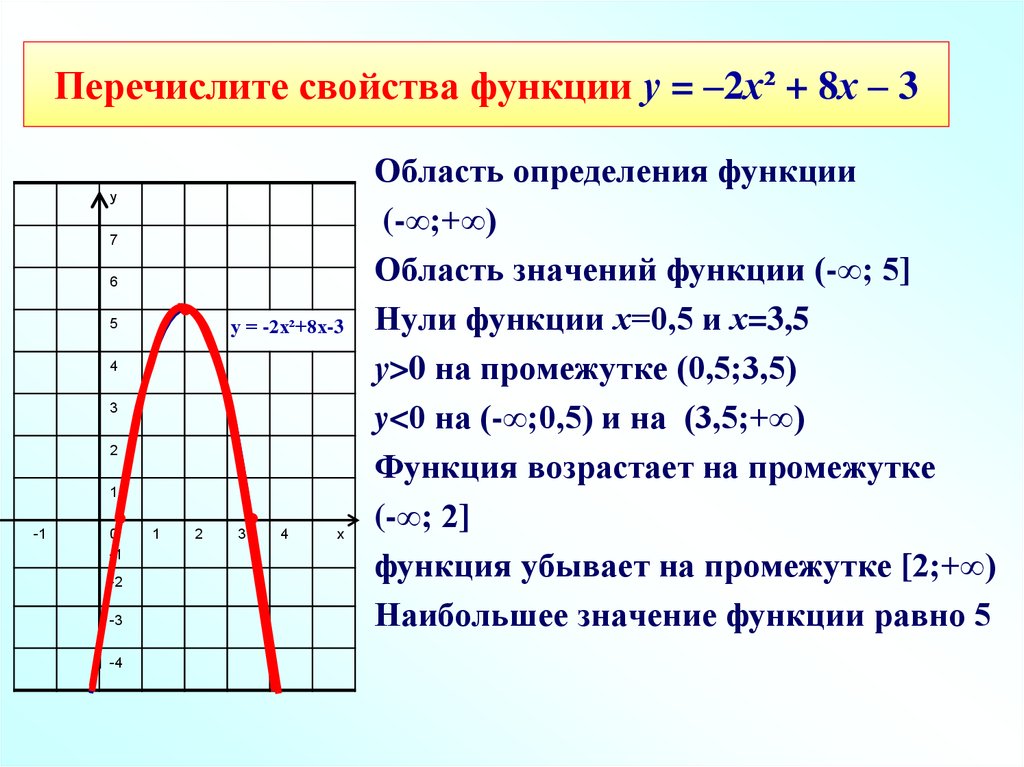
Запишется D(f)=D(f1)D(f2)…D(fn)
Пример 2Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1является постоянной функцией, f2
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x)– произведение постоянной функции и f. Область определения – это все действительные числа области определения

Естестввенным образом получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x – [0, +∞).
Области определения y=f(x) и y=−f(x)совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Пример 3Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2. В данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Пример 4Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞)
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Известно, что D(f)является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1)
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Пример 5Найти область определения y=ln x2.
Решение
Алгоритм решения этого уравнения или функции следующий.
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена.
Ответ: (−∞, 0)∪(0, +∞).
Пример 6Найти область определения функции y=(arcsin x)-12.
Решение
График решения следующий.
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x))))
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3– логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Пример 8Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3–это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4– это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Действия с корнями
Корни в математике, в частности, функцию с корнем можно определить следующим образом:
y=n√x. N здесь — натуральное число, большее за единицу.
Область определения корня зависит от того, каков показатель: четный или нечетный.
Если n является четным числом (n=2m). Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Если показатель корня — нечетное число, большее за единицу (n=2m+1 и m принадлежит к n), то областью определения корня будет множество всех действительных чисел.
Также важным является вопрос, как складывать корни.
Сложение и вычитание корней возможно при условии наличия одинакового подкоренного выражения. К примеру, сложение и вычитание корней возможно 2√3 и 4√3. Можно ли складывать корни или вычитать в случае 2√3 и 2√5? Ответ — нет.
Как решать корни во втором случае? Вы можете упростить подкоренное выражение и привести их корни к одинаковому подкоренному выражению. После этого вы сможете как считать корни, так и вычитать корни.
К основным действиям с корнями относят:
- умножение корней;
- деление корней;
- корень минус корень или плюс.
Область определения логарифма с переменной в основании
Определение 3Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
К аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Пример 9Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Пример 10Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.
| Функция | Ее область определения |
Сумма, разность, произведение функций f1, f2,…, fn | Пересечение множеств D(f1), D(f2), …, D(fn) |
Сложная функция y=f1(f2(f3(…fn(x))))
В частности, y=f1(f2(x)) | Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1)
x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y=k·x | R |
| Линейная y=k·x+b | R |
Обратная пропорциональность y=kx | -∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C – число | D(f) |
Дробная y=f1(x)f2(x)
В частности, если f1(x), f2(x) – многочлены | Множество всех x, которые одновременно удовлетворяют условиям
f2(x)≠0 |
| y=f(x)n, где n – четное | x∈D(f1), f(x)≥0 |
y=logf2(x)f1(x)
В частности, y=logaf1(x)
В частности, y=logf2(x)a | x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1
x∈D(f1), f1(x)>0
x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Функция ВПР – Служба поддержки Майкрософт
Excel
Формулы и функции
Для работы со ссылками
Для работы со ссылками
Функция ВПР
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Совет: Попробуйте использовать новую функцию ПРОСМОТРX, улучшенную версию функции ВПР, которая работает в любом направлении и по умолчанию возвращает точные совпадения, что делает ее проще и удобнее в использовании, чем предшественницу.
Находите данные по строкам в таблице или диапазоне с помощью функции ВПР. Например, можно найти цену автомобильной детали по ее номеру или найти имя сотрудника по его идентификатору.
Самая простая функция ВПР означает следующее:
=ВПР(искомое значение; место для его поиска; номер столбца в диапазоне с возвращаемым значением; возврат приблизительного или точного совпадения — указывается как 1/ИСТИНА или 0/ЛОЖЬ).
Совет: Секрет функции ВПР состоит в организации данных таким образом, чтобы искомое значение (Фрукт) отображалось слева от возвращаемого значения, которое нужно найти (Количество).
Используйте функцию ВПР для поиска значения в таблице.
Синтаксис
ВПР(искомое_значение, таблица, номер_столбца, [интервальный_просмотр])
Например:
- org/ListItem”>
-
=ВПР(“Иванов”;B2:E7;2;ЛОЖЬ)
-
=ВПР(A2;’Сведения о клиенте’!A:F;3;ЛОЖЬ)
=ВПР(A2;A10:C20;2;ИСТИНА)
|
Имя аргумента |
Описание |
|---|---|
|
искомое_значение (обязательный) |
Значение для поиска. Например, если таблица охватывает диапазон ячеек B2:D7, искомое_значение должно находиться в столбце B. Искомое_значение может являться значением или ссылкой на ячейку. |
|
таблица (обязательный) |
Диапазон ячеек, в котором будет выполнен поиск искомого_значения и возвращаемого значения с помощью функции ВПР. Вы можете использовать именованный диапазон или таблицу, а также имена в аргументе вместо ссылок на ячейки. Первый столбец в диапазоне ячеек должен содержать искомое_значение. Узнайте, как выбирать диапазоны на листе . |
|
номер_столбца (обязательный) |
Номер столбца (начиная с 1 для крайнего левого столбца таблицы), содержащий возвращаемое значение. |
|
интервальный_просмотр (необязательный) |
Логическое значение, определяющее, какое совпадение должна найти функция ВПР, — приблизительное или точное.
|
Начало работы
Для построения синтаксиса функции ВПР вам потребуется следующая информация:
-
Значение, которое вам нужно найти, то есть искомое значение.
-
Диапазон, в котором находится искомое значение.
 Помните, что для правильной работы функции ВПР искомое значение всегда должно находиться в первом столбце диапазона. Например, если искомое значение находится в ячейке C2, диапазон должен начинаться с C.
Помните, что для правильной работы функции ВПР искомое значение всегда должно находиться в первом столбце диапазона. Например, если искомое значение находится в ячейке C2, диапазон должен начинаться с C. -
Номер столбца в диапазоне, содержащий возвращаемое значение. Например, если в качестве диапазона вы указываете B2:D11, следует считать B первым столбцом, C — вторым и т. д.
-
При желании вы можете указать слово ИСТИНА, если вам достаточно приблизительного совпадения, или слово ЛОЖЬ, если вам требуется точное совпадение возвращаемого значения. Если вы ничего не указываете, по умолчанию всегда подразумевается вариант ИСТИНА, то есть приблизительное совпадение.
Теперь объедините все перечисленное выше аргументы следующим образом:
=ВПР(искомое значение; диапазон с искомым значением; номер столбца в диапазоне с возвращаемым значением; приблизительное совпадение (ИСТИНА) или точное совпадение (ЛОЖЬ)).
Примеры
Вот несколько примеров использования функции ВПР.
Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
С помощью функции ВПР вы можете объединить несколько таблиц в одну, если одна из таблиц содержит поля, общие для всех остальных. Это может быть особенно удобно, если вам нужно поделиться книгой с пользователями более старых версий Excel, которые не поддерживают функции данных с несколькими таблицами в качестве источников данных. Благодаря объединению источников в одну таблицу и изменению источника функции данных на новую таблицу, функцию данных можно использовать в более старых версиях Excel (при условии, что функция данных поддерживается в более старой версии).
|
Здесь столбцы A–F и H содержат значения или формулы, которые используют значения только на этом листе, а в остальных столбцах используется функция ВПР и значения столбца А (код клиента) и столбца B (адвокат) для получения данных из других таблиц. |
-
Скопируйте таблицу с общими полями на новый лист и присвойте имя.
-
Щелкните Данные > Работа с данными > Отношения, чтобы открыть диалоговое окно “Управление отношениями”.
org/ListItem”>
-
Поле, которое связывает таблицы (указано в скобках в диалоговом окне). Это искомое_значение для вашей формулы ВПР.
-
Имя связанной таблицы подстановки. Это таблица в вашей формуле ВПР.
-
Поле (столбец) в связанной таблице подстановки, содержащее данные, которые вам нужны в новом столбце. Эта информация не отображается в диалоговом окне “Управление отношениями”. Чтобы увидеть, какое поле нужно получить, посмотрите на связанную таблицу подстановки.
 Обратите внимание на номер столбца (A=1) — это номер_столбца в вашей формуле.
Обратите внимание на номер столбца (A=1) — это номер_столбца в вашей формуле. -
Чтобы добавить поле в новую таблицу, введите формулу ВПР в первом пустом столбце, используя сведения, собранные на шаге 3.
В нашем примере столбец G использует адвоката (искомое_значение) для получения данных ставки из четвертого столбца (номер_столбца = 4) из таблицы листа “Адвокаты”, тблАдвокаты (таблица), с помощью формулы =ВПР([@Адвокат];тбл_Адвокаты;4;ЛОЖЬ).
Формула также может использовать ссылку на ячейку и ссылку на диапазон. В нашем примере это =ВПР(A2;’Адвокаты’!A:D;4;ЛОЖЬ).
-
Продолжайте добавлять поля, пока не получите все необходимые поля.
 Если вы хотите подготовить книгу, содержащую функции данных, которые используют несколько таблиц, измените источник данных для функции данных на новую таблицу.
Если вы хотите подготовить книгу, содержащую функции данных, которые используют несколько таблиц, измените источник данных для функции данных на новую таблицу.
Для каждого отношения в списке обратите внимание на следующее.
|
Проблема |
Возможная причина |
|---|---|
|
Неправильное возвращаемое значение |
Если аргумент интервальный_просмотр имеет значение ИСТИНА или не указан, первый столбец должны быть отсортирован по алфавиту или по номерам. Если первый столбец не отсортирован, возвращаемое значение может быть непредвиденным. Отсортируйте первый столбец или используйте значение ЛОЖЬ для точного соответствия. |
|
#Н/Д в ячейке |
Дополнительные сведения об устранении ошибок #Н/Д в функции ВПР см. в статье Исправление ошибки #Н/Д в функции ВПР. |
|
#ССЫЛКА! в ячейке |
Если значение аргумента номер_столбца больше, чем число столбцов в таблице, появится значение ошибки #ССЫЛКА!. Дополнительные сведения об устранении ошибок #ССЫЛКА! в функции ВПР см. в статье Исправление ошибки #ССЫЛКА!. |
|
#ЗНАЧ! в ячейке |
Если значение аргумента таблица меньше 1, появится значение ошибки #ЗНАЧ!. Дополнительные сведения об устранении ошибок #ЗНАЧ! в функции ВПР см. в статье Исправление ошибки #ЗНАЧ! в функции ВПР. |
|
#ИМЯ? в ячейке |
Значение ошибки #ИМЯ? чаще всего появляется, если в формуле пропущены кавычки. Дополнительные сведения см. в статье Исправление ошибки #ИМЯ?. |
|
Ошибки #ПЕРЕНОС! в ячейке |
Эта конкретная ошибка #ПЕРЕНОС! обычно означает, что формула использует неявное пересечение для искомого значения и применяет весь столбец в качестве ссылки. Например, =ВПР(A:A;A:C;2;ЛОЖЬ). Вы можете устранить эту проблему, привязав ссылку подстановки с помощью оператора @, например: =ВПР(@A:A;A:C;2;ЛОЖЬ). Кроме того, вы можете использовать традиционный метод ВПР и ссылаться на одну ячейку вместо целого столбца: =ВПР(A2;A:C;2;ЛОЖЬ). |
|
Действие |
Примечания |
|---|---|
|
Используйте абсолютные ссылки в аргументе интервальный_просмотр |
Использование абсолютных ссылок позволяет заполнить формулу так, чтобы она всегда отображала один и тот же диапазон точных подстановок. Узнайте, как использовать абсолютные ссылки на ячейки. |
|
Не сохраняйте числовые значения или значения дат как текст. |
При поиске числовых значений или значений дат убедитесь, что данные в первом столбце аргумента таблица не являются текстовыми значениями. Иначе функция ВПР может вернуть неправильное или непредвиденное значение. |
|
Сортируйте первый столбец |
Если для аргумента интервальный_просмотр указано значение ИСТИНА, прежде чем использовать функцию ВПР, отсортируйте первый столбец таблицы. |
|
Используйте подстановочные знаки |
Если значение аргумента интервальный_просмотр — ЛОЖЬ, а аргумент искомое_значение представляет собой текст, то в аргументе искомое_значение допускается использование подстановочных знаков: вопросительного знака (?) и звездочки (*). Например, с помощью функции =ВПР(“Ивано?”;B2:E7;2;ЛОЖЬ) будет выполнен поиск всех случаев употребления Иванов с последней буквой, которая может меняться. |
|
Убедитесь, что данные не содержат ошибочных символов. |
При поиске текстовых значений в первом столбце убедитесь, что данные в нем не содержат начальных или конечных пробелов, недопустимых прямых (‘ или “) и изогнутых (‘ или “) кавычек либо непечатаемых символов. В этих случаях функция ВПР может возвращать непредвиденное значение. Для получения точных результатов попробуйте воспользоваться функциями ПЕЧСИМВ или СЖПРОБЕЛЫ. |
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Функция ПРОСМОТРX
Видео: когда и как использовать ВПР
Краткий справочник: функция ВПР
Исправление ошибки #Н/Д в функции ВПР
Поиск значений с помощью функций ВПР, ИНДЕКС и ПОИСКПОЗ
Функция ГПР
то, что вы найдете закопанным в грязи под Чарльзом Ф. кеттеринг старший средняя школа (детройт, мичиган)
кровь:
промокшая и запекшаяся на белых носках, на синих сетчатых футболках.
синяя палочка и барабанные палочки лидера группы.
Сера из спичечного коробка пролилась на окурки ньюпортских сигарет.
презервативы нескольких матовых оттенков. учебники по химии для десятого класса
моделирование атомарных жирных кислот.
наполовину высосанные оранжевые соски, спрятанные под талонами задержанных.
фото из черных волос, выстриженных для предварительного согласования с косметологом.
сломанные черные блестящие ремни с розовыми пряжками в форме губ.
свечной воск с прошлогоднего бдения, когда
де’андре «чаки» Браун рухнул на руки своему товарищу по команде
. отпечатки обуви товарища по команде качались взад и вперед
, где проводилось бдение, закусив губу.
сломанные мобильные телефоны. куски черного резинового коврика
под входом, который мы пересекали каждое утро,
зубы стиснуты. записки о согласии, которые девушки написали, но не имели в виду
и хотели бы, чтобы они не сдали обратно.
сломанные зубы. потерянные слуги. скомканные письма, написанные вожатым
и выброшенные из-за неразборчивого почерка. списки телефонов
клиник по прерыванию беременности. сдутые воздушные шары на день святого валентина с
растоптанной белой лентой. объявления о продаже комплектов люльки.
шарф для пианино моего первого парня. обложка альбома phyllis hymen
. путь от
выходная дверь за школой, через которую некоторые мальчики
не увидят, как уходят некоторые девочки.
разорванные отчеты о проделанной работе.
кастеты. два
афро кирки по разные стороны школы. микробы в коридоре проходят
от мальчика, держащегося за промежность.
пыль ржавой арматуры. голубиные кости. украденные номера телефонов.
т.о.т. автобус проходит с 1960 года, года закладки фундамента.
приостановлено действие водительских прав. разбитые очки изо льда
упакован в снежки. непрочитанные брошюры по номеру
charles f. Кеттеринг, фермер с плохим зрением,
Кеттеринг, фермер с плохим зрением,
, изобрел электростартер
и инкубатор для недоношенных.
хвосты опоссумов. оригинальные баллы. скрученные записи журнала
, написанные и подожженные, с подробным описанием злоупотреблений. половые жидкости.
ДНК. конверты с письмами-приемками
в страны дальние. украденные учителями математики ключи ответов
порваны и сожжены зажигалками.
зажигалки. сотни контейнеров для картофеля фри Mcdonald’s
, потому что они легко расплющиваются. сорняк.
имитация бриллиантов из диадемы возвращения на родину
инкрустированная грязью цвета дерьма. исследовательские работы по Кеттерингу
с подробным описанием его лечения
венерической болезни
, которое включало нагревание пациентов в термошкафах
до тех пор, пока температура их тела не поднималась до 130 градусов.
красные пометки учителей на сочинениях с подробным описанием злоупотреблений.
пустые карточки спринта.
шина, которую должен был носить футбольный капитан
, но решил, что он выглядит геем.
лента для толстяков. куски рваных синих и белых стартовых курток
от того, как мальчишки боролись друг с другом
весной на земле.
мой первый поэтический журнал. страницы его стихов
с тиснением в виде кедов первых известных брендов.
скомканные предсмертные записки, написанные карандашом и опаленные пеплом.
потерял ключи от дома. фото первых влюбленностей. пули.
неопубликованные статьи разочарованных учителей
которые кратко изучили результаты исследований,
используя charles f. kettering инструмент школьной оценки климата
с подробным описанием психологического воздействия
внешних стрессоров на учащихся, обычно связанных
с моделями домашнего насилия во взрослом возрасте. толстые шнурки.
гильзы. фляжка для виски Джим Бим, которую старый директор выбросил
думал, что кто-то идет.
план занятий моего последнего парня, тщательно структурированный
на обороте
комикса. отпечатки скромного маминого каблука
от пересечения бесплодной лобной площади на моем выпускном.
статьи в свободной прессе о неназванных несовершеннолетних, тела которых были найдены
в мусорных баках возле Кеттеринга. кристаллизованный блок образовался
из ткани, которую мой отец вручил мне на выпускном
от слез, которые я не мог объяснить.
Помощь в оплате лекарств | Medicare
Что такое дополнительная помощь?
«Дополнительная помощь» — это программа Medicare, помогающая людям с ограниченным доходом и ресурсами оплачивать Покрытие лекарств Medicare (часть D) премии, франшизы, совместное страхование и другие расходы. Что такое премия, франшиза, совместное страхование или доплата?
Вам также не придется платить штраф за позднюю регистрацию в части D, пока вы получаете дополнительную помощь.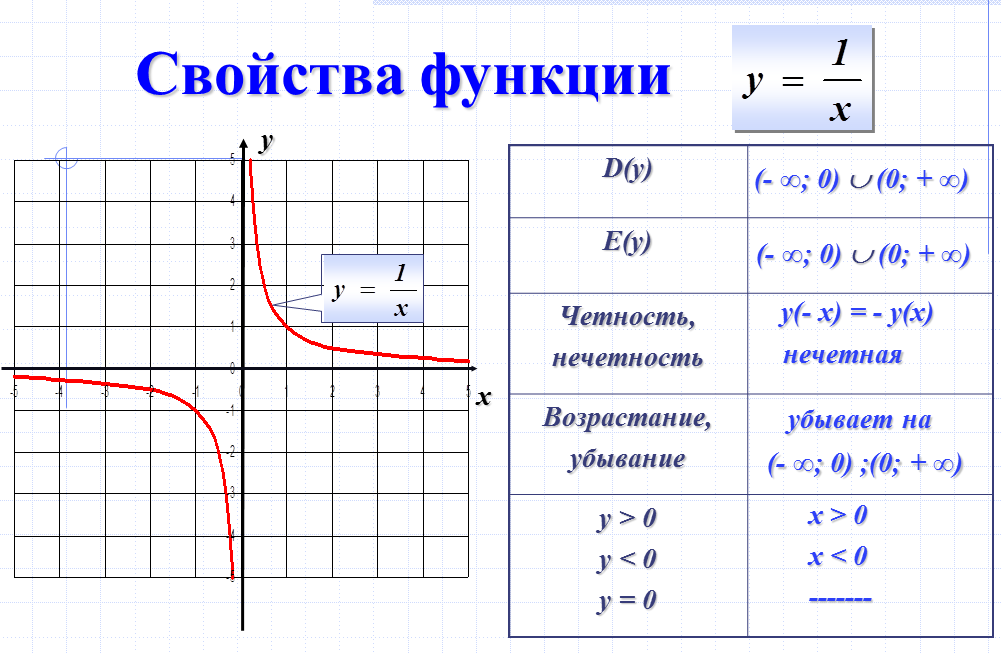 Каков штраф по Части D?
Каков штраф по Части D?
Некоторые люди получают дополнительную помощь автоматически, а другие должны подать заявку.
Кто автоматически получает дополнительную помощь?
Вы автоматически получите дополнительную помощь, если:
- Полное покрытие Medicaid
- Помощь от вашего штата в оплате страховых взносов по Части B (от Программа сбережений Medicare )
- Дополнительный социальный доход (SSI) льготы от социального обеспечения
Вы получите письмо о дополнительной помощи. В нем сообщается, например, сколько вы будете платить, и ваш новый план лекарств Medicare, если у вас его еще нет.
Если вы не получаете дополнительную помощь автоматически, вы можете подать заявку на нее:
Подать заявку на дополнительную помощь
Или позвонить в Службу социального обеспечения по номеру 1-800-772-1213. Пользователи TTY могут позвонить по номеру 1-800-325-0778.
Кому следует обращаться за дополнительной помощью?
В большинстве случаев, чтобы претендовать на дополнительную помощь, вы должны иметь доход и ресурсы ниже определенного предела. Эти лимиты увеличиваются каждый год.
Эти лимиты увеличиваются каждый год.
Предел дохода основан на вашем доходе за предыдущий год.
Ограничения доходов и ресурсов в 2022 году:
| Ваша ситуация: | Лимит дохода: | Лимит ресурсов: Что учитывается в ограничениях ресурсов? |
|---|---|---|
| Индивидуальный | 20 385 долл. США | 15 510 долл. США |
| Семейная пара | 27 465 долл. США | 30 950 долл. США |
Мы автоматически запишем вас в План лекарственного обеспечения Medicare (часть D) , если у вас его еще нет. Мы делаем это, чтобы вы могли получить экономию средств, на которую вы имеете право.
- Вы получите письмо, в котором будет сказано:
- О вашем новом плане.
 При желании вы можете выбрать другой план лекарственного обеспечения Medicare.
При желании вы можете выбрать другой план лекарственного обеспечения Medicare. - Сколько вы будете платить в зависимости от «уровня» дополнительной помощи, которую вы получаете.
- Чтобы вы получали дополнительную помощь до конца календарного года. Даже если ваш доход изменится в середине года, вы продолжите получать дополнительную помощь до 31 декабря.
- О вашем новом плане.
- Если вы достигнете лимита доходов и ресурсов на следующий год, , вы продолжите получать дополнительную помощь. Мы отправим вам письмо, только если:
- Изменения в дополнительной помощи.
- Вы больше не имеете права на дополнительную помощь.
- Вы перешли на другой план на следующий год.
- Если вы не получите письмо от Medicare или Social Security, вы сохраните тот же уровень Extra Help и тот же план на следующий год.
| Уровень дополнительной помощи: | В 2023 году вы будете платить: |
|---|---|
| Полная дополнительная помощь | Премия плана: $0 Франшиза плана: $0 Рецепты:
После того, как общая стоимость вашего препарата составит (сколько платите и вы, и ваш план) достигает 7400 долларов, вы будете платить 0 долларов за каждый покрываемый препарат. |
| Частичная дополнительная помощь | Премиальный план: Варьируется в зависимости от вашего дохода. Планируйте страховые взносы, если у вас есть Частичная дополнительная помощь Франшиза плана: не более 104 долларов США Рецепты: не более 15% стоимости каждого покрываемого лекарства Когда общая стоимость препарата (то, что платите и вы, и ваш план) достигнет 7400 долларов, вы заплатите не более:
|
Узнайте больше о письмах, которые вы получаете, когда имеете право на получение дополнительной помощи.
Считаете ли вы, что платите неправильную сумму за рецепт(ы)?
Если вы имеете право на получение дополнительной помощи и считаете, что платите неправильную сумму, вот что вы можете сделать:
- Свяжитесь с вашим планом лекарств.
 Ваш план может запросить подтверждение того, что вы получаете дополнительную помощь, чтобы они могли скорректировать ваши расходы.
Примеры доказательств того, что вы получаете дополнительную помощь
.
Ваш план может запросить подтверждение того, что вы получаете дополнительную помощь, чтобы они могли скорректировать ваши расходы.
Примеры доказательств того, что вы получаете дополнительную помощь
.
- Позвоните нам по телефону 1-800-MEDICARE (1-800-633-4227). Пользователи TTY могут позвонить по номеру 1-877-486-2048. Мы можем сообщить вам ваш уровень дополнительной помощи и помочь вам зафиксировать ваши расходы в рамках плана.
Вы можете получить часть денег обратно, если вы:
- Оплатили рецептурные препараты после того, как получили право на дополнительную помощь
- Не участвуете в плане лекарств Medicare
Сохраняйте квитанции с ценами на лекарства, отпускаемые по рецепту, и звоните в Medicare
Программа перехода с ограниченным доходом для новых участников (NET)
в
1-800-783-1307. Пользователи телетайпа могут позвонить по номеру 711.
Другие способы снизить расходы на лекарства, отпускаемые по рецепту:
- Присоединиться к страховому покрытию лекарств Medicare (часть D):
- Сравните планы лекарств Medicare, чтобы найти план с более низкой стоимостью лекарств.

- Сравните планы лекарств Medicare, чтобы найти план с более низкой стоимостью лекарств.


 Искомое значение должно находиться в первом столбце диапазона ячеек, указанного в аргументе таблица.
Искомое значение должно находиться в первом столбце диапазона ячеек, указанного в аргументе таблица. Диапазон ячеек также должен содержать возвращаемое значение, которое нужно найти.
Диапазон ячеек также должен содержать возвращаемое значение, которое нужно найти. Это способ по умолчанию, если не указан другой. Например, =ВПР(90;A1:B100;2;ЛОЖЬ).
Это способ по умолчанию, если не указан другой. Например, =ВПР(90;A1:B100;2;ЛОЖЬ). Помните, что для правильной работы функции ВПР искомое значение всегда должно находиться в первом столбце диапазона. Например, если искомое значение находится в ячейке C2, диапазон должен начинаться с C.
Помните, что для правильной работы функции ВПР искомое значение всегда должно находиться в первом столбце диапазона. Например, если искомое значение находится в ячейке C2, диапазон должен начинаться с C. Обратите внимание на номер столбца (A=1) — это номер_столбца в вашей формуле.
Обратите внимание на номер столбца (A=1) — это номер_столбца в вашей формуле. Если вы хотите подготовить книгу, содержащую функции данных, которые используют несколько таблиц, измените источник данных для функции данных на новую таблицу.
Если вы хотите подготовить книгу, содержащую функции данных, которые используют несколько таблиц, измените источник данных для функции данных на новую таблицу.

 Во время поиска имени сотрудника убедитесь, что имя в формуле взято в кавычки. Например, в функции =ВПР(“Иванов”;B2:E7;2;ЛОЖЬ) имя необходимо указать в формате “Иванов” и никак иначе.
Во время поиска имени сотрудника убедитесь, что имя в формуле взято в кавычки. Например, в функции =ВПР(“Иванов”;B2:E7;2;ЛОЖЬ) имя необходимо указать в формате “Иванов” и никак иначе.
 Вопросительный знак соответствует любому отдельно взятому символу. Звездочка — любой последовательности символов. Если требуется найти именно вопросительный знак или звездочку, следует ввести значок тильды (~) перед искомым символом.
Вопросительный знак соответствует любому отдельно взятому символу. Звездочка — любой последовательности символов. Если требуется найти именно вопросительный знак или звездочку, следует ввести значок тильды (~) перед искомым символом.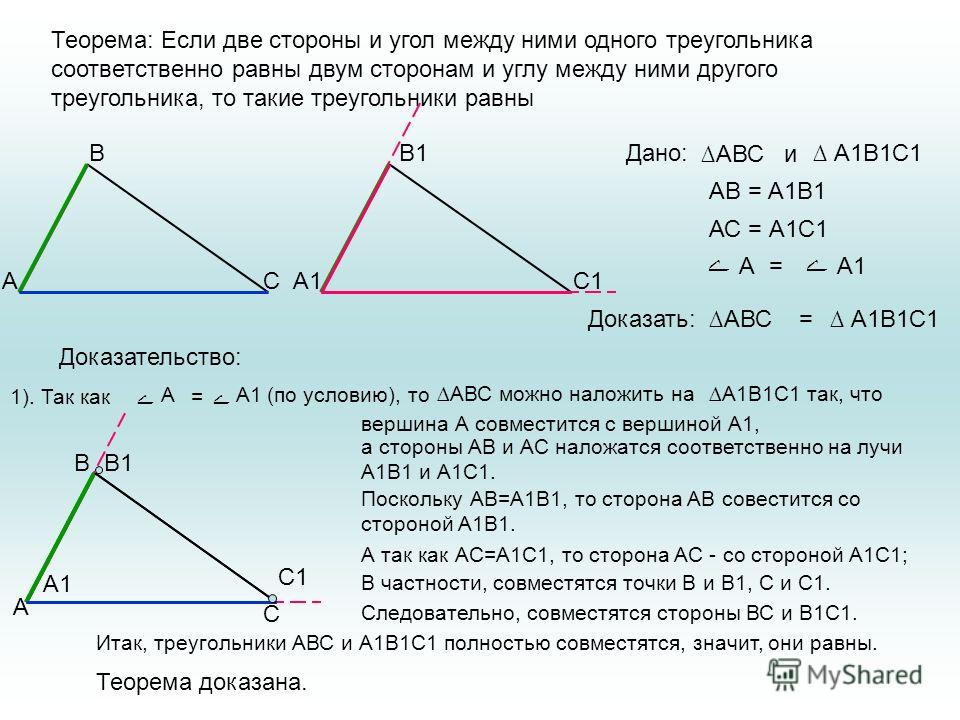
 При желании вы можете выбрать другой план лекарственного обеспечения Medicare.
При желании вы можете выбрать другой план лекарственного обеспечения Medicare.
 Ваш план может запросить подтверждение того, что вы получаете дополнительную помощь, чтобы они могли скорректировать ваши расходы.
Примеры доказательств того, что вы получаете дополнительную помощь
.
Ваш план может запросить подтверждение того, что вы получаете дополнительную помощь, чтобы они могли скорректировать ваши расходы.
Примеры доказательств того, что вы получаете дополнительную помощь
.