Урок 18. основное уравнение мкт – Физика – 10 класс
Физика, 10 класс
Урок 18. Основное уравнение МКТ
Перечень вопросов, рассматриваемых на уроке:
1) средняя кинетическая энергия молекулы;
2) давление газа;
3) основное уравнение МКТ;
Глоссарий по теме:
Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.
Средняя кинетическая энергия молекул – усреднённая величина, равная половине произведения массы молекулы на среднюю величину квадрата её скорости.
Концентрация – число молекул в единице объёма.
Масса молекулы (или атома) – чрезвычайно маленькая величина в макроскопических масштабах (граммах и килограммах), вычисляется через отношение массы вещества к количеству содержащихся в ней молекул (или атомов).
Изменение импульса тела – произведение силы на время действия силы.
Основная и дополнительная литература по теме урока:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 188 – 192.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. С. 111.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. С. 65 – 67.
Открытые электронные ресурсы по теме урока:
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
- http://kvant.mccme.ru/1983/10/davlenie_idealnogo_gaza.htm
- http://kvant.mccme.ru/1987/09/davlenie_gaza_v_sosude.htm
Теоретический материал для самостоятельного изучения
Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами – массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.
Это соотношение называется основным уравнением молекулярно-кинетической теории газа.
Давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы
Давление пропорционально второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:
, где m0 – масса одной молекулы газа,
n– концентрация молекул,
– среднее значение квадрата скорости молекул.
Коэффициент обусловлен трёхмерностью пространства – во время хаотического движения молекул все три направления равноправны.
Средняя кинетическая энергия поступательного движения
тогда уравнение примет вид:
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Примеры и разбор решения заданий.
1. К каждой позиции первого столбца подберите соответствующую позицию второго:
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
1) импульс тела | А) |
2) средняя кинетическая энергия молекул | Б) |
3) давление газа на стенку сосуда | В) |
4) концентрация молекул | Г) |
Правильный ответ: вспомнив формулы величин, устанавливаем соответствие:
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ |
1) импульс тела | В) |
2) средняя кинетическая энергия молекул | А) |
3) давление газа на стенку сосуда | Г) |
4) концентрация молекул | Б) |
2.
Решение:
Ответ: 460 м/с.
Идеальный газ — определение, свойства, условия
В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояний точно три?
На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Модель идеального газа
В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.
Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.
Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).
Важно знать
Модель идеального газа не может описать ситуацию, когда газ сжимают так сильно, что он конденсируется — переходит в жидкое состояние.
В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.
Свойства идеального газа
- Расстояние между молекулами значительно больше размеров молекул.

- Молекулы газа очень малы и представляют собой упругие шары.
- Силы притяжения между молекулами пренебрежимо малы.
- Молекулы взаимодействуют только при соударениях.
- Молекулы движутся хаотично.
- Молекулы движутся по законам Ньютона.
Среднеквадратичная скорость
Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.
На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.
Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.
Эта скорость называется средней квадратичной.
Средняя квадратичная скорость v1, v2, vn — скорости разных молекул [м/с] |
Давление идеального газа
Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению.
Эксперимент
Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление p = F/S F — сила [Н] S — площадь [м2] |
То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.
Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.
Рассмотрим аналогичный пример с двумя сосудами разной площади.
Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.
Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.
В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.
Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.
Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:
Эта зависимость называется законом Шарля в честь ученого, открывшего ее.
Основное уравнение МКТ
Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.
В основе молекулярно-кинетической теории лежат три положения.
- Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.
Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
- Атомы и молекулы находятся в непрерывном хаотическом движении.

- Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.
Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.
Основное уравнение МКТ p = nkT или p — давление газа [Па] n — концентрация [м-3] T — температура газа [К] m0 — масса одной молекулы [кг] v — средняя квадратичная скорость [м/с] |
Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.
Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.
Мы знаем, что кинетическая энергия вычисляется по следующей формуле:
Кинетическая энергия Ек = mv2/2 Ек — кинетическая энергия [Дж] m — масса тела [кг] v — скорость [м/с] |
Для молекулы газа формула примет вид:
Средняя кинетическая энергия поступательного движения молекулы Ек = m0v2/2 Ек — средняя кинетическая энергия поступательного движения молекулы [Дж] m0 — масса молекулы [кг] v — скорость молекулы [м/с] |
Из этой формулы можно выразить m0v2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Основное уравнение МКТ p — давление газа [Па] n — концентрация [м-3] E — средняя кинетическая энергия поступательного движения молекулы [Дж] |
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.
Давление идеального газа, теория и примеры
Общие понятия о давлении идеального газа
Молекулы в идеальном газе совершают движения, при этом они ударяются о стенки сосуда, в котором газ находится, создавая этим давление газа на стенки. Это давление (p) легко вычисляется исходя из представлений молекулярно-кинетической теории (МКТ). Для облегчения данной задачи вводят следующие упрощения:
- Так как давление газа не зависит от формы сосуда, в котором этот газ находится, поэтому будем считать, что сосуд имеет форму прямоугольного параллелепипеда, стороны которого .

- Пусть сталкивающиеся со стенкой молекулы газа испытывают зеркальное отражение от нее, без изменения величины скорости, взаимодействуют со стеной по закону абсолютно упругого удара.
- Все направления движения молекул следует считать равновероятными, если газ находится в равновесии. Для упрощения считаем, что молекулы движутся только в трех взаимно перпендикулярных направлениях, которые совпадают с ребрами параллелепипеда. Тогда, если в сосуде находится N молекул, то в каждом направлении движется молекул (вдоль одного ребра ).
Вычисление давления идеального газа
Выделим на стенке сосуда маленькую площадку , определим каково давление, которое газ оказывает на нее.
При соударении молекула, которая движется по нормали к площадке, передает ей импульс равный:
где – масса молекулы, v – скорость молекулы. За время равное выделенной площадки достигают только те молекулы, которые находятся в объеме цилиндра основание которого равно , а высота: . Количество таких молекул равно , где n – число молекул в единице объема газа. На самом деле молекулы движутся к выделенной площади под разными углами и имеют разные скорости, и скорость молекулы при каждом соударении со стенкой изменяется. Тогда принимая во внимание пункт 3 сделанных нами допусков имеем, что число ударов молекул о площадку будет равно: . Импульс, который получает стенка при ударах этого числа молекул, равен:
Количество таких молекул равно , где n – число молекул в единице объема газа. На самом деле молекулы движутся к выделенной площади под разными углами и имеют разные скорости, и скорость молекулы при каждом соударении со стенкой изменяется. Тогда принимая во внимание пункт 3 сделанных нами допусков имеем, что число ударов молекул о площадку будет равно: . Импульс, который получает стенка при ударах этого числа молекул, равен:
В таком случае давление газа на стенку получается равно:
Определим среднеквадратичную скорость (), которая характеризует всю совокупность молекул газа, как:
где N – число молекул в объема газа равном V. Тогда давление идеального газа равно:
Уравнение (5) называют основным уравнением МКТ. Приведенный вывод формулы (5) является очень приблизительным, но точный расчет давления с учетом движения молекул по всем направлениям даст такую же формулу.
Основное уравнение МКТ часто записывают в виде:
где – средняя кинетическая энергия поступательного перемещения молекул газа.
Давление идеального газа можно вычислить, применяя уравнения состояния:
где T – температура газа по абсолютной шкале температур (в К).
или уравнение состояния, называемое уравнением Менделеева — Клапейрона
где – молярная масса газа; R- универсальная газовая постоянная.
Примеры решения задач
Страница не найдена |
Страница не найдена |404. Страница не найдена
Архив за месяц
ПнВтСрЧтПтСбВс
262728293031
12
12
1
3031
12
15161718192021
25262728293031
123
45678910
12
17181920212223
31
2728293031
1
1234
567891011
12
891011121314
11121314151617
28293031
1234
12
12345
6789101112
567891011
12131415161718
19202122232425
3456789
17181920212223
24252627282930
12345
13141516171819
20212223242526
2728293031
15161718192021
22232425262728
2930
Архивы
Авг
Сен
Окт
Ноя
Дек
Метки
Настройки
для слабовидящих
СРОЧНО выведите формулу, связывающую давление идеального газа и среднюю кинетическую энергию
решите пожалуйста задачу 27 20 баллов
решите пожалуйста задачу 26 20 баллов
решите пожалуйста задачу 25 баллов
В калориметре находится кусок льда массой 85 г при температуре 0°С. Какую массу воды с начальной температурой 100 °С нужно налить в калориметр, чтобы
… весь лёд растаял, а температура образовавшейся воды стала равной 35 °С ? Ответ выразить в граммах [г]. Удельная теплота плавления льда 335 х 10″3 Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг×К). Тепловыми потерями в окружающую среду пренебречь.
Какую массу воды с начальной температурой 100 °С нужно налить в калориметр, чтобы
… весь лёд растаял, а температура образовавшейся воды стала равной 35 °С ? Ответ выразить в граммах [г]. Удельная теплота плавления льда 335 х 10″3 Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг×К). Тепловыми потерями в окружающую среду пренебречь.
С ПОДРОБНЫМ РЕШЕНИЕМ!!!Баржу перемещают с помощью двух буксиров, движущихся со скоростями 3 м/с и 5 м/с, образующими угол а (рис. 56), тангенс которог … о равен tga = 2. Тросы, с помощью которых буксируют баржу, нерастяжимы и прикреплены к одной точке баржи. Под каким углом В к скорости і, будет направлена скорость точки крепления тросов и че- му равна скорость этой точки? Воспользоваться формулой для косину- са разности двух углов cos(а – в) = cos a cos B + sin a sin В.
Какое количество теплоты выделится при конденсации водяного пара массой 3 кг при температуре 100оС? Удельная теплота парообразования воды равна 2,3∙10 … 6 Дж/кг. 2,3 МДж 6,9МДж 3 МДж 23 МДж
Погрешность измерения тока I специальным амперметром, рассчитанным на токи до Imax=50 мА, определяется только погрешностью считывания и равна ΔI=1 мА. … У вас в распоряжении много таких амперметров.
Какое наименьшее количество амперметров нужно использовать, чтобы можно было измерить ток 1 А с наименьшей относительной погрешностью?
Чему равна относительная погрешность измерения такого тока? Ответ выразите в процентах, округлите до целого числа.
… У вас в распоряжении много таких амперметров.
Какое наименьшее количество амперметров нужно использовать, чтобы можно было измерить ток 1 А с наименьшей относительной погрешностью?
Чему равна относительная погрешность измерения такого тока? Ответ выразите в процентах, округлите до целого числа.
222. Первую треть пути автомобиль проехал с постоянной скоростью 10 км/ч, вторую треть со скоростно 60 км/ч, третью 30 км/ч. Вычислите среднюю скорост … ь автомобиля на всем пути. (С РЕШЕНИЕМ!!!) Спасибо!!!!!
Извините, я не уловил мысль. Помогите понять, что имелось ввиду. “Как и в случае равномерного движения, можно пользоваться формулой [tex]s \: = ut[/t
… ex]для определения пути, пройденного за данный промежуток времени при определённой средней скорости, и формулой [tex]t \: = \frac{s}{u} [/tex]для определения времени, за которое пройден данный путь с данной средней скоростью. Но пользоваться этими формулами можно только для того участка пути и для того промежутка времени, для которых эта средняя скорость была рассчитана. Например, зная среднюю скорость на участке пути AB и зная длину AB, можно определить время, за которое был пройден этот участок, но нельзя найти время, за которое была пройдена половина участка АВ, т.к. средняя скорость на половине участка при неравномерном движении, вообще говоря, не будет равна средней скорости на всём участке.Что имеется ввиду под предпоследним предложением? Объясните просторно и понятно, даю 40 баллов
Например, зная среднюю скорость на участке пути AB и зная длину AB, можно определить время, за которое был пройден этот участок, но нельзя найти время, за которое была пройдена половина участка АВ, т.к. средняя скорость на половине участка при неравномерном движении, вообще говоря, не будет равна средней скорости на всём участке.Что имеется ввиду под предпоследним предложением? Объясните просторно и понятно, даю 40 баллов
ПОЖАЛУЙСТА, СРОЧНО! 1). Известно, что нота “до” первой октавы имеет частоту 262 Hz. Также известно, что частоты двух одноимённых нот соседних октав от … личаются ровно в 2 раза. В какой октаве находится звук, порождённые колебаниями, ищображенными на графике? (график приложен) 2). Нарисовать график 3). Определить музыкальный инструмент
Основное уравнение молекулярно-кинетической теории (МКТ) с выводом
В статье рассмотрена модель идеального газа, приведено основное уравнение молекулярно-кинетической теории и его вывод.
Чтобы объяснить свойства материи в газообразном состоянии, в физике применяется модель идеального газа. Идеальный газ – разреженный, состоящий из одного типа атомов газ, частицы которого не взаимодействуют между собой. Помимо основных положений МКТ эта модель предполагает, что:
- молекулы имеют пренебрежимо малый объем в сравнении с объемом емкости
- при сближении частиц друг с другом и с границами емкости имеют место силы отталкивания
Основное уравнение молекулярно-кинетической теории
Физический смысл основного уравнения МКТ заключается в том, что давление идеального газа – это совокупность всех ударов молекул о стенки сосуда. Это уравнение можно выразить через концентрацию частиц, их среднюю скорость и массу одной частицы:
p – давление молекул газа на границы емкости,
m0 – масса одной молекулы,
n – концентрация молекул, число частиц N в единице объема V;
v2 – средне квадратичная скорость молекул.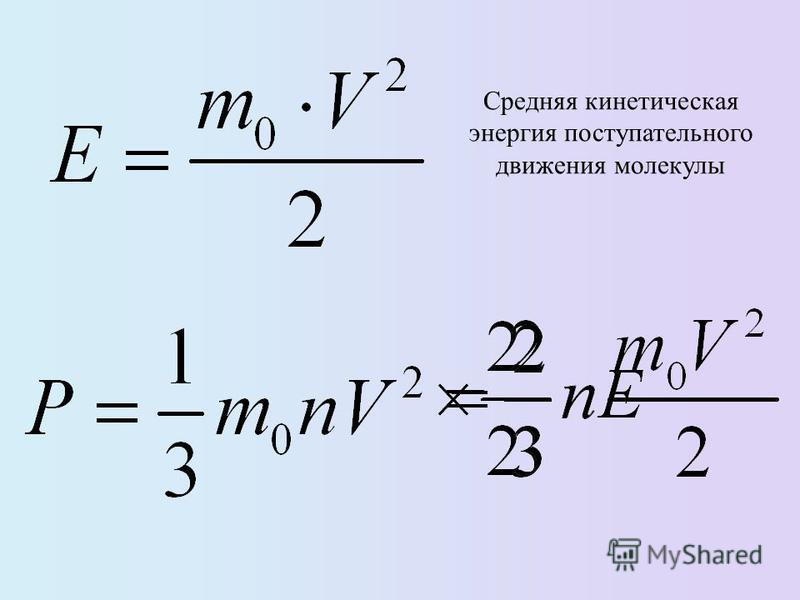
Вывод основного уравнения МКТ
Частицы идеального газа при соударениях с границами емкости ведут себя как упругие тела. Такое взаимодействие описывается согласно законам механики. При соприкосновении частицы с границей емкости проекция vx скоростного вектора на ось ОХ, проходящую под прямым углом к границе сосуда, меняет свой знак на противоположный, но сохраняется неизменной по модулю:
Поэтому после соударения частицы с границей емкости проекция импульса молекулы на ось ОХ меняется с mv1x = –mvx на mv2x = mvx.
Изменение импульса молекулы ΔP равняется удвоенному произведению массы молекулы на ее скорость:
Поскольку в каждом из шести основных направлений декартовой системы координат (вверх, вниз, вперед, назад, вправо, влево) движется одна шестая часть частиц N/6. Тогда число частиц, которые сталкиваются с каждой стенкой за время Δt равно:
S – площадь этой стенки
n – концентрация частиц
Давление p равно отношению силы F к площади S, на которую действует эта сила:
Суммарная сила, с которой частицы давят на стенку равна отношению произведения числа этих частиц N и изменения импульса ΔP ко времени, в течение которого происходит давление:
Исходя из вышенаписанного получаем:
Тогда
Если заменить среднее значение кинетической энергии поступательного движения молекул – E:
и подставить эту формулу в основное уравнение МКТ, получим давление идеального газа:
Давление идеального газа равняется двум третям средней кинетической энергии поступательного движения молекул на единицу объема. При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.
При решении задач реальный газ можно считать идеальным газом, если он одноатомный и можно пренебречь взаимодействием между частицами.
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
Давление идеального газа равно двум третьим средней кинетической энергии поступательного движения молекул, находящихся в единице объема.
2. Физический смысл понятия температуры
Умножим правую и левую части уравнения (10) на объем одного моля газа:
– число молекул в моле газа, оно равно постоянной Авогадро ;
Кроме того, по уравнению Менделеева-Клайперона , при ; ;
Отсюда:
(11)
Таким образом,
средняя кинетическая энергия
поступательного движения молекул непосредственно
связана с параметрами состояния газа
(давлением, объемом, температурой).
Из (11) имеем
(12)
Поскольку R и – постоянные, то и (13)
является постоянной величиной и называется постоянной Больцмана:
(11) может принять вид:
(14)
Следовательно, средняя кинетическая энергия является функцией только температуры и не зависит от массы молекулы.
Из уравнения (14) можно сделать весьма важный вывод: абсолютная температура есть величина, пропорциональная средней кинетической энергии движения молекул, находящихся в единице объема.
Этот вывод раскрывает смысл
молекулярно-кинетического определения
температуры как меры средней кинетической
энергии молекул,
а абсолютная шкала температур приобретает
непосредственный физический смысл. Согласно формуле (14) при абсолютном нуле
поступательное движение должно
прекратиться.
Согласно формуле (14) при абсолютном нуле
поступательное движение должно
прекратиться.
Предположение, сделанное при выводе основного уравнения кинетической теории газов, о том, что молекулы совершают только поступательное движение, уже не выполняется при низких температурах, т.к. все вещества с понижением температуры переходят в конденсированное состояние. Следовательно, теряют смысл выводы, сделанные на основе кинетической теории газов.
Отметим, что кинетическая энергия – величина существенно положительная, поэтому отрицательных температур быть не может.
Из формулы (14) и (10) видно, что температура, как и давление, определяется средней кинетической энергией молекулы идеального газа. Поэтому температура, как и давление, представляет собой статистическую величину, следовательно, бессмысленно говорить о температуре или давлении одной молекулы или немногих молекул.
Объединяя (14) и (11) в одно, получим:
(15)
3.
 Распределение энергии по степеням свободы
Распределение энергии по степеням свободыФормула (14) определяет энергию только поступательного движения молекулы. Однако, наряду с поступательным движением возможны также вращения молекул и колебания атомов, входящих в состав молекул. Оба эти движения связаны с некоторым запасом энергии, определить который позволяет устанавливаемое статистической физикой положение о равнораспределении энергии по степеням свободы молекул.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых можно задать положение системы.
Так, положение в пространстве материальной точки полностью определяется заданием значений 3-х ее координат (например, x, y, z – декартовых или – сферических). В соответствии с этим материальная точка имеет 3 степени свободы.
В молекулярной
физике, так же как и в механике, неизбежно
приходится схематизировать изучаемые
явления и пользоваться моделями,
упрощенно изображающими строение
вещества.
Простейшей моделью газа является идеальный газ. Это такая модель, в которой молекулы принимаются за материальные точки, не взаимодействующие между собой на расстоянии. Следовательно: суммарным объемам молекул можно пренебречь по сравнению с объемом занимаемого газом сосуда.
Модель молекулы идеального газа – материальная точка. Материальная точка имеет 3 степени свободы поступательного движения. Поэтому кинетическая энергия молекулы идеального газа может быть представлена суммой энергий , соответствующим трем составляющим скорости ее движения относительно трех координатных осей. Из-за хаотичности движения молекул и одно направление их движения не имеет преимущества перед другими и поэтому средние значения кинетической энергии по всем трем направлениям одинаковы:
.
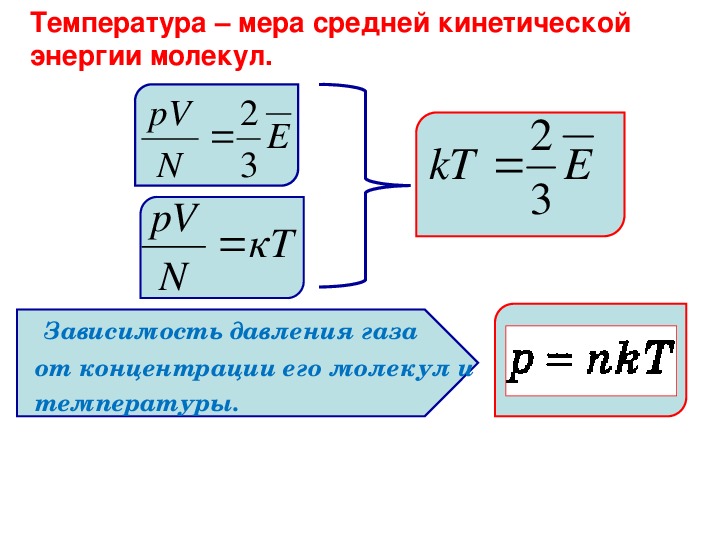
Так как средняя
кинетическая энергия поступательного
движения молекулы
,
то на долю каждой из составляющих
движения приходится одинаковая средняя
кинетическая энергия
.
В первом приближении двухатомную молекулу можно представить в виде двух жестко связанных между собой атомов. Такая система имеет пять степеней свободы, из которых три поступательные и две вращательные.
При взаимных столкновениях двухатомных молекул энергия вращательного движения молекулы может увеличиваться за счет энергии поступательного движения другой молекулы, либо наоборот. Таким путем устанавливается равновесие между средними знаниями энергии поступательного и вращательного движений молекул газа.
Так как при хаотическом движении ни один из видов движения не имеет преимущества перед другими, то можно считать, что средняя энергия, приходящаяся на каждую степень свободы вращательного движения, будет также .
Предположение о
том, что на
любую степень свободы молекулы в среднем
приходится одинаковая кинетическая
энергия, часто называют законом
равнораспределения энергии по степеням
свободы.
Молекула двухатомного газа обладает средней кинетической энергией:
(16)
Система из трех жестко связанных между собой материальных точек, не лежащих на одной прямой, имеет 6 степеней свободы: 3 – поступательных; 3 – вращательных.
Эти же шесть степеней свободы присущи любой молекуле, содержащей более трех атомов.
(17)
Модель молекулы, представляющая собой систему жестко связанных материальных точек, пригодна лишь тогда, когда не учитывают энергию колебания атомов в молекуле. Для учета этой энергии нужно перейти к другой модели молекулы в которой атомы связаны между собой упругой связью, например, пружиной, позволяющей совершать колебательные движения.
Колебательное
движение всегда связано с переходом
кинетической энергии в потенциальную
и обратно. В этом случае нужно учитывать
не только среднюю кинетическую энергию,
приходящуюся на одну колебательную
степень свободы, но и соответствующую
среднюю потенциальную энергию.
Предположим, что колебания атомов, например, в 2-х атомной молекуле, происходит по гармоническому закону. При гармонических колебаниях средние значения потенциальной и кинетической энергий одинаковы. Следовательно, можно считать что на колебательную степень свободы приходится в среднем : одна в виде кинетической энергии, другая – в виде потенциальной.
Иначе говоря, колебательная степень свободы обладает вдвое большей энергетической емкостью по сравнению с поступательной или вращательной.
Учитывая все это выражение для средней кинетической энергии молекулы можно преобразовать:
. (18)
Здесь i– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы;
. (20)
4. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
Полная энергия тела складывается из кинетической энергии движения тела как целого , из потенциальной энергии его во внешнем поле сил и внутренней энергии тела U:
. (20)
(20)
Под внутренней энергией тела обычно подразумевают кинетическую энергию хаотического (теплового) движения его частиц и их взаимную потенциальную энергию.
В зависимости от характера движения и взаимодействия частиц, образующих тело, внутренняя энергия включает в себя:
кинетическую энергию хаотического движения молекул,
потенциальную энергию взаимодействия между молекулами,
кинетическую и потенциальную энергию колебательного движения атомов в молекуле,
внутриатомную энергию.
Во многих физических явлениях, рассматриваемых в молекулярной физике, внутриатомная энергия не изменяется и поэтому ее часто не учитывают.
В идеальном газе
молекулы не взаимодействуют друг с
другом на расстоянии, и его внутренняя
энергия определяется лишь кинетической
энергией хаотического движения молекул.
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа равна . Умножив эту энергию на число Авогадро , получим значение внутренней энергии одного моля идеального газа
(21)
Внутренняя энергия произвольной массы идеального газа:
(22)
где m – масса газа, – масса моля газа, R – универсальная газовая постоянная.
Следовательно: внутренняя энергия данной массы идеального газа зависит только от его температуры и не зависит ни от давления, ни от объема.
ЗАКЛЮЧЕНИЕ
Развитая Ломоносовым молекулярно-кинетическая теория получила признание лишь спустя IOO лет, когда в конце XIX в. появились работы Р. Клаузиуса, Д. Максвелла, Л. Больцмана и другие.
С этого времени
молекулярно-кинетическая теория прочно
утверждается в физике, хотя и не все
ученые ее признавали. Например: Э.Мах,
В. Оствальд и другие отрицали реальность
существования атомов, считая их «плодом
человеческой фантазии». Больше того,
В. Оствальд в своих работах пытался
свести все многообразие явлений природы
к энергетическим представлениям.
Окончательным
подтверждением молекулярно-кинетической
теории
послужили работы французского физика
Ж. Перрена, исследовавшего в 1908 году
броуновское движение.
Например: Э.Мах,
В. Оствальд и другие отрицали реальность
существования атомов, считая их «плодом
человеческой фантазии». Больше того,
В. Оствальд в своих работах пытался
свести все многообразие явлений природы
к энергетическим представлениям.
Окончательным
подтверждением молекулярно-кинетической
теории
послужили работы французского физика
Ж. Перрена, исследовавшего в 1908 году
броуновское движение.
10
Кинетическая теория идеальных газов
Кинетическая теория идеальных газовКинетическая теория идеальных газов
ТЕОРИЯ
Идеальный газ – это газ, в котором атомы не действуют друг на друга, но сталкиваются со стенками контейнера (в упругих столкновениях). Основываясь на здравом смысле и эксперименте, закон идеального газа связывает давление, температуру, объем и количество молей идеального газа:
PV = nRT,
где R – постоянная, известная как универсальная газовая постоянная.
Комментарии:
- Будьте осторожны, все величины выражены в одной системе единиц!
- Температура T, должна быть выражена как абсолютная температура, Кельвин.
- n – количество молей газа, определяемое как
n º м образец / М
м º N A м атом
, где m sample – масса всей пробы газа, N A – число Авогадроса, а m atom – масса одного атома газа.M называется молекулярной массой газа (массой одного моля газа). Если под N мы подразумеваем общее количество атомов газа, то мы также можем написать
n = нет данных A
Это означает, что 1 моль состоит из N A атомов газа.
В классе I докажу на основе второго закона Ньютона и закона идеального газа
E int = 3/2 n R T (для одноатомного идеального газа = «m.i.g.»)
Следовательно,
- внутренняя энергия идеального газа зависит только от его абсолютной температуры, а Температура
- является мерой случайной кинетической энергии атомов.

- Это уравнение – замечательное уравнение, поскольку оно обеспечивает связь между макроскопическим миром (n, T) и микроскопическим миром (E int газа атомов)
Поскольку внутренняя энергия m.i.g. полностью кинетический у нас также есть
E int = m образец
, что дает среднеквадратичную скорость атома газа
против RMS = [3RT / M] 1/2 .
Внимание: держитесь прямо n, N, N A , m atom , m sample и M. Это шесть различных величин.
ПРИМЕРЫ
[в классе]
Давление, температура и среднеквадратичная скорость – University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните взаимосвязь между микроскопическими и макроскопическими величинами в газе
- Решение проблем, связанных со смесями газов
- Решение задач, связанных с расстоянием и временем между столкновениями молекул газа
Мы исследовали давление и температуру на основе их макроскопических определений. Давление – это сила, деленная на площадь, на которую действует сила, а температура измеряется термометром. Мы можем лучше понять давление и температуру из кинетической теории газов, теории, которая связывает макроскопические свойства газов с движением молекул, из которых они состоят. Во-первых, мы делаем два предположения о молекулах в идеальном газе.
Давление – это сила, деленная на площадь, на которую действует сила, а температура измеряется термометром. Мы можем лучше понять давление и температуру из кинетической теории газов, теории, которая связывает макроскопические свойства газов с движением молекул, из которых они состоят. Во-первых, мы делаем два предположения о молекулах в идеальном газе.
- Существует очень большое количество N молекул, все одинаковые и каждая имеет массу m .
- Молекулы подчиняются законам Ньютона и находятся в непрерывном движении, которое является случайным и изотропным, то есть одинаковым во всех направлениях.
Чтобы вывести закон идеального газа и связь между микроскопическими величинами, такими как энергия типичной молекулы, и макроскопическими величинами, такими как температура, мы анализируем образец идеального газа в жестком контейнере, о чем мы делаем еще два предположения:
- Молекулы намного меньше среднего расстояния между ними, поэтому их общий объем намного меньше, чем объем их контейнера (который имеет объем V ).
 Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малой по сравнению с объемом моля газа в контейнере.
Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малой по сравнению с объемом моля газа в контейнере. - Молекулы совершают совершенно упругие столкновения со стенками контейнера и друг с другом. Другие силы, действующие на них, включая гравитацию и притяжение, представленные постоянной Ван-дер-Ваальса a , незначительны (что необходимо для предположения об изотропии).
Столкновения между молекулами не фигурируют при выводе закона идеального газа.Они также не нарушают вывод, поскольку столкновения между молекулами, движущимися со случайными скоростями, дают новые случайные скорости. Более того, если скорости молекул газа в контейнере изначально не являются случайными и изотропными, именно столкновения молекул делают их случайными и изотропными.
Мы делаем дополнительные предположения, которые упрощают вычисления, но не влияют на результат. Во-первых, пусть контейнер будет прямоугольной коробкой. Во-вторых, мы начнем с рассмотрения одноатомных газов, то есть тех, молекулы которых состоят из отдельных атомов, таких как гелий.Тогда мы можем предположить, что атомы не имеют энергии, кроме своей поступательной кинетической энергии; например, у них нет ни вращательной, ни колебательной энергии. (Позже мы обсудим справедливость этого предположения для реальных одноатомных газов и откажемся от него, рассмотрев двухатомные и многоатомные газы.)
Во-вторых, мы начнем с рассмотрения одноатомных газов, то есть тех, молекулы которых состоят из отдельных атомов, таких как гелий.Тогда мы можем предположить, что атомы не имеют энергии, кроме своей поступательной кинетической энергии; например, у них нет ни вращательной, ни колебательной энергии. (Позже мы обсудим справедливость этого предположения для реальных одноатомных газов и откажемся от него, рассмотрев двухатомные и многоатомные газы.)
(рисунок) показано столкновение молекулы газа со стенкой контейнера, так что она оказывает на стенку силу (по третьему закону Ньютона). Эти столкновения являются источником давления в газе.По мере увеличения количества молекул количество столкновений и, следовательно, давление увеличивается. Точно так же, если средняя скорость молекул выше, давление газа выше.
Когда молекула сталкивается с жесткой стенкой, составляющая ее импульса, перпендикулярная стенке, меняется на противоположную. Таким образом, на стену действует сила, создающая давление.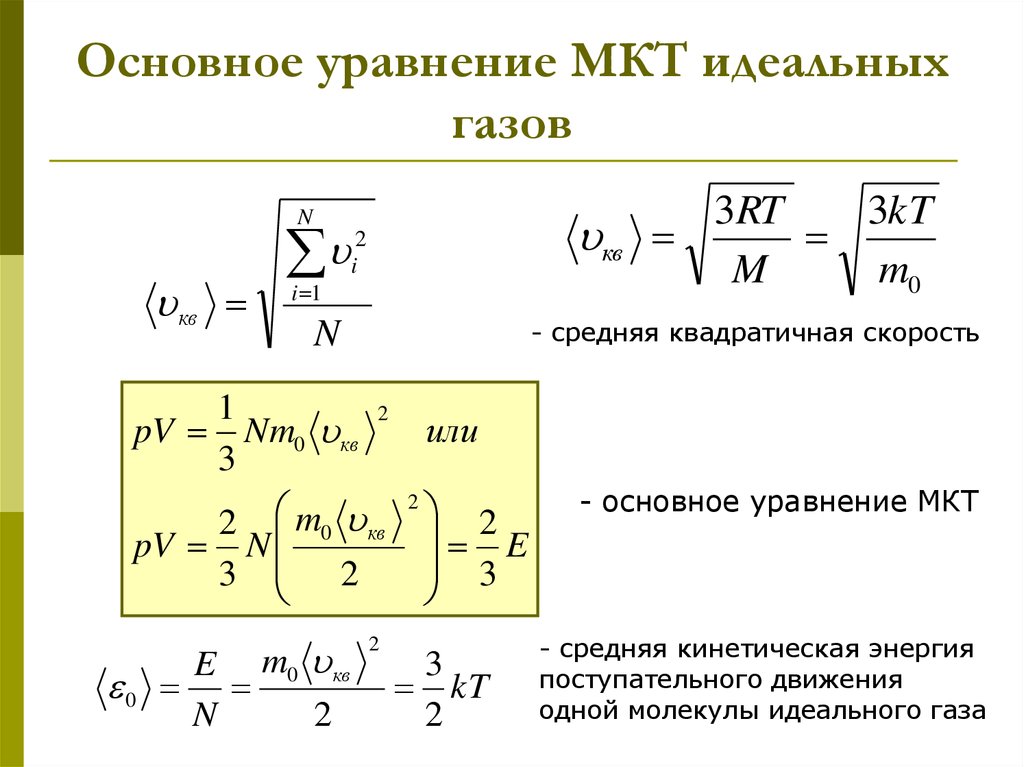
В пробе газа в контейнере случайность молекулярного движения вызывает колебания числа столкновений молекул с любой частью стенки в заданное время.Однако, поскольку огромное количество молекул сталкивается со стенкой за короткое время, количество столкновений в измеряемых нами масштабах времени и пространства колеблется лишь на крошечную, обычно ненаблюдаемую долю от среднего. Мы можем сравнить эту ситуацию с ситуацией в казино, где результаты ставок случайны, а выручка казино колеблется в зависимости от минуты и часа. Однако в течение длительного периода времени, например года, выручка казино очень близка к средним, ожидаемым по шансам. В резервуаре с газом гораздо больше молекул, чем в казино за год, и молекулы совершают гораздо больше столкновений за секунду, чем казино делает ставки.
Расчет средней силы, прилагаемой молекулами к стенкам ящика, приводит нас к закону идеального газа и к связи между температурой и молекулярной кинетической энергией. (Фактически, мы возьмем два средних значения: одно по времени, чтобы получить среднюю силу, действующую на одну молекулу с заданной скоростью, а затем другое среднее значение по молекулам с разными скоростями. ) Этот подход был разработан Даниэлем Бернулли (1700–1782). , который наиболее известен в физике своими работами по течению жидкости (гидродинамика).Примечательно, что Бернулли проделал эту работу до того, как Дальтон установил представление о материи как о состоящей из атомов.
) Этот подход был разработан Даниэлем Бернулли (1700–1782). , который наиболее известен в физике своими работами по течению жидкости (гидродинамика).Примечательно, что Бернулли проделал эту работу до того, как Дальтон установил представление о материи как о состоящей из атомов.
(Рисунок) показывает контейнер, полный газа, и увеличенный вид упругого столкновения молекулы газа со стенкой контейнера, разбитого на компоненты. Мы предположили, что молекула мала по сравнению с разделением молекул в газе, и что ее взаимодействием с другими молекулами можно пренебречь. В этих условиях экспериментально справедлив закон идеального газа.Поскольку мы также предположили, что стена жесткая, а частицы являются точками, столкновение является упругим (по закону сохранения энергии – кинетической энергии частицы некуда уйти). Следовательно, кинетическая энергия молекулы остается постоянной, а следовательно, ее скорость и величина ее количества движения также остаются постоянными. Это предположение не всегда верно, но результаты в остальной части этого модуля также получены в моделях, которые позволяют молекулам обмениваться энергией и импульсом со стенкой.
Газ в ящике оказывает внешнее давление на его стенки.Молекула, сталкивающаяся с твердой стенкой, меняет скорость и импульс в направлении x на противоположное. Это направление перпендикулярно стене. Компоненты его скорости и количества движения в направлениях y и z не изменяются, что означает отсутствие силы, параллельной стене.
Если скорость молекулы изменяется в направлении x , ее импульс изменяется с на Таким образом, ее изменение количества движения равно. -я молекула, где i обозначает молекулы от 1 до N , имеет вид
(Только в этом уравнении p представляет импульс, а не давление.) Между стенкой и молекулой нет силы, кроме случаев, когда молекула касается стенки. В течение короткого времени столкновения сила между молекулой и стенкой относительно велика, но это не та сила, которую мы ищем. Мы ищем среднюю силу, поэтому мы принимаем за среднее время между столкновениями данной молекулы с этой стенкой, то есть время, за которое мы ожидаем найти одно столкновение. Пусть l представляет длину коробки в направлении x .Тогда время, которое потребуется молекуле, чтобы пересечь коробку и обратно, расстояние 2 l , со скоростью Таким образом, и выражение для силы станет
Мы ищем среднюю силу, поэтому мы принимаем за среднее время между столкновениями данной молекулы с этой стенкой, то есть время, за которое мы ожидаем найти одно столкновение. Пусть l представляет длину коробки в направлении x .Тогда время, которое потребуется молекуле, чтобы пересечь коробку и обратно, расстояние 2 l , со скоростью Таким образом, и выражение для силы станет
Эта сила обусловлена одной молекулой . Чтобы найти полную силу на стене, F , нам нужно сложить вклады всех молекул N :
Теперь мы используем определение среднего, которое мы обозначаем чертой, чтобы найти силу:
Нам нужна сила в терминах скорости v , а не x -компонент скорости.Обратите внимание, что квадрат полной скорости представляет собой сумму квадратов ее компонентов, так что
В предположении изотропии три средних значения справа равны, поэтому
Подставляя это в выражение для F , получаем
Давление F / A , поэтому получаем
, где мы использовали для объема. Это дает важный результат
Это дает важный результат
Объединение этого уравнения с дает
Мы можем получить среднюю кинетическую энергию молекулы из левой части уравнения, разделив N и умножив на 3/2.
Средняя кинетическая энергия на молекулу
Средняя кинетическая энергия молекулы прямо пропорциональна ее абсолютной температуре:
Уравнение представляет собой среднюю кинетическую энергию на молекулу. Обратите внимание, в частности, что ничто в этом уравнении не зависит от молекулярной массы (или любого другого свойства) газа, давления или чего-либо еще, кроме температуры. Если образцы газообразного гелия и ксенона с очень разными молекулярными массами имеют одинаковую температуру, молекулы имеют одинаковую среднюю кинетическую энергию.
Внутренняя энергия термодинамической системы – это сумма механических энергий всех молекул в ней. Теперь мы можем дать уравнение для внутренней энергии одноатомного идеального газа. В таком газе единственной энергией молекул является их поступательная кинетическая энергия.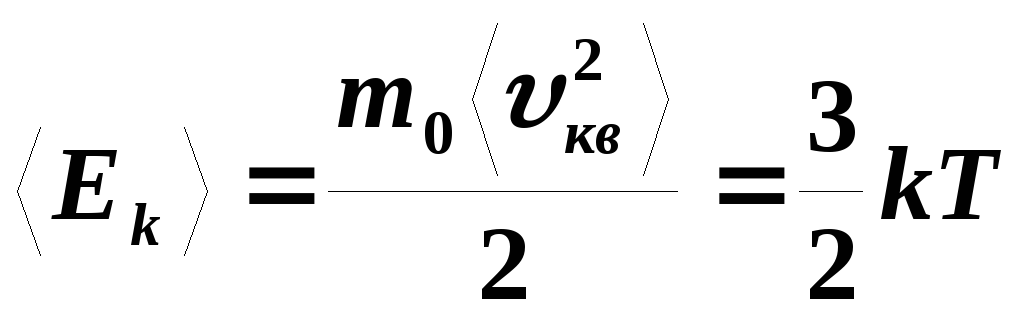 Следовательно, обозначая внутреннюю энергию, мы просто имеем или
Следовательно, обозначая внутреннюю энергию, мы просто имеем или
Часто мы хотели бы использовать это уравнение в отношении молей:
Мы можем решить для типичной скорости молекулы в идеальном газе с точки зрения температуры, чтобы определить так называемую среднеквадратичную ( среднеквадратичное значение ) скорость молекулы .
RMS скорость молекулы
Среднеквадратичная (RMS) скорость молекулы или квадратный корень из среднего квадрата скорости равна
Среднеквадратичная скорость – это не средняя или наиболее вероятная скорость молекул, как мы увидим в разделе «Распределение молекулярных скоростей», но она обеспечивает легко вычисляемую оценку скорости молекул, которая связана с их кинетической энергией. Мы снова можем записать это уравнение в терминах газовой постоянной R и молярной массы M в кг / моль:
Мы отвлеклись на мгновение, чтобы ответить на вопрос, который, возможно, возник у вас: когда мы применяем модель к атомам вместо теоретических точечных частиц, меняет ли кинетическая энергия вращения наши результаты? Чтобы ответить на этот вопрос, мы должны обратиться к квантовой механике.В квантовой механике кинетическая энергия вращения не может принимать никаких значений; он ограничен дискретным набором значений, а наименьшее значение обратно пропорционально инерции вращения. Инерция вращения атома крошечная, потому что почти вся его масса находится в ядре, которое обычно имеет радиус меньше чем. Таким образом, минимальная энергия вращения атома намного больше, чем для любой достижимой температуры, а доступной энергии недостаточно, чтобы заставить атом вращаться. Мы вернемся к этому вопросу при обсуждении двухатомных и многоатомных газов в следующем разделе.
Расчет кинетической энергии и скорости молекулы газа (а) Какова средняя кинетическая энергия молекулы газа при (комнатной температуре)? (б) Найдите среднеквадратичную скорость молекулы азота при этой температуре.
Стратегия (a) В уравнении для средней кинетической энергии известна температура:
Прежде чем подставлять значения в это уравнение, мы должны преобразовать заданную температуру в градусы Кельвина: мы можем найти среднеквадратичную скорость молекулы азота, используя уравнение
, но сначала мы должны найти массу молекулы азота.Получив молярную массу азота из периодической таблицы Менделеева, находим
Решение
- Для определения средней поступательной кинетической энергии достаточно одной температуры. Подстановка температуры в уравнение поступательной кинетической энергии дает
- Подставляя эту массу и значение для в уравнение для получения
Значение Обратите внимание, что средняя кинетическая энергия молекулы не зависит от типа молекулы.Средняя поступательная кинетическая энергия зависит только от абсолютной температуры. Кинетическая энергия очень мала по сравнению с макроскопической энергией, поэтому мы не чувствуем, когда молекула воздуха ударяется о нашу кожу. С другой стороны, это намного больше, чем типичная разница в гравитационной потенциальной энергии, когда молекула движется, скажем, из верхней части комнаты в нижнюю, поэтому наше пренебрежение гравитацией оправдано в типичных реальных ситуациях. Среднеквадратичная скорость молекулы азота удивительно велика.Эти большие скорости молекул не приводят к макроскопическому движению воздуха, поскольку молекулы движутся во всех направлениях с равной вероятностью. Длина свободного пробега (расстояние, на которое молекула перемещается в среднем между столкновениями, обсуждается немного позже в этом разделе) молекул в воздухе очень мала, поэтому молекулы движутся быстро, но не уходят очень далеко за секунду. Высокое значение среднеквадратичной скорости отражается на скорости звука, которая составляет около 340 м / с при комнатной температуре. Чем выше среднеквадратичная скорость молекул воздуха, тем быстрее звуковые колебания могут передаваться по воздуху.Скорость звука увеличивается с температурой и больше в газах с малой молекулярной массой, таких как гелий (см. (Рисунок)).
(а) В обычном газе так много молекул движутся так быстро, что сталкиваются миллиарды раз в секунду. (б) Отдельные молекулы не перемещаются очень далеко за небольшой промежуток времени, но возмущения, подобные звуковым волнам, передаются со скоростью, зависящей от молекулярных скоростей.
Расчет температуры: скорость убегания атомов гелия Чтобы избежать гравитации Земли, объект в верхней части атмосферы (на высоте 100 км) должен уйти от Земли на 11 °.1 км / с. Эта скорость называется второй скоростью . При какой температуре атомы гелия будут иметь среднеквадратичную скорость, равную космической скорости?
Стратегия Определите известные и неизвестные и определите, какие уравнения использовать для решения проблемы.
Решение
- Определите известные: v – космическая скорость, 11,1 км / с.
- Определите неизвестные: нам нужно найти температуру, T . Нам также нужно найти массу m атома гелия.
- Определите, какие уравнения необходимы.
- Чтобы получить массу m атома гелия, мы можем использовать информацию из периодической таблицы:
- Чтобы найти температуру T , мы можем переставить
, чтобы получить
- Чтобы получить массу m атома гелия, мы можем использовать информацию из периодической таблицы:
- Подставьте известные значения в уравнения и решите неизвестные,
и
Значение Эта температура намного выше, чем температура окружающей среды, которая составляет приблизительно 250 K на большой высоте.В атмосфере осталось очень мало атомов гелия, но многие из них присутствовали, когда атмосфера была сформирована, и всегда создается больше в результате радиоактивного распада (см. Главу по ядерной физике). Причина потери атомов гелия заключается в том, что небольшое количество атомов гелия имеет скорости, превышающие скорость убегания Земли даже при нормальных температурах. Скорость атома гелия изменяется от одного столкновения к другому, так что в любой момент существует небольшой, но ненулевой шанс, что скорость атома больше, чем скорость убегания.Вероятность достаточно высока, что за время жизни Земли почти все атомы гелия, которые были в атмосфере, достигли космической скорости на больших высотах и покинули земное гравитационное притяжение. Более тяжелые молекулы, такие как кислород, азот и вода, имеют меньшую среднеквадратичную скорость, поэтому гораздо менее вероятно, что какая-либо из них будет иметь скорости, превышающие скорость убегания. На самом деле вероятность настолько мала, что для потери значительного количества более тяжелых молекул из атмосферы требуются миллиарды лет.(Рисунок) показывает влияние отсутствия атмосферы на Луне. Поскольку гравитационное притяжение Луны намного слабее, она потеряла почти всю свою атмосферу. В упражнениях этой главы сравниваются атмосферы Земли и других тел.
Эта фотография командира Аполлона-17 Юджина Сернана, управляющего луноходом по Луне в 1972 году, выглядит так, как если бы она была сделана ночью с помощью большого прожектора. На самом деле свет исходит от Солнца. Поскольку ускорение свободного падения на Луне настолько низкое (примерно 1/6 от земного), космическая скорость Луны намного меньше.В результате молекулы газа очень легко убегают с Луны, практически не оставляя на ней атмосферы. Даже днем небо черное, потому что нет газа, рассеивающего солнечный свет. (Источник: Харрисон Х. Шмитт / НАСА)
Проверьте свое понимание Если вы рассмотрите очень маленький объект, такой как крупинка пыльцы, в газе, то количество молекул, ударяющихся о его поверхность, также будет относительно небольшим. Ожидаете ли вы, что пыльца будет испытывать какие-либо колебания давления из-за статистических колебаний количества молекул газа, ударяющихся о нее за заданный промежуток времени?
Да.Такие флуктуации действительно происходят для тела любого размера в газе, но поскольку количество молекул для макроскопических тел огромно, флуктуации составляют крошечный процент от количества столкновений, а средние значения, о которых говорится в этом разделе, меняются незаметно. Грубо говоря, флуктуации обратно пропорциональны квадратному корню из числа столкновений, поэтому для малых тел они могут стать значительными. Это действительно наблюдалось в девятнадцатом веке для пыльцевых зерен в воде и известно как броуновское движение.
Давление пара, парциальное давление и закон Дальтона
Давление, которое мог бы создать газ, если бы он занимал весь доступный объем, называется парциальным давлением газа. Если два или более газа смешиваются, они придут к тепловому равновесию в результате столкновений между молекулами; процесс аналогичен теплопроводности, описанной в главе о температуре и тепле. Как мы видели из кинетической теории, когда газы имеют одинаковую температуру, их молекулы имеют одинаковую среднюю кинетическую энергию.Таким образом, каждый газ по отдельности подчиняется закону идеального газа и оказывает такое же давление на стенки сосуда, как если бы он был один. Следовательно, в смеси газов полное давление является суммой парциальных давлений составляющих газов , при условии идеального поведения газа и отсутствия химических реакций между компонентами. Этот закон известен как закон парциальных давлений Дальтона в честь предложившего его английского ученого Джона Далтона (1766–1844). Закон Дальтона согласуется с тем фактом, что давление складывается согласно принципу Паскаля.
В смеси идеальных газов, находящихся в тепловом равновесии, количество молекул каждого газа пропорционально его парциальному давлению. Этот результат следует из применения закона идеального газа к каждому из них в форме Поскольку правая часть одинакова для любого газа при данной температуре в контейнере заданного объема, левая часть также такая же.
- Парциальное давление – это давление, которое мог бы создать газ, если бы он существовал сам по себе. Закон
- Дальтона гласит, что полное давление – это сумма парциальных давлений всех присутствующих газов.
- Для любых двух газов (обозначенных цифрами 1 и 2), находящихся в равновесии в контейнере,
Важное применение парциального давления состоит в том, что в химии оно действует как концентрация газа при определении скорости реакции. Здесь мы упоминаем только, что парциальное давление кислорода в легких человека имеет решающее значение для жизни и здоровья. Вдыхание воздуха с парциальным давлением кислорода ниже 0,16 атм может ухудшить координацию и рассудительность, особенно у людей, не привыкших к работе на большой высоте.Более низкие парциальные давления имеют более серьезные последствия; парциальное давление ниже 0,06 атм может быстро привести к летальному исходу и необратимым повреждениям, даже если человек будет спасен. Однако ощущение потребности дышать, как при задержке дыхания, вызвано в гораздо большей степени высокими концентрациями углекислого газа в крови, чем низкими концентрациями кислорода. Таким образом, если небольшая комната или туалет заполнены воздухом с низкой концентрацией кислорода, возможно, из-за того, что там хранится протекающий баллон со сжатым газом, человек не будет ощущать никакого «удушающего» ощущения и может впасть в конвульсии или потерять сознание. ничего не замечая.Инженеры по технике безопасности уделяют этой опасности большое внимание.
Другим важным применением парциального давления является давление пара, то есть парциальное давление пара, при котором он находится в равновесии с жидкой (или твердой, в случае сублимации) фазой того же вещества. При любой температуре парциальное давление воды в воздухе не может превышать давление пара воды при этой температуре, потому что всякий раз, когда парциальное давление достигает давления пара, вода конденсируется из воздуха.Роса является примером такой конденсации. Температура, при которой происходит конденсация пробы воздуха, называется точкой росы . Его легко измерить, медленно охладив металлический шар; точка росы – это температура, при которой на шаре впервые появляется конденсат.
Давление паров воды при некоторых температурах, представляющих интерес для метеорологии, приведено на (Рисунок).
| Т | Давление пара (Па) |
|---|---|
| 0 | 610.5 |
| 3 | 757,9 |
| 5 | 872,3 |
| 8 | 1073 |
| 10 | 1228 |
| 13 | 1497 |
| 15 | 1705 |
| 18 | 2063 |
| 20 | 2338 |
| 23 | 2809 |
| 25 | 3167 |
| 30 | 4243 |
| 35 | 5623 |
| 40 | 7376 |
Относительная влажность (R.Ч.) При температуре Т определяется по
Относительная влажность означает, что парциальное давление воды равно давлению пара; Другими словами, воздух насыщен водой.
Расчет относительной влажности Какова относительная влажность при температуре воздуха и точке росы?
СтратегияМы просто ищем давление пара при заданной температуре и давление в точке росы и находим соотношение.
Решение
Значение R.H. важен для нашего комфорта. Значение находится в диапазоне, рекомендованном для комфорта в помещении.
Как отмечалось в главе о температуре и тепле, температура редко опускается ниже точки росы, потому что, когда она достигает точки росы или точки замерзания, вода конденсируется и выделяет относительно большое количество скрытой теплоты испарения.
Средняя длина свободного пробега и средняя продолжительность свободного пробега
Теперь мы рассматриваем столкновения явно. Обычный первый шаг (это все, что мы сделаем) – это вычислить длину свободного пробега, среднее расстояние, которое проходит молекула между столкновениями с другими молекулами, и среднее время свободного пробега , , среднее время между столкновениями молекулы. .Если мы предположим, что все молекулы представляют собой сферы с радиусом r , то одна молекула столкнется с другой, если их центры будут находиться на расстоянии 2 r друг от друга. Для данной частицы мы говорим, что площадь круга с таким радиусом является «поперечным сечением» столкновений. Когда частица движется, она отслеживает цилиндр с этой площадью поперечного сечения. Средняя длина свободного пробега – это такая длина, при которой ожидаемое количество других молекул в цилиндре длины и поперечного сечения равно 1.Если мы временно проигнорируем движение молекул, отличных от той, на которую мы смотрим, ожидаемое число – это плотность молекул, N / V , умноженная на объем, и объем равен, поэтому мы имеем или
Учет движения всех молекул значительно усложняет расчет, но единственное изменение – коэффициент. Результат:
В идеальном газе можно заменить, чтобы получить
Среднее время свободного пробега – это просто средний свободный пробег, деленный на типичную скорость, и обычно выбирают среднеквадратичную скорость.Тогда
Проверьте свое понимание Что имеет более длинный свободный пробег, жидкую воду или водяной пар в воздухе?
В жидкости молекулы расположены очень близко друг к другу, постоянно сталкиваясь друг с другом. Чтобы газ был почти идеальным, как воздух в обычных условиях, молекулы должны находиться очень далеко друг от друга. Следовательно, длина свободного пробега в воздухе намного больше.
Сводка
- Кинетическая теория – это атомарное описание газов, а также жидкостей и твердых тел.Он моделирует свойства материи с точки зрения непрерывного случайного движения молекул.
- Закон идеального газа может быть выражен через массу молекул газа и средний квадрат скорости молекул, а не через температуру.
- Температура газов пропорциональна средней поступательной кинетической энергии молекул. Следовательно, типичная скорость молекул газа пропорциональна квадратному корню из температуры и обратно пропорциональна квадратному корню из молекулярной массы.
- В смеси газов каждый газ оказывает давление, равное общему давлению, умноженному на долю смеси, которую составляет газ.
- Средняя длина свободного пробега (среднее расстояние между столкновениями) и среднее время свободного пробега молекул газа пропорциональны температуре и обратно пропорциональны молярной плотности и площади поперечного сечения молекул.
Концептуальные вопросы
Как импульс связан с давлением газа? Объясните на молекулярном уровне, учитывая поведение молекул.
Если один вид молекул имеет двойной радиус другого и в восемь раз больше массы, как можно сравнить их средние длины свободного пробега при одинаковых условиях? Как сравнить их среднее свободное время?
Длина свободного пробега обратно пропорциональна квадрату радиуса, поэтому она уменьшается в 4 раза. Среднее время свободного пробега пропорционально длине свободного пробега и обратно пропорционально среднеквадратичной скорости, которая, в свою очередь, обратно пропорциональна квадратный корень из массы.Это дает коэффициент в числителе, поэтому среднее свободное время уменьшается в
раз.Какова средняя скорость молекул воздуха в комнате, где вы сейчас находитесь?
Почему атмосферы Юпитера, Сатурна, Урана и Нептуна, которые намного массивнее и дальше от Солнца, чем Земля, содержат большое количество водорода и гелия?
Поскольку они более массивны, их сила тяжести сильнее, поэтому скорость убегания от них выше.Поскольку они дальше от Солнца, они холоднее, поэтому скорости атмосферных молекул, включая водород и гелий, ниже. Сочетание этих фактов означает, что относительно небольшое количество молекул водорода и гелия покинуло внешние планеты.
Статистическая механика утверждает, что в газе, поддерживаемом при постоянной температуре за счет теплового контакта с более крупной системой («резервуаром») при этой температуре, колебания внутренней энергии обычно составляют часть внутренней энергии.Какова доля общей внутренней энергии моля газа, насколько велики флуктуации внутренней энергии? Имеем ли мы право игнорировать их?
Что более опасно: чулан, где хранятся резервуары с азотом, или тот, где хранятся резервуары с углекислым газом?
Тот, в котором хранится азот, так как избыток вызывает чувство удушья, а избыток азота и недостаток кислорода – нет.
Проблемы
В задачах этого раздела предполагается, что все газы идеальны.
Человек ударяет теннисным мячом массой 0,058 кг о стену. Средняя составляющая скорости мяча, перпендикулярная к стене, составляет 11 м / с, и мяч ударяется о стену в среднем каждые 2,1 с, отскакивая с противоположной перпендикулярной составляющей скорости. а) Какая средняя сила действует на стену? (б) Если часть стены, которую ударяет человек, имеет площадь, равную среднему давлению на эту площадь?
Человек находится в закрытом помещении (площадке для ракетбола), где наугад без пауз бьет по мячу.Средняя кинетическая энергия мяча составляет 2,30 Дж. (А) Какое среднее значение имеет значение. Имеет значение, в каком направлении вы выберете x ? б) Используя методы этой главы, найдите среднее давление на стены? (c) Помимо присутствия только одной «молекулы» в этой задаче, какое основное допущение в отношении давления, температуры и среднеквадратичной скорости здесь неприменимо?
Пять велосипедистов едут со следующими скоростями: 5,4 м / с, 5,7 м / с, 5,8 м / с, 6,0 м / с и 6.5 м / с. а) Какова их средняя скорость? (б) Какова их среднеквадратичная скорость?
Некоторые лампы накаливания заправлены аргоном. Что делать с атомами аргона возле нити накала, если их температура составляет 2500 К?
Типичные молекулярные скорости велики даже при низких температурах. Что такое атомы гелия при 5,00 К, что менее чем на один градус выше температуры ожижения гелия?
Какова средняя кинетическая энергия в джоулях атомов водорода на поверхности Солнца? (б) Какова средняя кинетическая энергия атомов гелия в области солнечной короны с температурой?
Каково отношение средней поступательной кинетической энергии молекулы азота при температуре 300 K к гравитационной потенциальной энергии системы азот-молекула-Земля на потолке комнаты высотой 3 м относительно того же система с молекулой на полу?
Какова полная поступательная кинетическая энергия молекул воздуха в помещении с объемом, если давление равно (комната находится на довольно большой высоте) и температура равна? Нет ли необходимости в каких-либо данных для решения?
Произведение давления и объема пробы газообразного водорода при ат равно 80.0 Дж. (А) Сколько молей водорода присутствует? б) Какова средняя поступательная кинетическая энергия молекул водорода? (c) Каково значение произведения давления на объем при
?а. 0,0352 моль; б. c. 139 Дж
Какое манометрическое давление в баллоне со сжатым азотом с объемом, равным 514 м / с?
Если среднеквадратичная скорость молекул кислорода внутри холодильника объемом 465 м / с, каково парциальное давление кислорода? Их 5.71 моль кислорода в холодильнике, а молярная масса кислорода составляет 32,0 г / моль.
Космическая скорость любого объекта с Земли составляет 11,1 км / с. При какой температуре молекулы кислорода (молярная масса равна 32,0 г / моль) имели бы среднеквадратичную скорость, равную космической скорости Земли, равной 11,1 км / с?
Космическая скорость с Луны намного меньше, чем с Земли, всего 2,38 км / с. При какой температуре прошли бы молекулы водорода (молярная масса равна 2.016 г / моль) имеют среднеквадратичную скорость, равную космической скорости Луны?
Ядерный синтез, источник энергии Солнца, водородных бомб и термоядерных реакторов, происходит гораздо легче, когда средняя кинетическая энергия атомов высока, то есть при высоких температурах. Предположим, вы хотите, чтобы атомы в вашем термоядерном эксперименте имели среднюю кинетическую энергию. Какая температура нужна?
Предположим, что типичная скорость молекул углекислого газа (молярная масса 44.0 г / моль) в пламени составляет 1350 м / с. На какую температуру это указывает?
(а) Молекулы водорода (молярная масса 2,016 г / моль) равна 193 м / с. Какая температура? (б) Большая часть газа около Солнца состоит из атомарного водорода (должна быть H, а не его температура, чтобы среднеквадратичная скорость равнялась скорости убегания от Солнца. Что это за скорость?
а. 1,004; б. 764 К; c. Эта температура эквивалентна, что является высоким, но достижимым.Таким образом, этот процесс осуществим. Однако при такой температуре могут быть другие факторы, затрудняющие процесс. (В общем, обогащение урана с помощью газовой диффузии действительно сложно и требует большого количества проходов.)
Парциальное давление углекислого газа в легких составляет около 470 Па, когда общее давление в легких составляет 1,0 атм. Какой процент молекул воздуха в легких составляет углекислый газ? Сравните свой результат с процентным содержанием углекислого газа в атмосфере, около 0.033%.
Сухой воздух примерно на моль состоит из следовых количеств других газов. Резервуар со сжатым сухим воздухом имеет объем 1,76 кубических футов при манометрическом давлении 2200 фунтов на квадратный дюйм и температуре 293 К. Сколько в молях кислорода содержится в нем?
(a) Используя данные из предыдущей задачи, найдите массу азота, кислорода и аргона в 1 моль сухого воздуха. Молярная масса 28,0 г / моль, 32,0 г / моль и аргона 39,9 г / моль.(b) Сухой воздух смешивается с пентаном с молярной массой 72,2 г / моль), важным компонентом бензина, в соотношении воздух-топливо 15: 1 по массе (примерно типично для автомобильных двигателей). Найдите парциальное давление пентана в этой смеси при общем давлении 1,00 атм.
(a) Учитывая, что воздух является кислородом, найдите минимальное атмосферное давление, которое дает относительно безопасное парциальное давление кислорода 0,16 атм. (b) Какое минимальное давление дает парциальное давление кислорода выше быстро смертельного уровня 0.06 атм? (c) Давление воздуха на вершине Эвереста (8848 м) составляет 0,334 атм. Почему несколько человек поднялись на нее без кислорода, в то время как некоторым, кто пытался, хотя они тренировались на большой высоте, пришлось повернуть назад?
а. 0,76 атм; б. 0,29 атм; c. Давление там едва превышает смертельный уровень.
(a) Если парциальное давление водяного пара составляет 8,05 торр, какова точка росы? б) В теплый день, когда температура воздуха и точка росы равны, каковы парциальное давление воды в воздухе и относительная влажность?
Глоссарий
- Закон парциальных давлений Дальтона
- физический закон, который гласит, что полное давление газа является суммой парциальных давлений составляющих газов
- внутренняя энергия
- сумма механических энергий всех входящих в него молекул
- кинетическая теория газов
- теория, которая выводит макроскопические свойства газов из движения молекул, из которых они состоят.
- длина свободного пробега
- среднее расстояние между столкновениями частицы
- среднее свободное время
- среднее время между столкновениями частицы
- парциальное давление
- давление, которое мог бы создать газ, если бы он занимал весь доступный объем
- Среднеквадратичная (среднеквадратичная) скорость
- корень квадратный из среднего квадрата (количества)
- Давление паров
- парциальное давление пара, при котором он находится в равновесии с жидкой (или твердой, в случае сублимации) фазой того же вещества
2.3: Давление, температура и среднеквадратичная скорость
Цели обучения
К концу этого раздела вы сможете:
- Объясните взаимосвязь между микроскопическими и макроскопическими величинами в газе
- Решение проблем, связанных со смесями газов
- Решение задач, связанных с расстоянием и временем между столкновениями молекул газа
Мы исследовали давление и температуру на основе их макроскопических определений.Давление – это сила, деленная на площадь, на которую действует сила, а температура измеряется термометром. Мы можем лучше понять давление и температуру из кинетической теории газов , теории, которая связывает макроскопические свойства газов с движением молекул, из которых они состоят. Во-первых, мы делаем два предположения о молекулах в идеальном газе.
- Существует очень большое количество N молекул, все одинаковые и каждая имеет массу m .
- Молекулы подчиняются законам Ньютона и находятся в непрерывном движении, которое является случайным и изотропным, то есть одинаковым во всех направлениях.
Чтобы вывести закон идеального газа и связь между микроскопическими величинами, такими как энергия типичной молекулы, и макроскопическими величинами, такими как температура, мы анализируем образец идеального газа в жестком контейнере, о чем мы делаем еще два предположения:
- Молекулы намного меньше среднего расстояния между ними, поэтому их общий объем намного меньше, чем объем их контейнера (который имеет объем V ).Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малой по сравнению с объемом моля газа в контейнере.
- Молекулы совершают совершенно упругие столкновения со стенками контейнера и друг с другом. Другие силы, действующие на них, включая гравитацию и притяжение, представленные постоянной Ван-дер-Ваальса a , пренебрежимо малы (что необходимо для предположения об изотропии).
Столкновения между молекулами не фигурируют при выводе закона идеального газа.Они также не нарушают вывод, поскольку столкновения между молекулами, движущимися со случайными скоростями, дают новые случайные скорости. Более того, если скорости молекул газа в контейнере изначально не являются случайными и изотропными, именно столкновения молекул делают их случайными и изотропными.
Мы делаем дополнительные предположения, которые упрощают вычисления, но не влияют на результат. Во-первых, пусть контейнер будет прямоугольной коробкой. Во-вторых, мы начнем с рассмотрения одноатомных газа, то есть тех, молекулы которых состоят из отдельных атомов, таких как гелий.Тогда мы можем предположить, что атомы не имеют энергии, кроме своей поступательной кинетической энергии; например, у них нет ни вращательной, ни колебательной энергии. (Позже мы обсудим справедливость этого предположения для реальных одноатомных газов и откажемся от него, рассмотрев двухатомные и многоатомные газы.)
На рисунке \ (\ PageIndex {1} \) показано столкновение молекулы газа со стенкой контейнера, так что она оказывает на стенку силу (по третьему закону Ньютона). Эти столкновения являются источником давления в газе.По мере увеличения количества молекул количество столкновений и, следовательно, давление увеличивается. Точно так же, если средняя скорость молекул выше, давление газа выше.
Рисунок \ (\ PageIndex {1} \): Когда молекула сталкивается с жесткой стенкой, составляющая ее импульса, перпендикулярная стенке, меняется на противоположную. Таким образом, на стену действует сила, создающая давление.В пробе газа в контейнере случайность молекулярного движения вызывает колебания числа столкновений молекул с любой частью стенки в заданное время.Однако, поскольку огромное количество молекул сталкивается со стенкой за короткое время, количество столкновений в измеряемых нами масштабах времени и пространства колеблется лишь на крошечную, обычно ненаблюдаемую долю от среднего. Мы можем сравнить эту ситуацию с ситуацией в казино, где результаты ставок случайны, а выручка казино колеблется в зависимости от минуты и часа. Однако в течение длительного периода времени, например года, выручка казино очень близка к средним, ожидаемым по шансам. В резервуаре с газом гораздо больше молекул, чем в казино за год, и молекулы совершают гораздо больше столкновений за секунду, чем казино делает ставки.
Расчет средней силы, прилагаемой молекулами к стенкам ящика, приводит нас к закону идеального газа и к связи между температурой и молекулярной кинетической энергией. (Фактически, мы возьмем два средних значения: одно по времени, чтобы получить среднюю силу, действующую на одну молекулу с заданной скоростью, а затем другое среднее по молекулам с разными скоростями.) Этот подход был разработан Дэниелом Бернулли (1700–1700 гг.) 1782), который наиболее известен в физике своими работами по течению жидкости (гидродинамика).Примечательно, что Бернулли проделал эту работу до того, как Дальтон установил представление о материи как о состоящей из атомов.
На рисунке \ (\ PageIndex {2} \) показан контейнер, полный газа, и увеличенный вид упругого столкновения молекулы газа со стенкой контейнера, разбитого на компоненты. Мы предположили, что молекула мала по сравнению с разделением молекул в газе, и что ее взаимодействием с другими молекулами можно пренебречь. В этих условиях экспериментально справедлив закон идеального газа.Поскольку мы также предположили, что стена жесткая, а частицы являются точками, столкновение является упругим (по закону сохранения энергии – кинетической энергии частицы некуда уйти). Следовательно, кинетическая энергия молекулы остается постоянной, а следовательно, ее скорость и величина ее количества движения также остаются постоянными. Это предположение не всегда верно, но результаты в остальной части этого модуля также получены в моделях, которые позволяют молекулам обмениваться энергией и импульсом со стенкой.
Рисунок \ (\ PageIndex {2} \): Газ в коробке оказывает внешнее давление на ее стенки.Молекула, сталкивающаяся с жесткой стенкой, меняет скорость и импульс в направлении оси x. Это направление перпендикулярно стене. Компоненты его скорости движения в направлениях y и z не изменяются, что означает отсутствие силы, параллельной стенке.Если скорость молекулы изменяется в направлении x , ее импульс изменяется с \ (- m_x \) на \ (+ mv_x \). Таким образом, его изменение импульса равно \ (\ Delta mv = + mv_x – (- mv_x) = 2mv_x \). Согласно теореме об импульсе-импульсе, приведенной в главе о линейном импульсе и столкновениях, сила, действующая на молекулу i , где i обозначает молекулы от 1 до N , определяется выражением \ [F_i = \ dfrac {\ Delta P_i} {\ Delta t} = \ dfrac {2mv_ {ix}} {\ Delta t}.\ nonumber \]
(Только в этом уравнении p представляет импульс, а не давление.) Между стенкой и молекулой нет силы, кроме тех случаев, когда молекула касается стенки. В течение короткого времени столкновения сила между молекулой и стенкой относительно велика, но это не та сила, которую мы ищем. Мы ищем среднюю силу, поэтому мы берем \ (\ Delta t \) как среднее время между столкновениями данной молекулы с этой стенкой, то есть время, за которое мы ожидаем найти одно столкновение.2 = \ dfrac {3} {2} k_BT. \ Nonumber \]
Уравнение \ (\ overline {K} = \ frac {3} {2} k_BT \) – это средняя кинетическая энергия на молекулу. Обратите внимание, в частности, что ничто в этом уравнении не зависит от молекулярной массы (или любого другого свойства) газа, давления или чего-либо еще, кроме температуры. Если образцы газообразного гелия и ксенона с очень разными молекулярными массами имеют одинаковую температуру, молекулы имеют одинаковую среднюю кинетическую энергию. 2 = \ frac {3} {2} k_BT \) для типичной скорости молекулы в идеале газа с точки зрения температуры, чтобы определить так называемую среднеквадратическую скорость ( среднеквадратичное значение ) скорость молекулы.2} = \ sqrt {\ dfrac {3k_BT} {m}}. \ Nonumber \]
Среднеквадратичная скорость – это не средняя или наиболее вероятная скорость молекул, как мы увидим в разделе «Распределение молекулярных скоростей», но она обеспечивает легко вычисляемую оценку скорости молекул, которая связана с их кинетической энергией. Мы снова можем записать это уравнение в терминах газовой постоянной R и молярной массы M в кг / моль:
\ [v_ {rms} = \ sqrt {\ dfrac {3 \, RT} {M}}. \ Nonumber \]
Мы отвлеклись на мгновение, чтобы ответить на вопрос, который, возможно, возник у вас: когда мы применяем модель к атомам вместо теоретических точечных частиц, меняет ли кинетическая энергия вращения наши результаты? Чтобы ответить на этот вопрос, мы должны обратиться к квантовой механике.{-26} \, кг}} = 511 \, м / с. \ Nonumber \]
Значение
Обратите внимание, что средняя кинетическая энергия молекулы не зависит от типа молекулы. Средняя поступательная кинетическая энергия зависит только от абсолютной температуры. Кинетическая энергия очень мала по сравнению с макроскопической энергией, поэтому мы не чувствуем, когда молекула воздуха ударяется о нашу кожу. С другой стороны, это намного больше, чем типичная разница в гравитационной потенциальной энергии, когда молекула движется, скажем, из верхней части комнаты в нижнюю, поэтому наше пренебрежение гравитацией оправдано в типичных реальных ситуациях.Среднеквадратичная скорость молекулы азота удивительно велика. Эти большие скорости молекул не приводят к макроскопическому движению воздуха, поскольку молекулы движутся во всех направлениях с равной вероятностью. Длина свободного пробега (расстояние, на которое молекула перемещается в среднем между столкновениями, обсуждается немного позже в этом разделе) молекул в воздухе очень мала, поэтому молекулы движутся быстро, но не уходят очень далеко за секунду. Высокое значение среднеквадратичной скорости отражается на скорости звука, которая составляет около 340 м / с при комнатной температуре.Чем выше среднеквадратичная скорость молекул воздуха, тем быстрее звуковые колебания могут передаваться по воздуху. Скорость звука увеличивается с температурой и больше у газов с малой молекулярной массой, таких как гелий (см. Рисунок \ (\ PageIndex {3} \)).
Рисунок \ (\ PageIndex {3} \): (а) В обычном газе так много молекул движутся так быстро, что сталкиваются миллиарды раз в секунду. (б) Отдельные молекулы не перемещаются очень далеко за небольшой промежуток времени, но возмущения, подобные звуковым волнам, передаются со скоростью, зависящей от молекулярных скоростей.Пример \ (\ PageIndex {2} \): Расчет температуры: скорость убегания атомов гелия
Чтобы избежать гравитации Земли, объект в верхней части атмосферы (на высоте 100 км) должен улететь от Земли со скоростью 11,1 км / с. Эта скорость называется второй скоростью . 2} {3k_B}.oF \)) на большой высоте. В атмосфере осталось очень мало атомов гелия, но многие из них присутствовали, когда атмосфера была сформирована, и всегда создается больше в результате радиоактивного распада (см. Главу по ядерной физике). Причина потери атомов гелия заключается в том, что небольшое количество атомов гелия имеет скорости, превышающие скорость убегания Земли даже при нормальных температурах. Скорость атома гелия изменяется от одного столкновения к другому, так что в любой момент существует небольшой, но ненулевой шанс, что скорость атома больше, чем скорость убегания.Вероятность достаточно высока, что за время жизни Земли почти все атомы гелия, которые были в атмосфере, достигли космической скорости на больших высотах и покинули земное гравитационное притяжение. Более тяжелые молекулы, такие как кислород, азот и вода, имеют меньшую среднеквадратичную скорость, поэтому гораздо менее вероятно, что какая-либо из них будет иметь скорости, превышающие скорость убегания. На самом деле вероятность настолько мала, что для потери значительного количества более тяжелых молекул из атмосферы требуются миллиарды лет.На рисунке \ (\ PageIndex {4} \) показано влияние отсутствия атмосферы на Луне. Поскольку гравитационное притяжение Луны намного слабее, она потеряла почти всю свою атмосферу. В упражнениях этой главы сравниваются атмосферы Земли и других тел.
Рис. \ (\ PageIndex {4} \): Эта фотография командира Аполлона-17 Юджина Сернана, управляющего луноходом на Луне в 1972 году, выглядит так, как если бы она была сделана ночью с помощью большого прожектора. На самом деле свет исходит от Солнца.Поскольку ускорение свободного падения на Луне настолько низкое (примерно 1/6 от земного), космическая скорость Луны намного меньше. В результате молекулы газа очень легко убегают с Луны, практически не оставляя на ней атмосферы. Даже днем небо черное, потому что нет газа, рассеивающего солнечный свет. (Источник: Харрисон Х. Шмитт / НАСА)Упражнение \ (\ PageIndex {2} \)
Если вы рассмотрите очень маленький объект, такой как крупинка пыльцы, в газе, то количество молекул, ударяющихся о его поверхность, также будет относительно небольшим.Ожидаете ли вы, что пыльца будет испытывать какие-либо колебания давления из-за статистических колебаний количества молекул газа, ударяющихся о нее за заданный промежуток времени?
- Ответ
Да. Такие флуктуации действительно происходят для тела любого размера в газе, но поскольку количество молекул для макроскопических тел огромно, флуктуации составляют крошечный процент от количества столкновений, а средние значения, о которых говорится в этом разделе, меняются незаметно.Грубо говоря, флуктуации обратно пропорциональны квадратному корню из числа столкновений, поэтому для малых тел они могут стать значительными. Это действительно наблюдалось в девятнадцатом веке для пыльцевых зерен в воде и известно как броуновское движение.
Давление пара, парциальное давление и закон Дальтона
Давление, которое газ создал бы, если бы он занимал весь доступный объем, называется парциальным давлением газа . Если два или более газа смешиваются, они придут к тепловому равновесию в результате столкновений между молекулами; процесс аналогичен теплопроводности, описанной в главе о температуре и тепле.Как мы видели из кинетической теории, когда газы имеют одинаковую температуру, их молекулы имеют одинаковую среднюю кинетическую энергию. Таким образом, каждый газ по отдельности подчиняется закону идеального газа и оказывает такое же давление на стенки сосуда, как если бы он был один. Следовательно, в смеси газов полное давление является суммой парциальных давлений составляющих газов , при условии идеального поведения газа и отсутствия химических реакций между компонентами. Этот закон известен как закон парциальных давлений Дальтона в честь предложившего его английского ученого Джона Далтона (1766–1844).Закон Дальтона согласуется с тем фактом, что давление складывается согласно принципу Паскаля.
В смеси идеальных газов, находящихся в тепловом равновесии, количество молекул каждого газа пропорционально его парциальному давлению. Этот результат следует из применения закона идеального газа к каждому из них в виде \ (p / n = RT / V \). Поскольку правая часть одинакова для любого газа при заданной температуре в контейнере заданного объема, левая сторона также такая же.
- Парциальное давление – это давление, которое мог бы создать газ, если бы он существовал сам по себе. Закон
- Дальтона гласит, что полное давление – это сумма парциальных давлений всех присутствующих газов.
- Для любых двух газов (обозначенных 1 и 2), находящихся в равновесии в контейнере, \ (\ frac {p_1} {n_1} = \ frac {p_2} {n_2}. \)
Важное применение парциального давления состоит в том, что в химии оно действует как концентрация газа при определении скорости реакции. Здесь мы упоминаем только, что парциальное давление кислорода в легких человека имеет решающее значение для жизни и здоровья.Вдыхание воздуха с парциальным давлением кислорода ниже 0,16 атм может ухудшить координацию и рассудительность, особенно у людей, не привыкших к работе на большой высоте. Более низкие парциальные давления \ (O_2 \) имеют более серьезные последствия; парциальное давление ниже 0,06 атм может быстро привести к летальному исходу и необратимым повреждениям, даже если человек будет спасен. Однако ощущение потребности дышать, как при задержке дыхания, вызвано в гораздо большей степени высокими концентрациями углекислого газа в крови, чем низкими концентрациями кислорода.Таким образом, если небольшая комната или туалет заполнены воздухом с низкой концентрацией кислорода, возможно, из-за того, что там хранится протекающий баллон со сжатым газом, человек не будет ощущать никакого «удушающего» ощущения и может впасть в конвульсии или потерять сознание. ничего не замечая. Инженеры по технике безопасности уделяют этой опасности большое внимание.
Другим важным приложением парциального давления является давление пара , которое представляет собой парциальное давление пара, при котором он находится в равновесии с жидкой (или твердой, в случае сублимации) фазой того же вещества.oC\))”> 40
Относительная влажность (R.Ч.) При температуре Т определяется по
\ [R.H. = \ dfrac {Парциальное \, давление \, из \, воды \, пара \, при \, T} {Пар \, давление \, из \, воды \, при \, T} \ раз 100 \%. \ nonumber \]
Относительная влажность \ (100 \% \) означает, что парциальное давление воды равно давлению пара; Другими словами, воздух насыщен водой.
Пример \ (\ PageIndex {3} \): расчет относительной влажности
Какова относительная влажность при температуре воздуха \ (25 ° C \) и точке росы \ (15 ° C \)?
Стратегия
Мы просто ищем давление пара при заданной температуре и давление в точке росы и находим соотношение.oC} \ times 100 \% = \ dfrac {1705 \, Pa} {3167 \, Pa} \ times 100 \% = 53,8 \%. \ nonumber \]
Значение
R.H. важен для нашего комфорта. Значение \ (53,8 \% \) находится в диапазоне от \ (40 \% \) до \ (60 \% \), рекомендованном для обеспечения комфорта в помещении.
Как отмечалось в главе о температуре и тепле, температура редко опускается ниже точки росы, потому что, когда она достигает точки росы или точки замерзания, вода конденсируется и выделяет относительно большое количество скрытой теплоты испарения.
Средняя длина свободного пробега и средняя продолжительность свободного пробега
Теперь мы рассматриваем столкновения явно. Обычный первый шаг (это все, что мы сделаем) – это вычислить длину свободного пробега \ (\ lambda \), среднее расстояние, которое проходит молекула между столкновениями с другими молекулами, и среднее время свободного пробега \ (\ тау \) – среднее время между столкновениями молекулы. Если мы предположим, что все молекулы представляют собой сферы с радиусом \ (r \), то одна молекула столкнется с другой, если их центры будут находиться на расстоянии 2 r друг от друга.{-10} \, s. \ Nonumber \]
Значение
Мы вряд ли можем сравнивать этот результат с нашей интуицией о молекулах газа, но он дает нам картину столкновения молекул с чрезвычайно высокой частотой.
Упражнение \ (\ PageIndex {4} \)
Что имеет большую длину свободного пробега, жидкую воду или водяной пар в воздухе?
- Ответ
В жидкости молекулы расположены очень близко друг к другу, постоянно сталкиваясь друг с другом.Чтобы газ был почти идеальным, как воздух в обычных условиях, молекулы должны находиться очень далеко друг от друга. Следовательно, длина свободного пробега в воздухе намного больше.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Идеальные газы и закон идеального газа: pV = nRT
Температура, Т
Температура должна быть в градусах Кельвина.Не забудьте добавить 273, если вам дана температура в градусах Цельсия.
Использование уравнения идеального газа
Расчеты с использованием уравнения идеального газа включены в мою книгу расчетов (см. Ссылку в самом низу страницы), и я не могу повторить их здесь. Однако есть пара вычислений, которые я не выполнил в книге, которые дают разумное представление о том, как работает уравнение идеального газа.
Молярный объем по стандарту
Если вы выполнили простые вычисления по уравнениям, вы, вероятно, использовали молярный объем газа.
1 моль любого газа занимает 22,4 дм 3 при stp (стандартные температура и давление, принимаемые как 0 ° C и давление в 1 атмосферу). Вы также могли использовать значение 24,0 дм 3 при комнатной температуре и давлении (принятое примерно за 20 ° C и 1 атмосферу).
Эти цифры верны только для идеального газа, и мы посмотрим, откуда они берутся.
Мы можем использовать уравнение идеального газа, чтобы вычислить объем 1 моля идеального газа при 0 ° C и давлении 1 атмосфера.
Во-первых, мы должны правильно определить единицы.
0 ° C составляет 273 К. T = 273 К.
1 атмосфера = 101325 Па. P = 101325 Па
Мы знаем, что n = 1, потому что мы пытаемся вычислить объем 1 моля газа.
И, наконец, R = 8.31441 J K -1 моль -1 .
Вставка всего этого в уравнение идеального газа и последующее преобразование дает:
И, наконец, поскольку нас интересует объем в кубических дециметрах, вы должны не забыть умножить его на 1000, чтобы преобразовать кубические метры в кубические дециметры.
Таким образом, молярный объем идеального газа составляет 22,4 дм. 3 на стандартном давлении.
И, конечно, вы можете повторить этот расчет, чтобы найти объем 1 моля идеального газа при комнатной температуре и давлении – или при любой другой температуре и давлении.
Определение относительной формулы массы газа по его плотности
Это примерно так же сложно, как и при использовании уравнения идеального газа.
Плотность этана 1.264 г дм -3 при 20 ° C и 1 атмосфере. Рассчитайте относительную формульную массу этана.
Значение плотности означает, что 1 дм 3 этана весит 1,264 г.
Опять же, прежде чем мы сделаем что-нибудь еще, разберитесь с неудобными юнитами.
Давление в 1 атмосферу составляет 101325 Па.
Объем 1 дм 3 нужно пересчитать в кубометры, разделив на 1000. У нас объем 0,001 м 3 .
Температура 293 К.
Теперь представьте все числа в форме уравнения идеального газа, которое позволяет вам работать с массами, и измените его так, чтобы вычислить массу 1 моля.
Масса 1 моля чего-либо – это просто относительная масса по формуле в граммах.
Таким образом, относительная формула массы этана равна 30,4, к 3 сиг.
Теперь, если вы сложите относительную формульную массу этана, C 2 H 6 , используя точные значения относительных атомных масс, вы получите ответ 30.07 до 4 значащих цифр. Что отличается от нашего ответа – так что не так?
Есть две возможности.
Возможно, я использовал неверное значение плотности. Я снова подсчитал, используя немного другое значение, указанное при другой температуре из другого источника. На этот раз я получил ответ 30,3. Таким образом, значения плотности могут быть не совсем точными, но они оба дают примерно одинаковый ответ.
Этан – не идеальный газ.Ну конечно не идеальный газ – такого не бывает! Однако, если предположить, что значения плотности близки к правильным, ошибка находится в пределах 1% от ожидаемого. Так что, хотя этан не совсем похож на идеальный газ, он не за горами.
Если вам нужно знать о настоящих газах, сейчас самое время прочитать о них.
Кинетическая теория газов
18.1. Константа Авогадро
законы классической термодинамики не показывают прямой зависимости наблюдаемые макроскопические переменные на микроскопических аспектах движения атомы и молекулы.Однако ясно, что давление оказывало газом связана с импульсом атомов и молекул, и что температура газа связана с кинетической энергией атомы и молекулы. В связи с эффектами движения атомы и молекулы до макроскопических наблюдаемых, таких как давление и температура, мы должны определить количество молекул в газе. моль – это мера количества молекул в образец, и он определяется как
” количество любого вещества, которое содержит столько атомов / молекул, сколько существует атомы в
а 12-граммовый образец 12С “
Лаборатория Эксперименты показывают, что количество атомов в образце 12С массой 12 г равно 6.02 х 1023 моль-1. Этот номер называется постоянной Авогадро , NA. Количество родинок в образец n определяется легко:
18.2. Идеальный газ
Авогадро сделал предположение, что все газы – при одинаковых температурных условиях и давление – содержат одинаковое количество молекул. Наоборот, если отбираем пробы различных газов объемом 1 моль, помещаем их в коробки одинаковых объема и удерживая их при той же температуре, мы обнаруживаем, что их измеренные давления почти одинаковы.Эксперименты показали, что газы подчиняются следующему соотношению (закон идеального газа ):
где n – количество молей газа, а R – газовая постоянная . R имеет одинаковое значение для всех газов:
Температура газа всегда должна выражаться в абсолютных единицах (Кельвинах).
Использование По закону идеального газа мы можем рассчитать работу, совершаемую идеальным газом.Предполагать образец n молей идеального газа заключен в начальный объем Vi. Газ расширяется перемещая поршень. Его окончательный объем – Vf. При расширении температура T газ поддерживается постоянным (этот процесс называется изотермическим расширением ). Дается работа, выполняемая расширяющимся газом. по
Закон идеального газа дает нам связь между давлением и том
С T остается постоянным, проделанная работа может быть легко рассчитана
Примечание:
Образец Задача 18-1
А баллон содержит кислород при температуре 20С и давлении 15 атм.при объеме 12 л. В температура повышается до 35С, а объем уменьшен до 8,5 л. Какое конечное давление газа ?
Закон идеального газа гласит, что
начальное состояние газа определяется Vi, pi и Ti; конечное состояние газа задается Vf, pf и Tf. Делаем вывод, что
Таким образом,
температура T в этой формуле должна быть выражена в Кельвинах:
Ti = 293 К
Tf = 308 К
единицы для объема и давления можно оставить в л и атм.так как только их соотношение входит в уравнение. Делаем вывод, что pf = 22 атм.
18,3. Давление и температура: взгляд на молекулы
Пусть n моль идеального газа заключено в кубический ящик объемом V. молекулы в ящике движутся во всех направлениях с разной скоростью, сталкиваясь друг с другом и со стенками ящика. На рисунке 18.1 показано молекула движется в коробке. Молекула столкнется с правая стена.Результатом столкновения является изменение направления движения на противоположное. x-компоненты импульса молекулы:
Рисунок 18.1. Молекула движется в коробке. |
y- и z-компоненты импульса молекулы не изменяются. В изменение импульса частицы, следовательно,
После молекула разлетелась по правой стенке, она столкнется с левой стена и, наконец, вернитесь к правой стене.Время, необходимое для завершить этот путь дается
Каждый когда молекула сталкивается с правой стенкой, она изменяет импульс стены по п. Сила, действующая на стену со стороны этой молекулы легко вычисляется
Для n моль газа, соответствующая сила равна
давление, оказываемое газом, равно силе на единицу площади, и, следовательно,
член в скобках можно переписать в терминах средней квадратичной скорости:
Таким образом, заключаем, что
где M – молекулярная масса газа.Для каждой молекулы общее скорость вычисляется легко
С есть много молекул, и поскольку нет предпочтительного направления, средний квадрат скоростей в направлениях x, y и z равен
и таким образом
Использование Из этого соотношения выражение для давления p можно переписать как
где vrms называется среднеквадратичной скоростью молекулы.Закон идеального газа говорит нам что
Объединение последние два уравнения заключаем, что
и
Для H при 300 K vrms = 1920 м / с; для 14N vrms = 517 м / с. Скорость звука в этих двух газах составляет 1350 м / с и 350 м / с соответственно. Скорость звука в газе всегда будет меньше v среднеквадратичного значения , поскольку звук распространяется через газ, вызывая возмущение. движение молекул .В возмущение передается от молекулы к молекуле посредством столкновений; а поэтому звуковая волна никогда не может двигаться быстрее, чем средняя скорость молекулы .
18,4. Поступательная кинетическая энергия
средняя поступательная кинетическая энергия молекулы, обсуждаемая в предыдущем разделе дается
Использование полученное ранее выражение для vrms, получаем
постоянная k называется постоянной Больцмана и равна отношению газовой постоянной R и постоянная Авогадро NA
Расчет показывает, что для данной температуры все молекулы газа – независимо от их массы – имеют одинаковую среднюю кинетическую поступательную энергия , а именно (3/2) кТ .Когда мы измеряем температуру газа, мы измеряем средняя поступательная кинетическая энергия его молекул.
18,5. Средняя длина свободного пробега
движение молекулы в газе затруднено. Помимо столкновения с стенки камеры удержания, молекулы сталкиваются друг с другом. А Полезным параметром для описания этого движения является длина свободного пробега л. В длина свободного пробега l – средняя расстояние, которое проходит молекула между столкновениями.Средне бесплатный путь молекулы связан с ее размером; чем больше размер тем короче его длина свободного пробега.
Предположим молекулы газа имеют сферическую форму и диаметр d. Две молекулы газа столкнутся, если их центры разделены менее чем на 2d. Предполагать среднее время между столкновениями t. За это время молекула путешествует на расстояние v. т, и подметает объем равный
Если в среднем он испытывает одно столкновение, количество молекул в объем V должен быть 1.Если N – количество молекул в единице объема, это означает, что
или
интервал времени t, определенный таким образом, является средним временем между столкновениями, а длина свободного пробега l равна
Здесь мы предположили, что движется только одна молекула, а все остальные неподвижны. Если проводим расчет правильно (все молекулы движутся), следующее для длины свободного пробега получено соотношение:
связь, полученная между макроскопическим давлением и микроскопическими аспектами движения молекул зависят только от средней среднеквадратичной скорости молекул в газе.Часто уходите, нам нужна дополнительная информация чем просто средняя среднеквадратичная скорость. Например, вопросы например, какая часть молекул имеет скорость больше v0, может иметь значение (ядерная реакция сечения резко увеличиваются с увеличением скорости). Это можно показать, что распределение скоростей молекул в газе описывается так называемым распределением скоростей Максвелла
product P (v) dv – доля молекул, скорость которых лежит в диапазоне с v на v + дв.Распределение нормализовано, а это значит, что
наиболее вероятная скорость , вп. пики распределения скорости. Наиболее вероятная скорость получается требуя, чтобы dP / dv = 0
ср заключаем, что dP / dv = 0, когда
и таким образом
Среднее значение скорость молекул газа можно рассчитать следующим образом:
Среднее значение квадратная скорость молекул может быть получена аналогичным манера.
Среднеквадратичное значение скорость , vrms, теперь можно получить
ср
обратите внимание, что vp внутренняя энергия газа связана с кинетической энергией
его молекулы. Предположим пока, что мы имеем дело с одноатомным
газ. В этом случае средняя поступательная кинетическая энергия каждого
молекула газа просто равна 3kT / 2.Если образец содержит n молей
такого газа он содержит молекулы нНК. В
полная внутренняя энергия газа равна ср
заметьте, что полная внутренняя энергия газа является функцией только
температура газа и не зависит от других переменных, таких как давление
и плотность. Для более сложных молекул (двухатомный N 2 и т. Д.) Ситуация осложняется тем, что
что кинетическая энергия молекул будет состоять не только из поступательного
движение, но и вне вращательного движения . Предположим
мы нагреваем n молей газа, сохраняя его объем постоянным. В
результатом добавления тепла в систему является повышение ее температуры Здесь,
CV – молярная теплоемкость при постоянном объеме , Q – добавленное тепло, а T – результирующее увеличение.
в температуре системы. Первый закон термодинамики
показывает, что С
объем остается постоянным (V = 0), мы заключаем, что и Использование
ранее полученное уравнение для U через T, мы можем показать, что и
таким образом Предположим
что при добавлении тепла в систему объем изменяется таким образом, что
давление газа не меняется. Опять же, изменение внутреннего
энергия системы дается где
Cp – молярная теплоемкость при постоянном давлении . Это выражение можно переписать как Для
идеальный газ (pV = nRT) мы можем связать V с T, если мы примем постоянную
давление Использование
это соотношение, первый закон термодинамики можно переписать как или Однако
внутренняя энергия U зависит только от температуры, а не от того, как
объем и / или давление меняется.Таким образом, U / T = 3/2 n R = n CV. Таким образом, предыдущее уравнение может
переписать как или ср
увидеть, что Cp CV. Во время адиабатическое расширение идеального газа без добавления или отвода тепла
из системы. Этого можно добиться, расширив газ
очень быстро (так, что не успевает течь тепло) или очень быстро
хорошо изолирующая система.Первый закон термодинамики говорит
нам что Закон идеального газа можно использовать, чтобы переписать p V: или удельная теплоемкость CV относится к U Использование
первый закон термодинамики мы можем написать или Объединение
два выражения, полученные для n. T получаем или Это
выражение можно переписать как Для
небольшие изменения это можно переписать как где
мы определили g как (Cp / CV).После интеграции этого
выражение получаем или Использование
закон идеального газа, чтобы исключить p из выражения, получаем Таким образом, 18,6. Теплоемкость идеального газа
18.6.1. Молярная теплоемкость при постоянном объеме
18.6.2. Молярная теплоемкость при постоянном давлении
18,7. Адиабатическое расширение идеального газа
Разработка закона об идеальном газе
Разработка закона об идеальном газе
Если газ сжимают при постоянной температуре, давление изменяется обратно пропорционально объему.Следовательно, закон Бойля можно сформулировать так: Произведение давления (P) и соответствующего ему объема (V) является константой. Математически PV = константа. Или, если P – исходное давление, V – исходный объем, P ′ представляет новое давление и V ′ – новый объем, соотношение будет
Закон Шарля / Гей-Люссака означает, что при постоянном давлении объем газа прямо пропорционален температуре Кельвина.В форме уравнения В = (константа) Т . Или, если В – исходный объем, Т – исходная температура Кельвина, В ′ – новый объем и Т ′ – новая температура Кельвина, соотношение будет
Закон Бойля и закон Шарля / Гей-Люссака можно объединить: PV = (константа) T . Объем увеличивается, когда масса газа (м) увеличивается, например, при закачке большего количества газа в шину; следовательно, объем газа также напрямую связан с массой газа и PV = (константа) mT .
Константа пропорциональности предыдущего уравнения одинакова для всех газов, если количество газа измеряется в молях , а не в единицах массы. Число молей (n) газа – это отношение массы (m) к молекулярной или атомной массе (M) , выраженной в граммах на моль:
Моль чистого вещества содержит массу в граммах, равную молекулярной массе или атомной массе вещества.Например, свинец имеет атомную массу 207 г / моль, или 207 г свинца – это 1 моль свинца.
Объединение закона Бойля, закона Шарля / Гей-Люссака и определения моля в одно выражение дает закон идеального газа PV = nRT , где R – универсальная газовая постоянная с значение R = 8,31 Дж / моль-градус × K в единицах СИ, где давление выражено в Н / м 2 (паскалях), объем – в кубических метрах, а температура – в градусах Кельвина.
Если температура, давление и объем изменяются для данного количества молей газа, формула будет
, где переменные без штриха относятся к одному набору условий, а переменные со штрихом относятся к другому. Часто набор условий температуры, давления и объема газа сравнивается со стандартной температурой и давлением (STP). Стандартное давление составляет 1 атмосферу, а стандартная температура составляет 0 градусов Цельсия (приблизительно 273 градуса Кельвина).
Амадео Авогадро (1776–1856) заявил, что один моль любого газа при стандартном давлении и температуре содержит такое же количество молекул. Значение, называемое Число Авогадро , равно N = 6,02 × 10 23 молекул / моль. Закон идеального газа может быть записан в терминах числа Авогадро как PV = NkT , где k , называемая постоянной Больцмана, имеет значение k = 1,38 × 10 −23 Дж / К. Один моль любого газа при стандартной температуре и давлении (STP) занимает стандартный объем из 22.4 литра.
Рассмотрим газ со следующими четырьмя идеализированными характеристиками:
- Он находится в тепловом равновесии со своим контейнером.
- Молекулы газа упруго сталкиваются с другими молекулами и стенками сосуда.
- Молекулы разделены расстояниями, большими по сравнению с их диаметром.
- Чистая скорость всех молекул газа должна быть равна нулю, чтобы в среднем в одном направлении двигалось столько же молекул, сколько в другом.
Эта модель газа как совокупности молекул в постоянном движении, претерпевающих упругие столкновения в соответствии с законами Ньютона, является кинетической теорией газов .
Из механики Ньютона, давление на стенку (P) может быть получено через среднюю кинетическую энергию молекул газа:
Результат показывает, что давление пропорционально количеству молекул в единице объема (N / V) и средней линейной кинетической энергии молекул.Используя эту формулу и закон идеального газа, можно найти связь между температурой и средней линейной кинетической энергией:
, где k – снова постоянная Больцмана; следовательно, средняя кинетическая энергия молекул газа прямо пропорциональна температуре газа в градусах Кельвина. Температура – это прямая мера средней молекулярной кинетической энергии идеального газа.
Эти результаты кажутся интуитивно оправданными. Если температура повышается, молекулы газа движутся с большей скоростью.Если объем останется неизменным, можно ожидать, что более горячие молекулы будут сталкиваться со стенками чаще, чем более холодные, что приведет к увеличению давления. Эти важные отношения связывают движения молекул газа в субатомном мире с их характеристиками, наблюдаемыми в макроскопическом мире.
Вывод уравнения идеального газа из кинетической теории газов ~ ChemistryGod
Уравнение идеального газа: PV = nRT . Это уравнение легко вывести из комбинации закона Бойля, закона Чарльза и закона Авогадро.Но здесь мы выведем уравнение из кинетической теории газов. Кинетическая теория газов – очень важная теория, которая связывает макроскопические величины, такие как давление, с микроскопическими величинами, такими как скорость молекул газа. Это уравнение применимо только для идеальных газов, но при некоторых условиях может быть приближено к реальному газу.
В 1856 году немецкий химик Август Крониг разработал простую модель газа. В своей модели он рассматривал только поступательное движение частиц газа.Позже, в 1857 году, Рудольф Клаузиус независимо от Кронига разработал изощренную версию кинетической теории газов. Клаузиус рассматривал не только поступательное движение, но также вращательное и колебательное движение молекул газа.
Допущения в уравнении идеального газа
Поведение газов значительно упрощается благодаря множеству предположений. Это необходимо, чтобы избежать сложностей. Теоретические допущения следующие:
- Газ состоит из очень маленьких частиц, известных как молекулы.
- Молекулы газа представляют собой твердые твердые одинаковые сферы.
- Все молекулы газа имеют одинаковую массу.
- Объем каждой молекулы ничтожно мал по сравнению с общим объемом газа. Другими словами, молекулы не занимают места по сравнению с размером контейнера, в котором они хранятся.
- Межмолекулярные силы между молекулами равны нулю. Молекулы между собой не действуют.
- Молекулы находятся в постоянном беспорядочном движении.Они путешествуют только по прямым линиям.
- Все столкновения между ними и между молекулами и стенкой контейнера имеют совершенно упругую природу. Таким образом, при столкновении нет потери кинетической энергии.
- Давление – это чистый результат столкновений молекул со стенкой контейнера.
- Средняя кинетическая энергия является функцией только температуры.
Вывод уравнения идеального газа
Визуализируйте куб в пространстве, как показано на рисунке ниже. L, – длина куба и площади, A . V – объем куба.
Куб заполнен идеальным газом под давлением P , при температуре T . Пусть n и N – моль и количество молекул газа в кубе. m и M – масса молекулы и газа.
Рисунок 1: Куб в пространстве длиной L и площадью AРассмотрим одиночную молекулу, движущуюся со скоростью v ⃗.Пусть v ⃗ x , v ⃗ y и v ⃗ z – компоненты скорости в направлениях x , y и z . соответственно.
Шаг 1. Определение частоты столкновений.
Для простоты мы начнем с направления x , как показано на рисунке ниже. Первоначально при x = 0 молекула с массой м движется со скоростью v ⃗ x .Он ударяется о стену размером x = L . Это первое столкновение. Общее расстояние, пройденное при первом столкновении, составляет L 0 , а затраченное время составляет t 1 . Второе столкновение происходит при t 1 + t , а расстояние между столкновением 1 -го и 2-м -м столкновением составляет 2 L . Интервал времени между столкновением 1 и 2 nd составляет ∆ t = ( t 1 + t ) – t 1 = t .Это также показано на рисунке ниже.
Рисунок 2: Положение молекулы в разный момент времениДля столкновения 3 rd , взятое время составляет t 1 + 2 t , но временной интервал между предыдущим столкновением такой же ∆ t = ( т 1 + 2 т ) – ( т 1 + т ) = т . Кроме того, расстояние, на которое проходит молекула между столкновением 2 nd и 3 rd , одинаково 2 L .Эти две величины, временной интервал и пройденное расстояние, останутся неизменными для всех последующих столкновений. Итак, мы можем вычислить скорость v x , которая представляет собой интервал времени, разделенный на расстояние, разделенное на время для всех столкновений, следующим образом:
Здесь v 1 , v 2 , v 3 , v 4 … – скорости для 1 st , 2 nd , 3 rd , 4 th ,… столкновений, и все они равны v x .
Следовательно, временные интервалы для соответствующих коллизий равны
Среднее время, затраченное t на k столкновений, равно
Когда k стремится к бесконечности, мы получаем
Это период времени для коллизии, и обратная величина – частота ( f ) столкновений.
Шаг 2: вычисление силы
Сила F определяется как скорость изменения количества движения ∆ p .
Изменение импульса – это разность импульса после столкновения (- mv x ) минус до столкновения ( mv x ).
Примечание: отрицательный импульс означает, что молекула потеряла импульс после столкновения.
Сила, прилагаемая стенкой F wm к молекуле, определяется как:
Закон Ньютона 3 rd гласит, что при каждом действии существует равная и противоположная реакция. Таким образом, сила, прилагаемая молекулой к стенке F mw , противоположна силе, прилагаемой стенкой к молекуле F wm .
Используя уравнения (1) и (2),
Вначале мы рассматривали только одну молекулу; Итак, приведенное выше уравнение силы относится только к одной молекуле.Сила со стороны молекул Н , движущихся в направлении x , равна,
Среднеквадратичная скорость v ̄ 2 дается как
Подставляя вышеприведенное уравнение в (3),
Примечание. сила, действующая со стороны молекулы на одну стенку куба.
Шаг 3. Определение давления газа
Зная силу, действующую на стену, мы можем определить давление ( P ), которое является силой на единицу площади.
Здесь V – объем куба.
В уравнение (4) мы включили только направление x . Нам нужно заменить v ̄ 2
x на v ̄ 2 .
Из математики связь между v ̄ 2
x , v ̄ 2
y и v ̄ 2
7
Кроме того, каждая из этих скоростей равна.
Из уравнений (5) и (6),
Подставляя уравнение (7) в (4),
Уравнение (8) связывает макроскопическое давление с микроскопической скоростью.
Шаг 4: Определение энергии, связанной с идеальным газом
Проблема с уравнением (8) заключается в том, что среднеквадратичная скорость v ̄ 2 не является удобной величиной для измерения. Мы заменим его на более удобную величину: температуру, которую легко измерить градусником.
Уравнение кинетической энергии из классической механики составляет половину массы, умноженной на квадрат скорости.
Кроме того, из статистической механики кинетическая энергия одноатомного газа дается как:
Здесь k – постоянная Больцмана, и ее приблизительное значение составляет 1,380 × 10 −23 Дж K −1 .
Использование уравнений (9) и (10)
Шаг 5: Определение уравнения идеального газа
Из уравнений (8) и (11),
Постоянная Больцмана ( k ) также является отношением газовой постоянной ( R ) к постоянной Авогадро ( N A ).Подставляя
в уравнение вышеупомянутого уравнения,В приведенном выше уравнении отношение
– это моль газа n .Наконец, уравнение идеального газа, PV = nRT , выводится с использованием кинетической теории газов.

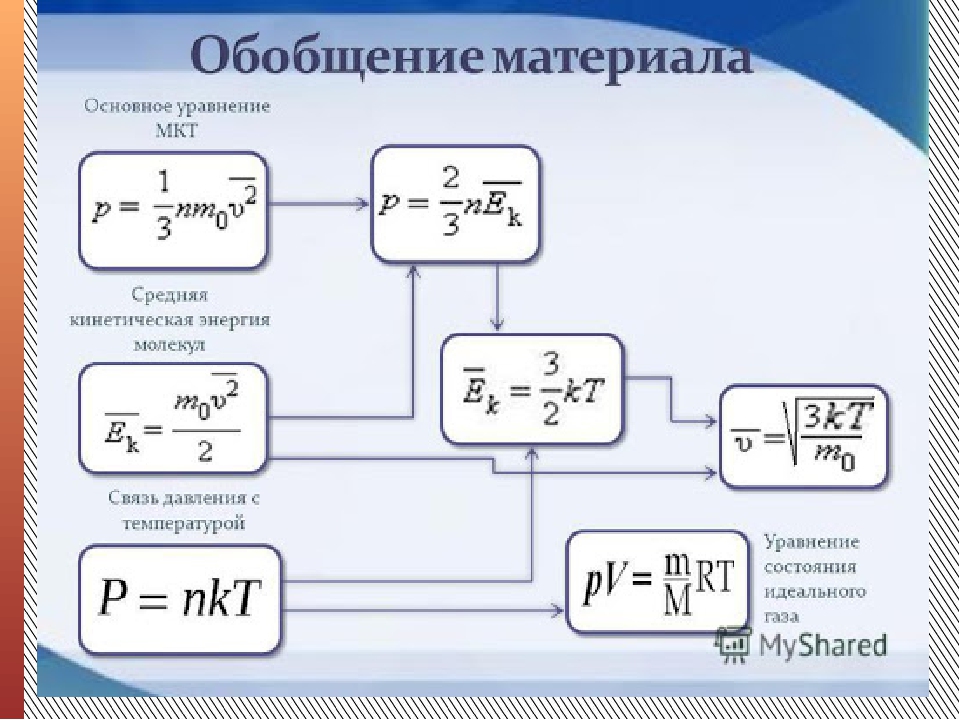



 Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малой по сравнению с объемом моля газа в контейнере.
Другими словами, мы принимаем постоянную Ван-дер-Ваальса b , объем моля молекул газа, пренебрежимо малой по сравнению с объемом моля газа в контейнере.