Давление идеального одноатомного газа формула: Давление идеального газа, теория и онлайн калькуляторы

Давление идеального газа, теория и онлайн калькуляторы

Давление идеального газа, теория и онлайн калькуляторы

Определение давления идеального газа

Определение

Давление идеального газа – это один из самых важных макроскопических параметров, при помощи которого характеризуют состояние системы в молекулярной физике.

Обозначают давление буквой $p$. Если для известной массы идеального газа определены давление и температура (или объем), то полагают, что состояние термодинамической системы в состоянии равновесия определяется однозначно, так как существующие законы и уравнения молекулярно кинетической теории (МКТ) позволяют все остальные параметры вычислить.

В общем случае давление определяют как:

\[p={\mathop{\lim }_{\Delta S\to 0} \frac{\Delta F_n}{\Delta S}\ }\left(1\right),\]

где $F_n$ проекция силы на нормаль к поверхности S данная сила оказывает воздействие, $\Delta S$- площадь поверхности. 2_i}},\ N\ $- количество молекул в объеме газа равном $V$. Уравнение (2) называют основным уравнением МКТ. Его можно записать в другом виде, используя среднюю кинетическую энергию молекул ($\left\langle E_k\right\rangle $):

\[p=\frac{2}{3}n\left\langle E_k\right\rangle \left(3\right).\]

С таким важным термодинамическим параметром как термодинамическая температура давление связывает формула:

\[p=nkT\ \left(4\right),\]

где $k$ – постоянная Больцмана. Уравнение (4) называют уравнением состояния идеального газа.

Если проводить изохорный процесс ($V=const$) с некоторой массой идеального газа, то давление его будет подчинено закону Шарля:

\[p_2=p_1\frac{T_2}{T_1}\left(5\right),\]

где $p_1$- давление газа имеющего температуру $T_1$.

При проведении изотермического процесса ($T=const$) c постоянной массой некоторого газа поведение давления можно характеризовать, используя уравнение:

\[p_1V_1=p_2V_2\left(6\right).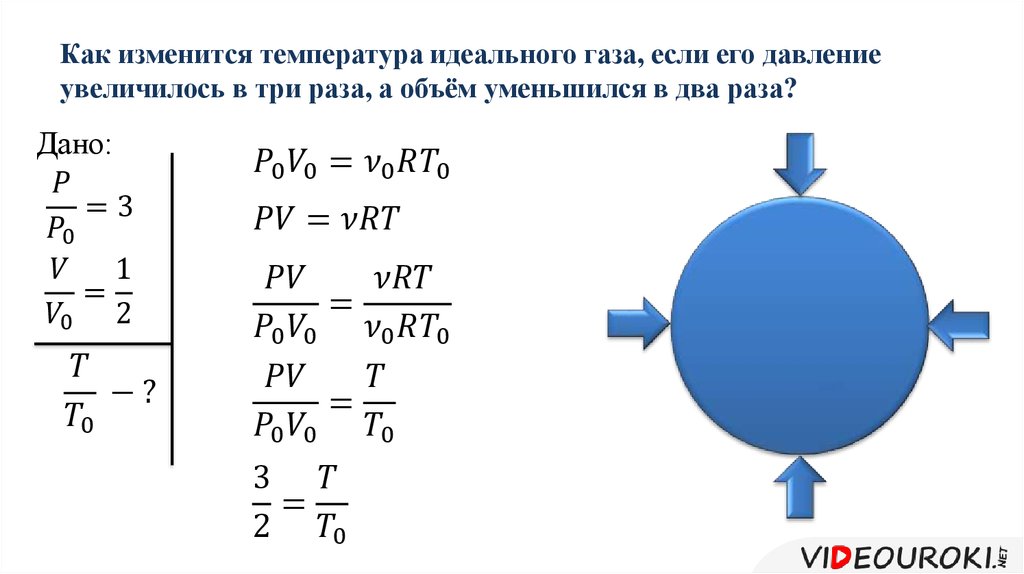 {V_2}_{V_1}{pdV}\left(9\right).\]

Соответственно, первое начало термодинамики для идеального газа в дифференциальном виде запишем как:

\[\delta Q=pdV+\frac{i}{2}\nu RdT\left(10\right),\]

где $i$ – число степеней свободы молекулы газа; $\delta Q$ – элементарное количество теплоты, которое получает идеальный газ; $\frac{i}{2}\nu RdT=dU$ – изменение внутренней энергии термодинамической системы.\textit{}

Примеры задач с решением

Пример 1

Задание. В идеальном газе проводят процесс, при котором $p=\frac{AU}{V},$ где $U$ – внутренняя энергия газа; $A=const$ для определенного газа. Сравните коэффициенты пропорциональности $A$, если в первом случае газ одноатомный, во втором двух атомный. \textit{}

Решение. Внутренняя энергия идеального газа для любого процесса равна:

\[U=\frac{i}{2}\nu RT\ \left(1.1\right).\]

Состояние идеального газа описывает уравнение Менделеева – Клайперона:

\[pV=\nu RT\ \left(1. 2\right).\]

Подставим правую часть уравнения, которое описывает заданный в условиях задачи процесс ($p=\frac{AU}{V}$) вместо давления в (1.2), имеем:

\[\frac{AU}{V}V=\nu RT\ \left(1.3\right).\]

Получим из (1.3), что внутренняя энергия вычисляется как:

\[U=\frac{1}{A}\nu RT\left(1.4\right).\]

Сравним выражения для внутренней энергии (1.1) и (1.4), имеем:

\[\frac{i}{2}=\frac{1}{A}\left(1.5\right).\]

Для одноатомного газа $i=3$; для двухатомного газа (без учета колебаний молекул) $i=5$.

\[\frac{3}{2}=\frac{1}{A_1};;\ \frac{5}{2}=\frac{1}{A_2}\to \frac{A_2}{A_1}=\frac{3}{2}\cdot \frac{2}{5}=\frac{3}{5}.\]

Ответ. $\frac{A_2}{A_1}=\frac{3}{5}$

Пример 2

Задание. На рис.1 представлены процессы, проводимые с постоянной массой идеального газа, укажите, как изменяются давления в процессах?

Решение. Уравнение процесса можно аналитически описать уравнением:

\[V(T)=AT-B\ \left(2.1\right),\]

где $A$ и $B$ положительные постоянные величины.

Состояние газа определим при помощи уравнения Менделеева – Клапейрона:

\[pV=\nu RT\ \left(2.2\right).\]

Вместо объема подставим уравнение процесса в (2.2):

\[p\left(AT-B\right)=\nu RT\left(2.3\right).\]

Раздели обе части (2.3) на температуру:

\[\frac{p\left(AT-B\right)}{T}=\nu R\to p\left(A-\frac{B}{T}\right)=\nu R\to p=\frac{\nu R}{A-\frac{B}{T}}\ \left(2.4\right).\]

Из уравнения (2.4) следует, что при увеличении температуры $\frac{B}{T}$ уменьшается, следовательно, знаменатель дроби правой части выражения (2.4) увеличивается, значит, давление уменьшается.

Ответ. Давление в заданном процессе уменьшается.

Читать дальше: диэлектрический гистерезис.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Какой величины достигает давление идеального одноатомного газа, масса молекул которого составляет

4,65·10^-26 кг, концентрация молекул равна 1,2·10²⁶ штук на кубический метр газа, а их скорость 500 м/с?

(Отв:465 кПа.)

2. Какую концентрацию имеют молекулы воздуха при условиях, когда давление достигает 100000 Па, а величина средней кинетической энергии их движения составляет 1,3·10^-21 Дж? (Отв:1,15·10²⁶ м^-3.)

Давление идеального газа

Для решения задач данного раздела необходимо знать обозначения и единицы измерения для следующих физических величин:

n – концентрация молекул идеального газ 1/м 3 Р – давление газа Па Т – абсолютная температура К k – постоянная Больцмана 1,38·10-23Дж/К (см. справочную таблицу)

ЗАДАЧА-ОБРАЗЕЦ: Определить концентрацию молекул идеального газа, давление которого составляет 200000 а температура составляет 20ºC

Внимательно ознакомьтесь с условием и решением этой задачи, обязательно найдите в учебнике указанную формулу и найдите в справочнике число Больцмана. Перепишите решение этой задачи себе в рабочую тетрадь, соблюдая правила оформления. Переписывать нужно только текст, выделенный курсивом, а пояснения, сделанные обычным шрифтом переписывать не нужно. Температуру запишите в Кельвинах, перевод сделайте по формуле:

Т=t+273[К]

Дано:	СИ:	Решение:
T=20ºС P=200000 Па k=1,38·10-23Дж/К	=293К
n-?
Откройте учебник, разыщите там формулу давление идеального газа: P=nkT Преобразуйте эту формулу, перенеся сомножители таким образом, чтобы формула годилась для вычисления концентрации молекул n: Вместо массы и молярной массы подставьте числа из «дано», из столбика «СИ», и посчитайте на калькуляторе результат: Проверьте, какая размерность у результата: Запишите ответ. Ответ: Концентрация идеального газа равна 4,95·1025 молекул в кубическом метре.

Вслед за первой, попробуйте решить самостоятельно следующие задачи, соблюдая все правила их оформления:

1. Какой величины может достигать давление идеального одноатомного газа при температуре -3ºС, если концентрация его молекул составляет 1,2·10²⁶ штук на один кубический метр газа? (Отв:4,8·10⁵ Па.)

2. Какую концентрацию имеют молекулы газа при давлении величиной 100000 Па, и температуре 17 ºС? (Отв:2,5·10²⁵ м^-3.)

3. При какой температуре концентрация молекул идеального газа достигает 3,8·10²⁵ штук на один литр газа при давлении 5 атмосфер? (Отв:953 К. )

Скорость молекул идеального газа

Для решения задач данного раздела необходимо знать обозначения и единицы измерения для следующих физических величин:

– средняя квадратичная скорость молекул м/с k – постоянная Больцмана 1,38·10-23Дж/К (см. справочную таблицу) Т – абсолютная температура К m0 – масса молекулы газа Кг R – газовая постоянная 8,31Дж/моль·К (см. справочную таблицу) M –молярная масса кг/моль (см. «таблицу Менделеева»)

ЗАДАЧА-ОБРАЗЕЦ: С какой средней скоростью двигаются молекулы азота при температуре 27ºС?

Для решения этой задачи воспользуйтесь периодической таблицей химических элементов («таблицей Менделеева») и найдите там молярную массу азота М=28 г/моль и переведите температуру газа в абсолютную шкалу по формуле:

Т=t+273[К]

Внимательно ознакомьтесь с условием и решением этой задачи, обязательно найдите в учебнике указанную формулу и найдите в справочнике табличные данные. Перепишите решение этой задачи себе в рабочую тетрадь, соблюдая правила оформления. Переписывать нужно только текст, выделенный курсивом, а пояснения, сделанные обычным шрифтом переписывать не нужно.

Дано:	СИ:	Решение:
М=28 г/моль Т=27ºС	=0,028кг/моль =300 К
=?
Откройте учебник, разыщите там формулу для вычисления средней скорости теплового движения молекул: или Какую из двух формул применить, решайте, исходя из тех данных, которые имеются в задаче. Поскольку в данном случае известна молярная масса азота М, правильным решением будет применить второй вариант: Подставьте числа из «дано», из столбика «СИ», и подсчитайте на калькуляторе результат: Проверьте, какая размерность у результата: Запишите ответ. Ответ: Средняя скорость молекул составляет 517м/с.

Вслед за первой, попробуйте решить самостоятельно следующие задачи, соблюдая все правила их оформления:

Использование анализа размерностей в разделе «Молекулярно-кинетическая теория. Законы идеального газа»

Библиографическое описание:

Мазейкина, М. Ю. Использование анализа размерностей в разделе «Молекулярно-кинетическая теория. Законы идеального газа» / М. Ю. Мазейкина. — Текст : непосредственный // Педагогическое мастерство : материалы II Междунар. науч. конф. (г. Москва, декабрь 2012 г.). — Москва : Буки-Веди, 2012. — С. 124-126. — URL: https://moluch.ru/conf/ped/archive/65/3168/ (дата обращения: 20.09.2022).

В работах [1-2] были представлены примеры использования анализа размерностей (далее АР) в геометрии и механике на уровне, доступном ученикам средней школы. Предлагаемую работу можно рассматривать как продолжение указанных работ. Здесь представлен пример использования АР в разделе «Молекулярно-кинетическая теория. Законы идеального газа».

1. ПОСТАНОВКА ЗАДАЧИ

Задача №МКТ1. Найти формулу давления идеального газа в сосуде (формулу основного уравнения молекулярно-кинетической теории).

Механической моделью идеального газа в рамках молекулярно-кинетической теории (далее МКТ) может служить замкнутое в сосуде ограниченное множество абсолютно упругих одинаковых точечных физических объектов (молекул).

Сосуд – это абсолютно упругая оболочка.

Сосуд может иметь дополнительные свойства, отраженные в условиях конкретной задачи.

Исходя из этой модели, давление на стенки сосуда есть следствие абсолютно упругого взаимодействия молекул газа со стенками сосуда. Следовательно, можно попытаться составить перечень физических параметров, от которых может зависеть давление.

1. Давление газа (p) может зависеть от концентрации (n) молекул – числа молекул в единице объема.

Логично предположить, что давление газа тем больше, чем больше молекул в сосуде заданного объема.

2. Естественным было бы и предположение о зависимости давления газа от массы молекулы (m₁).

Было бы логичным предположить, что чем больше масса молекул, тем больше будет давление при прочих постоянных величинах.

3. Предположим, что давление газа зависит от осредненной скорости (v) молекул газа.

Логично предположить, что при увеличении скоростей молекул газа давление газа будет возрастать при равных прочих величинах.

Указанные соображения (предположения) носят качественный характер. Они основаны на логике и интуиции исследователя (в данном случае ученика). Тем не менее, они позволяют поставить задачу в обобщенной форме: найти функциональную зависимость давления газа от концентрации молекул, их массы и скорости:

p = f (n, m₁, v). (1)

1. РЕШЕНИЕ ЗАДАЧИ

Для того, чтобы выявить функциональную зависимость (1), воспользуемся известным алгоритмом анализа размерностей (далее АР), представленным в работах [2-4].

За определяемый физический параметр примем давление газа. Тогда определяющими физическими параметрами будут служить: концентрация молекул, их масса и осредненная скорость.

Искомую функциональную зависимость будем искать в виде степенного одночлена:

p = K n^{xm₁yvz, (ИФ2)}

К = Сonst,

[К] = 1. (3)

Здесь и далее ИФ – итоговая формула.

За базисную систему размерностей примем систему LTM.

L – размерность длины, T– размерность времени, M – размерность массы, К – безразмерная постоянная величина.

Формулы размерностей концентрации, массы и скорости в системе LTM имеют вид:

[p] = L^-1 T^-2M; [n] = L^-3; [m₁] = M; [v] = L T^-1. (4)

Используя (2) и (3), составим уравнение размерностей:

L^-1T^-2M = L^-3х M^у L^zT^–z. (5)

После упрощения уравнение размерностей (5) примет вид

L^-1T^-2M= L^-3х+zT^–zM^у. (6)

Приравнивание показателей степеней при одинаковых основаниях обеих частей уравнения размерностей (6) дает систему линейных уравнений

-3х+z = -1

у = 1 (7)

-z = -2.

Решение системы (7) есть решение уравнения размерностей (6). Решая систему (7), получим:

х = у = 1, z = 2. (8)

Подставляя (8) в (ИФ2), получим итоговую формулу

р = K n m₁ v². (ИФ9)

Мы получили с точностью до постоянного безразмерного множителя (К) выражение (ИФ9), называемое основным уравнением МКТ.

Эксперимент и решение задачи иными методами дают для одноатомного газа следующее значение К:

К = (ИФ10)

1. АНАЛИЗ РЕШЕНИЯ ЗАДАЧИ

Давление газа, используя (ИФ9), можно выразить и так:

р = Kρv² (ИФ11)

ρ = nm₁= m / V, (12)

m = nm₁V = N m₁, (13)

где ρ – плотность газа, m – масса газа, V – объем газа (сосуда), N – число молекул газа.

Формулу (ИФ11) можно получить, если решать эту же задачу анализом размерностей, предполагая, что параметрами, определяющими давление, являются плотность газа (ρ) и осредненная скорость молекул (v).

Из (ИФ11) и (12) получим

p = Kmv² / V. (14)

Эту формулу можно записать иначе

p = K₁mv² / (2V), (15)

К₁ = 2K = , (16)

p = K₁Е/V= K₁U/V= K₁= K₁ (ИФ17)

где Е – суммарная кинетическая энергия молекул газа,

– объемная плотность суммарной кинетической энергии молекул газа, – объемная плотность внутренней энергии идеального газа, К₁ – безразмерная постоянная (равная для одноатомного газа).

Определение. Суммарная кинетическая энергия молекул газа (Е) называется внутренней энергией газа (U).

Е = U. (18)

Из (ИФ17) и (18) следует

pV = K₁Е = K₁U (ИФ19)

Из формулы (ИФ17) следует теорема 1, а из (ИФ19) – теорема 2.

Теорема 1. Давление идеального газа пропорционально объемной плотности суммарной кинетической энергии молекул газа (или объемной плотности внутренней энергии идеального газа).

Теорема 2. Произведение давления идеального газа на его объем пропорционально суммарной кинетической энергии молекул газа (или внутренней энергии идеального газа).

1. ЧАСТНЫЕ СЛУЧАИ ФОРМУЛЫ (ИФ19)

1. Если предположить, что суммарная кинетическая энергия (Е) молекул газа данной массы (m) величина постоянная, то формула (ИФ19) примет вид

pV = const₁.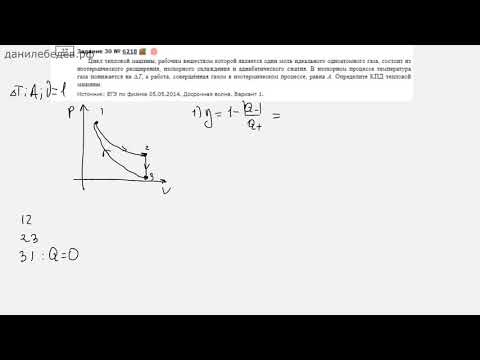 (ИФ20)

1. Если объем газа (V) данной массы газа (m) величина постоянная, то формула (ИФ19) примет вид

p/Е = const₂. (ИФ21)

1. Если давление газа (р) данной массы газа (m) величина постоянная, то формула (ИФ19) примет вид

V/Е = ( )^-1 = = const₃. (ИФ22)

В этом случае объемная плотность () суммарной кинетической энергии всех молекул газа есть величина постоянная.

Постоянные const₁ – const₃ имеют размерности левых частей формул.

Из трех термодинамических макроскопических параметров газа (объем, давление и температура), измеряемых простейшими приборами, в формулах (ИФ20-ИФ22) явным образом не содержится лишь температура.

Однако температура содержится в указанных формулах косвенно. Это можно установить, если поставить вопрос: «А не связана ли суммарная кинетическая энергия (Е) всех молекул газа с температурой газа?». На постановку этого вопроса указывает качественный анализ частных случаев формулы (ИФ19) – формул (ИФ20-22).

При этом следующие два предположения представляются вполне логичными.

Предположение П1. Предположим, что осредненная кинетическая энергия молекул газа (Е₁) есть функция абсолютной температуры (Т)

Е₁ = = = f (Т). (П1)

Предположение П2. Предположим, что эта функция – степенная и простейшая.

Т. е.

Е₁ = const₄ Т, (П2)

где const₄ – константа, имеющая размерность, удовлетворяющую требованиям АР.

Для того, чтобы формула (П2) удовлетворяла предельному случаю

Е₁ = 0 → Т = 0, (23)

необходимо, чтобы температура (Т) являлась «абсолютной температурой», измеряемой по шкале Кельвина.

Константа (const₄) определяется формулой Больцмана (для одноатомного газа):

Е₁= = k ·Т, (24)

где k – постоянная Больцмана (Дж/К – в системе SI).

Формула размерности постоянной Больцмана в системе размерностей LTMT^°.

[k] = L²T^-2M/T^°, где T^°-1 – размерность температуры, измеряемой в кельвинах.

Из (24) получим выражение для константы (const₄):

const₄ = k. (25)

Для двухатомного газа выражение для константы (const₄) таково:

const₄ = k. (26)

С учетом предположений П1 и П2 понятие «осредненной скорости» молекул обретает конкретный смысл: это средняя квадратичная скорость всех молекул.

v = (Σv_i² /N)^{0. 5,} (27)

где i – текущий номер молекулы; суммирование производится по числу (N) всех молекул газа.

В этом случае замена скоростей молекул на среднеквадратичную скорость не приведет к изменению суммарной кинетической энергии всех молекул газа, т. е. кинетическая энергия рассматриваемой системы абсолютно упругих частиц не изменится.

Предположения П1 и П2 (и соответствующие им формулы П1 и П2) отражают физический смысл понятия «абсолютная температура»: абсолютная температура – это осредненная кинетическая энергия молекул газа.

Из формул (П1), (П2), (24), (25) следует формула внутренней энергии для одноатомного газа

Е = U = N Е₁ = N k Т. (28)

Заметим, что для двухатомного газа аналогичная формула такова

Е = U = N Е₁ = N k Т. (29)

Подставляя (28) в формулы (ИФ19-ИФ22), получим

p V / Т = const, (ИФ19.1)

p V = const, (ИФ20.1)

p / Т = const, (ИФ21.1)

V / Т = const, (ИФ22.1)

где const – константы, имеющие размерности левых частей формул.

Формулы (ИФ19.1 – ИФ22.1) есть выражение законов идеального газа с позиций МКТ.

Полученные формулы законов идеального газа представлены в таблице.

№ п/п	№ формулы	Формула, выражающая закон	Наименование газового процесса, выраженного формулой	Наименование закона
1	(ИФ19. 1)	p V / Т = const	Для любого процесса	Уравнение Клапейрона состояния идеального газа
2	(ИФ20.1)	p V = const	Изотермический процесс	Бойля-Мариотта
3	(ИФ21.1)	p / Т = const	Изохорный процесс	Шарля
4	(ИФ22.1)	V / Т = const	Изобарный процесс	Гей-Люссака
5	(ИФ19. 2)	pV/Т= νR = const	Для любого процесса	Уравнение Клапейрона-Менделеева состояния идеального газа

Д. И. Менделеев придал формуле (ИФ19.1) более содержательный вид, установив физический смысл константы правой части (см. формулу 19.2):

p V / Т = ν R = const (ИФ19.2)

ν = m / M, (30)

где ν – число молей газа, m – масса газа, М – молярная масса газа,

R – универсальная газовая постоянная.

Отметим, что все формулы, представленные в таблице, справедливы для любого идеального газа: одноатомного, двухатомного, трехатомного. Специфика газа, определяемая его химическим составом, в формуле (ИФ19.2) отражена его молярной массой (М).

Заметим, что формула (ИФ11) представляет собой частный случай уравнения Бернулли для идеальной жидкости, если положить К= . В этом случае буква (v) означает скорость молекул в поперечном сечении струи. При этом предполагается, что скорости всех молекул в поперечном сечении струи одинаковы. В этой формуле давление, обозначенное буквой p, в аэродинамике называется динамическим давлением.

Таким образом, АР позволяет выявлять аналогии между формулами различных разделов физики. Часто эти аналогии имеют глубокий физический смысл. При этом выявляется новый уровень обобщения. В таких случаях АРП служит звеном, укрепляющим связи между разделами физики.

Литература:

1. Неграш А. С., Мазейкина М.Ю. Использование анализа размерностей в геометрии /А.С. Неграш, М.Ю. Мазейкина// Педагогическое мастерство: материалы междунар. заоч. науч. конф. (г. Москва, апрель 2012 г.). – М.: Буки-Веди, 2012. – С.165-169.

2. Неграш А. С., Мазейкина М.Ю. Использование алгоритма анализа размерностей физических величин в школе / А. С. Неграш, М.Ю. Мазейкина// Молодой учёный. – 2012. – №6. – С. 411 – 417

3. Дешковский А., Койфман Ю. Метод размерностей в решении задач //ФПВ. – 2002. – № 2. – С. 71–81.

4. Неграш, А. С. Алгоритм решения задач физики анализом размерностей с использованием линейной алгебры / Неграш, А.С., Мазейкина М.Ю. // Бюллетень лаборатории математического, естественнонаучного образования и информатизации: Реценз. сб. науч. тр.–М.: Научная книга. – 2012. Том III. – С. 232-235.

Основное уравнение МКТ идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23..n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13. .m0n−v2	m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2
p=13..ρ−v2	ρ — плотность газа
p=nkT	k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0. .=√3RTM..

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32..kT

T=2−Ek3k..

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

---

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3..

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1..=p2V2T2..

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13..p1

б) 2p1

в) 23..p1

г) 43..p1

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23..n−Ek

Составим уравнения для начального и конечного состояний:

p1=23..n1−Ek1=23..3n−Ek=2n−Ek

p2=23.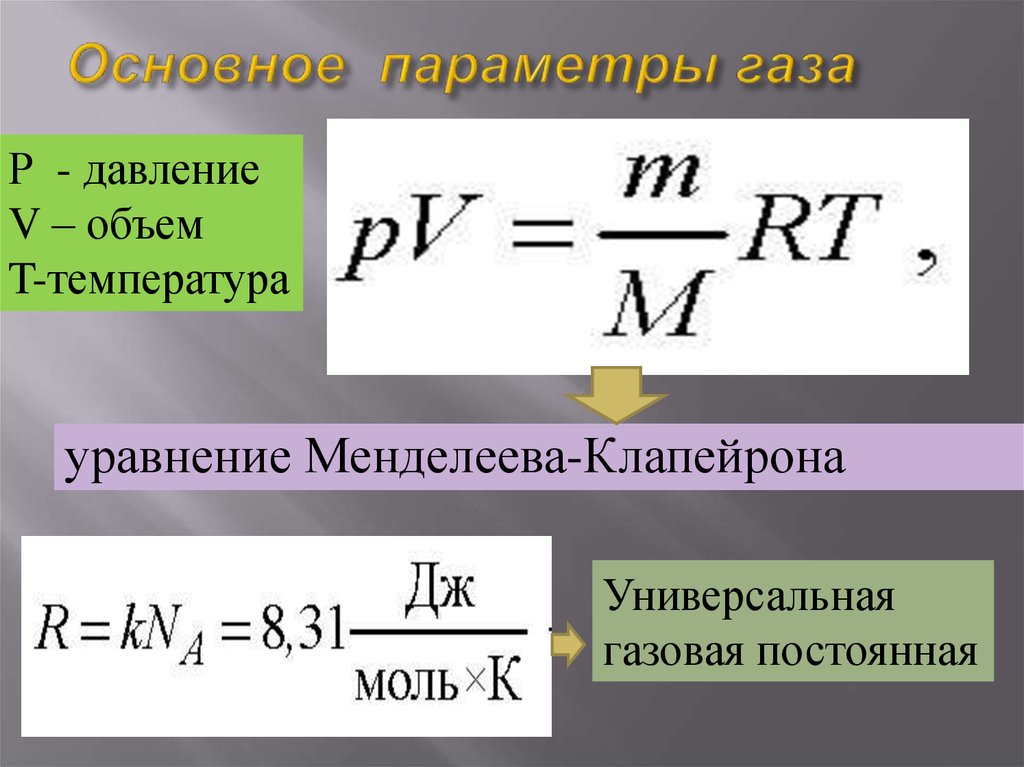 .n2−Ek2=23..n2−Ek=43..n−Ek

Отсюда:

n−Ek=p12..=3p24..

p2=4p16..=23..p1

.

.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18416 Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

---

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23..n−Ek

Применим его для обоих газов и получим:

p1=23..n1−Ek1 или 2p=23..n−Ek1 

p2=23..n2−Ek2 или p=23..n−Ek2 

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn..

−Ek2=3p2n..

Поделим уравнения друг на друга и получим:

−Ek1−Ek2..=3pn..·2n3p..=2

.

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18824 В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

---

Алгоритм решения

1. Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23..n−Ek

Применим его для обоих газов и получим:

p1=23..n1−Ek1 или 2p=23..n1−Ek 

p2=23..n2−Ek2 или p=23..n2−Ek 

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek..

n2=3p2−Ek..

Поделим уравнения друг на друга и получим:

n1n2..=3p−Ek..·2−Ek3p..=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 7. 2k | Оценить:

При увеличении объема газа в 2 раза его давление уменьшилось

Обновлено: 19.09.2022

Все эти задачи на одну формулу: PV = NkT, где P – давление газа, V – объем газа, N, k – некоторые постоянные величины, T – температура.
Тогда из этой формулы очевидно, что в первом вопросе температура не изменилась, то есть подрозумевается ответ изотермический
Для второго вопроса рассуждения не совсем верные, для того чтобы понять, поменялось ли давление или нет, выразим его из главной формулы: P = NkT/V. подставив начальные и конечные значения объема и температуры получим что давление не поменялось, следственно подрозумевается изобарический процесс

1. При увеличении объема идеального газа в 2 раза его температура увеличилась тоже в 2 раза. Какой процесс произошел с газом? Ответ А) Изобарический.

Какова удельная теплота сгорания торфа, если при сгорании 19 кг торфа выделяется 2,1 • 10 8 Дж энергии?

В течение 30с поезд двигался со скоростью 72 км\ч. Какой путь он прошёл ха это время ?

4. (2 бали) Потяг, рухаючись рівноприскорено, протягом часу t = 1хв збільшує свою швидкість від Vo = 36 км/год до у= 54 км/год. Знайти прискорення а п … отяга і визначити відстань Ѕ, яку він пройшов під час прискорення.. 5.(3 бали) Автобус рухається з постійною швидкістю 45 км/год протягом 4 год. Побудуйте графіки залежності: швидкості руху та шляху від часу.​

двигаясь со скоростью 72 км/ч мотоциклист притормозил и через 20 с достиг скорости 36 км/ч с каким ускорением он тормозил. км час перевести в си​

Чему будет равен путь, пройденный муравьем за 20 секунд равномерногодвижения, если за первые 4 секунды пройденный им путь состававил 2 см?​

Срочно! По рисункам первый и второй варианты очень нужно!

5. Велосипед движется со скоростью 14 м/с. Шины не скользят по поверхности дороги. Диаметр шины велосипеда равен 60 см. Чему равна угловая скорость ко … лес?​

3. Машина за 1/10 мин замедляет движение с 72 м/с до 36 м/с. Рассчитайте для машины: (а) Ускорение торможения. (б) Скорость через 2 с после начала то … рможения. (с) Скорость через 7 с после начала торможения.

В сосуде под поршнем находится идеальный газ. Если при нагревании газа его давление остается постоянным, то как изменятся величины: объем газа, его плотность и внутренняя энергия?

Для каждой величины определите соответствующий характер изменения:

3) не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Объем газа

Плотность газа

Внутренняя энергия газа

Идеальный газ в сосуде нагревается изобарически. Следовательно, согласно закону Гей-Люссака объем газа увеличивается. Плотность обратно пропорциональна объему, и так как количество газа не меняется, плотность газа уменьшается. Внутренняя энергия фиксированного количества идеального газа зависит только от температуры. При повышении температуры внутренняя энергия идеального газа увеличивается

При неизменной плотности одноатомного идеального газа давление этого газа увеличивают в 4 раза. Во сколько раз изменяется при этом среднеквадратичная скорость движения его атомов?

Давление идеального газа можно найти по формуле Концентрация равна где — масса всего газа. Следовательно, концентрация, также как и плотность газа, остаётся постоянной. Средняя кинетическая энергия атомов газа где — масса атомов газа. Подставим выражение для в уравнение для и выразим квадрат средней скорости.

Среднеквадратичная скорость движения атомов равна корню из среднего квадрата скорости атомов Следовательно, при увеличении давления в 4 раза среднеквадратичная скорость движения атомов газа возрастёт в 2 раза.

В закрытом сосуде находится идеальный газ. Как при охлаждении сосуда с газом изменятся величины: давление газа, его плотность и внутренняя энергия?

Для каждой величины определите соответствующий характер изменения:

3) не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Давление газа

Плотность газа

Внутренняя энергия газа

Идеальный газ в сосуде охлаждается изохорно. Следовательно, согласно закону Шарля давление газа уменьшается. Плотность газа не изменяется, так как объем, занимаемый газом и его количество не меняются. Внутренняя энергия фиксированного количества идеального газа зависит только от температуры. При понижении температуры внутренняя энергия идеального газа уменьшается

Здравствуйте я пиши не ради того чтобы узнать ответ на вопрос или сообщить об ошибки , а о том на сколько я признателен вам и этому сайту за проделанную работу , благодаря вашему сайту мои знания в области физики значительно стали лучше и за это вам огромное спасибо. Спасибо что вы есть !!(Я не знал куда написать слова благодарности поэтому и написал в коментарий под данной задачей )

Спасибо за то что вы делаете эту работу и помогаете простым школьникам вроде меня , Большое спасибо .

Очень приятно. А в целом, тут заготовлен целый раздел для приема благодарностей, называется “Сказать спасибо!”

в формуле U=(i/2)vRT, что значит символ i?

— число степеней свободы

Извините но плотность газа обратна пропорциональна температуре и прямо пропорциональна давлению по формуле:

Р =давление *на молярную массу / R T

Сама плотность, есть отношение массы и объема, объем не изменился.

В результате некоторого процесса концентрация молекул идеального одноатомного газа повышается. При этом среднеквадратичная скорость молекул остаётся прежней. Как в результате этого процесса изменяются давление газа и внутренняя энергия газа? Для каждой величины определите соответствующий характер её изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

1. Давление газа. Из основного уравнения идеального газа Так как средняя квадратичная скорость не меняется, а концентрация увеличивается, то давление увеличивается.

2. Внутренняя энергия газа. Внутренняя энергия идеального одноатомного газа равна Поскольку средняя квадратичная скорость постоянна, то температура газа не меняется; количество вещества не меняется, поэтому и внутренняя энергия остаётся неизменной.

Одноатомный идеальный газ неизменной массы совершает положительную работу в изотермическом процессе. Как изменяются в этом процессе объем, давление и внутренняя энергия газа? К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под со-ответствующими буквами.

Для каждой величины определите соответствующий характер изменения:

3) не изменяется.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Объём газа

Давление газа

Внутренняя энергия газа

Поскольку газ совершает положительную работу, его объем увеличивается. Процесс изменения состояния газа изотермический, а значит, согласно закону Бойля-Мариотта, величина должна оставаться постоянной. Таким образом, давление газа уменьшается в ходе этого процесса. Наконец, внутренняя энергия одноатомного идеального газа пропорциональна его температуре: следовательно, внутренняя энергия в этом процессе не изменяется.

Дан неправильный ответ 231 задача N83 “Оптимальный банк заданий для подготовки учащихся ” В.А.Орлов,М.Ю.Демидова. ЕГЭ-2013

Данная задача решена правильно. Еще раз сверьте условие, может в предложенной Вами книге порядок вопросов отличается?

Уважаемый Алексей! Да, действительно, по крайней мере, в сборнике «Универсальные материалы для подготовки учащихся. ЕГЭ-2011 Физика», В.А.Орлов, М.Ю.Демидова и др., – есть аналогичная задача (N 83). Только, в условии задачи в указанном сборнике, возможные характеры изменения соответствующих величин (А – объёма газа, Б – давления газа, В – внутренней энергии газа) , в отличие от условия задачи на данном сайте, нумеруются следующими цифрами: 1) не изменяется; 2) увеличивается; 3) уменьшается.

Спасибо! Теперь все встало на свои места.

Постоянное количество идеального газа охлаждается так, что его давление изменяется прямо пропорционально температуре. Как в этом процессе изменяются следующие физические величины: объем газа; внутренняя энергия газа?

Для каждой величины определите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Уравнение состояния идеального газа: По условию давление изменяется прямо пропорционально температуре: значит, объём газа не изменялся.

Процесс, происходящий при постоянном объеме — изохорный процесс.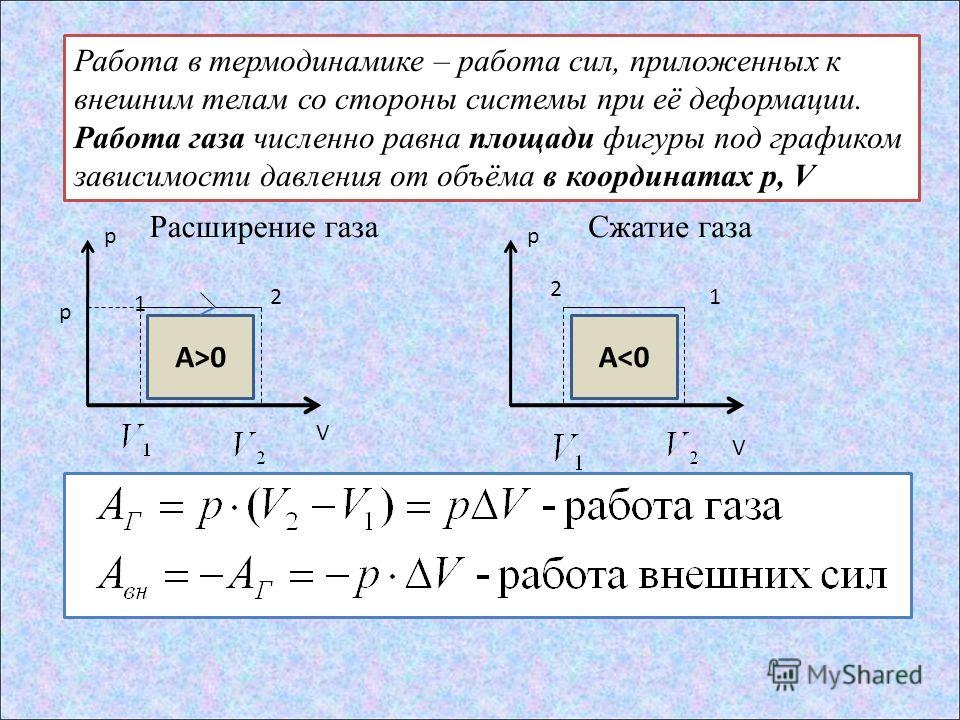 При этом процессе газ не совершает работы, а внутренняя энергия т. е. изменение внутренней энергии пропорционально изменению температуры. По условию газ охлаждается, значит, внутренняя энергия газа уменьшается.

Один моль одноатомного идеального газа участвует в процессе 1–2, график которого изображён на рисунке в координатах V–T (V — объём и T — абсолютная температура газа). Как изменяются в ходе этого процесса внутренняя энергия газа и его давление?

Для каждой величины определите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины.

Цифры в ответе могут повторяться.

Внутренняя энергия фиксированного количества идеального газа зависит только от температуры, т.е. уменьшение температуры приведет к уменьшению внутренней энергии газа.

На графике изображен изобарный процесс, т.к. следовательно, давление газа остается постоянным.

На графике зависимости объёма V от абсолютной температуры Т изображён процесс перехода идеального одноатомного газа из состояния 1 в состояние 2. Известно, что масса газа в этом процессе не изменялась. Как изменились при этом переходе плотность и давление газа?

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

А) плотность газа

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Так как формула для плотности газа имеет вид то увеличение объёма приводит к уменьшению плотности.

Уравнение состояния: Из графика видно, что объем и температура изменяются линейным образом, а значит давление в этом процессе не изменится.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом объём газа и его внутренняя энергия?

Для каждой величины определите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

На графике представлен изотермический процесс. При изотермическом процессе внутренняя энергия системы не меняется, а при уменьшении давления объем газа увеличивается.

На рисунке показан график зависимости модуля среднеквадратичной скорости V_ср.кв. атомов одноатомного идеального газа от объёма V газа в некотором процессе 1→2. Количество атомов газа в течение этого процесса не изменяется.

На основании анализа представленного графика выберите все верные утверждения.

1) В процессе 1→2 газ совершает положительную работу.

2) В процессе 1→2 внутренняя энергия газа уменьшается.

3) В процессе 1→2 давление p газа возрастает прямо пропорционально объёму V газа.

4) В процессе 1→2 газ отдаёт некоторое количество теплоты окружающим телам.

5) Процесс 1→2 является изобарическим.

1) В процессе 1→2 объем газа увеличивается, значит, газ совершает положительную работу. Утверждение 1 — верно.

2) Среднеквадратичная скорость газа в процессе увеличивается, значит, увеличивается и внутренняя энергия. Утверждение 2 — неверно.

3) Среднеквадратичная скорость связана с давлением как

В изображенном процессе среднеквадратичная скорость возрастает прямо пропорционально объему газа, значит, давление газа будет также возрастать прямо пропорционально объему газа. Утверждение 3 — верно.

4) В процессе 1→2 внутренняя энергия газа увеличивается и газ совершает положительную работу. Согласно первому началу термодинамики к газу подводится некоторое количество теплоты. Утверждение 4 — неверно.

5) Давление газа увеличивается, процесс не является изобарическим. Утверждение 5 — неверно.

Процесс, происходящий с идеальным газом, представлен на графике зависимости концентрации газа от его давления. При проведении опыта количество вещества оставалось постоянным. Постройте график зависимости давления от объёма для этого процесса. Опишите данные процессы опираясь на известные законы.

Концентрация газа связана с объёмом соотношением По условию количество молекул газа оставалось постоянным

В процессе 1–2 концентрация, а следовательно, и объём оставались неизменными, т. е. процесс был изохорным. Этому процессу на pV-диаграмме соответствует вертикальная линия. Как видно из графика, давление при этом изменилось от 2 до 4 единиц.

В процессе 2–3 выполняется соотношение а значит, — это закон Бойля — Мариотта, т. е. процесс был изотермический. Этому процессу на pV-диаграмме соответствует гипербола. Давление в процессе 2–3 изменилось от 4 до 8 единиц, т. е. увеличилось в 2 раза, следовательно, объём в процессе 2–3 уменьшился в 2 раза.

В итоге график выглядит следующим образом:

Источник: ЕГЭ 28.06.2018. Резервный день. Вариант 1 (Часть С)

На VT-диаграмме изображён процесс перехода одного моля идеального газа из состояния 1 в состояние 2.

Определите, как при этом переходе изменяются давление газа и плотность газа. Для каждой величины определите соответствующий характер её изменения:

3) не изменяется.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Из диаграммы видно, что процесс изотермический. При увеличении объёма в изотермическом процессе давление газа уменьшается.

Плотность газа уменьшается с увеличением его объёма.

В цилиндрическом сосуде, расположенном горизонтально, находится идеальный газ. Сосуд закрыт поршнем, который может перемещаться без трения. Давление снаружи атмосферное. Сосуд с газом нагревают так, что температура газа повышается. Как изменятся в результате этого объём газа в сосуде и внутренняя энергия газа?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Объём газа в сосуде

Внутренняя энергия газа

Температура газа увеличивается, так как сосуд с поршнем, то давление газа в сосуде будет постоянным, значит, объем газа будет увеличиваться. А следовательно, внутренняя энергия газа тоже увеличивается.

Источник: Тренировочная работа по физике 21.12.2016, вариант ФИ10203

В закрытом сосуде объёмом 8,3 литра находится одноатомный идеальный газ при температуре 127 °C. Начиная с момента времени t = 0 давление p газа изменяется так, как показано на приведённом графике.

На основании анализа графика выберите все верные утверждения.

1) Количество теплоты, переданное газу за первые 10 минут, равно 74,7 Дж.

2) Работа газа за первые 10 минут больше, чем работа газа за следующие 10 минут.

3) Изменение внутренней энергии газа за первые 20 минут равно 149,4 Дж.

4) В момент времени t = 25 мин температура газа станет равной 407,5 °С.

5) По заданным в задаче параметрам определить число молей газа в сосуде не представляется возможным.

Сосуд закрытый, поэтому объём газа не будет меняться. Количество теплоты, переданное газу за первые 10 минут, равно:

Значит, 1 утверждение верно.

В изохорном процессе работа газа равна нулю (за любой промежуток времени). Значит, утверждение 2 неверно.

Изменение внутренней энергии газа за первые 20 минут равно:

Значит, 3 утверждение верно.

В момент времени t = 25 мин температура газа по закону Шарля станет:

Значит, утверждение 4 неверно.

Из уравнения Клапейрона — Менделеева найдём число молей в газе

Значит, утверждение 5 неверно.

Источник: Тренировочная работа по физике 21.12.2016, вариант ФИ10203

В двух сосудах (1) и (2) объёмом V₀ каждый находятся одинаковые идеальные одноатомные газы. Исходные состояния этих газов соответствуют точкам А и В на VT-диаграмме (см. рисунок). Известно, что сначала давление в обоих сосудах одинаковое. Затем из исходных состояний газы переводят в новые конечные состояния А‘ и В‘.

Выберите все верные утверждения на основании анализа представленного графика.

1) В исходном состоянии концентрация молекул газа в сосуде (1) равна концентрации молекул газа в сосуде (2).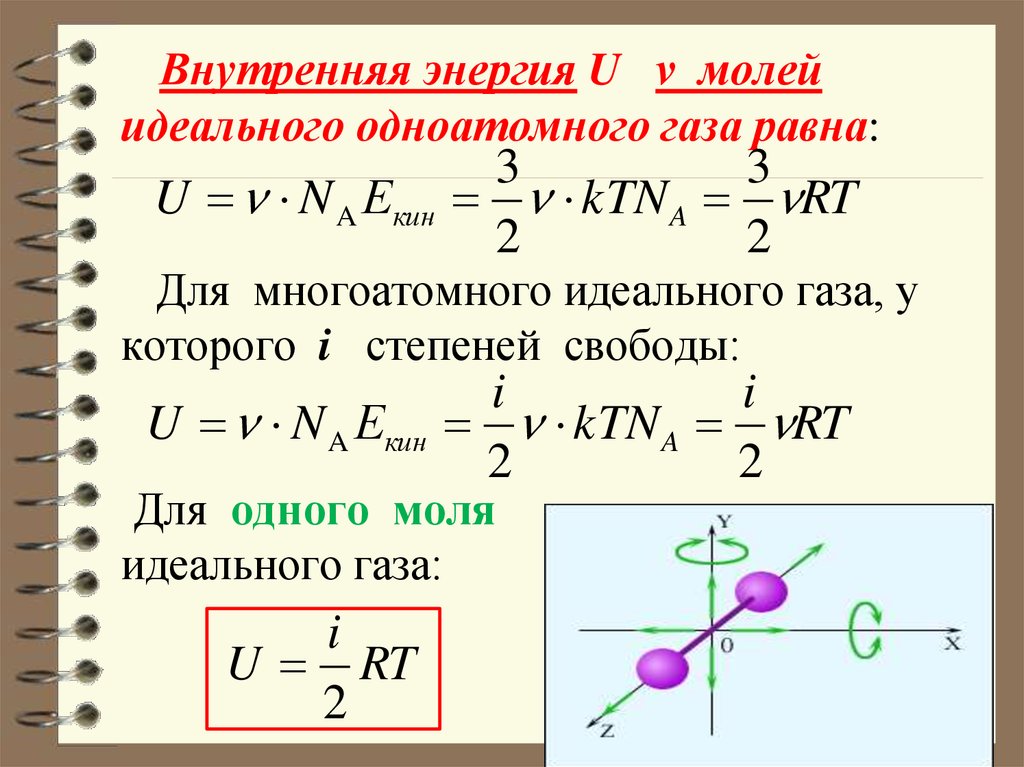

2) В конечном состоянии средняя кинетическая энергия хаотического движения молекул газа в сосуде (1) больше средней кинетической энергии хаотического движения молекул газа в сосуде (2).

3) Масса газа в сосуде (1) больше массы газа в сосуде (2).

4) Изменение внутренней энергии газа, находящегося в сосуде (1), при его переходе из состояния А в состояние А‘ равно изменению внутренней энергии газа, находящегося в сосуде (2), при его переходе из состояния В в состояние В‘.

5) Работа, совершённая газом, находящимся в сосуде (1) в процессе А→А‘, больше работы, совершённой газом, находящимся в сосуде (2) в процессе В→В‘.

1) Из условия задачи следует, что в начальный момент времени давление и объем в сосудах были одинаковы, а температура во втором сосуде в 2 раза больше, чем в первом сосуде. Согласно уравнению Менделеева — Клапейрона

откуда следует, что масса газа в первом сосуде в 2 раза больше, чем во втором. Утверждение 3 — верно.

Концентрация частиц может быть найдена как

Таким образом, концентрация газа в первом сосуде в 2 раза больше, чем во втором. Утверждение 1 — неверно.

2) Средняя кинетическая энергия поступательного движения молекул одноатомного идеального газа связана с его абсолютной температурой соотношением: В конечном состоянии температура газа выше во втором сосуде, а значит, частицы газа в этом сосуде обладают большей средней кинетической энергией. Утверждение 2 — неверно.

4) Внутренняя энергия одноатомного идеального газа пропорциональна его температуре

Учитывая, что в первом сосуде газа находится больше, внутренняя энергия в обоих сосудах изменилась на одинаковую величину. Утверждение 4 — верно.

5) Как видно из графика, в обоих сосудах происходит изобарный процесс, в котором работа газа может быть вычислена по формуле

Первоначальное давление в обоих сосудах равно, а объем изменился на одну и ту же величину. Таким образом, работа, совершённая газом, находящимся в сосуде (1) в процессе А→А‘, равна работе, совершённой газом, находящимся в сосуде (2) в процессе В→В‘. Утверждение 5 — неверно.

1.абсолютная температура газа увеличилась в 2 раза,а его объём увеличился при этом в 3 раза.изменилось ли при этом давление газа?если да,то во сколько раз?
2.абсолютная температура газа уменьшилась в 2 раза,а его давление уменьшилось при этом в 1,5 раза.изменился ли при этом объём газа?если да,то во сколько раз?

Решение не сложное. Тут надо применить уравнение Менделеева-Клайперона для идеальных газов РV=(m*RT)/M здесь Р – давление V -объем, m-масса газа, М – масса одного моля газа, Т – температура, R -газовая постоянная 8,31 дж/мольК (но это не надо) . Так вот. По условию массу не меняли, молярную массу не меняли, газовая постоянная вообще неизменна, значит менялись только давление, объем и температура. Ну вот, подставим первый случай Р*3=2, значит Р=2/3. Получается, что давление упало на 33,33% или в 0,66 раз

Теперь второй случай также подставим в уравнение V/1,5=1/2, решаем V=0,75 Получается, что объем сдулся на 25% или в 0,75 раз.

Читайте также:

  
• Факторио расчет схем
  
• Прототипы персонажей сталкер
  
• Симс 4 черта характера угасающий род
  
• Террария вики тактики
  
• Концовка doom 1

значение в термодинамике, правила определения, формулы

Физика

12. 11.21

14 мин.

Тепловые явления можно описать при помощи специальных макроскопических параметров, измеряемых термометром либо манометром. Эти приборы не реагируют на воздействие отдельных частиц. Термодинамикой называется теоретическая часть тепловых процессов, когда не берётся во внимание молекулярное строение тел. На уроках физики в 10 классе изучают внутреннюю энергию идеального газа, которая позволяет определить скорость движения молекул.

Оглавление:

• Краткое описание
• Свойства газа
• Использование высоких температур
• Особенности теплообмена
• Макроскопические параметры
• Воздействие внешних факторов
• Принцип определения ВЭ

Краткое описание

На уроках физики можно узнать, что основной функцией состояния термодинамической системы является внутренняя энергия (ВЭ) идеального газа. Необходимые параметры определяются набором макроскопических параметров, которые не зависят от того, какие данные фиксировались ранее. Например, если система перешла из одного состояния в другое, тогда изменения ВЭ будут заметны только на начальном и конечном этапе. Если всё будет возвращено в исходное положение, тогда и колебание показателей будет равно нулю. Это утверждение касается как одноатомных, так и двухатомных газов.

В физике описывается только два варианта изменения внутренней энергии тела:

• Теплопередача.
• Выполнение механической работы.

Потенциальная энергия взаимодействия частиц идеального газа равна нулю. По этой причине итоговые параметры одноатомного идеального газа будут сведены к суммарной кинетической энергии поступательного движения атомов. Если речь касается многоатомного агрегатного состояния, тогда дополнительно должно быть учтено вращение молекул и колебания атомов. В противном случае результат будет ошибочным.

Когда нужно найти энергию, то число атомов необходимо умножить на кинетическую энергию. На этот случай в физике существует специальная формула: U = NE = N *(3/2) kT = vNa * 3/2 kT = 3/2 vRT либо U = 3 m /2M RT. Химический состав и масса идеального газа останутся неизменными. Полученный результат можно рассматривать только как показатель температуры. У твёрдого тела, жидкости либо газа итоговая величина ВЭ во многом зависит от объёма, при изменении которого меняется расположение входящих в состав частиц.

Свойства газа

В физике газ описывается как агрегатное состояние какого-либо вещества, для которого свойственна большая подвижность входящих в состав частиц. Дополнительно можно выделить минимальную связь между атомами и молекулами. Вещество не имеет определённой формы в газообразном состоянии. Из-за чего стандартные способы решения сложных задач являются неактуальными. Если правильно подобрать температурный режим и параметры давления, то практически любое вещество можно будет перевести в газообразное состояние.

Идеальным можно назвать только тот газ, который обладает следующими свойствами:

• Молекулы не взаимодействуют между собой. Это связано с тем, что отсутствуют силы притяжения и отталкивания.
• Молекулы отличаются небольшим размером.
• Движение частиц происходит по принципу закона Ньютона.
• Молекулы могут отталкиваться друг от друга и от стенок ёмкости, в которую они помещены. Такие соударения подробно описаны формулами из раздела механики.
• Расстояние между молекулами существенно превышает их размер.

Если присутствуют все эти свойств, тогда можно говорить, что работать предстоит с идеальным газом.

Использование высоких температур

Многочисленные эксперименты доказали, что при нагревании частицы газа начинают двигаться гораздо быстрее. Изобретение термометров и введение величины температуры позволило учёным наблюдать за различными явлениями, которые связаны с нагревом и охлаждением. В результате усердной работы физикам удалось получить уравнение состояния идеальных газов: p*V = (m/µ) * (R * T). Речь касается соотношения между давлением, объёмом и абсолютной температурой по шкале Кельвина. Расшифровка формулы:

• Молярная масса — µ (R = 8.3157).
• Температура — T.
• Объём — V.
• Давление — p.

Это уравнение можно использовать только тогда, когда речь касается одноатомного газа. У молекул с большим количеством атомов дополнительно присутствуют колебательные и вращательные движения. К примеру, молекула О2 (кислорода) имеет энергию (7/2) * k * T, что существенного превышает стандартное значение одноатомного газа.

Особенности теплообмена

Перенос внутренней энергии в газах или жидкостях под воздействием циркуляции потоков называется конвекцией. Вблизи отопительных радиаторов воздух постепенно нагревается и расширяется. В действие вступает сила тяжести, не меняющая своих значений, а вот выталкивающие способности постепенно увеличиваются, из-за чего воздух поднимается. По такому алгоритму в природе образуется ветер.

Смена потоков задаёт темп циркуляции воздуха, что и является примером конвекции. Тепло распространяется по комнате благодаря воздушным потокам. Аналогичный процесс можно наблюдать и в случае использования жидкостей. Например, если поставить на плиту кастрюлю с водой, то её нагрев будет происходить благодаря конвекции. Многое зависит от теплопроводности используемой жидкости.

Конвекции невозможно добиться в том случае, если используются твёрдые тела. Силы взаимодействия частиц настолько велики, что они колеблются вблизи фиксированных пространственных точек.

Если циркуляция конвекционных потоков будет использоваться для отопления помещения, тогда нужно позаботиться о том, чтобы нагретому воздуху было куда подниматься. Если попробовать установить радиатор под потолком, то тепло не опустится. Отопительные приборы должны быть расположены максимально близко к полу. А вот климатическое оборудование нужно фиксировать как можно выше. Холодный воздух будет постепенно опускаться, вытесняя более тёплые потоки. В этом случае циркуляция будет действовать в обратном направлении.

Макроскопические параметры

Чтобы на практике использовать формулу изменения внутренней энергии, нужно учесть, что итоговый результат во многом зависит от температуры. Средняя потенциальная энергия взаимодействия молекул у реальных газов, твёрдых тел и жидкостей не равна нулю. Всё зависит от объёма вещества. В каждой ситуации можно наблюдать разное расстояние между молекулами. В термодинамике ВЭ реального газа зависит от объёма V и температуры T. Аналогичное правило действует и по отношению к макроскопическим телам.

Невозможно правильно вычислить внутреннюю энергию, если брать во внимание только движение отдельных молекул и их расположение относительно друг друга. Это связано с тем, что в макроскопических телах слишком много молекул.

Нужно уметь определять значение ВЭ с использованием тех параметров, которые можно измерить при помощи термометра или манометра.

Воздействие внешних факторов

Если по отношению к объекту были совершены какие-либо действия, тогда показатель ВЭ возрастёт. В качестве примера можно рассмотреть ситуацию, когда после нескольких ударов молотком гвоздь нагревается, а также немного деформируется.

Такой результат свидетельствует об увеличении кинетической энергии. Микроскопические частицы разгоняются от удара молотком и трения гвоздя о материал.

Деформацию можно расценивать как элементарное смещение частиц относительно друг друга. После удара молотком происходит сжатие. Частицы постепенно сближаются, из-за чего между ними возрастает сила отталкивания, что приводит к приращению потенциальной энергии. Так как над гвоздём была совершена работа, его ВЭ возросла.

В других ситуациях внутренняя энергия тела может существенно уменьшиться. Например, в теплоизолированной трубе сжатый воздух под поршнем постепенно расширяется, из-за чего поднимается определённый груз, совершая тем самым работу. Этот процесс отличается тем, что молекулы будут ударяться о стены, отдавая при этом часть своей кинетической энергии. ВЭ будет постепенно уменьшаться. Определённую работу совершает только воздух, у которого имеется достаточный запас энергии. Так как труба теплоизолированная, отсутствует приток кислорода, который мог бы пополнить запасы ВЭ.

Принцип определения ВЭ

Используя формулы внутренней энергии газа, нужно учитывать, что полученное значение будет прямо пропорционально его абсолютной температуре. Чёткое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. На уроках физики в 10 классе чаще всего используют следующую формулу: U = Ek + En. Расшифровка выглядит так:

• ВЭ газа — U.
• Кинетическая энергия хаотичного теплового движения — Ek.
• Показатель потенциальной энергии взаимодействия присутствующих в составе молекул — En.

Если по условиям задачи нужно правильно определить ВЭ газа (Ud), тогда в используемой формуле можно убрать потенциальную составляющую энергии. К примеру: Ud = Ek. Только благодаря сложению всех отдельных частиц рассчитывается кинетическая энергия вещества Eew. Если всё сделать правильно, то в итоге формула будет выглядеть так: Eew = E1 + E2 + E3 + E4 +… En. Буква n обозначает общее количество частиц в идеальном газе.

В разделе механики используется следующая формула: Ek = (m*v2)/2. Для обозначения массы используется буква m, скорость — v, а кинетическая энергия — Ek. Такой подход актуален на уроках физики, когда не подразумевается углублённое изучение темы. Но если нужно будет максимально точно рассчитать ВЭ частиц газа, тогда должен быть применён немного другой подход.

Для решения более сложных задач необходимо знать массу всех частиц, а также их суммарное количество. Но даже в одном моле вещества содержится большое количество молекул, которых просто не сосчитать. Именно поэтому понадобятся такие макроскопические параметры, как температура и давление.

Идеальный одноатомный газ | Азимут

Сегодня в Институте Топоса Софи Либкинд, Оуэн Линч и я провели некоторое время, беседуя о термодинамике, двигателях Карно и тому подобном. В результате я хочу выяснить для себя некоторые основные факты об идеальном газе. Все это хорошо известно, но мне трудно найти именно то, что я хочу — и не более того, спасибо — собранное в одном месте.

Просто для фона цикл Карно выглядит примерно так:

На самом деле это очень неточная картина, но она ясна. У нас есть сосуд с газом, и мы заставляем его совершать циклические движения, так что его давление и объем описывают на плоскости петлю. Как видите, эта петля состоит из четырех кривых:

• В первом, от a до b, мы помещаем контейнер с газом в контакт с горячей средой. Затем мы подвергаем его изотермическому расширению, то есть расширению при постоянной температуре.

• Во втором случае, от b до c, мы изолируем контейнер и допускаем адиабатическое обратимое расширение газа, т. е. расширение без поступления и отвода тепла. Температура падает, но только потому, что контейнер расширяется, а не потому, что уходит тепло. Достигает более низкой температуры. Затем снимаем изоляцию.

• В третьем, от c до d, мы помещаем контейнер в контакт с холодной средой, соответствующей его температуре. Затем мы подвергаем его изотермическому сжатию, то есть сжатию при постоянной температуре.

• В четвертом, от d до a, мы изолируем контейнер и допускаем адиабатическое обратимое сжатие газа, т. е. сжатие без поступления и отвода тепла. Температура повышается до тех пор, пока не сравняется с температурой горячей среды. Затем снимаем изоляцию.

Цикл Карно имеет историческое значение, потому что это пример максимально эффективного теплового двигателя: он выполняет максимально возможную работу для заданного количества тепла, передаваемого от горячей среды к холодной. Но я не хочу вникать в это. Я просто хочу вычислить формулы для всего, что здесь происходит, включая формулы для четырех кривых на этом рисунке!

Чтобы получить конкретные формулы, я рассмотрю идеальный одноатомный газ, то есть газ, состоящий из отдельных атомов, например гелий. Некоторые характеристики идеального газа, например формула зависимости энергии от температуры, зависят от того, является ли он одноатомным.

В качестве причудливого дополнительного бонуса я хотел бы подчеркнуть, как некоторые свойства идеального одноатомного газа зависят от размерности пространства. Есть определенный фрагмент теории, который не зависит от размерности пространства, если вы интерпретируете «объем» как n -мерный аналог объема. Но число 3 появляется в формуле энергии идеального одноатомного газа. И это потому, что пространство трехмерно! Так что просто для интереса, я сделаю весь анализ в и размеры.

Нам нужно знать четыре основные формулы.

Во-первых, у нас есть закон идеального газа:

где

• давление.
• n -мерный объем.
• число молекул в сосуде с газом.
• является постоянной, называемой постоянной Больцмана.
• температура.

Во-вторых, у нас есть формула для энергии или, точнее, внутренней энергии одноатомного идеального газа:

где

• внутренняя энергия.
• размерность пространства.

Множитель n /2 проявляется благодаря теореме о равнораспределении: классически гармонический осциллятор при температуре имеет ожидаемую энергию, равную количеству его степеней свободы. Грубо говоря, дело в том, что в n измерениях имеется n различных направлений, в которых может двигаться атом.

В-третьих, у нас есть связь между внутренней энергией, работой и теплотой:

Здесь

• дифференциал внутренней энергии.
• бесконечно малая работа, совершенная в газом.
• есть бесконечно малая теплота, переданная газу .

Интуиция проста: чтобы увеличить энергию некоторого газа, вы можете совершить с ним работу или передать ему тепло. Но математика может показаться немного туманной, поэтому позвольте мне объяснить.

Я подчеркиваю «до», потому что это влияет на знак: например, работа, выполненная на газа, минус работа, выполненная 9от 0022 до газ. Работа, совершенная с по , газ увеличивает на его внутреннюю энергию, а работа, совершенная с на , уменьшает его внутреннюю энергию. Аналогично для тепла.

Но что это за «бесконечно малые» штуки и эти странные символы?

Через минуту я все выражу через и Итак, и будут функции на плоскости с координатами и будет 1-форма на этой плоскости: это дифференциал функции

Но и есть не дифференциал функций а Нет функций на плоскости под названием а Нельзя взять коробку газа и измерить ее работу или нагрев! Есть только 1-формы, называемые и описывающие изменение в работе или тепле. Это не точные 1-формы, то есть не дифференциалы функций.

Четвертое и последнее:

Это должно быть интуитивно понятно. Работа, совершенная на газа во внешнем мире при небольшом изменении его объема, равна произведению давления на изменение объема. Итак, работа сделана 9От 0022 до газ равен минус давление, умноженное на изменение объема.

Одна приятная особенность 1-формы заключается в следующем: когда мы интегрируем ее вокруг простой замкнутой кривой, идущей против часовой стрелки, мы получаем площадь, ограниченную этой кривой. Итак, площадь этой области:

— это работа, совершенная на нашего сосуда с газом во время цикла Карно. (Здесь есть много минусов, о которых стоит беспокоиться, но не волнуйтесь, я их контролирую. Наша кривая идет по часовой стрелке, так что проделанная работа 9От 0022 до наш контейнер с газом отрицателен, и это минус площадь в регионе.)

Хорошо, теперь, когда у нас есть четыре основных уравнения, мы можем поиграть с ними и вывести следствия. Предположим, что число атомов в нашем сосуде с газом фиксировано — константа. Тогда мы думаем обо всем как о функции двух переменных: и

Во-первых, поскольку у нас есть

Таким образом, температура пропорциональна давлению, умноженному на объем.

Второй, так как и у нас

Итак, как и температура, внутренняя энергия газа пропорциональна произведению давления на объем, но зависит от размерности пространства!

Отсюда получаем

Отсюда и по нашим формулам получаем

Вот и все!

Но теперь мы знаем, как разобраться во всем, что касается цикла Карно. Я не буду делать все это здесь, но я разработаю формулы для кривых в этом цикле:

Изотермические кривые просты, так как мы видели, что температура пропорциональна давлению, умноженному на объем:

Итак, изотермическая кривая — это любая кривая с

Адиабатические обратимые кривые, или сокращенно «адиабаты», гораздо интереснее. Кривая на плоскости представляет собой адиабату , если при изменении давления и объема сосуда с газом при движении по этой кривой теплота не передается ни к газу, ни от газа. То есть:

, где забавный символ означает, что я ограничиваю 1-форму кривой и получаю 1-форму на этой кривой (которая оказывается равной нулю).

Давайте разберемся, как выглядит адиабата! По нашей формуле для мы имеем

или

или

Теперь мы сможем интегрировать обе стороны вдоль части кривой и получить

или

. , поскольку вы позволяете газу расширяться адиабатически — скажем, помещая его в изолированный цилиндр, чтобы тепло не могло проникать внутрь или наружу, — его давление падает по мере увеличения его объема. Но для одноатомного газа оно падает особым образом: давление уменьшается, как и объем, в степени -5/3.

В любом измерении давление одноатомного газа падает более круто, когда контейнер расширяется адиабатически, чем когда он расширяется при постоянной температуре. Почему? Поскольку падает быстрее, чем с

Но по мере ,

адиабаты становятся все ближе и ближе к изотермическим кривым в больших размерностях. Это не важно для понимания концептуально значимых особенностей цикла Карно! Но это любопытно, и я хотел бы улучшить свое понимание, думая об этом, пока это не станет очевидным. Пока нет.

Эта запись была опубликована в четверг, 15 июля 2021 г., в 4:38 и находится в разделе химия, физика. Вы можете следить за любыми ответами на эту запись через ленту RSS 2.0. Вы можете оставить отзыв или вернуться со своего сайта.

Удельная теплоемкость газов

Удельная теплоемкость газов

Удельная теплоемкость газов обычно выражается в молярной удельной нагревает. Для одноатомного идеального газа вся внутренняя энергия выражается в форме кинетической энергии, и кинетическая теория дает выражение для этой энергии, связанное с кинетической температурой. Выражение для внутренней энергии равно Для газов определены две удельные теплоемкости: одна для постоянного объема ( C V ) и один для постоянного давления ( C P ). Для процесса постоянного объема с одноатомным идеальным газом первый закон термодинамики дает: Более общий случай Дальнейшее применение закона идеального газа и первого закона дает соотношение Показать Отношение удельных теплоемкостей γ = C P /C V является фактором адиабатических процессов в двигателе и определяет скорость звука в газе. Это отношение γ = 1,66 для идеального одноатомного газа и γ = 1,4 для воздуха, который является преимущественно двухатомным газом.

Индекс Концепции газового закона Концепции кинетической теории

Гиперфизика***** Термодинамика R Ступица

Вернуться

Молярная удельная теплоемкость при постоянном объеме определяется как Постоянный объем Используя первый закон термодинамики, это можно представить в виде . , но поскольку ΔV = 0, выражение для C V становится равным Для одноатомного идеального газа , поэтому Это значение хорошо согласуется с экспериментом для одноатомных благородных газов, таких как гелий и аргон, но не описывает двухатомные или многоатомные газы, поскольку их молекулярные вращения и колебания вносят вклад в удельную теплоемкость. Равнораспределение энергии предсказывает

Index Концепции газового права Концепции кинетической теории

Гиперфизика***** Термодинамика R Неф

Вернуться

Молярная удельная теплоемкость при постоянном давлении определяется выражением Постоянное давление Используя первый закон термодинамики для процесса с постоянным давлением, это можно представить в виде Из закона идеального газа (PV=nRT) в условиях постоянного давления видно, что Поскольку удельная теплоемкость при постоянном объеме равна , отсюда следует, что Для идеального одноатомного газа	Index Концепции кинетической теории
Гиперфизика***** Термодинамика R Nave	Вернуться

Молярная удельная теплоёмкость идеальных одноатомных газов равна: Для двухатомных или линейных многоатомных молекул добавляются две вращательные степени свободы, соответствующие вращению вокруг двух перпендикулярных осей, проходящих через центр молекулы. Можно было бы ожидать, что это даст C V = 5/2 R, что подтверждается примерами, подобными азоту и кислороду. Нелинейная многоатомная молекула сможет вращаться вокруг трех перпендикулярных осей, что, как ожидается, даст С В = 3R. Наблюдаемое отклонение от этого значения указывает на необходимость учета колебательных степеней свободы для полного описания удельных теплоемкостей газов. Примеры Таблица молярных теплоемкостей

Index Концепции кинетической теории Sears & Salinger, Sec 9-7

Гиперфизика***** Термодинамика R Ступица

Вернуться

Модели постоянной объемной теплоемкости, основанные на равнораспределении энергии и включающие вращательные степени свободы, а также поступательные, могут объяснить теплоемкость двухатомных молекул. Отход от этой модели в случае нелинейных многоатомных молекул свидетельствует о колебательном участии. Удельная теплоемкость при постоянном давлении связана со значением постоянного объема как C P = C V + R. Отношение удельных теплоемкостей γ = C P /C V является фактором адиабатических процессов двигателя и при определении скорости звука в газе. Водород как пример двухатомной молекулы

Индекс Концепции кинетической теории Sears & Salinger, разделы 9-7

Гиперфизика***** Термодинамика R Ступица

Вернуться

Поведение удельной теплоемкости водорода при изменении температуры в начале 20-го века было крайне загадочным. При низких температурах он вел себя как одноатомный газ, но при более высоких температурах его удельная теплоемкость принимала значение, подобное другим двухатомным молекулам. Потребовалось развитие квантовой теории, чтобы показать, что двухатомный водород с его крошечной инерцией вращения требует большого количества энергии для возбуждения своего первого квантового состояния возбужденного молекулярного вращения. Поскольку он не мог получить такое количество энергии при низких температурах, он вел себя как одноатомный газ. Удельная теплоемкость газов Равнораспределение энергии

Index Концепции кинетической теории

9 Гиперфизика***** Термодинамика R Nave 9 Назад 3.5 Теплоемкость идеального газа – University Physics Volume 2 Глава 3. Первый закон термодинамики Цели обучения К концу этого раздела вы сможете: Определить теплоемкость идеального газа для конкретного процесса Рассчитайте удельную теплоемкость идеального газа для изобарного или изохорного процесса Объясните разницу между теплоемкостью идеального газа и реального газа Оценка изменения удельной теплоемкости газа в диапазоне температур Мы узнали об удельной теплоемкости и молярной теплоемкости в Температуре и Теплоте; однако мы не рассматривали процесс, в котором добавляется тепло. Мы делаем это в этом разделе. Сначала мы исследуем процесс, в котором система имеет постоянный объем, затем сопоставляем его с системой при постоянном давлении и показываем, как связаны их удельные теплоемкости. Начнем с рисунка 3.12, на котором показаны два сосуда A и B , каждый из которых содержит 1 моль идеального газа одного и того же типа при температуре T и объеме V . Единственная разница между двумя сосудами заключается в том, что поршень в верхней части A зафиксирован, тогда как поршень в верхней части B может свободно перемещаться против постоянного внешнего давления p . Теперь рассмотрим, что происходит, когда температура газа в каждом сосуде медленно повышается до [латекс]Т+дТ[/латекс] при добавлении тепла. Рисунок 3.12  Два сосуда идентичны, за исключением того, что поршень в верхней части A зафиксирован, тогда как поршень в верхней части B может свободно перемещаться против постоянного внешнего давления p. Поскольку поршень сосуда A зафиксирован, объем заключенного газа не меняется. Следовательно, газ не работает, и мы имеем по первому закону [латекс] d {E} _ {\ text {int}} = dQ-dW = dQ. [/ латекс] Тот факт, что теплота обменивается при постоянном объеме, представим, написав [латекс]dQ={C}_{V}dT,[/латекс] , где [латекс]{C}_{V}[/латекс] — молярная теплоемкость при постоянном объеме газа. Кроме того, поскольку [latex]d{E}_{\text{int}}=dQ[/latex] для этого конкретного процесса, [латекс] d {E} _ {\ text {int}} = {C} _ {V} dT. [/latex] Мы получили это уравнение, предполагая, что объем газа фиксирован. Однако внутренняя энергия — это функция состояния, зависящая только от температуры идеального газа. Следовательно, [latex]d{E}_{\text{int}}={C}_{V}dT[/latex] дает изменение внутренней энергии идеального газа для любого процесса, связанного с изменением температуры дТ . Когда газ в сосуде B нагревается, он расширяется против подвижного поршня и совершает работу [латекс]dW=pdV. [/латекс] В этом случае тепло добавляется при постоянном давлении, и мы пишем [латекс]dQ={C}_{p}dT,[/латекс] , где [латекс]{C}_{p}[/латекс] — молярная теплоемкость газа при постоянном давлении . Кроме того, поскольку идеальный газ расширяется против постоянного давления, [латекс]d\левый(pV\правый)=d\левый(RT\правый)[/латекс] становится [латекс]pdV=RdT.[/латекс] Наконец, подставляя выражения для dQ и pdV в первый закон, получаем [латекс]d{E}_{\text{int}}=dQ-pdV=\left({C}_{p}-R\right)dT.[/latex] Мы нашли [латекс]d{E}_{\text{int}}[/latex] как для изохорного, так и для изобарического процесса. Поскольку внутренняя энергия идеального газа зависит только от температуры, [latex]d{E}_{\text{int}}[/latex] должен быть одинаковым для обоих процессов. Таким образом, [латекс] {C}_{V}dT=\left({C}_{p}-R\right)dT,[/latex] и [латекс]{C}_{p}={C}_{V}+R.[/латекс] Вывод уравнения 3. 10 был основан только на законе идеального газа. Следовательно, это соотношение приблизительно справедливо для всех разбавленных газов, будь то одноатомные, такие как He, двухатомные, такие как [латекс] {\ text {O}} _ {2}, [/ латекс], или многоатомные, такие как [латекс] {\ текст {CO} }_{2}{\phantom{\rule{0.2em}{0ex}}\text{или NH}}_{3}\text{.}[/latex] В предыдущей главе мы нашли, что молярная теплоемкость идеального газа при постоянном объеме равна [латекс]{C}_{V}=\frac{d}{2}R,[/латекс] , где d — число степеней свободы молекулы в системе. В таблице 3.3 показаны молярные теплоемкости некоторых разбавленных идеальных газов при комнатной температуре. Теплоемкости реальных газов несколько выше, чем те, которые предсказываются выражениями [латекс]{C}_{V}[/латекс] и [латекс]{С}_{р}[/латекс], приведенными в уравнении 3.10. Это указывает на то, что колебательное движение в многоатомных молекулах существенно даже при комнатной температуре. Тем не менее разница в молярных теплоемкостях, [латекс]{C}_{p}-{C}_{V},[/latex] очень близка к R даже для многоатомных газов. Таблица 3.3 Молярная теплоемкость разбавленных идеальных газов при комнатной температуре Тип молекулы Газ [латекс]{C}_{p}[/латекс] (Дж/моль К) [латекс]{C}_{V}[/латекс] (Дж/моль К) [латекс]{C}_{p}-{C}_{V}[/латекс] (Дж/моль·К) Одноатомный Идеал [латекс]\фракция{5}{2}R=20,79[/латекс] [латекс]\фракция{3}{2}R=12,47[/латекс] [латекс]R=8,31[/латекс] Двухатомный Идеал [латекс]\frac{7}{2}R=29,10[/латекс] [латекс]\фракция{5}{2}R=20,79[/латекс] [латекс]R=8,31[/латекс] Многоатомный Идеал [латекс]4R=33,26[/латекс] [латекс]3R=24,94[/латекс] [латекс]R=8,31[/латекс] Резюме Для идеального газа молярная емкость при постоянном давлении [латекс]{C}_{p}[/латекс] определяется как [латекс]{C}_{p}={C}_{V}+R =dR\text{/}2+R[/latex], где d — количество степеней свободы каждой молекулы/объекта в системе. У реального газа удельная теплоемкость близка, но немного выше, чем у соответствующего идеального газа с [латексом]{C}_{p}\simeq {C}_{V}+R.[/latex] Концептуальные вопросы Как объект может передавать тепло, если объект не обладает дискретным количеством тепла? Большинство материалов расширяются при нагревании. Одним заметным исключением является вода между [латексом]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] и [латексом]4\phantom{\rule{0.2em }{0ex}}\text{°}\text{C,}[/latex], объем которого фактически уменьшается с повышением температуры. Что лучше для воды в этом температурном диапазоне, [латекс]{C}_{p}[/латекс] или [латекс]{C}_{V}[/латекс]? Показать решение Обычно [латекс]{C}_{p}[/латекс] больше, чем [латекс]{C}_{V}[/латекс], потому что, когда расширение происходит при постоянном давлении, оно действует на окружение. Следовательно, теплота может переходить во внутреннюю энергию и совершать работу. При постоянном объеме все тепло переходит во внутреннюю энергию. В этом примере вода сжимается при нагревании, поэтому, если мы добавляем тепло при постоянном давлении, работа над водой выполняется окружающей средой, и, следовательно, [латекс]{С}_{р}[/латекс] меньше, чем [латекс]{ C}_{V}[/латекс]. Почему для газов [латекс]{C}_{p}[/латекс] и [латекс]{C}_{V}[/латекс] указаны две удельные теплоемкости, а для твердого тела – только одна? Задачи Температура идеального одноатомного газа повышается на 8,0 К. Как изменится внутренняя энергия 1 моль газа при постоянном объеме? Показать раствор 100 Дж При повышении температуры на [латекс]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] при постоянном объеме, какое количество тепла поглощается (a) 3,0 моль разбавленного одноатомного газа; б) 0,50 моль разбавленного двухатомного газа; в) 15 моль разбавленного многоатомного газа? Если газы из предыдущей задачи изначально имеют температуру 300 К, какова их внутренняя энергия после того, как они поглотят тепло? Показать раствор а. 370 Дж; б. 100 Дж; в. 500 Дж Рассмотрим 0,40 моль разбавленного углекислого газа при давлении 0,50 атм и объеме 50 л. Какова внутренняя энергия газа? Когда 400 Дж тепла медленно добавляют к 10 молям идеального одноатомного газа, его температура повышается на [латекс]10\phantom{\rule{0.2em}{0ex}}\text{°}\text{C} [/латекс]. Какую работу совершил газ? Показать решение 850 J Один моль разбавленного двухатомного газа, занимающий объем 10,00 л, расширяется при постоянном давлении 2000 атм при медленном нагревании. Если температура газа повышается на 10,00 К и при этом выделяется 400,0 Дж теплоты, каков его конечный объем? Глоссарий молярная теплоемкость при постоянном давлении количественно определяет отношение количества подведенного тепла к температуре при измерении при постоянном давлении молярная теплоемкость при постоянном объеме количественно определяет отношение количества подведенного тепла к температуре при измерении при постоянном объеме Лицензии и атрибуты Теплоемкость идеального газа. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/3-5-heat-capacities-of-an-ideal-gas. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction Общая физика II Q21.13 Идеальный газ находится в сосуде при температуре 300 К. Если температура увеличивается до 900 К, (а) во сколько раз среднеквадратичная скорость каждой молекулы сдача? Температура повысилась в 3 раза. Среднеквадратическая скорость равна квадратному корню из температуры, поэтому мы увеличили среднеквадратичную скорость на КОРЕНЬ(3)=1,732 (б) от какого фактора зависит давление в сосуде сдача? Закон идеального газа остается в силе, P V = n R T. Если объем остается постоянным, увеличение температура в 3 раза означает увеличение давления с тем же коэффициентом 3. SQRT[] означает «Квадратный корень из», потому что для меня это проще написать SQRT, чем идти в графический редактор и строить квадратный корень знак.   21.*. Найти среднеквадратичную скорость молекул азота при стандартных условиях, 0,0 o С и давление 1,00 атм. Напомним, что 1 моль любого газа занимает объемом 22,4 литра в стандартных условиях. Уравнение 21.7 на стр. 590 говорит нам T = 0 o C = 273 K R = 8,31 Дж/моль-К M = 28 г/моль = 28 x 10 – 3 кг/моль v среднеквадратичное значение = SQRT[ 3 (8,31 Дж/моль-K)(273 K)/(28 x 10 – 3 кг/моль)] v среднеквадратичное значение = SQRT [2,43 x 10 5 (Дж/моль-К)(К)/(кг/моль)] v среднеквадратичное значение = SQRT [2,43 x 10 5 (Дж/кг)(Н-м/Дж)(кг-м/с 2 /Н)] v среднеквадратичное значение = SQRT [2,43 x 10 5 (м 2 /с 2 )] v rms = 493 м/с Будьте осторожны с единицами измерения. Они важны! Они не просто запоздалая мысль. 21,3 За 30-секундный интервал в оконное стекло площадью 0,60 ударилось 500 градин. м 2 под углом 45 o к поверхности окна. Каждый Градины имеют массу 5,0 г (0,005 кг) и скорость 8,0 м/с. Если удары упругие, найти среднюю силу и давление на окно. v x = v cos 45 o v x = (8,0 м/с)(0,707) = 5,66 м/с p x = m v x = (0,005 кг)(5,66 м/с) = 2,83 x 10 – 2 кг-м/с р x = 2 p x = 5,66 x 10 – 2 кг-м/с F = p xtot /t F = (500)(5,66 х 10 – 2 кг-м/с)/30 с F = 0,943 кг-м/с 2 F = 0,943 Н П = Ф/А P = 0,943 Н / 0,60 м 2 P = 1,57 Н/м2 P = 1,57 Па 21. ** Рассчитайте среднеквадратичную скорость молекулы H 2 при температуре 250 o C. Конечно, это в основном то же самое, что и задача 2 выше. Но всегда полезно работать с похожими задачами — просто посмотреть что идея одна и та же даже с разными номерами. Этот время Т = 250 или С = 523 К М = 2 г/моль = 2 x 10 – 3 кг/моль Как и в случае с 21.1, начнем с уравнения 21.7 со стр. 590, R = 8,31 Дж/моль-К v среднеквадратичное значение = SQRT[ 3 (8,31 Дж/моль-K)(523 K)/(2 x 10 – 3 кг/моль)] v среднеквадратичное значение = SQRT [6,52 x 10 6 (Дж/моль-К)(К)/(кг/моль)] v среднеквадратичное значение = SQRT [6,52 x 10 6 (Дж/кг)(Н-м/Дж)(кг-м/с 2 /Н)] v среднеквадратичное значение = SQRT [6,52 x 10 6 (м 2 /с 2 )] v среднеквадратичное значение = 2 550 м/с 21,8 Если среднеквадратическая скорость атома гелия при комнатной температуре равна 1350 м/с, какова среднеквадратичная скорость молекулы кислорода (O 2 ) при этой температуре? (Молярная масса O 2 равно 32, а молярная масса He равна 4. ) Эта задача также начинается с уравнения 21.7, T/M O ] / SQRT[3 R T/M H ] v rmsO /v rmsH = SQRT[ (3 R Т/М О ) / (3 Р Т/М Х )] v rmsO /v rmsH = SQRT[ М Н / М О ] v rmsO /v rmsH = SQRT[ 4/16 ] v rmsO /v rmsH = SQRT[ 1/4 ] v среднеквадратичное значение /v среднеквадратичное значение = 1/2 v среднеквадратичное значение /v среднеквадратичное значение = 0,5 В среднеквадратичное значение = 0,5 В среднеквадратичное значение v среднеквадратичное значение O = 0,5 (1350 м/с) v rmsO = 675 м/с 21. *** Один моль газообразного ксенона при 20,0 o C занимает 0,0224 м 3 . Какое давление оказывают атомы Хе на стенки сосуда? П В = н Р Т Р = н Р Т / В P = (1 моль) (8,31 Дж/моль-К) (293 К) / 0,0224 м 3 P = 1,09 x 10 5 (Дж/м 3 ) Что такое J/m 3 ? P = 1,09 x 10 5 ( Дж /м 3 ) [ Н-м / Дж ] P = 1,09 x 10 5 Н/м 2 P = 1,09 x 10 5 Па P = 1,09 x 10 5 Па [1 атм / 1,013 x 10 5 Па] P = 0,029 атм 21.13 Рассчитайте изменение внутренней энергии 3,0 молей газообразного гелия при повышении его температуры на 2,0 К. Для идеального газа мы получили бы U = (3/2) n R T У = (3/2) n R T У = (3/2) (3 моля) (8,31 Дж/моль-К) (2,0 К) У = 74,8 Дж В то время как гелий ведет себя почти как идеальный газ, мы можем сделать этот расчет для фактического поведения гелия. У = н С v Т Из таблицы 21.2 на странице 647 текста мы находим, что для гелия c v = 12,5 Дж/моль-К У = (3 моль)(12,5 Дж/моль-К)(2,0 К) У = 75,0 Дж   21.**** Один моль идеального одноатомного газа имеет начальную температуру 300 К. Газ подвергается изоволюметрическому процессу, приобретая 500 Дж нагревать. Затем он подвергается изобарическому процессу, теряя такое же количество тепла. Определить: а) новую температуру газа и б) работу, совершенную над газ. [[ Примечание: Часть из более ранних решений , размещенных в Интернете, было неправильным.]] Для изоволюметрического (постоянного объема) процесса от А до B, работа не выполняется, W AB = 0 Q = У = 500 Дж Для изобарического (постоянного давления) процесса от В до С работа З БК = П В Нам известна начальная температура, T A = 300 К. Найти W BC нам понадобятся температуры T B и T C в состояниях B и C, поэтому мы можем найти P V для выражения выше. Q AB = н С В Т = 500 Дж (н) ( (3/2) Р) (Т) = 500 Дж (1 моль) ( (3/2) 8,31 Дж/моль-К) (Т) = 500 Дж (12,5 Дж/К) Т = 500 Дж Т = (500/12,5) К Т = 40 К Т В = 300 К + 40 К Т Б = 340 К Q BC = n C P T – 500 Дж = (n) ( (5/2) R) (T) – 500 Дж = (1 моль) ( (5/2) 8,31 Дж/моль-К) (Т) – 500 Дж = (20,8 Дж/К) Т Т = – (500/20,8) К Т = – 24,1 К Т С = 340 К – 24,1 К Т С = 315,9 К W до = W AB + W BC Вт АВ = 0 З БК = П В Q до = W до + U до Q to = 500 Дж + (- 500 Дж) = 0 Ш до = – U до У = п С В Т У = (n) ( (3/2) R) (T to ) Т = 40,0 К – 24,1 К Т = 15,9 К· У = (n) ( (3/2) R) (T to ) У = (1 моль)(12,5 Дж/моль-К)(15,9 К) У = 199 Дж Ш до = – U до Вт = – 199 Дж [[ Этот окончательный ответ такой же, как был опубликован ранее, но часть из предыдущее решение было неправильно . ]]   21,25 Два моля идеального газа ( = 1,40) медленно и адиабатически расширяется от давления 5,0 атм и объемом 12,0 литров до конечного объема 30,0 литров. а) Каково конечное давление газа? “Адиабатически” означает или P f = (5,0 атм) (12,0 л/30,0 л) 1,4 P f = (5,0 атм) (0,4) 1,4 P f = (5,0 атм) (0,2773) P f = 1,386 атм (b) Каковы начальная и конечная температуры? Снова (или “как обычно”?!?!?) найдем Закон Идеального Газа очень полезно; П В = н Р Т Т = П В / н Р T i = P i V i / n R T i = (5,0 атм) (12,0 л)/[(2,0 моль) (8,31 Дж/моль-К)] Будьте осторожны! Хотя это уравнение верно, оно также неуклюже или камберсон, так как у нас есть такие странные или смешанные подразделения. С тех пор, как мы иметь давление в атмосферах и объем в литрах, мы будем далеко лучше использовать R в единицах л-атм вместо джоулей! Опять таки (и снова, и снова, и снова!), следите за единицами! Единицы не «дополнение»; они важны — даже жизненно важны! T i = (5,0 атм) (12,0 л)/[(2,0 моль) (0,0821 л-атм/моль-К)] Т i = 365,4 К T f = P f V f / n R T f = (1,386 атм) (30,0 л)/[(2,0 моль) (0,0821 л-атм/моль-К)] T f = 253,2 К 21,***** Четыре литра двухатомного идеального газа ( = 1,40), заключенные в цилиндр, проходят через замкнутый цикл. Газ первоначально при 1,0 атм и при 300 К. Во-первых, его давление увеличивается втрое при постоянный объем. Затем он адиабатически расширяется до исходного давления. и, наконец, изобарически сжимается до исходного объема. (z) Каково его начальное давление? П В = н Р Т P = n R T / V (а) Начертите PV-диаграмму этого цикла. Вот набросок: (b) Определите объем в конце адиабатического расширение. При движении по адиабате или или   в) Найдите температуру газа в начале адиабатическое расширение В состоянии A, P A V A = n R T A n = P А В А / Р Т А А В состоянии B начало адиабатического расширения, P B V B = n R T B B T B = P B V B / N R Т Б = П Б В Б /[(P A V A / R T A ) Р] Т Б = Т А [ П Б В Б Б /(П А В А ) ] Т Б = Т А (P B /P A ) (V B /V A ) [ или мы могли бы получить это примерно так же просто, заметив P V = n R T П В / Т = н Р П А В А /Т А = Р Б В Б /Т Б Т Б = Т А (P B /P A ) (V B /V A ) способ кажется заметно легче. Но, конечно, результат то же.] Т Б = Т А (P B /P A ) (V B /V A ) Конечно, V B = V A T B = 300 К (3 атм/1 атм) (1) Т В = 300 К (3) Т Б = 900 К (d) Найдите температуру в конце цикла. Мы знаем давление и объем для состояния C, конец адиабатическое расширение, P C = 1 атм В С = 8,77 л П В = н Р Т P V / T = константа П А В А / Т А = Р С В С / Т С Т С = Т А (P C /P A ) (V C /VA) T C = 300 K (1 атм/1 атм) (8,77 л/4 л) Т С = 300 К (1) (2,19) Т С = 657,5 К (e) Какая чистая работа была совершена за этот цикл? Посмотрите на работу для каждой части, а затем просуммируйте те; Вт АВ = 0 Ш ВС = – У Т = T f – T i = T C – T B Т = 657,5 К – 900 К Т = – 242,5 У = н С В Т У = n [ (5/2) R ] [ – 242,5 K ] Сколько у нас родинок? Вернитесь в состояние А и найдите вне; П В = н Р Т n = [ PV/T ] [1/R] n = [1 атм – 4 л / 300 K] [1/R] У = [ 1 атм – 4 л / 300 K] [1/R] [ (5/2) R ] [- 242,5 К ] У = [ 4 атм – л / 300 ] [ (5/2)] [ – 242,5 ] У = – 8,08 л-атм Мы делали это покрытие блока раньше. Мы могли бы просто пойти вернись и получи. Но стоит делать “с нуля”, слишком; У = – 8,08 л-атм [0,001 м3/л] [1,013 x 10 5 (Н/м 2 )/атм] У = – 819 Дж Вт ВС = + 819 Дж З СА = П В Вт CA = (1 атм) (4 л – 8,77 л) Вт CA = – 4,77 л-атм Вт CA = – 4,77 л-атм [0,001 м 3 /л] [1,013 x 10 5 (Н/м 2 )/атм] Вт СА = – 483 Дж Вт до = Вт АВ + Ш ВС + В КА Вт до = 0 + 819 Дж – 483 Дж Вт до = 336 J Хотя я пометил это W tot , так как в всего работает, мы могли бы также назовите это net work и назовите его W нетто . 21.****** Сосуд объемом 5,0 л содержит 0,125 моль идеального газа при 1,50 банкомат Какова средняя поступательная кинетическая энергия одной молекулы? = (1/2) м 2 > = (1/2) м 2 > = (1/2) к T Итак, сначала мы должны найти температуру T P V = n R T Т = П В / н Р T = (1,5 атм) (5,0 л) / [(0,125 моль) (0,0821 л-атм/моль-К)] Т = 731 К = (1/2) k T = (1/2) (1,38 x 10 – 23 Дж/К) (731 К) = 5,04 x 10 – 21 Дж 21,33 Рассмотрим 2,0 моля идеального двухатомного газа. Найдите общее тепло емкость при постоянном объеме и постоянном давлении, если (а) молекулы вращаются, но не колеблются и C V = (5/2) R C tot = n C V = 5 R (б) молекулы вращаются и вибрируют. С В = (7/2) Р C tot = n C V = 7 R Pagina niet gevonden | Digitaal Wetenschapshistorisch Centrum Institut d’Història de la Ciència iHC, Universitat Autonoma de Barcelona приглашает к участию в международном семинаре Small Science: Perspectives on Contemporary Small-Scale Research . Мероприятие состоится 2-3 февраля 2023 года в Institut d’Història de la Ciència, Universitat Autònoma de Barcelona. Тем не менее, для тех, кто предпочитает дистанционное участие, также будет виртуальный вариант. Лиз Мир… An der Fakultät Biologie ist zum nächstmöglichen Zeitpunkt die Juniorprofessur (W1) für Geschichte der Botanik und des Gartenbaus für zunächst vier Jahre zu besetzen. Nach Positiver Zwischenevaluation wird das Dienstverhältnis auf insgesamt sechs Jahre verlängert. Lees meer… История исторических отношений между наукой и империей часто излагается мазками, а ученые, приехавшие из-за пределов Европы, отводятся на второстепенные роли. В последние годы этот подход подвергался сомнению как внутри академии, так и за ее пределами: ученые и журналисты в равной степени призывают к проведению дополнительных исследований, направленных на понимание активной роли отдельных ученых, происходящих из коренных колониальных общин. Лиз Мир… С 2014 года междисциплинарный исследовательский проект «Наука и религия: изучение спектра глобальных перспектив» направлен на то, чтобы лучше понять, как профессиональные ученые и представители общественности видят взаимосвязь между эволюцией и религией, и, соответственно, , отношения между наукой, рациональностью и религией. Совместно с исследователями из восьми стран мира, включая Великобританию, США, Канаду, Испанию, Германию, Аргентину, Австралию и Шри-Ланку, проект изучил исторические, культурные, социальные и психологические факторы, действующие в общественных дискуссиях об отношениях между эволюция и личная вера. Лиз Мир… При изучении истории микроскопии естественно начать с Рима. Именно в Риме под эгидой Accademia dei Lincei Федерико Чези опубликовал свои микроскопические наблюдения за пчелами в своих Melissographia (1625 г.) и Apiarium (1626 г.). В честь недавно избранного Барберини Папы Урбана VIII, на фамильном гербе которого изображены три пчелы, пчела стала первым объектом визуального представления исследований, которые стали возможными благодаря новому прибору, который вскоре назовут «микроскопом». Подробнее читайте на веб-странице семинара Конференция Gewina, которая проводится раз в два года (обычно) открыта для регистрации. Организаторы хотят поблагодарить всех за их восторженный отклик на призыв к докладам и с нетерпением ждут презентаций. Программу можно найти здесь. Вопросы о регистрации, программе или другие организационные вопросы можно направлять по адресу [email protected] Подробнее на Gewina.nl В 1746 году verschijnt in opdracht van de Staten van Holland een prachtig gegraveerde kaart van de Maasmonding bij Rotterdam (afbeelding 1). De kaart heeft een schaal van 1:20.000 en toint daarmee een zeer gedetailleerd beeld van de toenmalige waterstaatkundige situatie ter plekke. Старший картограф, работавший ландметром Мельхиором Болстра (1703/4–1776). Het resultaat mag er zijn: een fraaie, bijna drie meter lange kaart van een gebied dat de eeuwen erna drastisch zou veranderen. En met de nieuwe technieken van tegenwoordig kunnen we die veranderingen vanuit onze luie stoel op ons gemak bestuderen! Lees Verder Op Academischerfgoed.nl Wetenschappers En Antortings, Leraren En Priest , te beleren en te vermaken. Ze brachten niet zelden een publiek op de was van meer dan duizend toeschouwers per keer. В zekere zin legde de moderniteit hiermee de grondslag voor de film, maar ook voor de diaprojector en zijn actuele digitale varianten. Лиз Мир… История Нобелевской премии, самой престижной и заметной научной награды в мире, с самого начала в 1901 году переплетается с историей науки Нидерландов. Насчитывая на сегодняшний день более двадцати голландских лауреатов, в том числе Эйнтховена, ван ’т Хоффа и Тинбергена, Нидерланды входят в первую десятку стран по статистике Нобелевских лауреатов на страну. При этом наше понимание того, как награды использовались и используются как символ превосходства, остается слабым. На примере Нидерландов этот симпозиум направлен на изучение того, как научные премии в целом и Нобелевская премия в частности присуждаются в различных условиях (музеи, университеты, города) и для различных целей. Опираясь на текущие дискуссии о «героях» в науке (по сравнению с командной работой), мы хотим изучить значение и мотивы научных наград в Нидерландах и за их пределами. Подробнее читайте на веб-сайте конференции Департамент истории науки и идей Университета Упсалы приглашает к приему заявок на одну постдокторскую должность, связанную с исследовательским проектом  Ранняя гражданская наука: как общественность использовала инструкции Линнея для сбора Мир с. 1750-1850 , финансируется Фондом Кнута и Алисы Валленберг. Проект рассчитан на период с 2021 по 2026 год и включает в себя постдокторантов и приглашенных исследователей. Мы ищем соискателей со степенью кандидата наук. степень и исследовательские интересы, имеющие отношение к изучению истории науки и колониального коллекционирования. Работа связана с проектом, и успешный кандидат будет планировать и проводить свои исследования в сотрудничестве с главным исследователем, доктором Линдой Андерссон Бернетт. Лиз Мир… Решено: Если давление идеального одноатомного газа равно Учебники / Физика / Университетская физика Сирса и Земанского с современной физикой 13 / Глава 18 / Задача 17DQ 4 5 1 377 Отзывы Задача 17DQ Задача 17DQ Если давление идеального одноатомного газа увеличить, а число молей оставить постоянным, что произойдет со средней поступательной кинетической энергией одного атома газа? Можно ли изменить как объем, так и давление идеального газа, сохранив при этом среднюю поступательную кинетическую энергию атомов постоянной? Объяснять. Пошаговое решение: Шаг 1 из 3 Решение задачи 17DQ Когда [давление идеального одноатомного газа увеличивается, сохраняя число молей постоянным, температура увеличивается, а значит, увеличивается и средняя кинетическая энергия. PV=nRT P=2N(средний KE)/3V Таким образом, при увеличении P средний KE также будет увеличиваться. Да, можно изменить давление и объем идеального одноатомного газа без изменения температуры. Это возможно, если расширение носит изотермический характер, когда nRT сохраняется постоянным. Шаг 2 из 3 Глава 18, проблема 17DQ решена Просмотреть полное решение Шаг 3 из 3 Это руководство по выживанию в учебнике было создано для учебника: Sears and Zemansky’s University Physics with Modern Physics, выпуск: 13. Поскольку был дан ответ на решение 17DQ из 18 главы, более 269 студентов просмотрели полный пошаговый ответ. Университетская физика Сирса и Земанского с современной физикой была написана и связана с ISBN: 9780321696861. Это полное решение охватывает следующие ключевые темы: газ, кинетика, среднее значение, давление, поступательное движение. Этот обширный учебник по выживанию охватывает 44 главы и 8517 решений. На полное пошаговое решение задачи: 17DQ из главы: 18 ответил , наш главный эксперт по решениям в области физики, 09.09.17, 04:08. Ответ на вопрос: «Если давление идеального одноатомного газа увеличить, а число молей оставить постоянным, что произойдет со средней поступательной кинетической энергией одного атома газа? Можно ли изменить и объем, и давление идеального газа, сохранив при этом среднюю поступательную кинетическую энергию атомов постоянной? Объяснять.” разбит на несколько простых шагов, и 59слова. Другие растворы 18. 1: В баке объемом 20,0 л находится гелий. Молярная масса гелия равна (а)… Физика Университетская физика Сирса и Земанского с современной физикой 13 издание 3 / 5 из 3 отзывов Посмотреть весь материал 18.2: Газообразный гелий объемом 2,60 л при давлении 0,180 атм. Физика Университетская физика Сирса и Земанского с современной физикой 13 издание 3 / 5 из 4 отзывов Посмотреть весь материал 18. 3: Цилиндрический резервуар имеет плотно прилегающий поршень, который позволяет объему… Физика Университетская физика Сирса и Земанского с современной физикой 13 издание 3 / 5 из 3 отзывов Посмотреть весь материал 18.4: Резервуар объемом 3,00 л содержит воздух под давлением 3,00 атм. Бак герметичен и… Физика Университетская физика Сирса и Земанского с современной физикой 13 издание 3 / 5 из 11 отзывов Посмотреть весь материал 18. 5: Планетарные атмосферы. а) Рассчитайте плотность атмосферы… Физика Университетская физика Сирса и Земанского с современной физикой 13 издание 3 / 5 из 3 отзывов Посмотреть весь материал 18.6: У вас есть несколько одинаковых шариков. Вы экспериментально определяете т… Физика Университетская физика Сирса и Земанского с современной физикой 13 издание 3 / 5 из 3 отзывов Посмотреть весь материал исчисление: ранние трансцендентальные функции: Метод Ньютона ?Используя метод Ньютона В упражнениях 1–4 выполните две итерации метода Ньютона, чтобы аппроксимировать ноль функции, используя заданное начальное предположение Исчисление: ранние трансцендентные функции: Площадь области между двумя кривыми ?Нахождение области В упражнениях 7-12 подынтегральная функция определенного интеграла представляет собой разность двух функций. Нарисуйте график каждой функции и ша Химия: центральная наука: Введение: Материя, Энергия и Измерение Вы идете в горы и находите блестящий золотой самородок. Это может быть элемент золота или «золото дураков», которое является прозвищем железа Химия: центральная наука: Реакции в водном растворе ?Объясните, как в окислительно-восстановительной реакции участвуют электроны так же, как в реакции нейтрализации участвуют протоны. [Разделы 4.3 и 4.4] 9{-2} M \math Химия: Центральная наука: Химия окружающей среды ?(a) Напишите химическое уравнение, описывающее воздействие кислотных дождей на известняк, \(\mathrm{CaCO}_{3}\). (b) Если бы известняковая скульптура была Химия: центральная наука: Жидкости и межмолекулярные силы (a) Какова связь между поверхностным натяжением и температурой? б) Какова связь между вязкостью и температурой? (с) Почему Статистика: обоснованные решения с использованием данных: Приложения нормального распределения ?В задачах 5–12 найдите указанные области. Для каждой проблемы обязательно нарисуйте стандартную кривую нормалей и заштрихуйте область, которую необходимо найти. Det Статистика: обоснованные решения с использованием данных: Сравнение трех или более средств «Защитное вождение» Следователь полиции штата хочет определить эффективность трех различных программ обучения безопасному вождению до 9{+}\) ион, имеют ли 2s- и 2p-орбитали одинаковую энергию? Если нет, то какая орбиталь имеет меньшую энергию? (б) Если мы добавим Люди также купили 7P: Оцените давление, оказываемое на пол (а) одним остроконечным стулом… Физика Физика: принципы с приложениями 6 издание 5 / 5 из 7 отзывов Посмотреть весь материал 75E: Атомная масса меди составляет 63,546 а. е.м. Имеются ли изотопы меди… Химия Химия: молекулярный подход 3 издание 4 / 5 из 4 отзывов Посмотреть весь материал 12SAQ: «Здесь показана структура Льюиса для иона ацетата: какая структура… Химия Химия: молекулярный подход 3 издание 4 / 5 из 10 отзывов Посмотреть весь материал 97P: Сколько теплоты в килоджоулях требуется, чтобы нагреть 56 литров воды из. .. Химия Введение в химию 5 издание 3 / 5 из 7 отзывов Посмотреть весь материал 30E: Сколько строк появляется в таблице истинности для каждого из этих составных p… Математика Дискретная математика и ее приложения 7 издание 3 / 5 из 7 отзывов Посмотреть весь материал 4E: БИО Травмы позвоночника. ? При лечении травм позвоночника… Физика Университетская физика 13 издание 4 / 5 из 8 отзывов Посмотреть весь материал Родственные разделы Глава 4.4: Дискретная математика и ее приложения | 7-е издание Математика Дискретная математика и ее приложения 7 издание 3 / 5 из 97 отзывов Посмотреть весь материал Глава 2. 6: Статистика для инженеров и ученых | 4-е издание Статистика Статистика для инженеров и ученых 4 издание 4 / 5 из 48 отзывов Посмотреть весь материал Глава 5.6: Статистика для инженеров и ученых | 4-е издание Статистика Статистика для инженеров и ученых 4 издание 4 / 5 из 48 отзывов Посмотреть весь материал Глава 5. 9: Статистика для инженеров и ученых | 4-е издание Статистика Статистика для инженеров и ученых 4 издание 4 / 5 из 48 отзывов Посмотреть весь материал Глава 6.11: Статистика для инженеров и ученых | 4-е издание Статистика Статистика для инженеров и ученых 4 издание 4 / 5 из 48 отзывов Посмотреть весь материал Глава 9. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: