Давление в жидкости в чем измеряется: Давление в жидкости — урок. Физика, 7 класс.

Манометр — из чего состоит? Виды и типы

Что такое манометр

Термин «манометр» в основе имеет два греческих слова: «измерять» и «неплотный». Из этого понятны его назначение и основные функции — измерения в неких неплотных средах (жидкостях и газах).

Манометр — это прибор для измерения искусственно созданного давления газа или жидкости в замкнутой системе.

Не следует путать его с барометром, который тоже показывает давление, но только атмосферное. В то время как с помощью манометра можно измерить, с какой силой жидкость или газ давит на стенки герметично закрытой емкости. Условно говоря, он показывает плотность воздуха внутри закрытого пространства.

Единица измерения давления: паскаль (Па). Она отражает силу в 1 Н, которая равномерно действует на площадь 1 кв. м. Также давление иногда измеряют в барах, атмосферах, миллиметрах ртутного или водяного столба.

Для чего нужен манометр

В зависимости от модификации манометры могут использоваться в самых разных сферах:

• при накачивании автомобильных шин;

• в обслуживании систем кондиционирования и отопления;

• в гидравлических узлах для передвижения железнодорожной стрелки;

• для контроля давления в пневматических агрегатах на производстве;

• в нефтяной и газодобывающей промышленности;

• для обслуживания двигателей на морских судах и т. д.

Основное назначение манометра — проинформировать об избыточном или недостаточном давлении воды, пара, газа или иной рабочей среды. В промышленности также выделяют сигнальные приборы, которые помогают предотвратить взрывы и техногенные катастрофы из-за разрыва емкостей с опасными веществами (например, аммиаком или горячим паром).

Полезные подарки для родителей

В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!

Жидкостный манометр

Этот тип манометров появился первым еще в XVII веке. Он ведет свое начало от опытов Торричелли — одного из учеников Галилео Галилея.

Итальянский ученый погружал в емкость запаянную с одного конца и наполненную ртутью трубку. Некоторое количество ртути выливалось из трубки, и в ее верхней части получался вакуум. Соответственно, при повышении атмосферного давления ртутный столбик в трубке поднимался, а при понижении — опускался.

Принцип работы жидкостного манометра в целом похож на принцип работы системы из опыта Торричелли.

Этот прибор представляет собой систему сообщающихся сосудов — две трубки, соединенные в U-образную конструкцию. Система наполовину заполнена жидкостью (обычно ртутью), и если на нее действует только атмосферное давление — уровень жидкости в обеих трубках будет одинаков.

Если одну из трубок подключить к накачивающему устройству или к закрытой емкости, на жидкость в ней будет действовать измеряемое давление (Р₁). В то время как на жидкость во второй трубке действует только атмосферное давление (Р₂). При изменении Р₁ уровень жидкости во второй трубке тоже будет меняться.

Измерив разность высоты столба Δh = h₁ − h₂, можно узнать, насколько изменилось давление Δp = p₁ − p₂.

Результат измерений, полученный в сантиметрах ртутного столба, переводят в паскали из расчета:

1 см ртутного столба (при 0°C) = 1333,22 Па.

Для получения результата сразу в паскалях можно воспользоваться формулой, которая определяет давление воды на стенки емкости:

Р = ρgh, где ρ — плотность жидкости, g — ускорение свободного падения, h — высота столба.

Ускорение свободного падения (g) равно 9,8 H/кг.

Интересный факт!

Слава изобретателя манометра принадлежит Торричелли, но на самом деле он был придуман на столетие раньше Леонардо да Винчи. Гениальный художник и ученый написал трактат по гидравлике, в котором рассказал о замере давления воды с помощью U-образной системы. Однако этот труд до широкой публики дошел только в XIX веке.

Другие виды манометров

Жидкостный манометр дает возможность точных измерений, но у него есть большой недостаток: конструкция боится ударов и вибраций.

Поэтому сегодня такие приборы используются в основном в лабораториях. С развитием промышленности возникли другие типы манометров, которые могут измерять давление в любых условиях — на подвижных механизмах, при сильных вибрациях и т. д. По конструкции выделяют деформационные и поршневые (грузопоршневые) приборы.

Деформационные манометры

Манометр деформационного типа — это компактное механическое устройство, измеряющее давление сразу в паскалях (без перевода из других единиц). Его рабочим элементом является дугообразная или спиральная трубка Бурдона, в которую накачивается газ. Если давление внутри трубки повышается, она начинает распрямляться, и это движение через систему тяг передается на стрелку. При снятии давления она возвращается в свое первоначальное положение.

Вместо трубки может быть использована пружина, мембрана или другой чувствительный элемент, который деформируется под давлением. Принцип действия манометра остается тем же: деформация передается на стрелку, движущуюся по шкале.

Деформационные металлические манометры чаще всего используются в быту и на производстве. Они компактны, отлично переносят вибрации, не требуют строго вертикальной установки. Если нужно выбрать, к примеру, автомобильный манометр, он будет именно такого типа.

Интересный факт!

Деформационный манометр был изобретен случайно. В 1845 году швейцарский ученый Р. Шинц наблюдал, как на производстве рабочие восстанавливали сплющенную металлическую трубку, заглушив один ее конец и закачав внутрь воду. Под действием давления трубка разогнулась, а ученому пришла в голову мысль использовать такой же элемент для измерений, но работать с воздухом, а не с водой.

Поршневые манометры

Несмотря на то, что поршневые манометры были созданы раньше деформационных, они получили меньшее распространение. Сегодня такие приборы используются для исследования скважин в нефте- и газодобывающей промышленности, а также для сверки показаний в лабораториях.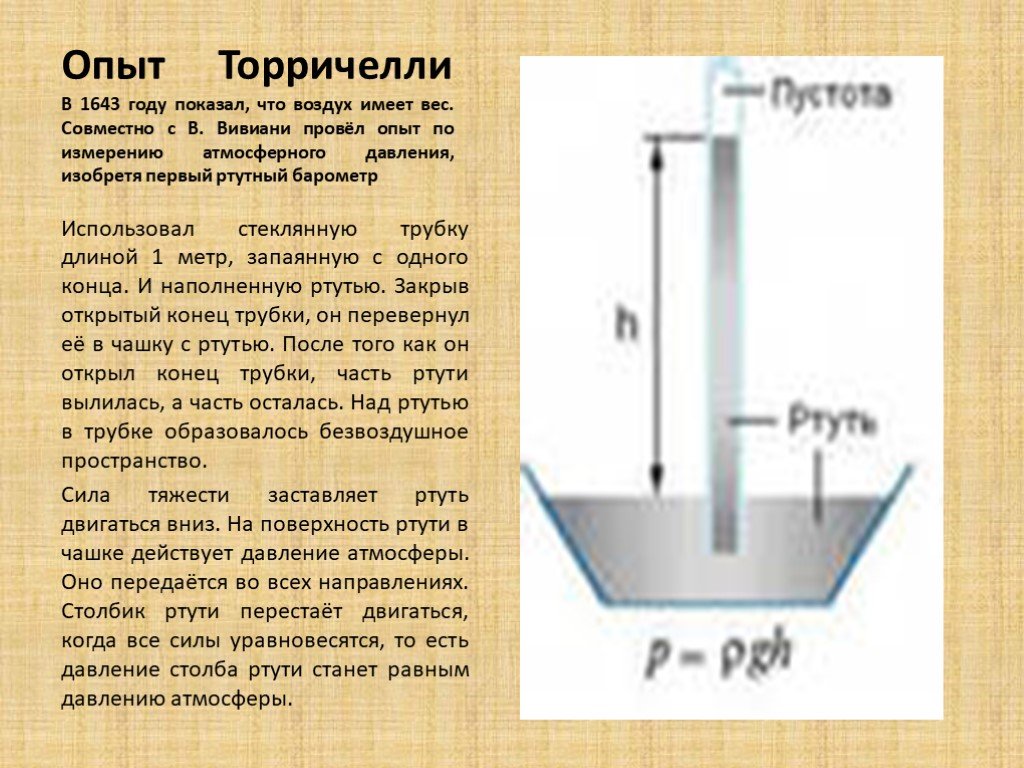

На рисунке ниже можно увидеть, из чего состоит манометр поршневого типа. В самом простом варианте это емкость с маслом, соединенная при помощи штуцера с измеряемой средой. В емкость погружен цилиндр с тщательно притертым поршнем (зазор между стенками цилиндра и поршнем должен быть минимальным). На торце поршня закреплена тарель, на которую могут укладываться грузы.

Снизу на поршень действует измеряемое давление Р, сверху оно уравновешивается некой силой, создаваемой весом самого поршня и грузов G₁+ G₂.

Давление под поршнем рассчитывается по формуле:

, где G₁— масса грузов, G₂— масса поршня с тарелью, g — ускорение свободного падения, F — площадь поршня.

Также давление можно выразить через силу согласно закону Паскаля:

P = F / S, где F — сила, действующая на поршень, S — площадь поршня.

С помощью поршневых маномеров впервые измеряли давление ученые-физики Георг Паррот и Эмиль Ленц. Но широкое распространение эти приборы получили благодаря некому Рухгольцу, который запустил их в массовое производство.

Задачи

Чтобы научиться решать задачи под руководством опытного преподавателя, приходите на онлайн-курсы по физике для 9 класса!

Задача 1

В канистру налит бензин и высота столба составляет 0,6 м. Плотность бензина — 710 кг/м². Определите давление бензина на дно канистры. Ускорение g равно 9,8 H/кг.

Решение:

Нам известно:

h = 0,6 м;

ρ = 710 кг/м².

Согласно формуле, определяющей давление жидкости на стенки сосуда:

Р = ρgh;

P = 710 × 9,8 × 0,6 = 4174,8 Па = 4,7 кПа.

Ответ: 4,7 кПа.

Задача 2

На поршень, погруженный в цилиндр с маслом, положили груз весом 3 кг. Площадь поршня составляет 2 см2, а его вес — 300 гр. Чему равна сила давления под поршнем?

Решение:

Итак, у нас дано:

G₁= 3 кг;

G₂= 300 гр = 0,3 кг;

F = 2 см² = 0,0002 м²;

Ускорение g равно 9,8 H/кг.

Ответ: 161,7 кПа.

на дно и стенки сосуда, понятие гидростатического давления

Содержание:

• Что такое давление жидкости
• История открытия
• Факторы, влияющие на показатель
• Давление на дно и стенку сосуда
• Расчет давления жидкости на дно и стенки сосуда
• Единицы измерения
• Формулы расчета
• Применение на практике
• Гидростатический парадокс

Содержание

• Что такое давление жидкости
• История открытия
• Факторы, влияющие на показатель
• Давление на дно и стенку сосуда
• Расчет давления жидкости на дно и стенки сосуда
• Единицы измерения
• Формулы расчета
• Применение на практике
• Гидростатический парадокс

Что такое давление жидкости

Наука гидростатика исследует ситуации, когда движение в жидкости отсутствует или скорость пренебрежимо мала, и позволяет понять некоторые свойства такой важной гидродинамической величины, как давление.

Теорема

Давление — физическая величина, описывающая силу, которая действует перпендикулярно поверхности на единицу ее площади. Для ее обозначения используется символ р или Р.

На опору под действием силы тяжести давят и твердые, и сыпучие вещества, но их воздействие отличается от гидростатического давления. Воздействие твердого тела определяется его весом, жидкости — ее глубиной. В газе и жидкости давящее воздействие на поверхности создается за счет хаотических столкновений молекул и связано с другими параметрами состояния вещества — например, температурой Т и плотностью \(\rho.\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для жидкости, учитывая ее малую сжимаемость, вместо уравнения Клапейрона, учитывающего температуру и молярную массу газа, обычно используют условие несжимаемости, которое существенно упрощает уравнения гидроаэромеханики:

\(\rho = const. \)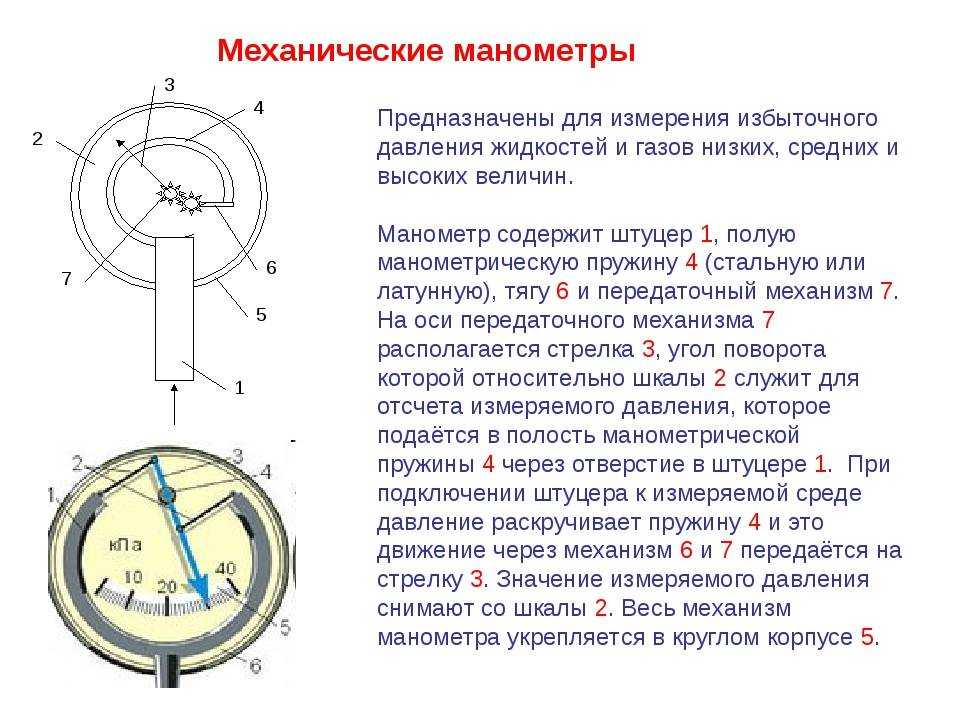

Сила гидростатического давления р на дно сосуда не зависит от его формы и изменяется пропорционально уровню налитой в сосуд жидкости и ее плотности в соответствии с основной гидростатической формулой:

\(р = р_{0} + \rho\times g\times h.\)

\(\rho\) здесь — плотность вещества, \(р_{0}\) — атмосферное давление, g — ускорение свободного падения, h — глубина погружения.

История открытия

Гидростатика как наука была достаточно хорошо известна еще в античные времена, поскольку она тесно связана с практической деятельностью людей. Для строительства лодок и кораблей, колодцев и различных гидравлических аппаратов, например, поршневых насосов, необходимо было понимать, как вода взаимодействует с твердыми материальными предметами.

Различие между давлением твердого тела и воды очень эффектно пояснил на опыте Блез Паскаль: всего лишь стакан воды, вылитый в высокую тонкую трубку, соединенную с наполненной водой закрытой бочкой, создал такое избыточное давление, что вода через щели брызнула наружу.

Определение

В 1653 году Паскаль сформулировал свой закон: давление, производимое на жидкость или газ, передается в любую точку одинаково.

Позже был сконструирован прибор, демонстрирующий действие закона Паскаля. Он называется шар Паскаля и представляет собой заполняемый водой шар с маленькими отверстиями, соединенный с цилиндрической рукояткой, внутри которой движется поршень. Внешнее давление, производимое поршнем, передается во все точки воды одинаково, и она выплескивается в виде одинаковых струек. Поэтому струйки, вытекающие из отверстий, расположенных в горизонтальной плоскости, оставляют на полу следы равной длины.

Факторы, влияющие на показатель

На давление жидкости могут влиять:

• ее плотность;
• атмосферное давление;
• температура;
• глубина сосуда;
• площадь дна сосуда.

Давление на дно и стенку сосуда

Закон Паскаля утверждает, что давление в любом месте покоящейся жидкости или газа по всем направлениям одинаково, причем оно одинаково передается по всему объему вещества. Таким образом, разницы между давлением на дно и на стенку нет.

Расчет давления жидкости на дно и стенки сосуда

Чтобы найти давление на дно сосуда, нужно взять приведенное выше основное уравнение гидростатики и подставить туда глубину, плотность и атмосферное давление.

В случае стенок непосредственно прилагать эту формулу можно только к бесконечно малым горизонтальным полоскам на боковых стенках сосуда. Чтобы рассчитать давление на стенки, нужно суммировать давление на все горизонтальные элементы их поверхности, используя правила интегрального исчисления. Паскаль, проведя эти расчеты, доказал, что от формы сосуда давление жидкости не зависит.

Единицы измерения

В международной системе единиц давление измеряется в Паскалях. Один Паскаль равен силе в один ньютон, производящей равномерное давление на единицу поверхности в один метр. Но на практике часто используют такую единицу измерения, как атмосфера, равную 76 см ртутного столба при нулевой температуре по Цельсию.

Определение

Атмосфера — внесистемная единица измерения, которая примерно означает давление атмосферы Земли на уровне Мирового океана.

Формулы расчета

Для описания процессов в гидравлических прессах или любых других системах, в которых давление собственно жидкостей ничтожно мало по сравнению с передаваемым им извне, используется формула закона Паскаля:

\(р = \frac{F}{S}.\)

F — сила, с которой происходит воздействие на поверхности сосуда, S — площадь этой поверхности.

В учебных задачах обычно опускают такой параметр, как атмосферное давление, и используют для расчетов формулу:

\(р = \rho\times g\times h.\)

Можно вывести эту формулу для сосудов, имеющих форму прямой призмы или цилиндра, из закона Паскаля.

\(m = \rho\times V = \rho\times S\times h\)

Вес \(Р = g \times m = g\times \rho\times S\times h. \)

Вес столба, давящего на дно сосуда, равен силе, и тогда:

\(р = \frac{Р}{S} = g\times \rho\times S\times \frac{h}{S} = g\times \rho\times h.\)

Применение на практике

Для гидравлических механизмов, например, прессов, можно рассчитать пропорциональный изменению площади выигрыш в силе, зная, во сколько раз увеличивается площадь большего поршня по сравнению с меньшим.

 

Соотношение между полезной и затраченной работой описывается понятием КПД, коэффициент полезного действия, и рассчитывается по формуле:

\(\frac{F_{2}h_{2}}{F_{1}h_{1}}\)

Также закон Паскаля описывает работу жидкостных манометров, приборов для измерения давления, отличного от атмосферного. Давление в одном колене манометра вызывает повышение жидкости в другом колене — это явление называется избыточным столбом. По его высоте, соотнося ее с нанесенной шкалой, пользователь прибора узнает точную цифру в миллиметрах ртутного столба.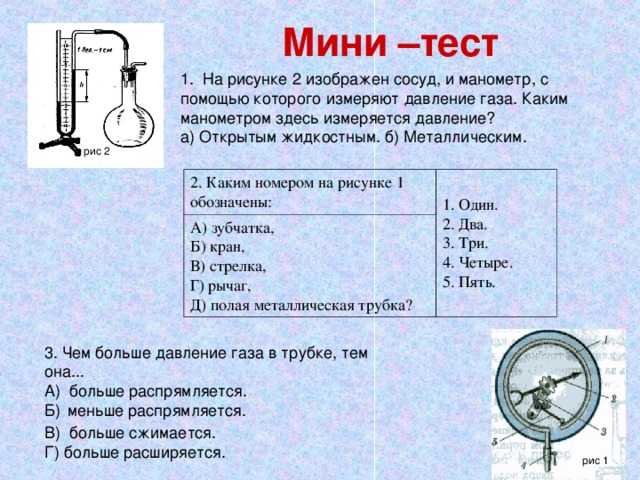

Гидростатический парадокс

Согласно гидростатическому парадоксу, давление жидкости на любую плоскую стенку равняется весу столба этой жидкости, давящему на основание, площадь которого равна площади этой стенки. Поэтому от формы емкости давление не зависит. Если емкость расширяется к горлышку, то вес содержимого распределяется по наклонным стенкам и передается вниз через стенки, не давя на дно, а если емкость к горлышку сужается, то содержимое давит на стенки снизу вверх, что уменьшает его воздействие на дно.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Давление жидкости и его измерение

Давление жидкости в точке

Источник:http://wwwmdp.eng.cam.ac.uk/web/library/enginfo/aerothermal_dvd_only/aero/fprops/statics/node4.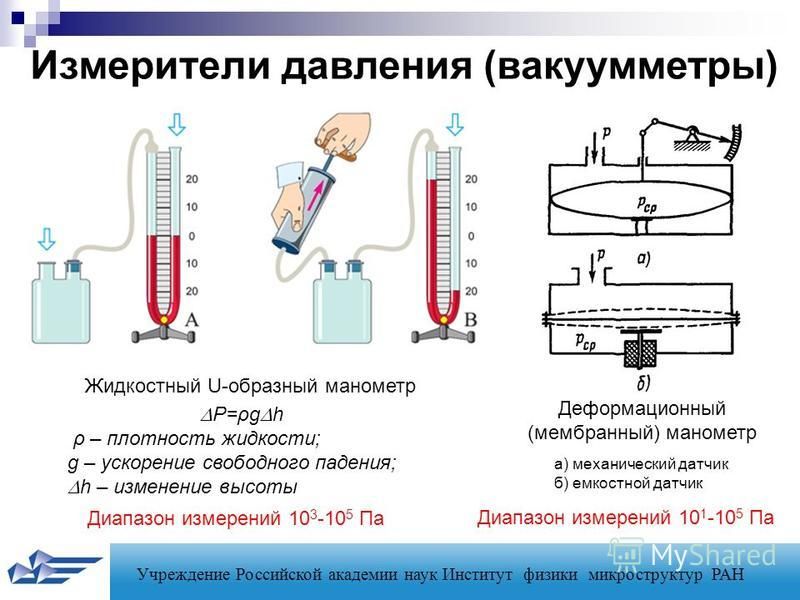 html

Рассмотрим небольшую площадь dA в большой массе жидкости. Если жидкость неподвижна, то сила, действующая со стороны окружающей среды, а затем сила, действующая со стороны окружающей жидкости на площадь dA, всегда будет перпендикулярна поверхности dA. Пусть dF — сила, действующая на площадь dA в нормальном направлении. Тогда отношение dF/dA известно как интенсивность давления или просто давление, и это отношение представлено P.

Математически,

Давление в точке покоящейся жидкости (P) = dF/dA

Если сила (F) равномерно распределена по площади (A),

Тогда,

Давление (P) = Сила (F)/Площадь (A)

Также

Сила или сила давления (F) = Давление (P) * Площадь (A)

Единицы давления:

1. кгс/м ² и кгс/см ² в единицах МКС.
2. Н/м ² и Н/мм ² в единицах СИ.

ПРИМЕЧАНИЕ: KPA = Kilo Pascal = 1000 Н/ м ²

бар = 100 кПа = N/ M ²

Закон Паскаля

ПАСКАЛЬНЫЙ точка в статической жидкости — это все направления».

Интенсивность давления в точке покоящейся жидкости одинакова во всех направлениях:

Элемент жидкости имеет очень малые размеры, т.е. dx, dy и ds.

Рассмотрим произвольный элемент жидкости клиновидной формы в покоящейся массе жидкости, как показано на рисунке. Пусть ширина элемента, перпендикулярного плоскости бумаги, равна единице и P _x , P _y и P _z – давление или интенсивность давления, действующие на силы AB, AC и BC соответственно.

Затем

Сила со стороны AB = P _x * Площадь поверхности AB

Или Сила со стороны AB = P _x *dy*1

Или Сила со стороны AB = P _x dy

Аналогично,

Сила со стороны AC = P _y dx

Сила со стороны BC = P _z ds

Вес (W) = Площадь треугольного элемента*глубина*Удельный вес

Или, W = 1/2* AB * AC *1*

Или, W = * dxdy * ρg

Разложение сил в направлении x

P _x dy = P _z ds sin ( 90- θ)

или, стр. _x DY = P _Z DS COS θ

Также с рисунка,

DY = DS COS θ

СЕЙЧАС,

P _x DY = P _Z . dy

Или, P _x = P _z                     …………………. (i) 

Аналогично,

Разложение сил в направлении y

Pydx = Pzds cos(90- θ) + 1/2* dxdy * ρg

Кроме того,

dscos θ = dx {также элемент очень мал и, следовательно, вес пренебрежимо мал}

Теперь,

P _Y DX = P _Z DX

или, P _Y = P _Z ……………… .. (II)

(I) и ( ii), мы имеем

P _x = P _y = P _z

Приведенное выше уравнение показывает, что давление в любой точке в направлениях x, y и z одинаково.

Абсолютное, манометрическое и атмосферное давление в точке и их взаимосвязь:

Абсолютное давление

Абсолютное давление – это давление, которое относительно нулевого давления в пустом, свободном от воздуха пространстве Вселенной. Это эталонное давление является идеальным или абсолютным вакуумом. Кроме того, это сумма манометрического давления и атмосферного давления.

т.е. P _ab = P _{манометр} +P _атм

Где,

Абсолютное давление = P _ab

Манометрическое давление = P _{манометр}

Атмосферное давление = P _атм

Манометрическое давление

Манометрическое давление определяется как разница между абсолютным и атмосферным давлением.

, т.е. P _Датчик = P _AB – P _ATM

Где,

Абсолютное давление = P _AB

Дайч.0061 атм

Атмосферное давление

Атмосферное давление также известно как барометрическое давление, это давление в атмосфере земли.

, т. Е. P _ATM = P _AB – P _Датчик

Где,

Абсолютное давление = P _AB

давление. Давление вакуума

Давление ниже атмосферного называется давлением вакуума.

Графическое представление соотношения между абсолютным, манометрическим и атмосферным давлением в точке :

Давление жидкости измеряется следующими приборами:

Манометр :

Манометры измерение давления в точке жидкости путем уравновешивания столба жидкости тем же или другим столбом жидкости. Они классифицируются как:

• Одиночные манометры
• Дифференциальные манометры

2. Механические манометры:

Механические манометры определяются как устройства, используемые для измерения давления путем уравновешивания столба жидкости пружиной или собственным весом.

Обычно используемые механические датчики:

1. Дальний давление в диафрагме
2. Давление давления в трубке Бурдона
3. Мертвый веса.0004

   Простой манометр состоит из стеклянной трубки, один конец которой соединен с точкой измерения давления, а другой конец остается открытым для атмосферы.

   Типы простых манометров:

   1. Пьезометр
   2. U-образный манометр и
   3. Одноколонный манометр
   1. Пьезометр /home-work. определения/пьезометр-8

      Пьезометр – простейшая форма манометра, используемая для измерения манометрического давления. Один конец этого манометра подсоединен к точке измерения давления, а другой конец открыт для атмосферы, как показано на рисунке. Подъем жидкости дает напор в точке. Если в точке А высота жидкости, пропускаемой водой, равна «h» в трубке пьезометра, то давление в точке А = ρgh

      Единицей измерения в системе СИ является Н/м ² .

      2. U-образный манометр

      U-образный манометр состоит из стеклянной трубки, изогнутой в форме буквы U, один конец которой соединен с точкой, в которой измеряется давление, а другой конец остается открытым для атмосферы. Трубка обычно содержит ртуть или любую другую жидкость, удельный вес которой больше, чем удельный вес жидкости, давление которой необходимо измерить.

      Типы U-образных манометров:

      • Для манометрического давления
      • Для вакуумметрического давления

      A. Для манометрического давления

      Пусть B — точка, в которой должно быть измерено давление, значение которой равно P. Базовая линия — A-A.

      Let,

      h ₁ = Высота легкой жидкости над базовой линией.

      h ₂ = Высота тяжелой жидкости над базовой линией.

      s ₁ = Удельный вес легкой жидкости.

      s ₂ = Удельный вес тяжелой жидкости.

      ρ ₁ = Плотность легкой жидкости. = 1000 * с ₁

      ρ ₂   = плотность тяжелой жидкости. = 1000 * с ₂

      Поскольку давление одинаково для горизонтальной поверхности. Следовательно, давление над горизонтальной исходной линией А-А в левом и правом столбцах U-образного манометра должно быть одинаковым.

      Давление над А-А в левой колонке = P + ρ ₁ г ч ₁

      Давление над А-А в правой колонке = ρ ₂ g h ₂

      Hence, equating the two pressure

      P + ρ ₁ g h ₁ = ρ ₂ g h ₂

       Or,    P =    ρ ₂ g h _{2 –} ρ ₁ g h ₁

      B. Для измерения вакуумметрического давления

      Для измерения вакуумметрического давления уровень тяжелой жидкости в манометре будет таким, как показано на рисунке.

      Let,

      h ₁ = Высота легкой жидкости над базовой линией.

      h ₂ = Высота тяжелой жидкости над базовой линией.

      s ₁ = Удельный вес легкой жидкости.

      s ₂ = Удельный вес тяжелой жидкости.

      ρ ₁  = плотность легкой жидкости. = 1000 * с ₁

      ρ ₂ = Плотность тяжелой жидкости. = 1000 * с ₂

      Тогда

      Давление над А-А в левой колонке = P + ρ ₁ g h ₁ + ρ ₂ g h ₂

      Давление над A-A в правых столбцах = 0

      Следовательно, приравнивая два давления

      P + ρ ₁ G H _{1 +} ρ ₂ G H ₂ = 0

      , P. = – (ρ ₁ g h _{1 +} ρ ₂ g h ₂ )

      3. Одноколонный манометр

      Одноколонный манометр представляет собой модифицированную форму U-образного манометра с резервуаром большая площадь поперечного сечения (примерно в 100 раз) по сравнению с площадью трубки соединена с одним из плеч манометра. Из-за большой площади поперечного сечения резервуара при любом изменении давления изменение уровня жидкости в резервуаре будет очень небольшим, которым можно пренебречь, и, следовательно, давление определяется высотой жидкости в другом отводе. Другая конечность может быть вертикальной или наклонной. Таким образом, существует два типа одноколонных манометров:

      • Вертикальный одноколонный манометр
      • Наклонный одноколонный манометр

      A. Вертикальный одноколонный манометр

      На рисунке выше показан вертикальный одноколонный манометр. Пусть X-X будет исходной линией в резервуаре и в правом колене манометра, когда он не подключен к трубе из-за высокого давления в точке А, тяжелая жидкость в резервуаре будет выталкиваться вниз и подниматься в правом колене

      Пусть,

      ч ₁ = Высота легкой жидкости над базовой линией.

      h ₂ = Высота тяжелой жидкости над базовой линией.

        s ₁ = Удельный вес легкой жидкости.

      s ₂ = Удельный вес тяжелой жидкости.

      ρ ₁ = Плотность легкой жидкости.

      ρ ₂ = Плотность тяжелой жидкости.

      △h= Падение тяжелой жидкости.

      P = Давление в A.

      A = Площадь поперечного сечения резервуара.

      а = площадь поперечного сечения правой конечности.

      Падение тяжелой жидкости в резервуар вызовет подъем уровня тяжелой жидкости в правой конечности (a)

      Теперь рассмотрим базовую линию Y-Y, как показано на рисунке.

      Затем,

       Давление в правой конечности выше Y-Y = ρ ₂ g (△h + h ₂ )                     (b)

      Давление в левой конечности выше Y-Y = ρ ₁ г (△h + h ₁ ) + P                      (c)

      △ H + H ₂ ) = ρ ₁ G (△ H + H ₁ ) + P

      или P = ρ ₂ G (△ H + H ₂ ) – ρ ₁ г (△h + h ₁ )

      Или, P = △h [ρ ₂ г – ρ ₁ г] + h ₂ ρ ₂ г – h 9

      Из уравнения (а) ρ ₂ g – h ₁ ρ ₁ g

      Поскольку площадь A очень велика по сравнению с a, следовательно, отношение a/A становится очень малым, и им можно пренебречь.

      Таким образом,

      P= h ₂ ρ ₂ г – h ₁ ρ ₁ г

      B. Наклонный одноколонный манометр

      На рисунке выше показан наклонный одноколонный манометр. Этот манометр более чувствителен. Из-за наклона расстояние, пройденное тяжелой жидкостью в правой конечности, будет больше.

      Let,

      L= длина перемещения тяжелой жидкости в правом колене из X-X

      θ = наклон правого колена к горизонтали

      h ₂ = вертикальный подъем тяжелой жидкости в правом колене из X-X   = Lsinθ

      Сейчас,

      Из уравнения давления в A

      P = H ₂ ρ ₂ G – H ₁ ρ ₁ G

      Заменить значение, мы получаем

      P = LSINθ ρ ₂ G – H ₁ ρ ₂ G – H ₁ ρ ₂ G – H ₁ ρ ₂ G – H ₁ ρ ₂ G – H ₁ ρ г

      Дифференциальный манометр

      Дифференциальный манометр – это устройства, используемые для измерения разницы давлений между двумя точками в трубе или в двух разных трубах. Дифференциальный манометр состоит из U-образной трубки, содержащей тяжелую жидкость, два конца которой соединены с точками, в которых измеряется разность давлений. Наиболее распространенные типы дифференциальных манометров:

      • Дифференциальный манометр с U-образной трубкой
      • Перевернутый дифференциальный манометр с U-образной трубкой
      1. Дифференциальный манометр с U-образной трубкой

      Наиболее распространенные типы дифференциального манометра с U-образной трубкой:

   2. Две трубы на одном уровне
   Источник: https://www.hkdivedi.com/2018/01/дифференциальный-манометр-and-its.html
   1. Две трубы на разных уровнях

   На приведенном выше рисунке две точки A и B находятся на разных уровнях и также содержат жидкости с разным удельным весом. Эти точки подключены к дифференциальному манометру с U-образной трубкой. Предположим, что давление в точках A и B равно

   P _A и P _B соответственно.

   Let,

   h= разница уровней ртути в U-образной трубке

   y = расстояние центра B от уровня ртути в правой конечности

   x= расстояние центра A от уровня ртути в правая конечность

   ρ ₁ = Плотность жидкости в точке А

   ρ ₂ = Плотность жидкости в точке В

   ρ _м = Плотность тяжелой жидкости или ртути

   1 ρ = 1

   Давление выше X-X в левой g(h+x) + P _A

   Давление выше X-X в правой конечности = ρ _m gh + ρ ₂ gy + P _B

   Приравнивая два давления, имеем 7 ρ

   ₁ g(h+x) + P _A = ρ _m gh + ρ ₂ gy + P _B

    Or, P _A – P _B = ρ _m gh + ρ ₂ gy – ρ ₁ g(h+x

   Or, P _A – P _B = HG (ρ _M – ρ ₁ )+ ρ ₂ GY – ρ ₁ GX

   • Две трубы находятся на уровне
   3. . Дифференциальный манометр с U-образной трубкой
      Источник: https://www.theengineerspost.com/types-of-manometers/

      Он состоит из перевернутой U-образной трубки, содержащей легкую жидкость. Два конца трубки соединены с точками разность давлений которого необходимо измерить.Применяется для измерения перепада низкого давления.

      На приведенном выше рисунке показан перевернутый U-образный дифференциальный манометр, соединенный с двумя точками A и B. Пусть давление в точке A больше, чем давление в точке B.

      Пусть,

      h ₁ = Высота жидкости в левой части ниже нулевой линии X-X

      h ₂ = высота жидкости в правой части ниже нулевой линии X-X

      h = разница легкой жидкости

      ρ ₁ = плотность жидкости в точке A

      1

      2 = Плотность жидкости в B

      ρ _L = плотность световой жидкости

      P _A = давление при

      P _B = давление при B

      Затем

      Давление в левой конечности ниже x-x = P _A –

      ρ ₁ G H ₁

      Давление в левой правой конечности ниже x-X = P _B -ρ ₂ г ч ₂ -ρ _L GH

      , уравнение двух давления

      . – ρ ₁  г ч ₁ = P _B – ρ ₂ G H ₂ – ρ _L GH

      OR, P _A – P _B = ρ ₁ G _{1 – 2 1111111111111911 2 1 2 1 1 – ρ 1 г. g h 2  – ρ L gh}

      Ссылки: 1. Учебник по гидромеханике и гидравлическим машинам, доктор Р.К. Бансал, (2008), Laxmi Publication(P) LTD.

      Регулятор давления жидкости • Новости регулирования давления • Fluid Handling Pro

      Регулятор давления жидкости контролирует и регулирует разницу давлений, создаваемых жидкостями, газами и плазмой в гидравлических системах между двумя уровнями. Измерение давления жидкостей измеряет силу на единицу площади, прикладываемую жидкостями, газами и плазмой.

      Показать производителей для контроля и измерения давления

      Статьи о контроле и измерении давления

      Если вы когда-либо замечали неожиданное падение давления и в итоге тратили время на поиски несуществующей утечки, вас, вероятно, обманули. by the…

      Подробнее

      31 января 2023 г.

      OleumTech®, ведущий поставщик решений для промышленной автоматизации и IoT, объявил о добавлении интеллектуального преобразователя перепада давления (DP) к своим…

      Подробнее

      28 сентября 2022 г.

      Цифровые манометры — это полезные инструменты для считывания значений давления, которые обеспечивают быстрые и четкие результаты. Серия DPG с цифровым…

      Подробнее

      24 сентября 2022 г.

      Компания ControlAir LLC, ведущий производитель прецизионных пневматических и электропневматических средств управления, сегодня объявила о выпуске серии 855BP…

      Подробнее

      21 сентября 2022 г.

      Решение проблемы отсутствия отраслевых стандартов для испытаний на совместимость с водородом…

      Подробнее

      7 сентября 2022 г. до четырех независимых измерительных каналов с любой комбинацией…

      Подробнее

      28 июля 2022 г.

      Эксперты по контролю и измерению давления

      Дэйв Грумни (Hawk Measurement Systems) Дэйв является вице-президентом по продажам компании Hawk Measurement (HAWK) и имеет более чем 40-летний опыт работы в отрасли КИПиА. Дэйв начал работать внешним инженером по продажам в 19 лет.79 для компании своего отца, AO Grumney. Пока … Задайте вопрос Ян Кристенсен (Brooks Instrument) Ян Кристенсен имеет почти 40-летний опыт работы с прецизионными приборами для контроля расхода и давления. Он начал свою карьеру в качестве специалиста по обслуживанию в Канаде, где он выезжал на месторождение и ремонтировал контрольно-измерительные приборы и клапаны … Задайте вопрос Эрик Тименсма (Bronkhorst High-Tech B.V.) Эрик Тименсма, менеджер по продажам, имеет более чем 20-летний опыт измерения и контроля расхода и давления газа, жидкости и пара. В течение многих лет Эрик работал инженером по продажам, поддерживая каналы продаж по всему миру в поиске … Задайте вопрос

      Водород считается сложной средой, потому что его особенно маленькие молекулы могут проникать даже в нержавеющую сталь и повреждать структуру материала…

      Подробнее

      28 июня 2022 г.

      Газовый фильтр HD от WITT для установки в трубопроводе обеспечивает надежность защита от мелкодисперсных загрязнений и конденсатов в системе газоснабжения. С…

      Подробнее

      31 мая 2022 г.

      Это захватывающее время для биотехнологии. Многие химические и фармацевтические процессы в настоящее время трансформируются в биотехнологические процессы. Прямо в…

      Читать подробности

      25 мая, 2022

      Новые технологические преимущества, суперкритические и другие требовательные процессы…

      Читать дальше

      19 мая 2022

      .

      Получите обширное покрытие для профессионалов по работе с жидкостями, которые покупают, обслуживают, управляют или эксплуатируют оборудование, доставленное на ваш почтовый ящик.

      Регистрируясь в нашем списке, вы соглашаетесь с нашими Положениями и условиями. Мы выпускаем два электронных бюллетеня каждую неделю, еженедельный электронный бюллетень (выходит каждый вторник) с общими новостями отрасли и один бюллетень «Рынок/электронный продукт» (выходит каждый четверг), посвященный конкретному рынку или технологии.

      Партнеры

      VEGA Grieshaber KG

      Ассортимент продукции VEGA Grieshaber KG простирается от датчиков для измерения уровня, предельного уровня и давления до оборудования и программного обеспечения для интеграции в системы управления технологическими процессами. Подробнее ➜

      Hawk Measurement Systems

      Компания HAWK является мировым лидером в области решений для уровня, позиционирования, мониторинга оборудования и измерения расхода и получила несколько наград за свои технологии. Подробнее ➜

      Titan Enterprises Ltd

      Titan поставляет ряд готовых расходомеров, расходомеров для конкретных приложений, а также комплектных/индивидуальных расходомеров и решений. Подробнее ➜

      Panametrics

      Panametrics, подразделение Baker Hughes, разрабатывает решения для измерения и анализа расхода влаги, кислорода, жидкости, пара и газа с использованием проверенных технологий. Подробнее ➜

      Clarke Valve

      Clarke Valve производит высококачественные прецизионные регулирующие клапаны для нефтегазовой, нефтехимической и нефтеперерабатывающей промышленности по всему миру. Сертифицированы по API 641 и ISO 15848-1, имеют меньший вес и меньшую занимаемую площадь. Подробнее ➜

      Bronkhorst High-Tech B.V.

      Bronkhorst High-Tech B.V. является ведущим производителем измерителей массового расхода и давления/контроллеров для газов и жидкостей. Подробнее ➜

      Silverson

      Уже более 70 лет компания Silverson специализируется на производстве качественных мешалок с большими сдвиговыми усилиями для перерабатывающей и обрабатывающей промышленности по всему миру. Подробнее ➜

      Brooks Instrument

      Вот уже более 75 лет компания Brooks Instrument является надежным партнером в области приборов для измерения расхода, давления и испарения по всему миру. Подробнее ➜

      Industrial Flow Solutions

      Industrial Flow Solutions специализируется на разработке, производстве, продаже и обслуживании насосов и решений по управлению потоками для суровых условий эксплуатации. Подробнее ➜

      Watson-Marlow Fluid Technology Solutions

      Watson-Marlow Fluid Technology Solutions (WFTG) — мировой лидер в области нишевых перистальтических насосов и связанных с ними технологий прохождения жидкости. Подробнее ➜

      Siemens Industry, Inc.

      Siemens Process Instrumentation предлагает инновационные измерительные решения для повышения эффективности предприятия и улучшения качества продукции. Подробнее ➜

      Vögtlin Instruments GmbH

      Vögtlin — швейцарский разработчик прецизионных цифровых массовых расходомеров и контроллеров для газов, предназначенных для широкого спектра применений: науки о жизни, биотехнологии, OEM и многие другие. Подробнее ➜

      Kecol Pumping Systems Ltd

      Kecol Pumping Systems Ltd является британским лидером в разработке и производстве гигиенических насосов и насосных систем из нержавеющей стали для вязких материалов. Подробнее ➜

      GF Piping Systems

      GF Piping Systems является ведущим мировым поставщиком решений для потоков, обеспечивающих безопасную и устойчивую транспортировку жидкостей. Подробнее ➜

      HERMETIC-Pumpen GmbH

      HERMETIC-Pumpen GmbH является ведущим разработчиком и производителем герметичных насосов и насосных технологий. Подробнее ➜

      HRS Heat Exchangers

      HRS Group работает в авангарде тепловых технологий, предлагая инновационные и эффективные продукты для теплопередачи по всему миру, уделяя особое внимание эффективному управлению энергопотреблением. Подробнее ➜

      О нас

      С 2010 года мы предоставляем промышленным специалистам последние инновации, тематические исследования и наиболее полное руководство по оборудованию в области технологий обработки жидкостей на различных рынках.