Как работает деление матриц GNU Octave? Получение неожиданного поведения.
Матричное деление с Октавом объясняло:
Формальное описание Octave Matrix Division отсюда
http://www.gnu.org/software/octave/doc /interpreter/Arithmetic-Ops.html
x/y
Right division. This is conceptually equivalent to the expression
(inverse (y') * x')'
But it is computed without forming the inverse of y'.
If the system is not square, or if the coefficient matrix is
singular, a minimum norm solution is computed.
Это означает, что эти два должны быть одинаковыми:
[3 4]/[4 5; 6 7]
ans =
1.50000 -0.50000
(inverse([4 5; 6 7]') * [3 4]')'
ans =
1.50000 -0.50000
Во-первых, поймите, что деление матрицы Октавы не является коммутативным, как матрица. Умножение не является коммутативным.
Это означает, что A/B не равен B/A
1/[1;1] ans = 0.50000 0.50000 [1;1]/1 ans = 1 1
Один делится на матрицу с одним значением один:
1/[1]
ans = 1
Один делится на матрицу с одним значением три = 0.33333:
1/[3]
ans = .33333
Один делится на матрицу (1×2):
1/[1;1]
ans =
0.50000 0.50000
Эквивалент:
([1/2;1/2] * 1)'
ans =
0.50000 0.50000
Обратите внимание, что, как и в приведенных инструкциях, мы берем норму вектора. Итак, вы видите, как [1; 1] был преобразован в [1/2; 1/2] . «2» исходит из длины вектора, 1 - из поставленного вектора. Мы сделаем еще одно:
Один делится на матрицу (1×3):
1/[1;1;1]
ans =
0.33333 0.33333 0.33333
Эквивалент:
([1/3;1/3;1/3] * 1)'
ans =
0.33333 0.33333 0.33333
Что делать, если один из элементов отрицательный . ..
..
1/[1;1;-1]
ans =
0.33333 0.33333 -0.33333
Эквивалент:
([1/3;1/3;-1/3] * 1)'
ans =
0.33333 0.33333 -0.33333
Итак, теперь у вас есть общее представление о том, что делает Octave, когда вы не снабжаете его квадратной матрицей. Чтобы понять, что делает деление матрицы Octave, когда вы передаете ей квадратную матрицу, вам нужно понять, что делает обратная функция.
Я нормализую ваши векторы вручную, если вы хотите, чтобы октава делала их, вы можете добавлять пакеты для этого, я думаю, что следующий пакет будет делать то, что я делал, с нормализацией вектора:
http://octave.sourceforge.net/geometry/function/normalizeVector.html
Итак, теперь вы можете преобразовать деление в эквивалентное умножение. Прочтите эту статью о том, как работает матричное умножение, и вы можете отступить и выяснить, что происходит под капотом матричного деления.
http://www.purplemath.com/modules/mtrxmult2.
%d0%b4%d0%b5%d0%bb%d0%b5%d0%bd%d0%b8%d0%b5%20%d0%bc%d0%b0%d1%82%d1%80%d0%b8%d1%86 — со всех языков на все языки
Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАканАлтайскийАрагонскийАрабскийАстурийскийАймараАзербайджанскийБашкирскийБагобоБелорусскийБолгарскийТибетскийБурятскийКаталанскийЧеченскийШорскийЧерокиШайенскогоКриЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийВаллийскийДатскийНемецкийДолганскийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГэльскийГуараниКлингонскийЭльзасскийИвритХиндиХорватскийВерхнелужицкийГаитянскийВенгерскийАрмянскийИндонезийскийИнупиакИнгушскийИсландскийИтальянскийЯпонскийГрузинскийКарачаевскийЧеркесскийКазахскийКхмерскийКорейскийКумыкскийКурдскийКомиКиргизскийЛатинскийЛюксембургскийСефардскийЛингалаЛитовскийЛатышскийМаньчжурскийМикенскийМокшанскийМаориМарийскийМакедонскийКомиМонгольскийМалайскийМайяЭрзянскийНидерландскийНорвежскийНауатльОрокскийНогайскийОсетинскийОсманскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПортугальскийКечуаКвеньяРумынский, МолдавскийАрумынскийРусскийСанскритСеверносаамскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиШумерскийСилезскийТофаларскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийТувинскийТвиУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВьетнамскийВепсскийВарайскийЮпийскийИдишЙорубаКитайский
Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАлтайскийАрабскийАварскийАймараАзербайджанскийБашкирскийБелорусскийБолгарскийКаталанскийЧеченскийЧаморроШорскийЧерокиЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийДатскийНемецкийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГалисийскийКлингонскийЭльзасскийИвритХиндиХорватскийГаитянскийВенгерскийАрмянскийИндонезийскийИнгушскийИсландскийИтальянскийИжорскийЯпонскийЛожбанГрузинскийКарачаевскийКазахскийКхмерскийКорейскийКумыкскийКурдскийЛатинскийЛингалаЛитовскийЛатышскийМокшанскийМаориМарийскийМакедонскийМонгольскийМалайскийМальтийскийМайяЭрзянскийНидерландскийНорвежскийОсетинскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПуштуПортугальскийКечуаКвеньяРумынский, МолдавскийРусскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиТамильскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВодскийВьетнамскийВепсскийИдишЙорубаКитайский
Умножение матрицы на число – Энциклопедия по машиностроению XXL
В алгебре матриц определяются следующие действия над матрицами а) сложение матриц б) умножение матрицы на число в) умножение матриц. Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.
Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.
Умножение матрицы на число. Если к—вещественное или комплексное число, то произведение ХА матрицы А на число к определяется формулой [c.95]
Умножение матрицы на число I (которое можно записать справа, так и слева матрицы) эквивалентно умножению на I кв дого элемента этой матрицы если [c.40]
При умножении матрицы на некоторое число необходимо умножить на это число все элементы матрицы, т. е. [c.144]
Умножение (деление) матрицы на число. Для этого необходимо каждый элемент матрицы умножить (разделить) на это число. [c.181]
Определение 4. Произведением матрицы Л размера тХп на число а называется матрица С тех же размеров, элементы которой получаются из соответствующих элементов матрицы Л умножением их на число а, т. е.
[c.41]
е.
[c.41]
Л]- -[В] умножение тензора на число Тв=%ТА, гле матрица [В]—%[А умножение тензора на тензор (скаляр-ное) Тс=Гл7 в, где матрица [С]=[А][В]. [c.61]
Еще большее число показателей требует для своего расчета применение умножения матриц на векторы. Вектор — это матрица с одной строкой или одним столбцом. Данная операция, таким образом, есть частный случай умножения матриц. Ее результатом является вектор. Примером такой операции является вычисление потребностей в материалах.
В табл. 7.1 приведена скорость выполнения операции умножения матрицы на вектор. В первой колонке представлены выражения для числа тактовых циклов, необходимых для завершения одной операции умножения. Умножение матрицы тХп на вектор /гХ1 требует 2тп операций сложения и умножения. Если предположить, что биты данных проходят в системе с частотой 10 МГц (величина 0,1 мкс/бит является достаточно обоснованной для существующих электронных устройств), то можно вычислить скорость выполнения операций.
В символьных вычислениях центральное место занимает операция вычисления внутреннего произведения, эквивалентная умножению составляющих элементов на вектор (векторное умножение), на матрицу (умножение матрицы на матрицу) или на корреляционную функцию. В предыдущих разделах была установлена общность процедур вычисления внутреннего произведения для большого числа алгоритмов из области цифровых вычислений. В одном типичном представлении символьных вычислений отношения знаний выражаются в терминах логического сопоставления с образцом, процедура которого определяется поиском соглашения по предпосылке-условию (с левой стороны) соотношения если [А], тогда [В] (см.
Умножение матрицы на скаляр р равносильно умножению всех ее элементов на это число Ьу = р ау 1 = 1,2,] =1,2,…,11. [c.156]
Умножение матрицы [Aij] на скаляр X дает матрицу [КАц. Произведение двух матриц [Aij] и определено только в том случае, если число столб- [c.18]
Суммой двух матриц А и В одинакового порядка (тХп) называется матрица того же порядка, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц. Перемножать можно только матрицы, у которых число столбцов в первой матрице совпадает с числом строк во второй. Каждый элемент матрицы — произведения С=ВА — определяется по правилу умножения строки на столбец, которое для квадратных матриц приводит к формуле [c.46]
Мы уже говорили, что, записывая уравнение (4.19) в виде г = кг, мы просто пользуемся символическим обозначением для указания определенной операции А, совершаемой над координатной системой (или над вектором). Но, расширяя наше понятие о матрицах, можно сделать так, что эта запись будет указывать на действительное умножение на умножение матриц. Матрицы, рассматривавшиеся нами до сих пор, были квадратными, т. е. число их строк равнялось числу столбцов. Однако можно рассматривать также матрицы, состоящие всего лишь из одного столбца, такие, как
[c.119]
Но, расширяя наше понятие о матрицах, можно сделать так, что эта запись будет указывать на действительное умножение на умножение матриц. Матрицы, рассматривавшиеся нами до сих пор, были квадратными, т. е. число их строк равнялось числу столбцов. Однако можно рассматривать также матрицы, состоящие всего лишь из одного столбца, такие, как
[c.119]
Любую матрицу при помощи элементарных преобразований строк и столбцов, заключающихся в перестановке строк (столбцов), умножении строки (столбца) на число и сложении строк (столбцов) между собой, можно привести к каноническому виду. Ранг канонической матрицы равен числу единиц на ее главной диагонали. [c.16]
Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимаются замена строк столбцами, а столбцов соответствующими строками перестановка строк матрицы вычеркивание строки, все элементы которой равны нулю умножение какой-либо строки на число, отличное от нуля прибавление к элементам одной строки соответствующих элементов другой строки.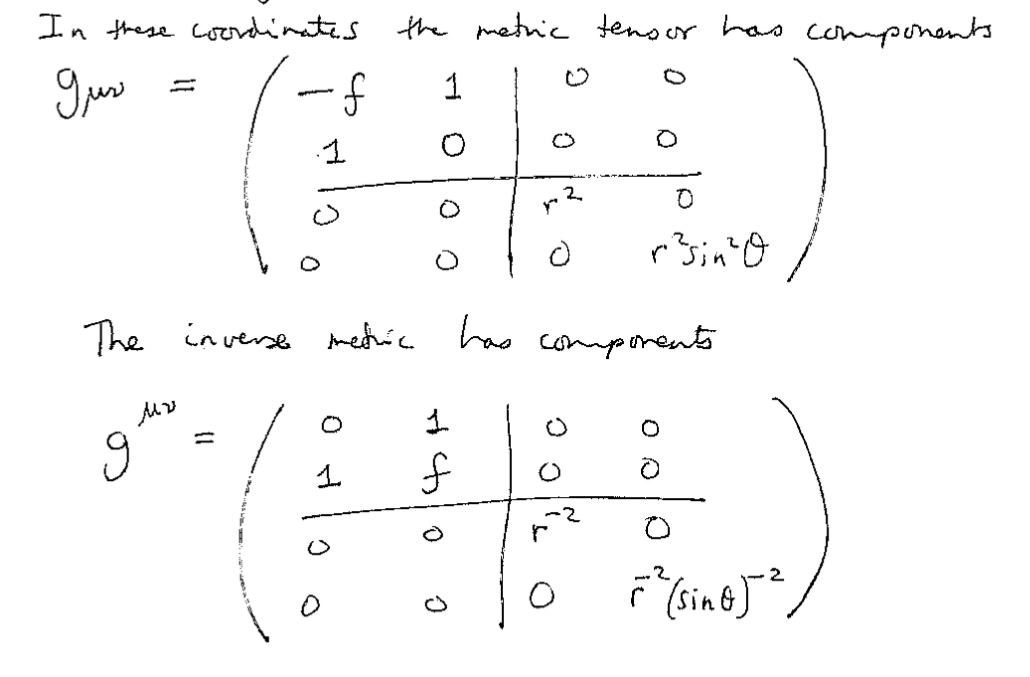 [c.53]
[c.53]
Г. Умножение матриц. Рассмотрим (т X Р) Матрицу а и (/ X ) Матрицу Ъ—число столбцов а равно числу строк Ъ. Такие матрицы, взятые в указанной последовательности а, Ь, называются конформными. Действие умножения определено для конформных матриц. Произведением их с — аЬ называется (т X )”Матрица, элемент /-Й строки и /г-го столбца которой ра ен сумме произведений элементов /-й строки матрицы а на элементы /г-го столбца матрицы Ь [c.762]
Матрицы, имеющие одинаковое число строк и столбцов, можно складывать (или вычитать) поэлементно. Умножение матрицы [Л,/] на скаляр X дает матрицу [М,у]. Произведение двух матриц определено только в том случае, когда число столбцов в первом множителе Л равно числу строк во втором множителе Произведением (М X Р)-матрицы на (Р X Л )-матрицу будет (М х Ы)-матрица. Умножение матриц обычно обозначается простым написанием их символов один за другим, например [c.32]
Гамильтониан (2. 8), (2.9) зависит от 21 параметра. Существует три типа простейших преобразований, которые изменяют (в частности, исключают) параметры в гамильтониане без изменения уравнений движения. К первому типу относятся групповые преобразования 30(3) х 30(3). С их помощью в представлении (2.9) матрицы А и С могут быть одновременно приведены к диагональному виду. Добавление к гамильтониану произвольной линейной комбинации функций Казимира Рг,Р2, которые являются однородными квадратичными функциями, позволяет исключить еще два параметра. Умножение гамильтониана на произвольную константу Н аН с заменой времени t 1, также позволяет уменьшить число параметров на единицу. Таким образом, квадратичное семейство гамильтонианов (2.8) либо (2.9)) определяется двенадцатью параметрами.
[c.181]
8), (2.9) зависит от 21 параметра. Существует три типа простейших преобразований, которые изменяют (в частности, исключают) параметры в гамильтониане без изменения уравнений движения. К первому типу относятся групповые преобразования 30(3) х 30(3). С их помощью в представлении (2.9) матрицы А и С могут быть одновременно приведены к диагональному виду. Добавление к гамильтониану произвольной линейной комбинации функций Казимира Рг,Р2, которые являются однородными квадратичными функциями, позволяет исключить еще два параметра. Умножение гамильтониана на произвольную константу Н аН с заменой времени t 1, также позволяет уменьшить число параметров на единицу. Таким образом, квадратичное семейство гамильтонианов (2.8) либо (2.9)) определяется двенадцатью параметрами.
[c.181]
Второй способ состоит в умножении соответствующего диагонального элемента матрицы на некоторое большое число, скажем 10 , перед модификацией соответствующего коэффициента нагрузки. В рассматриваемом случае мы бы получили
[c. 486]
486]
Матрица рассеяния 5(Л) не зависит от Л и также сводится к умножению на число (б). [c.109]
Таком образом, для выполнения алгоритма (55) требуются два прямых и одно обратное преобразование Ф/рье, а также прямое умножение матрицы на матрицу. Если в качестве дижретного преобразования Фурье использовать алгоритм БПФ, число опера дай сложения составит 2N og2 , а число операций умножения -. [c.63]
Однако этот критерий, строго говоря, не имеет смысла. Путем почленного умножения уравнений на числа, большие единицы, определитель системы линейных алгебраических уравнений можно сделать сколь угодно большим. Обусловленность системы при этом не изменится. В теории матриц вводятся числа обусловленности, инвариантные относительно подобных преобразований. К таким числам относятся числа Тюринга и Тодда. [c.181]
SUBROUTINE SKM (А, S, М, N) — программа умножения матрицы на скаляр. А — исходная и результирующая матрица S — скалярная величина М, N — целые числа, определяющие размер матрицы.
[c.251]
А — исходная и результирующая матрица S — скалярная величина М, N — целые числа, определяющие размер матрицы.
[c.251]
Рассмотрение данного примера было вызвано необходимостью обеспечить высокую скорость при выполнении операции внутреннего произведения в линейной алгебре (например, для умножения матрицы на вектор или матрицы на матрицу), в противном случае эти операции становятся бессысленными. Операции внутреннего произведения включают умножение двух чисел и сложение результата с третьим числом. Например, 2-разрядный умножитель-сумматор умножает два 2-раз-рядных числа М ц Ы, прибавляет результат к 5-разрядному входному числу X и выводит результаты в виде 5-разрядного числа У. В синхронизированном режиме работы выходной сигнал У мог бы подаваться по цепи обратной связи на вход X для того, чтобы достичь эффекта многократного накопления результата (если имеется возможность накопления до трех произведений и при этом не возникает переполнение). [c.155]
Одна из целей цифровых оптических вычислений состоит в достижении большей гибкости системы, чем у их аналоговых предшественников. Особенность оптических компьютеров состоит в том, что они скорее выполняют не монолитные операции, а ряд простых операций, которые можно объединить для выполнения широкого круга задач. Однако в данном случае это не так плохо, поскольку при построении оптических процессоров, осуществляющих функции регистра, их возможности поднимутся на качественно новый уровень. С этой точки зрения матричное умножение (под которым подразумевают либо умножение матрицы на вектор, либо матрицы на матрицу), возможно, является наиболее полезной операцией среднего уровня из числа тех, которые только можно придумать. Многие сложные проблемы, например калмановское фильтрование,
[c.183]
Особенность оптических компьютеров состоит в том, что они скорее выполняют не монолитные операции, а ряд простых операций, которые можно объединить для выполнения широкого круга задач. Однако в данном случае это не так плохо, поскольку при построении оптических процессоров, осуществляющих функции регистра, их возможности поднимутся на качественно новый уровень. С этой точки зрения матричное умножение (под которым подразумевают либо умножение матрицы на вектор, либо матрицы на матрицу), возможно, является наиболее полезной операцией среднего уровня из числа тех, которые только можно придумать. Многие сложные проблемы, например калмановское фильтрование,
[c.183]
Разновидности основной архитектуры. Сообщалось и о других способах преобразования схем вычисления свертки в схемы умножителей матрицы на матрицу. В [16] для получения промежуточного произведения при вычислении внутреннего произведения двух векторов используется основная схема вычисления свертки с интегрированием по времени. Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из п элементов, с точностью в I знаков требуется п входов для каждого вектора, 21—1 фотодетекторных элементов и 21—1 тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет п1 Ь—1) . Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы тХп и вектора пХ все т умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов тп), а элементы вектора Ь сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий т 21—1) циклов при этом i используется т(21—1) детекторов выходного сигнала.
Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из п элементов, с точностью в I знаков требуется п входов для каждого вектора, 21—1 фотодетекторных элементов и 21—1 тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет п1 Ь—1) . Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы тХп и вектора пХ все т умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов тп), а элементы вектора Ь сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий т 21—1) циклов при этом i используется т(21—1) детекторов выходного сигнала. Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов Ь при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также тп входов для одной матрицы и п входов для другой, а также т 21—1) детекторов выходного сигнала. Затраты времени на вычисления составляют k + m—1) 21—1) тактовых циклов.
[c.200]
Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов Ь при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также тп входов для одной матрицы и п входов для другой, а также т 21—1) детекторов выходного сигнала. Затраты времени на вычисления составляют k + m—1) 21—1) тактовых циклов.
[c.200]
Правильный результат получают уже в смешанном формате, путем умножения исходной матрицы на дополненный вектор. Эта процедура может быть выполнена с помощью любого из обсуждавшихся выше вариантов умножения матрицы на матрицу. Ценой этого будет служить увеличение объема памяти, необходимое для записи вектора, и задача класса умножение матрицы на вектор оказывается отданной в уплату за задачу класса матрица — матрица. В целом же кажется более выгодным использовать оптические методы для выполнения суммирования вдоль противодиагоналей. В число возможных оптических способов решения такой задачи входит сегментация цилиндрических линз, сегментация голографических линз или применение матриц оптических волокон, соединяющих соответствующие элементы с детекторами, на которых происходит суммирование. [c.203]
[c.203]
В работе [20] предлолсхемы построения процессоров внешнего произведения. В первом случае используется перекрестное включение одномерных входных модуляторов (рис. 7.14). Для умножения матрицы на вектор в один из модуляторов вводят целый столбец матрицы, а элементы вектора размещаются в другом модуляторе. Матричный модулятор должен обладать т1 разрядами, а модулятор для ввода вектора должен иметь I разрядов. Когда оба модулятора загружены, то от источника света подается импульс света и перекрестное произведение записывается на матрице пг1х1 интегрирующих по времени детекторов. Если суммирование осуществляется оптически, необходимо только т(21—1) детекторов. Каждое промежуточное произведение может быть накоплено на детекторе за время загрузки входного сигнала в модулятор, которое полагаем равным т1. Полное число тактовых импульсов для операции умножения матрицы на вектор составляет пт1. Для умножения матрицы на матрицу требуется кт 21—1) детекторов, при этом необходимое число тактовых циклов составляет лишь пт1 (если т>к). [c.203]
[c.203]
Все процессоры характеризуются тем, что чем больше объем задачи, тем быстрее они работают. Например, умножители матрицы на вектор (за одним исключением) работают со скоростью в десятки мегаопераций в секунду, характерной для небольших по объему задач. Процессоры умножения матрицы на матрицу работают со скоростями порядка гигаопераций в секунду, что характерно для задач большего масштаба. Очевиден выигрыш в быстродействии, получаемый для параллельной обработки. Более неопределенной характеристикой является абсолютная величина быстродействия. Представленные здесь цифры являются лишь оценками, но они действительно отражают общие свойства оптических вычислений. За небольшим числом исключений имеется очень небольшая разница (менее чем на порядок по величине) между разными видами оптических процессоров, используемых для решения заданной задачи. Возможности оптических процессоров, как представляется, достаточно жестко ограничены определенными скоростями. При сравнении с возможностями электронных процессоров скорости вряд ли произведут на читателя глубокое впечатление. На момент написания книги на промышленно освоенных электронных устройств удается достичь скоростей около 50 мегаопераций в секунду. Разрабатываемые в настоящее время умножители матрицы на вектор не позволят превзойти эту величину. Умножители матрицы на матрицу демонстрируют существенно более высокие возможности.
[c.208]
На момент написания книги на промышленно освоенных электронных устройств удается достичь скоростей около 50 мегаопераций в секунду. Разрабатываемые в настоящее время умножители матрицы на вектор не позволят превзойти эту величину. Умножители матрицы на матрицу демонстрируют существенно более высокие возможности.
[c.208]
Матрица S обладает рядом универсальных свойств, вытекаюших из симметрии задачи и закона сохранения энергии. Отметим одно из них. Известно, что при умножении столбца или строки матрицы на число q ее детерминант увеличивается в q раз. Умножая первый и третий столбец мат- [c.96]
Поэтому математической моделью излучающей системы может служить соотношение (2.24) или (2.27), т. е. систему излучателей можно описывать матрицей как [/)], так и [/)] . Размерности матриц [ )] и [/)] одинаковы, и для хранения их в ЭВМ требуются одинаковые объемы памяти. В модели (2.24) нахождение коэффициентов мод токов [/] связано с решением системы линейных алгебраических уравнений, а в модели (2.27) эти коэффициенты находятся путем умножения матрицы на вектор, что требует существенно меньшего числа операций. Матрицы [В] и имеют порядок MNxMN), т. е. с ростом числа излучателей и числа учитываемых мод он быстро увеличивается.
[c.62]
В модели (2.24) нахождение коэффициентов мод токов [/] связано с решением системы линейных алгебраических уравнений, а в модели (2.27) эти коэффициенты находятся путем умножения матрицы на вектор, что требует существенно меньшего числа операций. Матрицы [В] и имеют порядок MNxMN), т. е. с ростом числа излучателей и числа учитываемых мод он быстро увеличивается.
[c.62]
В АР с большим числом излучателей матрица [ )] содержит много элементов с малой абсолютной величиной, которые соответствуют излучателям, далеко отстоящим друг от друга. Поскольку в итерационных методах умножение матрицы на вектор является единственной операцией с матрицей, то это позволяет легко исключить операции с элементами матрицы [О], имеющими малое значение. Сохраняя в матрице [1>] только те элементы, которые соответствуют учету взаимодействия не более чем с Ь ближайшими излучателями, можно существенно уменьшить затраты машинного времени (8, 9 в табл. 3.1). Например, расчет токов АР из 21X21 полуволновых вибраторов над экраном ( =с у=0,6Я,) методом сопряженных градиентов с учетом взаимодействия
[c. 110]
110]
Умножение двух матриц возможно, если число столбцов первой равно числу строк второй матрицы. Произведением матрицы А = = [aij] размера тХР на матрицу В = [Ьр,] размера рХп является матрица С = [с,/,] размера тХп, в которой каждый элемент iu определяется по правилу умножения строки на столбец элементы /-Н строки первой матрицы умножаются на соответствуюн не элементы kio столбца второй матрицы и полученные произведения складываются [c.104]
В случае, когда элементами матрицы являются матрицы-блоки, умножение выполняется по тем же правилам, как если бы элементами матриц были числа, т. е. строки первой матрицы-сомно-жителя умножаются на столбцы второй матрицы-сомножителя (см., например, Г а н т м а х е р Ф. Р., Теория матриц, 5), [c.184]
Умножение на скаляр а тензора Т ь любого ранга вследствие инва-риашносга первого можно выполнять в любом множестве координат. Для этого необходамо каждую компоненту матрицы тензора в выбранной множестве координат умножить на число, характеризующее скал ф. Ранг тензора, получаемого в результате такого умножения, равен рангу тензора, участвующему в этом действии
[c.242]
Ранг тензора, получаемого в результате такого умножения, равен рангу тензора, участвующему в этом действии
[c.242]
Произведением матрицы [A]—[aik]m,n на число а называется матрица a,[A]=[aaik]m.n, полученная умножением всех элементов матрицы [Л] на число сг. пример [c.37]
Быстродействие оптических матричных умножителей было уже описано в табл. 7.1 и 7.2. При вычислении отношения Псалтиса числа в табл. 7.1 и 7.2 имеют коэффициент запаса 2, поскольку были учтены операции умножения и сложения. Для умножителей матриц на векторы соотношение Псалтиса показано в табл. 7.3. Умножители матрицы на матрицы показаны в табл. 7.4. Вычисления проведены для тех же случаев, что и в табл. 7.1 и 7.2. Второй столбец табл. 7.3 предполагает значение / = 16, п=т = 32, в то время как для третьего столбца /=32, п = т= 28. В табл. 7.4 второй столбец соответствует значениям /=16, n = m = = 32, а третий столбец относится к / = 32, п=т = k=l28.
[c. 210]
210]
Полученный результат справедлив при любом выборе ортонор-мированной системы функций Если система // выбрана произвольно, то для построения матрицы гамильтониана потребуется большое число функций //, и соответствующее представление группы симметрии будет иметь очень высокую размерность. Если, с другой стороны, взять в качестве функций /г собственные состояния гамильтониана, то действие на них гамильтониана сведется к умножению их на некоторое число (собственное значение энергии), и матрица гамильтониана окажется диагональной. Любое преобразование симметрии должно поэтому переводить либо в себя, либо в вырожденное состояние. Размерность представления, порожденного данной функцией / , не может превышать степень вырождения состояния. Таким образом, между размерностью представления группы и степенью вырождения состояния, породившего это представление, существует тесная связь. В частности, если под действием неприводимого представления все состояния некоторой совокупности преобразуются друг через друга, то это означает, что и под действием операции симметрии эти состояния будут преобразовываться друг через друга, т. е. мы не можем найти никакой линейной комбинации (никакого унитарного преобразования), представляющей исключение. Из симметрии гамильтониана поэтому следует, что эти состояния должны быть вырожденными. Мы пришли тем самым, правда с помощью интуитивных соображений, к одному из важных результатов теории групп. Если группа симметрии гамильтониана имеет многомерные неприводимые представления, это означает, что собственные состояния гамильтониана должны быть вырожденными.
[c.38]
е. мы не можем найти никакой линейной комбинации (никакого унитарного преобразования), представляющей исключение. Из симметрии гамильтониана поэтому следует, что эти состояния должны быть вырожденными. Мы пришли тем самым, правда с помощью интуитивных соображений, к одному из важных результатов теории групп. Если группа симметрии гамильтониана имеет многомерные неприводимые представления, это означает, что собственные состояния гамильтониана должны быть вырожденными.
[c.38]
Путь ячейки в Golden Ratio. Доходность. Деление матриц Фибоначчи на investuga.com
В этой статье я разберу основные моменты матричного маркетинга проекта Golden Ratio. Какой путь проходит ячейка и что происходит с закрывшимися матрицами? Что такое числа Фибоначчи?
Числа Фибоначчи
Числа Фибоначчи – эта последовательность чисел начиная с 0 или 1, а каждое последующее число равно сумме двух предыдущих чисел. Например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и т. д. Принцип работы маркетинга матрицы Фибоначчи основан на строго математических расчетах и основатель проекта Golden Ratio Искандер Хасанов решил, что крайнее число в маркетинге Золотого Сечения будет 233.
д. Принцип работы маркетинга матрицы Фибоначчи основан на строго математических расчетах и основатель проекта Golden Ratio Искандер Хасанов решил, что крайнее число в маркетинге Золотого Сечения будет 233.
Покупка и вход в матрицу
Для того чтобы попасть в матрицу ваша ячейка проходит общую очередь. Примерно 54 места. Т.е. после вашей покупки должно быть совершено еще 54 покупки и после этого ячейка окажется в матрице. Причем проходя общую очередь ваша ячейка получает +67% к своей стоимости. Это бонус компании. Стоит заметить, что ячейки могут стоить по-разному., это зависит в какой Гильдии вы ее покупаете.
После общей очереди ячейка попадает в матрицу Х2. В матрице есть 20 мест. Первое место это 1, последнее – 20. Ячейки попадая в матрице движутся от большего места к меньшему. И когда вы занимаете 1 место ваша ячейка переходит на более высокий уровень матриц. Всего 5 уровней матриц Х2, Х3, Х5, Х8, Х13. Каждая из которых отличается размером доходности.
Каждая из которых отличается размером доходности.
Доходность матриц в Golden Ratio
Первая Ф-матрица удваивает ваши вложения. Допустим на входе было 1 WEC, на выходе стало 2 WEC. 20% (0,4 WEC) от данной суммы отправляется на баланс для вывода, остальные 80% — в матрицу второго уровня. Здесь ваши вложения умножаются на 3, то есть вместо 1,6 WEC Вы получите 4,8 WEC , из которых 30% (1.44 WEC) идут на баланс для выплат, а остальные 3,36 WEC переходят на Ф-матрицу третьего уровня.
На этом уровне ваши инвестиции увеличиваются в 5 раз – общий доход составит 16,8 WEC, 50% (8,4 WEC) из которых доступны для вывода. Остальные попадают в Ф-матрицу четвертого уровня, в которой ваш депозит увеличивается в восемь раз. Закрыв матрицу четвертого уровня, вы получите 67,2 WEC; из них вы сможете вывести 80% (53,76 WEC), а 13,44 перейдет на Ф-матрицу пятого уровня. Матрица высшего уровня умножает ваши деньги на 13, и вы получите 100% = 174,72 WEC на выходе доступные к выводу. Общая доходность проекта составляет почти 40 000%! И это только с одной ячейкой. Количество покупаемых вами ячеек неограниченно и зависит только от вас.
Общая доходность проекта составляет почти 40 000%! И это только с одной ячейкой. Количество покупаемых вами ячеек неограниченно и зависит только от вас.
Деление матриц и блоков
Когда заполняется одна матрица полностью, заняты все ячейки, то происходит деление одной матрицы на две. При этом первая ячейка переходит на новый уровень матрицы, а остальные равномерно и поочереди распределяются между 2 новообразовавшимися матрицами.
Когда заполняются 2 матрицы (за счет покупок новых ячеек), то они делятся на 3 матрицы. Причем ячейки с первым местом переходят на новый уровень матрицы, а остальные ячейки равномерно заполняют три новых матрицы. Когда 3 матрицы заполняются происходит деление на 5 матриц. Потом 5 матриц делятся на 8 и т.д. до 233 матриц (в соответствии с последовательностью чисел Фибоначчи). Таким образом получается в процессе нескольких делений ваши ячейки перемещаются с последних мест на первые, а именно сдвиг в 1,61 раз.
После того как блок – все 233 матрицы будут заполнены ячейками начинается перезапуск или строительство матрицы с нуля. Это предусмотрено для уравнивания шансов на получение прибыли между всеми участниками. В этот момент еще большее количество ячеек переходят на новый уровень матриц. Все незакрытые ячейки изымаются и выстраиваются в новую очередь в порядке номеров, создаются 2 блока с одной пустой матрицей в каждом. Подобных блоков может быть не более пяти. Создаётся эффект рекурсии. Все матрицы заполняются по новой с учетом всех операций делений. Все происходит по схеме которая описана выше. В результате происходит серия делений и переходов первых ячеек на высший уровень. В этот момент происходит сужение матрицы, так называемое освобождение ячеек в следствии перехода их на новый уровень. Такое перераспределение позволяет ускорить процесс закрытия матриц новыми ячейками и обеспечить выплаты всем участникам проекта.
Блоки в свою очередь делятся на 2, 3, 5, 10, 15, 25, 50, 75, 125, 250, 375, 625 и т. {-1}\), где \(\mathbb{A}\) – первая матрица, \(\mathbb{B}\) – вторая матрица. То есть это умножение на обратную матрицу. Следует иметь ввиду, что вторая матрица должна быть квадратной.
{-1}\), где \(\mathbb{A}\) – первая матрица, \(\mathbb{B}\) – вторая матрица. То есть это умножение на обратную матрицу. Следует иметь ввиду, что вторая матрица должна быть квадратной.
При поэлементном возведении в степень вместо второй матрицы должно быть просто число. Каждый элемент матрицы возводится в степень, равную этому числу.
Матричное возведение в степень \(n\) – это матричное умножение матрицы саму на себя \(n\) раз. То есть во второе поле ввода должно быть вписано целое число. Для получения обратной матрицы введите в правую часть «\(-1\)»
Решение линейных уравнений – в этом режиме первая матрица содержит коэффициенты уравнения в левой части, вторая – в правой части. Например, чтобы решить систему уравнений \[\left\lbrace\begin{aligned}2x+3y&=5;\\10x-y&=6,\end{aligned}\right.\] нужно ввести в левое поле ввода:
2 3 10 -1в правое:
5 6
Концепция Пикселя – CoderLessons.com
Пиксель — это самый маленький элемент изображения. Каждый пиксель соответствует какому-либо одному значению. В 8-битном изображении серой шкалы значение пикселя находится в диапазоне от 0 до 255. Значение пикселя в любой точке соответствует интенсивности световых фотонов, падающих в эту точку. Каждый пиксель хранит значение, пропорциональное интенсивности света в этом конкретном месте.
Каждый пиксель соответствует какому-либо одному значению. В 8-битном изображении серой шкалы значение пикселя находится в диапазоне от 0 до 255. Значение пикселя в любой точке соответствует интенсивности световых фотонов, падающих в эту точку. Каждый пиксель хранит значение, пропорциональное интенсивности света в этом конкретном месте.
PEL
Пиксель также известен как PEL. Вы можете лучше понять пиксель из рисунков, приведенных ниже.
На изображении выше могут быть тысячи пикселей, которые вместе составляют это изображение. Мы будем увеличивать это изображение до такой степени, чтобы мы могли видеть некоторые пиксельные деления. Это показано на изображении ниже.
Связь с массивом CCD
Мы видели, как образ формируется в матрице CCD. Таким образом, пиксель также может быть определен как
Наименьшее деление матрицы ПЗС также известно как пиксель.
Каждое деление матрицы ПЗС содержит значение в зависимости от интенсивности фотона, ударяющего в него. Это значение также можно назвать пикселем.
Это значение также можно назвать пикселем.
Расчет общего количества пикселей
Мы должны определить изображение как двумерный сигнал или матрицу. Тогда в этом случае количество PEL будет равно числу строк, умноженному на количество столбцов.
Это может быть математически представлено ниже:
Общее количество пикселей = количество строк (X) количество столбцов
Или мы можем сказать, что количество (x, y) координатных пар составляет общее количество пикселей.
Мы рассмотрим более подробно в руководстве по типам изображений, как рассчитать пиксели в цветном изображении.
Уровень серого
Значение пикселя в любой точке обозначает интенсивность изображения в этом месте, что также называется уровнем серого.
Мы увидим более подробно о значении пикселей в хранилище изображений и учебнике по битам на пиксель, но сейчас мы просто рассмотрим концепцию значения только одного пикселя.
Значение пикселя.
 (0)
(0)Как уже было определено в начале этого урока, каждый пиксель может иметь только одно значение, а каждое значение обозначает интенсивность света в этой точке изображения.
Теперь мы рассмотрим очень уникальное значение 0. Значение 0 означает отсутствие света. Это означает, что 0 обозначает темный, и это также означает, что когда пиксель имеет значение 0, это означает, что в этой точке будет сформирован черный цвет.
Посмотрите на эту матрицу изображений
Теперь эта матрица изображений заполнена нулями. Все пиксели имеют значение 0. Если бы мы рассчитали общее количество пикселей в этой матрице, это то, как мы собираемся это сделать.
Общее количество пикселей = общее количество из строк X всего № колонн
= 3 х 3
= 9
Это означает, что изображение будет сформировано с 9 пикселями, и это изображение будет иметь размер 3 строки и 3 столбца, и что наиболее важно, это изображение будет черным.
Полученное изображение будет примерно таким
Теперь, почему это изображение все черное. Потому что все пиксели в изображении имели значение 0.
Потому что все пиксели в изображении имели значение 0.
Введение в матрицы и матричную арифметику для машинного обучения
Дата публикации 2018-02-07
Матрицы являются основополагающим элементом линейной алгебры.
Матрицы используются во всей области машинного обучения при описании алгоритмов и процессов, таких как переменная входных данных (X) при обучении алгоритма.
В этом уроке вы узнаете о матрицах в линейной алгебре и о том, как манипулировать ими в Python.
После завершения этого урока вы узнаете:
- Что такое матрица и как ее определить в Python с помощью NumPy.
- Как выполнять поэлементные операции, такие как сложение, вычитание и произведение Адамара.
- Как умножить матрицы вместе и интуиция за операцией.
Давайте начнем.
Обзор учебника
Этот урок разделен на 6 частей; они есть:
- Что такое матрица?
- Определение матрицы
- Матричная арифметика
- Матрица-матричное умножение (точечный продукт)
- Матрично-векторное умножение
- Матрично-скалярное умножение
Что такое матрица?
Матрица – это двумерный массив скаляров с одним или несколькими столбцами и одной или несколькими строками.
Матрица – это двумерный массив (таблица) чисел.
– страница 115,Руководство по линейной алгебре, 2017
Обозначение матрицы часто представляет собой заглавную букву, такую как A, а записи обозначаются их двумерным индексом строки (i) и столбца (j), например aij. Например:
A = ((a11, a12), (a21, 22), (a31, a32))Чаще встречаются матрицы, определенные с помощью горизонтальной записи.
a11, a12
A = (a21, a22)
a31, a32Вероятно, первое место, с которым вы можете столкнуться с матрицей в машинном обучении, – это данные обучения модели, состоящие из множества строк и столбцов и часто представленные заглавной буквой «X».
Геометрическая аналогия, используемая, чтобы помочь понять векторы и некоторые из их операций, не выполняется с матрицами. Кроме того, сам вектор может рассматриваться как матрица с одним столбцом и несколькими строками.
Зачастую размеры матрицы обозначаются как m и n для количества строк и количества столбцов.
Теперь, когда мы знаем, что такое матрица, давайте рассмотрим ее определение в Python.
Определение матрицы
Мы можем представить матрицу в Python, используя двумерный массив NumPy.
Массив NumPy может быть создан с учетом списка списков. Например, ниже приведена матрица из 3 строк и 2 столбцов.
# create matrix
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)При выполнении примера печатается созданная матрица, показывающая ожидаемую структуру.
[[1 2 3]
[4 5 6]]Матричная арифметика
В этом разделе будет продемонстрирована простая матрично-матричная арифметика, где все операции выполняются поэлементно между двумя матрицами одинакового размера, что приводит к созданию новой матрицы с тем же размером.
Дополнение матрицы
Две матрицы с одинаковыми размерами могут быть добавлены вместе, чтобы создать новую третью матрицу.
C = A + BСкалярные элементы в результирующей матрице рассчитываются как сложение элементов в каждой из добавляемых матриц.
a11 + b11, a12 + b12
A + B = (a21 + b21, a22 + b22)
a31 + b31, a32 + b32Или, говоря по-другому:
C[0,0] = A[0,0] + B[0,0]
C[1,0] = A[1,0] + B[1,0]
C[2,0] = A[2,0] + B[2,0]
C[0,1] = A[0,1] + B[0,1]
C[1,1] = A[1,1] + B[1,1]
C[2,1] = A[2,1] + B[2,1]Мы можем реализовать это в python, используя оператор плюс непосредственно на двух массивах NumPy.
# add matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A + B
print(C)В примере сначала определяются две матрицы 2 × 3, а затем складываются их вместе.
При выполнении примера сначала распечатываются две родительские матрицы, а затем результат их сложения.
[[1 2 3]
[4 5 6]]
[[1 2 3]
[4 5 6]]
[[ 2 4 6]
[ 8 10 12]]Матричное вычитание
Аналогично, одна матрица может быть вычтена из другой матрицы с такими же размерами.
C = A - BСкалярные элементы в результирующей матрице рассчитываются как вычитание элементов в каждой из матриц.
a11 - b11, a12 - b12
A - B = (a21 - b21, a22 - b22)
a31 - b31, a32 - b32Или, говоря по-другому:
C[0,0] = A[0,0] - B[0,0]
C[1,0] = A[1,0] - B[1,0]
C[2,0] = A[2,0] - B[2,0]
C[0,1] = A[0,1] - B[0,1]
C[1,1] = A[1,1] - B[1,1]
C[2,1] = A[2,1] - B[2,1]Мы можем реализовать это в python, используя оператор минус непосредственно на двух массивах NumPy.
# subtract matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[0.5, 0.5, 0.5], [0.5, 0.5, 0.5]])
print(B)
C = A - B
print(C)В примере сначала определяются две матрицы 2 × 3, а затем вычитается одна из другой.
Выполнение примера сначала печатает две родительские матрицы, а затем вычитает первую матрицу из второй.
[[1 2 3]
[4 5 6]]
[[ 0.5 0.5 0.5]
[ 0.5 0.5 0.5]]
[[ 0.5 1.5 2.5]
[ 3.5 4.5 5.5]]Умножение матриц (продукт Адамара)
Две матрицы с одинаковым размером могут быть умножены вместе, и это часто называют поэлементным умножением матриц или произведением Адамара.
Это не типичная операция, предназначенная для обозначения умножения матриц, поэтому часто используется другой оператор, такой как круг «o».
C = A o BКак и в случае поэлементного вычитания и сложения, поэлементное умножение включает в себя умножение элементов из каждой родительской матрицы для вычисления значений в новой матрице.
a11 * b11, a12 * b12
A o B = (a21 * b21, a22 * b22)
a31 * b31, a32 * b32Или, говоря по-другому:
C[0,0] = A[0,0] * B[0,0]
C[1,0] = A[1,0] * B[1,0]
C[2,0] = A[2,0] * B[2,0]
C[0,1] = A[0,1] * B[0,1]
C[1,1] = A[1,1] * B[1,1]
C[2,1] = A[2,1] * B[2,1]Мы можем реализовать это в python, используя оператор star непосредственно на двух массивах NumPy.
# element-wise multiply matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A * B
print(C)В примере сначала определяются две матрицы 2 × 3, а затем они умножаются вместе.
При выполнении примера сначала распечатываются две родительские матрицы, а затем результат их умножения на продукт Адамара.
[[1 2 3]
[4 5 6]]
[[1 2 3]
[4 5 6]]
[[ 1 4 9]
[16 25 36]]Матричный отдел
Одна матрица может быть разделена на другую матрицу с такими же размерами.
C = A / BСкалярные элементы в результирующей матрице рассчитываются как деление элементов в каждой из матриц.
a11 / b11, a12 / b12
A / B = (a21 / b21, a22 / b22)
a31 / b31, a32 / b32Или, говоря по-другому:
C[0,0] = A[0,0] / B[0,0]
C[1,0] = A[1,0] / B[1,0]
C[2,0] = A[2,0] / B[2,0]
C[0,1] = A[0,1] / B[0,1]
C[1,1] = A[1,1] / B[1,1]
C[2,1] = A[2,1] / B[2,1]Мы можем реализовать это в python, используя оператор деления непосредственно на двух массивах NumPy
# divide matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A / B
print(C)В примере сначала определяются две матрицы 2 × 3, а затем делится первая и вторая матрицы.
Выполнение примера сначала печатает две родительские матрицы, а затем делит первую матрицу на вторую.
[[1 2 3]
[4 5 6]]
[[1 2 3]
[4 5 6]]
[[ 1. 1. 1.]
[ 1. 1. 1.]]Матрица-матричное умножение (точечный продукт)
Умножение матриц, также называемое произведением матричных точек, является более сложным, чем предыдущие операции, и включает в себя правило, поскольку не все матрицы могут быть умножены вместе.
C = A * Bили же
C = ABПравило умножения матриц следующее:
- Количество столбцов (n) в первой матрице (A) должно равняться количеству строк (m) во второй матрице (B).
Например, матрица A имеет размеры m строк и n столбцов, а матрица B имеет размеры n и k. N столбцов в A и n строк b равны. В результате получается новая матрица с m строками и k столбцами.
C(m,k) = A(m,n) * B(n,k)Это правило применяется к цепочке умножений матриц, где количество столбцов в одной матрице в цепочке должно соответствовать количеству строк в следующей матрице в цепочке.
Одной из наиболее важных операций с участием матриц является умножение двух матриц. Матричный продукт матриц A и B является третьей матрицей C. Для того чтобы этот продукт был определен, A должно иметь такое же количество столбцов, что и B имеет строки. Если A имеет форму m × n, а B имеет форму n × p, то C имеет форму m × p.
– страница 34,Глубокое обучение, 2016
Интуиция для умножения матрицы состоит в том, что мы вычисляем скалярное произведение между каждой строкой в матрице A и каждым столбцом в матрице B. Например, мы можем уменьшить количество строк столбца A и умножить каждый на столбец 1 в B, чтобы получить скаляр значения в колонке 1 кл.
Это ясно из следующего изображения.
Ниже описывается матричное умножение с использованием матричной записи.
a11, a12
A = (a21, a22)
a31, a32
b11, b12
B = (b21, b22)
a11 * b11 + a12 * b21, a11 * b12 + a12 * b22
C = (a21 * b11 + a22 * b21, a21 * b12 + a22 * b22)
a31 * b11 + a32 * b21, a31 * b12 + a32 * b22Это можно упростить, удалив знаки умножения следующим образом:
a11b11 + a12b21, a11b12 + a12b22
C = (a21b11 + a22b21, a21b12 + a22b22)
a31b11 + a32b21, a31b12 + a32b22Мы можем описать операцию умножения матриц, используя обозначение массива.
C[0,0] = A[0,0] * B[0,0] + A[0,1] * B[1,0]
C[1,0] = A[1,0] * B[0,0] + A[1,1] * B[1,0]
C[2,0] = A[2,0] * B[0,0] + A[2,1] * B[1,0]
C[0,1] = A[0,0] * B[0,1] + A[0,1] * B[1,1]
C[1,1] = A[1,0] * B[0,1] + A[1,1] * B[1,1]
C[2,1] = A[2,0] * B[0,1] + A[2,1] * B[1,1]Операция умножения матриц может быть реализована в NumPy с помощью функции dot ().
# matrix dot product
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
B = array([[1, 2], [3, 4]])
print(B)
C = A.dot(B)
print(C)В примере сначала определяются две матрицы 2 × 3, а затем вычисляется их точечное произведение.
При выполнении примера сначала распечатываются две родительские матрицы, а затем результат скалярного произведения.
[[1 2]
[3 4]
[5 6]]
[[1 2]
[3 4]]
[[ 7 10]
[15 22]
[23 34]]Матрично-векторное умножение
Матрица и вектор могут быть умножены вместе при условии соблюдения правила умножения матриц.
В частности, что количество столбцов в матрице должно равняться количеству элементов в векторе. Как и в случае умножения матриц, операция может быть записана с использованием точечной нотации. Поскольку вектор имеет только один столбец, результатом всегда будет вектор.
c = A . vИли без точки в компактной форме.
c = AvРезультатом является вектор с тем же количеством строк, что и у родительской матрицы.
a11, a12
A = (a21, a22)
a31, a32
v1
v = (v2)
a11 * v1 + a12 * v2
c = (a21 * v1 + a22 * v2)
a31 * v1 + a32 * v2Или более компактно.
a11v1 + a12v2
c = (a21v1 + a22v2)
a31v1 + a32v2Умножение матрицы на вектор может быть реализовано в NumPy с помощью функции dot ().
# matrix-vector multiplication
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
B = array([0.5, 0.5])
print(B)
C = A.dot(B)
print(C)Вначале пример определяет матрицу 2 × 3 и вектор из 2 элементов, а затем умножает их вместе.
При выполнении примера сначала печатается родительская матрица и вектор, а затем результат их умножения.
[[1 2]
[3 4]
[5 6]]
[ 0.5 0.5]
[ 1.5 3.5 5.5]Матрично-скалярное умножение
Матрица может быть умножена на скаляр.
Это может быть представлено с использованием точечной нотации между матрицей и скаляром.
C = A . bИли без точечной записи.
C = AbВ результате получается матрица того же размера, что и родительская матрица, в которой каждый элемент матрицы умножается на скалярное значение.
a11, a12
A = (a21, a22)
a31, a32
b
a11 * b, a12 * b
C = (a21 * b, a22 * b)
a31 * b, a32 * bили же
a11b, a12b
C = (a21b, a22b)
a31b, a32bМы также можем представить это с помощью обозначения массива.
C[0,0] = A[0,0] * b
C[1,0] = A[1,0] * b
C[2,0] = A[2,0] * b
C[0,1] = A[0,1] * b
C[1,1] = A[1,1] * b
C[2,1] = A[2,1] * bЭто можно реализовать непосредственно в NumPy с помощью оператора умножения.
# matrix-scalar multiplication
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
b = 0.5
print(b)
C = A * b
print(C)В этом примере сначала определяется матрица 2 × 3 и скаляр, а затем они умножаются вместе.
При выполнении примера сначала распечатывается родительская матрица и скаляр, а затем результат их умножения.
[[1 2]
[3 4]
[5 6]]
0.5
[[ 0.5 1. ]
[ 1.5 2. ]
[ 2.5 3. ]]расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
- Создайте 5 примеров, используя каждую операцию, используя ваши собственные данные.
- Реализуйте каждую матричную операцию вручную для матриц, определенных как списки списков.
- Найдите документы по машинному обучению и найдите 1 пример каждой используемой операции.
Если вы исследуете какое-либо из этих расширений, я хотел бы знать.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.
книги
- Раздел 2.3, Матричные операции.Руководство по линейной алгебре, 2017
- Раздел 3.3, Матричное умножение.Руководство по линейной алгебре, 2017
- Раздел 1.3 Матрицы,Введение в линейную алгебру, Пятое издание, 2016.
- Раздел 2.4 Правила для матричных операций,Введение в линейную алгебру, Пятое издание, 2016.
- Раздел 2.1 Скаляры, векторы, матрицы и тензоры,Глубокое обучение, 2016
- Раздел 2.2. Умножение матриц и векторов,Глубокое обучение, 2016
API
статьи
Резюме
В этом уроке вы обнаружили матрицы в линейной алгебре и способы управления ими в Python.
В частности, вы узнали:
- Что такое матрица и как ее определить в Python с помощью NumPy.
- Как выполнять поэлементные операции, такие как сложение, вычитание и произведение Адамара.
- Как умножить матрицы вместе и интуиция за операцией.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Оригинальная статья
Калькулятор деления матрицы– eMathHelp
Калькулятор найдет частное двух матриц (если возможно) с указанием шагов. Он разделяет матрицы любого размера до 7×7 (2×2, 3×3, 4×4 и т. Д.).
Ваш ввод
Вычислить $$$ \ frac {\ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \\ 1 & 2 & 3 \ end {array} \ right]} {\ left [\ begin {array} {ccc} 1 & 1 & 1 \\ 2 & 3 & 4 \\ 3 & 1 & 1 \ end {array} \ right]}.{-1} = \ left [\ begin {array} {ccc} – \ frac {1} {2} & 0 & \ frac {1} {2} \\ 5 & -1 & -1 \\ – \ frac {7} {2} & 1 & \ frac {1} {2} \ end {array} \ right] $$$ (шаги см. В калькуляторе обратной матрицы).
Наконец, перемножьте матрицы: $$$ \ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \\ 1 & 2 & 3 \ end {array} \ right] \ cdot \ left [\ begin {array} {ccc} – \ frac {1} {2} & 0 & \ frac {1} {2} \\ 5 & -1 & -1 \\ – \ frac {7} { 2} & 1 & \ frac {1} {2} \ end {array} \ right] = \ left [\ begin {array} {ccc} – \ frac {3} {2} & 2 & \ frac {1} {2} \\ 4 & -1 & 0 \\ – 1 & 1 & 0 \ end {array} \ right] $$$ (шаги см. В калькуляторе умножения матриц).
Ответ
$$$ \ frac {\ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \\ 1 & 2 & 3 \ end {array} \ right]} {\ left [\ begin {array} {ccc} 1 & 1 & 1 \\ 2 & 3 & 4 \\ 3 & 1 & 1 \ end {array} \ right]} = \ left [\ begin {array} {ccc} – \ frac {3} {2} & 2 & \ frac {1} {2} \\ 4 & -1 & 0 \\ – 1 & 1 & 0 \ end {array} \ right] = \ left [\ begin { array} {ccc} -1,5 & 2 & 0,5 \\ 4 & -1 & 0 \\ – 1 & 1 & 0 \ end {array} \ right] $$$ A
Matrix Division – Сообщество PTC
>> Ни в одной книге по математике я не могу найти. Используется ли он обычно или нет, это совсем другой вопрос.
>> Скаляр, разделенный на матрицу, не более определен, чем матрица, разделенная на матрицу. <<
Да, это так. Проблема с B / A заключается в том, что его можно использовать для решения либо Ax = B, либо xA = B. Но если B – скаляр, оба решения имеют одно и то же решение, поэтому обозначения однозначны.
>> Большинство математических обозначений очень стандартны <<
Большинство – это далеко не все. Что еще хуже, компьютеры глупы. Если вы что-то закодируете, они применит это ко всем.Даже если ты действительно имел в виду больше всего.
>> На тривиальном уровне, как часто вы видели сложение, обозначенное чем-либо, кроме “+”? <<
В некоторой степени зависит от того, что вы подразумеваете под сложением. Но да, сложение реальных чисел довольно часто обозначается знаком +. И что? То, что существует одна или даже несколько практически универсальных конвенций, ничего не говорит о моем тезисе.
И я видел, что + используется не только для сложения действительных чисел. Я видел, как он используется для обозначения логики или операции.Я также видел, как он используется для представления логической операции исключающее ИЛИ. Я видел некоторые типы сложения, представленные знаком + с кружком вокруг них (и того же типа в разных текстах, просто +). Я видел различные формы сложения, представленные знаком + с нижним индексом. Множество вариаций, даже с такой простой концепцией, как дополнение.
>> Многие следуют в большей степени, хотя <<
Верно. Хотя это может немного зависеть от того, как вы считаете. Разумеется, за ним следят достаточно широко, чтобы попытки Mathcad быть «стандартными» оказались полезными.Тем не менее, нужно понимать, что, хотя многие условности в значительной степени соблюдаются, многие другие – нет, и что даже среди тех, которые в значительной степени соблюдаются, часто бывают важные исключения. И глупый компьютер должен сделать твердый выбор.
Предположим, вы видели G / K в математическом тексте. Что вы ожидаете от этого значения? Или a b c b . Что вы ожидаете от этого?
А в целом интерес людей к “эталону” весьма ограничен. Их обычно вполне устраивает просто «понятное».Несмотря на то, что стандартное обозначение cos 2 θ возможно в Mathcad, я не думаю, что видел, чтобы кто-то использовал его вместо нестандартного cos (θ) 2 . Я также не вижу, чтобы люди использовали стандартную форму cos -1 x вместо нестандартной формы acos (x).
>> Так зачем включать что-то, что не определено математически <<
1 / M не является неопределенным – оно просто не используется (в основном). Я не думаю, что у какого-либо математика возникли бы проблемы с тем, чтобы точно знать, что это значит, если бы его использовали.
>> Итак, я придерживаюсь своего утверждения, что 1 / M, или a / M, или A / B и т. Д. Должны быть неопределенными. <<
Я никогда не говорил, что они должны быть определены. Я сказал, что если 1 / M был определен, он должен быть обратным M. Для B / A я сказал, что, начиная с нуля, оно должно быть, если оно вообще определено, решением AX = B. Но, учитывая, что в настоящее время он реализован как решение XA = B, лучше оставить это так.
Однако в контексте новой версии Mathcad я буду придерживаться позиции, что, поскольку эти формы уже определены и определены разумно, нет причин для их внезапного отмены.Не многие люди используют эти формы, но какая польза от противодействия даже этим немногим?
Tom Gutman
Left Matrix Division and Numpy Solve
Из документации MathWorks для левой матрицы:
Если A – это матрица размером m на n с m ~ = n, а B – вектор-столбец с m компонентов, или матрица с несколькими такими столбцами, то X = A \ B – это решение в смысле наименьших квадратов для недо- или переопределенных система уравнений AX = B.Другими словами, X минимизирует норму (A * X – B), длина вектора AX – B.
Эквивалент в numpy: np.linalg.lstsq:
В [15]: B = np.array ([[2], [4]])
В [16]: b = np.array ([[4], [4]])
В [18]: x, остаток, ранг, s = np.linalg.lstsq (B, b)
В [19]: x
Out [19]: массив ([[1.2]])
Matlab фактически выполняет ряд различных операций, когда используется оператор \, в зависимости от формы задействованных матриц (подробнее см. Здесь).В вашем примере Matlab возвращает решение методом наименьших квадратов, а не напрямую решает линейное уравнение, как это произошло бы с квадратной матрицей. Чтобы получить такое же поведение в numpy, сделайте следующее:
импортировать numpy как np
импортировать numpy.linalg как lin
B = np.array ([[2], [4]])
b = np.array ([[4], [4]])
напечатать np.linalg.lstsq (B, b) [0]
, который должен дать вам то же решение, что и Matlab.
Можно сформировать левую инверсию:
импортировать numpy как np
import numpy.линалг как лин
B = np.array ([[2], [4]])
b = np.array ([[4], [4]])
B_linv = lin.solve (B.T.dot (B), B.T)
c = B_linv.dot (б)
печать ('c \ n', c)
Результат:
c
[[1.2]]
На самом деле, мы можем просто запустить решатель один раз, не создавая инверсию, например:
c = лин. Раствор (B.T.dot (B), B.T.dot (b))
печать ('c \ n', c)
Результат:
c
[[1.2]]
…. как раньше
Почему? Потому что:
У нас:
Умножаем на B.Т , дает:
Итак, B.T.dot (B) – квадрат, полный ранг, имеет обратное. И поэтому мы можем умножить на обратное значение B.T.dot (B) или использовать решатель, как указано выше, чтобы получить c .
(подразделение / план): стратегическое планирование
Планирование является важным инструментом управления. Стратегическое планирование всегда было частью процесса принятия управленческих решений в DEQ. Ежегодные встречи по планированию проводятся каждую весну отдельными подразделениями и департаментом в целом.Эти выездные семинары являются частью ежегодного процесса планирования, присущего собственной системе управления департамента, и включают в себя миссию, видение и ценности департамента. Основная цель процессов планирования как DEQ, так и EPA состоит в том, чтобы способствовать более значимому и эффективному планированию, которое расширяет сотрудничество, коммуникацию и координацию между агентствами, гражданами, клиентурой и заинтересованными сторонами для достижения желаемых экологических результатов.
Кроме того, у Департамента также есть требования к планированию, которые являются компонентами требований к выдаче разрешений, требований к грантам и нашего собственного плана управления качеством.Эта матрица планирования определяет многие инициативы по планированию, которыми занимается Департамент.
Департамент качества окружающей среды (DEQ)
Департамент качества окружающей среды сотрудничает с Агентством по охране окружающей среды США (EPA), 12 местными департаментами здравоохранения штата Юта и другими агентствами в рамках партнерских усилий по разработке и реализации планов для достижения желаемых рабочих целей. Эти планы включают Национальное соглашение о партнерстве в области экологической результативности с EPA, разработку плана оказания экологических услуг с местными департаментами здравоохранения и разработку плана информационных технологий для всего департамента.
Отдел реагирования на окружающую среду и восстановления (DERR)
Отдел реагирования на окружающую среду и восстановления реализует планы очистки отходов и реагирования на окружающую среду. Отдел также несет главную ответственность за разработку плана действий Департамента в чрезвычайных ситуациях, который требуется каждому государственному учреждению, которому возложены функции и обязанности по оказанию помощи при стихийных бедствиях. Этот План реагирования на чрезвычайные ситуации и стихийные бедствия DEQ был подготовлен в соответствии с этим требованием, чтобы обеспечить общее руководство для персонала DEQ в управлении, координации и реагировании на чрезвычайные ситуации или стихийные бедствия, влияющие на здоровье людей, жизнь, имущество и окружающую среду по всему штату.
- План реагирования на чрезвычайные ситуации и стихийные бедствия Департамента: требуется штатом и DEQ; Орган: UCA 53-2-104 и UCA 19-1-201 (2)
Отделение твердых и опасных отходов (ТБО)
Подразделение твердых и опасных отходов несет ответственность за защиту здоровья населения и окружающей среды путем обеспечения надлежащего обращения с твердыми и опасными отходами в штате Юта.
- Государственный план обращения с твердыми отходами: требуется Советом по контролю за твердыми и опасными отходами; Администрация: UCA 19-6-104 (2)
Отдел питьевой воды (DDW)
Отдел питьевой воды несет ответственность за защиту населения от рисков для здоровья, связанных с водой, посредством обучения, помощи и надзора.Приняты правила по охране общественных источников питьевой воды. Эти правила требуют, чтобы каждый поставщик коммунальной питьевой воды подготовил план защиты источника. Этот план должен быть рассмотрен и утвержден Отделом питьевой воды.
Отдел качества воды (DWQ)
Загрязнение из неточечных источников (НПВ), в отличие от загрязнения от промышленных предприятий и очистных сооружений, происходит из многих диффузных источников. Загрязнение из неточечных источников вызывается дождем или таянием снега, перемещающимся над землей и сквозь нее.По мере движения сток собирает и уносит природные и антропогенные загрязнители. Некоторые общие источники загрязнения НПВ включают городские улицы и автостоянки, сельскохозяйственные угодья и производственные объекты, строительные площадки и стоки с заброшенных шахт.
- План управления неточечным источником: требуется EPA и DEQ; Авторитет: CWA Раздел 319
- 305 (b) Отчет: Требуется EPA и DEQ; Орган: CWA Section 319
- 303 (d) Список загрязненных вод: требуется EPA и DEQ; Орган: CWA Section 319
- Стратегия мониторинга (долгосрочная): требуется EPA и DEQ; Орган: CWA Section 319
- Годовой план работ по мониторингу: требуется EPA и DEQ; Орган: CWA Section 319
- План предполагаемого использования SRF: требуется EPA и DEQ; Орган: CWA Section 319
Отдел качества воздуха (DAQ)
В целях защиты здоровья населения Закон о чистом воздухе (42 U.S.C. Section 7401) требует, чтобы федеральные стандарты ограничивали максимальные уровни загрязняющих веществ в наружном воздухе. Каждый штат несет ответственность за разработку планов, демонстрирующих, как эти стандарты будут достигнуты, поддерживаться и обеспечивать соблюдение. Эти планы составляют Государственный план реализации. Связанные с ними планы и правила соблюдаются государством, и после утверждения на федеральном уровне они также подлежат исполнению на федеральном уровне. Эти планы составляют основу программы каждого штата по защите воздуха.
- Государственный план реализации: требуется EPA и DAQ; Орган: 19-2-104 (3) и Федеральный закон о чистом воздухе, раздел 110 .
- Планы выделенных объектов: требуется DAQ; Орган: 40 CFR 60.23
- План управления задымлением: требуется DAQ; Орган: 40 CFR
- Обзор сети мониторинга: требуется органом DAQ: 51.309
- План действий при стихийных бедствиях: требуется DAQ; Орган: 40 CFR 58, подраздел C План работы программы соответствия
- : Требуется DAQ; Орган: CAA Section 319CAA / PPA
Отдел радиационного контроля (DRC)
Отдел радиационного контроля регулирует использование радиоактивных материалов и оборудования для производства рентгеновских лучей.Сюда входят низкоактивные радиоактивные отходы, урановые заводы, пользователи медицинских рентгеновских лучей, а также коммерческое, исследовательское и промышленное использование радиоактивных материалов.
- План рекультивации и вывода из эксплуатации хвостов: требуется DRC и Milling / Mining Co .; Авторитет: 10 CFR 40 App. A Политика применения разрешений на доступ к участку генератора
- : Требуется DRC / Generators; Авторитет: R313-24, R313-26 и R313-14-15
Свяжитесь с командой по коммуникациям DEQ ([email protected]) с вопросами или комментариями.
Quick-R: Матричная алгебра
Большинство методов на этом веб-сайте фактически описывают программирование матриц. Он глубоко встроен в язык R. В этом разделе просто рассматриваются операторы и функции, специально предназначенные для линейной алгебры. Перед тем, как продолжить, многие захотят просмотреть разделы, посвященные типам данных и операторам.
Матричный комплекс
В следующих примерах A и B – это матрицы, а x и b – векторы.
| Оператор или функция | Описание |
| А * В | Поэлементное умножение |
| A% *% B | Умножение матриц |
| A% o% B | Внешний продукт. АБ ‘ |
| крестовина (A, B) крестовина (A) | A’B и A’A соответственно. |
| т (A) | Транспонировать |
| диаг (x) | Создает диагональную матрицу с элементами x по главной диагонали |
| диаг (A) | Возвращает вектор, содержащий элементы главной диагонали |
| диаг (к) | Если k – скаляр, это создает единичную матрицу k x k.Иди разберись. |
| решить (A, b) | Возвращает вектор x в уравнении b = Ax (т.е. A -1 b ) |
| решить (A) | Инверсия A , где A – квадратная матрица. |
| гинв (А) | Обобщенная инверсия Мура-Пенроуза A . ginv (A) требует загрузки пакета MASS . |
| y <-eigen (A) | y $ val – собственные значения A y $ vec – собственные векторы A |
| y <-svd (A) | Разложение на одно значение A . y $ d = вектор, содержащий сингулярные значения A y $ u = матрица со столбцами, содержащая левые сингулярные векторы A y $ v = матрица со столбцами, содержащая правые сингулярные векторы А |
| R <- хол (A) | Факторизация Холецкого A .Возвращает множитель верхнего треугольника, так что R’R = A . |
| y <- qr (A) | QR-разложение A . y $ qr имеет верхний треугольник, содержащий разложение, и нижний треугольник, содержащий информацию о разложении Q. y $ rank – это ранг A. y $ qraux вектор, который содержит дополнительную информацию о Q. y $ pivot содержит информацию об используемой стратегии поворота. |
| cbind (A, B, …) | Объедините матрицы (векторы) по горизонтали. Возвращает матрицу. |
| rbind (A, B, …) | Объедините матрицы (векторы) по вертикали. Возвращает матрицу. |
| Ряд Средств (A) | Возвращает вектор средних значений строки. |
| ряд Суммы (A) | Возвращает вектор сумм строк. |
| СРЕДСТВА (A) | Возвращает вектор средних значений столбца. |
| КолСуммы (A) | Возвращает вектор сумм столбцов. |
Эмуляция Matlab
Пакет matlab содержит функции-оболочки и переменные, используемые для наилучшей репликации вызовов функций MATLAB. Это может помочь в переносе приложений и кода MATLAB на R.
Идем дальше
Пакет Matrix содержит функции, расширяющие R для поддержки очень плотных или разреженных матриц. Он обеспечивает эффективный доступ к BLAS (основные подпрограммы линейной алгебры), Lapack (плотная матрица), TAUCS (разреженная матрица) и UMFPACK (разреженная матрица) рутины.
к практике
Попробуйте выполнить некоторые из упражнений по матричной алгебре из этого курса, посвященного статистике с R.
Matrix Division в Python для науки о данных || Обучено на Vimeo
#Data_Science_Course #Datascience #Data_science_Training #Python #Matrix_division
Обзор: изучите применение ключевых математических тем, связанных с линейной алгеброй, с языком программирования Python.
Ожидаемая продолжительность: 1 час 10 минут. После завершения этого курса вы должны быть в состоянии выполнить цели следующих уроков и тем.
Урок математики для науки о данных и машинного обучения:
1. Поймите, как работать с векторами в Python
2. Базис и проекция векторов: Поймите базис и проекцию векторов в Python
3. Работа с матрицами: Уясните, как работать с матрицами в Python
4. Умножение матриц: узнайте, как умножать матрицы в Python
5.Разделение матриц: понять, как делить матрицы в Python
5. Линейные преобразования: понять, как работать с линейными преобразованиями в Python
7. Исключение Гаусса: понять, как применять исключение Гаусса
8. Детерминанты: понять, как работать с определителями в Python
9. Ортогональные матрицы: понять, как работать с ортогональными матрицами в Python
10. Собственные значения: узнать, как получить собственные значения из восьми разложений в Python
11. Собственные векторы: узнать, как получить собственные векторы из собственного разложения в Python
12.PseudoInverse: узнайте, как получить псевдообратную версию в Python
13. Упражнение: математика для науки о данных и машинного обучения
Мы предоставляем 6-месячный курс DataTrained по науке о данных с гарантированным размещением. Этот курс был создан и разработан двумя профессиональными специалистами по данным, работающими с MathsoMania, чтобы мы могли делиться отраслевыми знаниями в области машинного обучения и помогать людям изучать и понимать сложные теории, алгоритмы и библиотеки кодирования гораздо более простым способом.
Мы шаг за шагом проведем вас во вселенную Data Science.Обучение будет настолько простым и изобретательным, что с каждым уроком вы будете развивать новые навыки и улучшать свое понимание этой сложной, но прибыльной области науки о данных.
Этот курс полон веселья и азарта, но в то же время мы глубоко погружаемся в тонкости науки о данных и ее алгоритмов.
Кроме того, курс насыщен практическими упражнениями, основанными на реальных примерах. Таким образом, вы не только изучите теорию, но и получите практическую практику построения собственных моделей.
И в качестве бонуса этот курс включает в себя шаблоны кода Python и R, которые вы можете загрузить и использовать в своих собственных проектах.
Вы должны быть как минимум выпускником или на последнем году обучения. Для прохождения теста требуется лишь немного математики на уровне средней школы.
****** ПОДПИСАТЬСЯ НА НАШУ СОЦИАЛЬНУЮ ССЫЛКУ *******
Ознакомьтесь с нашим 6-месячным курсом по науке о данных с гарантированным размещением здесь: datatrained.com/data-science-program
Facebook: facebook.com / datatrained
Twitter: twitter.com/datatrained
LinkedIn: linkedin.com/company/datatrained/
Для получения дополнительной информации напишите нам по адресу [email protected] или позвоните нам по телефону IND: 0120-4298471-72 / Mob: 7303485574
Математика для науки о данных
Математика для науки о данных и машинного обучения
Математика для анализа данных
Математика для курса по науке о данных
Математика для аналитика данных
Математика для интеллектуального анализа данных
Математика, необходимая для науки о данных
Математические приемы для интерпретации данных
Математика обработки данных
Интерпретация математических данных
Разделение труда при производстве матриц биопленок
Такие простые организмы, как бактерии, могут участвовать в сложных коллективных действиях, таких как групповая подвижность и формирование плодовых тел.Некоторые из этих действий включают разделение труда, при котором фенотипически специализированные клональные субпопуляции или генетически различные клоны взаимодействуют друг с другом, выполняя дополнительные задачи. Здесь мы объединяем экспериментальные и вычислительные подходы для изучения потенциальных выгод, возникающих в результате разделения труда во время производства матрицы биопленки. Мы показываем, что как фенотипические, так и генетические стратегии разделения труда могут способствовать формированию коллективной биопленки в почвенной бактерии Bacillus subtilis.У этого вида матрикс биопленки состоит из двух основных компонентов: экзополисахаридов (ЭПС) и TasA. Мы наблюдали, что клональные группы B. subtilis фенотипически разделяются на три субпопуляции, состоящие из непродуцентов матрикса, продуцентов EPS и генералистов, которые продуцируют как EPS, так и TasA. Эта неполная фенотипическая специализация была превзойдена генетическим разделением труда, когда два мутанта, созданные как специалисты, дополняли друг друга, обмениваясь EPS и TasA.

 50000
[1;1]/1
ans =
1
1
50000
[1;1]/1
ans =
1
1