Деление матрицы на число: Деление матриц, формулы и примеры - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

(-1) = (1/∆)•B, где ∆ – определитель матрицы, который должен быть отличен от нуля. Если это не так, то обратная матрица не существует. B – матрица, состоящая из алгебраических дополнений исходной матрицы А.

Например, выполните деление заданных матриц.

Найдите матрицу, обратную ко второй. Для этого вычислите ее определитель и матрицу алгебраических дополнений. Запишите формулу определителя для квадратной матрицы третьего порядка:∆ = a11·a22·a33 + a12·a23·a31 + a21·a32·a13 – a31·a22·a13 – a12·a21·a33 – a11·a23·a32 = 27.

Определите алгебраические дополнения по указанным формулам:A11 = a22•a33 – a23•a32 = 1•2 – (-2)•2 = 2 + 4 = 6;A12 = -(a21•a33 – a23•a31) = -(2•2 – (-2)•1) = -(4 + 2) = -6;A13 = a21•a32 – a22•a31 = 2•2 – 1•1 = 4 – 1 = 3;A21 = -(a12•a33 – a13•a32) = -((-2)•2 – 1•2) = -(-4 – 2) = 6;A22 = a11•a33 – a13•a31 = 2•2 – 1•1 = 4 – 1 = 3;A23 = -(a11•a32 – a12•a31) = -(2•2 – (-2)•1) = -(4 + 2) = -6;A31 = a12•a23 – a13•a22 = (-2)•(-2) – 1•1 = 4 – 1 = 3;A32 = -(a11•a23 – a13•a21) = -(2•(-2) – 1•2) = -(-4 – 2) = 6;A33 = a11•a22 – a12•a21 = 2•1 – (-2)•2 = 2 + 4 = 6.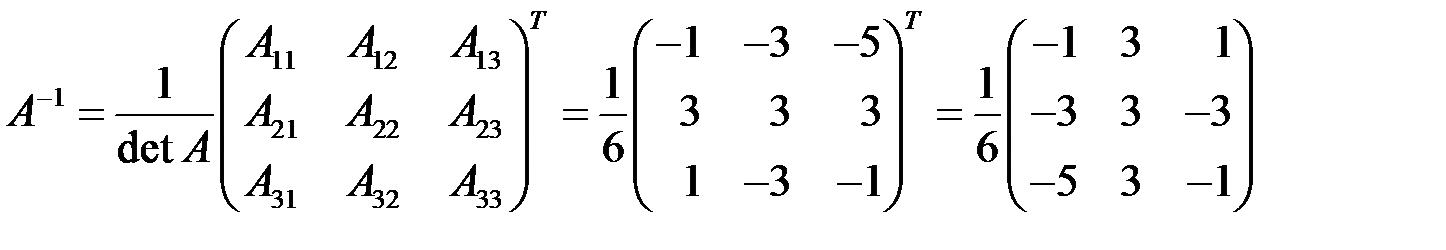

Разделите элементы матрицы алгебраических дополнений на величину определителя, равную 27. Таким образом, вы получили матрицу, обратную ко второй. Теперь задача сводится к умножению первой матрицы на новую.

Выполните умножение матриц по формуле C = A*B:c11 = a11•b11 + a12•b21 + a13•b31 = 1/3;c12 = a11•b12 + a12•b22 + a13•b23 = -2/3;c13 = a11•b13 + a12•b23 + a13•b33 = -1;c21 = a21•b11 + a22•b21 + a23•b31 = 4/9;c22 = a21•b12 + a22•b22 + a23•b23 = 2/9;c23 = a21•b13 + a22•b23 + a23•b33 = 5/9;c31 = a31•b11 + a32•b21 + a33•b31 = 7/3;c32 = a31•b12 + a32•b22 + a33•b23 = 1/3;c33 = a31•b13 + a32•b23 + a33•b33 = 0.

Содержание

умножение на число, сложение, вычитание, умножение матриц.

Свойства операций над матрицами.

Сложение матриц:

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В c_ij = a_ij + b_ij Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента

матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что

b_ij = k × a_ij. В = k × A b_ij = k × a_ij. Матрица – А = (-1) × А называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А – А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С – матрицы, α и β – числа.

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы А_m×n на матрицу В_n×p, называется матрица С_m×p такая, что с_ik = a_i1 × b_1k + a_i2 × b_2k + . .. + a_in × b_nk, т. е. находиться сумма произведений элементов i – ой строки

матрицы А на соответствующие элементы j – ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е – единичная матрица того же размера.

Свойства умножения матриц:

Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная

матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А

Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ)^Т = В^ТА^Т; 7. (АВС)^Т = С^ТВ^ТА^Т; 8. (А + В)^Т = А^Т + В^Т;

2. Определители 2-го и 3-го порядков. Свойства определителей.

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6

Свойства определителей матриц

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|^Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов

определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой

определитель матрицы равен нулю.

Свойство № 5:

Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы:

Деление столбцов матрицы на элементы вектора

Я выясняю, как разделить N-й столбец матрицы на N-й элемент вектора строк.

Например, пусть матрица a и вектор b:

a <- matrix(1:9, byrow = TRUE,  nrow = 3)
b <- c(3:5)

дающий

[[1]]
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9

[[2]]
[1] 3 4 5

В этом случае я ищу код, который делит первый столбец матрицы на 3, второй на 4 и третий на 5.

Я пытался использовать функцию apply без успеха

c <- apply(a, 2, function(x) x / b)

Есть ли какой-нибудь код, который может сделать это с помощью apply и предпочтительно без использования циклов?

r
Поделиться Источник Adrian 08 января 2018 в 13:25
3 ответа
Деление строк на члены вектора в R
Этот вопрос очень прост. Он состоит в делении каждой строки матрицы на соответствующий ей номер вектора. Например. У меня есть эта матрица: [3 6 9 12] И этот вектор: 5, 10 Я хочу разделить первую строку матрицы на первое число вектора, а вторую строку матрицы-на второе число вектора. Так что…
Как разделить элементы матрицы на суммы столбцов *non-zero* в MATLAB?
Я вижу этот вопрос: Как разделить элементы матрицы на суммы столбцов в MATLAB? Но кроме того, я хочу сделать деление только в том случае, если сумма столбца ( sum(A) ) отлична от нуля. Будет ли работать какой-либо из перечисленных там методов, кроме метода цикла, так как он очень медленный для…

5

Вы могли бы использовать sweep для этого:
#same as apply the second argument needs to be 1 for row or 2 for column sweep(a, 2, b, FUN = '/') # [,1] [,2] [,3] #[1,] 0.3333333 0.50 0.6 #[2,] 1.3333333 1.25 1.2 #[3,] 2.3333333 2.00 1.8
Поделиться LyzandeR 08 января 2018 в 13:27

3

Другой вариант- mapply , т. е.
mapply(`/`, data.frame(a), b)
что дает
X1 X2 X3 [1,] 0.3333333 0.50 0.6 [2,] 1.3333333 1.25 1.2 [3,] 2.3333333 2.00 1.8
Поделиться Sotos 08 января 2018 в 13:33

2

Вы можете взять транспонирование матрицы, разделить и снова транспонировать результат.
t(t(a)/b) # [,1] [,2] [,3] #[1,] 0.3333333 0.50 0.6 #[2,] 1.3333333 1.25 1.2 #[3,] 2.3333333 2.00 1.8
Поделиться Esteban PS 08 января 2018 в 13:47
Возвращает IDs матрицы, содержащей все элементы вектора
Я знаю, что ответ совершенно прост, но я не мог получить его до сих пор. Также я пытался найти ответ через подобные вопросы, но не смог. В любом случае, мне нужно вернуть ID матрицы m , которая имеет все элементы вектора ( NoN ). в Примере, который я подготовил ниже, мне нужно вернуть IDs 1 и 3….
Numpy Способ построения NXD матрицы из мультипликации матрицы и элементов вектора
У меня есть вектор v, который имеет размер D, и я хочу умножить его на каждый элемент вектора y, который имеет размер N, так что каждый столбец i новой матрицы X является произведением v и индексированного элемента вектора y. Я пытаюсь избежать создания пустой матрицы NXD и запустить с for loop…
Похожие вопросы:

Matlab поэлементное деление на ноль
У меня есть две матрицы, скажем X = [1 2; 3 4; 5 6] и Y = [0 1; -1 1; 1 1]. Я хочу выполнить поэлементное деление X./Y, но мне нужен способ игнорировать все нули в Y. Я попробовал использовать…

Векторизованное поэлементное деление на разреженные матрицы в R
A/B в R выполняет поэлементное деление матрицы. Однако если я сгенерирую разреженную матрицу из пакета Matrix и попытаюсь разделить A/B,, то получу эту ошибку: > class(N) [1] dgCMatrix…

Использование столбца или строк матрицы для ссылки на элементы вектора
У меня есть вектор. Я выбираю группы из n=4 последовательных значений, используя матрицу, полученную с помощью mapply(seq,starts,ends) . Я использую столбцы матрицы для ссылки на элементы в моем…

Деление строк на члены вектора в R
Этот вопрос очень прост. Он состоит в делении каждой строки матрицы на соответствующий ей номер вектора. Например. У меня есть эта матрица: [3 6 9 12] И этот вектор: 5, 10 Я хочу разделить первую…

Как разделить элементы матрицы на суммы столбцов *non-zero* в MATLAB?
Я вижу этот вопрос: Как разделить элементы матрицы на суммы столбцов в MATLAB? Но кроме того, я хочу сделать деление только в том случае, если сумма столбца ( sum(A) ) отлична от нуля. Будет ли…

Возвращает IDs матрицы, содержащей все элементы вектора
Я знаю, что ответ совершенно прост, но я не мог получить его до сих пор. Также я пытался найти ответ через подобные вопросы, но не смог. В любом случае, мне нужно вернуть ID матрицы m , которая…

Numpy Способ построения NXD матрицы из мультипликации матрицы и элементов вектора
У меня есть вектор v, который имеет размер D, и я хочу умножить его на каждый элемент вектора y, который имеет размер N, так что каждый столбец i новой матрицы X является произведением v и. ..

деление строк матрицы на вектор столбцов
Как я могу разделить каждый элемент строк симметричной матрицы NxN на вектор столбца (Nx1), так что я могу получить не Вектор Nx1, а снова симметричную матрицу NxN, где каждый элемент вдоль строк…

Как сопоставить элементы списка с именами столбцов матрицы в R
У меня есть матрица без colnames, которая выглядит следующим образом: >my_matrix [,1] [,2] [,3] ENSG00000000345 1.324266e+03 1.071842e+03 1.024920e+03 ENSG00000000105 3.750147e+01 8.081121e+02…

Как заполнить конкретные элементы матрицы, зная их индексы, значениями из вектора столбцов
Как я могу заполнить элементы нижней треугольной части матрицы, включая диагональ, значениями из вектора столбцов? Например у меня есть : m=np.zeros((3,3)) n=np.array([[1],[1],[1],[1],[1],[1]])…
Функции для работы с матрицами в Excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
Выделить диапазон, где должен появиться результат действия формулы.
Ввести формулу (как и положено, со знака «=»).
Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.

Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Матрицы в Excel
Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.
Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.
Формулы массива
В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
Выделить набор ячеек, где будут выводиться значения.
Непосредственно введение формулы.
Нажатие последовательности клавиш Ctrl + Shift + Ввод.
После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.
Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.
Что можно делать с матрицами
В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.
Транспонирование
Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Далее есть несколько методов, как можно осуществить транспонирование.
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».
Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
Выделить набор ячеек, отведенных под транспонированную матрицу.
Нажать клавишу F2.
Нажать на горячие клавиши Ctrl + Shift + Enter.
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.
Сложение
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.
В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.
=Первый элемент первой матрицы + Первый элемент второй матрицы
Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.
Умножение
Предположим, у нас есть такая таблица, которую следует умножить на 12.
Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.
При этом важно указывать абсолютные ссылки на ячейки.
Итого, получится такая формула.
=A1*$E$3
Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:h21). Не стоит забыть нажать Ctrl + Shift + Enter.
Обратная матрица
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР.
Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4). В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.
Поиск определителя матрицы
Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.
Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)
Несколько примеров
Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.
Умножение и деление
Метод 1
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке h5. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.
Не стоит забывать о том, ячейку h5, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.
Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.
Метод 2
Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
Деление осуществляется аналогичным образом, только знак * нужно заменить на /.
Сложение и вычитание
Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.
Метод 1
Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:
=B3+h4
Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.
Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.
Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.
Метод 2
Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.
Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Пример транспонирования матрицы
Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП().
Выделяем диапазон для ячеек матрицы АТ.
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП. После этого свои действия подтверждаются кнопкой ОК.
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».
Важно. Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.
Поиск обратной матрицы
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР().
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР. После того, как мы ее выберем, нужно нажать на клавишу ОК. Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Выводы
Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.
Оцените качество статьи. Нам важно ваше мнение:
Умножение матриц
Каталин Дэвид
Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Алгоритм умножения матриц
Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.
Умножаем элементы первой строки на элементы первого столбца.
Умножаем первый элемент первой строки на первый элемент первого столбца.
Умножаем второй элемент первой строки на второй элемент первого столбца.
Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
Складываем полученные произведения.
Полученный результат будет первым элементом первой строки произведения матриц.
Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
Умножаем первый элемент первой строки на первый элемент второго столбца.
Умножаем второй элемент первой строки на второй элемент второго столбца.
Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
Складываем полученные произведения.
Полученный результат будет вторым элементом первой строки произведения матриц.
Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.
Пример 7
$A= \begin{pmatrix} 1 & 2 & 2\\ 3 & 1 & 1 \end{pmatrix}$
$B=\begin{pmatrix} 4 & 2 \\ 3 & 1 \\ 1 & 5\\ \end{pmatrix}$
Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.
$A \cdot B=$ $\begin{pmatrix} \color{red}1 &\color{blue}2 & \color{green}2\\ \color{red}3 &\color{blue}1 & \color{green}1 \end{pmatrix} \begin{pmatrix} \color{red}4 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \\ \color{green}1 & \color{green}5 \end{pmatrix}=$ $\begin{pmatrix} \color{red}{1\cdot4}+\color{blue}{2\cdot3}+\color{green}{2\cdot1} & \color{red}{1\cdot2}+\color{blue}{2\cdot1}+\color{green}{2\cdot5}\\ \color{red}{3\cdot4}+\color{blue}{1\cdot3}+\color{green}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}+\color{green}{1\cdot5} \end{pmatrix}=$ $\begin{pmatrix} 12 & 14\\ 16 & 12\\ \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}4 &\color{blue}2 \\ \color{red}3 & \color{blue}1 \\ \color{red}1 & \color{blue}5 \end{pmatrix} \begin{pmatrix} \color{red}1 &\color{red}2 & \color{red}2\\ \color{blue}3 &\color{blue}1 & \color{blue}1 \end{pmatrix}=$
$\begin{pmatrix} \color{red}{4\cdot1}+\color{blue}{2\cdot3} & \color{red}{4\cdot2}+\color{blue}{2\cdot1} & \color{red}{4\cdot2}+\color{blue}{2\cdot1}\\ \color{red}{3\cdot1}+\color{blue}{1\cdot3} & \color{red}{3\cdot2}+\color{blue}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}\\ \color{red}{1\cdot1}+\color{blue}{5\cdot3} & \color{red}{1\cdot2}+\color{blue}{5\cdot1} & \color{red}{1\cdot2}+ \color{blue}{5\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 10 & 10 & 10 \\ 6 & 7 & 7 \\ 16 & 7 & 7 \end{pmatrix}$
Заметим, что $A \cdot B \neq B \cdot A$
Пример 8
$A= \begin{pmatrix} 5 & 2 \\ 3 & 1 \end{pmatrix} B= \begin{pmatrix} 4 & 6 \\ 5 & 2 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}5 & \color{blue}2 \\ \color{red}3 & \color{blue}1 \end{pmatrix} \cdot \begin{pmatrix} \color{red}4 & \color{red}6 \\ \color{blue}5 & \color{blue}2 \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot4}+\color{blue}{2\cdot5} & \color{red}{5\cdot6}+\color{blue}{2\cdot2} \\ \color{red}{3\cdot4}+\color{blue}{1\cdot5} & \color{red}{3\cdot6}+\color{blue}{1\cdot2} \end{pmatrix} =$ $\begin{pmatrix} 30 & 34\\ 17 & 20 \end{pmatrix}$
$B \cdot A= \begin{pmatrix} \color{red}4 & \color{blue}6 \\ \color{red}5 & \color{blue}2 \end{pmatrix} \cdot \begin{pmatrix} \color{red}5 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \end{pmatrix} =\begin{pmatrix} \color{red}{4\cdot5}+\color{blue}{6\cdot3} & \color{red}{4\cdot2}+\color{blue}{5\cdot1} \\ \color{red}{5\cdot5}+\color{blue}{2\cdot3} & \color{red}{5\cdot2}+\color{blue}{2\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 38 & 14\\ 31 & 12 \end{pmatrix}$
Опять-таки $A \cdot B \neq B \cdot A$.
Пример 9
$A= \begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} B= \begin{pmatrix} 5 & 2 & 1 \\ 4 & 3 & 2 \\ 2 & 1 & 5 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} & \color{red}{1} \\ \color{blue}{4} & \color{blue}{3} & \color{blue}{2} \\ \color{green}{2} & \color{green}{1} & \color{green}{5} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot5} + \color{blue}{4\cdot4} + \color{green}{3\cdot2} & \color{red}{1\cdot2} + \color{blue}{4\cdot3} + \color{green}{3\cdot1} & \color{red}{1\cdot1} + \color{blue}{4\cdot2} + \color{green}{3\cdot5} \\ \color{red}{2\cdot5} + \color{blue}{1\cdot4} + \color{green}{5\cdot2} & \color{red}{2\cdot2} + \color{blue}{1\cdot3} + \color{green}{5\cdot1} & \color{red}{2\cdot1} + \color{blue}{1\cdot2} + \color{green}{5\cdot5}\\ \color{red}{3\cdot5} + \color{blue}{2\cdot4} + \color{green}{1\cdot2} & \color{red}{3\cdot2} + \color{blue}{2\cdot3} + \color{green}{1\cdot1} & \color{red}{3\cdot1} + \color{blue}{2\cdot2} + \color{green}{1\cdot5} \end{pmatrix}=$
$=\begin{pmatrix} 27 & 17 & 24\\ 24 & 12 & 29\\ 25 & 13 & 12 \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}{5} & \color{blue}{2} & \color{green}{1}\\ \color{red}{4} & \color{blue}{3} & \color{green}{2}\\ \color{red}{2} & \color{blue}{1} & \color{green}{5} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{4} & \color{red}{3} \\ \color{blue}{2} & \color{blue}{1} & \color{blue}{5} \\ \color{green}{3} & \color{green}{2} & \color{green}{1} \end{pmatrix}=$ $\begin{pmatrix} \color{red}{5\cdot1} + \color{blue}{2\cdot2} + \color{green}{1\cdot2} & \color{red}{5\cdot4} + \color{blue}{2\cdot1} + \color{green}{1\cdot2} & \color{red}{5\cdot3} + \color{blue}{2\cdot5} + \color{green}{1\cdot1} \\ \color{red}{4\cdot1} + \color{blue}{3\cdot2} + \color{green}{2\cdot3} & \color{red}{4\cdot4} + \color{blue}{3\cdot1} + \color{green}{2\cdot2} & \color{red}{4\cdot3} + \color{blue}{3\cdot5} + \color{green}{2\cdot1}\\ \color{red}{2\cdot1} + \color{blue}{1\cdot2} + \color{green}{5\cdot3} & \color{red}{2\cdot4} + \color{blue}{1\cdot1} + \color{green}{5\cdot2} & \color{red}{2\cdot3} + \color{blue}{1\cdot5} + \color{green}{5\cdot1} \end{pmatrix}=$
$=\begin{pmatrix} 11 & 24 & 26\\ 16 & 23 & 29\\ 19 & 19 & 16 \end{pmatrix}$
Опять-таки $A \cdot B \neq B \cdot A$.
Пример 10
$A= \begin{pmatrix} 5 & 2\\ 3 & 1\\ \end{pmatrix} I_{2}= \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{5} & \color{blue}{2}\\ \color{red}{3} & \color{blue}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{0} \\ \color{blue}{0} & \color{blue}{1} \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot1}+\color{blue}{2\cdot0} & \color{red}{5\cdot0}+\color{blue}{2\cdot1} \\ \color{red}{3\cdot1}+\color{blue}{1\cdot0} & \color{red}{3\cdot0}+\color{blue}{1\cdot1} \end{pmatrix} = \begin{pmatrix} 5 & 2\\ 3 & 1 \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}{1} & \color{blue}{0} \\ \color{red}{0} & \color{blue}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} \\ \color{blue}{3} & \color{blue}{1} \\ \end{pmatrix} =\begin{pmatrix} \color{red}{1\cdot5}+\color{blue}{0\cdot3} & \color{red}{1\cdot2}+\color{blue}{0\cdot1} \\ \color{red}{0\cdot5}+\color{blue}{1\cdot3} & \color{red}{0\cdot2}+\color{blue}{1\cdot1} \end{pmatrix} = \begin{pmatrix} 5 & 2\\ 3 & 1 \end{pmatrix}$
Заметим, что $A \cdot I_{2} = I_{2} \cdot A=A$.
Пример 11
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} I_{3}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{0} & \color{red}{0} \\ \color{blue}{0} & \color{blue}{1} & \color{blue}{0} \\ \color{green}{0} & \color{green}{0} & \color{green}{1} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot1} + \color{blue}{4\cdot0} + \color{green}{3\cdot0} & \color{red}{1\cdot0} + \color{blue}{4\cdot1} + \color{green}{3\cdot0} & \color{red}{1\cdot0} + \color{blue}{4\cdot0} + \color{green}{3\cdot1} \\ \color{red}{2\cdot1} + \color{blue}{1\cdot0} + \color{green}{5\cdot0} & \color{red}{2\cdot0} + \color{blue}{1\cdot1} + \color{green}{5\cdot0} & \color{red}{2\cdot0} + \color{blue}{1\cdot0} + \color{green}{5\cdot1}\\ \color{red}{3\cdot1} + \color{blue}{2\cdot0} + \color{green}{1\cdot0} & \color{red}{3\cdot0} + \color{blue}{2\cdot1} + \color{green}{1\cdot0} & \color{red}{3\cdot0} + \color{blue}{2\cdot0} + \color{green}{1\cdot1} \end{pmatrix}=$
$=\begin{pmatrix} 1 & 4 & 3\\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}{1} & \color{blue}{0} & \color{green}{0} \\ \color{red}{0} & \color{blue}{1} & \color{green}{0}\\ \color{red}{0} & \color{blue}{0} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{4} & \color{red}{3} \\ \color{blue}{2} & \color{blue}{1} & \color{blue}{5} \\ \color{green}{3} & \color{green}{2} & \color{green}{1} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot1} + \color{blue}{0\cdot2} + \color{green}{0\cdot2} & \color{red}{1\cdot4} + \color{blue}{0\cdot1} + \color{green}{0\cdot2} & \color{red}{1\cdot3} + \color{blue}{0\cdot5} + \color{green}{0\cdot1} \\ \color{red}{0\cdot1} + \color{blue}{1\cdot2} + \color{green}{0\cdot3} & \color{red}{0\cdot4} + \color{blue}{1\cdot1} + \color{green}{0\cdot2} & \color{red}{0\cdot3} + \color{blue}{1\cdot5} + \color{green}{0\cdot1}\\ \color{red}{0\cdot1} + \color{blue}{0\cdot2} + \color{green}{1\cdot3} & \color{red}{0\cdot4} + \color{blue}{0\cdot1} + \color{green}{1\cdot2} & \color{red}{0\cdot3} + \color{blue}{0\cdot5} + \color{green}{1\cdot1} \end{pmatrix} =$
$=\begin{pmatrix} 1 & 4 & 3\\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix}$
Опять-таки $A \cdot I_{3} = I_{3} \cdot A = A$.
Примечание:
В общем случае умножение матриц некоммуникативно.
$A\cdot I_{n} = I_{n} \cdot A = A$ для любой матрицы A, имеющей n столбцов.
Как делить матрицы
2 методика:Деление матрицы на числоДеление матрицы на матрицу
Матрицы — это векторные математические объекты, содержащие 2 или более скалярных элемента. Матрицы используются для нахождения многих неизвестных в системах скалярных уравнений, и для операций с большими массивами чисел. Как и со скалярными величинами (например, числами 1, 2, 3, 4), с векторами можно производить математические вычисления, такие как сложение, вычитание и умножение. Однако матрицы нельзя непосредственно разделить одну на другую. Для деления матриц необходимо произвести действие, состоящее из двух этапов. Вначале определяется матрица, обратная делителю (знаменателю). Затем на эту матрицу умножается та, которую делят, или матрица-числитель. Такой метод позволяет получить искомый результат, не производя деление непосредственно. В этой статье рассказывается, как делить матрицы.
Шаги
Метод 1 из 2: Деление матрицы на число
1 Поделите матрицу на скалярную величину. Хотя деление матрицы на другую матрицу не определено строго, матрицу всегда можно разделить на скалярную величину. Такое деление заключается в делении каждого элемента матрицы на данное число.
Метод 2 из 2: Деление матрицы на матрицу
1 Определите матрицу, обратную матрице-знаменателю. Методы нахождения обратных матриц и других действий с матрицами можно найти в учебниках и справочниках по математике.
Вычислите детерминант матрицы-знаменателя. Процедура нахождения детерминанта матрицы описана в математических учебниках. Цель данного шага заключается в том, чтобы определить, отличен ли детерминант матрицы от нуля. Если детерминант матрицы-делителя равен нулю, это означает, что данная матрица необратима, то есть для нее не существует обратной матрицы.
В этом случае прекратите дальнейшие действия. Если матрица, обратная матрице-делителю не существует, дальше можно не продолжать. Такая ситуация подобна делению на ноль, не допустимому для скалярных величин.
Если детерминант не равен нулю, найдите матрицу, обратную матрице-знаменателю. Наиболее распространенные способы нахождения обратной матрицы — метод Гаусса-Жордана и процедура нахождения матрицы алгебраических дополнений.
Проверьте, правильно ли вы нашли обратную матрицу. Умножьте обратную матрицу на пряму, в результате вы должны получить единичную матрицу. Единичная матрица — это такая, все элементы которой равны нулю, кроме диагональных, которые равны единице.
2 Умножьте матрицу-числитель на обратную знаменателю матрицу. Учтите, что, в отличие от умножения скалярных величин, в данном случае порядок множителей имеет значение. При умножении чисел 2, умноженное на 4 дает тот же результат, что и 4, умноженное на 2. В векторной математике умножение матрицы-числителя на обратную знаменателю матрицу дает результат, отличный от того, если бы обратная матрица была помножена на матрицу-числитель.
3 Заметьте, что результат умножения матриц соответствует искомому. Матрица, не определенная строго в матричной алгебре, вычисляется путем нахождения обратной матрицы и умножения на нее делимой матрицы.
Нахождение обратной матрицы
Матрица Инверсия:
Нахождение обратной матрицы (стр. 1 из 2)
Для матриц есть нет такого понятия, как разделение. Можете добавить, вычесть и умножить матрицы, но их нельзя разделить.Однако есть и связанная с этим концепция: что называется «инверсия». Сначала я расскажу, почему инверсия полезно, а затем я покажу вам, как сделать это.
Вспомните, когда вы впервые узнал о том, как решить линейные уравнения. Если бы вам дали что-то вроде “3 x = 6 “, вы бы решите, разделив обе стороны на 3. Поскольку умножение на 1/3 это то же самое, что и разделение на 3, вы также можете умножить обе стороны на 1/3 чтобы получить тот же ответ: х = 2.Если вам нужно было решить что-то вроде “(3/2) x = 6 “, вы могли бы все равно разделите обе стороны на 3/2, но, вероятно, было легче умножить обе стороны на 2/3. Обратная дробь 2/3 – это обратное 3/2 потому что, если умножить две дроби, вы получите 1, которая в данном контексте называется «(мультипликативной) идентичностью»: 1 называется тождеством, потому что умножение чего-либо на 1 не меняет своего значения.
Эта терминология и эти факты очень важны для матриц. Если вам дано матричное уравнение как AX = C , где вы даны А и C и им предлагается вычислить X , вы хотите «поделить» матрицу А . Но нельзя делать деление с помощью матриц.С другой стороны, что если вы можно было найти инверсию A , что-то похожее на нахождение обратной дроби выше? Обратный из А , г. записывается как “ A ¹” и произносится как “ A ” обратный », позволит вам отменить A из матричного уравнения, а затем решите относительно X .
Как появился “ A ¹ AX ” в левой части уравнения превратиться в “ X “? Вспомните природу обратных чисел для обычных чисел.Если у тебя есть число (например, 3/2) и его обратная (в данном случае 2/3) и вы их умножаете, вы получаете 1. И 1 это тождество, так называемое, потому что 1 x = x для любого числа х . То же самое и с матрицами. Если вы умножите матрицу (например, А ) и его обратное (в данном случае
A ¹), вы получаете личность матрица I . А суть единичной матрицы в том, что IX = X для любой матрицы Х (имеется в виду, конечно, «любая матрица правильного размера»).
Следует отметить, что порядок умножения приведенное выше важно и вовсе не произвольно. Напомним, что для матриц умножение не коммутативно. То есть AB почти никогда не равно BA .Таким образом, умножая матричное уравнение «слева» (чтобы получить A ¹ AX ) это совсем не то же самое, что умножение «справа» (чтобы получить AXA ¹). И нельзя сказать, что продукт AXA ¹ равен A ¹ AX , потому что вы не можете изменить порядок умножения. Вместо, надо умножить A ¹ слева, поставив рядом с A в исходном матричном уравнении.И так как вы должны делать то же самое к обеим сторонам уравнения, когда вы решаете, вы должны умножить на “слева” и в правой части уравнения, в результате получается A ¹ C . Вы не можете быть случайным с размещением матриц; Ты должен быть точный, правильный и последовательный. Это единственный способ успешно отменить A и решим матричное уравнение.
Как вы видели выше, обратные матрицы могут быть очень полезны для решения матрицы уравнения. Но, учитывая матрицу, как вы ее инвертируете? Как ты находишь обратное? Техника инвертирования матриц довольно хитрая. Для заданная матрица A и его обратная A ¹, мы знаем, что у нас есть A ¹ A = I . Собирались использовать единичную матрицу I в процесс инвертирования матрицы.
Найти обратное следующая матрица.
Сначала я записываю записи в матрицу A , но я пишу их в матрице двойной ширины:
В другой половине двойной ширины, пишу единичную матрицу:
Сейчас сделаю матрицу строковые операции чтобы преобразовать левую часть двойной ширины в тождество. (Как всегда с операциями со строками, не существует единственного “правильного” способа сделать это. Ниже приведены лишь шаги, которые произошли с мне. Ваши расчеты легко могут выглядеть совершенно иначе.)
Теперь, когда левый сторона двойной ширины содержит тождество, правая часть содержит обратное. То есть обратная матрица следующая:
Обратите внимание, что мы можем подтвердить что эта матрица является инверсией A умножив две матрицы и убедившись, что мы получили тождество: Авторские права Элизабет Stapel 2003-2011 Все права защищены
Обратите внимание, что в “реальном жизнь », инверсия редко бывает матрицей, заполненной красивыми аккуратными целыми такие числа.Если повезет, особенно если вы делаете обратное от руки вам дадут вот такие милые дела.
Верх | 1 | 2 | Возвращение к указателю След. >>
Цитируйте эту статью как:
Стапель, Елизавета. «Обращение матрицы: поиск обратной матрицы.« Purplemath . Доступно по номеру
https://www.purplemath.com/modules/mtrxinvr.htm . Доступ [Дата] [Месяц] 2016 г.
матрицы – Как я могу разделить на матрицу?
Для матрицы $$ A = \ begin {bmatrix} d & e & f \\ g & h & i \\ j & k & l \ end {bmatrix} $$
и вектор $ y = \ begin {bmatrix} a \\ b \\ c \ end {bmatrix} $
продукт $ y \ cdot A $ равен , а не .
Продукт $ A \ cdot y $, с другой стороны, определяется
$$ Ay = \ begin {bmatrix} ad + be + cf \\ ag + bh + ci \\ aj + bk + al \ end {bmatrix} $$
Но ваш вопрос, как разделить по матрице, и ответ: это сложно. В общем, деление на матрицу не очень хорошо определено и обычно не упоминается как деление на матрицу.
Во-первых, давайте посмотрим на деление в действительных числах. Что на самом деле означает $ x = \ frac {a} b $ ? $ x = \ frac ab $ на самом деле означает, что $ x $ – единственное решение уравнения
$$ bx = a $$
Например, $ \ frac12 $ – это число, которое мы должны умножить на $ 2 $, чтобы получить результат $ 1 $.
Точно так же, когда вы хотите спросить: «Сколько $ y $ делится на $ A $», вы действительно спрашиваете
Какой вектор $ x $ мне нужно умножить на $ A $, чтобы получить $ y $?
Или, другими словами, вы решаете уравнение $$ Ax = y $$ и вы хотите решить его за $ x $.
Теперь вы столкнулись с проблемой.
Что, если все элементы $ A $ равны $ 0 $, но не все $ y $ равны нулю? Тогда очевидно, что любой вектор $ x $, умноженный на $ A $, будет равен $ 0 $, так что не существует решения для $ Ax = y $.
Что, если все элементы $ A $ и $ y $ оба равны нулю? Тогда любой вектор $ x $ будет решением $ Ax = y $.
Эти две задачи аналогичны задаче деления на $ 0 $ в действительных числах: уравнение $ 0 \ cdot x = 1 $ не имеет решений, а $ 0 \ cdot x = 0 $ имеет бесконечно много решений.
Однако становится еще хуже. Матрица
$$ A = \ begin {bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \ end {bmatrix} $$
также вызывает проблемы, поскольку $$ A \ cdot \ begin {bmatrix} a \\ b \\ c \ end {bmatrix} = \ begin {bmatrix} a \\ a \\ a \ end {bmatrix} $$
независимо от того, что такое $ b, c $.{-1} $.
Однако вообще не стоит думать о делении матриц. Причина в том, что единственная причина существования матриц – это представление линейного преобразования и упрощение вычислений, связанных с линейным преобразованием (иногда).
Линейное преобразование – это функция $ T: V \ to W $ между векторными пространствами, удовлетворяющая некоторым свойствам. В частности, линейным преобразованиям $ T: V \ to V $, где размерность $ V $ равна $ n $, соответствует матрица (на самом деле много матриц), представляющая $ T $.Хотя матрица – это просто блок чисел, может возникнуть соблазн рассмотреть деление, но для линейного преобразования $ T: V \ to V $ это не так. Имеет смысл спросить, где могут быть добавлены два линейных преобразования $ T, S: V \ to V $ (и это будет соответствовать сложению матриц), а также имеет смысл поговорить о композиции $ T \ circ S $ ( который будет соответствовать умножению матриц (и объясняет, почему умножение матриц определено именно так)). Имеет смысл спросить, является ли $ T: V \ to V $ обратимым (и это будет соответствовать обратной матрице, о которой я упоминал выше).
Не знаю, видели вы уже линейные преобразования или нет. Очень часто предпочтительнее (ошибочно) вводить матрицы перед введением линейных преобразований. Причина, по которой это предпочтительнее, заключается в том, что матрица – это просто блок чисел, поэтому это легко. Причина, по которой это неправильно, заключается в том, что у математика нет абсолютно никаких причин просыпаться утром и просто говорить: «Эй, было бы здорово иметь блоки чисел, складывать их таким образом, умножать их таким образом и» играть с этими вещами ».Он изображает неправильное представление о том, что такое математика. Причина рассмотрения матриц – изучение линейных преобразований. Вопросы, которые вы должны задать о матрицах, должны быть связаны с линейными преобразованиями. Вот почему в математике мы не изучаем, например, треугольные блоки чисел или пятиугольные блоки чисел. Они ничего не представляют (мы знаем).
Матрицы – умножение, деление, сложение и вычитание
Умножение
Умножение

Дивизион

Матрица – это массив чисел, в котором есть строки и столбцы, показывающие размер или размеры матриц.
Умножить матрицу всего на одно число очень просто –
Расчеты производятся по следующей формуле –
Все мы знаем, что число 2 в этом условии – скаляр, поэтому оно известно как скалярное умножение.
Умножение матрицы на другую матрицу
Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это означает? Теперь давайте посмотрим на пример этого для выработки ответа или решения для строки 1 ^st и столбца 1 ^st.
Скалярное произведение – это умножение совпадающих элементов с последующим суммированием –
(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48
Мы должны сопоставить 1 элементов, которые равны 1 и 7, затем умножить их на 2 ^и элементов, таких как 2 и 9, и 3 ^rd элементов, которые равны 3 и 10, а затем, наконец, просуммировать это. все до.
Хотите решить другой пример? Тогда вот это для 1-го ряда и 2-го столбца –
(2, 3, 4).(7, 8, 9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74
Теперь мы можем сделать то же самое для строки 2 ^и и 1-го столбца –
(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12
А потом для 2 ^{ой строки} и 2 столбца –
(3, 1, 2). (1, 2, 3) = 3 * 1 +1 * 2 + 2 * 3 = 3 + 2 + 6 = 11
Тогда наконец-то мы получили результат.
Надеюсь, вы теперь ясно понимаете метод и решения?
Дивизия
А что такое деление? На самом деле мы не делим матрицы, как мы это делаем.
X / Y = X * (1 / Y) = X * B ^-1
Где, B инверсия означает инверсию матрицы B., поэтому здесь нам не нужно ее делить, мы умножаем ее на инверсию матрицы. Есть несколько специальных способов найти инверсию матрицы.
Для обратной матрицы вам необходимо записать матрицу и отождествить матрицу рядом, а также выполнить некоторые операции со строками, чтобы сделать матрицу B отождествляемой с матрицей. Выполняя операции со строками, B станет затем единичной матрицей, а фактическая единичная матрица станет обратной по отношению к матрице B, поскольку все операции будут выполняться в единичной матрице.
После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.
Сложение и вычитание

Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют равные размеры. Для добавления двух матриц просто сложите записи и получите сумму вместо полученной матрицы.
Давайте решим некоторые из примеров и разберемся с этим подробно –
Пример – 1
[1 2] + [2-3]
Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем их сложить.
[1 2] + [2-3]
= [1 + 2 2 + (- 3)]
= [3 -1]
Вычитание – это также очень простая процедура с матрицами. Давайте рассмотрим несколько примеров, чтобы иметь о них четкое представление.
Пример – 2
[4 5] – [2 1]
Сначала четко посмотрите, что обе матрицы имеют одинаковую размерность, а затем начните вычитание –
[4 5] – [2 1]
= [4-2 5-1]
= [2 4]
Добавить матрицу очень просто, и это делается для каждой записи.
Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:
Добавьте указанные ниже матрицы
Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.
Итак, окончательный ответ –
До сих пор вы научились складывать две вещи в матрицы, такие как переменные, числа, уравнения и многое другое. Но сложение не всегда работает с матрицами.
Оцените задачу, указанную ниже, или, если это невозможно, укажите причину.
Хотя матрицы добавляются с каждой записью, нам нужно добавить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7, которые не имеют прямые числа в другой матрице? Итак, ответ –
Эти матрицы нельзя добавить, так как они имеют разные размеры и размеры.
Это всегда имеет место при добавлении матриц, вам нужны обе матрицы одинаковых размеров.Если они не равны по размеру, то сложение не применяется. Он не создает никакой математической логики для сложения неравных матриц.
Вычитание также работает с каждой записью и с одинаковыми условиями. Матричное вычитание, как и сложение, невозможно выполнить, если матрицы не одинакового размера или размеров. Это справедливо как для сложения, так и для вычитания матриц.
Найдите значения x и y для следующих уравнений –
Во-первых, нужно легко оценить левую часть со стороны и входа –
Таким образом, при равенстве матрицы работает с элементами записи, мы сравниваем эти элементы для создания простых уравнений, которые мы можем решить.В таких случаях
X + 6 = 7 и 2y -3 = -5
X = 7-6
X = 1
и
2y – 3 = -5
Y = -5 + 3/2
Y = -2/2
Y = -1
Матрица R
Матрица в R
В программировании на R матрица представляет собой объект с элементами, расположенными в виде двухмерного массива, например таблицы. Матрица R может содержать элементы только одного и того же атомарного типа.
В аналитике или обработке данных мы в основном используем Matrix с числовым типом данных.Таким образом, было бы полезно иметь практический опыт работы с матрицами.
В этом руководстве мы рассмотрим учебные пособия, которые помогут создавать и обрабатывать матрицы в программировании на R.
R Matrix Tutorials
R Matrix – Access Elements
Вы можете получить доступ к элементам матрицы R, используя столбец и индекс строки элемента.
MatrixName [row_index, column_index]
Давайте выберем элемент в row = 3 и column = 2.
> M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M1 [3,2] [1] 7
Если индекс строки не упоминается, а индекс столбца упоминается, возвращается весь столбец.
> M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M1 [, 2] [1] 5 6 7 8
M1 [, 2] выбирает второй столбец матрицы M1 .
Если указан индекс строки, а индекс столбца не указан, возвращается вся строка.
> M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M1 [3,] [1] 3 7 11
M1 [3,] выбирает третью строку матрицы M1 .
Добавление матрицы R
В R мы можем добавить две матрицы. Чтобы сложить две матрицы, используйте оператор сложения (+). Результатом является матрица с суммой двух операндов Matrix.
При сложении двух матриц размер двух матриц, т.е. количество строк и столбцов, должно быть одинаковым.
> M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M2 [, 1] [, 2] [, 3] [1,] 5 9 13 [2,] 6 10 14 [3,] 7 11 15 [4,] 8 12 16 > M3 = M1 + M2 > M3 [, 1] [, 2] [, 3] [1,] 6 14 22 [2,] 8 16 24 [3,] 10 18 26 [4,] 12 20 28
R Вычитание матрицы
В R мы можем вычесть матрицу из другой.Чтобы вычесть матрицу, используйте оператор вычитания (-). Результатом является матрица с разницей между первой и второй матрицами.
При вычитании двух матриц размер двух матриц, т.е. количество строк и столбцов, должно быть одинаковым.
> М2 [, 1] [, 2] [, 3] [1,] 5 9 13 [2,] 6 10 14 [3,] 7 11 15 [4,] 8 12 16 > M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M3 = M2 - M1 > M3 [, 1] [, 2] [, 3] [1,] 4 4 4 [2,] 4 4 4 [3,] 4 4 4 [4,] 4 4 4 >
R Умножение матрицы – один к одному
Чтобы умножить элементы матрицы на соответствующие элементы другой матрицы, используйте оператор умножения (*).Умножение происходит только между (i, j) первой матрицы и (i, j) второй матрицы.
> M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M2 [, 1] [, 2] [, 3] [1,] 5 9 13 [2,] 6 10 14 [3,] 7 11 15 [4,] 8 12 16 > M3 = M1 * M2 > M3 [, 1] [, 2] [, 3] [1,] 5 45 117 [2,] 12 60 140 [3,] 21 77 165 [4,] 32 96 192 >
R Деление матрицы
Чтобы разделить элементы матрицы на соответствующие элементы другой матрицы, используйте оператор деления (/).Умножение происходит только между (i, j) первой матрицы и (i, j) второй матрицы.
> M1 [, 1] [, 2] [, 3] [1,] 1 5 9 [2,] 2 6 10 [3,] 3 7 11 [4,] 4 8 12 > M2 [, 1] [, 2] [, 3] [1,] 5 9 13 [2,] 6 10 14 [3,] 7 11 15 [4,] 8 12 16 > M3 = M2 / M1 > M3 [, 1] [, 2] [, 3] [1,] 5,000000 1,800000 1,444444 [2,] 3.000000 1.666667 1.400000 [3,] 2,333333 1,571429 1,363636 [4,] 2.000000 1.500000 1.333333 >
Заключение
В этом руководстве по R мы узнали о матрицах R: как инициализировать матрицу R, как получить доступ и выполнять арифметические операции с матрицами R.
Матрица «деление»
Тема: Линейная алгебра
Имя: Hoda
Кто спрашивает: Студент
Уровень: Все
Вопрос:
У меня вопрос об умножении матриц; ну собственно матричное деление.Я предполагаю, что матрицы делятся так же, как умножаются; то есть строка за столбцом. Но что произойдет, если вам придется разделить на ноль? Как это повлияет на итоговую матрицу?
В частности, проблема, о которой я говорю:
Чтобы решить для A, вы разделите правую матрицу на матрицу слева.
Я придумываю следующее:
Что мне делать с этим 6/0?
Привет Хода,
К сожалению, операция “деления” матрицы, которую вы определили, работает не так, как вы хотите.
Сравните свою проблему с проблемой с числами:
6x = 3 Чтобы найти x = 1/2, вы можете разделить обе стороны на 6 или умножьте обе части на (1/6). Если вы сделаете последнее, вы получите (1/6) (6) x = (1/6) (3). Обратите внимание, что (1/6) (6) = 1, и 1, умноженное на x, равно x. Следовательно, мы имеем х = (1/6) (3) = 1/2
Смысл этого очень простого примера – проиллюстрировать ту же технику для матрицы. При матричном умножении единичная матрица I превосходит 1, поскольку для любой матрицы A 2 на 2 I x A = A.
Обратите внимание, что если мы умножим
матрицей в левой части уравнения,
получаем
единичная матрица I
по сравнению с
(1/6) (6) = 1
Следовательно, ваша система умножает обе стороны на матрицу выше. Ты получить:
что сводится к вашему ответу:
Для получения дополнительной информации о таких инверсных матрицах и о том, как их найти (выглядит как мы “вытащили это из шляпы”) обратитесь к тексту по линейной алгебре.
Надеюсь, это даст вам начало,
Патрик и Пенни
Перейти в Центр математики
Разделить каждую строку матрицы и кадра данных вектором в R (2 примера)
В этом руководстве объясняется, как разделить строки матрицы данных на элементы вектора в R.
Учебник будет содержать следующую информацию:
Начнем прямо сейчас.
Пример 1. Разделение каждой строки матрицы на элементы вектора
В этом примере показано, как разделить каждую строку матрицы на элементы векторного объекта на языке программирования R.
Во-первых, мы должны создать примерную матрицу в R:
mat <- matrix (1:20, ncol = 4) # Создать пример матрицы mat # Распечатать пример матрицы
mat <- matrix (1:20, ncol = 4) # Создать пример матрицы mat # Пример печати матрицы
Выходные данные предыдущего программного кода R показаны в таблице 1. Мы создали числовую матрицу с пятью строками и четырьмя столбцами.
Далее нам нужно создать векторный объект:
vec <- c (5, 1, 8, 3) # Создать пример вектора vec # Распечатать пример вектора # [1] 5 1 8 3
vec <- c (5, 1, 8, 3) # Создать пример вектора vec # Распечатать пример вектора # [1] 5 1 8 3
Наш вектор содержит четыре числовых элемента, т.е.е. такой же длины, как и количество столбцов нашей матрицы.
Теперь мы можем использовать функцию t () (t означает транспонирование) и оператор /, чтобы разделить каждую строку нашей матрицы на элементы нашего вектора:
mat_div <- t (t (mat) / vec) # Разделить строки матрицы на вектор mat_div # Вывести разделенную матрицу
mat_div <- t (t (mat) / vec) # Разделить строки матрицы на вектор mat_div # Вывести разделенную матрицу
Выполнив предыдущий синтаксис, мы создали Таблицу 2, т.е.е. новый объект матрицы, содержащий результаты делений.
Пример 2: Разделение каждой строки фрейма данных на элементы вектора
В примере 2 я объясню, как выполнить математическое деление каждой строки фрейма данных на элементы вектора.
Для этого мы можем преобразовать нашу матрицу, созданную в примере 1, в класс data.frame с помощью функции as.data.frame.
data <- as.data.frame (mat) # Создать пример кадра данных data # Напечатать пример кадра данных
data <- as.data.frame (mat) # Создать пример фрейма данных data # Пример печати кадра данных
В таблице 3 показано, что мы создали фрейм данных, содержащий те же значения, что и матрица нашего примера, которую мы использовали в примере 1.
Теперь мы можем использовать в основном тот же код, что и в примере 1, чтобы разделить каждую строку нашего фрейма данных на вектор. Единственная разница в том, что мы используем as.data.frame еще раз, чтобы также вернуть результаты в объекте фрейма данных.
Взгляните на следующий код R и его результат:
data_div <- as.data.frame (t (t (data) / vec)) # Разделить строки кадра данных на вектор data_div # Распечатать разделенный кадр данных
data_div <- as.data.frame (t (t (data) / vec)) # Разделить строки кадра данных на вектор data_div # Распечатать разделенный фрейм данных
Выходные данные предыдущего синтаксиса программирования R показаны в Таблице 4: Фрейм данных, содержащий результаты нашего матричного / векторного деления.
Видео и другие ресурсы
Вам нужны дополнительные пояснения по содержанию этого руководства? Тогда вы можете посмотреть следующее видео с моего канала на YouTube. Я объясняю программные коды R этого руководства в видео:
Видео на YouTube скоро будет добавлено.
Кроме того, вы можете ознакомиться с некоторыми из соответствующих руководств на моем веб-сайте. Я уже выпустил несколько статей о матричных вычислениях.
Резюме: На этом этапе вы должны знать, как использовать функцию t () для деления строк на вектор в R. Если у вас есть дополнительные вопросы, дайте мне знать в разделе комментариев.
/ * Добавьте свои собственные переопределения стиля формы MailChimp в таблицу стилей вашего сайта или в этот блок стилей.
Мы рекомендуем переместить этот блок и предыдущую ссылку CSS в HEAD вашего HTML-файла. * /
]]> .