Дифференциал что это математика: Дифференциал и его применение | Творческие проекты и работы учащихся - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Дифференциал – это… Что такое Дифференциал?

в математике, главная линейная часть приращения функции. Если функция y = f (x) одного переменного х имеет при х = х₀ производную, то приращение

Δy = f (x₀ + Δx) – f (x₀)

функции f (x) можно представить в виде

Δy = f’ (x₀) Δx + R,

где член R бесконечно мал по сравнению с Δх. Первый член

dy = f’ (x₀) Δх

в этом разложении и называется дифференциалом функции f (x) в точке x₀. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Δx, а равенство

Δy = dy + R

показывает, в каком смысле Д.

dy является главной частью приращения Δy.

Обобщение понятия дифференциала. Обобщение понятия Д. на вектор-функции, начало которому положили в начале 20 в. французские математики Р. Гато и М. Фреше, позволяет лучше выяснить смысл понятия «дифференциал» для функций нескольких переменных, а в применении к Функционалам приводит к понятию вариации, лежащему в основе вариационного исчисления (См. Вариационное исчисление).

Важную роль в этом обобщении играет понятие линейной функции (линейного отображения). Функция L

(x) векторного аргумента х называется линейной, если она непрерывна и удовлетворяет равенству

L (x’ + х “) = L (x’) + L (x “)

для любых х’ и х “ из области определения. Линейная функция n-мерного аргумента х = {x₁,…, x_n} всегда имеет вид

L (x) = a₁x₁ +. .. + a_nx_n,

где a₁,…, a_n — постоянные. Приращение

ΔL = L (x + h) – L (x)

линейной функции L (x) имеет вид

ΔL = L (h),

т. е. зависит только от векторного приращения h, и притом линейно. Функция f (x) называется дифференцируемой при значении аргумента х, если её приращение Δf = f (x + h) – f (x), рассматриваемое как функция от h, имеет главную линейную часть L (h), т. е. выражается в виде

Δf = L (h) + R (h

где остаток R (h) при h → 0 бесконечно мал по сравнению с h. Главная линейная часть L (h) приращения Δf и называется дифференциалом df функции f в точке x. При этом в зависимости от того, в каком смысле понимается бесконечная малость R (h) по сравнению с h, различают слабый дифференциал, или дифференциал Гато, и сильный дифференциал, или дифференциал Фреше. Если существует сильный Д., то существует и слабый Д., равный сильному Д. Слабый Д. может существовать и тогда, когда сильный не существует.

В случае f (x) ≡ x из общего определения следует, что df = h, т. е. можно приращение h считать Д. аргумента x и обозначать dx.

Если сделать теперь переменной точку x, в которой определяется Д. df, то он будет функцией двух переменных:

df (x; h).

Далее, считая h = h₁ постоянным, можно найти Д. от дифференциала df (x; h₁) как главную часть приращения

df (x + h₂; h₁) — df (x; h

1),

где h₂ — некоторое второе, не связанное с h₁ приращение x. Получаемый таким образом второй дифференциал d²f = d²f (x; h₁, h₂) является функцией трёх векторных аргументов x, h₁ и h₂, линейной по каждому из двух последних аргументов. Если d²f непрерывно зависит от x, то он симметричен относительно h₁ и h₂:

d²f (x

; h₁, h₂) = d²f (x; h₂, h₁).

Аналогично определяется дифференциал dⁿf = dⁿf (x; h₁,…, h_n) любого порядка n.

В вариационном исчислении сам векторный аргумент x является функцией x (t), а дифференциалы df и d²f функционала f [x (t)] называются его первой и второй вариациями и обозначаются δf и δ²f.

Всюду выше речь шла об обобщении понятия Д. на числовые функции векторного аргумента. Существует обобщение понятия Д. и на случай вектор-функций, принимающих значения в банаховых пространствах.

Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 2 изд., М., 1967; Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 2 изд., М., 1968; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970; Рудин У., Основы математического анализа, пер. с англ., М., 1966; Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964.

А. Н. Колмогоров.

Дифференциал и производная | Математика, которая мне нравится

Определение. Пусть функция задана на множестве , . Производная функции в точке есть

Доказательство равносильности двух определений.

Рассмотрим разность

Функция задана и

Если произвольным образом задать значение функции при , то последнее равенство будет выполняться и при .

Определение. Пусть , . Функция называется дифференцируемой в точке , если существует такое число и такая функция , что имеет место равенство

Функция, которая каждому числу ставит в соответствие число , называется дифференциалом функции в точке .

Мы доказали, что если у функции есть производная в точке , то дифференцируема в этой точке (за число можно взять число ).

Докажем, что если функция дифференцируема в точке , то у нее есть производная в точке .

Попутно мы доказали, что число в правой части равенства определяется однозначно и равно .

Обозначение.

— дифференциал функции в точке .

Дифференциал — линейная функция приращения :

Пример.

— обозначение дифференциала тождественной функции

Обозначения.

Задачи. 1) Вычислите приращения для данных функций и данной точки , постройте соответствующие графики функций , постройте графики функций , найдите , если он существует.

а) ;

б) ;

в) ;

г) .

2) Для данных функций и данной точки вычислите производную

составьте выражение

и докажите, что , найдите .

а) ;

б) .

3) Выясните, для каких из данных функций найдется такое число , что при всех функция (при ) может быть представлена в виде , где

а) , б) .

1. ;

2. ;

4) Найдите дифференциал функции и с его помощью приближенно вычислите значение данной функции в точке .

5) Приведите примеры функций, имеющих производные везде, кроме: а) одной точки; б) двух точек; в) трех точек; г) целых чисел.

6) Выясните, имеют ли данные функции производную в точке :

а)

б)

7) Найдите все значения параметров и , такие, что функция

а) непрерывна в ;
б) дифференцируема в .

8 ) Исследуйте функции на дифференцируемость

а) ;
б) ;
в)

Производная и дифференциал

Дифференциальное исчисление – это раздел математики, который исследует свойства функций, которые заданы на интервалах (сплошных множествах), с помощью определения предела функций.

Свойство непрерывности свидетельствует о том, что точке х₀ при малом отклонении аргумента Δx от х₀ функция отклоняется мало. В связи с этим, непрерывную функцию в окрестности точки х₀, приближенно можно заменить константой, значением в х₀. В таком случае, при Δx?0 к нулю стремится абсолютная ошибка приближения. Однако данная аппроксимация не отражает изменения функции при переходе переменной х в точке 0 – убывая или возрастая, медленно или быстро. Для того, чтобы это выяснить и введены производная и дифференциал, которые и дают более точную аппроксимацию функции в окрестности х₀ линейной функцией, а не константой. Производная и дифференциал отражает величину и тенденцию изменения в точке х₀ функции.

Производная и дифференциал на наглядном примере выглядит так. Возьмем функцию y = f ( x), которая имеет действительные значения и задана на оси R. Внутреннюю точку x₀ ε I фиксируем и берем еще любую точку xεI . Приращением независимой переменной в точке х₀ является разность Δx = x – x₀. Предел разностного отношения, при котором х стремится к х0 называется производной функции f (x) в точке х₀.

Функция, для которой возможно разложение, называется дифференцируемой в точке х₀. Дифференциалом функции f в точке х₀ называется слагаемое f’ (х₀)(х-х₀). Таким образом, наличие в точке производной эквивалентно и дифференцируемости в этой же точке.

Дифференциал также имеет и специальное обозначение:

df(x₀)=dy(x₀)= f’ (х₀)(х-х₀)

Создано дифференциальное исчисление одновременно, а также независимо друг от друга Готфиридом Вильгельмом Лейбницем и Исааком Ньютоном.

Производная и дифференциал

Приращение функции y = f(x), соответствующее приращению Δx аргумента x

Δy = f(x + Δx) – f(x)

Определение производной

y’ =

dy
dx

lim
Δx → 0

Δy
Δx

Геометрически y’ = f'(x) – угловой коэффициент касательной
к графику функции y = f(x) в точке с абсциссой x

Правила дифференцирования

c’ = 0
(cu)’ = cu’
(u + v)’ = u’ + v’
(u – v)’ = u’ – v’
(uv)’ = u’v + uv’

где y = f(z) и z = φ(x), т.

е y = f(φ(x)).

где x

‘
y

– производная обратной функции

Производные элементарных функций

)’ = nx

n – 1

, x’ = 1

(log

x)’ =

1
xln(a)

(sinx)’ = cosx

(cosx)’ = – sinx

(secx)’ = secx * tgx

(cosecx)’ = -cosecx * ctgx

Свойства дифференциала

d(af(x)) = a * df(x)

d(f

(x) + f

(x) – f

(x)) = df

(x) + df

(x) – df

(x)

df(x) = f'(x)dx

da = 0 (a = const)

d(ax + b) = Δ(ax + b) = a Δx

Дифференциал второго порядка функции y = f(x),

где x – независимая переменная (d

x = 0)

Производные высших порядков некоторых функций

)

(n)

= m(m – 1)(m – 2).

..(m – n + 1)x

m – n

(ln(x))

(n)

= (-1)

n – 1

(n – 1)

(log

(n)

= (-1)

n – 1

(n – 1)!
ln(a)

)

(n)

= ln(a)

)

(n)

= (k * ln(a))

(sinx)

(n)

= sin(x +

nπ
2

)

(cosx)

(n)

= cos(x +

nπ
2

)

Правило Лопиталя для неопределенностей вида

0
0

или

∞
∞

lim
x → a

φ(x)
ψ(x)

lim
x → a

φ'(x)
ψ'(x)

если правый предел существует

Формула Тэйлора с остаточным членом в форме Лагранжа

f(x) = f(x

) +

(x – x

) +

(x – x

)

+ .

… +

(x – x

)

(x – x

)

n + 1

где ξ – такое число, что x

Формула Маклорена

f(x) = f(0) +

x +

+ …

где ξ – такое число, что 0

Дифференциал


	Главная > Учебные материалы > Математика: Дифференциал


	1. Понятие дифференциала. 2.Свойства дифференциала. 3.Дифференциал сложной функции. 4.Приближенные вычисления с помощью дифференциала.

	9 10 11 12 13 14 15 16 17


	1.Понятие дифференциала. Допустим функция y=f(x) определена на промежутке Х и дифференцируема в некоторой окресности точки xϵX, т.е. существует производная y’. Согласно теореме о связи бесконечно малых величин с пределами функции запишем:
	из рисунка 1 видно, что угол β равен сумме двух углов: ϕ и γ. tg ϕ = f'(x) в точке М, tg β – tg ϕ = а(∆x) представляет собой бесконечно малую величину, зависящую от ∆x. ∆y/∆x = f'(x) + а(∆x) где а(∆x) – бесконечно малая величина при ∆х →0, откуда ∆y = f'(x)∆x + а(∆x)∆x из формулы можно увидеть, что приращение функции ∆y состоит из двух слагаемых: линейного относительно ∆x и нелинейного. Таким образом, дифференциалом функции называется главная, линейная часть приращения функции относительно ∆x, равная произведению производной на приращение независимой переменной. dy =f'(x) ∆x или dy = f'(x) dx
	2. Геометрический смысл дифференциала. Допустим задана функция y = f(x). Возьмем произвольную точку М(x,y). Дадим переменной x приращение ∆x. Тогда функция получит приращение ∆y = f(x+∆x) – f(x). (см.рис. 1). Проведем касательную к кривой y = f(x) в точке М, которая образует угол ϕ с положительным направлением оси Ох, т.е f'(x) = tg ϕ. Из прямоугольного треугольника МAB AB = MB · tg ϕ = ∆x tg ϕ = f’ (x)∆x т.е. dy = AB. Можно сказать что, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда х получает приращение ∆x.		Рис 1. Геометрический смысл дифференциала.

	3.Свойства дифференциала. Дифференциал имеет следующие свойства. 1. dc=0 2. d(cu)= c du 3. d(u+v)=du+dv 4. d(uv)=v du + u dv 5. d(u/v) = (v du – u dv) / v²



	3.Дифференциал сложной функции. Дифференциал функции dy = f'(x) dx. Рассмотрим функцию y = f(u), где f(u) является сложной функцией, т.е. y = f(g(x)). Если функции y = f(u) и u = g(x) – дифференцируемые функции от своих аргументов, то производная сложной функции равна: dy = f'(x) dx = f'(u) · u’dx = f'(u) du. т.е. dy = f'(u) du

	4. Приближенные вычисления с помощью дифференциала.

	Из формулы ∆y = f'(x)∆x + а(∆x)∆x можно увидеть, что приращение функции приблизительно равно ее дифференциалу, т.к. величина а(∆x)∆x бесконечно малая. Именно поэтому, при достаточно малых значениях ∆x можно считать, что ∆y≈ dy т.е. f(x+∆x)≈f(x)+f ‘(x)∆x. Данная формула тем точнее, чем меньше значение ∆x. Это приближенное равенство можно применить в приближенных вычислениях.
	Пример:




	9 10 11 12 13 14 15 16 17

Разница между дифференциальным и производным (Математика и статистика)

Чтобы лучше понять разницу между дифференциалом и производной функции, вам нужно сначала понять концепцию функции.

Функция – это одно из основных понятий в математике, которое определяет взаимосвязь между набором входов и набором возможных выходов, где каждый вход связан с одним выходом. Одна переменная является независимой переменной, а другая переменная является зависимой переменной.

Понятие функции – одна из самых недооцененных тем в математике, но она необходима для определения физических отношений. Возьмем, к примеру: утверждение «у есть функция х» означает, что что-то, связанное с у, напрямую связано с х по некоторой формуле. Скажем, если на входе 6 и функция добавить 5 на вход 6. Результат будет 6 + 5 = 11, что является вашим выходом.

Есть несколько исключений в математике, или вы можете сказать, проблемы, которые не могут быть решены с помощью обычных методов геометрии и алгебры. Новая ветвь математики, известная как исчисление, используется для решения этих проблем..

Исчисление принципиально отличается от математики, которая не только использует идеи из геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.

Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других разделов математики. Дифференциал – это подполе исчисления, которое относится к бесконечно малой разнице в некоторой изменяющейся величине и является одним из двух фундаментальных делений исчисления. Другая ветвь называется интегральным исчислением.

Что такое дифференциал?

Дифференциал является одним из основных разделов исчисления наряду с интегральным исчислением. Это подполе исчисления, которое имеет дело с бесконечно малым изменением в некоторой изменяющейся величине. Мир, в котором мы живем, полон взаимосвязанных величин, которые периодически меняются.

Например, площадь круглого тела, которое изменяется по мере изменения радиуса, или снаряда, который изменяется со скоростью. Эти изменяющиеся объекты в математических терминах называются переменными, и скорость изменения одной переменной по отношению к другой является производной. И уравнение, которое представляет отношения между этими переменными, называется дифференциальным уравнением.

Дифференциальные уравнения – это уравнения, которые содержат неизвестные функции и некоторые их производные.

Что такое производная?

Понятие производной функции является одним из самых мощных понятий в математике. Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.

Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной относительно изменения значения независимой переменной. Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной линии. Он измеряет, насколько крутой график функции находится в некоторой заданной точке на графике..

Проще говоря, производная – это скорость, с которой функция изменяется в определенной точке..

Разница между дифференциальным и производным

Определение дифференциала против.

производный

Термины дифференциальный и производный тесно связаны друг с другом с точки зрения взаимосвязи. В математике изменяющиеся объекты называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.

Уравнения, которые определяют связь между этими переменными и их производными, называются дифференциальными уравнениями. Дифференциация – это процесс поиска производной. Производная функции – это скорость изменения выходного значения по отношению к ее входному значению, тогда как дифференциал – это фактическое изменение функции..

Дифференциальные отношения против. производный

Дифференцирование – это метод вычисления производной, которая представляет собой скорость изменения выхода y функции по отношению к изменению переменной x.

Проще говоря, производная относится к скорости изменения y относительно x, и это соотношение выражается как y = f (x), что означает, что y является функцией от x. Производная функции f (x) определяется как функция, значение которой генерирует наклон функции f (x), где она определена и f (x) является дифференцируемой. Это относится к наклону графика в данной точке.

Представление Дифференциала Vs. производный

Дифференциалы представлены как dИкс, dY, dт, и так далее, где dх представляет небольшое изменение в х, dу представляет небольшое изменение у, и dт небольшое изменение т. При сравнении изменений в связанных величинах, где у – функция х, дифференциал dу можно записать как:

dу = ф^‘(Икс) dИкс

Производная функции является наклоном функции в любой точке и записывается как d/dИкс. Например, производная от sin (x) может быть записана как:

d/dх грех (х) = грех (х)^‘ = cos (x)

Дифференциальный и производный: Сравнительная таблица

Краткое изложение дифференциала производный

В математике скорость изменения одной переменной по отношению к другой переменной называется производной, а уравнения, выражающие взаимосвязь между этими переменными и их производными, называются дифференциальными уравнениями. В двух словах, дифференциальные уравнения включают производные, которые фактически указывают, как величина изменяется по отношению к другой. Решая дифференциальное уравнение, вы получаете формулу для количества, которое не содержит производных. Метод вычисления производной называется дифференцированием. Проще говоря, производная функции – это скорость изменения выходного значения относительно его входного значения, тогда как дифференциал – это фактическое изменение функции..

Решение высшей математики онлайн

‹– Назад

Пусть функция задана в некоторой области , и — внутренняя точка этой области. Пусть — произвольная точка этой же области . Разность называется приращением аргумента ; , где . Разность значений функции называется приращением, или полным приращением функции в точке , соответствующим приращению аргумента ; — это функция от точки и приращения .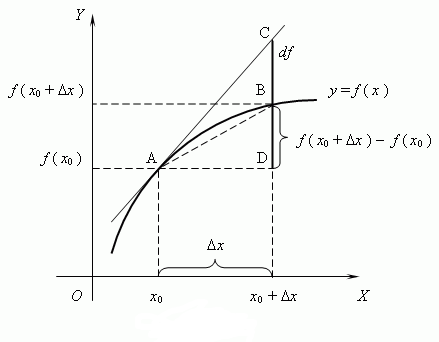

Предположим, что приращение функции можно представить в виде

где — некоторые числа. Подчеркнём, что эти числа не зависят от , но могут измениться, если сменить точку . Относительно величины мы предположим, что это функция, при базе являющаяся величиной большего порядка малости, чем . Это означает, если вспомнить определение бесконечно малой величины большего порядка малости относительно другой бесконечно малой, что Заметим, что сумма всех слагаемых левой части (7.2), кроме последнего, — это линейная функция от приращения аргумента , если точка фиксирована. Условие большей малости последнего слагаемого (7.2) относительно означает, что эта линейная функция — главная часть приращения функции.

Таким образом, приращение дифференцируемой функции можно представить в виде суммы дифференциала , то есть линейной части приращения, и остатка , который имеет более высокий порядок малости, чем приращение :

Теорема 7. 8 Дифференцируемая в точке функция является непрерывной в этой точке.

Доказательство. Действительно, если , то стремятся к 0 все слагаемые дифференциала: они имеют вид ; множитель не зависит от , то есть постоянен, а , поскольку Величина также стремится к 0, так как имеет даже больший порядок малости, чем . Значит, . Но условие как раз и означает, что при , то есть что функция непрерывна в точке .

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Основные правила дифференцирования, применяемые в математике

Для начала стоит вспомнить о том, что такое дифференциал и какой математический смысл он несет.

Дифференциалом функции называется произведение производной функции от аргумента на дифференциал самого аргумента. Математически данное понятие можно записать, как выражение: dy=y’*dx.

В свою очередь, по определению производной функции справедливо равенство y’=lim dx-0(dy/dx), а по определению предела – выражение dy/dx=x’+α, где параметром α является бесконечно малая математическая величина.

Следовательно, обе части выражения стоит умножить на dx, что в итоге дает dy=y’*dx+α*dx, где dx – это бесконечно малое изменение аргумента, (α*dx) – величина, которой можно пренебречь, тогда dy – приращение функции, а (y*dx) – главная часть приращения или дифференциал.

Дифференциалом функции называется произведение производной функции на дифференциал аргумента.

Теперь стоит рассмотреть основные правила дифференцирования, которые довольно часто используют в математическом анализе.

Теорема. Производная суммы равна сумме производных, полученных от слагаемых: (а+с)’=а’+с’.

Аналогичным образом это правило будет действовать и для нахождения производной разности.
Следствием даного правила дифференцирования является утверждение о том, что производная от некоторого числа слагаемых равна сумме производных, полученных от данных слагаемых.

Например, если необходимо найти производную от выражения (а+с-к)’, тогда результатом будет выражение а’+с’-к’.

Теорема. Производная произведения математических функций, дифференцируемых в точке, равна сумме, состоящей из произведения первого множителя на производную второго и произведения второго множителя на производную первого.

Математически теорема будет записана следующим образом: (a*c)’=а*с’+а’*с. Следствием теоремы является вывод о том, что постоянный множитель в производной произведения можно выносить за производную функции.

В виде алгебраического выражение данное правило будет записано следующим образом: (а*с)’=а*с’, где а=const.

Например, если необходимо найти производную выражения (2а3)’, то результатом будет ответ: 2*(а3)’=2*3*а2=6*а2.

Теорема. Производная отношения функций равна отношению между разностью производной числителя, умноженной на знаменатель, и числителя, умноженного на производную знаменателя и квадрата знаменателя.

Математически теорема будет записана следующим образом: (a/c)’=(а’*с-а*с’)/с².

В заключение необходимо рассмотреть правила дифференцирования сложных функций.

Теорема. Пусть задана фукция у=ф(х), где х=с(т), тогда функция у, по отношению к переменной т, называется сложной.

Таким образом, в математическом анализе производная сложной функции трактуется, как производная самой функции, умноженная на производную ее подфункции. Для удобства правила дифференцирования сложных функций представляют в виде таблицы.

f(x)	f^‘(x)
(1/с)’	-(1/с²)*с’
(а^с)’	а^с(ln а)с’
(е^с)’	е^с*с’
(ln с)’	(1/с)*с’
(log a^c)’	1/(сlg a)c’
(sin c)’	cos с*с’
(cos с)’	-sin с*с’

При регулярном использовании данной таблицы производные легко запоминаются. Остальные производные сложных функций можно найти, если применить правила дифференцирования функций, которые были изложены в теоремах и следствиях к ним.

Дифференциал функции

Определение дифференциала функции

Рассмотрим функцию \ (y = f \ left (x \ right), \), которая непрерывна в интервале \ (\ left [{a, b} \ right]. \). Предположим, что в некоторой точке \ ({x_0 } \ in \ left [{a, b} \ right] \) независимая переменная увеличивается на \ (\ Delta x. \) приращение функции \ (\ Delta y \), соответствующее изменению независимой переменной \ (\ Delta x \) дается

\ [\ Delta y = \ Delta f \ left ({{x_0}} \ right) = f \ left ({{x_0} + \ Delta x} \ right) – f \ left ({{x_0}} \ right ).\]

Для любой дифференцируемой функции приращение \ (\ Delta y \) может быть представлено как сумма двух членов:

\ [\ Delta y = A \ Delta x + \ omicron \ left ({\ Delta x} \ right), \]

, где первый член (называемый главной частью приращения) линейно зависит от приращения \ (\ Delta x, \), а второй член имеет более высокий порядок малости по отношению к \ (\ Delta x. \) Выражение \ (A \ Delta x \) называется дифференциалом функции и обозначается \ (dy \) или \ (df \ left ({{x_0}} \ right).2. \)

Обратите внимание, что в этом примере коэффициент \ (A \) равен значению производной от \ (S \) в точке \ ({x_0}: \)

\ [A = 2 {x_0}. \]

Оказывается, для любой дифференцируемой функции справедлива следующая теорема:

Коэффициент \ (A \) в главной части приращения функции в точке \ ({x_0} \) равен значению производной \ (f ‘\ left ({{x_0}} \ right ) \) в этой точке, то есть приращение \ (\ Delta y \) равно

\ [\ Delta y = A \ Delta x + \ omicron \ left ({\ Delta x} \ right) = f ‘\ left ({{x_0}} \ right) \ Delta x + \ omicron \ left ({\ Дельта x} \ вправо).\]

Разделив обе части уравнения на \ (\ Delta x \ ne 0 \), получим

\ [\ frac {{\ Delta y}} {{\ Delta x}} = A + \ frac {{\ omicron \ left ({\ Delta x} \ right)}} {{\ Delta x}} = f ‘\ left ({{x_0}} \ right) + \ frac {{\ omicron \ left ({\ Delta x} \ right)}} {{\ Delta x}}. \]

В пределе как \ (\ Delta x \ to 0 \) получаем значение производной в точке \ ({x_0}: \)

\ [y ‘\ left ({{x_0}} \ right) = \ lim \ limits _ {\ Delta x \ to 0} \ frac {{\ Delta y}} {{\ Delta x}} = A = f’ \ left ({{x_0}} \ right).\]

Здесь мы учли, что для небольшого количества \ (\ omicron \ left ({\ Delta x} \ right) \) более высокого порядка малости, чем \ (\ Delta x, \), предел равен

\ [\ lim \ limits _ {\ Delta x \ to 0} \ frac {{\ omicron \ left ({\ Delta x} \ right)}} {{\ Delta x}} = 0. \]

Предполагая, что дифференциал независимой переменной \ (dx \) равен ее приращению \ (\ Delta x: \)

\ [dx = \ Delta x, \]

получаем из соотношения

\ [dy = A \ Delta x = y’dx \]

, что

\ [y ‘= \ frac {{dy}} {{dx}}, \]

и.е. производная функции может быть представлена как отношение двух дифференциалов.

Геометрическое значение дифференциала функции

На рисунке \ (2 \) схематично показано разделение приращения \ (\ Delta y \) на главную часть \ (A \ Delta x \) (дифференциал функции) и член более высокого порядка малости \ (\ omicron \ left ({\ Delta x} \ right). \)

Рис. 2.
Касательная \ (MN \), проведенная к кривой функции \ (y = f \ left (x \ right) \) в точке \ (M, \), как известно, имеет угол наклона \ (\ alpha, \), касательная к которой равна производной:
\ [\ tan \ alpha = f ‘\ left ({{x_0}} \ right).\]
Когда независимая переменная изменяется на \ (\ Delta x \), тангенс увеличивается на \ (A \ Delta x. \). Это линейное приращение, образованное касательной, является просто дифференциалом функции. Оставшаяся часть полного приращения \ (\ Delta y \) (отрезок \ (N {M_1} \)) соответствует «нелинейной» добавке более высокого порядка малости по отношению к \ (\ Delta x. \)
Свойства дифференциала
Пусть \ (u \) и \ (v \) – функции переменной \ (x \).Дифференциал имеет следующие свойства:

За знаком дифференциала можно вынести константу:
\ [d \ left ({Cu} \ right) = Cdu, \]
где \ (C \) – постоянное число.
Дифференциал суммы (разности) двух функций равен сумме (разности) их дифференциалов:
\ [d \ left ({u \ pm v} \ right) = du \ pm dv. \]
Дифференциал постоянной равен нулю:
\ [d \ left (C \ right) = 0. \]

Дифференциал независимой переменной \ (x \) равен ее приращению:
\ [dx = \ Delta x.{n – 1}} dx, \; \; \; d \ left ({\ ln x} \ right) = \ frac {{dx}} {x}, \; \; \; d \ left ({\ sin x} \ right) = \ cos x dx, \]
и так далее.
Формальная инвариантность дифференциала
Рассмотрим композицию двух функций \ (y = f \ left (u \ right) \) и \ (u = g \ left (x \ right). \) Ее производную можно найти по цепному правилу:
\ [{y’_x} = {y’_u} \ cdot {u’_x}, \]
, где субиндекс обозначает переменную дифференцирования.
Дифференциал “внешней” функции \ (y = f \ left (u \ right) \) можно записать как
\ [dy = {y’_u} \, du.\]
Дифференциал «внутренней» функции \ (u = g \ left (x \ right) \) может быть представлен аналогичным образом:
\ [du = {u’_x} \, dx. \]
Если мы подставим \ (du \) в последнюю формулу, получим
\ [dy = {y’_u} \, du = {y’_u} {u’_x} \, dx. 2}}} = – \ frac {\ pi} { 2}.2} dx. \]
См. Другие проблемы на странице 2.
Дифференциальные уравнения | Математика
Элементарные дифференциальные уравнения с краевыми задачами (Бойс, ДиПрима, Мид, 11-е издание)
Раздел Тема Домашнее задание
2,1 Линейные уравнения; Метод интегрирующих факторов 2c, 4c, 6c, 9, 12, 14 (b, c), 21
2.2 Разделимые дифференциальные уравнения 2, 3, 5, 10 (а, в), 14 (а, в), 18
2,3 Моделирование с помощью дифференциальных уравнений первого порядка 1, 2, 5, 17 (а, б), 18 (а, б)
2,6 Точные уравнения и интегрирующие множители 1, 2, 4, 7, 11, 15, 19, 20 (см. Задачу 17)
3,1 Однородные дифференциальные уравнения с постоянными коэффициентами 3, 6, 10, 13, 15, 17
3. 2 Решения линейных однородных уравнений; Вронскианец 3, 7, 9, 10, 12, 13, 14, 15, 18, 19, 21, 24, 25, 27, 28
3,3 Комплексные корни характеристического уравнения 1, 6, 11, 12, 13, 15, 19
3,4 Повторяющиеся корни; Редукция заказа 1, 2, 6, 10, 13, 19, 20
3,5 Неоднородные уравнения; Метод неопределенных коэффициентов 1, 2, 5, 12, 14
3.6 Изменение параметров 4, 6, 9, 10, 13
3,7 Механические колебания 1, 4, 5, 8, 17, 18 (а, б)
3,8 Принудительные периодические колебания 4, 5, 7, 8
6,1 Определение преобразования Лапласа 1-3, 4 (а, в), 6, 10, 12, 16
6,2 Решение задач начального значения 3, 6, 7, 11, 15, 16, 17
6. 3 Шаговые функции 1, 2, 5, 7, 9, 10, 14, 15, 16, 30
6,4 Дифференциальные уравнения с разрывными вынуждающими функциями 1-4, 9, 11 (а, б)
6,5 Импульсные функции 1, 3, 4, 6, 10 (а, б)
6,6 Интеграл свертки 1 (а), 4, 5, 7, 9, 11, 12
2.7 Численные аппроксимации: метод Эйлера 1,2,4
8,1 Метод Эйлера или касательной линии 4, 5, 8, 22
Плоские системы дифференциальных уравнений (дополнительные примечания)
1 Введение 1,1, 1,2
2 Некоторые понятия из теории матриц и линейной алгебры 2. 1, 2,2 (1,4,6,7,8), 2,3 (1), 2,4 (3), 2,5 (1,2,3)
3 Общая теория линейных систем 2×2 3,1, 3,3, 3,4
4 Случай 1 (однородный, линейный, постоянный коэффициент) 4,1, 4,2, 4,4, 4,5
5 Корпус 2 5,1, 5,2, 5,3
6 Корпус 3 6,1, 6,2, 6,4, 6,5
7 Решения негосударственных систем 2.6 (1,3), 7,1, 7,3, 7,4
8 Качественные методы 8,1, 8,2, 8,3
9 Линеаризация нелинейных систем в изолированных точках покоя (если позволяет время) 9,1, 9,4, 9,5, 9,7
World Web Math: нотация
World Web Math: нотация Предлагаемые пререквесты: Определение производной
Часто самая запутанная вещь для студента, знакомого с дифференциация – это обозначение, связанное с ним. Здесь попытка будет сделано, чтобы ввести как можно больше типов обозначений.
Производная всегда является производной функции относительно к переменной . Когда мы записываем определение производной как
мы имеем в виду производную функции f ( x ) при относительно переменной x .
Один тип обозначение для производных иногда называют простым обозначение . Функция f ´ ( x ), который будет читаться как “ f -prime x ”, означает производная f ( x ) относительно х .Если мы скажем y = f ( x ), то y ´ (читается как “ y -prime ”) = f ´ ( x ). Иногда это даже воспринимается как чтобы писать такие вещи, как, для y = x ⁴ + 3x (например), y ´ = ( x ⁴ + 3 x ) ´.
Производные высшего порядка в простых обозначениях представлен увеличением количества простых чисел. Например, второй производная y относительно x будет записана в качестве
Помимо второй или третьей производной, все эти простые числа становятся беспорядочными, поэтому часто порядок производной вместо этого записывается как римский верхний индекс в скобках, так что девятая производная от f ( x ) относительно x записывается как f ⁽⁹⁾ ( x ) или f ^(ix) ( x ).
Секунда тип записи для производных иногда называют оператором обозначение . Оператор D _x есть применяется к функции для выполнения дифференцирования. Затем производная f ( x ) = y с относительно x можно записать как D _x y (читать “ D – sub – x из y ”) или как D _x f ( x (читать “ D – sub x – из – f ( x ) ”).
Производные высшего порядка записываются добавлением верхнего индекса к D _x , так что, например, третья производная от y = ( x ² + sin ( x )) относительно x будет записано как
Другой широко используемые обозначения были разработаны Лейбница и соответственно называется Лейбниц. обозначение . В этих обозначениях, если y = f ( x ), затем производная y относительно x может быть записана в качестве
(его читают как “ dy – dx ”, но не “ dy minus dx ” или иногда “ dy over dx ”).С y = f ( x ), мы также можем написать
Это обозначение предполагает, что, возможно, производные можно рассматривать как дроби, что в некоторых случаях верно в ограниченном смысле. (Для пример с цепным правилом.) Это тоже называется дифференциальное обозначение , где dy и dx – это дифференциалы . Это обозначение становится очень полезным при работе с дифференциальными уравнениями.
Вместо этого вариант дифференциальной записи Лейбница записывается как
который напоминает приведенный выше оператор обозначение, с ( d / dx в качестве оператора).
Производные высшего порядка с использованием записи Лейбница можно записать как
Во второй форме экспоненты могут показаться в странных местах, но это имеет смысл, если вы посмотрите на первую форму.
Итак, это наиболее часто используемые обозначения для дифференциация. Возможно, существуют другие, непонятные обозначения, используемые некоторыми, но эти непонятные формы не будут включены здесь. Полезно знать различные обозначения.
Когда функция дифференцируема?
Вернуться на страницу исчисления | Вернуться на главную страницу World Web Math

watko @ mit.edu
Последнее обновление: 24 августа 1998 г.
Онлайн-курс по дифференциальным уравнениям – Расчет расстояний
Дифференциальные уравнения лучше всего можно описать как «теорию интеграции более высокого уровня». Простейшие дифференциальные уравнения. есть решения, которые являются простыми интегралами, как вы узнали в Исчислении II. Но очень быстро дифференциальные уравнения становятся более сложными, как и решения. Физики думают о дифференциальных уравнениях как о уравнениях которые выплевывают из их анализа различных физических ситуаций, и поэтому их нужно решить, чтобы понять физика.К сожалению, большинство дифференциальных уравнений не могут быть решены алгебраически, но основное внимание уделяется классу / учебнику. Курсы обычно заключаются в том, чтобы просто попытаться исчерпать все дифференциальные уравнения, которые можно решить вручную.
Наш онлайн-курс по дифференциальным уравнениям через Distance Calculus @ Roger Williams University использует другой подход: что делают эти дифференциальные уравнения имеют в виду? Что означают их решения? Что означают их графические или числовые решения? С помощью такого электроинструмента, как Mathematica, мы не связаны только теми дифференциальными уравнениями, которые имеют вычисленные вручную решения, но, скорее, все дифференциальные уравнения – это честная игра, и мы исследуем концепции дифференциальных уравнений с точки зрения лабораторных исследований.
Первый курс по изучению дифференциальных уравнений часто называется Обычные дифференциальные уравнения ; другие названия этого курса включают:
Вводные дифференциальные уравнения
Обыкновенные дифференциальные уравнения
Первый курс дифференциальных уравнений
Дифференциальные уравнения с одной переменной
Завершение курса математики 317 – Дифференциальные уравнения дает 3 академических кредита в течение семестра с официальной академической справкой из Университета Роджера Уильямса, в Провиденсе, Род-Айленд, США, который регионально аккредитован Новой Англией Комиссия высшего образования (NECHE), способствующая передаче кредитов по всей стране другим колледжам и университетам.
Онлайн-курс по дифференциальным уравнениям Вводные видеоролики
Введение в онлайн-курс по дифференциальным уравнениям
Дифференциальные уравнения можно рассматривать как «задачу интегрирования с (все более и более) сложностями».
Простое алгебраическое интегрирование функции f (x) можно переинтерпретировать в терминах этого интеграла. являясь решением дифференциального уравнения y ‘= f (x) , и наша задача решить для y – как интегрирование – это «обратная» операция дифференцирования, мы видим, что y – алгебраический интеграл из ф (х) .
Уравнение y ‘= f (x) является самым основным из возможных дифференциальных уравнений . Мы быстро приходим к исследовать более сложные формы уравнений, включающие дифференцирование , например: y ‘= y + f (x) , который спрашивает: найти функцию y = y (x) , который имеет свойство, заключающееся в том, что его производная y ‘ равна самой себе y добавляется к функции f (x) . Непростой вопрос перед началом курса Дифференциальные уравнения , но по завершении этого курса, на такие вопросы – а также на экспоненциально более сложные и сложные уравнения – даны ответы со знанием дела и понимание.
Более чем просто «алгебраическая игра с интегралами», тема Дифференциальные уравнения не изучает только алгебраические решения таких уравнений (когда это возможно!), но и качественное понимание свойств и решений этих уравнений.
Традиционные дифференциальные уравнения Курсы часто посвящены изучению этих “расширенных” методы интегрирования »для изучения решений этих уравнений чисто с алгебраической точки зрения.Хотя этот подход имеет свои достоинства, типы дифференциальных уравнений, встречающиеся «в реальном мире» (например, физика, химия, инженерия и т. д.) требуют решения и методов анализа, выходящих за рамки того, что возможно. только с помощью алгебры.
Учебная программа нашего онлайн-курса по дифференциальным уравнениям основана на Differential Equations & Mathematica от Carpenter / Davis / Uhl, и использует мощную компьютерную алгебру и систему построения графиков Mathematica ™ от Wolfram Research.Привлечение к алгебраическим исследованиям изучаемых классов дифференциальных уравнений вкратце, учебная программа быстро переходит к изучению гораздо более богатых концепций. доступный через Mathematica ™ и его числовой и графический дифференциал решатели уравнений, открывающие вводное изучение дифференциальных уравнений за пределами традиционный учебник по предмету.
Список курсов Университета Роджера Вильямса: Математика 317 – Дифференциальные уравнения
МАТЕМАТИКА 317: Дифференциальные уравнения [3 кредитных часа]
Описание курса : Изучает методы решения обыкновенных дифференциальных уравнений с приложения в науке и технике.Широко используются метод преобразований Лапласа.
Предпосылка : Исчисление II
Подробная программа курса в PDF
Материалы курса по дифференциальным уравнениям Онлайн-курс
Темы учебной программы по дифференциальным уравнениям включают:
Линейные дифференциальные уравнения первого порядка
Темы включают :
Невыполненные уравнения (однородные)
Принудительные уравнения (неоднородные)
Решения устойчивого состояния
Приложения к личным финансам
Шаговая функция и дельта-функция Дирака
Касательные векторы
Начальные условия
Коэффициенты интеграции
Линейные дифференциальные уравнения второго порядка
Темы включают :
Осцилляторы с избыточным и недостаточным демпфированием
Линейные принудительные и ненагруженные генераторы
Однородные уравнения
Неоднородные уравнения – изменение параметров
Характеристические уравнения
Формула Эйлера
Импульсное форсирование
Методы сверточных интегралов
Пружины и электрические заряды
Резонанс
Уравнения высшего порядка
Преобразования Лапласа
Темы включают :
Вычисление преобразований Лапласа
Преобразование дифференциальных уравнений с помощью преобразования Лапласа
Обратное преобразование Лапласа
Вводный анализ Фурье
Быстрые преобразования Фурье в приближенные периодические функции
Преобразования Лапласа и быстрая аппроксимация Фурье
Графический анализ дифференциальных уравнений
Темы включают :
Метод Эйлера
Графики и траектории потоков
Фазовые линии
Хищник-жертва Модель
Логистическая уборка
точки бифуркации
Чувствительность к начальным условиям
Нелинейные дифференциальные уравнения первого порядка
Темы включают :
Автономные уравнения
Неавтономные и другие типы уравнений
Многофазные линии
Участки бифуркации
Метод решения разделения переменных
Линейные системы дифференциальных уравнений
Темы включают :
Потоки, траектории и векторные поля
Преобразование между ODE высшего порядка и линейными системами
Собственные значения, собственные векторы и классификация решений
Онлайн-курс по дифференциальным уравнениям Кредит: 3 семестровых кредитных часа
Старшеклассники – курс дифференциальных уравнений
Многие продвинутые старшеклассники, завершившие курсы AP Calculus AB и BC, которые эквивалентны Calculus I и Calculus II, соответственно, часто оказываются в старшем классе средней школы, не имея дополнительных курсов математики в старшей школе.
Нет других курсов AP Calculus, кроме курса AP Calculus BC (Calculus II).
Отличный следующий шаг в учебе для этих продвинутых студентов-математиков средней школы – это пройти один или несколько из следующих курсов по дистанционному исчислению:
Математика 351 – Многопараметрическое исчисление
Math 317 – Дифференциальные уравнения
Math 331 – Линейная алгебра
Математика 315 – Теория вероятностей (статистика на основе вычислений)
В отличие от программы AP Calculus, эти курсы не содержат обязательных стандартных экзаменов, которые нужно сдать, а скорее позволяют получить настоящие университетские академические кредиты. через Университет Роджера Уильямса для этих продвинутых старшеклассников.
Вот видео, в котором обсуждаются некоторые варианты для этих продвинутых старшеклассников.
Продвинутый математический план средней школы для старших классов
После исчисления AP
Онлайн-курс по дифференциальным уравнениям Кредит: 3 семестра зачетных часов университетского уровня
Что такое обыкновенные дифференциальные уравнения?
«Обычный» означает, что изучаемые нами функции являются функциями одной переменной .Обычно: y = f (x)
Исторически этот курс назывался «Обыкновенные дифференциальные уравнения», часто сокращенно ODE , и вы увидите ODE используется взаимозаменяемо с DE для сокращения термина «дифференциальные уравнения».
Что такое неординарное дифференциальное уравнение? Это называется Уравнения с частными производными , и они включают рассмотрение уравнения, включающие частные производные функций двух или более переменных, например: z = f (x, y).
Уравнения в частных производных – это, как правило, курс математики для младших классов, который изучают все математические специальности и многие специальности физики и инженерии. предпримете, чтобы узнать о следующих шагах в изучении дифференциальных уравнений.
Термин «обычный» в обыкновенных дифференциальных уравнениях помогает вам определить уровень курса дифференциальных уравнений, который вы может потребоваться взять. Этот онлайн-курс по дифференциальным уравнениям – Математика 317 – является первым курсом по обыкновенным дифференциальным уравнениям.
В разговорной речи вы можете слышать, как другие студенты называют этот курс «Diff-E-Q» или «DiffyQ».
Существует также курс высшего, младшего уровня по дифференциальным уравнениям, обычно называемый «Расширенные дифференциальные уравнения» или «Промежуточные дифференциальные уравнения». который продолжает изучение обыкновенных дифференциальных уравнений, но на более продвинутом уровне и совершенно отличен от курсов по уравнениям в частных производных. Наша математика 317 – Дифференциальные уравнения не считается одним из этих курсов более высокого уровня для младших классов и выше.
Дифференциальные уравнения Примеры учебной программы
Ниже приведены распечатки некоторых из них в формате PDF. ноутбуков Mathematica ™ из Differential Equations & Mathematica Автор: Карпентер / Дэвис / Уль. Также прилагается пример тетради с домашним заданием, выполненной учеником. в курсе, демонстрируя, как записные книжки для домашних заданий становятся «обычной классной доской». что и ученики, и преподаватель пишут в своем «разговоре» о тетради.
Это похоже на программный код!
Да, Mathematica ™ – это система компьютерной алгебры на основе синтаксиса, т. Е. инструкции для создания графиков и вычислений выглядят как код языка программирования (что это такое).
Этот курс не является курсом программирования. Мы не обучаем программированию и не ожидайте, что студенты будут изучать программирование или даже что-нибудь знать о программировании. В этом курсе важна математика , а не код.
Помня об этом принципе, авторы книги «Дифференциальные уравнения » и «Математика » обучающие программы разработали записные книжки с объяснениями (Основы и учебные пособия) и записные книжки с домашними заданиями (попробуйте) таким образом, чтобы их было легко копировать / вставлять из пояснения в тетради для домашних заданий и внесение незначительных изменений (очевидных) для получения желаемого аналогичного (но другого) вывода. Таким образом, мы можем строго придерживайтесь имеющейся математики и обращайтесь с программным кодом как как можно меньше.
Онлайн-курс по дифференциальным уравнениям Кредит: 3 семестра зачетных часов университетского уровня
Расчет расстояний – Отзывы студентов
Дифференциальное исчисление – обзор
2.5 Математические основы динамики Фалька II: системы
Давайте теперь рассмотрим случай, когда функции M – G не работают в области физических величин Ⴚ _{r + 1}, но в их диапазоне Вт. Не является строгим, что основные теоретико-множественные аксиомы, с помощью которых могут быть введены кольца полиномов, все еще действительны, если отображения выполняются из Ⴚ _{r + 1} на W. Это особенно верно для задачи соединения некоторых Ⴚ _{r + 1} элементов процессами дифференцирования, основанными исключительно на алгебраических правилах, упомянутых выше. Хотя эти правила гарантируют, что отображения обычно удовлетворяют всем условиям непрерывности в W, следует соблюдать одно отмеченное исключение: Составление системы S из всех отображений Z из Ⴚ _{r +} 1 на W = ℝ, то есть в набор действительных чисел, тем самым включается специальное отображение, согласно которому элемент M – G F ( X ₀; X ₁;…; X _r ) рассматриваемой системы переводится в нулевой элемент.Уравнение (2.59), которое управляет этим переносом во всех случаях, можно применить напрямую:
(2.71) Z [FX0; X1;…; Xr = Fξ0; ξ1;…; ξ≡0forallZ∈S.
Уравнение F (ξ ₀;…; ξ _r) ≡ 0, конечно, не что иное, как основное уравнение Гиббса системы S , описывающее связь между сопряженными значениями ξ _j ( j = 1 (1) r ) и их независимые родовые типы X ₀; X ₁; …; X _r
Строго говоря, не все значения r + 1 ξ ₀; ξ ₁; …; ξ _r .поэтому разрешено быть независимыми переменными в смысле математического анализа. Тем не менее, функция F может обрабатываться как неявная функция с учетом этих самых переменных. Другими словами:
Что касается дифференциального исчисления, ξ ₀; ξ ₁; …; Ξ _r можно использовать просто как набор независимых переменных (поскольку они являются просто маркерами положения позиции ), но по отношению к значениям базовых обобщений фундаментальное уравнение Гиббса является просто вырожденной функцией, другими словами, постоянный ноль.
На следующем этапе и в качестве обоснованного подхода элемент M – G F = F ( X ₀; X ₁;…; X _r ) считается разрешимым относительно X ₀. Тогда систему S не нужно описывать напрямую с помощью F ( X ₀; X ₁;…; X _r ), но также может быть представлена Функция M – G X ₀ = X ₀ ( F; X ₁;…; X _r ) с учетом (2.00; ξ1;…; ξr = Gξ1;…; ξr
между значениями ξ ₀ = Z [ X ₀] и ξ ₁ = Z [ X ₁],…, ξ _r = Z [ X _r ].
Следовательно, интенсивные элементы (2.59) могут быть легко отображены из Ⴚ _{r + 1} на ℝ на
(2.73) ZYi: = τi = ∂Gξ1… ξr∂ξi; i = 11r.
Эта форма соответствует общепринятому использованию, особенно если также рассматривать пределы ряда действительных чисел со ссылкой на дифференциальное исчисление.
Что касается существенного неравенства между концепциями дифференцирования в алгебре и анализе, комментарий к (2.73) может быть разрешен, потому что каждое отображение Z является членом семейства отображений, посредством которого любая общая величина X _i set Ⴚ _{r +} i отображается на непрерывный интервал значений ξ _i , тогда как любая другая величина X _k из общей коллекции { F, X _l; …; X _r} превращается в фиксированное число ξ _k. По этой причине в математической физике необходим континуум действительных чисел, и поэтому, следуя Фальку (1990, стр. 275), хорошо известное условие непрерывности Гиббса действительно хорошо обосновано.
Теперь рассмотрим однородность первого порядка элемента M – G F ( X ₀; X ₁;…; X _r ). Уравнение (2.72) сразу допускает два математических вывода из этого свойства:
(2.74) dξ0 = ∑j = 1rτjdξj; ξ0 = ∑j = 1rτjξj
Ясно, что оба уравнения лежат в основе общего формализма, предложенного Гиббсом и заключенного Фальком. .Здесь мы должны увидеть, что теория Гиббса – Фалькиана не ограничивается в своих приложениях термодинамикой или физикой, но может также использоваться в таких областях науки, как математическая экономика и так называемая общая теория систем.
В этом контексте следует упомянуть грамотную книгу Мировского. Автор излагает многочисленные и разнообразные попытки экономистов связать физические понятия и отношения с основными терминами ранней неоклассической экономической теории. Выдающаяся докторская диссертация Ирвинга Фишера 1892 года дала поразительное сравнение соответствующих аналогий (см.Мировский, 1990, с. 224). Мировски объясняет такие подходы постоянным влиянием классической механики на ведущих ученых-экономистов. Прежде всего, он подчеркивает влияние энергетики, в основном пропагандируется книгой Хельма (1898 г.), на которую значительное влияние оказала термостатика Гиббса. Однако любопытно, что энергетика как якобы социальная теория (см. Helm, 1898, стр. 207) была разнообразной и широко распространенной на рубеже девятнадцатого века и все же быстро ушла в затмение в 1930-х и 1940-х годах; тогда как неоклассицизм сохранился до наших дней.Можно отметить две причины: «Во-первых, неоклассической экономике (непреднамеренно?) Удалось отделить себя от более широкой программы энергетики до такой степени, что она не имела очевидной связи с ней; во-вторых, события в физике подорвали претензии невозмутимой энергетики основываться на принятой и заслуживающей доверия физической теории, что сделало ее предполагаемое научное преимущество перед другими теориями жалким »(Mirowski, 1990, p.269). С этой точки зрения подход Гиббса-Фалькиана, представленный в этой главе, предлагает, прежде всего, новые возможности исследования списка соответствия Фишера для основных терминов физики и экономики с помощью гораздо более эффективных инструментов.
Преобразуя (2.65) со ссылкой на (2.71), получается -кратное -кратное преобразование Лежандра
(2.75) ξ⋄0 = ξ0m = ξ0 − ∑j = 1mξj∂ξ0∂ξj
для приложения к уровень состояний, то есть самой рассматриваемой системы.
Мы можем оценить еще одно важное уравнение относительно обоих выражений в (2.74), которые взаимно согласованы только при условии
(2.76) ∑j = 1rξjdτj≡0.
Это тождество относится к соотношению Гиббса – Дюгема – Маргулеса (2.70), в котором говорится, что r интенсивные параметры τ _j зависят от самих себя. Следовательно, соотношение
(2.77) hτ1τ2… τr≡0
становится неизбежным и типичным для ансамбля состояний S так же, как основное уравнение (2.71) или функция M – G (2.72). Другими словами, если предположить, что система фактически определяется своей однородной функцией M – G первого порядка, эта система также подчиняется своему соответствующему уравнению (2.77). Поэтому Фальк (1990, стр. 277) предложил называть это тождество внутренним фундаментальным уравнением рассматриваемой системы.
Давайте сначала рассмотрим пример, связанный с термодинамической системой, использованной в качестве стандартного случая в предыдущих разделах. Рассмотрим функцию M – G U = U ( S ; V ; n ), полученную из основного уравнения Гиббса Г ( U ; S ; V ; n ) ≡ 0 . При подготовке расчетов и рассмотрении (2.54) безразмерные переменные ξ _j умножаются на соответствующие им международные единицы следующим образом:
(2.78) U: = ξ0 × J; S: = ξ1 × JK − 1; V: = ξ2 × m3; n: = ξ3 × моль; T ∗: = τ1 × K; p ∗: = τ2 × Па.
Следующая последовательность следствий всесторонне объясняет полную взаимозависимость как математических, так и физических соотношений:
(2.79) Fξ0ξ1… ξr≡0⇒ΓUSVn≡0⇒U = ξ0⇒ξ0 = Gξ1… ξr⇒ξ⋄0 = ξ0V = U − V∂U / ∂Vs; n = U − V − p ∗ = U + p ∗ V: = H ∗
Результат хорошо известен: преобразованием Лежандра согласно (2.∗ все даются формулами (2.26). Функция, обозначенная (2.80), поясняет различные шаги, которые необходимо предпринять от однородной M – G-функции первого порядка U ( S ; V ; n ) к неоднородной M – G-функции H _⁎ ( S ; p _⁎; n ).
Второй пример относится к изотропному излучению черного тела, для которого фотоны или фононы, соответственно, находятся в тепловом и химическом равновесии.Его внутреннее фундаментальное уравнение хорошо известно (Фальк, 1990, стр. 281) и может быть записано с использованием общих обозначений этой книги:
(2.81) hτ1τ2: = a • τ14 + 3 • τ2≡0.
Предполагается, что число a является естественной постоянной радиационной системы.
Посредством преобразования Лежандра согласно (2.75) и относительно экстенсивной переменной ξ ₁ простые соотношения
ξ01 = ξ0 − ξ1 • τ1 = ξ2 • τ2 = ξ2 • −3−1a • τ14
получены с использованием соотношения однородности (2.74) и тождество (2.81). Таким образом, ξ ₁ легко вычисляется с помощью производной
ξ1 = ∂ξ01τ1ξ2∂τ1 = 43aξ2τ13,
, с помощью которой зависимая экстенсивная переменная ξ ₀ может быть выражена в переменных τ ₁ и ξ ₂:
ξ0 = τ1ξ1 + τ2ξ2 = a • ξ2 • τ14.
Путем исключения τ ₁ функция M – G (2.72), а также основное уравнение (2.71) радиационной системы могут быть определены в следующем виде
ξ0 = Gξ1ξ2 = 3434a13ξ143ξ2−13; Fξ0ξ1ξ3 = ξ0ξ23−34334aξ1ξ2≡0.
Используя размерные величины согласно (2.78), можно легко получить хорошо известные уравнения для давления p _⁎, энтропии S и внутренней энергии U излучающего газа. :
p ∗ = b3T ∗ 4; S = 43bVT * 3; U = bVT * 4. ∗, по сравнению с размерными количества U , V , S , p _⁎ и T _⁎, впервые представленные в (2.78). Для получения дополнительной информации см. Falk (1990, стр. 283).
Для продолжения общей теории целесообразно работать в диапазоне значений, присвоенных набору Ⴚ . Примечательно, что однородность элемента M – G F ( X ₀;…; X _r ), а также его функция изображения F (ξ ₀;…; ξ _r ) всегда относится к полному ансамблю переменных r + 1. Если, например, значение ξ _k предполагается фиксированным, то элемент F (ξ ₀; … ; ξ _{k –1}; ξ _{k + 1};… ξ _r ) остается однородным только при особом условии, что выполняется ξ _k ≡ 0.Следовательно, основное отношение однородности задано для
(2.82) Fλξ0;…; λξk − 1; 0; λξk + 1;…; λξr = λωFξ0;…; ξk − 1; 0; ξk + 1;…; ξr ,
, который не зависит от степени однородности ω и действителен для каждого действительного числа λ ≠ 0. Это простое утверждение приводит нас к важному выводу, касающемуся точной процедуры для установления подмножеств S , с помощью которых могут быть конкретно представлены физические системы. . Это связано с тем, что F (ξ ₀; … ; ξ _{k –1}; 0; ξ _{k + 1};… ξ _r ) для ξ _k = 0 представляет собой еще раз фундаментальное уравнение системы.Для краткости такую систему можно назвать сокращенной системой S ‘.
Что касается редукции каждой системы, следует отметить, что это может быть выполнено не только путем допущения любой отдельной переменной, но также с помощью каждой допустимой линейной комбинации переменных ξ _j или τ _{j ;}, что тождественно нулю. Например, преобразования
(2.83) ξ1 ′: = 2−1 / 2ξ1 + ξ2; ξ2 ′: = 2−1 / 2ξ1 − ξ2ξi ′: = ξi, i = 31rτj ′: = 2−1 / 2τ1 + τ2 ; τ2 ′: = 2−1 / 2τ1 − τ2τj ′: = τj, j = 31r
демонстрируют эквивалентность случая ξ ₂ ′ ≡ 0 с соотношением ξ ₁, = ξ ₂, а также как и для случая τ ₂ ′ ≡ 0 с соотношением τ ₁ = τ ₂.Эта гибкость внутри системы имеет большое значение для физических приложений.
Необходимость критериев допустимости возникает также в рамках кардинальных связей (2.74). Если предположить, что τ _j ⁰ постоянное, то из первого соотношения
(2.84) dG ′ = dG − τj0ξj = ∑l = 1rτl − τj0δljdξl = ∑l = 1rτl′ξl
следует, что завершается вторым соотношением
(2.85) G ′ = G − τj0ξj = ∑l = 1rτl − τj0δjldξl = ∑l = 1rτl′ξl
Соответственно, интенсивная переменная τ _j предполагается постоянной τ _j ⁰ сразу равняется преобразованной переменной τ _j ′, принимаемой равной нулю.Это по совпадению сопровождается заменой функции G ‘на функцию M – G G . Таким образом, обе простейшие редукции ξ _j = 0 или τ _j = константа означают, что пара переменных ξ _j , τ _j не входит в приведенную систему .
В общем, частный случай τ _j ′ = 0 представляет большой интерес для определения событий равновесия, которые можно охарактеризовать с помощью основных понятий физики и, прежде всего, термодинамики.Это верно для хорошо известных примеров любого силового равновесия в механике или для термического и химического равновесия. Наоборот, однако, нельзя с легкостью сделать вывод, что любые относящиеся к интенсивным переменным, наблюдаемые как нулевые, должны быть связаны с каким-либо реализуемым явлением равновесия.
Математически легко доказать, что свойство экстремума положений равновесия может быть гарантировано однородностью функции M – G. Интенсивная переменная, скажем, τ _j , предполагаемая равной нулю, задается через (2.74) частной производной функции M – G ξ ₀ = G по соответствующей обширной переменной ξ _j . Из следующего уравнения мы получаем с
∂∂ξjξ0 = τjξ1;…; ξr≡0
условие, которое должно выполняться в связи с преобразованной Лежандром M – G-функцией (2.75) системы, приведенной к равновесию. В отличие от ξ ₀ (ξ ₁;…; ξ _{j – 1}; ξ _j ; ξ _{j + 1};… ξ _r ξ) эта преобразованная функция ₀ ^◊ = ξ ₀ = τ _j ξ _j зависит от переменных ξ ₁; …; Ξ _{j – 1}; τ _j ; ξ _{j + 1}; … Ξ _r при этом τ _j дополнительно заменяется нулем.Однако для разрешения этого тождества относительно выделенного ξ _j производная ∂τ _j / ∂ξ _j не должна исчезать в окрестности τ _j = 0 Следовательно, существует два класса репрезентативных функций M – G: максимальный класс и минимальный класс, определяемый соответствующим знаком производной ∂τ _j / ∂ξ _j каждый.
Фальк (1990, стр.295) обобщил простой случай одного равновесия на полную систему из на степеней свободы при условии уменьшения на одновременно работающих равновесий. Его анализ приводит к следующим условиям устойчивости, которым должна удовлетворять функция M – G рассматриваемой системы вместе с ее m -кратными преобразованиями Лежандра согласно (2.75). Учитывая
Ξξm − 1: = ∂2G∂ξ12τ1 = 0 • ∂2G1∂ξ22τ2 = 0 • ⋯ • ∂2Gm − 1∂ξm2τm = 0
, мы получаем
(2,86) Ξξm − 1> 0минимальный класс энергии как минимум и класс энергии, если класс энергии>
Чтобы гарантировать, что любое сокращение системы снова приведет к новым системам в смысле термодинамики, эти системы должны быть очень стабильными по отношению к любым возможным изменениям в смысле Гиббса (1961, стр.57). Такое поведение устойчивости вблизи необязательных состояний равновесия важно для общих классификаций веществ в различных неравновесных состояниях. Это особенно верно ввиду некоторых характерных свойств жидкостей, которые в принципе можно считать нечувствительными к изменениям состояния. Хорошо известными примерами являются теплоемкость, изоэнтропическая и изотермическая сжимаемость газов, жидкостей, твердых тел, а также их смесей.
Если взглянуть на некоторые другие механические аспекты, возникает некоторый спрос на основные свойства материи.Предполагая, что P _i является одной из составляющих векторного (линейного) импульса P , тогда условие устойчивости
(2.87) ∂2E∂Pi2 = ∂vi∂Pi> 0
напрямую требует, чтобы изменения импульса P и скорость v рассматриваемой системы всегда равнонаправлены. Следовательно, в механике масс-точки допускаются только положительные значения массы m , здесь определяемой энергией E одной масс-точки E : = P ²/2 m + E ₀.По той же причине (2.87) применяет положительные значения энергии, определенные формулой E ²: = c ² P ² + E ₀ ² в механике Эйнштейна. Оба случая будут играть важную роль в следующих разделах.
Существует вариант, при котором редукция системы открывает некоторые аспекты фундаментального интереса математической физики. Имейте в виду, что система характеризуется конечным числом r степеней свободы.Следовательно, любое уменьшение числа переменных может быть выполнено только посредством сокращения системы, определенного выше, а не за счет какого-либо непрерывного уменьшения в смысле математической непрерывности. Это также ключ к пониманию предыстории и решения знаменитого парадокса Гиббса, который будет обсуждаться позже в этом разделе.
Вариант сокращения любой данной системы в принципе основан на соответствующем свойстве, присущем предписанной функции M – G. Однако это исключительная особенность структуры Ⴚ _{r + 1}, позволяющая разбить систему на подсистемы или собрать некоторые системы в новую, более сложную систему.
Фальк (1990, стр. 312) доказал, что оба эти варианта могут быть сведены к простому обратному соотношению. Начнем с того, что три системы I , II и III определяются своими соответствующими функциями M – G
(2.88) ξI0 = GIστI1;…; τIσ; ξσ + 1; 0jξIσ + 3;…; ξIr, ξII0 = GIIστII1;…; τIIσ; 0jξσ + 2; ξIIσ + 3;…; ξIIr, ξIII0 = GIIIστIII1;…; τIIIσ; 0jξIIIσ + 3;…; ξIIIr,
, где индекс σ означает, что эти функции зависят от как интенсивные переменные, так и экстенсивные.Каждая функция отличается одной характеристической переменной, которая не имеет отношения к двум другим функциям. Тогда предполагается, что вся система устанавливается (нередуцированной) системой M – G
(2.89) Gσ = GσIτ1I;…; τσI; ξσ + 1; ξIσ + 3;…; ξIr + GIIστII1;…; τσII; ξσ + 2; ξIIσ + 3;…; ξIIr + GσIIIτ1III;…; τσIII; ξIIIσ + 3;…; ξIIIr,
, где теперь выполняется набор из 3 r – 4 степени свободы.
Теперь уравнение (2.89) будет сокращено в два этапа: первый выполняется посредством редукции через интенсивных переменных,
(2.90) τ1I = τ1II = τ1III: = τ1;…; τσI = τσII = τσIII: = τσ,
второй с помощью расширенных переменных
(2,91) ξIσ + 3 = ξIIσ + 3 = ξIIIσ + 3: = ξσ + 3;…; ξIr = ξIIr = ξIIIr = ξr.
Таким образом, уравнение (2.90) представляет собой равновесие в точном соответствии с (2.84) и (2.85).
Комбинируя (2.90) и (2.91) с функцией M – G (2.89), возникает тип системного синтеза, который можно точно рассматривать как аналог разложения.
Это можно легко продемонстрировать с помощью M – G функции с преобразованием Лежандра G , на этот раз исключительно в зависимости от обширных переменных:
(2.92) G = τ1Iξ1I + τ1IIξ1II + τ1IIIξ1III + ⋯ + τσIξσI + τσIIξσII + τσIIIξσIII + τσ + 3Iξσ + 3I + τσ + 3IIξσ + 3II + τσ + 3IIIξσ + 3III + ⋯ + + τrIξrI + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσIII + τξσi + τξσIII + τξσIII + τξσI + τξσIII + τξσIII + τξσIII + τξσIII + τξσi + τξσI + τξσ 2IIξσ + 2II.
Используя (2.90) и (2.91) функция M – G (2.92) превращается в следующий набор соотношений
(2.93) ξ0 = ξ0I + ξ0II + ξ0III; ξj = ξjI + ξjII + ξjIII; j = 11σ; τk = τkI + τkII + τkIII; k = σ + 11r,
, где последнее соотношение означает для k = σ + 1: τ _{σ + 1} = τ _{σ + 1} ^I и τ _{σ + 1} ^II = τ _{σ + 1} ^III ≡ 0 и т. Д.Условия (2.93) подчеркивают, что при преобладающих условиях различные переменные должны быть объединены уникальным образом для проверки подхода (2.89). Таким образом, очевидно, что разложение (2.89) может быть выполнено, если ограничения, например, записаны
(2.94) ∂2Gσ∂ξσ + 1∂ξσ + 2 = ∂τσ + 1∂ξσ + 2 = ∂τσ + 2 ∂ξσ + 1≡0
может быть выполнено. В этом случае получатся три M – G-функции I, II и III согласно (2.88). Расширения и вариации пунктов, рассматриваемых в (2.94) легко вывести.
Общую теорию разложения, обсужденную выше, можно применить к случаю, который будет преобладающим. Для этого условия предполагается, что функция M – G G зависит только от r расширенных переменных (т.е. σ сокращается), которые могут быть разделены на две подгруппы: ξ ₁…; ξ _q и ξ _{q + 1}; …; ξ _r. Следовательно, каждая смешанная вторая производная от G должна одинаково обращаться в нуль для любой пары переменных, принадлежащих разным подгруппам.Это согласуется с формулой
(2.95) ∂2G∂ξj∂ξk = ∂τj∂ξk = ∂τk∂ξj≡0; j = 11q; k = q + 11r,
, которая допускает простое разложение
(2.96 ) Gξ1;…; ξr = GIξ1;…; ξq + GIIξq + 1;…; ξr.
Конечно, идея состоит в том, что «композиция» системы просто означает отмену соответствующей декомпозиции. Позже уравнение (2.95) будет играть важную роль для формулировки альтернативной теории.
В заключение этой главы мы продемонстрируем, как разложить систему, определяемую четырьмя степенями свободы.Выбор температуры T _⁎, объема V, и двух удельных молярных величин n ₁ и n ₂ измерения соответствующего частичного количества двух задействованных веществ, свободная энергия F равна равной соответствующей функции M – G. Две подсистемы, I и II, могут быть описаны с помощью T _⁎, V, и одного из двух чисел молей n ₁ и n ₂ каждая.∗ выбрана постоянной.
Математическая структура этого примера точно соответствует теоретическому подходу, представленному системой уравнений от (2.88) до (2.96). Таким образом, условие исключения (2.94) можно сформулировать в терминах двух первых подсистем следующим образом:
(2.97) ∂2F∂n1∂n2 = ∂μ1 ∗ ∂μ2 = ∂n2 ∗ ∂n1≡0.
Следовательно, структура функции M – G F изоморфна структуре (2.89):
(2.98) FT ∗; V; n1; n2 = FIT ∗; V; n1 + FIIT ∗; V; n2 + FIIIT ∗; V.
Условия, относящиеся к восстановлению (2.90) и (2.91), а также заключительные соотношения (2.93) прямо приводят к соответствующим условиям равновесия для температуры и объема:
(2.99) TI = TII = TIII: = Т; VI + VII + VIII: = V.
В итоге, учитывая ограничения на процессную реализацию задачи, получаем:
(2.100) pI + pII + pIII: = p; SI + SII + SIII: = S.
В этом контексте, с точки зрения практического применения, представляется уместным обсудить понятие разнообразия веществ. Этот термин, по-видимому, понятен простой интуицией, однако он напоминает знаменитый парадокс Гиббса ’. Этот парадокс озадачил термодинамиков с самого начала. Следовательно, на мой взгляд, одно из главных преимуществ динамики Фалька – исключить этот парадокс простым, но правильным и прозрачным способом.
Рассмотрим два идеальных газов (нижние индексы 1 и 2), которые, как предполагается, подпадают под условие исключения (2.97). Давайте далее всегда рассматривать два разных состояния со ссылкой на общий объем.Их отличает тот факт, что в состоянии (2) оба газа заключены в единый объем, тогда как в состоянии (1) они разделены по разным объемам каждый, но при этом соприкасаются друг с другом.
Очевидно, что состояние (2) соответствует выбранному примеру, но без учета указанной выше подсистемы. Таким образом, оба состояния могут быть определены следующими условиями, при условии, что n _l и n ₂ являются переменными.
1TI = TII: = T; pI = pII: = p; реализуется посредством VI + VII: = V1.2TI = TII: = T; pI2 + pII2: = p; реализуется посредством VIVII⇒V2.
Обсуждение парадокса Гиббса требует вычисления полной разности энтропии между (1) и (2), таким образом, ясно представляя эффект перемешивания, при условии, что (1) и (2) считаются начальным состоянием. и последний соответственно. Возьмем случай двух газов, где изотермически-изобарическое изменение энтропии определяется выражением
(2,101) ΔS = S2 − S1 = −nRχ1lnχ1 + χ2lnχ2,
, так что n : = n ₁ 906 + N ₂ и χ _k: = n _k / n (при k = 1, 2) обозначают общее число молей и, соответственно, мольную долю kth составная часть.
Из-за типа реализации процесса (2.101) справедливо для энтропии перемешивания как характеристической меры необратимости. В этом случае сначала выберем n ₂ << n ₁ (или наоборот), в результате чего Δ S , тем не менее, сохранит свое конечное значение. Во-вторых, рассмотрим физически сомнительные, но математически допустимые пределы χ ₁ → 1 или χ ₂ → 0 соответственно.Затем энтропия смешения резко стремится к нулю, что указывает на то, что диффузия не может происходить в однородных газах.
Такой формальный вывод довольно хрупок, особенно с учетом того интересного факта, что (2.101) также можно вывести и интерпретировать совершенно по-другому, как это могло бы иметь место для состояний (1) и (2): Состояние (2) заменяется состоянием (3), определяемым как
3TI = TII: = T; pI3 + pII3: = p; реализовано как VI + VII: = V3.
Физически (3) может быть реализовано обратимым расширением V ^I и V ^II или даже необратимым расширением Гей-Люссака (см. Раздел 8.3.2) таким образом, чтобы давление, присвоенное V ₍₃₎, равнялось значению p из (1). Смешивание двух газов не происходит. В этом случае, очевидно, для Δ S не имеет значения, достигается ли конечное состояние (3) необратимо и, кроме того, различаются ли идеальные газы 1 и 2 или нет.
После этой подготовки следует сделать несколько замечаний о значении парадокса Гиббса с учетом динамики Фалька. Гиббс (1961, стр. 166) впервые заметил, что значение Δ S не зависит от различных видов рассматриваемого газа, «если количества таковы, как предполагалось, за исключением того, что смешанные газы должны иметь разные дети.Если бы мы соприкоснулись с двумя массами одного и того же газа, они тоже смешались бы, но энтропии не увеличилось бы ».
Другими словами, (2.101) не содержит параметров, типизирующих некоторые виды материи. Тем не менее, I согласны с Фальком (1990, стр. 319), что этот факт подтверждает, что человеческое воображение иногда притворяется – даже в физике – уместностью понятия, даже если это именно то убеждение, которое должно быть опровергнуто любой рациональной теорией. Соответственно, динамика Фалька не использует термин «материал» как релевантную величину; он даже отвергает такое несвязанное свойство как источник базовой информации.На самом деле теория знает только степени свободы; в лучшем случае некоторые переменные «количества» могут быть отделены от общего числа r степеней свободы. Например, любой газ с тремя степенями свободы, представленными T _⁎, V, и n , может состоять из неопределенного числа материалов, которые все находятся в равновесии друг с другом.
Термин чистый материал применяется к системе с одной независимой переменной «количество» n. То же самое верно и для так называемого материала, составляющего r ‘, при условии, что это обозначение относится к r’ степеням свободы.
Чтобы использовать такие термины в рамках динамики Фалька, необходимо соблюдать два вывода:
1.
Термин материал может быть оправдан только в том случае, если он используется как синоним в связи с соответствующим числом r степеней свободы.
2.
Что касается пункта (1), теории известно только определенное число r универсально физических величин, для которых бесконечно малое изменение во времени или с помощью другого управляющего параметра недопустимо во всех смыслах и целей.
Аргументы, ведущие к парадоксу Гиббса, основаны на идее «количественного разнообразия веществ», интуитивно возникшей из меняющихся значений конечного числа величин, для которых математический континуум составляет запас переменных. По этой причине нельзя бесконечно варьировать количество различных веществ; то есть разные вещества нельзя непрерывно переводить в идентичные, так как категорически запрещено, например, произвольно изменять размерность пространственных координат.
Конечно, можно уменьшить количество переменных, но только сокращением системы, а не бесконечно малым предельным процессом в смысле математического анализа. Ergo, Парадокса Гиббса не существует в рамках математически непротиворечивой теории.
Существенный вопрос: какую роль играет время в динамике Фалька? Чтобы предвосхитить основную часть соответствующего ответа, я процитирую отрывок из книги Фалька:
В отличие от механики, электродинамики и теории относительности в методе динамического описания, основанном на термодинамике, пространство и время не составляют естественный порядок, в котором должны быть размещены все события.Следовательно, пространство и время не играют никакой конкретной роли, даже не важной. Напротив, понятие универсально физической величины является элементарным для метода динамического описания. Верно, что координаты пространства и времени принадлежат этим величинам, но они не отличаются от всех остальных. Напротив, часто бывает полезно оставить пространство и время в стороне и сосредоточиться на отношениях, в которых координаты x ; y ; z; т не фигурируют.Все такие связи принадлежат тем отношениям, которые описывают то, что обычно называют «системой». (Falk, 1990, p. 118; перевод автора)
Несомненно, это утверждение хорошо подтверждается математической трактовкой и аппаратом динамики Фалька. Однако следует подчеркнуть, что существует скорее прямое, но менее прозрачное сходство между понятием времени и представленной теорией. Это происходит исключительно благодаря хорошо известному свойству времени констатировать синхронные события.Это означает, что такие операции, как декомпозиция системы или взаимодействие между двумя или более системами, неявно предполагается, что они выполняются одновременно во времени. Кстати, синхронизация не привязана к каким-либо фиксированным точкам времени. Ссылки на временные интервалы являются обычной практикой, особенно в технической термодинамике, но также и в экономике (см. Fischer, 1996)
Конечно, сегодня ученые и инженеры узнают, что в современной физике временная координата является частью соглашения о целом. семейство величин.По этой причине процитированное выше утверждение Фалька верно до тех пор, пока оно действительно относится к классическому ньютоновскому понятию времени, но не включает возможность установления характерных соотношений между координатой времени и другими физическими величинами. Это будут некоторые из тем следующих глав.
Вариационное исчисление и дифференциальные уравнения с частными производными
Вариационное исчисление и уравнения в частных производных привлекает и собирает многие важные высококачественные материалы в этой области исследований и подчеркивает взаимодействие между аналитиками, геометрами и физиками.
Охват журнала включает:
• Задачи минимизации вариационных интегралов, теория существования и регулярности минимизаторов и критических точек, геометрическая теория меры
• Вариационные методы для уравнений в частных производных, линейные и нелинейные задачи на собственные значения, теория бифуркаций
• Вариационные задачи в дифференциальной и комплексной геометрии
• Вариационные методы в глобальном анализе и топологии
• Динамические системы, симплектическая геометрия, периодические решения гамильтоновых систем
• Вариационные методы в математической физике, нелинейная упругость, кристаллы , асимптотические вариационные задачи, усреднение, явления капиллярности, задачи со свободными границами и фазовые переходы
• Уравнения Монжа-Ампера и другие полностью нелинейные уравнения в частных производных, связанные с задачами дифференциальной геометрии, сложной геометрии и физики.
Привлекает и собирает многие важные высококачественные материалы в этой области исследований
Подчеркивает взаимодействие между аналитиками, геометрами и физиками
92% авторов, ответивших на опрос, сообщили, что они обязательно опубликуют или, возможно, опубликуют в журнал снова
Информация журнала
Главные редакторы
Андреа Мондино,
Андре Арроха Невес,
Ласло Секелихиди
Издательская модель
Гибрид (трансформирующий журнал).Узнайте о публикации открытого доступа у нас
Показатели журнала
1,945 (2020)
Импакт-фактор
2,478 (2020)
Пятилетний импакт-фактор
85 дней
Подача первого решения
122 дня
Приемка
155,340 (2020)
Загрузки
Syllabus for Math 1530: «Дифференциальное исчисление»
Math 1530 (дифференциальное исчисление) и Math 1540 (интегральное исчисление) – это 3-часовые курсы, которые вместе охватывают материал 5-часового Math 1550 (дифференциальное и интегральное исчисление) , который представляет собой вводный курс математического анализа, предназначенный в первую очередь для инженерных специальностей и некоторых других технических специальностей.
Предполагается, что учащийся математики 1530 разбирается в стандартных темах, предшествующих вычислению, таких как функции, построение графиков, решение уравнений, а также экспоненциальные, логарифмические и тригонометрические функции. Начинающий преподаватель должен знать, что у некоторых студентов могут быть проблемы с алгеброй и триггером, которые могут помешать их успеху в математике 1530. Преподаватели этого класса не предполагают предварительного знакомства с дифференциальным исчислением (хотя многие студенты уже имели математическое знание раньше). Тестирование и оценка каждого класса полностью на усмотрение инструктора.Никакой ведомственной политики по использованию сложных калькуляторов в Math 1530 не существует; это решение остается за инструктором.
Базовые навыки, которые студенты должны приобрести в течение курса
Пределы и непрерывность
Оценить пределы по графику
Оценить пределы в точках непрерывности
Оцените пределы неопределенных форм, используя алгебраические упрощения и правило Л’Опиталя
Знать, что подразумевает непрерывность графика и поведения функции
Определение точек разрыва для функций, определяемых формулами или графиками
Дифференциация
Знать различные интерпретации производной (скорость, скорость изменения, наклон касательной)
Вычислить производные простых функций, используя коэффициент разности
Вычислить производные комбинаций основных элементарных функций
Возьмите производную, используя неявное и логарифмическое дифференцирование
Найдите касательные и уметь использовать их в качестве линейных приближений
Найти критические значения, локальные экстремумы и интервалы вогнутости для дифференцируемых функций
Найти абсолютные экстремумы ограниченных функций
Понимание теоремы о среднем значении производных
Решить проблемы, связанные со связанными ставками
Текст: «Исчисление, ранние трансцендентальные представления», 8-е издание, Джеймс Стюарт
Конкретная поэтапная программа для текста Стюарта и комментариев показана ниже.Рекомендуемый набор домашних заданий не предоставляется. Учебник затрагивает широкий круг задач, от уровня упражнений до концептуального анализа. Инструктору предлагается назначить широкий круг задач из каждого раздела. Не просто назначайте задачи сверления. Необычные, сложные задачи должны составлять часть каждого домашнего задания.
Программа
Глава 1. Функции и модели
Необязательно. Это глава, посвященная предварительному анализу, и ее можно кратко обсудить или назначить на усмотрение преподавателя.Хотя поступающие студенты должны быть знакомы с темами этой главы, некоторые могут быть плохо подготовлены к расчету. Некоторые преподаватели начали требовать от студентов прохождения диагностического теста на основе этой первой главы. Тест может показать учащемуся, какие области перед расчетом им необходимо улучшить. Многие преподаватели просто пропускают эту главу.
Глава 2: Лимиты и производные
Раздел 2.1
Задачи касательной и скорости: Автор использует понятия касательных и скорости, чтобы мотивировать идею предела.Многие студенты лучше относятся к ограничениям, если им дают какое-то объяснение для их изучения.
Раздел 2.2
Предел функции: Это стандартный нестрогий подход к ограничению. Большинство преподавателей используют эту последовательную версию ограничений, прежде чем применять строгий подход в Разделе 2.4. Студентам полезно использовать большое количество примеров, в основном графических, но также следует использовать некоторые числовые примеры.
Раздел 2.3
Расчет пределов с использованием законов пределов: В этом разделе изложены стандартные теоремы о пределах сумм, разностей, произведений и т. Д. Доказательства следует отложить до тех пор, пока строгое определение пределов не будет дано в разделе 2.4.
Раздел 2.4
Точное определение лимита: Преподаватель должен действовать по своему усмотрению в этом разделе. Этот материал более абстрактный, чем все остальные в этом курсе. Если вы новичок в преподавании, вы можете встретиться с координатором курса или проконсультироваться с некоторыми из ваших коллег по этой теме.При представлении его следует подробно и медленно объяснять. Автор откладывает пределы на бесконечность до раздела 2.6. Вы можете представить точное определение пределов бесконечности, когда дойдете до раздела 2.6.
Раздел 2.5
Непрерывность: Непрерывность – одна из самых важных идей в курсе. Преподаватель должен подробно изучить тему, чтобы в дальнейшем избежать путаницы. В тексте используются последовательные критерии преемственности в точках, а затем обсуждение расширяется до интервалов.Студенты должны знать о непрерывности стандартных функций и о том, как их комбинировать, чтобы получить более сложные непрерывные функции. Студентов следует научить оценивать пределы непрерывных функций с помощью простых замен.
Раздел 2.6
Пределы на бесконечности и горизонтальные асимптоты: Это стандартный раздел. Некоторые студенты могут быть знакомы с вычислением горизонтальных асимптот на уроках алгебры.
Раздел 2.7 и раздел 2.8
Производные финансовые инструменты и темпы изменения и производные финансовые инструменты как функции: Это введение в производные инструменты как предел разницы частных. Учащийся должен знать, что производная представляет собой мгновенную скорость изменения, наклон касательной и скорость частицы. Слишком много студентов выходит из начальных классов по математическому анализу со способностью вычислять сложные производные, практически не имея представления о природе производной.Инструктору рекомендуется на протяжении всего курса подчеркивать интерпретацию того, что нам сообщает производная. Это раздел, с которого начинается эта инструкция. Студенты должны быть ознакомлены с идеей о том, что дифференцируемость означает локальную линейность.
Глава 3: Правила дифференциации
Раздел 3.1
Производные многочленов и экспоненциальные функции: Автор проверяет правило степени для натуральных чисел, но затем утверждает, что оно верно для действительных чисел.После этого он начинает использовать правило силы для реалов. Просто помните об этом факте. Стандартные начальные правила линейности производной представлены и используются для вычисления производных полиномов. Затем автор использует наивный предельный подход к производной естественной экспоненциальной функции.
Раздел 3.2
Правила произведения и коэффициента: Это довольно стандартное представление, использующее эти два мощных правила дифференциации.Инструктор может проверить правила и привести многочисленные примеры. У большинства студентов эта тема не вызывает особых затруднений.
Раздел 3.3
Производные от тригонометрических функций: Материал стандартный. Студенты могут не вспомнить столько триггеров, сколько инструктор сочтет нужным. В некотором роде вы обнаружите, что ваши ученики в основном не могут работать с основными тождествами или решать тригонометрические уравнения.
Раздел 3.4
Цепное правило: Эта тема вызывает беспокойство у учащегося. Проблема начинается с их алгебраической слабости с композицией. Они не могут легко различать составные функции, потому что на самом деле не понимают саму композицию. Преподаватель должен будет представить большое количество примеров.
Раздел 3.5
Неявная дифференциация: Начинающему преподавателю следует сообщить, что эта, казалось бы, простая тема поставит перед их учениками множество проблем.Не подозревайте, что вы сможете быстро освоить этот материал и быстро усвоить его учениками. Помните, они еще не совсем понимают правило цепочки.
Раздел 3.6
Производные логарифмических функций: Автор использует неявное дифференцирование для вывода формулы для производных логарифмов. Этот раздел также включает логарифмическое дифференцирование и проверку правила мощности для действительных чисел. Студентам будет сложно различать функции башни.
Раздел 3.7
Темпы изменений в естественных и социальных науках: В этом разделе подчеркивается скорость изменения и скоростная интерпретация производной. В этом разделе приведены примеры деривативов, используемых в других областях. Студенты должны знать, что деривативы используются не только в математике, но и в других курсах. Раздел также продолжает описание интерпретации производных и напоминает студентам, что производная – это не просто формула.
Раздел 3.8
Экспоненциальный рост и спад: Необязательно. Эта тема действительно должна быть освещена в классах дифференциальных уравнений.
Раздел 3.9
Соответствующие ставки: Эта тема доставляет учащимся некоторые проблемы, поскольку они не понимают правила цепочки. Два основных правила для связанных задач скорости: 1 – дифференцировать по времени и 2 – никогда не заменять числовые значения, пока вы не дифференцируете.Эти два правила должны помочь большинству студентов.
Раздел 3.10
Линейные приближения и дифференциалы: В этом разделе снова рассматривается касательная линия и идет речь о линеаризации функций. Преподаватель может пожелать упомянуть, что это наилучшее полиномиальное приближение первой степени для функции. Студент должен понимать геометрическую интерпретацию dy .
Раздел 3.11
Гиперболические функции: Гиперболические функции будут новыми для большинства студентов.Преподаватель должен охватить их, поскольку они предоставляют дополнительные базовые функции для примеров и интересных задач с ограничениями. Обратные гиперболические функции следует считать необязательными.
Глава 4: Применение дифференциации
Раздел 4.1
Максимальные и минимальные значения: Этот раздел включает определения абсолютных экстремумов, локальных экстремумов и критических значений. Этот раздел посвящен поиску экстремумов непрерывных функций на отрезках.Начинающий инструктор должен подчеркнуть алгебраические аспекты поиска критических значений. Разделы с 4.1 по 4.3 очень важны.
Раздел 4.2
Теорема о среднем значении: Этот раздел включает теорему Ролля и теорему о среднем значении. MVT является строительным блоком для доказательства многих других теорем и требует внимательного представления.
Раздел 4.3
Как производные влияют на форму графика: Этот раздел начинается с теста увеличения и уменьшения.Это, возможно, самое важное, что студенты могут узнать по математике. Далее следует тест первой производной. Автор вводит понятие вогнутости и ее обозначение второй производной. Этот раздел завершается вторым производным тестом. Чтобы хорошо проработать этот раздел, потребуется не один день. Алгебра и тригонометрия в этом разделе могут быть интенсивными. Предупреждение студентам может быть уместным.
Раздел 4.4
Неопределенные формы и правило Госпиталя: Это довольно стандартная презентация.
Раздел 4.5
Краткое описание построения кривых: В этом разделе кратко описаны методы построения графиков. Многие задачи, связанные с тригонометрическими и экспоненциальными функциями, являются сложными. Начинающий инструктор, возможно, пожелает проявить осторожность при постановке некоторых из этих задач на экзаменах.
Раздел 4.6
Построение графиков с помощью исчислений и калькуляторов : опустить.
Раздел 4.5 – последний раздел, рассматриваемый в Math 1530.Раздел 4.6 пропускается в Math 1530, 1540 и 1550.

Элементарные дифференциальные уравнения с краевыми задачами (Бойс, ДиПрима, Мид, 11-е издание)
Раздел	Тема	Домашнее задание
2,1	Линейные уравнения; Метод интегрирующих факторов	2c, 4c, 6c, 9, 12, 14 (b, c), 21
2.2	Разделимые дифференциальные уравнения	2, 3, 5, 10 (а, в), 14 (а, в), 18
2,3	Моделирование с помощью дифференциальных уравнений первого порядка	1, 2, 5, 17 (а, б), 18 (а, б)
2,6	Точные уравнения и интегрирующие множители	1, 2, 4, 7, 11, 15, 19, 20 (см. Задачу 17)

3,1	Однородные дифференциальные уравнения с постоянными коэффициентами	3, 6, 10, 13, 15, 17
3. 2	Решения линейных однородных уравнений; Вронскианец	3, 7, 9, 10, 12, 13, 14, 15, 18, 19, 21, 24, 25, 27, 28
3,3	Комплексные корни характеристического уравнения	1, 6, 11, 12, 13, 15, 19
3,4	Повторяющиеся корни; Редукция заказа	1, 2, 6, 10, 13, 19, 20
3,5	Неоднородные уравнения; Метод неопределенных коэффициентов	1, 2, 5, 12, 14
3.6	Изменение параметров	4, 6, 9, 10, 13
3,7	Механические колебания	1, 4, 5, 8, 17, 18 (а, б)
3,8	Принудительные периодические колебания	4, 5, 7, 8

6,1	Определение преобразования Лапласа	1-3, 4 (а, в), 6, 10, 12, 16
6,2	Решение задач начального значения	3, 6, 7, 11, 15, 16, 17
6. 3	Шаговые функции	1, 2, 5, 7, 9, 10, 14, 15, 16, 30
6,4	Дифференциальные уравнения с разрывными вынуждающими функциями	1-4, 9, 11 (а, б)
6,5	Импульсные функции	1, 3, 4, 6, 10 (а, б)
6,6	Интеграл свертки	1 (а), 4, 5, 7, 9, 11, 12

2.7	Численные аппроксимации: метод Эйлера	1,2,4
8,1	Метод Эйлера или касательной линии	4, 5, 8, 22

Плоские системы дифференциальных уравнений (дополнительные примечания)
1	Введение	1,1, 1,2
2	Некоторые понятия из теории матриц и линейной алгебры	2. 1, 2,2 (1,4,6,7,8), 2,3 (1), 2,4 (3), 2,5 (1,2,3)
3	Общая теория линейных систем 2×2	3,1, 3,3, 3,4
4	Случай 1 (однородный, линейный, постоянный коэффициент)	4,1, 4,2, 4,4, 4,5
5	Корпус 2	5,1, 5,2, 5,3
6	Корпус 3	6,1, 6,2, 6,4, 6,5
7	Решения негосударственных систем	2.6 (1,3), 7,1, 7,3, 7,4
8	Качественные методы	8,1, 8,2, 8,3
9	Линеаризация нелинейных систем в изолированных точках покоя (если позволяет время)	9,1, 9,4, 9,5, 9,7

Дифференциал – это… Что такое Дифференциал?

Дифференциал и производная | Математика, которая мне нравится

Производная и дифференциал

Производная и дифференциал

Дифференциал

1.Понятие дифференциала.

2. Геометрический смысл дифференциала.

3.Свойства дифференциала.

3.Дифференциал сложной функции.

4.

Разница между дифференциальным и производным (Математика и статистика)

Что такое дифференциал?

Что такое производная?

Разница между дифференциальным и производным

Определение дифференциала против.

Дифференциальные отношения против. производный

Представление Дифференциала Vs. производный

Дифференциальный и производный: Сравнительная таблица

Краткое изложение дифференциала производный

Решение высшей математики онлайн

Основные правила дифференцирования, применяемые в математике

Дифференциал функции

Определение дифференциала функции

Геометрическое значение дифференциала функции

Свойства дифференциала

Формальная инвариантность дифференциала

Дифференциальные уравнения | Математика

World Web Math: нотация

Онлайн-курс по дифференциальным уравнениям – Расчет расстояний

Онлайн-курс по дифференциальным уравнениям Вводные видеоролики

Введение в онлайн-курс по дифференциальным уравнениям

Список курсов Университета Роджера Вильямса: Математика 317 – Дифференциальные уравнения

Материалы курса по дифференциальным уравнениям Онлайн-курс

Старшеклассники – курс дифференциальных уравнений

Продвинутый математический план средней школы для старших классов

После исчисления AP

Что такое обыкновенные дифференциальные уравнения?

Дифференциальные уравнения Примеры учебной программы

Это похоже на программный код!

Расчет расстояний – Отзывы студентов

Дифференциальное исчисление – обзор

2.5 Математические основы динамики Фалька II: системы

Вариационное исчисление и дифференциальные уравнения с частными производными

Информация журнала

Показатели журнала

Syllabus for Math 1530: «Дифференциальное исчисление»

Базовые навыки, которые студенты должны приобрести в течение курса

Текст: «Исчисление, ранние трансцендентальные представления», 8-е издание, Джеймс Стюарт

Программа

Глава 1. Функции и модели

Глава 2: Лимиты и производные

Глава 3: Правила дифференциации

Глава 4: Применение дифференциации

Оставить комментарий Отменить ответ