Дифференциал функции
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
или
или же
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину (см. рисунок).
Дифференциал функции в точке x и обозначают
или
Следовательно,
(1)
или
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а – наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
(3)
или
(4)
Пример 1. Найти дифференциалы функций:
1) ;
2) ;
3) ;
4) .
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) ;
2) ;
3) ;
4) .
Найти дифференциалы самостоятельно, а затем посмотреть решения
Пример 2.
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции
в точке x.
В основном же задачи на дифференциалы – это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
(С – постоянная величина) (5)
(6)
(7)
(8)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .
Одно из особеннейших свойств дифференциала – инвариантность формы дифференциала в случае сложных функций.
Установленное во втором параграфе приближенное равенство
или
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
а
то
или
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид
Положим
тогда
Следовательно,
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Решение. Число
является одним из значений функции
Так как производная этой функции
то формула (11) примет вид
Полагая
и
получаем
(табличное значение
).
Вычислить приближенно самостоятельно, а затем посмотреть решение
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:
(12)
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
(13)
Если точное число неизвестно, то
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину.
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.
Решение. Рассмотрим функцию
Её производная равна
а формула (11) примет вид
В данном случае было бы нерационально вычислять приближенно следующим образом:
так как значение
не является малым по сравнению со значением производной в точке
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3.
Тогда
Теперь, полагая
получим
Умножая на 4/3, находим
Принимая табличное значение корня
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
Весь блок “Производная”
Поделиться с друзьями
Дифференциал (математика) – это… Что такое Дифференциал (математика)?
Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.
Обозначения
Обычно дифференциал функции обозначается . Некоторые авторы предпочитают обозначать шрифтом прямого начертания, желая подчеркнуть, что дифференциал является оператором.
Дифференциал в точке обозначается , а иногда или , а также , если значение ясно из контекста.
Соответственно, значение дифференциала в точке от может обозначаться как , а иногда или , а также , если значение ясно из контекста.
Использование знака дифференциала
Определения
Для функций
Дифференциал функции в точке может быть определён как линейная функция
где обозначает производную в точке .
Таким образом есть функция двух аргументов .
Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция линейно зависящая от и для которой верно следующее соотношение
Для отображений
Дифференциалом отображения в точке называют линейный оператор такой, что выполняется условие
Связанные определения
- Отображение называется дифференцируемым в точке если определён дифференциал .
Свойства
- Матрица линейного оператора равна матрице Якоби; её элементами являются частные производные .
- Отметим, частные производные могут быть определены в точке, где дифференциал не определён.
- Дифференциал функции связан с её градиентом следующим определяющим соотношением
История
Термин «дифференциал» введён Лейбницем. Изначально применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики за исключением нестандартного анализа.
Вариации и обобщения
Литература
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления»
Производная и дифференциал
Дифференциальное исчисление – это раздел математики, который исследует свойства функций, которые заданы на интервалах (сплошных множествах), с помощью определения предела функций.
Свойство непрерывности свидетельствует о том, что точке х0 при малом отклонении аргумента Δx от х0 функция отклоняется мало.
В связи с этим, непрерывную функцию в окрестности точки х0, приближенно можно заменить константой, значением в х0. В таком случае, при Δx?0 к нулю стремится абсолютная ошибка приближения. Однако данная аппроксимация не отражает изменения функции при переходе переменной х в точке 0 – убывая или возрастая, медленно или быстро. Для того, чтобы это выяснить и введены производная и дифференциал, которые и дают более точную аппроксимацию функции в окрестности х0 линейной функцией, а не константой. Производная и дифференциал отражает величину и тенденцию изменения в точке х0 функции.
Производная и дифференциал на наглядном примере выглядит так. Возьмем функцию y = f ( x), которая имеет действительные значения и задана на оси R. Внутреннюю точку x0 ε I фиксируем и берем еще любую точку xεI . Приращением независимой переменной в точке х0 является разность Δx = x – x0. Предел разностного отношения, при котором х стремится к х0 называется производной функции f (x) в точке х0.
Функция, для которой возможно разложение, называется дифференцируемой в точке х0. Дифференциалом функции f в точке х0 называется слагаемое f’ (х0)(х-х0). Таким образом, наличие в точке производной эквивалентно и дифференцируемости в этой же точке.
Дифференциал также имеет и специальное обозначение:
df(x0)=dy(x0)= f’ (х0)(х-х0)
Создано дифференциальное исчисление одновременно, а также независимо друг от друга Готфиридом Вильгельмом Лейбницем и Исааком Ньютоном.
Производная и дифференциал | |||||||||||||
| Приращение функции y = f(x), соответствующее приращению Δx аргумента x | |||||||||||||
| Δy = f(x + Δx) – f(x) | |||||||||||||
Определение производной | |||||||||||||
| |||||||||||||
| Геометрически y’ = f'(x) – угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой x | |||||||||||||
Правила дифференцирования | |||||||||||||
| c’ = 0 (cu)’ = cu’ (u + v)’ = u’ + v’ (u – v)’ = u’ – v’ (uv)’ = u’v + uv’ | |||||||||||||
где y = f(z) и z = φ(x), т. е y = f(φ(x)). | |||||||||||||
| |||||||||||||
Производные элементарных функций | |||||||||||||
| |||||||||||||
| |||||||||||||
| (sinx)’ = cosx | |||||||||||||
| (cosx)’ = – sinx | |||||||||||||
| |||||||||||||
| |||||||||||||
| (secx)’ = secx * tgx | |||||||||||||
| (cosecx)’ = -cosecx * ctgx | |||||||||||||
| |||||||||||||
| |||||||||||||
Свойства дифференциала | |||||||||||||
| d(af(x)) = a * df(x) | |||||||||||||
| |||||||||||||
| df(x) = f'(x)dx | |||||||||||||
| da = 0 (a = const) | |||||||||||||
| d(ax + b) = Δ(ax + b) = a Δx | |||||||||||||
Дифференциал второго порядка функции y = f(x), | |||||||||||||
| |||||||||||||
Производные высших порядков некоторых функций | |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| если правый предел существует | |||||||||||||
Формула Тэйлора с остаточным членом в форме Лагранжа | |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
Формула Маклорена | |||||||||||||
| |||||||||||||
| где ξ – такое число, что 0 |
..(m – n + 1)x
..Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение».
За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту [email protected]
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Математический портал. Высшая математика. Математический анализ.
Литература: Сборник задач по математике.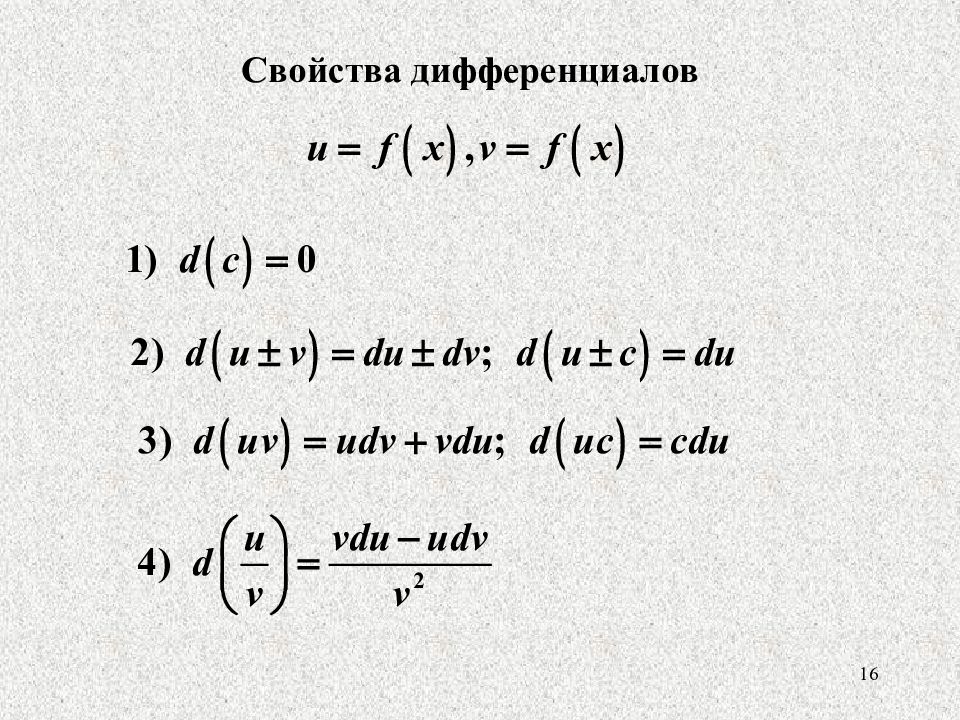
Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Определение. Функция $y=f(x)$ называется дифференцируемой в точке $x_0,$ если ее приращение $\Delta y(x_0, \Delta x)$ может быть представлено в виде $$\Delta y(x_0, \Delta x)=A\Delta x+o(\Delta x).$$
Главная линейная часть $A\Delta x$ приращения $\Delta y$ называется дифференциалом этой функции в точке $x_0,$ соответствующим приращению $\Delta x,$ и обозначается символом $dy(x_0, \Delta x).$
Для того, чтобы функция $y=f(x)$ была дифференцируема в точке $x_0,$ необходимо и достаточно, чтобы существовала производная $f'(x_0),$ при этом справедливо равенство $A=f'(x_0).$
Выражение для дифференциала имеет вид $$dy(x_0, dx)=f'(x_0)dx,$$ где $dx=\Delta x.$
Свойства дифференциала:1. $d(C)=0,$ где $C -$ постоянная;
2. $d(C_1u+C_2v)=C_1du+C_2dv;$
3. $d(uv)=udv+vdu;$
4.
2}.$
Ответ: $\frac{x+y}{x-y}dx.$
математический-анализ / Дифференциал независимой переменной. / Математика
Объявляю конкурс на лучшее определение понятия “дифференциал независимой переменной”.
Пояснение. Это понятие только кажется простым, на самом у него есть много разных интерпретаций. Например, в физике это просто достаточно малая величина, которая часто имеет ограничение не только сверху, но и снизу (я уже приводил пример распределения температуры в среде, аналогичная ситуация с давлением, плотностью и т.д.). Хотелось бы услышать мнения, как наиболее корректно определить понятие дифференциала независимой переменной в матанализе?
Дополнение для DocentI. Т.к. лимит комментариев исчерпан, пишу здесь. Я прекрасно знаю содержание учебников матана, я сам все это читаю. Если бы там содержался ответ на мой вопрос, я бы его не задавал. В матане совершенно четко и строго определены понятия “предел” и “производная”, здесь даже нечего обсуждать.{b}f(x)dx$% ? Ведь это предел интегральных сумм!
Я жду ответ на вопрос в виде “Дифференциал независимой переменной $%dx$% – это …”, где вместо точек стоит математическое определение.
Дополнение 3 для DocentI. Рождение раздела математики под названием Математический анализ произошло практически одновременно в двух близких, но все-таки различных формах – Ньютона и Лейбница. У Ньютона все формулировалось через пределы, у Лейбница – через бесконечно малые, как самостоятельные сущности. И обе эти интерпретации всегда сосуществовали. Во второй половине 20 века в теоретической математике прочно утвердилась Ньютоновская интерпретация, которую Вы блестяще изложили в своем ответе. Но во многих более прикладных облестях, в частности в физике, всегда больше склонялись к подходу Лейбница. Возьмите любой учебник общей физики, как там выводится практически любое дифференциальное уравнение? Что-то типа “выделим параллелепипед $%dxdydz$% и подсчитаем количество частиц в нем” и т.д. Но в этом случае $%dx,dy,dz$% не могут быть любыми! Они дожны быть достаточно малыми (но не совсем, а так, чтобы достаточное количество частиц туда бы все-таки поместилось)! Меня, между прочим, еще в студенческие годы очень удивляло это идеологическое противоречие между математикой и физикой. Нужно сказать, что Лейбнецевский подход все-таки нет-нет, но проявлялся в математике. Например, трансфинитные числа можно рассматривать как “обратные бесконечно малые”. Сейчас на основе Лейбнецевского подхода развивается нестандарнный анализ.В общем, дуализм в самом-самом основании математического анализа имеет место, я просто хотел это подчеркнуть и, возможно, увидеть какие-то интересные идеи на этот счет.
Дополнение 4 (для DocentI). Да, аксиома Архимеда для бесконечно малых не выполняется, но ведь в математике сейчас известно достаточно много неархимедовых полей. Вопрос, конечно, куда деть бесконечно малые на числовой прямой? Между действительными числами они не поместятся – там все плотно. Если считать, что они в ортогональном направлении “утолщают” прямую – нелогично, т.к. они должны легко превращаться в действительные приращения. Единственный вариант – считать, что они входят в структуру действительного числа, т.е. являются элементами внутренней структуры точки. Весьма экзотично – но ничему не противоречит.
Методы | |
1. Организационный момент – взаимное приветствие – проверка состава студентов | Беседа Визуально |
2. Проверка знаний студентов по теме «Производная функции»: Вопросы:
– производная суммы или разности двух функций – производная произведения функций – производная частного функций – производная сложной функции с) Производные основных элементарных функции d) Применение производной Индивидуальные задания по нахождению производных | Устный фронтальный опрос Индивидуальная работа по карточкам с элементами взаимоконтроля |
3. Подведение итогов проверки знаний студентов | Анализ, комментарии преподавателя |
4. Сообщение темы и целей урока. Начальная мотивация учебной познавательной деятельности. | Беседа |
5. Изложение нового материала по теме «Дифференциал функции» | Объяснительно-иллюстративный с применением мультимедиа |
6. Закрепление изученного материала.
| Решение задач письменно с комментариями преподавателя |
6. Подведение итогов урока, выставление оценок. | Обобщение с комментариями преподавателя |
7. Задание для самостоятельной работы студентов во внеурочное время: сборник домашних работ, работа №5, конспект | Пояснение |
3 вариант | |
2 вариант | 4 вариант | 3 вариант |
2 ВАРИАНТ | 4 ВАРИАНТ |
– Что такое дифференциал?
Правильный вопрос – не “Что такое дифференциал?” но «Как ведут себя дифференциалы?».
Позвольте мне объяснить это с помощью аналогии. Предположим, я научу вас всем правилам сложения и умножения рациональных чисел. Затем вы спрашиваете меня: «Но что такое , – рациональные числа?»
Ответ: это все, что подчиняется этим правилам. Теперь, чтобы это имело смысл, мы должны знать, что есть по крайней мере одна вещь, которая подчиняется этим правилам.
Итак, математики решают эту проблему следующим образом: сначала они определяют упорядоченные пары целых чисел. Затем они определяют две упорядоченные пары $ (a, b) $ и $ (c, d) $ как эквивалент , если $ ad = bc $. Затем они определяют класс эквивалентности как любой набор упорядоченных пар, все из которых эквивалентны друг другу, и ни одна из которых не эквивалентна чему-либо вне этого набора. Затем они определяют рациональное число $ a / b $ как класс эквивалентности упорядоченной пары $ (a, b) $, где $ a $ – любое целое число, а $ b $ – любое целое число, отличное от нуля.Затем они описывают сложение и умножение классов эквивалентности в терминах лежащих в основе упорядоченных пар. Например, они определяют $ a / b + c / d $ равным $ (ad + bc) / bd $ (помня, что каждое из этих выражений обозначает набор упорядоченных пар. Затем они проверяют, имеет ли определение смысл – – например, если $ a / b = e / f $, тогда $ a / b + c / d $ лучше равняется $ e / f + c / d $, поэтому они проверяют это и множество других свойств. , они говорят: “Хорошо. Мы нашли структуру, которая подчиняется всем правилам” рациональных чисел “, поэтому мы знаем, что рациональные числа существуют.Теперь, когда мы это знаем, мы можем перестать думать обо всей этой структуре и просто работать с правилами.
Итак, никто никогда не думает о рациональном числе 2/3 как о наборе упорядоченных пар, даже несмотря на то, что, согласно вышеизложенному, это то, что оно «есть».
Дифференциалы такие же, за исключением того, что их построение значительно сложнее, чем построение рациональных чисел.
Но вы начали работать с рациональными числами еще в начальной школе, задолго до того, как научились их составлять.Все, что вам нужно было знать, – это правила манипулирования ими. Много позже, если вам было интересно, вы спросили кого-нибудь: «Что такое – это рациональное число?» и, возможно, у вас есть объяснение, подобное тому, которое я вам только что дал.
Важно знать, что такая конструкция существует, потому что она гарантирует, что правила, которые вы использовали, не приведут к противоречию. Но для того, чтобы усвоить правила, совсем не обязательно знать конструкцию.
Итог: было бы безумием ждать, пока у вас будет объяснение на этом уровне, прежде чем вы начнете заниматься арифметикой рациональных чисел.
Если вам интересно и любопытно – а это похоже на то, – вы со временем научитесь строить дифференциалы на строгой основе. Я не использую эту конструкцию в этом ответе, потому что рассмотрение всех деталей займет слишком много времени. Но это аналог построения рациональных чисел. И, как и в этом случае, единственная цель построения – показать, что или удовлетворяет правилам, с которыми вы работали все эти годы, чтобы гарантировать, что эти правила не противоречат друг другу.
Реальный анализ– строгое определение «дифференциала»
Я думаю, что версия с дифференциальными формами заслуживает более подробного описания:
Пусть $ x, y, z, \ ldots $ – все используемые (скалярные) переменные. Напишите $ p $ для кортежа, который присваивает значения этим переменным: $ (x_p, y_p, z_p, \ ldots) $. Тогда переменная величина – это (математическая) функция, которая присваивает (действительное или векторное) значение каждому кортежу $ p $. Обратите внимание, что переменных являются четко определенными переменными величинами, заданными
.$$ x (x_p, y_p, z_p, \ ldots) = x_p \\ y (x_p, y_p, z_p, \ ldots) = y_p \\ z (x_p, y_p, z_p, \ ldots) = z_p \\ \ vdots $$
Для каждого переменного количества $ E $ мы собираемся определить другое количество $ dE $.В частности, если $ E $ является вещественной переменной величиной, дифференциал $ E $ $ dE $ будет (частичной функцией), которая присваивает каждому назначению $ p $ линейное преобразование из векторного пространства назначений. в векторное пространство действительных чисел (при сложении). Если $ E $ – векторная переменная, $ dE $ отобразит каждый $ p $ в линейное преобразование из векторного пространства назначений в векторное пространство, где $ E $ принимает свои значения (это обобщение определения для вещественных переменных. ).
Если $ \ Delta p $ – небольшое смещение присваивания $ p $, мы хотим, чтобы $ E (p) + dE (p) \ Delta p $ было хорошим приближением к $ E (p + \ Delta p) $. . Прежде всего отметим, что $$ dE (p) \ Delta p \ to 0 \ text {as} \ Delta p \ to 0 $$ по определению, поскольку мы хотим, чтобы $ dE (p) $ было линейным. Так что если $$ E (p + \ Delta p) \ to 0 \ text {as} \ Delta p \ to 0 $$ т.е. $ E $ – это непрерывных , $ E (p) + dE (p) \ Delta p $ никогда не будет хорошим приближением к $ E (p + \ Delta p) $. Итак, мы собираемся рассматривать только точки $ p $, где $ E $ непрерывно (таких точек может и не быть).2 $ переходят в 0 на различных скоростях как $ x \ на 0 $. Мы можем использовать эту идею, чтобы более точно определить $ dE (p) $. Как минимум, мы хотим, чтобы $ E (p) + dE (p) \ Delta p $ перешло в $ E (p) $ быстрее, чем $ \ Delta p $ перешло в 0. Мы можем записать это формально (строго) в виде $$ \ frac {E (p + \ Delta p) – E (p) – dE (p) \ Delta p} {\ | \ Delta p \ |} \ to 0 \ text {as} \ Delta p \ to 0 $$ Обратите внимание, что это в точности то же самое, что и определение $ dE (p) $ как (векторной) производной от $ E $ в точке $ p $. Уникальность линейного преобразования (если оно существует), удовлетворяющего этому свойству (наилучшее линейное приближение к $ E $ при $ p $ ), является основной теоремой, доказываемой в любом учебнике векторного анализа.
Переменная величина $ f (x) $ на самом деле является композицией: $ f (x) (p) $ на самом деле означает $ f (x (p)) $. Итак, правило $$ d (f (x)) = f ‘(x) dx $$ (что на самом деле означает $$ d (f (x)) (p) = f’ (x (p)) (dx (p )) $$) – это простое применение цепного правила.
Разница между дифференциалом и производной
Чтобы лучше понять разницу между дифференциалом и производной функции, вам необходимо сначала понять концепцию функции.
Функция – это одно из основных понятий в математике, которое определяет взаимосвязь между набором входов и набором возможных выходов, где каждый вход связан с одним выходом.Одна переменная является независимой, а другая – зависимой.
Концепция функции – одна из наиболее недооцененных тем в математике, но она необходима для определения физических отношений. Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x некоторой формулой. Скажем, если на входе 6, а функция должна прибавить 5 ко входу 6. Результат будет 6 + 5 = 11, что и будет вашим выходом.
В математике есть несколько исключений, или, можно сказать, задачи, которые нельзя решить обычными методами геометрии и алгебры.Для решения этих задач используется новый раздел математики, известный как исчисление.
Исчисление фундаментально отличается от математики, которая не только использует идеи геометрии, арифметики и алгебры, но также занимается изменением и движением.
Исчисление как инструмент определяет производную функции как предел определенного вида. Концепция производной функции отличает исчисление от других разделов математики. Дифференциальный – это подполе исчисления, которое относится к бесконечно малой разнице в некоторой переменной величине и является одним из двух основных разделов исчисления.Другая ветвь называется интегральным исчислением.
Что такое дифференциал?
Дифференциал – это один из основных разделов исчисления, наряду с интегральным исчислением. Это подполе исчисления, которое имеет дело с бесконечно малыми изменениями некоторой переменной величины. Мир, в котором мы живем, полон взаимосвязанных величин, которые периодически меняются.
Например, площадь круглого тела, которая изменяется при изменении радиуса, или снаряда, который изменяется в зависимости от скорости.Эти изменяющиеся сущности, в математических терминах, называются переменными, а скорость изменения одной переменной по отношению к другой является производной. А уравнение, которое представляет собой взаимосвязь между этими переменными, называется дифференциальным уравнением.
Дифференциальные уравнения – это уравнения, содержащие неизвестные функции и некоторые их производные.
Что такое производная?
Понятие производной функции – одно из самых мощных понятий в математике.Производная функции обычно представляет собой новую функцию, которая называется производной функцией или функцией скорости.
Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной по отношению к изменению значения независимой переменной. Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной. Он измеряет, насколько крутым является график функции в определенной точке графика.
Проще говоря, производная – это скорость, с которой функция изменяется в определенной точке.
Разница между дифференциалом и производной
Определение дифференциала Vs. Производная
И термины «дифференциал», и «производная» тесно связаны друг с другом с точки зрения взаимосвязи. В математике изменяющиеся объекты называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.
Уравнения, определяющие взаимосвязь между этими переменными и их производными, называются дифференциальными уравнениями.Дифференциация – это процесс поиска производной. Производная функции – это скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал – это фактическое изменение функции.
Взаимосвязь дифференциала и дифференциала. Производная
Дифференциация – это метод вычисления производной, которая представляет собой скорость изменения выхода y функции по отношению к изменению переменной x.
Проще говоря, производная относится к скорости изменения y по отношению к x, и это соотношение выражается как y = f (x), что означает, что y является функцией x.Производная функции f (x) определяется как функция, значение которой порождает наклон f (x), где она определена, и f (x) дифференцируема. Это относится к наклону графика в данной точке.
Представление дифференциала Vs. Производная
Дифференциалы представлены как d x, d y, d t и т. Д., Где d x представляет небольшое изменение x, d y представляет небольшое изменение y и d т – небольшое изменение т.При сравнении изменений связанных величин, где y является функцией x, дифференциал d y может быть записан как:
d y = f ’ (x) d x
Производная функции – это наклон функции в любой точке и записывается как d / d x. Например, производная sin (x) может быть записана как:
d / d x sin (x) = sin (x) ’ = cos (x)
Дифференциальный vs.Производная: сравнительная таблица
Сводка дифференциала против Производная
В математике скорость изменения одной переменной по отношению к другой называется производной, а уравнения, которые выражают взаимосвязь между этими переменными и их производными, называются дифференциальными уравнениями. Короче говоря, дифференциальные уравнения включают производные, которые фактически определяют, как величина изменяется по отношению к другой. Решая дифференциальное уравнение, вы получаете формулу для величины, не содержащую производных.Метод вычисления производной называется дифференцированием. Проще говоря, производная функции – это скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал – это фактическое изменение функции.
Сагар Хиллар – плодовитый автор контента / статей / блогов, работающий старшим разработчиком / писателем контента в известной фирме по обслуживанию клиентов, базирующейся в Индии. У него есть желание исследовать разноплановые темы и разрабатывать высококачественный контент, чтобы его можно было лучше всего читать.Благодаря своей страсти к писательству, он имеет более 7 лет профессионального опыта в написании и редактировании услуг на самых разных печатных и электронных платформах.Вне своей профессиональной жизни Сагар любит общаться с людьми разных культур и происхождения. Можно сказать, что он любопытен по натуре. Он считает, что каждый – это опыт обучения, и это приносит определенное волнение, своего рода любопытство, чтобы продолжать работать. Поначалу это может показаться глупым, но через некоторое время это расслабляет и облегчает начало разговора с совершенно незнакомыми людьми – вот что он сказал.”
Последние сообщения Sagar Khillar (посмотреть все): Если вам понравилась эта статья или наш сайт. Пожалуйста, расскажите об этом. Поделитесь им с друзьями / семьей.
Cite
APA 7
Khillar, S. (20 сентября 2018 г.). Разница между дифференциалом и производной. Разница между похожими терминами и объектами. http://www.differencebetween.net/science/mat Mathematics-statistics/difference-between-differential-and-derivative/.
MLA 8
Хиллар, Сагар.«Разница между дифференциалом и производной». Разница между похожими терминами и объектами, 20 сентября 2018 г., http://www.differencebetween.net/science/mat Mathematics-statistics/difference-between-differential-and-derivative/.
| ’62 Центр театра и танца, 62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Программа позитивных действий, Хопкинс-холл, | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотостудия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / фотостудия, Spencer Studio Art | 597-3193 | |
| Asian Studies, Hollander | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочный домик, Озеро Онота | 443-9851 | |
| Тренеры | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическая культура | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
| Центр экологических исследований, класс 1966 г. Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория наук об окружающей среде, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабоведение, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Холландер | 597-2391 | 597-3028 факс |
| Языковой кабинет | 597-3260 | |
| Россия, Холландер | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молельная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Химия, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| Маршал колледжа, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Операции по развитию, Мирс-Уэст | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс-Уэст | 597-4151 | 597-4178 факс |
| Почтовые службы для выпускников / разработчиков, Мирс-Уэст | 597-4369 | |
| Девелопмент, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Grants Office, Mears West | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Mears | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Веб-команда, Саутвортская школа | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Conferences & Events, Парески | 597-2591 | 597-4748 факс |
| Запросы Elm Tree House, Mt.Ферма Надежды, | 597-2591 | |
| Офис контролера, Хопкинс Холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Financial Information Systems, Hopkins Hall | 597-4023 | |
| Purchasing Cards, Hopkins Hall | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Jenness House | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Grill, Парески | 597-4585 | |
| Булочная, Парески | 597-4511 | |
| Общественное питание, факультет | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Парески | 597-2889 | |
| Экономика, Шапиро | 597-2476 | 597-4045 факс |
| Английский, Холландер | 597-2114 | 597-4032 факс |
| Сооружения, сооружения, служебное здание | 597-2301 | |
| Запрос на получение автомобиля в колледже | 597-2302 | |
| Экстренная ситуация вечером / в выходные дни | 597-4444 | |
| Запросы на работу производственных помещений | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Клуб преподавателей, Дом факультетов / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Geosciences, Clark Hall | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Программа магистратуры по истории искусств, Кларк | 458-2317 факс | |
| Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Медицинское просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с опасностью для жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Хопкинс Форест | 597-4353 | |
| Центр Розенбурга | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Погодная линия (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курса, Drop Box для офисных услуг | 597-4090 | |
| Центр ссуды на оборудование, Додд Приложение | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [электронная почта] | 597-4090 | |
| Медиауслуги и справочная информация в классе | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / телефоны | 597-4090 | |
| Междисциплинарные исследования, Hollander | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Офис в Бостоне | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Справедливость и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Хопкинс-холл | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Performance Studies, ’62 Center | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр старой обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс-холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Арендное жилье для преподавателей / сотрудников | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 Дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Службы каталогизации / метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Schow, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Вовлеченность студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Паресский почтовый кабинет | 597-2150 | |
| Устойчивое развитие / Центр Зилха, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямса | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| вице-президент по кампусной жизни, Хопкинс-холл, | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрированию, Hopkins Hall | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Williams Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Хопкинс-холл | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
Инженерная математика: Изучите дифференциальные уравнения
Что, если бы я сказал вам, что существует концепция инженерной математики : Дифференциальные уравнения, , которая настолько универсальна во всем, что мы делаем, что она почти обязательна хотя бы знать, что это такое, если не владеть им? Вы мне поверите? Кроме того, что, если бы я добавил, что эта концепция чаще всего ассоциируется с инженерной математикой , но ее можно найти в экономике, развитии технологий и так далее? Как насчет сейчас? Что ж, такая концепция действительно существует, и она называется дифференциальными уравнениями, которая широко используется в инженерной математике .В этом курсе «Инженерная математика: Дифференциальные уравнения» мы будем выяснять и решать дифференциальные уравнения – читайте дальше, если я вас заинтересовал.
В чем смысл решения дифференциальных уравнений?
Если математика – это последнее, что в этом мире ассоциируется со словом «развлечение», вы, вероятно, не очень обрадуетесь, узнав, что обыкновенные дифференциальные уравнения можно найти почти везде и где угодно в нашей повседневной жизни. Вдобавок ко всему, во многих местах, предлагающих карьерные возможности, на самом деле очень важно знать процессы решения дифференциальных уравнений, будь то однородные дифференциальные уравнения или другие.Но почему это понятие так важно? Какой смысл знать разницу между разделимыми дифференциальными уравнениями и обыкновенными? Что ж, различия на самом деле довольно заметны.
Проще говоря, обыкновенные дифференциальные уравнения – это математические уравнения, которые используются для связи функций с их производными. Функции обычно представляют собой какую-то физическую величину, а производные обозначают скорость изменения. Уравнение используется для определения отношения между этими двумя.Как вы, наверное, догадались, эти типы отношений чрезвычайно распространены во всех сферах жизни (биология, химия, экономика) – вот почему очень важно знать методы решения дифференциальных уравнений – однородные дифференциальные уравнения, разделяемые дифференциальные уравнения и все, что связано с между.
Почему этот курс?
Хорошо, я доказал вам, что знание методов решения дифференциальных уравнений важно – но почему вы должны получать эту информацию от меня? Почему бы не выбрать другое руководство? Что ж, я преподаю математику в университете последние 15 лет – я опубликовал множество успешных рукописей и имею бесчисленный опыт решения дифференциальных уравнений.Я говорю все это не для того, чтобы хвастаться своими достижениями – я говорю это для того, чтобы вы поняли мою гарантию качества этого курса. Выбрав этот учебник, вы можете быть уверены, что получите информацию только самого высокого качества.
Вдобавок к этому, вы можете быть уверены, что, закончив этот курс дифференциальных уравнений, вы получите гораздо более широкое и глубокое понимание концепции дифференциальных уравнений (при условии, что вы, конечно, приложите усилия). Я научу вас шаг за шагом решать дифференциальные уравнения.Вам не нужен какой-либо предыдущий опыт работы в этой области, чтобы начать обучение с этого курса – мы возьмем все сверху, поэтому у вас будет возможность либо изучить все, либо пересмотреть его, в зависимости от ваших предыдущих навыков. Не упустите эту возможность – зарегистрируйтесь сегодня и изучите все методы решения дифференциальных уравнений!
Этот курс охватывает все области, связанные с инженерией, физикой, экономикой, прикладной химией, биоматематикой, медицинскими науками, затратами и менеджментом, банковским и финансовым сектором, коммерцией и бизнесом, технологиями и многими другими областями.
Благодаря широкому применению во всех сферах жизни, это самая актуальная и актуальная тема в современном мире. Он описывает физическое поведение объектов и скорость их изменения в особых обстоятельствах.
Я описал различные особенности и решения обыкновенных уравнений и уравнений в частных производных вместе с преобразованием Лапласа.
Курс имеет свою ценность с точки зрения его применения и преподавания во всех областях.
Степень и порядок дифференциального уравнения
Разделение переменных и различные примеры вместе с деталями
Решения однородных и неоднородных дифференциальных уравнений первого порядка
Решения точных дифференциальных уравнений
Решения неточно дифференциальных уравнений
Интегрирующий коэффициент
Решения дифференциальных уравнений первого порядка по ортогональным траекториям
Решения линейных дифференциальных уравнений первого порядка
Решения дифференциальных уравнений высшего порядка
Преобразование Лапласа и его приложение
Производные
Функции нескольких переменных
Производные n-го порядка
Гарантия возврата денег
Это не похоже на то, что я зря потратил время где-нибудь на курсе.Я даю вам подлинные презентации содержания курса. Поэтому я обещаю вам, что вы не потратите зря свои деньги. Также Udemy имеет 30-дневную гарантию возврата денег, и если вы чувствуете, что курс не такой, как вы искали, вы можете вернуть свои деньги.
ЧТО СПРАШИВАЮТ О МОИХ КУРСАХ
Вот некоторые отзывы студентов о моих курсах.
1- Brava Man: Отличный курс !!
Преподаватель очень хорошо осведомлен и подробно и методично излагает концепции квантовой физики.
Мы рассмотрели такие аспекты, как исследование и внедрение, на примерах, которым мы можем следовать в дополнение к реальным математическим задачам, которые нам предлагают решить.
2- Манокаран Масикова: Это хороший курс для изучения квантовой механики с базового уровня, и он объяснил на примерах, чтобы понять концепцию.
3- Д-р Б. Баскаран: очень приятно участвовать в курсе, а также очень интересно и полезно.
4- Машрур Бхуйян: Ну, в настоящее время я студент инженерного факультета и забыл основы своего исчисления.но этот курс помог мне получить хорошее представление о дифференциации и интеграции. В целом метод обучения хорош.
5- Kaleem Ul Haq: Действительно отличные объяснения, и каждый шаг хорошо объясняет. Мне нравится этот курс. Он знакомый преподаватель математического анализа. Я видел много лекций этого инструктора перед тем, как пройти этот курс.
Надеюсь, вы присоединитесь ко мне в этом курсе
AD CHAUHDRY
Дифференциальные уравнения – История и обзор | Хесус Наджера
Математики и физики часто не во всем согласны.Одна неопровержимая истина, которая, кажется, пронизывает каждую тему STEM и объединяет обе стороны, однако, это принципиальное убеждение, что анализ динамических отношений между отдельными компонентами приводит к большему пониманию системы в целом. В отличие от более абстрактных тем, исследуемых в этой серии, таких как теория логики, теория чисел и теория множеств, мы сейчас переходим к универсально применимому миру измерения и интерпретации изменений .
Дифференциальные уравнения – это раздел математики, который начинается с одного или нескольких записанных наблюдений за изменением и заканчивается одной или несколькими функциями, которые предсказывают будущие результаты. Алгебраическое уравнение , такое как квадратное уравнение, решается со значением или набором значений; Дифференциальное уравнение , напротив, решается с помощью функции или класса функций. «DFQ» для краткости, практически все программы бакалавриата STEM квалифицируют его как основное требование по простой причине: DFQ – фантастический инструмент для моделирования ситуаций в любой области или отрасли.
Первоначально опубликовано в SetzeusВ реальных приложениях модели обычно включают объекты и зарегистрированные скорости изменения между ними (производные / дифференциалы) – цель DFQ – определить общую взаимосвязь между ними. Системы такого типа чрезвычайно распространены в явлениях природы, и именно поэтому DFQ играет важную роль в самых разных областях, от физики до экономики и биологии.
Учитывая его долговечность и длительное влияние как основную часть репертуара любого математика или ученого, неудивительно, что история DFQ довольно плотная.Как мы вскоре увидим, современный DFQ – это результат многовековых усовершенствований, многие из которых носят нарицательный характер. Однако это совместное, постепенное продвижение к устоявшейся ветви стало возможным только благодаря двум гигантам математики: Исааку Ньютону и Готфриду Лейбницу.
Как показывает история, оба человека спорно утверждали, что независимо друг от друга изобрели исчисление примерно в один и тот же период времени. Это ключевой момент, поскольку исчисление с буквальным развитием интегралов и производных заложило основу для будущих математиков.
Неопределенность определения точных моментов происхождения является результатом множества факторов, таких как общая аура конкуренции / секретности и своевременность частных публикаций (некоторые записи были обнаружены только спустя десятилетия). Одно можно сказать наверняка: они оба заслуживают уважения за происхождение DFQ, как видно из следующих примеров.
Предположительно еще в 1671 году Ньютон в грубых неопубликованных заметках выдвинул следующие три «типа» дифференциальных уравнений:
Первые два уравнения выше содержат только обыкновенные производные или нескольких зависимых переменных; сегодня они называются обыкновенными дифференциальными уравнениями .Последнее уравнение содержит частные производные зависимых переменных, таким образом, номенклатура, уравнений в частных производных . Обратите внимание, оба этих термина являются современными ; , когда Ньютон, наконец, опубликовал эти уравнения (около 1736 г.), он первоначально назвал их « флюксий ».
Примерно в тот же период времени (~ 1675 г.) немецкий математик Готфрид Лейбниц, также в неопубликованных заметках, представил две ключевые идеи: свой собственный дифференциал и самый первый зарегистрированный экземпляр интегрального символа:
Несмотря на раннее происхождение этих идей сейчас -открытые черновики, математическое сообщество впервые услышит об этой теме в ближайшие двадцать лет (~ 20).В частности, в 1693 году и Лейбниц, и Ньютон , наконец, , официально опубликовали и распространили решения своих дифференциальных вопросов, отметив 1693 год как зарождение дифференциальных уравнений как отдельной области математики.
Готфрид Вильгельм Лейбниц и Исаак НьютонС заложенными основами путь к DFQ был медленным и устойчивым – попытки решить физические проблемы постепенно привели к созданию моделей, которые, в свою очередь, требовали инновационных решений. Эти проблемы и их решения привели к росту независимой дисциплины.Усилия сообщества быстро ускорили эволюцию этой области, несмотря на вклад Ньютона и Лейбница.
Ниже приведен список как исторически значимых проблем DQF, так и математика с атрибутами, опубликовавшего удовлетворительное решение:
Приведенный выше список является лишь фрагментом всех проблем, способствующих DFQ; однако даже этот сокращенный список подчеркивает уровень математиков, которые внесли свой вклад в отрасль, которая считается одной из основ STEM. Из таких узнаваемых имен, как Лагранж, Эйлер и Бернулли, а также по оригиналам Ньютон и Лейбниц, при свете дня становится ясно, насколько важны математики для дальнейшего развития DFQ.
В этой серииКогда дело доходит до анализа реального мира, DFQ – это реальное дело. Предсказание химических реакций с помощью уравнений полураспада, прогнозирование подсчета культур экосистемы с ростом населения или описание траектории волн – базовое понимание DFQ является обязательным для любого, кто серьезно интересуется карьерой в STEM.
Куда мы идем дальше? Во-первых, чтобы изучить нотацию DFQ и просмотреть различные типы заказов. Далее мы рассмотрим механику Лагранжа и уравнения движения.После этого мы рассмотрим одну из самых важных формул прикладной математики: преобразование Лапласа. И, наконец, мы исследуем область теплового потока глазами Жозефа Фурье.
Источники
Дифференциальные уравнения
Персональный сайт Сетцеуса
Дифференциальные уравнения – краткий курс
[Дифференциальная диагностика первичной и вторичной математической неспособности к обучению – показания теста на дискалькурию Basis-Math 4–8]
Исследования детей с AD (H) D без нарушения математической способности к обучению (MLD), а также исследования влияния метилфенидата на арифметику показали, что большинство недостатков в математике и большинство типов ошибок, обычно описываемых как специфические для дискалькулии развития (например,g., подсчет пальцев, дефицит поиска фактов, сложный подсчет, трудности с процедурами переноса / заимствования, самокоррекции) не могут быть классифицированы как таковые и, следовательно, не должны использоваться для дифференциальной диагностики первичной дискалькулии и вторичной MLD. В этой статье предлагается использовать общий балл в тесте на дискалькулию Basis-Math 4-8 (Moser Opitz et al., 2010), а также неправдоподобные ошибки вычитания в качестве маркера дискалькулии и количества самокоррекций, сделанных во время теста, в качестве критерия. когнитивный маркер дефицита внимания.Иерархический кластерный анализ был рассчитан на выборке из 51 клинически направленного ребенка с нормальным IQ и подозрением на MLD с использованием IQ, количества лет обучения, общего балла Basis-Math 4–8 и количества самокоррекций в этом тесте в качестве переменных. Результаты выявили подгруппу с первичной дискалькулией, а также три подгруппы с вторичным MLD (две с синдромом дефицита внимания с гиперактивностью, одна с депрессией и одна небольшая подгруппа с высоким IQ).