Что такое дифференциальные уравнения? | Наука в Сибири
Как известно, в современной науке, стремящейся к описанию наблюдаемых природных или общественных явлений, значительная роль принадлежит математике. Теория дифференциальных уравнений, являясь одним из крупных разделов математики, в то же время всегда была и остается тесно связанной с приложениями.
Рассматривая математику как способ проникновения в тайны окружающего нас мира, можно сказать, что основным приемом исследования является формирование и изучение математических моделей реальных явлений. Исследуя какие-либо явления, ученый в первую очередь создает математическую идеализацию или, иначе говоря, математическую модель. Математическая модель есть не что иное, как запись основных законов, описывающих явление, в математической форме. И очень часто эти законы можно выразить в виде дифференциальных уравнений, соотношений между функциями и их производными: в приложениях функции обычно представляют изменяющиеся величины, а производные описывают скорость их изменения.
Изучая полученные дифференциальные уравнения, исследователь извлекает полезные сведения о происходящих явлениях, часто может узнать их прошлое и предсказать будущее, получить качественные оценки происходящих в течение процесса изменений и даже открыть новые феномены, выдвинуть новые гипотезы, которые, быть может, приведут к более совершенным научным воззрениям и приоткроют завесу тайны окружающего мира. Таким образом, теория дифференциальных уравнений широко используется при решении научных проблем как для точной формулировки их содержания, так и для получения новых результатов.
Вместе с тем следует помнить, что математическая модель сама по себе является объектом и может обладать собственными свойствами, не имеющими отношения к моделируемому процессу. Модель не всегда адекватна конкретному явлению: так, например, из существования решения реальной задачи (существование наблюдаемого процесса обычно не вызывает сомнений ученых) не следует существование решения соответствующей математической задачи; или же может оказаться, что решений математической задачи много; или же решение неустойчиво к изменениям данных.
В настоящее время теория дифференциальных уравнений представляет собой обширную и широко разветвленную теорию, находящуюся в постоянном взаимодействии с другими науками. Приложения снабжают ее новыми проблемами, решая которые, теория дифференциальных уравнений обращается к остальным разделам математики, таким как алгебра, функциональный анализ, теория функций, геометрия, теория вероятностей, вычислительная математика.
Фото и изображение предоставлены исследователем
Дифференциальные уравнения и продление жизни / Хабр
188. Гектора ж, в бегстве преследуя, гнал Ахиллес непрестанно. Словно как пёс по горам молодого гонит оленя.<…> 199. Словно во сне человек изловить человека не может, Сей убежать, а другой уловить напрягается тщетно, — Так и герои, ни сей не догонит, ни тот не уходит.
Задача №1.
 Ахиллес и Смерть
Ахиллес и СмертьВ некоей альтернативной вселенной герою по имени Ахиллес предрекли, что жить ему осталось ровно m лет. Но мать Ахиллеса благодаря своему волшебству (она ж нимфа по легенде), продлевает ему жизнь таким образом, что каждые k (k > 1) лет продолжительность жизни увеличивается на 1 год. Сколько Ахиллес проживет в итоге, если считать, что увеличение происходит непрерывно?
Пусть x – это сколько осталось жить нашему герою. Ахиллес проживает первые m лет, но за эти годы получает лет прибавки к ПЖ. Он проживает эти лет, но за это время получает еще лет (прибавку разделить на k). И так далее, до бесконечности и можно подумать, что герой никогда не умрет. Но это не так: Смерть все таки догонит Ахиллеса, потому что все эти прибавки образуют бесконечную геометрическую прогрессию:
И тут стоит обратить внимание на условие: k > 1 из чего следует, что а это значит, что геометрическая прогрессия бесконечно убывающая. А бесконечно убывающая геометрическая прогрессия сходится к конечному значению:
вывод формулы суммы бесконечной геометрической прогрессииПусть у нас есть вот такая сумма:
И тут кому-то пришла в голову гениальная мысль: “а что если обе части равенства умножить на q?”. Так чего же мы ждем! Умножаем:
Так чего же мы ждем! Умножаем:
А теперь вычтем из первого второе и получим красивую формулу для суммы:
Если q < 1, то при n стремящемся к бесконечности очевидно получаем:
Так как стремится к нулю
В период с 2000 по 2019 год ожидаемая продолжительность жизни голландских мужчин, например, увеличилась с 75.5 до 80.5 лет (то есть примерно на год каждые четыре года), что согласуется с данными по Европе в среднем. Таким образом, если человеку на текущий момент осталось жить 40 лет, а ожидаемая ПЖ увеличивается на год каждые четыре года, то имеем:
то есть мужчина-европеец в возрасте примерно 38 лет может прожить не 40 лет в среднем, а примерно на 13 лет дольше из-за прогресса в медицине (конечно, данные расчеты много чего не учитывают, нельзя их воспринимать как надежные предсказания).
А вот если k <= 1, то имеем уже бесконечность и это и есть та самая пресловутая longevity escape velocity о которой много говорит знаменитый борец со старением Обри Ди Грей. То есть Смерть никогда не догонит Ахиллеса.
То есть Смерть никогда не догонит Ахиллеса.
А теперь давайте посмотрим насколько эта же задача легче и логичнее решается при помощи дифференциальных уравнений:
dx – это насколько изменилось количество оставшихся лет до смерти за период dt. В отсутствии медицинского прогресса dx просто уменьшается на величину dt (логично, черт возьми). А прогресс добавляет определенное количество лет, такое что оно равно 1, если dt=k годам. Решается это уравнение тоже элементарно:
Совершенно очевидно, что x(0) = m, откуда C = m. А теперь подставим это в уравнение выше и выразим время t через которое Ахиллес помрет (x(t) = 0):
Получилось просто и красиво, более того, есть задачи на которые можно дать ответ только с помощью дифференциальных уравнений. Например, если k зависит от времени. Давайте помечтаем немного и представим, что в какой-то момент времени наука развилась до такого уровня, что требуется все меньше и меньше времени для продления ожидаемой ПЖ на год, то есть k уменьшается со временем.
Пусть, например, k уменьшается по экспоненте с периодом полураспада в n лет. И давайте попробуем ответить на такой вопрос: какой должен быть минимальный m, чтобы человек мог достигнуть longevity escape velocity при таком k(t)?
Чтобы ответить на данный вопрос давайте составим дифференциальное уравнение:
Надо, пожалуй, пояснить откуда взялось b в экспоненте и чему равняетсяМы определили k(t) = k0*exp(-bt). Так как через n лет значение k(t) должно быть вдвое меньше, то имеем
откуда:
Интегрируем уравнение и получаем:
Чтобы определить C, воспользуемся начальным условием: x(0)=m:
Получаем следующую запись функции дожития:
Давайте взглянем на ее график:
Функция x(t) имеет минимум и нам нужно, чтобы этот минимум был выше оси абсцисс (фиолетовая кривая)Наша функция дожития имеет минимум и все, что нам нужно, это найти значение минимума как функции от m и найти значение m при котором этот минимум больше нуля. Как мы помним еще со школы, для того, чтобы найти минимум функции надо сначала найти ее производную и приравнять к нулю. Причем производную-то мы уже знаем из уравнения (1):
Причем производную-то мы уже знаем из уравнения (1):
Мы точно знаем, что это минимум, потому что вторая производная положительна на всей области определения, а значит функция выпукла вниз и, следовательно, найденный экстремум является минимумом.
Теперь необходимо найти :
А отсюда уже выразим ограничение для m:
При и необходимо иметь в запасе примерно 9.2 года ожидаемой продолжительности жизни, чтобы достичь longevity escape velocity, то есть быть, например, мужчиной моложе 79 лет. Каждый может прикинуть свои шансы на достижение longevity escape velocity исходя из своего возраста. Но возможно ли в принципе бессмертие? Есть ли какие-то фундаментальные математические (не физические) ограничения? Об этом я расскажу в следующей статье, а пока давайте поговорим о более практических вещах.
Задача 2. Плазмаферез
Конечно, медицинская наука еще очень далека от достижения LEV (а может быть этого и вовсе никогда не случится), однако попытки отсрочить старение ведутся уже сейчас. Одной из самых интересных интервенций, возможно, способной немного продлить молодость и продолжительность жизни является терапевтическое разбавление плазмы. Известные геронтологи супруги Конбои продемонстрировали, что если мышкам заменить половину плазмы на физраствор с альбумином, то у них существенно улучшаются многие показатели жизнедеятельности. Предполагается, что это происходит за счет удаления из организма токсичных продуктов, которые образуются из-за старения организма. Более подробно все описано, например, тут. Более того, некоторые отчаянные биохакеры даже пробуют этот метод на себе и замечают улучшение ряда биомаркеров. Конечно, пройдет еще немало времени прежде чем установят эффективность (или неэффективность) этого метода на людях, но мы тем не менее постараемся ответить на вполне конкретный вопрос: а сколько раз нам необходимо сдать плазму, чтобы заменить половину, если за один раз забирается v мл?
Одной из самых интересных интервенций, возможно, способной немного продлить молодость и продолжительность жизни является терапевтическое разбавление плазмы. Известные геронтологи супруги Конбои продемонстрировали, что если мышкам заменить половину плазмы на физраствор с альбумином, то у них существенно улучшаются многие показатели жизнедеятельности. Предполагается, что это происходит за счет удаления из организма токсичных продуктов, которые образуются из-за старения организма. Более подробно все описано, например, тут. Более того, некоторые отчаянные биохакеры даже пробуют этот метод на себе и замечают улучшение ряда биомаркеров. Конечно, пройдет еще немало времени прежде чем установят эффективность (или неэффективность) этого метода на людях, но мы тем не менее постараемся ответить на вполне конкретный вопрос: а сколько раз нам необходимо сдать плазму, чтобы заменить половину, если за один раз забирается v мл?
Поскольку нам надо найти такой k при котором обновится половина плазмы, то приравняем правую часть уравнения выше к 1/2, прологарифмируем обе части равенства и воспользуемся свойствами логарифма, чтобы получить формулу для k:
Удельный объем плазмы взрослого мужчины составляет, в среднем, 46. 7 мл/кг. Возьмем к примеру мужчину массой 80 кг и v=450 мл (стандартный объем плазмы при донорстве):
7 мл/кг. Возьмем к примеру мужчину массой 80 кг и v=450 мл (стандартный объем плазмы при донорстве):
То есть взрослому сорокалетнему мужчине массой 80 кг необходимо за короткий срок 6 раз пожертвовать плазму, чтобы ее обновить чуть более чем наполовину.
Пусть X(t) – доля старой плазмы в момент времени t. Пусть скорость вытекания плазмы равна r мл/мин. Чему же будет равна концентрация старой плазмы в момент времени t + dt? А концентрация равна:
Давайте разберем каждое составляющее этого равенства:
X(t)V: концентрация старой плазмы помноженная на общий объем – очевидно это объем старой плазмы во всем организме в момент t
X(t)rdt: это объем старой плазмы, который вытечет за время dt (rdt – это скорость истечения, помноженная на время, что соответствует объему, а X(t) – это доля старой плазмы в этом объеме).
Затем мы делим получившийся объем старой плазмы на общий объем (который остается неизменным, потому что физраствор втекает с той же скоростью) и получим концентрацию. А теперь узнаем чему равно изменение концентрации (разница между концентрацией в моменты времени t+dt и t):
А теперь узнаем чему равно изменение концентрации (разница между концентрацией в моменты времени t+dt и t):
Разделяем переменные и решаем это дифференциальное уравнение:
Отсюда:
Мы знаем, что вначале концентрация старой плазмы равнялась 1:
X(0) = 1 => C = 1
Поэтому , а теперь найдем время, за которое обновится половина плазмы:
На практике это означает примерно 259 минут (4 с лишним часа!), если руководствоваться средней скоростью 10 мл/мин (обычно забирают 450 мл плазмы и уходит на это примерно 45 минут):
Конечно, это время абсолютно неприемлемо, однако процедуру можно существенно ускорить. Например, в этой статье описан метод, который позволяет изымать плазму со скоростью 24 мл/мин, что позволяет заменить половину плазмы за 108 минут. Весьма неплохо! Однако неизвестно выдержит ли организм замену половины плазмы за один раз 🙂 Но это уже выходит за рамки математики, оставим этот вопрос врачам. Тем более, что различные клинические исследования по влиянию плазмафереза на старение людей уже начались.
Дифференциальные уравнения, динамические системы и оптимальное управление
О профессии
Областью профессиональной деятельности аспиранта по направлению «Математика и механика» являются научные исследования и математическое моделирование, связь, информационные и коммуникационные технологи в сферах разработки и тестирования программного обеспечения, создания, поддержки и администрирования информационно-коммуникационных систем, а также образование в сферах общего, профессионального и дополнительного обучения.
Выпускники, освоившие программу, обладают социальной мобильностью, конкурентоспособностью и устойчивостью на современном рынке труда, способны к инновационной деятельности в сфере науки, образования и управления, востребованы во всех организациях и структурах, где используются компьютерные технологии. Они могут заниматься исследовательской деятельностью, способны решать актуальные задачи фундаментальной и прикладной математики, совершенствовать и реализовывать новые математические методы решения прикладных задач, разрабатывать математические модели и проводить их анализ при решении задач в области профессиональной деятельности, комбинировать и адаптировать существующие информационно-коммуникационные технологи для решения задач в области профессиональной деятельности с учетом требований информационной безопасности.
Учебный процесс
Программа аспирантуры ставит перед собой цель сформировать у будущих специалистов современные знания в сфере решения теоретических и прикладных задач, а также навыки самостоятельной научно-исследовательской и педагогической деятельности. Обязательная часть программы включает в себя фундаментальную подготовку по математике, изучение современных математических методов и активную научно-исследовательскую работу.
Программа обучения состоит из набора дисциплин базовой части, обязательных к освоению, и набора дисциплин по выбору аспирантов. На первых двух курсах аспиранты изучают следующий набор дисциплин: «Иностранный язык», «История и философия науки», «Педагогика высшей школы», «Методология научных исследований», «Краевые задачи для дифференциальных уравнений», «Теория экстремальных задач».
Третий и четвертый курсы посвящены по большей части научно-исследовательской работе студента, работе в команде исследователей и написанию кандидатской диссертации. Весь учебный процесс и научные исследования проводятся в мультимедийных аудиториях и научно-учебных лабораториях и центрах Математического института имени академика С.М. Никольского, а также в компьютерных классах, оснащенных современным оборудованием и программным обеспечением для проведения вычислительных экспериментов.
Весь учебный процесс и научные исследования проводятся в мультимедийных аудиториях и научно-учебных лабораториях и центрах Математического института имени академика С.М. Никольского, а также в компьютерных классах, оснащенных современным оборудованием и программным обеспечением для проведения вычислительных экспериментов.
Практика
Учебным планом предусмотрены научно-исследовательская и педагогическая практики, которые проводятся на базе Научного центра нелинейных задач математической физики Математического института имени академика С.М. Никольского.
Для аспирантов ежегодно проводятся мастер-классы ведущих экспертов и представителей работодателей реальных секторов экономики, российских и зарубежных ученых из ведущих вузов и научных центров. Действует научный семинар по дифференциальным и функционально-дифференциальным уравнениям, в котором принимают участие крупные российские и зарубежные математики, преподаватели, студенты, аспиранты и докторанты. Математический институт им. С.М. Никольского тесно сотрудничает с МГУ им. М.В. Ломоносова, Математическим институтом им. В.А. Стеклова РАН, Вычислительным центром РАН им. А.А. Дородницына, Московским авиационным институтом.
С.М. Никольского тесно сотрудничает с МГУ им. М.В. Ломоносова, Математическим институтом им. В.А. Стеклова РАН, Вычислительным центром РАН им. А.А. Дородницына, Московским авиационным институтом.
Карьера
Полученные знания и практические навыки позволяют выпускникам аспирантуры работать в сфере образования, науки, финансов и промышленности, в инвестиционных фондах на должностях аналитика-программиста, научного сотрудника, разработчика математических моделей процессов, консультанта по математическому моделированию, администратора базы данных, преподавателя математики и информатики. Выпускники, освоившие программу, могут осуществлять профессиональную деятельность и в других областях в соответствии полученными компетенциями, необходимыми для квалификации работника, способны работать в междисциплинарной команде.
Издания | Библиотечно-издательский комплекс СФУ
Все года изданияТекущий годПоследние 2 годаПоследние 5 летПоследние 10 лет
Все виды изданийУчебная литератураНаучная литератураЖурналыМатериалы конференций
Все темыЕстественные и точные наукиАстрономияБиологияГеографияГеодезия. КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография. ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство.
КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография. ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство. ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литератураХудожественные произведения
ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литератураХудожественные произведения
Все институтыВоенно-инженерный институтБазовая кафедра специальных радиотехнических системВоенная кафедраУчебно-военный центрГуманитарный институтКафедра ИТ в креативных и культурных индустрияхКафедра истории России, мировых и региональных цивилизацийКафедра культурологии и искусствоведенияКафедра рекламы и социально-культурной деятельностиКафедра философииЖелезногорский филиал СФУИнженерно-строительный институтКафедра автомобильных дорог и городских сооруженийКафедра инженерных систем, зданий и сооруженийКафедра проектирования зданий и экспертизы недвижимостиКафедра строительных конструкций и управляемых системКафедра строительных материалов и технологий строительстваИнститут архитектуры и дизайнаКафедра архитектурного проектированияКафедра градостроительстваКафедра дизайнаКафедра дизайна архитектурной средыКафедра изобразительного искусства и компьютерной графикиИнститут горного дела, геологии и геотехнологийКафедра геологии месторождений и методики разведкиКафедра геологии, минералогии и петрографииКафедра горных машин и комплексовКафедра инженерной графикиКафедра маркшейдерского делаКафедра открытых горных работКафедра подземной разработки месторожденийКафедра технической механикиКафедра технологии и техники разведкиКафедра шахтного и подземного строительстваКафедра электрификации горно-металлургического производстваИнститут инженерной физики и радиоэлектроникиБазовая кафедра “Радиоэлектронная техника информационных систем”Базовая кафедра инфокоммуникацийБазовая кафедра физики конденсированного состояния веществаБазовая кафедра фотоники и лазерных технологийКафедра нанофазных материалов и нанотехнологийКафедра общей физикиКафедра приборостроения и наноэлектроникиКафедра радиотехникиКафедра радиоэлектронных системКафедра современного естествознанияКафедра теоретической физики и волновых явленийКафедра теплофизикиКафедра экспериментальной физики и инновационных технологийКафедры физикиИнститут космических и информационных технологийБазовая кафедра “Интеллектуальные системы управления”Базовая кафедра геоинформационных системКафедра высокопроизводительных вычисленийКафедра вычислительной техникиКафедра информатикиКафедра информационных системКафедра прикладной математики и компьютерной безопасностиКафедра разговорного иностранного языкаКафедра систем автоматики, автоматизированного управления и проектированияКафедра систем искусственного интеллектаИнститут математики и фундаментальной информатикиБазовая кафедра вычислительных и информационных технологийБазовая кафедра математического моделирования и процессов управленияКафедра алгебры и математической логикиКафедра высшей и прикладной математикиКафедра математического анализа и дифференциальных уравненийКафедра математического обеспечения дискретных устройств и системКафедры высшей математики №2афедра теории функцийИнститут нефти и газаБазовая кафедра пожарной и промышленной безопасностиБазовая кафедра проектирования объектов нефтегазового комплексаБазовая кафедра химии и технологии природных энергоносителей и углеродных материаловКафедра авиационных горюче-смазочных материаловКафедра бурения нефтяных и газовых скважинКафедра геологии нефти и газаКафедра геофизикиКафедра машин и оборудования нефтяных и газовых промысловКафедра разработки и эксплуатации нефтяных и газовых месторожденийКафедра технологических машин и оборудования нефтегазового комплексаКафедра топливообеспеченя и горюче-смазочных материаловИнститут педагогики, психологии и социологииКафедра информационных технологий обучения и непрерывного образованияКафедра общей и социальной педагогикиКафедра психологии развития и консультированияКафедра современных образовательных технологийКафедра социологииИнститут торговли и сферы услугБазовая кафедра таможенного делаКафедра бухгалтерского учета, анализа и аудитаКафедра гостиничного делаКафедра математических методов и информационных технологий в торговле и сфере услугКафедра технологии и организации общественного питанияКафедра товароведения и экспертизы товаровКафедра торгового дела и маркетингаОтделение среднего профессионального образования (ОСПО)Институт управления бизнес-процессамиКафедра бизнес-информатики и моделирования бизнес-процессовКафедра маркетинга и международного администрированияКафедра менеджмент производственных и социальных технологийКафедра цифровых технологий управленияКафедра экономики и управления бизнес-процессамиКафедра экономической и финансовой безопасностиИнститут физ. культуры, спорта и туризмаКафедра медико-биологических основ физической культуры и оздоровительных технологийКафедра теоретических основ и менеджмента физической культуры и туризмаКафедра теории и методики спортивных дисциплинКафедра физической культурыИнститут филологии и языковой коммуникацииКафедра восточных языковКафедра журналистики и литературоведенияКафедра иностранных языков для гуманитарных направленийКафедра иностранных языков для естественнонаучных направленийКафедра иностранных языков для инженерных направленийКафедра романских языков и прикладной лингвистикиКафедра русского языка и речевой коммуникацииКафедра русского языка как иностранногоКафедра теории германских языков и межкультурной коммуникацииИнститут фундаментальной биологии и биотехнологииБазовая кафедра “Медико-биологические системы и комплексы”Базовая кафедра биотехнологииКафедра биофизикиКафедра водных и наземных экосистемКафедра геномики и биоинформатикиКафедра медицинской биологииИнститут цветных металлов и материаловеденияБазовая кафедра “Технологии золотосодержащих руд”Кафедра автоматизации производственных процессов в металлургииКафедра аналитической и органической химииКафедра инженерного бакалавриата СDIOКафедра композиционных материалов и физико-химии металлургических процессовКафедра литейного производстваКафедра металловедения и термической обработки металловКафедра металлургии цветных металловКафедра обогащения полезных ископаемыхКафедра обработки металлов давлениемКафедра общаей металлургииКафедра техносферной безопасности горного и металлургического производстваКафедра физической и неорганической химииКафедра фундаментального естественнонаучного образованияИнститут экологии и географииКафедра географииКафедра охотничьего ресурсоведения и заповедного делаКафедра экологии и природопользованияИнститут экономики, государственного управления и финансовКафедра бухгалтерского учета и статистикиКафедра международной и управленческой экономикиКафедра социально-экономического планированияКафедра теоретической экономикиКафедра управления человеческими ресурсамиКафедра финансов и управления рискамиКрасноярская государственная архитектурно-строительная академияКрасноярский государственный технический университетКрасноярский государственный университетМежинститутские базовые кафедрыМежинститутская базовая кафедра “Прикладная физика и космические технологии”Политехнический институтБазовая кафедра высшей школы автомобильного сервисаКафедра конструкторско-технологического обеспечения машиностроительных производствКафедра материаловедения и технологии обработки материаловКафедра машиностроенияКафедра прикладной механикиКафедра робототехники и технической кибернетикиКафедра стандартизации, метрологии и управления качествомКафедра тепловых электрических станцийКафедра теплотехники и гидрогазодинамикиКафедра техногенных и экологических рисков в техносфереКафедра техносферной и экологической безопасностиКафедра транспортаКафедра транспортных и технологических машинКафедра химииКафедра электроэнергетикиХакасский технический иститутЮридический институтКафедра гражданского праваКафедра иностранного права и сравнительного правоведенияКафедра конституционного, административного и муниципального праваКафедра международного праваКафедра предпринимательского, конкурентного и финансового праваКафедра теории и истории государства и праваКафедра теории и методики социальной работыКафедра трудового и экологического праваКафедра уголовного праваКафедра уголовного процеса и криминалистики
культуры, спорта и туризмаКафедра медико-биологических основ физической культуры и оздоровительных технологийКафедра теоретических основ и менеджмента физической культуры и туризмаКафедра теории и методики спортивных дисциплинКафедра физической культурыИнститут филологии и языковой коммуникацииКафедра восточных языковКафедра журналистики и литературоведенияКафедра иностранных языков для гуманитарных направленийКафедра иностранных языков для естественнонаучных направленийКафедра иностранных языков для инженерных направленийКафедра романских языков и прикладной лингвистикиКафедра русского языка и речевой коммуникацииКафедра русского языка как иностранногоКафедра теории германских языков и межкультурной коммуникацииИнститут фундаментальной биологии и биотехнологииБазовая кафедра “Медико-биологические системы и комплексы”Базовая кафедра биотехнологииКафедра биофизикиКафедра водных и наземных экосистемКафедра геномики и биоинформатикиКафедра медицинской биологииИнститут цветных металлов и материаловеденияБазовая кафедра “Технологии золотосодержащих руд”Кафедра автоматизации производственных процессов в металлургииКафедра аналитической и органической химииКафедра инженерного бакалавриата СDIOКафедра композиционных материалов и физико-химии металлургических процессовКафедра литейного производстваКафедра металловедения и термической обработки металловКафедра металлургии цветных металловКафедра обогащения полезных ископаемыхКафедра обработки металлов давлениемКафедра общаей металлургииКафедра техносферной безопасности горного и металлургического производстваКафедра физической и неорганической химииКафедра фундаментального естественнонаучного образованияИнститут экологии и географииКафедра географииКафедра охотничьего ресурсоведения и заповедного делаКафедра экологии и природопользованияИнститут экономики, государственного управления и финансовКафедра бухгалтерского учета и статистикиКафедра международной и управленческой экономикиКафедра социально-экономического планированияКафедра теоретической экономикиКафедра управления человеческими ресурсамиКафедра финансов и управления рискамиКрасноярская государственная архитектурно-строительная академияКрасноярский государственный технический университетКрасноярский государственный университетМежинститутские базовые кафедрыМежинститутская базовая кафедра “Прикладная физика и космические технологии”Политехнический институтБазовая кафедра высшей школы автомобильного сервисаКафедра конструкторско-технологического обеспечения машиностроительных производствКафедра материаловедения и технологии обработки материаловКафедра машиностроенияКафедра прикладной механикиКафедра робототехники и технической кибернетикиКафедра стандартизации, метрологии и управления качествомКафедра тепловых электрических станцийКафедра теплотехники и гидрогазодинамикиКафедра техногенных и экологических рисков в техносфереКафедра техносферной и экологической безопасностиКафедра транспортаКафедра транспортных и технологических машинКафедра химииКафедра электроэнергетикиХакасский технический иститутЮридический институтКафедра гражданского праваКафедра иностранного права и сравнительного правоведенияКафедра конституционного, административного и муниципального праваКафедра международного праваКафедра предпринимательского, конкурентного и финансового праваКафедра теории и истории государства и праваКафедра теории и методики социальной работыКафедра трудового и экологического праваКафедра уголовного праваКафедра уголовного процеса и криминалистики
По релевантностиСначала новыеСначала старыеПо дате поступленияПо названиюПо автору
Урок 26.
 простейшие дифференциальные уравнения – Алгебра и начала математического анализа – 11 класс
простейшие дифференциальные уравнения – Алгебра и начала математического анализа – 11 классАлгебра и начала математического анализа, 11 класс
Урок №26. Простейшие дифференциальные уравнения.
Перечень вопросов, рассматриваемых в теме
1) Нахождение области применения дифференциальных уравнений
2) Определение дифференциального уравнения
3) Решение простейших дифференциальных уравнений
Таблица первообразных.
Функция f(x) | Первообразная F(x) |
0 | C = const |
1 | x + C |
cos x | sin x + C |
sin x | -cos x + C |
Основная литература:
Колягин Ю. М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для выполняется равенство F’ (x) = f(x).
Дифференциальным уравнением называется соотношение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные.
Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного уравнения. ( Пример: y’ – y = 0 – дифференциальное уравнение 1-го порядка; y’’ + y = 0 – дифференциальное уравнение 2-го порядка).
Решением дифференциального уравнения называется любая функция y = f(x), которая при подстановке в это уравнение обращает его в тождество.
Примеры и разбор решения заданий тренировочного модуля
№1. Тело движется по оси абсцисс, начиная движение от точки А(10; 0) со скоростью v=4t+4 Найдите уравнение движения тела, и определите координату х через 1 с
Решение
Воспользуемся определением первообразной, т.к. х(t)=v0t+at2/2
х’(t) = v(t) .
Найдем все первообразные функции 4t+4
х(t)= 4t+2t2 +c.
При этом с=10, т.к. это есть начальная координата тела из условия задачи.
Следовательно, закон движения будет выглядеть следующим образом:
х=2t2+4t+10
Подставим t=1c в данное уравнение и найдем координату тела за данное время х = 2+4+10=16
Ответ: х=2t2+4t+10
№2. Найдите c при частном решении, у’ = x, если при х = 1 у = 0 .
Решение:
Найдем все первообразные уравнения у’ , это будет общее решение уравнения :
Найдем число С , такое х = 1 у = 0 .
Подставим х = 1, y = 0 , в общее решение и получим:
0=(1)2/2 +с
С=-1/2
Ответ с = -0,5
№3. Используя уравнение у'(x)= 4х+5, найди его решение и определи число С, если у(-2)=10
Решение
Найдем все первообразные функции 4х+5
Найдем число С , такое, у(-2)=10
Подставим х = – 2, y = 10 , получим:
10=(-2)2 +5(-2)+с
С=12
Следовательно, у=5х +2х2 +12 ,
Ответ: у=5х +2х2 +С, где С= 12
Заметки по R: Дифференциальные уравнения
library("knitr")
opts_chunk$set(
# cache=FALSE,
message=FALSE, warning=FALSE)
library("ggplot2") # для построения графиков
library("rasterVis")
library("fields")
library("deSolve") # решение дифф. уравнений с начальными условиями
library("bvpSolve") # решение дифф. уравнений с краевыми условиями
library("dplyr") # манипуляции с даннымиПакет rasterVis предназначен для изображения данных на реальных географических картах, поэтому там нужно понятие проекции.
Строим классический график со стрелочками
vectorplot(rast, isField = TRUE)Строим няку с капельками
streamplot(rast, isField = TRUE)Простой график можно руками построить без доп. пакетов. При этом нам нужно самостоятельно уменьшить количество стрелочек.
y1 <- seq(-6, 6, 0.5) y2 <- seq(-6, 6, 0.5) df <- expand.grid(y1 = y1, y2 = y2) df <- mutate(df, y1dot = y2, y2dot = y1 + cos(y2)) plot(df$y1, df$y2, pch = ".", xlab = expression(paste(y[1])), ylab = expression(paste(y[2])), main = "График векторного поля") arrow.plot(df$y1, df$y2, df$y1dot, df$y2dot, arrow.ex = 0.03, length = 0.05)
Решим ОДУ с начальным условиями
Решим систему ОДУ с начальными условиями
Описываем саму систему:
eq1 <- function(t, y, parampampam) {
return(list(c(
y[2],
y[1] + cos(y[2])
)))
}Начальные условия:
y. start <- c(y1 = 1, y2 = 4)
start <- c(y1 = 1, y2 = 4) Точки, в которых компьютер будет считать функцию:
t <- seq(0, 10, by = 0.01)Решаем
sol <- ode(y = y.start, times = t, func = eq1)
sol <- data.frame(sol)
head(sol)## time y1 y2
## 1 0.00 1.000000 4.000000
## 2 0.01 1.040018 4.003678
## 3 0.02 1.080076 4.007785
## 4 0.03 1.120176 4.012326
## 5 0.04 1.160324 4.017305
## 6 0.05 1.200524 4.022725str(sol)## 'data.frame': 1001 obs. of 3 variables:
## $ time: num 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 ...
## $ y1 : num 1 1.04 1.08 1.12 1.16 ...
## $ y2 : num 4 4 4.01 4.01 4.02 ...ggplot(sol) + geom_line(aes(time, y1), size = 2) + labs(x = "t",
y = expression(paste(y[1])), title = "Решение ОДУ с начальными условиями")Функция ode возвращает матрицу, а для рисования графиков удобнее табличка с данными, data. frame. Строчка
frame. Строчка sol <- data.frame(sol) переделывает матрицу в таблицу с данными.
Решим систему ОДУ с краевыми условиями
Описываем саму систему:
eq1 <- function(t, y, parampampam) {
return(list(c(
y[2],
y[1] + cos(y[2])
)))
}Граничные условия:
y.start <- c(y1 = 1, y2 = NA)
y.final <- c(y1 = 42, y2 = NA)Точки, в которых компьютер будет считать функцию:
t <- seq(0, 10, by = 0.01)Решаем
sol <- bvptwp(yini = y.start, yend = y.final,
x = t, func = eq1,
nmax = 2000)
sol <- data.frame(sol)
head(sol)## x y1 y2
## 1 0.00 1.0000000 -1.553150
## 2 0.01 0.9845193 -1.543001
## 3 0.02 0.9691398 -1.532904
## 4 0.03 0.9538610 -1.522860
## 5 0.04 0.9386824 -1.512868
## 6 0.05 0.9236035 -1.502928ggplot(sol) + geom_line(aes(x, y1), size = 2) + labs(x = "x",
y = expression(paste(y[1])), title = "Решение ОДУ с краевыми условиями")Бесплатное приложение.
 2))
2))r <- rasterFromXYZ(df, crs = proj)Линии уровня функции z
contour(r)Капельки текущие по градиенту
streamplot(r)Направление градиентов, заодно вид сбоку для графика функции
vectorplot(r)3.8: Неявное дифференцирование – Математика LibreTexts
Мы уже изучали, как находить уравнения касательных линий к функциям и скорость изменения функции в конкретной точке. Во всех этих случаях мы имели явное уравнение для функции и явно дифференцировали эти функции. Предположим вместо этого, что мы хотим определить уравнение касательной к произвольной кривой или скорость изменения произвольной кривой в точке. В этом разделе мы решаем эти проблемы, находя производные функций, которые неявно определяют \(y\) через \(x\).2+1\) неявно.
Неявное дифференцирование позволяет нам находить наклоны касательных к кривым, которые явно не являются функциями (они не проходят проверку вертикальной прямой). 2=25\).2}\). Однако не всегда легко решить функцию, неявно заданную уравнением. К счастью, техника неявного дифференцирования позволяет нам найти производную неявно определенной функции без явного решения этой функции. Процесс нахождения \(\dfrac{dy}{dx}\) с использованием неявного дифференцирования описан в следующей стратегии решения задач.
2=25\).2}\). Однако не всегда легко решить функцию, неявно заданную уравнением. К счастью, техника неявного дифференцирования позволяет нам найти производную неявно определенной функции без явного решения этой функции. Процесс нахождения \(\dfrac{dy}{dx}\) с использованием неявного дифференцирования описан в следующей стратегии решения задач.
Стратегия решения проблем: неявная дифференциация
Чтобы выполнить неявное дифференцирование уравнения, которое неявно определяет функцию \(y\) через переменную \(x\), выполните следующие действия:
- Возьмите производную от обеих частей уравнения.Имейте в виду, что \(y\) является функцией \(x\). Следовательно, тогда как \[\dfrac{d}{dx}(\sin x)=\cos x\nonumber\] и \[\dfrac{d}{dx}(\sin y)=\cos y\cdot\dfrac {dy}{dx}\nonumber\], потому что мы должны использовать цепное правило, чтобы дифференцировать \(\sin y\) относительно \(x\).
- Перепишите уравнение так, чтобы все члены, содержащие \(dy/dx\), находились слева, а все члены, не содержащие \(dy/dx\), — справа.

- Вынести \(dy/dx\) слева.
- Найдите \(dy/dx\), разделив обе части уравнения на соответствующее алгебраическое выражение.2)=2y\dfrac{dy}{dx}\).
\(2y\dfrac{dy}{dx}=-2x\) Шаг 2. Оставьте члены с \(\dfrac{dy}{dx}\) слева. Переместите оставшиеся члены вправо. \(\dfrac{dy}{dx}=-\dfrac{x}{y}\) Шаг 4. Разделите обе части уравнения на \(2y\). (Шаг 3 в этом случае не применяется.) Анализ
Обратите внимание, что результирующее выражение для \(\dfrac{dy}{dx}\) выражено как независимой переменной \(x\), так и зависимой переменной \(y\).2=25\) в точке \((3,−4)\).
Раствор
Хотя мы могли бы найти это уравнение без использования неявного дифференцирования, использование этого метода значительно упрощает задачу. В примере \(\PageIndex{1}\) мы нашли \(\dfrac{dy}{dx}=-\dfrac{x}{y}\).

Наклон касательной определяется подстановкой \((3,−4)\) в это выражение. Следовательно, наклон касательной равен \(\dfrac{dy}{dx}\Big|_{(3,−4)}=−\dfrac{3}{−4}=\dfrac{3}{4 }\).
Используя точку \((3,−4)\) и наклон \(\dfrac{3}{4}\) в уравнении точка-наклон линии, мы получаем уравнение \(y=\dfrac{ 3}{4}x−\dfrac{25}{4}\) (рисунок).2=100\) в точке \(\left(3,\frac{8}{3}\right)\) пересекает ось \(x\). Начните с неявного нахождения \(\dfrac{dy}{dx}\).
Дифференцируя, у нас есть
\(8x+50y\dfrac{dy}{dx}=0.\)
Решение для \(\dfrac{dy}{dx}\),
у нас есть
\(\dfrac{dy}{dx}=-\dfrac{4x}{25y}\).
Наклон касательной равен \(\dfrac{dy}{dx}\Bigg|_{\left(3,\frac{8}{3}\right)}=-\dfrac{9}{50} \). Уравнение касательной имеет вид \(y=−\dfrac{9}{50}x+\dfrac{183}{200}\).2=16\) в точке \((5,3)\).
- Подсказка
\(\dfrac{dy}{dx}=\dfrac{x}{y}\)
- Ответить
\(y=\dfrac{5}{3}x−\dfrac{16}{3}\)
Неявное дифференцирование
Если функция описывается уравнением \(y = f\left( x \right)\), где переменная \(y\) стоит в левой части, а правая часть зависит только от независимой переменной \(x \), то говорят, что функция задана явно.
 2} = 0, \;\;\;xy – \sin\left( {x + y} \right) = 0.\]
2} = 0, \;\;\;xy – \sin\left( {x + y} \right) = 0.\]Хорошей новостью является то, что нам не нужно преобразовывать неявно определенную функцию в явную форму, чтобы найти производную \(y’\left( x \right).\) Если \(y\) определено неявно как функция \(x\) уравнением \(F\left( {x,y} \right) = 0,\) поступим следующим образом:
- Продифференцируйте обе части уравнения по \(x\), предполагая, что \(y\) является дифференцируемой функцией \(x\), и используя цепное правило.Производная нуля (в правой части) также будет равна нулю.
Примечание: Если правая часть отлична от нуля, то неявное уравнение имеет вид
\[f\влево( {x,y} \вправо) = g\влево({x,y} \вправо),\]
затем дифференцируем левую и правую части уравнения. - Решите полученное уравнение для производной \(y’\left( x \right)\).
В приведенных ниже примерах найдите производную неявной функции.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
 \основной },\;\; \Стрелка вправо 2yy’ = 2p,\;\; \Rightarrow y’ = \frac{p}{y},\;\;\text{где}\;\;y \ne 0. \]
\основной },\;\; \Стрелка вправо 2yy’ = 2p,\;\; \Rightarrow y’ = \frac{p}{y},\;\;\text{где}\;\;y \ne 0. \]Пример 2.
Неявно дифференцировать функцию \(y\left( x \right)\), заданную уравнением \(y = \cos \left( {x + y} \right).\)
Раствор.
Дифференцировать обе стороны относительно \(x:\)
\[\frac{{dy}}{{dx}} = \frac{d}{{dx}}\cos \left( {x + y} \right),\;\; \Rightarrow y’ = – \sin \left( {x + y} \right) \cdot \left( {1 + y’} \right), \Rightarrow y’ = – \sin \left( {x + y} \right) – y’\sin \left( {x + y} \right), \rightarrow y’\left( {1 + \sin \left( {x + y} \right)} \right) = – \ грех \влево( {х + у} \вправо), \]
что дает
\[y’ = – \frac{{\sin \left( {x + y} \right)}}{{1 + \sin \left({x + y} \right)}}.4}}} = \frac{2}{2} = 1.\]
Дополнительные проблемы см. на стр. 2.
World Web Math: неявное дифференцирование
World Web Math: неявное дифференцирование Предлагаемые предпосылки: Определение производной, Цепное правилоСуществует два способа определения функций: неявно и явно .  Большинство уравнений, с которыми мы имели дело, имеют
были явными уравнениями, такими как y = 2 x -3, так что мы можем написать y = f ( x ), где f ( x ) = 2 x -3.Но
уравнение 2 x – y = 3 описывает то же самое
функция. Это второе уравнение является неявным определением y как функция x . Так как нет настоящего
различие между появлением x или y в
второй форме, это уравнение также является неявным определением x как функция y
Большинство уравнений, с которыми мы имели дело, имеют
были явными уравнениями, такими как y = 2 x -3, так что мы можем написать y = f ( x ), где f ( x ) = 2 x -3.Но
уравнение 2 x – y = 3 описывает то же самое
функция. Это второе уравнение является неявным определением y как функция x . Так как нет настоящего
различие между появлением x или y в
второй форме, это уравнение также является неявным определением x как функция y Не все неявные уравнения можно явно переформулировать в одном уравнение.Например, неявное уравнение x 2 + y 2 = 9 потребностей два явных уравнения,
которые являются верхней и нижней половинками криле соответственно, чтобы полностью определить функциональное отношение.

И xy = sin( y )+ x 2 y 2 (пурпурные кривые на рисунке слева) не могут быть решены для либо y как явная функция x , либо x как явная функция y .Это неявное функция рассматривается в примере 2. Как ни странно, мы можем взять производную от неявных функций точно так же, как мы берем производную от явных функций. Мы просто берем производная каждой части уравнения, не забывая рассматривать зависимая переменная как функция независимой переменной, применить правила дифференцирования и найти производную. Возвращаясь к наш исходный пример:
Это, конечно, то, что мы получаем, дифференцируя явную форму, y = 2 x -3 по отношению к x .
Этот простой пример может быть не очень информативным. Рассмотрим второй пример, уравнение, описывающее окружность радиуса 3, с центром в начале координат.
 Взяв производную обеих частей с
относительно x , используя правило мощности для производной г ,
Взяв производную обеих частей с
относительно x , используя правило мощности для производной г ,Из рисунков видно, что для любой части круга наклон касательной имеет противоположный знак отношения x / y , и величина наклона становится тем больше, чем точка касания приближается к оси x .
(В этом случае нахождение dy/dx как явной функции x требует использования правила мощности для дробных степеней, обычно считается позже. Этот пример можно рассматривать как вкус дела впереди.)
Некоторые примеры:
-
Обратите внимание, что это выражение можно решить, чтобы получить 90 510 x 90 511 в качестве явная функция y путем решения кубического уравнения, и нахождение y как явной функции x будет включают в себя решение уравнения четвертой степени, ни одно из которых не входит в нашу план.
Используя цепное правило и рассматривая y как неявная функция x ,
Как и в большинстве случаев, требующих неявного дифференцирования, результат с точки зрения как x , так и y .
 В общем, если давать
результат в плане х одни были возможны, оригинал
выражение может быть решено для y как явная функция x , и неявное дифференцирование, хотя и правильное, будет
не быть необходимым.
В общем, если давать
результат в плане х одни были возможны, оригинал
выражение может быть решено для y как явная функция x , и неявное дифференцирование, хотя и правильное, будет
не быть необходимым. -
В этом случае правило цепочки и правило продукта используются для преимущество:
-
Использование обратных тригонометрических функций позволяет решить эту задачу. y как явная функция x и графически, как показано. Однако эта функция служит хорошим примером неявного дифференциация:
Упражнения:
- Продифференцируйте явно следующие уравнения, найдя y как функция x .Решить для y ´= dy/dx .
-
-
-
-
Решения к упражнениям | Вернуться на страницу исчисления | Вернуться на главную страницу World Web Math
watko@mit.
 edu Последнее изменение: 29 июля 2002 г.
edu Последнее изменение: 29 июля 2002 г.Неявное дифференцирование
Неявное дифференцированиеНеявное дифференцирование
Во многих примерах, особенно тех, которые получены из дифференциального уравнения, участвующие переменные не связаны друг с другом в явный способ.Чаще всего они связаны через неявная формула, например F ( x , y ) =0. Как только x будет исправлено, мы можем найдите и с помощью численных вычислений. (По некоторым причудливым теоремам мы можем формально показать, что y действительно можно рассматривать как функцию x через определенный интервал). Возникает вопрос, что такое производная , по крайней мере в определенный точка? Метод неявного дифференцирования ответов это беспокойство.Проиллюстрируем это с помощью следующего пример.
Пример. Найдите уравнение касательной к
эллипс
25 х 2 + у 2 = 109
в точке (2,3).
 Один из способов — найти y как функцию x из приведенного выше уравнения, затем продифференцируйте, чтобы найти наклон
касательной линии. Мы предоставим читателю сделать
подробности расчетов.Здесь мы будем использовать другой
метод. В приведенном выше уравнении рассматривают и как
функция x :
Один из способов — найти y как функцию x из приведенного выше уравнения, затем продифференцируйте, чтобы найти наклон
касательной линии. Мы предоставим читателю сделать
подробности расчетов.Здесь мы будем использовать другой
метод. В приведенном выше уравнении рассматривают и как
функция x :25 х 2 + у ( х ) 2 = 109,
и использовать приемы дифференцирования, чтобы получить
Отсюда получаем
что подразумевает, что в точке (2,3). Итак, уравнение касательной имеет вид данный
или эквивалентно
3 у + 50 х = 109.
Вы можете задаться вопросом, зачем беспокоиться, если это просто другой способ найти производную? Рассмотрим следующий пример! Это может быть очень сложно или фактически невозможно решить явно для и как функция x .
Пример. Найти и ‘, если
Найти и ‘, если
Это прекрасный пример неявной связи между x и y . Так как же нам найти и ‘? Продифференцируем вышеизложенное уравнение относительно x , где y считается функция x .Мы получили
Простые алгебраические манипуляции дают
Мы также можем найти более высокие производные от y , такие как y ” в этом способ. Нам нужно только дифференцировать приведенный выше результат. Из Конечно, расчеты становятся немного более грязными.
Упражнение 1. Найдите y ‘, если xy 3 + x 2 y 2 + 3 x 2 – 6 = 1.
Ответ.
Упражнение 2. Докажите, что уравнение касательной к
график гиперболы
в точку P ( x 0 , y 0 )
Ответ.

Упражнение 3. Покажите, что если провести нормаль к каждой точке эллипс проходит через центр эллипса, то эллипс это круг.
Ответ.
[Назад] [Следующий] [Тригонометрия] [Исчисление] [Геометрия] [Алгебра] [Дифференциальные уравнения] [Комплексные переменные] [Матричная алгебра] С.Домашняя страница OS MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Мохамед А. Хамси Copyright 1999-2022 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Математика Медикс, ООО. – П.О. Box 12395 – Эль-Пасо, Техас 79913 – США
пользователей онлайн за последний час
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
 Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. x$ и $\ln x$, поскольку эти функции
являются обратными.y$ нам нужно знать, что функция $y$ имеет производная. Все, что мы показали, это то, что , если имеет производную
тогда эта производная должна быть $1/x$. При использовании этого метода мы будем
всегда приходится предполагать, что искомая производная существует, но
к счастью, это надежное предположение для большинства таких проблем.
x$ и $\ln x$, поскольку эти функции
являются обратными.y$ нам нужно знать, что функция $y$ имеет производная. Все, что мы показали, это то, что , если имеет производную
тогда эта производная должна быть $1/x$. При использовании этого метода мы будем
всегда приходится предполагать, что искомая производная существует, но
к счастью, это надежное предположение для большинства таких проблем.
В примере $y=\ln x$ использовалась обратная функция, определенная неявно,
но другие функции могут быть определены неявно, а иногда и одна
уравнение может использоваться для неявного определения более чем одного
функция.2)\кр
0&=2x+2yy’\cr
y’&={-2x\over 2y}=-{x\over y}\cr
}$$
Теперь у нас есть выражение для $y’$, но оно содержит как $y$, так и
$х$. Это означает, что если мы хотим вычислить $y’$ для некоторого конкретного
значение $x$, мы должны будем знать или вычислить $y$ при этом значении $x$ как
Что ж. Именно в этот момент нам нужно будет знать, является ли $y$
$U(x)$ или $L(x)$. 2$ в точке
$\ds (1,-\sqrt{3})$.2}},$$
без явного вычисления производной от $L(x)$. Тогда мы
подставьте $x=1$ и получите тот же ответ, что и раньше.
$\квадрат$
2$ в точке
$\ds (1,-\sqrt{3})$.2}},$$
без явного вычисления производной от $L(x)$. Тогда мы
подставьте $x=1$ и получите тот же ответ, что и раньше.
$\квадрат$
В случае окружности можно найти функции $U(x)$ и $L(x)$ явно, но есть потенциальные преимущества использования неявное дифференцирование в любом случае. В некоторых случаях это сложнее или невозможно найти явную формулу для $y$ и неявную дифференцирование – единственный способ найти производную.
Пример 4.8.y=x$ для $y$, поэтому, возможно, после взятия производной мы получим
то, что трудно решить за $y’$. На самом деле это никогда
бывает. Все вхождения $y’$ происходят из-за применения цепного правила,
и всякий раз, когда используется цепное правило, он вносит один $y’$
умножить на какое-то другое выражение. Так что всегда можно будет
сгруппируйте термины, содержащие $y’$ вместе, и вынесите $y’$ на множители, просто
как в предыдущем примере. Если у вас когда-нибудь возникнет что-то более сложное
вы допустили ошибку и должны исправить ее, прежде чем пытаться продолжить. 2}=2a.2$
(отвечать)
2}=2a.2$
(отвечать)
Пример 4.8.4 $\ds 4\cos x \sin y = 1$ (отвечать)
Пример 4.8.5 $\ds\sqrt{x} + \sqrt{y} = 9$ (отвечать)
Пример 4.8.6 $\ds \tan(x/y) = x+ y$ (отвечать)
Пример 4.8.7 $\ds\sin(x+y)=xy$ (отвечать)
Пример 4.8.8 $\ds{1\над х} + {1\над у} = 7$ (отвечать)
Пример 4.8.9 Гипербола, проходящая через $(8,6)$, состоит из всех точек, расстояние до которых от начала координат постоянная больше, чем его расстояние от точки (5,2).2 = 9$ — эллипс. Найдите прямые, касающиеся этой кривой в двух точках. точки пересечения с осью $x$. Покажите, что эти линии параллельно. (отвечать)
Пример 4.8.13 Повторите предыдущую задачу для точек, в которых эллипс пересекает ось $y$. (отвечать)
Пример 4.8.14 Найдите точки на эллипсе из двух предыдущих задач. где наклон горизонтален, а где вертикальен. (отвечать)
Пример 4. 2 =k$ ортогонален
$ух=с$.2 =0$ и $yx=0$
ортогональны друг другу?
2 =k$ ортогонален
$ух=с$.2 =0$ и $yx=0$
ортогональны друг другу?
Пример 4.8.21 Предположим, что $m\neq 0$. Покажите, что семейство кривых $\ds \{y=mx+b \mid b\in \R \}$ ортогонален семейство кривых $\ds \{y=-(x/m)+c \mid c \in \R\}$.
4 Базовая дифференциация
4 Базовая дифференциация 4 Базовая дифференциация
Дифференциация заключается в вычислении наклона или градиент кривой y ( x ) в заданной точке, х .
Градиент – это
Подумайте о дорожных знаках: холм 1 из 10 означает, что вы проезжаете 1 метр. вверх на каждые 10 метров, которые вы проезжаете.
Обозначение : Мы используем символ Δ дельта для обозначения
(большое) изменение значения переменной. Если, скажем, x меняется со значения x 1 на новое
значение, x 2 , затем
Δ x = x 2 – x 1
Таким образом, градиент кривой y ( x ) можно записать как:
градиент = Линейные уравнения
Для прямолинейного графика уравнения y ( x ) = m x + c , градиент задается просто значением м .
Примеры
- y = 3 x + 6, градиент = 3
- у = 5 х – 3, градиент = 5
- y = -2 x + 1, градиент = -2
- y = 6 – 3 x , градиент = -3
Измерение градиентов
Если мы не знаем уравнения прямой, мы можем работать
из градиента, сведя в таблицу значения y vs. х и построение графика.
Пример Значения y и x приведены ниже,
какой градиент?
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у | -11 | -8 | -5 | -2 | 1 | 4 | 7 |
Графический метод
(i) График
(ii) Выберите любые 2 точки вдоль линии ( x 1 , y 1 ) и ( x 2 , у 2 )
(iii) Нарисуйте треугольники (как на диаграмме) или просто рассчитайте х и у .
(iv) Рассчитать градиент из: градиент =
Численный метод : выберите точки, для которых у нас есть значения,
скажем, (-2, -8) и (1,1). Теперь у нас есть:
Поскольку точка пересечения находится в точке y = -2, мы знаем, что уравнение.
этой строки должно быть
Нахождение градиента общей функции
Линейные кривые просты, но как найти наклон любого ?
кривая, y ( x ) в точке x ?
Градиент кривой в точке A такой же, как и у касательной в точке A .Итак, все, что нам нужно сделать, это построить касательной и измерьте ее градиент, Δ y / Δ x .
Пример Каков градиент y ( x ) = x 2 – 4 x – 1, когда x = 4?
Решение Постройте кривую, затем постройте касательную
когда х = 4 на глаз, как умеешь. Измерьте градиент
Δ y / Δ x , завершив треугольник.
Измерьте градиент
Δ y / Δ x , завершив треугольник.
Графически находим, что = 4.
Аналитическая дифференциация
Рисование касательных — довольно громоздкий метод получения градиентов.
Существует ли аналитический метод?
Ответ: дифференцирование . Упрощенный вывод
об этом дано в раздаточном материале, но нам нужно только действительно узнать
«волшебная формула» (см. ниже) .
Обозначение : наклон или градиент, или дифференциал, или производная может быть записана многими эквивалентными способами:
Для других имен переменных и функций существует эквивалент
обозначение.
напр. для с ( т ), у нас есть,
для E(ν) имеем
для φ(λ) имеем
Дифференциация «волшебная формула» (для стандартных
полиномы)
Чтобы дифференцировать полиномиальную функцию, нужно умножить
ведущий множитель, a , и показатель степени (мощность). н ,
затем вычтите единицу из показателя степени.
н ,
затем вычтите единицу из показателя степени.
Примеры
1. у = х 2 ,
= 2 х
2. у = 2 х 3 ,
= 6 х
3. у = 9 х 27 , = 243 х 26
4. u = 3 м 6 , = 18 м 5
5.φ = 7λ, = 7
6. Ψ= ,
7. р = -5 q 2 ,
= -10 q
8. y = 5, = 0 Дифференциал константы всегда равен нулю, т. е. . его наклон равен нулю, как и следовало ожидать.
Следующая лекция .


 start <- c(y1 = 1, y2 = 4)
start <- c(y1 = 1, y2 = 4) 
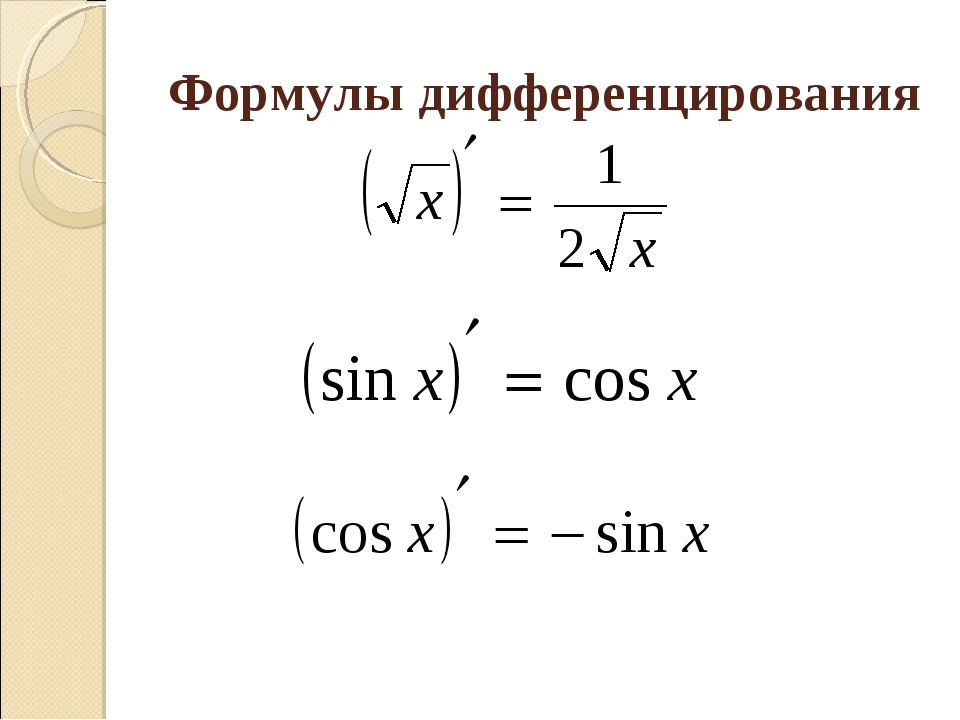
 2} = 0, \;\;\;xy – \sin\left( {x + y} \right) = 0.\]
2} = 0, \;\;\;xy – \sin\left( {x + y} \right) = 0.\] \основной },\;\; \Стрелка вправо 2yy’ = 2p,\;\; \Rightarrow y’ = \frac{p}{y},\;\;\text{где}\;\;y \ne 0. \]
\основной },\;\; \Стрелка вправо 2yy’ = 2p,\;\; \Rightarrow y’ = \frac{p}{y},\;\;\text{где}\;\;y \ne 0. \] Большинство уравнений, с которыми мы имели дело, имеют
были явными уравнениями, такими как y = 2 x -3, так что мы можем написать y = f ( x ), где f ( x ) = 2 x -3.Но
уравнение 2 x – y = 3 описывает то же самое
функция. Это второе уравнение является неявным определением y как функция x . Так как нет настоящего
различие между появлением x или y в
второй форме, это уравнение также является неявным определением x как функция y
Большинство уравнений, с которыми мы имели дело, имеют
были явными уравнениями, такими как y = 2 x -3, так что мы можем написать y = f ( x ), где f ( x ) = 2 x -3.Но
уравнение 2 x – y = 3 описывает то же самое
функция. Это второе уравнение является неявным определением y как функция x . Так как нет настоящего
различие между появлением x или y в
второй форме, это уравнение также является неявным определением x как функция y 
 Взяв производную обеих частей с
относительно x , используя правило мощности для производной г ,
Взяв производную обеих частей с
относительно x , используя правило мощности для производной г , В общем, если давать
результат в плане х одни были возможны, оригинал
выражение может быть решено для y как явная функция x , и неявное дифференцирование, хотя и правильное, будет
не быть необходимым.
В общем, если давать
результат в плане х одни были возможны, оригинал
выражение может быть решено для y как явная функция x , и неявное дифференцирование, хотя и правильное, будет
не быть необходимым. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.