Производная как смысл жизни или что такое дифференциал(d) / Хабр
Frog_cry_tooВремя на прочтение 2 мин
Количество просмотров 17KМатематика *
Туториал
Пролог:
Эта одна из статей серии “Производная как смысл жизни”, сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной(скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:
-напоминаю, что Δx – приращение аргумента, Δy – приращение функции.
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю “неточность”.
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение “неточности”(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.
Как мы видим приращение функции(Δy) как бы разделено на две части: BC и CD.
И ведь по-сути нам ведь интересна именно та часть, которая показывает на сколько изменился у относительно касательной – то есть BC, а CD – это лишь та “погрешность” которая нам не особо интересна, поэтому введем понятие дифференциала:
Дифференциал(d) – это линейная часть приращения функции.
Дифференциал функции(dy) – это главная линейная часть приращения функции.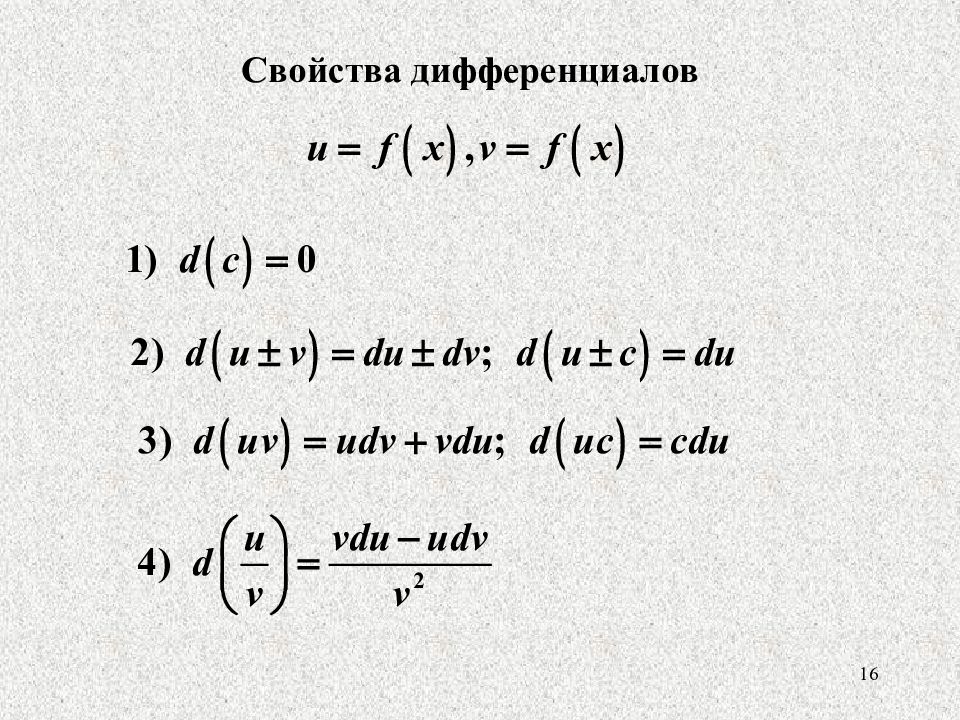
Зная это введем обозначение на графике:
Вернемся к равенству
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
Добавим с левой части и с правой предел
Тогда:
В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:
Зная, что f'(x)Δx = dy, мы делаем вывод, что:
Тогда так же мы можем сказать, что дифференциал функции – это приращения функции у которой приращение аргумента стремиться к нулю, ну и это следуется из того же графика.
В свою очередь dx по прежнему Δx
Теги:- дифференциал
- дифференцирование
- производная
- матанализ
- функция
- Математика
Дифференциал функции. Производные идифференциалы высших порядков
2.2.
Дифференциал функции. Производные и дифференциалы высших порядков
Сегодня вы изучите вопросы
-
Дифференциал функции
-
Геометрический смысл дифференциала функции
-
Основные формулы дифференциалов
-
Инвариантность формы первого дифференциала
-
Производные и дифференциалы высших порядков
Изучив тему занятия, вы сможете
Основные понятия
-
дифференциал функции и его геометрический смысл
-
производные высших порядков
дифференциалы высших порядков
2. 2.1.
2.1.
Дифференциал функции
Пусть на множестве Х задана функция , которая имеет в каждой ее точке производную:
. (113)
По теореме о существовании предела переменной имеем:
, где .
Отсюда находим:
. (114)
Приращение функции в произвольной точке в равенстве (114) представлено в виде суммы двух слагаемых, каждое из которых стремится к нулю при , т.е. является б.м.в. при . Однако второе слагаемое в правой части равенства (114) является б.м.в. более высокого порядка, чем первое, в точках, где производная отлична от 0.
Действительно, .
Следовательно, первое слагаемое, линейное относительно , является главной частью приращения дифференцируемой функции . Эта часть приращения функции называется дифференциалом функции и символически обозначается через :
(115)
Найдем дифференциал независимой переменной х:
Т.к. , то:
(116)
Из равенства (115) с учетом (116) имеем:
(117)
Из формулы (117) следует, что производную по Лейбницу можно рассматривать как дробь, где — числитель, а f — знаменатель.
Следовательно, производную функции можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
В приближенных вычислениях приращение функции заменяют ее дифференциалом Как было доказано выше, второе слагаемое (114) есть б.м.в. более высокого порядка, а следовательно, разность есть б.м.в. при .
Поэтому можно положить, что:
(118)
или
Отсюда находим, что:
. (119)
Формула (119) позволяет выразить приближенно новое значение функции через старое и дифференциал этой функции.
Например, пусть требуется найти приближенное значение корня . По форме заданной величины находится функция: .
По формуле (119) находим:
2.2.2.
Геометрический смысл дифференциала функции
Пусть функция дифференцируема на множестве Х; тогда на плоскости Оху график функции представляется гладкой линией L (в каждой точке этой линии имеется единственная касательная) (рис. 2.10).
2.10).
Пусть М — произвольная точка графика функции .
Построим в точке М касательную к графику функции .
Пусть т. — точка графика функции с абсциссой Сделаем дополнительные построения (см. рис. 2.10).
По рисунку 2.10, Найдем величину :
.
Т.к. , то:
. (120)
Правая часть равенства (120) есть выражение дифференциала функции .
Следовательно,
, (121)
т.е. левая часть равенства (121) есть приращение ординаты касательной. Отсюда краткое заключение.
Дифференциал функции геометрически представляет приращение ординаты касательной.
2.2.3.
Основные формулы дифференциалов
Пусть функции дифференцируемы на множестве Х. Найдем формулы дифференциалов для функций:
(последнее в точках, где ).
По определению дифференциала функции и формул дифференцирования имеем:
или .
или .
или .
В частности, если — константа или — константа, получим:
.
Найдем дифференциалы основных элементарных функций:
Из полученных равенств следует, что формулы дифференциалов аналогичны формулам для производных функции с той лишь только разницей, что вместо производных мы имеем дифференциалы .
2.2.4.
Инвариантность формы первого дифференциала
Пусть функция дифференцируема на множестве Х. Дифференциал первого порядка этой функции, как известно, равен:
(122)
Пусть , где — дифференцируемая функция на множестве Т, областью значений которой является множество Х. В этом случае переменная y является сложной функцией переменной t на множестве Т:
(123)
Найдем дифференциал сложной функции:
.
Мы видим, что форма первого дифференциала не изменилась. В этом и состоит инвариантность формы первого дифференциала.
2.2.5.
роизводные и дифференциалы высших порядков
Рассмотрим функцию Первая ее производная равна , т.е. тоже является функцией от х на множестве .
Найдем вторую ее производную:
.
Мы видим, что вторая производная также является функцией от х, которая, в свою очередь, может иметь производную, уже третьего порядка, и т.д.
Производной n-го порядка от функции называется производная от производной ()-го порядка:
.
В некоторых частных случаях иногда удается найти формулу для производной n-го порядка.
Например, пусть
Пусть требуется найти дифференциал функции :
, т.е. дифференциал функции, есть, вообще говоря, тоже функция — поэтому, в свою очередь, может иметь дифференциал (дифференциал второго порядка):
Дифференциалом n-го порядка называется дифференциал от дифференциала (n — 1)-го порядка: .
По определению,
По аналогии:
(124)
Формулу (124) легко доказать методом полной математической индукции.
Пусть формула (124) справедлива для дифференциала
-го порядка, т.е.
. (125)
Покажем, что в этих предположениях она верна и для дифференциала (k + 1)-го порядка:
Из равенства (124) следует, что , т. е. n-ую производную, по Лейбницу, можно рассматривать как дробь, где — числитель, а — знаменатель.
е. n-ую производную, по Лейбницу, можно рассматривать как дробь, где — числитель, а — знаменатель.
Рассмотрим приложения изложенной теоремы.
Пример 1. Дана металлическая квадратная пластинка с ребром х = 100 мм. При нагревании ребро пластинки удлиняется на ∆х = 0,1 мм. Насколько увеличится при этом площадь пластинки?
Пусть S(х) — первоначальная площадь пластинки, а ∆S — приращение этой площади после нагревании.
По условию задачи .
Найдем приближенное приращение площади пластинки, заменив ее полным дифференциалом:
∆S ≈ ds = (x2)’dx = 2x ∙ dx = 2x ∙ ∆x.
По условию задачи х = 100 мм, ∆x = 0,1 мм.
Отсюда находим, что:
∆S ≈ 2 ∙ 100 мм ∙ 0,1 мм = 20 мм2.
Для оценки погрешности вычисления найдем полное приращение по формуле:
∆S = (х + ∆x)2 — х2 = 2х ∙ ∆х + ∆х2.
Следовательно, погрешность замены равна:
∆х2 = (0,1 мм)2 = 0,01 мм2.
Последнее и есть неглавная часть приращения функции , равная
Пример 2. Найти дифференциал функции y = xn.
По определению дифференциала функции имеем:
Пример 3. Найти дифференциал функции y = ax.
Имеем:
Пример 4. Найти дифференциал функции у = sinx.
Имеем:
Пример 5. Заменив приращение функции дифференциалом, найти приближенное значение arctg 1,02.
Формула применительно к данной функции перепишется так:
Отсюда находим: .
В данном случае х + ∆x = 1,02, х = 1, ∆x = 0,02.
Следовательно, .
Пример 6. Найти n-ую производную функции
Имеем: или
Отсюда можно положить, что:
.
Данное утверждение можно доказать методом полной математической индукции.
Контрольные вопросы
-
Из каких двух частей состоит полное приращение функции?
-
Чем является для функции ее линейная часть относительно приращения независимой переменной?
-
Сравните неглавную часть с главной частью.
 Ваши выводы.
Ваши выводы. -
Может ли функция иметь дифференциал в точке, если она не имеет производной в этой точке?
-
-
В чем состоит инвариантность формы первого дифференциала?
Задания для самостоятельной работы
-
Найдите дифференциал функции y = x3 в точке x = 0, если по определению дифференциала.
-
Найдите дифференциал функции по формуле :
;
;
;
;
;
;
;
;
.
-
Найдите приближенное значение .
-
Найдите приближенное значение функций:
-
Найдите производные указанного порядка от заданных функций:
Дифференциал – Математическая энциклопедия
Основная линейная часть приращения функции.
1) Действительнозначная функция $ f $ вещественной переменной $ x $ называется дифференцируемой в точке $ x $ если она определена в некоторой окрестности этой точки и существует число $ A $ так что приращение
$$ \Delta y = f ( x + \Delta x ) – f ( x) $$
можно записать(если точка $ x + \Delta x $ лежит в этой окрестности) в виде
$$ \Дельта у = А \Дельта х + \омега , $$
где $ \omega / \Delta x \rightarrow 0 $
как $ \Delta x \rightarrow 0 $.
Здесь $A\Deltax$
обычно обозначается $dy$
и называется дифференциалом $f$
в $х$.
Для заданного $ x $
дифференциал $dy$
пропорциональна $ \Delta x $,
т.е. является линейной функцией от $\Delta x $.
По определению при $ \Delta x \rightarrow 0 $
дополнительный член $ \omega $
бесконечно мала более высокого порядка, чем $ \Delta x $(
а также чем $dy$
если $A \neq 0 $).
Вот почему говорят, что дифференциал является основной частью приращения функции.
9{ \prime } ( x ) = dy / dx $,
т. е. производная равна отношению дифференциалов $dy$
и $дх$. Если $A\neq0$,
тогда $ \Delta y / dy \rightarrow 1 $
как $ \Delta x \rightarrow 0 $,
т. е. если $ A \neq 0 $,
тогда $ \Delta y $
и $ды$
являются бесконечно малыми того же порядка, что и $ \Delta x \rightarrow 0 $;
этот факт, наряду с простой структурой дифференциала (т.е. линейностью по отношению к $\Delta x $),
часто используется в приближенных вычислениях, предполагая, что $ \Delta y \ приблизительно dy $
для малых $ \Delta x $.
Например, если требуется вычислить $ f ( x + \Delta x ) $
по известному $f(x)$
когда $ \Delta x $
мало, предполагается, что
9{ \prime } ( x _ {0} ) \Delta x $.
Правая часть представляет собой значение дифференциала функции $f$
в точке $ x _ {0} $
соответствующее значению $ \Delta x $
рассматривается. Таким образом, дифференциал идентичен соответствующему приращению ординаты касательной к кривой $ y = f ( x) $(
ср. отрезок $NT$
на рис. а). Здесь $\omega = \Delta y – dy$,
то есть значение $ | \омега | $
совпадает с длиной отрезка $TS$.
Если $A\neq0$,
тогда $ \Delta y / dy \rightarrow 1 $
как $ \Delta x \rightarrow 0 $,
т. е. если $ A \neq 0 $,
тогда $ \Delta y $
и $ды$
являются бесконечно малыми того же порядка, что и $ \Delta x \rightarrow 0 $;
этот факт, наряду с простой структурой дифференциала (т.е. линейностью по отношению к $\Delta x $),
часто используется в приближенных вычислениях, предполагая, что $ \Delta y \ приблизительно dy $
для малых $ \Delta x $.
Например, если требуется вычислить $ f ( x + \Delta x ) $
по известному $f(x)$
когда $ \Delta x $
мало, предполагается, что
9{ \prime } ( x _ {0} ) \Delta x $.
Правая часть представляет собой значение дифференциала функции $f$
в точке $ x _ {0} $
соответствующее значению $ \Delta x $
рассматривается. Таким образом, дифференциал идентичен соответствующему приращению ординаты касательной к кривой $ y = f ( x) $(
ср. отрезок $NT$
на рис. а). Здесь $\omega = \Delta y – dy$,
то есть значение $ | \омега | $
совпадает с длиной отрезка $TS$.
Рисунок: d031810a
2) Определения дифференцируемости и дифференциала легко распространяются на вещественнозначные функции от $ n $
реальные переменные. Таким образом, в случае $ n = 2 $
говорят, что вещественнозначная функция дифференцируема в точке $(x,y)$
по обеим переменным $ x $
и $ у $
если она определена в некоторой окрестности этой точки и если ее полное приращение
Таким образом, в случае $ n = 2 $
говорят, что вещественнозначная функция дифференцируема в точке $(x,y)$
по обеим переменным $ x $
и $ у $
если она определена в некоторой окрестности этой точки и если ее полное приращение
$$ \Delta z = f (x + \Delta x, y + \Delta y) – f (x, y) $$ 9{2} } $; предполагается, что точка $ ( x + \Delta x , y + \Delta y ) $ принадлежит упомянутой выше окрестности (рис. б).
Рисунок: d031810b
Вводится обозначение
$$ d z = d f ( x , y ) = A \Delta x + B \Delta y; $$
$ дз $
называется полным дифференциалом или просто дифференциалом функции $f$
в точке $(x,y)$(
иногда добавляется фраза «по обеим переменным x и y»). Для заданной точки $(x,y)$
дифференциал $ dz $
является линейной функцией от $ \Delta x $
и $ \Delta y $;
разница $\alpha=\Delta z – dz$
бесконечно мала более высокого порядка, чем $\rho$.
В этом смысле $dz$
— главная линейная часть приращения $\Delta z$.
9{ \prime } ( x , y ) dy $
является частным дифференциалом по $y$. { \prime } $
непрерывны или б) $A$
и $В$
всюду дифференцируемы в $D$
по обеим переменным $ x $
и $y$[7], [8].
{ \prime } $
непрерывны или б) $A$
и $В$
всюду дифференцируемы в $D$
по обеим переменным $ x $
и $y$[7], [8].
См. также Дифференциальное исчисление для дифференциалов вещественных функций одной или нескольких действительных переменных и для дифференциалов высших порядков.
3) Пусть функция $f$ быть определено на некотором множестве $ E $ действительных чисел, пусть $ x $ — предельная точка этого множества, пусть $x\inE$, $ x + \Delta x \in E $, $ \Delta y = A \Delta x + \alpha $, где $ \alpha / \Delta x \rightarrow 0 $ если $ \Delta x \rightarrow 0 $; то функция $f$ называется дифференцируемым по множеству $E$ в $х$, а $ dy = A \Delta x $ называется его дифференциалом по множеству $ E $ в $х$. Это обобщение дифференциала действительнозначной функции одной действительной переменной. К специальным видам этого обобщения относятся дифференциалы в концах отрезка, внутри которого функция определена, и аппроксимативный дифференциал (ср. Приближенная дифференцируемость).
Аналогичным образом вводятся дифференциалы по множеству для вещественнозначных функций нескольких действительных переменных.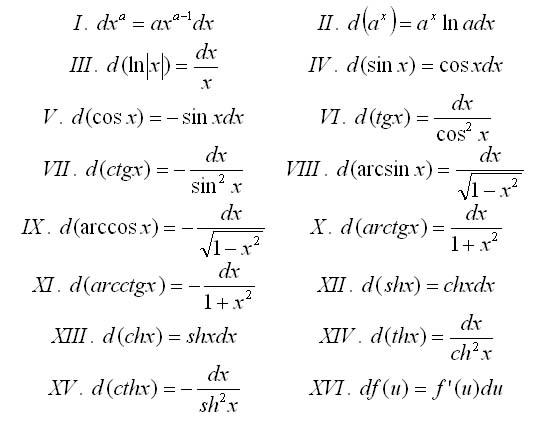
4) Все определения дифференцируемости и дифференциала, данные выше, почти без изменений могут быть распространены на комплекснозначные функции одной или нескольких действительных переменных; к вещественнозначным и комплекснозначным вектор-функциям одной или нескольких действительных переменных; и к комплексным функциям и вектор-функциям одной или нескольких комплексных переменных. В функциональном анализе они распространяются на функции точек абстрактного пространства. Можно говорить о дифференцируемости и о дифференциале функции множества по некоторой мере.
Ссылки
| [1] | Г.П. Толстов, “Элементы математического анализа”, 1–2 , Москва (1974) (на русском языке) Fichtenholz, “Differential und Integralrechnung”, 1 , Deutsch. Verlag Wissenschaft. (1964 г.) 6 Збл 0143.27002 |
| [3] | Л.Д. Кудрявцев, “Математический анализ”, 1 , Москва (1973) 14 Збл 1080. 00002 Збл 1080.00001 Збл 1060.26002 Збл 0869.00003 Збл 0696.26002 Збл 0703.26001 Збл 0609.00001 Збл 0632.26001 Збл 0485.26002 Збл 0 485.26001 00002 Збл 1080.00001 Збл 1060.26002 Збл 0869.00003 Збл 0696.26002 Збл 0703.26001 Збл 0609.00001 Збл 0632.26001 Збл 0485.26002 Збл 0 485.26001 |
| [4] | С.М. Никольский, “Курс математического анализа”, 1 , МИР (1977) Збл 0397.00003 Збл 0384.00004 |
| 301 | |
| [6] | А.Н. Колмогоров, С.В. Фомин, “Элементы теории функций и функционального анализа”, 1–2 , Graylock (1957–1961) (Перевод с русского) 1879 г.6 MR1530727 MR0118795 MR0085462 MR0070045 Збл 0932.46001 Збл 0672.46001 Збл 0501.46001 Збл 0501.46002 Збл 0235.46001 Збл 0103.08801 |
| [7] | Г.П. Толстов, “О криволинейных и повторных интегралах”, , Тр. Инст. Стеклов. , 35 (1950) MR44612 |
| [8] | Г.П. Толстов, «О полном дифференциале», УМН. наук , 3 : 5 (1948) стр. 167–170 MR0027044 167–170 MR0027044 |
Комментарии
См. также Дифференциация; Дифференциация отображения.
Для дифференциации функций набора см. Установить функцию; Теорема Радона–Никодима, [a7].
Для обобщения функций между абстрактными пространствами см. также производную Фреше; Производная Гато.
Для производной функции $ f : \mathbf C \rightarrow \mathbf C $ см. Аналитическая функция.
Каталожные номера
| [a1] | Т.М. Апостол, «Исчисление», 1–2 , Блейсделл (1964) MR0261376 MR0250092 MR0236734 MR0236733 MR0214705 MR1532185 MR1531712 MR0087718 Zbl 0123.25902 |
| [a2] | 9011 6 Т.М. Апостол, “Математический анализ”, Addison-Wesley (1974) MR0344384 Zbl 0309.26002|
| [a3] | В. Флеминг, “Функции многих переменных”, Springer (1977) МР0422527 Збл 0348.26002 |
| [а4] | К. Р. Stromberg, “Introduction to classic real analysis”, Wadsworth (1981) MR0604364 Zbl 0454.26001 Р. Stromberg, “Introduction to classic real analysis”, Wadsworth (1981) MR0604364 Zbl 0454.26001 |
| [a5] | R. Courant, “Vorlesungen über Differential- und Integralrechnung”, 9011 9 1–2 , Спрингер (1971–1972 гг.) ) MR01 MR1521849 MR1521664 Zbl 0224.26001 Zbl 0217.37201 Zbl 0121.28904 Zbl 0066.30303 Zbl 0064.04704 Zbl 0003.05401 Zbl 57.0246.01 Zbl 56.0193.01 Збл 53.0200.13 Збл 55.0728.02 |
| [а6] | И.П. Натансон, “Theorie der Funktionen einer reellen Veränderlichen”, H. Deutsch, Frankfurt a.M. Г.Э. Шилов, Б.Л. Гуревич, “Интеграл, мера и производная: единый подход”, Довер, переиздание (1977) (перевод с русского) MR0466463 Zbl 0391.28007 |
| [a8] | функции переменные réelles», Готье-Виллар (1937) Збл 0017.10504 Збл 63.0177.02 Збл 63.0177.01 |
Как процитировать эту запись:
Дифференциал. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Differential&oldid=53429
Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Differential&oldid=53429
Эта статья была адаптирована из оригинальной статьи Г.П. Толстова (создатель), который появился в Encyclopedia of Mathematics – ISBN 1402006098. См. Оригинальную статью
Mathematical Methods for Fractional Differential Equations in Applied Sciences
Journal of Mathematics
Journal of Mathematics / Open Special Issues / Special Issue
Дата публикации
01 июля 2023
Крайний срок подачи
02 июня 2023
Ведущий редактор
Юсуф Пандир 3
Приглашенные редакторы
Юсуф Гурефе 1 | J.F. G´omez-Aguilar 2
1 Факультет математики, Мерсинский университет, Турция
2 CONACyT-Tecnol´ogico Nacional de M´exico/CENIDET, Interior Internado Palmira S/N, Col. Palmira, C.P. 62490, Куэрнавака, Морелос, Мексика, Мексика
3 Университет Бозок, Турция
Прием статей
Этот выпуск открыт для подачи.
Статьи публикуются при приеме, независимо от даты выхода спецвыпуска.
Отправить в этот специальный выпускОписание
В последнее десятилетие дробные дифференциальные уравнения эффективно использовались при моделировании задач, возникающих в науке и технике. Исследования дробных дифференциальных уравнений являются междисциплинарными и встречаются в различных областях, таких как биоматематика, физика плазмы, системы управления, математическая биология, упругость, квантовая механика, гидромеханика, оптика, биоинженерия, сложные системы и т. д.
Моделирование задач с дробными дифференциальными уравнениями и нахождение аналитических, численных и точных решений этих моделей является важным явлением. Многие математические методы были усовершенствованы в литературе. Кроме того, различные подходы к дробному анализу обнаруживаются путем создания различных определений дробной производной и интегралов. Научные исследования по этим предметам выявили новые и различные методы дробного анализа, теории и приложений.
Целью этого специального выпуска является вклад в новые определения, теории и приложения дробной производной. Кроме того, мы хотим внести свой вклад в разработку и применение новых методов аналитического, численного и точного решения задач, возникающих в различных дисциплинах. Оригинальные исследовательские и обзорные статьи приветствуются.
Возможные темы включают, но не ограничиваются следующим:
- Новые определения и теории в дробном исчислении
- Применение дробного исчисления в науке и технике
- Дробные математические модели в прикладной математике
- Аналитические методы для дробных дифференциальных уравнений
- Численные методы дробных дифференциальных уравнений
- Новые численные схемы для дробных операторов
- Динамические и биологические системы, связанные к дробное исчисление
- Дифференциальное уравнение дробного порядка в математической физике
- Уединенные волновые решения во фрактальных средах
Статьи
Математическое моделирование чувств с точки зрения анализа поэзии Ольвидо с дробными операторами
Мустафа Али Докуйюку | Бурак Армаган | .

 Ваши выводы.
Ваши выводы.