Дифракционный параметр: 11.6. Дифракционные текстуры

11.6. Дифракционные текстуры

11.6. Дифракционные текстуры

11.6.1. Общая информация

Рисунок 11.214. Два примера дифракции.

Этот фильтр находится в Фильтры → Визуализация → Текстура → Дифракционные текстуры.

Этот фильтр позволяет создавать дифракционные текстуры или текстуры интерференции волн. Для каждого канала RGB можно установить частоту, контуры, рассеяние, и другие параметры.

Этот фильтр особенно полезен для создания замысловатых текстур, отлично подходит для создания психоделических текстур типа батик и для имитации узоров цветного стекла (как у окон церквей).

Фильтр старается имитировать эффект света, падающего на дифракционную решётку. К сожалению, авторы фильтра не написали теорию работы фильтра, или что означают параметры. К счастью, почти всё производимое этим фильтром выглядит интересным.

Можно, однако, сделать несколько замечаний по работе фильтра. Фильтр имеет двойную симметрию: левая сторона равна правой, верх – низу. Изображение напоминает структуру света после дифракции вокруг круглой апертуры (для низких значений параметра частоты). Проще говоря, изображение (для низких частот) – концентические круги. Цветной круг расположен в центре, затем тёмное кольцо, затем цветное и т.д. Чёткость границ перехода от цвета к чёрному в какой-то мере определяется параметром резкости границ. Каждая цветная область называется контур. При возрастающих значениях частоты круг в середине разбивается на пять кругов поменьше: в центре, вверху, внизу, справа и слева. При высоких значениях частоты краевые круги копируются до края изображения и соедены дугами. Это относится для каждого канала RGB в отдельности. Результаты отдельных каналов накладываются друг на друга для конечного изображения.

11.

6.2. Параметры

Просмотр

Этот фильтр требует много ресурсов, поэтому «Просмотр» автоматически не обновляется. Результат изменения настроек можно увидеть, нажав кнопку Просмотр. Этот фильтр не использует изображение, а просто заменяет его на свой результат.

Все параметры дают возможность ввести значения при помощи ползунка и поля ввода.

Частота

Частота: Определяет частоту падающего света. При низких значениях ( <1) получаются концентрические круги, при высоких количество кругов возрастает, и яркие элементы тяготеют к крестообразной форме. При значении 0 изображение покрывается одним тоном.

Красный; Зелёный; Синий

Частоту можно установить для каждого основного цвета отдельно.

Контуры

Определяет число подконтуров в начальных контурах. Начальный контур – та цветная область, которая получается при предельно малом значении этого параметра. При увеличения значения, каждый контур разбивается на чередующие цветные и тёмные области той же формы, что и начальный контур.

Для тех, кто любит математику. Представте себе, что яркость цвета по ширине контура описывается косинусом от -90° до 90°, т.е. положительные значения cos(kx). В диапазон от -90° до 90° помещается только один «холм» функции. При возрастании значения параметра больше холмов помещается в тот же диапазон, т.е. параметр увеличивает значение «k» (частота) в формуле cos(kx).

Это только приближённое представление работы фильтра, так как середина контура периодически бывает тёмной при возрастании значения параметра.

Красный; Зелёный; Синий

Число контуров можно установить для каждого основного цвета отдельно.

Резкие края

Определяет плавность перехода между цветной и тёмной областями.

Красный; Зелёный; Синий

Резкость можно установить для каждого основного цвета отдельно.

Другие параметры

Эти параметры относятся ко всем каналам.

Яркость

Определяет интенсивность света для всего изображения (от 0,0 до 1,0).

Рассеяние

Определяет степень наложения контуров друг на друга (от 0,0 до 1,0). При большем значении чёткость уменьшается.

Поляризация

Определяет степень дифференции (от -1,0 до 1,0). Значение 0 не влияет на результат. Значения -1,0 и 1,0 дают одинаковый результат. При значении около 0.7 интерференция максимальна и напоминает классическую интерференцию волн из двух источников.

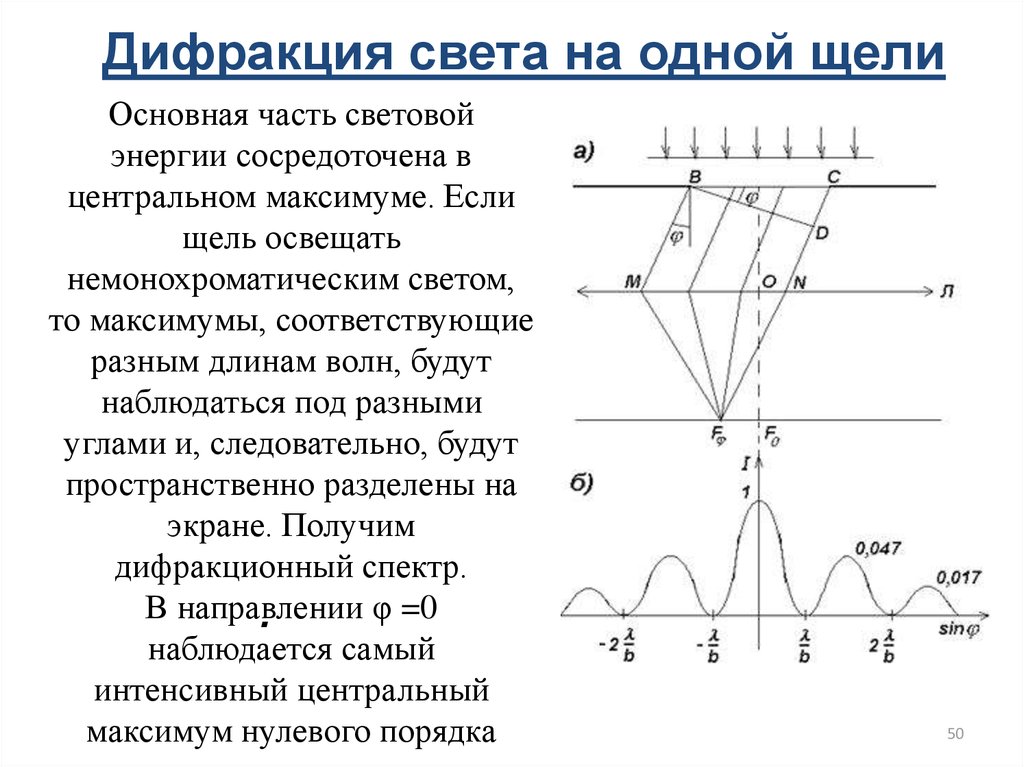
1. Дифракция света

Дифракция Фраунгофера на щели и дифракционной решетке

Цель работы: ознакомиться с теорией дифракции Фраунгофера на щели и дифракционной решетке, ознакомиться с теорией дифракционной решетки как спектрального прибора, а также с методом приближенного определения периода дифракционной решетки и ширины раздвижной щели.

Приборы и принадлежности: лазер ЛГН-109 на подставке, столик с измерительными линейками и держателем, дифракционная решетка на пропускание, раздвижная щель с микрометрическим винтом.

Теория

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например, вблизи границ непрозрачных тел, сквозь малые отверстия) и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.

Огибание препятствий звуковыми волнами (т.е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни. Для наблюдения же дифракции световых волн необходимо создание специальных условий. Это обусловлено тем, что длина световой волны очень мала.

Между дифракцией и интерференцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть

интерференцией волн. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией волн. Поэтому говорят о дифракционной картине от одной щели и интерференционной картине от двух узких щелей.

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, которая распространяется от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.

Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля.

Более строго характер дифракции зависит от значения безразмерного параметра a²¤(Ll), где

a – это ширина щели, L – расстояние от щели до экрана.

Если этот параметр много меньше единицы – наблюдается дифракция Фраунгофера, если он порядка единицы – дифракция Френеля, если же этот параметр много больше единицы – оказывается применимым приближение геометрической оптики.

Дифракцию Фраунгофера можно наблюдать, если поместить за источником света S и перед точкой наблюдения P на экране Э по одной линзе Л так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы (рис. 1).

Пусть на бесконечно длинную щель Щ шириной а падает плоская световая волна. Поместим за щелью собирающую линзу Л₂, а в фокальной плоскости этой линзы экран Э. Волновая поверхность падающей волны, плоскость щели и экран параллельны друг другу (см. рис. 1). Поскольку щель бесконечна, дифракционная картина, наблюдаемая в любой плоскости перпендикулярной к щели, будет одинакова. Поэтому достаточно исследовать характер картины в одной такой плоскости, например, в плоскости (рис.1).

На рис. 1 показаны вторичные лучи дифрагированные на угол j. В направлении, которое соответствует случаю когда j = 0 – разность хода крайних и любых других вторичных лучей равна нулю. В этом направлении (j = 0, D = 0) наблюдается главный максимум дифракционной картины.

В направлениях, для которых j = j_m и когда для вторичных лучей выполняется условие

D=a sin j_m=ml, где m – целое число – наблюдаются нулевые минимумы дифракционной картины m–го порядка.

Рассмотрим распределение интенсивности света на экране. Разобьем щель Щ на элементарные полоски. Ширину элементарной полоски обозначим dx (см. рис. 2). Возмущение, вызванное каждой полоской в плоскости щели, описывается уравнением dE_o = c dx cos wt, где c – постоянная.

Если амплитуду падающей волны, соответствующей всей ширине щели, обозначить через Е_о, то очевидно, что , откуда . Следовательно

. (1)

Для нахождения результирующей амплитуды в любой точке экрана наблюдения, определяемой углом дифракции j, необходимо знать распределение фаз всех колебаний, приходящих в эту точку. Так как линза не вносит добавочной разности хода, то распределение фазы в точке Р_j будет таким же, как в плоскости MF, образующей с плоскостью щели угол j. Поэтому надо найти распределение фаз для элементарных полос в плоскости MF (рис. 2).

Рассмотрим элементарную полоску, расположенную на расстоянии х от точки М, т.е. от левого края щели MN. Для лучей, дифрагированных под углом j, средняя точка этой полоски перемещается в точку F₁ плоскости MF. Возмущение, обусловленное произвольной полоской шириной dx, расположенной на расстоянии x от точки М в плоскости MF, выразится уравнением:

(2)

где k – волновое число.

Следовательно, вследствие добавочной сравнительно с точкой М разности хода лучей, возникает разность фаз между полоской точки М и полоской, находящейся на расстоянии х (в плоскости MF) от нее, равная: .

Дифракция

Дифракция

Справочный веб-сайт JPL по беспроводной связи Глава: Беспроводные каналы распространения Раздел: Потеря пути

Рисунок: Модель профиля пути для (одной) дифракции на кромке ножа

Если прямой видимости препятствует одно остроконечное препятствие высотой h _м мы определяем следующий параметр дифракции v :

где d _t и d _R — конечные расстояния от кромки ножа. Дифракционные потери, дополнительные к потерям в свободном пространстве и выраженные в дБ, могут быть точно аппроксимированы выражением

	A D =0	если v < 0
	A D =2 + 0 9 =2 + 9 900 0020 В 2	если 0 < В < 2,4
	A D =13 + 20 log v	, если v >2,4

Затухание над округлыми препятствиями обычно выше A _D в приведенной выше формуле.

Калькулятор кромки одного ножа

Приближенные методы расчета дифракционных потерь на нескольких кромках ножей были предложены

• Буллингтон
  
  Рисунок: Конструкция для приблизительного расчета дифракционных потерь на множественных ножевых кромках, предложенная Bullington

  Метод Буллингтона определяет новое “эффективное” препятствие в точке, где пересекаются линии прямой видимости двух антенн.

• Эпштейн и Петерсон
  
  Рисунок: Конструкция для приближенного расчета дифракционных потерь на множественных ножевых кромках, предложенная Эпштейном и Петерсоном

  Эпштейн и Петерсон предложили провести линии прямой видимости между соответствующими препятствиями и добавить дифракционные потери на каждом препятствии.

• Дейгу
  
  Рисунок: Конструкция для приближенного расчета дифракционных потерь Multiple Knife-Edge, предложенная Deygout

  Deygout предложил искать “главное” препятствие, т.е. точку с наибольшим значением v на пути. Дифракционные потери над «второстепенными» препятствиями добавляются к дифракционным потерям над основным препятствием.

Представленные ранее методы определения потерь на отражение от земли и дифракционных потерь предполагают «мондриановскую» интерпретацию профиля трассы: препятствия представляют собой прямые вертикальные линии, тогда как горизонтальные плоскости вызывают отражения. То есть путь распространения рассматривается как совокупность горизонтальных и вертикальных элементов. Точный расчет потерь на трассе на трассах вне прямой видимости с отражениями от земли является сложной задачей и не допускает таких упрощений.

Многие измерения потерь при распространении для трасс с комбинированными потерями из-за дифракции и отражения от земли показывают, что препятствия остроконечного типа значительно снижают потери от земной волны. Блумквист предложил два метода нахождения общей потери:

.

и эмпирическая формула

где A _fs потери в свободном пространстве, A _R потери на отражение от земли и A _D кратные потери в dB.

Справочный веб-сайт JPL по беспроводной связи 1993, 1995.

Размерная зависимость параметров решетки наночастиц платины на углеродном носителе: рентгеноструктурный анализ и теоретические соображения

Размерная зависимость параметров решетки наночастиц платины на углеродном носителе: рентгеноструктурный анализ и теоретические соображения 90–164

В. Леонтьев* ^абв А. Б. Куриганова, ^д Н. Г. Леонтьева, ^е Л. Хеннет, ^и А. Рахматуллина, ^и Н. В. Смирнова ^д и В. Дмитриев ^ф

Принадлежности автора

* Соответствующие авторы

^и CNRS, CEMHTI UPR 3079, ун-т. Орлеан, F-45071 Орлеан, Франция
Электронная почта: i. [email protected]
Тел: +79185524024

^б LE STUDIUM, Институт перспективных исследований долины Луары Орлеанские туры, Франция

^с Южный федеральный университет, физический факультет, ул. Зорге, 5, Ростов-на-Дону, Россия

^д Южно-Российский государственный технический университет, ул. Просвещения, 132, Новочеркасск, Россия

^и Азово-Черноморская государственная сельскохозяйственная академия, ул. Ленина, 21, г. Зерноград, Ростовская область, 347740, Россия

^ф Швейцарско-норвежские линии луча в ESRF, BoitePostale 220, F-38043 Гренобль, Франция

Аннотация

rsc.org/schema/rscart38″> Наночастицы Pt диаметром от 2 до 28 нм, нанесенные на углерод, были исследованы методом рентгеновской дифракции. Параметр элементарной ячейки синтезированных наночастиц Pt/C всегда ниже, чем у массивной Pt. При уменьшении среднего размера частиц D примерно до 2 нм параметр элементарной ячейки a нелинейно уменьшается примерно на 0,03 Å, что соответствует изменению на 0,7 % по сравнению с объемной Pt, а размерный эффект преобладает в диапазоне размеров от 2 до 10 нм. Зависимость a (1/ D ) хорошо аппроксимируется прямой линией с наклоном -0,0555 ± 0,0067 нм ^-1 и точкой пересечения -3,9230 ± 0,0017 Å. Для интерпретации полученной экспериментальной зависимости параметра элементарной ячейки наночастиц Pt/C использовались четыре различных теоретических подхода, таких как термовакансионный механизм, модель сплошной среды, давление Лапласа и механизм корреляции порядок-длина-прочность связи. Сравнение расчетных зависимостей, основанных на приведенных выше моделях, с экспериментальными показывает, что модель сплошной среды лучше всего согласуется с экспериментально найденной зависимостью параметра элементарной ячейки наших наночастиц Pt на углеродном носителе.