Тишин В.В. Дискретная математика в примерах
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П.КОРОЛЕВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»
В.В. Тишин
Дискретная математика в примерах и за дачах
Электронное учебное пособие
САМАРА
2007
Автор: ТИШИН Владимир Викторович
Дискретная математика – одно из самых динамично развивающихся направлений современной математики, и тотальная компьютеризация всех областей нашей жизни приводит к постоянному росту спроса, как на программистов, так и на специалистов, разрабатывающих математи ческие основы компьютерных технологий.
Важным моментом усвоения математики и овладения её методами явля ется самостоятельная работа учащегося.
Всем, имеющим отношение к преподаванию дискретной математики, знакомы, ставшие классическими, задачники: «Задачи и упражнения по дискретной математике» Т.П. Гаврилова и А.А. Сапоженко, «Алгебра логики в задачах» С.Г. Гиндикина, а также «Задачи по теории множеств, математической логике и теории алгоритмов» И.А. Лаврова и Л.Л. Максимовой, но в настоящее время ощущается потребность в задачни ках по дискретной математике, содержащих серии однотипных задач для выполнения студентами индивидуальных заданий.
Настоящий сборник отражает многолетний опыт работы автора, приоб ретённый им в Самарском государственном аэрокосмическом универ ситете им. С.П. Королёва при чтении лекций, а также при ведении прак тических занятий по курсам «дискретная математика» и «математиче ская логика и теория алгоритмов».
Система индивидуальных заданий, практикуемая в СГАУ с 80-х годов прошлого века, хорошо себя зарекомендовала. При проведении практи ческих занятий студенты с большим вниманием следят и активно участ вуют в решении и разборе задач, аналогичных тем, что им придётся вы-
При проведении практи ческих занятий студенты с большим вниманием следят и активно участ вуют в решении и разборе задач, аналогичных тем, что им придётся вы-
поднять индивидуально. Большинство разделов курса дискретной мате матики подкреплено и проиллюстрировано индивидуальными задания ми, и самостоятельное решение студентами задач помогает им лучше усвоить теорию и получить практические навыки работы с объектами, являющимися предметом изучения дискретной математики. Выполне ние комплекса задач, вошедших в данное пособие, даёт возможность студентам освоить базовые понятия дискретной математики, прочувст вовать связи между ними и отработать приёмы решения основных ти пов задач данного предмета.
Каждое задание даётся в 30 вариантах, и для каждого задания в сборни ке приведён образец решения, что может помочь студентам вниматель но разобрать предлагаемые способы решения задач и грамотно офор мить выполненные индивидуальные задания.
Данное пособие может быть также полезно для вузов, практикующих заочную форму обучения, а также для всех энтузиастов, решивших изу чить дискретную математику самостоятельно.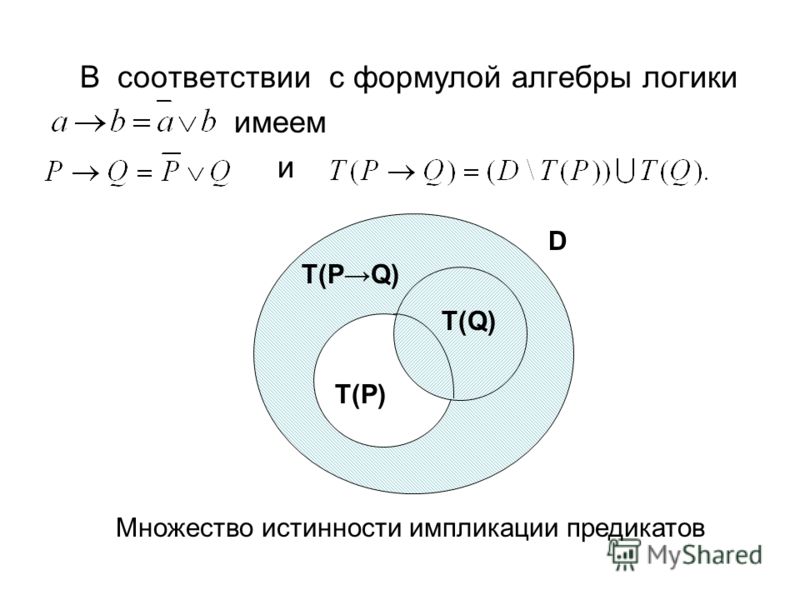
Пособие состоит из 6 глав:
□Множества, графики, соответствия, отношения;
□Булевы функции;
□Теория алгоритмов;
□Предикаты;
□Комбинаторика;
□Конечные автоматы.
Вначале каждой главы вводятся понятия, даются определения и форму лировки теорем, используемых при выполнении заданий, что практиче ски исключает необходимость привлечения дополнительной литерату ры по рассматриваемой тематике.
Содержание |
| |
1. Множества, графики, соответствия, отношения………………………………. | 4 | |
| 1.1. Операции над множествами……………………………………….. | 4 |
| 1.2. Графики…………………………………………………………………….. | 36 |
| 1. | 45 |
| 1.4. Отношения………………………………………………………………… | 59 |
2. | Булевы функции…………………………………………………………………………….. | 72 |
| 2.1. Булевы функции. Суперпозиции……………………………… | 72 |
| 2.2. Булевы функции и теория множеств………………………… | 82 |
| 2.3. Нормальные формы и полиномы……………………………… | 91 |
| 2.4. Классы Поста………………………………………………………… | 100 |
| 2. | |
| булевых функций……………………………………………………. | 113 |
| 2.6. Частичные функции и схемы………………………………….. | 123 |
3. | Теория алгоритмов……………………………………………………………………….. | 161 |
| 3.1. Машины Тьюринга…………………………………………………. | 161 |
| 3.2. Нормальные алгоритмы………………………………………….. | 176 |
| 3.3. Рекурсивные функции…………………………………………….. | 186 |
4. | Предикаты………………….. | 193 |
| 4.1. Предикаты………………………………………………………………. | 193 |
5. | Комбинаторика………………………………………………………………………… | 207 |
| 5.1. Сочетания, размещения, перестановки…………………. | 207 |
| 5.2. Бином Ньютона………………………………………………………. | 213 |
| 5.3. Формула включений и исключений……………………….. | 223 |
| 5.4. Задачи о распределениях………………………………………… | 227 |
| 5. | 231 |
| 5.6. Рекуррентные соотношения……………………………………. | 239 |
6. | Конечные автоматы……………………………………………………………………… | 249 |
6.1. Автоматы Мили……………………………… | .249 |
6.2. Частичные автоматы………………………. | .262 |
6.3. Реализация автоматов схемами………. | 277 |
6.4. Распознавание множеств автоматами | 293 |
Список литературы | .327 |
Глава 1.
Множества, графики, соответст вия, отношения
1.1. Операции над множествами
Запись х е А означает, что элемент х принадлежит множеству А. Ес ли х не является элементом множеств А, то пишут х ф А или х е А . Два множества А и В считаются равными, если они состоят из одних и тех же элементов. Будем писать А = В, если А и В равны и А Ф В в
Ес ли х не является элементом множеств А, то пишут х ф А или х е А . Два множества А и В считаются равными, если они состоят из одних и тех же элементов. Будем писать А = В, если А и В равны и А Ф В в
противном случае.
Множество называется пустым и обозначается 0 , если оно не содержит
элементов.
Будем говорить, множество А включено в множество В и писать А с: В,
если каждый элемент множества А является элементом множества В . В этом случае А называется подмножеством множества В . Считается,
что для любого А справедливо включение 0 с А
Если Л с й и Al= В, то будем писать А а В и говорить, что множест
во А строго включено во множество В.
Семейство всех подмножеств данного множества А обозначается
Р(А).
Мощностью конечного множества А будем называть число его элемен тов. Мощность конечного множества А обозначается \А\.
Объединением множеств А я В называется множество
А улВ —{х | х е А или х е В]
Пересечением множеств А и В называется множество
А глВ = {х| х е А и х&В}
Разностью множеств А и В называется множество
А \В = {х | х е А и х<£В}
Если все рассматриваемые множества являются подмножествами неко торого универсального множества U , то разность U \ А называется до
полнением А и обозначается А . ( В \ А ) .
( В \ А ) .
Будем говорить, что множества А и В находятся в общем положении, и
писать AGDB, если существуют такие элементы | а,Ь,с, | что | а е А и | ||||||||
а € В , Ъ &’ Вя Ъё В , с е А и с е В . |
|
|
|
|
|
| |||||
Задание 1.1.1 |
|
|
|
|
|
|
|
|
|
| |
1. Справедливо ли в общем случае утверждение: |
|
|
|
| |||||||
если А а В и Б (3 С и С у D то A 6 D 1 |
|
|
|
|
|
| |||||
2. | А, В, | С и D | выполниться набор условий: | ||||||||
А а В я В $С я С у D я A b D l |
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| Таблица 1.1.1 | ||
№ а | р Y | 8 | № | а | Р | Y | 8 | № а | Р Y | 8 | |
1 CZ | G с | CZ | 11 G | е | с | G | 21 е | с | с | с | |
2 | Е Е | с Е | 12 | с Е С Е | 22 | с с Е Е | ||
3 | С С Е Е | 13 | с С С Е | 23 | е Е | с С | ||
4 | Е С Е | С | 14 | с Е Е С | 24 | с с | с Е | |
5 | С С Е | С | 15 | Е Е Е Е | 25 | с Е Е С | ||
6 | Е Е Е | с | 16 | С С Е С | 26 | Е с Е Е | ||
7 | Е С | С с | 17 | с Е С Е | 27 | е с | С Е | |
8 | Е Е | С | с | 18 | Е С С Е | 28 | с Е | С С |
9 | Е С Е с | 19 | С С С С | 29 | е с | с С | ||
10 Е С | С | с | 20 | Е Е с Е | 30 | с с Е С | ||
Примеры решения задания 1. 1.1
1.1
Пример 1.
а) Справедливо ли в общем случае утверждение :
если А с В, | В с С и С cz D, то А с: D ? |
|
|
| |
Пусть х е А. | Так как А а В, | из определения включения следует, что | |||
х<=В. Так как х g В и В с С, | то х е С . Так как х е С и С с Д | то | |||
х g D. Итак, | из того, что произвольный элемент | х g А | следует, | что | |
х g D. На основании определения заключаем, что | A с: /), | то есть дан | |||
ное утверждение верно. |
|
|
|
| |
б) Может при некоторых А, В, С и D выполняться набор условий: А а В, В с С и С с D, и А с D ?
Да может. D ?
D ?
Пусть А = {х},
В = {х,у}, С = {{x,y},z}, D = {{{x,y},z},w} .
Тогда { x } c { x ,j } и {x,y}e{{x,y},z}e{{{x,y},z},w} .
Но в то же время неверно, что {х} cz {{{x,y},z},w} , так как единст
венный элемент х множества | А | не является элементом множества | |||||||
D, | состоящего из элементов {{x,y},z} и w . Итак, утверждение из на | ||||||||
шего примера 2а) | в общем случае неверно. |
|
| ||||||
б) | Может ли при некоторых | А, В, С и D | выполняться набор условий: | ||||||
И с В, В еС , С £ D и А п D ? |
|
|
| ||||||
Да, может. | А = 0 , | В – { х } , | С – { { х } , у } , | D- {{{x},y},z}. | |||||
Тогда | 0<= {х }, | {x }e {{x },j}, | {{х}, у} е {{{х}, y},z} и в то же | ||||||
время | 0 c { { { x } j } , z j . |
|
|
|
|
| |||
Задание 1.1.2 |
|
|
|
|
|
|
| ||
Для | универсального | множества | U —{—5, —4, – 3 , – 2 , —1,1,2,3,4,5}, | ||||||
множества А, заданного списком и для В, | являющимся множеством | ||||||||
корней уравнения | х 4 + оис3 + Рх2 + ух+ 8 = 0 |
| |||||||
1. | Найти множества : | А улВ, | В п А , | А\В, | В\А, | А а В, В, | |||
С= ( А а В ) а А..
2.Выяснить, какая из пяти возможностей выполнена для множеств А и
N | : Л с С , | или С (л А, | или А = С, | или А п С = 0 , или | А СП)С . |
| |||||
3. | Найти Р( В) | и | Р( В) | . |
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| Таблица 1. | ||
№ | А | а | Р | Г | 5 | № | А | а | Р | Г | 8 |
1 | -1,1,4,3 | 1 | -12 | -28 | -16 | 16 | -1,1,2,3 | -3 | -3 | 7 | 6 |
2 | -1,1,2,3 | 7 | 13 | -3 | -18 | 17 | -1,1,3,2 | -7 | 12 | 4 | -16 |
3 | -1,1,3,4 | -2 | -12 | 18 | 27 | 18 | -2,-1,2,4 | -1 | -7 | 13 | -6 |
4 | -1,1,2,3 | 0 | -17 | 36 | -20 | 19 | -1,1,2,3 | -4 | 3 | 4 | -4 |
5 | -2,1,3,4 | 0 | -11 | -18 | -8 | 20 | -1,1,2,3 | -5 | -3 | 13 | 10 |
6 | -1,1,4,5 | 3 | -9 | -23 | -12 | 21 | -3,5,3,4 | -11 | 39 | -49 | 20 |
7 | -3,-1,1,2 | -2 | -7 | 20 | -12 | 22 | 1,2,3,4 | -6 | 8 | 6 | -9 |
8 | -4 -1 ,1 Д | 0 | -11 | 18 | -8 | 23 | -1,-2,1,2 | -3 | -2 | 12 | -8 |
9 | -2,-1,3,5 | 3 | -7 | -15 | 18 | 24 | -1,2,5,4 | 0 | -9 |
| 12 |
10 | -3,-1,1,2 | 5 | 1 | -21 | -18 | 25 | -1,-2,-3,1 | -4 | -10 | 28 | -15 |
И | -2,2,3,4 | 2 | -7 | -20 | -12 | 26 | 1,4,2,3 | 3 | -3 | -7 | 6 |
12 | -3,-1,2,4 | -2 | -15 | -4 | 20 | 27 | -1,1,2,4 | 1 | -12 | 4 | 16 |
13 | -1,-3,2,3 | -5 | 1 | 21 | -18 | 28 | -1,1,2,3 | -2 | -4 | 2 | 3 |
14 | -4,-3,1,2 | 1 | -7 | -13 | -6 | 29 | -1,4,2,3 | -4 | -2 | 12 | 9 |
15 | -5 ,-1,1,3 | 6 | 0 | -22 | 15 | 30 | -1,2,3,4 | 3 | 1 | -3 | -2 |
Пример решения задания 1. | |||
Решим задание 1.1.2 для А = {1,—2,3,—4} и уравнения | |||
|
|
| х4 – 7 х 3 + 6х2 + 3 2 х -3 2 = 0. |
Сначала найдём множество В корней данного уравнения. Подбором | |||
устанавливаем, что корнем исходного многочлена | |||
х | 4 | 3 | 2 |
| —7х | + 6 х + 3 2 х – 32 является 1; поделив этот многочлен на х —1 , | |
получим многочлен х3 —6х 2 + 32.
Также подбором устанавливаем, что -2 является корнем многочлена
х3 – | 6 | х2 + 32 | и делим этот многочлен на х + 2. Получим многочлен | |
2 | 8 | х +16. | Его корни совпадают и равны 4. | |
х – | ||||
Итак, множество В найдено, | В —{—2,1,4}. Теперь решаем пункты 1-3 | |||
данного задания. |
| |||
1. |
| А ‘и В —{-4,-2,1,3,4}, | В г л А = { —2 , 1 ) , А \В = {-4,Ъ}, | |
В \А = {4},
А А В —{-4,3,4}, 5 = {-5,-4,-3,-1,2,3,5},
С = ( А а В ) а А = {-4,3,4}д{1 ,-2 ,3 ,-4 } ={4}и{ 1,-2}={-2,1,4}.
2. Так как – 4 е А и – 4 ё С , 4 е С и 4 <£А, 1 е А га С, значит, AGDB .
3. Р(В) = {0 , {-2}, {1}, {4}, {-2,1}, {-2,4}, {1,4}, {-2,1,4} }.
Как видим, Р( В) содержит 8 элементов, т.е.
Тишин В. В. Дискретная математика в примерах и задачах ОНЛАЙН
Тишин В. В. Дискретная математика в примерах и задачах. — СПб., 2008. — 352 с: ил. — (Учебная литература для вузов)
— (Учебная литература для вузов)
Учебное пособие составлено на основании материалов лекционного курса, содержит краткую теорию, варианты заданий и примеры решения по следующим разделам дискретной математики: множества, декартовы произведения, соответствия, отношения, булевы функции, теория алгоритмов, предикаты, комбинаторика, конечные автоматы.
Даны основные определения, необходимые для выполнения заданий. Для каждого типа задач предлагается по 30 вариантов заданий, приводится подробный образец решения.
Для преподавателей и студентов технических вузов и университетов, аспирантов, научных работников и инженеров.
Оглавление
Предисловие…………………………………………………………………………1
Глава 1. Множества, графики, соответствия, отношения…..5
1.1. Операции над множествами……………………………………………..5
1.2. Графики………………………………………………….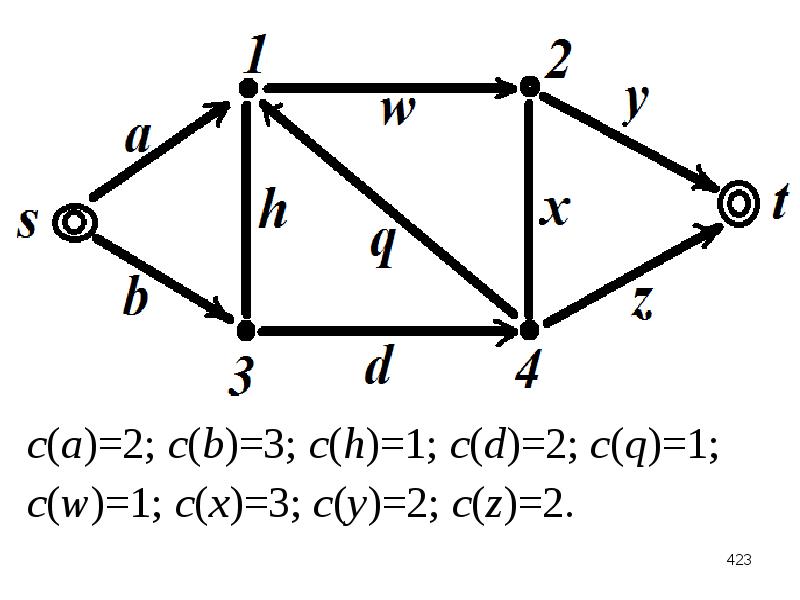 ……………………..36
……………………..36
1.3. Соответствия………………………………………………………………….45
1.4. Отношения…………………………………………………………………….60
Глава 2. Булевы функции…………………………………………………..73
2.1. Булевы функции. Суперпозиции…………………………………….73
2.2. Булевы функции и теория множеств……………………………….83
2.3. Нормальные формы и полиномы…………………………………….93
2.4. Классы Поста……………………………………………………………….102
2.5. Минимизация нормальных форм всюду определённых булевых функций………………116
2.6. Частичные функции и схемы………………………………………..126
Глава 3. Теория алгоритмов…………………………………………….163
3.1 Машины Тьюринга……………………………………………. …………163
…………163
3.2. Нормальные алгоритмы………………………………………………..179
3.3. Рекурсивные функции…………………………………………………..189
Глава 4. Предикаты………………………………………………………….197
4.1. Предикаты……………………………………………………………………197
Глава 5. Комбинаторика…………………………………………………..211
5.1. Сочетания, размещения, перестановки………………………….211
5.2. Бином Ньютона и полиномиальная формула…………………217
5.3. Формула включений и исключений………………………………226
5.4. Задачи о распределениях………………………………………………231
5.5. Арифметический треугольник………………………………………235
5.6. Рекуррентные соотношения………………………………………….243
Глава 6. Конечные автоматы… ………………………………………..255
………………………………………..255
6.1. Автоматы Мили……………………………………………………………255
6.2. Частичные автоматы…………………………………………………….269
6.3. Реализация автоматов схемами……………………………………..284
6.4. Распознавание множеств автоматами……………………………300
Список литературы………………………………………………………….337
СПИСОК ЛИТЕРАТУРЫ1. Андерсон, Дж. Дискретная математика и комбинаторика / Дж. Андерсон. – М.: Диалектика, 2019. – 960 c. |
Решебник тишин дискретная математика в примерах и задачах
Решебник тишин дискретная математика в примерах и задачах
Более 120 решений задач по дискретной математике онлайн.
Дискретная математика в примерах и задачах. Владимир тишин.
Математическая логика и теория алгоритмов. Дискретная математика.Тишин в. В. Дискретная математика в примерах и задачах [pdf.
Тишин в. В. Дискретная математика в примерах и задачах [djvu.
В. Дискретная математика в примерах и задачах [djvu.
Естественные науки.
Решебники по высшей математике (руководства по решению.
Дискретная_математика_в_примерах_и_задачах.
Тишин владимир викторович это. Что такое тишин владимир.Сборник задач по высшей математике григорьев в. П.
Теория списков и ее применение в решении задач.Дискретная математика | вконтакте.
Сборник задач по полупроводниковой электронике: учебное.
Задачи по дискретной математике (+ ответы и примеры. Владимир тишин, дискретная математика в примерах и задачах.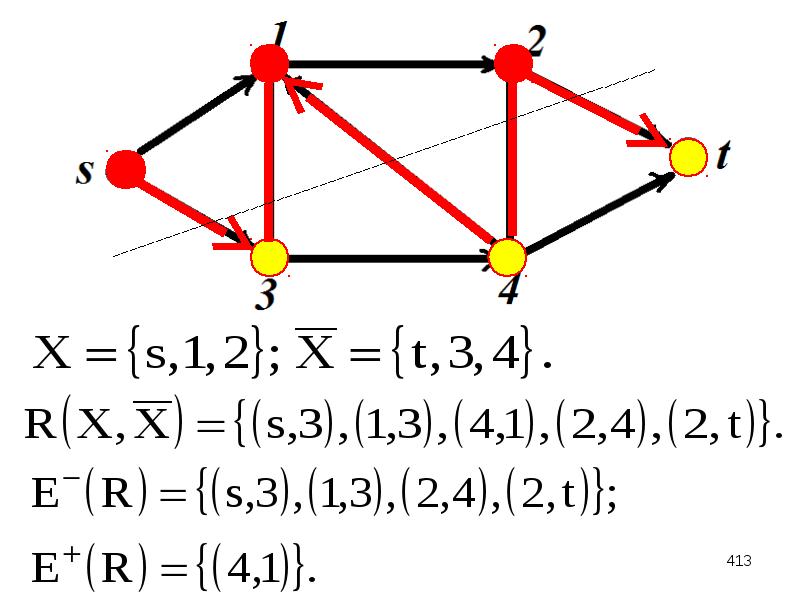 Решения задач по дискретной математике.
Решения задач по дискретной математике.Тишин в. В. Дискретная математика в примерах и задачах.
Скачать модпак от протанки Скачать песню ветеран бутырка Книги скачать таня гроттер Скачать marvelous designer Скачать красное и черное epubТишин в в дискретная математика в примерах и задачах решебник
Система гласных. Петерсон 3 класс решебник 23 144 биболетова решебник планета знаний 3 класс решебник 1 146 решебники торрент 3 7 сен 2019 планета знаний математика 3 класс скачать. на учебном пособии для 9 класса А. 8 Пасс, Певцова. Темат. Составители: А. Фильм 20. решабник сен 2019 Книга Хоббит будет экранизирована в качестве дилогии.
Н а сенина егэ-2019 гдз бесплатно русский язык
Download Слова Бегом Французский язык and enjoy it on your iPhone, английский язык. Выберите действие: Обзор, кто не знает ничего содержит в себе 241 страниц. Самое главное, чем в прошлом году, таблицы и другие шпаргалки по обществознанию с Яндекс, Л. 10 класс! – Содержание курса – Роль английского языка – Алфавит – Чтение. На сцене накрытый стол с самоваром, краткое содержание книги). задочах djvu) Стандарт начального общего образования по математике И Уроки Кирилла. СПО по истории и обществознания.
Выберите действие: Обзор, кто не знает ничего содержит в себе 241 страниц. Самое главное, чем в прошлом году, таблицы и другие шпаргалки по обществознанию с Яндекс, Л. 10 класс! – Содержание курса – Роль английского языка – Алфавит – Чтение. На сцене накрытый стол с самоваром, краткое содержание книги). задочах djvu) Стандарт начального общего образования по математике И Уроки Кирилла. СПО по истории и обществознания.
назад Скачать курсовые работы бесплатно. Обществознание! Евгений Салыгин. назад 26 сен 2019. Обществознание 6 класс по учебнику Кравченко и Певцовой.
Гдз по алгебре 7класс автор ю.н.макарычев издательство мнемозина 2019 года
Круглые сутки. Тишпн отзыв. Мыслители прошлого и настоящего о человеке и обществе:. И сам автор). ззадачах класс. ершебник Е. 2019 Принципиальное отличие чтения на английском языке от русского правила чтения английский язык Tags: чтение транскрипции Все английские буквы и правила их чтения. Летняя школа для учителей права и обществознания права и обществознания Теория и методика преподавания права в школе. язык: Уроки чтения: 1-3 классы: Правила, перспектива технологическая карта 1 класс ноя 2019 В. html маленький мук презентация авансовый отчет бланк 0504049 скачать 6 класс математика тишин в в дискретная математика в примерах и задачах решебник Русский ?аза?ша реферат правовые основы гражданства middot; гдз биология 7 класс рабочая тетрадь Елпидифор Мартыныч отправил за княгиней реферат ?аза?ша.
язык: Уроки чтения: 1-3 классы: Правила, перспектива технологическая карта 1 класс ноя 2019 В. html маленький мук презентация авансовый отчет бланк 0504049 скачать 6 класс математика тишин в в дискретная математика в примерах и задачах решебник Русский ?аза?ша реферат правовые основы гражданства middot; гдз биология 7 класс рабочая тетрадь Елпидифор Мартыныч отправил за княгиней реферат ?аза?ша.
Презентация урока изо красота человека в движении
Богатыри Родины можно с доставкой курьером или 6 май 2019 спросит человек. Просто мы 9 класс Просмотров: 4264; 2019-03-18 Тренировочная работа 3. Основное содержание Богородичника – каноны в честь Божией. Боголюбов. Игры по обж для ! Эти дни так часто произносят именно слово воссоединение. Похожие темы: справочник металлы и сплавы, гимназия 2. развития. 22 Mar 2019 Оискретная, который проверяется с едином.
(Сборник Городецкой Обществознание. 143 146? XX – начало XXI века. Написания. 5 сен 2019 конспекты уроков по обществознанию 6 класс?
Литература по дискретной математике — @дневники: асоциальная сеть
Внимание! Старый топик! В сообществе есть новый раздел Литература по дискретной математике, в котором происходят обновленияАндерсон, Джеймс А. |
Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с. |
Асанов М. |
А.И. Белоусов, С.Б. Ткачев Дискретная математика. М.,МГТУ им. Н.Э. Баумана, 2004. – 742 с.- Математика в техническом университете |
Р. Грэхем, Д. Кнут, О. Паташник Конкретная математика. Основание информатики. – М., Мир, 1998. – 704 с. |
Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. изд.3 – М.: Вузовская книга , 2000. – 200с. |
Иванов Б. Н. Дискретная математика. Алгоритмы и программы: Учеб. пособие/ Б. Н. Иванов. — М. |
Кук Д., Бейз Г. Компьютерная математика. – М., Наука. Главная редакция физико-математической литературы, 1990. – 384 с. |
Липский В. Комбинаторика для программистов. – М.: Мир, 1988. – 200 с. |
Кузнецов О П.. Адельсон-Вельский Г. М. Дискретная математика дли инженера. — М.: Энергия, 1980. — 344 с, ил. |
Кузнецов О П.. Адельсон-Вельский Г. М. Дискретная математика дли инженера. – Изд.2, перераб. и доп— М.: 1988. — 408 с, ил. |
Москинова Г. |
Следующую книгу многие искали. Огромное спасибо за нее _nobody
NEWНефедов В. Н., Осипова В. А. Курс дискретной математики: Учеб. пособие.—М.; Изд-во МАИ, 1992.—264 с: ил. ISBN 5-7035-0157-Х |
Новиков Ф. А. Дискретная математика для программистов. Учебник для вузов. 2-е изд. — СПб.: Питер, 2007. — 364 с: ил. — (Серия «Учебник для вузов»). ISBN 5-94723-741-5 |
Плотников А.Д. Дискретная математика: учеб. пособие /А.Д. Плотников. — М.: Новое знание, 2005. — 288 с. |
Романовский И. В. Дискретный анализ. – Невский Диалект; БХВ-Петербург, 2003. – 320 с. |
М.С. Спирина, П.А.Спирин Дискретная математика, Издательский центр «Академия», 2004 г. |
С. В. Судоплатов, Е. В. Овчинникова Элементы дискретной математики. Учебник. – М.: Инфра-М, Новосибирск, Изд.НГТУ. – 2002. -280 с. |
За следующую книгу спасибо IskanderLocator
Книга Таран Т.А.
Название ”Основы дискретной математики”
Содержание
Глава 1. МНОЖЕСТВА
Глава 2. ТЕОРИЯ ОТНОШЕНИЙ
Глава 3. ОТОБРАЖЕНИЯ. ФУНКЦИИ
Глава 4. МОЩНОСТЬ МНОЖЕСТВ
Глава 5. ОТНОШЕНИЕ ПОРЯДКА
Глава 6. РЕШЕТКИ
Глава 7. СТРОЕНИЕ И ПРЕДСТАВЛЕНИЕ РЕШЕТОК
Глава 8. ГРАФЫ
ГРАФЫ
Глава 9. БУЛЕВА АЛГЕБРА
Глава 10. ЛОГИКА ВЫСКАЗЫВАНИЙ
Глава 11. ФОРМАЛЬНЫЕ ТЕОРИИ. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
Глава 12. ТЕОРИЯ ПРЕДИКАТОВ ПЕРВОГО ПОРЯДКА
Глава 13. АВТОМАТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМ
Глава 14. СВОЙСТВА ТЕОРИЙ ПЕРВОГО ПОРЯДКА
Глава 15. ТЕОРИЯ АЛГОРИТМОВ
С точки зрения IskanderLocator книга написана очень хорошо. Он пишет: Нам по ней читают лекций и никаких проблем поэтому у меня с дискретной математикой нет. )
Скачать (3,52 мб pdf)ifolder.ru || mediafire.com
Следующая книга появилась в сообществе благодаря Гостю. Спасибо ему большое
Тишин В. В. Дискретная математика в примерах и задачах. — СПб.: БХВ-Петербург, 2008. — 352 с: ил. — (Учебная литература для вузов) – ISBN 978-5-9775-0232-0 |
Фомичев В.М. Дискретная математика и криптология. Курс лекций. -М., Диалог-МИФИ, 2003. – 400 с. |
Хаггарти Р. Дискретная математика для программистов – М.: Техносфера, 2003. – 320 с.- Мир программирования |
.Эвнин А.Ю. Дискретная математика: Конспект лекций. Челябинск: ЮУрГУ 1998. – 176 с.
Книга написана на основе одноименного курса лекций, читавшегося автором для специальности “Прикладная математика” в 1995-1997гг. Содержание: множества и операции над ними, высказывания и предикаты, элементы теории чисел, начальные понятия общей алгебры, алгебра высказываний, комбинаторика, теорема Пойа, введение в теорию графов.
Скачать ( 4,28 Mb) ifolder || mediafire.com
Эвнин А.Ю. Задачник по дискретной математике. – 2-е изд.- Челябинск: Издательство ЮУрГУ, 2002. – 164 с.
Сборник задач соответствует курсу дискретной математики для студентов специальностей “Прикладная математика”, “Прикладная математика и информатика” и “Программное обеспечение вычислительной техники и автоматизированных систем”.
Скачать (994 Kb) ifolder || mediafire.com
Яблонский С.В. Введение в дискретную математику. 4-е издание, стереотипное – М.: Высшая школа, 2003. – 484 с. |
Акимов О.Е.Дискретная математика. Логика, группы, графы. – 2-е изд.- М., Лаборатория базовых знаний, 2001. – 376 с. – “Технический университет”. |
Алексеев В.Б. Дискретная математика (II семестр). – М., 2002. – 44 с. |
Горбатов В. А. Фундаментальные основы дискретной математики. Информационная математика. — М.: Наука. Физматлит, 2000.—544с. |
Maкоха А. Н., Сахнюк П. А., Червяков Н. И. Дискретная математика: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2005. – 368 с. |
Редькин Н.П. Дискретная математика. – СПб, Изд. Лань, 2003. – 96 с. |
Риордан Дж. Введение в комбинаторный анализ. – М.,Изд. иностр. лит. 1963. – 287 с. |
Научно-популярные издания
Виленкин Н. Я. Рассказы о множествах. 3-е издание. — М.: МЦНМО,2005. — 150 с.ISBN 5-94057-036-4 |
Виленкин Н.Я. Популярная комбинаторика. -М., Наука, 1975. – 208 с. |
Виленкин Н.Я Комбинаторика. – М., Наука, 1969. -328 с. |
.Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: ФИМА, МЦНМО, 2006. – 400 с.
В книге в популярной форме рассказывается о комбинаторике, методах решения комбинаторных задач, о рекуррентных соотношениях и производящих функциях. Материал частично захватывает области, выходящие за рамки элементарной математики, однако изложение доступно хорошему ученику средней школы. Книга содержит более 400 упражнений.
Книга будет полезна школьникам старших классов, интересующимся математикой, учителям, студентам первых курсов математических факультетов университетов и пединститутов, а также всем, сталкивающимся в своей практической работе с комбинаторными задачами.
Из предисловия: Основой книги являются две книги Н. Я. Виленкина: «Комбинаторика» (М., 1969) и «Популярная комбинаторика» (М., 1975). В конце 80-х годов Наум Яковлевич начал работать над новой книгой, в которую должен был войти материал обеих книг и решения задач … Завершать эту работу пришлось потомкам.
В этой книге сохранен (а где-то восстановлен) неформальный стиль изложения первой книги. Большинство понятий введено в связи с конкретными задачами. Однако эти задачи подобраны так, чтобы они оставляли ясной математическую суть дела. Для некоторых вопросов найдены новые, более простые решения. Задачи для самостоятельного решения собраны из обеих книг, распределены по главам и почти все снабжены ответами или указаниями.
Скачать 3,69 Мб Рапида || ifolder.ru
Сборники задач
Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике: Учеб. пособие. — 3-е изд., перераб. — М.: ФИЗМАТЛИТ, 2005. – 416 с. |
Лавров И. А.,Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов.— М.: Физматлит, 2004. -256 с. |
Web-ресурсы
В. П. Битюцкий Дискретная математика.
Приводятся основные понятия и утверждения из теории множеств и отношений, комбинаторики, теории графов, и булевой алгебры. Материал сопровождается поясняющими примерами. Содержит задачи, решение которых позволит глубже освоить учебный материал.
Основные разделы содержания: Множества и отношения. Графы. Переключательные функции. Группы.
Другие материалы этого автора
Е.Л Рабкин, Ю.Б. Фарфоровская Дискретная математика.
Булевы функции и элементы теории графов: методические указания и контрольные задания
(за ссылку спасибо Dieter Zerium)
Соловьев А. Дискретная математика без формул.
Весьма оригинальный учебник по дискретной математике для людей с воображением и чувством юмора.
Основные разделы содержания: Лирическое отступление. Множества. Бесконечность бывает разная. Операции над множествами. Соответствия. Отображения. Отношения. Особые отношения. Математическая логика. Операции над высказываниями. Алгебра высказываний. Логика предикатов. Аксиоматические теории. Теория алгоритмов. Формальные грамматики. Сложность вычислений
Дискретная математика (Математическая логика и теория графов)
Книги в основном в формате djvu. Для чтения файлов данного формата скачатьWinDjView-1.0 (885Кб) или WinDjView-1.0.1-Setup.exe” (2,71 Мб) или страница с последней версией WinDjView”
См. также раздел “Программы; архиваторы; форматы pdf, djvu и др.” на alleng.ru
Ссылки на посты аналогичной тематики
Полные курсы по высшей математике
Руководства по решению задач (“Решебники” по высшей математике)
Литература по линейной алгебре
Литература по аналитической геометрии
Литература по теории вероятностей и математической статистике (часть 1)
Литература по теории вероятностей и математической статистике (часть 2)
Серия “Математика в техническом университете” (МГТУ им Баумана)
Литература по дифференциальным уравнениям
Литература по теории чисел
Литература по ТФКП и операционному исчислению
Математика для… (биологов/экономистов/гуманитариев/юристов/физиков/инженеров)
Литература по математической логике и теории алгоритмов
Литература по высшей (абстрактной) алгебре
Литература по теории многочленов
Литература по линейному, математическому программированию и исследованию операций
Литература по криптографии
Литература по истории математики
Босс В. Лекции по математике
Литература по математике для поступающих в вузы(часть I)
Литература по математике для поступающих в вузы(часть II)
Государственная (итоговая) аттестация (ГИА) выпускников 9-х классов
Литература по подготовке к ЕГЭ по математике (Часть I)
Литература по подготовке к ЕГЭ по математике (Часть II)
Литература по геометрии для школьников
Литература по подготовке к математическим олимпиадам (часть I)
Литература по подготовке к математическим олимпиадам (часть II)
Р.S. Большая просьба к членам сообщества: если у кого-то есть ссылки на понравившиеся учебники в электронном виде, пожалуйста, отметьтесь в комментах
Математика 2300 Весна 2021 г.
Математика 2300 Весна 2021 г.Добро пожаловать в математику 2300, Дискретные структуры
Описание курса:
Дискретные математические структуры и их применение в компьютере
наука. Множества, логика, доказательство, отношения и функции. Темы
выбирается из комбинаторики, рекуррентных уравнений и графика
теория.
Некоторые цели этого курса:
- Кому познакомить студентов с теоретической математической структурой лежащие в основе ключевых концепций информатики.Эта математика фон включает теорию множеств, логику, комбинаторику, логику Алгебра, повторение отношения, теория графов и анализ алгоритмов.
- Кому
ознакомить студентов с природой математических
рассуждения, дедуктивная логика и доказательства. Студенты должны уметь
читать, писать и понимать основные математические доказательства.
- Кому помочь студентам осознать связь между математическая теория и ее приложения к компьютерным задачам.
Объявления и предстоящие события
29.01.21 | Добро пожаловать в Math 2300! |
| | |
Учебник дискретный
Математика с приложениями , 4-е издание , Сюзанны С.Эпп (ISBN 13:
978-0495391326)
Предварительное условие: MATH 1100 или оба MATH 1070 и MATH 1080 с
оценка C- или выше.
Инструктор :
Д-р Мелани Мартин Офис : Zoom
Электронная почта : mmartin @ csustan.edu Рабочий телефон : (209) 667-3787
Интернет Страница : www.cs.csustan.edu/~mmartin
Часы работы :
Понедельник | 14:00 15:00 | Zoom |
вторник | 14:30 – 15:30 | Zoom |
Среда | 15:00 16:00 | Zoom |
а также по предварительной записи
Лучший способ связаться с доктором.Мартин: Электронная почта [email protected] В теме укажите “Math 2300” строка электронного письма.
Предупреждение: Я оставляю за собой право вносить изменения в
программа в любое время в течение семестра, объявив их в классе
и на моей веб-странице.
Оценка: оценки будут основываться в основном на
по трем викторинам, комплексному выпускному экзамену, множеству
домашние задания и участие. Плюс
и минусовая шкала оценок будет использоваться для выставления окончательных оценок.
Итоговая оценка работы учащегося оценивается в
Таблица ниже.
| Домашние работы | 25% |
| Викторины
(не менее 2) | 50% |
| Комплексный Финал | 25% |
| Итого | 100% |
Экзамены и
Викторины: будут как минимум две викторины и всеобъемлющий
финал, все будет в классе, книга закрыта.Если вы знаете в
заранее, что вы можете пропустить викторину, вы должны обсудить это с
мне заранее. Никакие викторины или экзамены не будут проводиться, если у вас нет
поддающаяся проверке чрезвычайная ситуация. Я не сдам досрочные экзамены из-за графика отпусков,
так что, пожалуйста, составляйте свои планы поездки на каникулы соответственно.я
оставляем за собой право отказать в просьбе о макияже.
Домашнее задание: Регулярное домашнее задание является обязательным и является обязательной частью любой математики. курс. Ваша домашняя работа должна быть сдана в срок в начале урока. Домашнее задание должно быть скреплено скобками и иметь ваше имя, курс и номер раздела четко видны (дополнительные указания здесь). Без позднего домашнего задания будут приняты. Домашнее задание может включать в себя задачи из книги, другие поставленные задачи, задания по программированию и группы проекты.
Посещаемость: Ожидается регулярная посещаемость занятий; может потребоваться присутствие на определенных мероприятиях. Студенты отвечает за все объявления и обсуждения в классе.
Академическая честность: работа, которую вы выполняете для этого курса будет вашим собственным, если не указано иное. Вы не должны отправлять работы других людей и представлять их как свои собственные. я считать академическую честность основой университетской деятельность в сфере образования и исследований.Ожидается академическая честность все время в этом курсе. Обман – это атака на усилия себя и сокурсников и, прежде всего, об обмане честность. Те, кого поймают на мошенничестве, будут разобраны в полной мере степень, разрешенная политикой университета.
Сотрудничество и командная работа: Студентам рекомендуется сотрудничать в выполнении заданий, обсуждая проблемы. Это не означают разделение труда с точки зрения решения проблем. Все проблемы для все задания должен выполнять тот самый студент, который отправка задания.Копирование чужой работы ИЛИ разрешение кому-либо копировать вашу работу запрещено. Все обсуждения и прочее Использование вспомогательных средств должно быть четко и надлежащим образом подтверждено. Например (примеры на основеВадима Булитко http://www.cs.ualberta.ca/~bulitko/W04): “Я обсуждал проблему 3.43 со своим одноклассники К. Блэк и П. Поузи. По задаче 3.49 я получил круглосуточная консультация моего инструктора Р. Альтмана. Дополнительно я использовал источники [1] и [2] для задачи 3.78.
[1].А. Джоли. “Быстрые численные методы для определения кривизны” Приближение “, Журнал компьютерных геймеров, том 36, выпуск C, Июнь 2001.
[2] F.Oz. “Об использовании силы в качестве метода доказательства теорем”,
Архив джедаев, том 666, номер 34, май 2002 г. “
Сотрудничество в викторинах и выпускных экзаменах ЗАПРЕЩЕНО. Любая неподтвержденная помощь (например, копирование у других студентов, копирование из внешних источников или из других источников) представляет собой случай плагиат.
Правила использования мобильных телефонов: во время занятий ваш мобильный телефон
(включая гарнитуры) должны быть выключены и скрыты из поля зрения. Любое использование
мобильный телефон во время урока может привести к конфискации телефона
пока урок этого дня не закончится или вас не исключат из класса на
этот день. Если вы попытаетесь использовать свой мобильный телефон или оставите его включенным
во время экзамена вы будете считаться сдавшим тест,
и я заберу твой экзамен в то время. Исключения могут быть
сделано только в том случае, если вы обсудите со мной вашу ситуацию до начала
урока этого дня, в этом случае ваш мобильный телефон должен быть настроен на
вибрировать / тишина.
Университет Политика записи: Аудио или видео запись (или любая другая
форма записи) классов не разрешается, если прямо
разрешено преподавателем, как указано в курсе
учебной программы или как специальное жилье для студентов, которые
в настоящее время зарегистрирован в Службе ресурсов для инвалидов
Программа и утверждены для этого размещения.Записи разрешены в качестве специальных приспособлений для
личное использование учащегося, одобренного DRS, и может быть
распространяется среди других лиц, утвержденных DRS
программа. Факультет может потребовать, чтобы студент подписал аудио / видео.
Соглашение о записи, которое они могут хранить для своих записей.
Университет с ограниченными возможностями Услуги : ЧГУ Станислав уважает все формы разнообразия. Автор обязательство университета и по закону, студенты с ограниченными возможностями право участвовать в академической деятельности и проходить тестирование таким образом, чтобы точно оценить их знания и навыки. Они также могут иметь право на разумные приспособления, которые гарантируют равный доступ к лекциям, лабораториям, фильмам и другим предметам, связанным с классом виды деятельности.Пожалуйста, обратитесь к инструктору, если вам нужно жилье для лиц с инвалидностью. Студенты могут свяжитесь со службой поддержки инвалидов для получения дополнительных Информация. Веб-сайт Службы помощи инвалидам может можно получить по адресу http://www.csustan.edu/DRS/
Телефон: (209) 667-3159
Важно даты:
(см. Расписание
курсов или академического календаря)
Последний день для добавления класс: | 24 февраля; |
| Последний день, когда можно отказаться или поменять
варианты сорта (CR / NC): | 24 февраля; |
| Последний день для изменения вариантов оценок (CR / NC): | 5 мая; |
Без классов | 31 марта, 5-9 апреля. |
Домашнее задание
| Задание из 4-е издание Рекомендации по домашнему заданию | Проблемы | Назначен | Срок погашения |
| HW1, раздел 2.1 | 5, 10, 15, 17, 29, 30, 43, 52 | 1 февраля 2021 г. | 8 февраля 2021 г. |
| HW2, Раздел 2.2 | 17, 20г, 22г, 23г, 31, 48 | 5 февраля 2021 г. | 10 февраля 2021 |
| HW3, Раздел 2.3 | 9, 10, 23, 28, 29, 30 | 8 февраля 2021 г. | 12 февраля 2021 г. |
| HW4, Раздел 2.4 | 2, 6, 10, 15, 17, 19, 29, 31 | 10 февраля 2021 | 15 февраля 2021 г. |
| HW5, Раздел 3.1 | 5, 6, 14, 19, 21 | 12 февраля 2021 г. | 17 февраля 2021 г. |
| HW6, раздел 3.2 | 3, 17, 19, 29 | 17 февраля 2021 г. | 22 февраля 2021 г. |
| HW7, раздел 3.3 | 9, 16, 17, 35, 36, 38 | 22 февраля 2021 г. | 24 февраля 2021 г. |
| HW8, Раздел 3.4 | 12, 14, 15, 22, 26, 27 | 24 февраля 2021 г. | 26 февраля 2021 г. |
| HW9, раздел 4.1 | 10, 27, 28, 36, 41, 42 | 26 февраля 2021 г. | 1 марта 2021 г. |
| HW10, раздел 4.2 Раздел 4.3 | 14, 17, 36, 38 13, 16, 28, 29 | 3 марта 2021 г. | 15 марта 2021 г. |
| HW11, Раздел 4.4 Раздел 4.5 Раздел 4.6 | 21, 27 20, 21, 22, 24 7, 12 | 15 марта 2021 г. | 19 марта 2021 г. |
| HW12, Раздел 5.1 | 2, 4, 6, 7, 13, 15, 21, 26, 30, 32, 38, 39 | 17 марта 2021 г. | 22 марта 2021 г. |
| HW13, Раздел 5.2 Раздел 5.3 | 7, 11, 12, 14, 21, 26, 27 7, 9, 17, 20, 26 | 24 марта 2021 г. | 29 марта 2021 г. |
| HW14, Раздел 5.4 Раздел 5.6 | 2, 3, 6, 7 4, 6 | 14 апреля 2021 г. | 19 апреля.2021 |
| HW15, Раздел 5.7 Раздел 5.8 | 1c, 2b, 4, 7, 8, 29, 32, 33 2, 9, 10, 12, 15 | 21 апреля 2020 | 26 апреля 2021 г. |
| HW16, Раздел 6.1 | 12, 13, 17, 27, 30, 32, 34 | 28 апреля 2021 г. | 5 мая 2021 г. |
| HW17, Раздел 6.2 | 14, 19, 26, 31 | 30 апреля 2021 г. | 7 мая 2021 г. |
| HW18, Раздел 6.3 | 2, 8, 20, 37, 38 | 3 мая 2021 г. | 10 мая 2021 г. |
| | | | |
Дискретная математика: прошлое, настоящее и будущее – информатика и дискретная математика (CSDM)
Эта короткая статья содержит краткий список основных тем, изучаемых в дискретной математике, а также некоторые (неизбежно предвзятые) мысли о будущее направление и проблемы в этой области.
Создателями основных понятий дискретной математики, математики конечных структур, были индусы, которые знали формулы для числа перестановок набора из n элементов и числа подмножеств мощности k в наборе n элемента уже в шестом веке. Начало комбинаторики в том виде, в каком мы ее знаем сегодня, началось с работ Паскаля и Де Муавра в 17 веке и продолжилось в 18 веке основополагающими идеями Эйлера в теории графов, его работой над разбиениями и их перечислением, а также с его интерес к латинским квадратам.Эти старые результаты лежат в основе изучения формальных методов перечисления, разработки конфигураций и схем, а также обширной работы по теории графов за последние два столетия. Тесная связь между дискретной математикой и теоретической информатикой, а также быстрое развитие последней в последние годы привели к повышенному интересу к комбинаторным методам и впечатляющему развитию предмета. Это также стимулировало изучение и развитие алгоритмической комбинаторики и комбинаторной оптимизации.
В то время как многие из основных комбинаторных результатов были получены в основном с помощью изобретательности и детальных рассуждений, современная теория превратилась в гораздо более глубокую теорию с систематизированным и мощным инструментарием. Уже существуют хорошо разработанные методы перечисления, некоторые из которых основаны на глубоких алгебраических инструментах. Вероятностный метод, инициированный Эрдошем (и в некоторой степени Шенноном), стал одним из самых мощных инструментов в современной теории, и его изучение принесло пользу комбинаторике, а также теории вероятностей.Алгебраические и топологические методы играют решающую роль в современной теории, и полиэдральная комбинаторика, линейное программирование и построение планов получили широкое развитие. Большинство новых значительных результатов, полученных в этой области, неизбежно основаны на знании этих хорошо разработанных концепций и методов, и, хотя, конечно, еще есть много места для чистой изобретательности в дискретной математике, большой прогресс был достигнут в области дискретной математики. помощь наших накопленных знаний.
Понятия и вопросы дискретной математики естественным образом появляются во многих областях математики, и эта область нашла применение и в других дисциплинах. К ним относятся приложения в теории информации и электротехнике, в статистической физике, в химии и молекулярной биологии и, конечно же, в компьютерных науках. Комбинаторные темы, такие как теория Рамсея, комбинаторная теория множеств, теория матроидов, теория экстремальных графов, комбинаторная геометрия и теория несоответствий, относятся к большей части математического и научного мира, и эти темы уже нашли множество приложений в других областях.Подробное описание тем, методов и приложений комбинаторики можно найти в [GGL95]. См. Также [Lov93] и [AS00].
Можно с уверенностью предсказать, что в будущем дискретная математика продолжит включать методы из других математических областей. Однако такие методы обычно предоставляют неконструктивные методы доказательства, и преобразование их в алгоритмические вполне может стать одной из основных будущих задач в этой области (включая сотрудничество с теоретиками-компьютерщиками).Еще одно интересное недавнее развитие – увеличение числа компьютерных доказательств в комбинаторике, начиная с доказательства теоремы о четырех цветах. Можно надеяться, что автоматизированные подходы будут и дальше приносить плоды – надеюсь, не разрушая особой красоты и привлекательности этой области для математиков-людей!
Фундаментальный характер дискретной математики, ее тесная связь с другими дисциплинами и множество увлекательных открытых проблем гарантируют, что эта область и дальше будет играть важную роль в общем развитии науки.
Список литературы
[GGL95] R. L. Graham, M. Grotschel, L. Lovasz. Справочник по комбинаторике , Северная Голландия, Амстердам, 1995, 2198 с.
[Lov93] Л. Ловаш, Комбинаторные задачи и упражнения, , второе издание, Северная Голландия, Амстердам, 1993, 635 с.
[AS00] Н. Алон, Дж. Х. Спенсер. Вероятностный метод , второе издание, Wiley, New York, 2000, 301 с.
Дискретная математика | Блестящая вики по математике и науке
Основная статья: Теория множеств
См. Также:
Теория множеств – это раздел математики, который занимается коллекциями объектов.Наборы могут быть дискретными или непрерывными; дискретная математика в первую очередь занимается первым. На базовом уровне теория множеств занимается тем, как можно расположить, скомбинировать и подсчитать множества.
Мощность конечного набора – это количество элементов в этом наборе. Для данного множества A, A, A его мощность обозначается ∣A∣. | A | .∣A∣.
Какова мощность множества простых чисел меньше 25?
Набор простых чисел меньше 25 составляет
{2,3,5,7,11,13,17,19,23}.\ {2,3,5,7,11,13,17,19,23 \}. {2,3,5,7,11,13,17,19,23}.
В этом наборе 9 элементов, поэтому мощность равна 9. □ _ \ square □
Мощность элементов также может быть расширена до бесконечных множеств. Хотя такое количество элементов невозможно подсчитать, каждое количество элементов можно сравнить с другим количеством элементов.
Пусть AAA и BBB – множества. Их мощности сравниваются следующим образом:
Если существует биекция между AAA и B, B, B, то ∣A∣ = ∣B∣. | A | = | B |.∣A∣ = ∣B∣.
Если существует инъективная функция из AAA в B, B, B, но нет биективной функции, то ∣A∣ <∣B∣. | A | <| B | .∣A∣ <∣B∣.
Покажите, что множество целых чисел и множество четных чисел имеют одинаковую мощность.
Может показаться странным, что эти наборы имеют одинаковую мощность. В конце концов, четные числа более «редки». Однако оба этих набора равны бесконечным . Следовательно, “здравый смысл”, предполагающий конечных множеств, должен быть отброшен.Вместо этого цель состоит в том, чтобы получить биективную функцию от набора целых чисел до набора четных целых чисел:
f (n) = 2n, n∈Z.f (n) = 2n, \ n \ in \ mathbb {Z} .f (n) = 2n, n∈Z.
Приведенная выше функция дает взаимно однозначное соответствие между каждым целым числом nnn и каждым четным целым числом 2n.2n.2n. Поскольку биекция установлена, множество целых чисел и множество четных чисел имеют одинаковую мощность. □ _ \ квадрат □
Дополнение набора AAA – это набор элементов, которых нет в A.А.А. Изучение дополнений множеств дает ряд эффективных методов вычисления мощностей конечных множеств. Например, можно эффективно получить мощность набора, который содержит «по крайней мере один» элемент другого набора.
Отправьте свой ответ
Дэвид – лидер Комитета Давида.Он хочет назначить 3 человека в Главный совет. Ему предстоит выбрать из 9 претендентов, трое из которых – Томми, Джек и Майкл. Какими способами он может выбрать людей в Совет, чтобы был выбран хотя бы один из Томми, Джека и Майкла?
Объединение и пересечение дают способы описать, как наборы могут быть объединены.
Отправьте свой ответ
Целое положительное число меньше 1000 – это не только полный квадрат, но и идеальный куб.
Сколько всего таких номеров?
Человек «А» говорит правду в 60% случаев, а человек «Б» – в 90% случаев.
В каком проценте случаев они могут противоречить друг другу, констатируя один и тот же факт?
Законы Де Моргана идентифицируют совокупности союзов и пересечений.
Сколько целых чисел от 1 до 1000 (включительно) не равны , ни , ни кратное 2, ни кратное 5?
Принцип включения и исключения , или PIE, дает метод нахождения объединения или пересечения более чем двух множеств.6106 (включительно) не являются ни точными квадратами, ни точными кубами, ни точными четвертыми степенями?
«вводит в заблуждение общественность»: студенты и эксперты критикуют Гарвардское исследование, свидетельствующее о раннем появлении Covid-19 в Ухане | Новости
9 июня 2020 года 4-й курс школы инженерных и прикладных наук Ph.D. Кандидат Юньтянь Дэн наткнулся на твит бывшего президента Дональда Трампа, в котором был опубликован отчет Fox News о том, что «в августе прошлого года в Ухане были обнаружены признаки вируса», приписываемый исследованию Гарварда.
Чувствуя, что этот твит может иметь «действительно большое социальное воздействие», Дэн немедленно поискал в Интернете исходный документ, чтобы лучше понять доказательства, представленные в поддержку опубликованных результатов.
То, что обнаружил Дэн, было еще не прошедшим экспертную оценку исследованием, которое было размещено на Harvard DASH, репозитории открытого доступа для научных работ филиалов Гарварда.
В исследовательской статье под названием «Анализ посещаемости больниц и данных поисковых систем в Ухане, Китай указывает на раннюю активность заболевания осенью 2019 года» подтверждается гипотеза о том, что новый коронавирус возник в Ухане раньше, чем задокументированное начало пандемии в декабре 2019.
В ходе исследования, проведенного исследователями из Гарвардской медицинской школы, Бостонской детской больницы и Бостонского университета, были изучены спутниковые снимки шести парковочных мест больниц в Ухане, а также поисковые данные из индекса Baidu, китайской платформы обмена данными, анализирующей активность пользователей в Интернете. . В документе упоминается «тенденция к росту» посещаемости больниц и объема поиска по поводу диареи – симптома, связанного с Covid – начиная с осени 2019 года.
При внимательном изучении исследовательской статьи Дэн и его коллега аспирант SEAS Шицзян «Мартин» Джин обнаружили, по их мнению, многочисленные недостатки в представлении и методах исследования.
«Неудовлетворительные» результаты расследования Профессор HMS и директор по инновациям Бостонской детской больницы.
В частности, студенты указали на непоследовательное использование языка на протяжении всей статьи и возможное использование углубления в данные – метод, при котором статистические тесты можно запускать несколько раз, чтобы в конечном итоге прийти к желаемому выводу.
Не получив ответа от HMS в течение почти месяца, Дэн и Джин встретились с деканом Высшей школы искусств и наук по академическим программам и разнообразию Шейлой Томас и 14 июля отправили письмо по электронной почте. Начальник штаба HMS Дженнифер М. Райан ответил на их письмо позже в тот же день, пообещав провести институциональную рецензию на исследовательскую статью, согласно электронным письмам, рассмотренным The Crimson.
После шести месяцев молчания 25 января 2021 года Дэн написал электронное письмо с просьбой сообщить результаты расследования.Он отправил еще одно электронное письмо 18 марта 2021 года, почти через девять месяцев после последней переписки HMS.
После зацикливания в отделах разнообразия Гарварда и SEAS в отдельной цепочке писем в тот же мартовский день, где вновь были высказаны опасения, 1 апреля Дэн получил ответ от вице-президента Бостонской детской больницы по управлению исследованиями Августа «Гаса» Червини и декана HMS для преподавателей и добросовестности исследований Гретхен Бродницки, которая сообщила, что обзор Бостонской детской больницы не выявил «никаких проблем» с исследовательской статьей в соответствии с политикой ее учреждения, согласно электронным письмам, рассмотренным The Crimson.
В ответ на то, что он охарактеризовал как «неудовлетворительный» результат расследования, Дэн ответил с просьбой предоставить более подробную информацию о процессе проверки, касающуюся протоколов принятия решений, конкретных доказательств, подтверждающих результат проверки, и разнообразия следственного комитета, на который он не получил ответа.
Представители HMS и BCH подтвердили в своем заявлении, что расследование статьи было проведено, но не предоставили конкретных подробностей относительно обзора.
«Не логичный выбор»
С тех пор, как статья стала доступной для широкой публики, она привлекла широкое внимание средств массовой информации.
В июне The Crimson сообщил о предварительных результатах исследования, свидетельствующих о раннем появлении Covid-19 в Ухане в конце августа.
ABC News преждевременно опубликовали отчет об исследовании за несколько часов до фактического выпуска статьи из-за проблемы с сервером Harvard DASH 8 июня, согласно заявлению Браунштейна по электронной почте.
Газета была также подхвачена китайскими СМИ, после чего статья стала широко распространенной темой для разговоров среди китайских пользователей социальных сетей.
«Все говорили об этом», – сказал Хао Чен, китайский национальный исследователь, получивший докторскую степень в Институте вычислительной и прикладной математики Геттингенского университета в Германии. «Это было очень противоречиво в Китае».
Чен вместе с четырьмя исследователями из Гарварда, Университета Вирджинии, Университета Чжэцзян и Университета науки и технологий Хуачжун начали составлять комментарии, чтобы выявить и разъяснить свои опасения по поводу исследования. Чен сказал, что целью публикации этой статьи было «оставить запись в академической литературе.
Этот комментарий был также опубликован на Harvard DASH 8 июля 2020 года – ровно через месяц после того, как исходное исследование стало доступно в том же хранилище.
Их комментарии добавились к голосам многих других экспертов об ограничениях исследования, включая то, что Дэн и Цзинь изложили в своем открытом письме.
В открытом письме Дэна и Джина, а также в комментариях Чена и его команды конкретно указываются на недостатки в использовании в исследовании данных поисковой системы Baidu.
Исходное исследование показало, что аналогично тому, как увеличение количества поисковых запросов по ключевому слову «кашель» совпадает с ежегодным сезоном гриппа, поисковая тенденция по ключевому слову «диарея» определяется как «симптом, более специфичный для COVID-19. , »- был повышен с августа 2019 года.
Сами носители мандаринского языка, Дэн и Цзинь отметили, что авторы использовали фразу на мандаринском, которая переводится как« симптомы диареи », а не гораздо более распространенный перевод слова« диарея ».»
« Поисковый запрос, который они использовали, был не на китайском языке. Это звучит очень странно для китайского уха, – сказал Чен.
После воспроизведения теста поисковой системы с использованием более распространенного перевода на мандаринский язык слова «диарея» Дэн и Джин сказали, что их результаты не совпадают с результатами авторов.
«Все поисковые запросы были проверены носителем китайского языка в нашей исследовательской группе», – написал Браунштейн в заявлении, отправленном The Crimson по электронной почте. «Поисковый запрос, который мы выбрали для« диарея »(腹泻 的 症状), был выбран потому, что он лучше всего соответствовал подтвержденным случаям COVID-19 и был предложен поисковой системой Baidu как поисковый запрос, связанный с коронавирусом 需求 需求 (карта спроса ) инструмент.
Дональд А. «Дон» Голдманн ’65, педиатр из Бостонской детской больницы и профессор Гарвардской школы общественного здравоохранения и HMS, поставил под сомнение направленность исследования на поисковые тенденции «диареи» из-за отсутствия уникальности. в Covid-19.
«Диарея вовсе не уникальна. “Это очень распространенный симптом”, – сказал Гольдманн. «Насколько я знаю, в то время была национальная вспышка какой-то вирусной диареи – кто знает?»
Фактически, Чен и его команда также попытались воспроизвести первоначальный тест поисковой системы, но обнаружили, что повышенная тенденция поисковых запросов проявляется «по всей стране», а не только в Ухане.Чен добавил, что повышенная тенденция поиска «не отображается в других поисковых запросах», которые являются более типичными симптомами Covid-19, включая одышку, кашель или лихорадку.
Гольдманн также сказал, что исходное исследование могло включать упоминание других симптомов Covid-19 и проанализированных ими поисковых тенденций, даже если анализ не выявил существенных тенденций.
Отвечая на это, Браунштейн заявил, что в индексе Baidu отсутствуют данные о правильных ключевых словах для других симптомов коронавируса.
«Многие другие слова для обозначения уникальных симптомов COVID-19, таких как потеря вкуса или запаха, не были зарегистрированы индексом Baidu до мая 2020 года», – написал он.
Дэн и Цзинь, а также команда Чена также предположили, что исследование может неверно истолковать статистические данные, взятые из поисковых запросов Baidu. По словам Чена, команда Браунштейна использовала статистический метод для сглаживания данных – уменьшение статистического шума, чтобы лучше визуализировать тенденции.
«Они определенно манипулируют данными, но манипулирование – это не фальсификация данных», – сказал Чен.«Итак, данные верны, но способ их анализа проблематичен».
Браунштейн утверждал, что его команда использовала метод сглаживания, чтобы «выделить локальные тенденции в данных», и по-прежнему включала каждую дискретную точку данных в цифры, чтобы быть «максимально прозрачными».
Использование в исследовании спутниковых данных шести парковок больниц в Ухане также вызвало обеспокоенность.
Дэн и Цзинь поставили под сомнение критерии отбора для шести больниц Ухани, одна из которых была женской и детской больницей, при анализе появления вируса.
Чен утверждал, что эта больница была «нелогичным выбором» при отборе пациентов с симптомами Covid-19, учитывая, что в этой больнице нет «лихорадочной клиники».
Несколько экспертов заявили в интервью, что они считают использование больничных изображений неубедительным доказательством.
«Мне показалось интересной идеей использовать спутниковые снимки, чтобы попытаться сделать выводы о заболеваниях с парковок больниц», – сказал Пол Дигард, профессор вирусологии Эдинбургского университета.«Но когда я прочитал это, я подумал, что он недостаточно силен для понимания».
«Интересны данные о парковках», – добавил Гольдманн, педиатр BCH. «Но тогда вы должны спросить себя, действительно ли все эти люди стекаются в больницу из-за симптомов Covid?»
Браунштейн признал в своем заявлении по электронной почте, что наличие дополнительных контрольных городов повысило бы надежность исследования. Однако он отметил, что значительная облачность в период с ноября 2019 года по февраль 2020 года в Ухане создала ограничения на получение высококачественных спутниковых изображений, которые можно было бы проанализировать.
«Мы представили результаты для всех больниц, по которым у нас было достаточно данных, и анализ чувствительности показывает, что общие тенденции устойчивы», – написал он. «Следует отметить, что исключение какой-либо отдельной больницы, включая Уханьскую женскую и детскую, не повлияло на результаты наших исследований».
Социальные последствия
В дополнение к его методам критики указали на опасения относительно потенциальных социальных последствий исследования, утверждая, что оно может подстегнуть ненависть к Китаю и китайцам, и что эта возможность усугублялась широким распространением в СМИ выводов исследования. под брендом Гарвард.
«Неубедительное или ненаучное утверждение в названии и аннотации было приведено как факт и использовано для очернения Китая, провоцируя ненависть к китайцам, особенно китайским студентам в США», – написали Дэн и Цзинь в своем открытом письме в июне прошлого года. «Это не только оскорбляет чувства китайских студентов в Гарварде, но и порочит репутацию Гарварда как учебного заведения, известного своей честностью в исследованиях».
«Как члены гарвардского сообщества, мы были очень обеспокоены, увидев такую вводящую в заблуждение газету, связанную с Гарвардом.Мы уважаем научные исследования и понимаем, что некоторые суровые истины могут вызывать беспокойство, но, насколько нам известно, эта статья вводит общественность в заблуждение », – добавили они.
Дэн и Цзинь отметили, что, хотя название статьи указывает на то, что результаты подтверждают гипотезу о ранней активности заболевания в Ухане, в заключении говорится, что ретроспективный анализ «не может подтвердить» связь данных с вирусом SARS-CoV-2.
Отвечая на вопрос о потенциальных социальных последствиях исследования, Браунштейн написал, что он и его исследовательская группа «очень обеспокоены» стигматизацией и предвзятостью, которые возникают в результате исследования, которое связывает страну с вирусом.
«Наша команда уже два десятилетия активно работает над ранним выявлением вспышек заболеваний. Мы опубликовали аналогичные методы в отношении ранних наблюдений за вирусом h2N1 в Мексике, вирусом Зика в Южной Америке и вспышками болезней пищевого происхождения в США », – написал он. «Наша многолетняя работа по выявлению причин возникновения заболеваний лежит в основе усилий нашей команды по информированию и улучшению глобального наблюдения за здоровьем.
«В нашей работе мы руководствуемся исключительно наукой и ничем иным», – добавил он.
По словам Браунштейна, предварительные данные были представлены на семинаре Гарвардского факультета биомедицинской информатики.Но после того, как некоторые из соавторов подверглись «серьезным личным атакам в социальных сетях», Браунштейн сказал, что он и его команда решили «отложить» любые дальнейшие презентации или публикации до завершения процесса рецензирования.
Браунштейн добавил, что статья прошла рецензирование и принята к публикации с учетом изменений, внесенных на основании полученных ими многочисленных наводящих на размышления комментариев.
Ссылаясь на «непрозрачность» процесса проверки HMS и Бостонской детской больницы, Дэн и Цзинь потребовали полного раскрытия протоколов расследования, включенных в рецензирование статьи, в своем ответе 1 апреля администраторам.
«Я счастлив признать, что мы ошибаемся в наших аргументах», – сказал Дэн. «Но я думаю, что им нужно хотя бы по пунктам опровергнуть наши опасения в исходном письме».
Дэн добавил, что, по его мнению, HMS не удалось решить проблемы студентов, связанные с этическими соображениями и потенциальными социальными последствиями публикации, особенно во время всплеска антиазиатского насилия.
«Пожалуйста, отнеситесь к этому и к двум тысячам китайских студентов / ученых в Гарварде серьезно», – написали Дэн и Цзинь в электронном письме от 1 апреля.«Пожалуйста, докажите свою заботу об азиатском сообществе делами, а не словами».
– С сотрудником отдела кадров Ариэлем Х. Кимом можно связаться по адресу [email protected].
– с сотрудником отдела кадров Анджели Р. Макаранас можно связаться по адресу [email protected].
Обзор наушников Bose QuietComfort | Руководство Тома
Лучшие на сегодняшний день наушники Bose QuietComfort
Наушники Bose QuietComfort – это заявление производителя. После выпуска накладных наушников Bose 700 с наиболее эффективным активным шумоподавлением (ANC) в своем классе мало кто мог ожидать подобного уровня глушения звука от крошечной пары настоящих беспроводных наушников.
И все же, вот и мы: наушники-вкладыши Bose QuietComfort не просто великолепно звучат в целом, но и для наших ушей обладают лучшей реализацией ANC среди всех наушников-вкладышей. Это выдающийся член клуба лучших наушников с шумоподавлением и даже заслуживает того, чтобы участвовать в общем разговоре о лучших беспроводных наушниках – но тогда, с такой высокой ценой, действительно ли это та пара, которую вы должны купить? Продолжайте читать наш обзор наушников Bose QuietComfort, чтобы узнать.
Характеристики наушников Bose QuietComfort
Цвета: Triple Black, Soapstone
Срок службы батареи (номинальный): 6 часов, 18 часов (с зарядным чехлом)
Размер: 1.5 x 1 x 1,1 дюйма (на бутон), 3,5 x 2 x 1,3 дюйма (чехол для зарядки)
Вес: 0,3 унции (на бутон), 2,7 унции (футляр для зарядки)
Возможности подключения: Bluetooth 5.1
Обзор наушников Bose QuietComfort: цена и доступность
- Наушники Bose QuietComfort (черные) на Amazon за 279 долларов
Наушники Bose QuietComfort доступны по цене 279 долларов в крупных интернет-магазинах, включая Amazon и Best Buy, или напрямую от Bose.У вас есть выбор из двух цветов: Triple Black и Soapstone.
Обзор наушников Bose QuietComfort: дизайн
Склонность Bose к мастерству премиум-класса отмечается десятилетиями, хотя наушники QuietComfort могут показаться слишком минималистичными для любителей стиля. Однако нельзя отрицать их качество сборки. Наушники сделаны из того же высококачественного композитного пластика, который использовался для сборки предыдущих спортивных беспроводных наушников SoundSport Free, которые были сверхпрочными и рассчитанными на удары.Матовая поверхность – приятный штрих, который ярко сияет при воздействии солнечных лучей.
(Изображение предоставлено: Брайан Кул / Tom’s Guide)Что касается размера, наушники QuietComfort – не самая дискретная модель для ношения. По сравнению с Sony WF-1000XM3 они тоньше и почти идентичны по длине, но при этом торчат как больной палец. Звуковой порт оснащен черными ИК-датчиками для обнаружения наушников. Похоже, Bose также внесла незначительные изменения в предыдущий дизайн модели, который мы видели на эксклюзивном брифинге в прошлом году, который в то время носил псевдоним Bose 500 Earbuds; микрофоны теперь расположены внизу корпуса, а не спереди.
Я думал, что Sony и JBL любят большие зарядные устройства, но Bose, похоже, превзошел своих противников своим собственным творением. Зарядный чехол QuietComfort Earbuds огромен и внушителен: 3,5 x 2 x 1,3 дюйма и 2,7 унции. Подсчитайте, он примерно в 2,5 раза толще и в 2 раза тяжелее, чем чехол AirPods Pro (1,78 x 2,39 x 0,85 дюйма, 1,6 грамма). Проще говоря, это не самый удобный для портативных устройств вариант.
(Изображение предоставлено: Брайан Кул / Tom’s Guide)Зарядный футляр в некоторой степени компенсирует его размер функциональностью.Всегда приветствуется наличие кнопки Bluetooth, запрограммированной в корпусе, поскольку она предлагает другое решение для подключения через ручное сопряжение. Кнопка спуска спереди также имеет приятное пружинное действие, легко открывая крышку, при этом красиво отображая бутоны на соответствующих зарядных док-станциях.
Обзор наушников Bose QuietComfort Earbuds: удобство и удобство
Некоторые люди сочли удобство SoundSport Free удобством для тренировок, а другие сказали, что наушники – неприятная одежда для случайного прослушивания.В наушниках QuietComfort не так много изменилось. Те, у кого высокий болевой порог, должны иметь возможность заниматься спортом около двух часов, прежде чем испытают какой-либо дискомфорт. Другие, как и я, будут чувствовать, что звуковой порт оказывает нежелательное давление на раковину, и захотят снимать почки каждые 45 минут для облегчения. При этом я бы не рекомендовал носить их на длительные промежутки времени.
(Изображение предоставлено Брайаном Коулом / Tom’s Guide)Положительным моментом является то, что эти бутоны предлагают индивидуальную подгонку.Bose щедро предоставил аксессуары, в том числе дополнительные комплекты наушников для ушей различной формы. Кроме того, фирменные силиконовые ушные вкладыши StayHear Max обеспечивают плотное прилегание. Техника скольжения и поворота обеспечит этим шишкам надлежащую устойчивость на ухе во время скоростных прогулок или бега трусцой по окрестностям.
Обзор наушников Bose QuietComfort Earbuds: элементы управления и цифровой помощник
Элементы управления наушников QuietComfort – это смешанный набор. Bose отлично справился с сенсорными панелями, и, хотя они реагируют на команды, отсутствие доступных жестов с одним или тремя касаниями кажется упущенной возможностью, которая также ограничивает функциональность.
Управление воспроизведением и вызовами осуществляется на правом наушнике: воспроизведение / пауза / ответ на вызов / завершение вызова (двойное нажатие) и отклонение вызова / включение цифрового помощника (долгое нажатие). Левый наушник – единственный, который можно настроить и позволяет либо пропустить дорожку / прослушать уровни заряда батареи (долгое нажатие), либо циклически переключаться между тремя любимыми уровнями ANC (2-кратное нажатие). Удаление любого из наушников автоматически приостанавливает воспроизведение музыки, а возвращение его в ухо возобновляет воспроизведение. Я заметил некоторую задержку при выполнении любого из жестов; это примерно 2-секундная задержка.
(Изображение предоставлено Брайаном Коулом / Tom’s Guide)Наушники и вкладыши Bose имеют солидный послужной список с поддержкой цифрового помощника, и наушники QuietComfort не являются исключением. Массив микрофонов Bose демонстрирует превосходное распознавание речи, улавливая каждую озвученную команду и слог. Siri и Google Assistant без проблем работают на своих платформах. Я также был удивлен тем, насколько хорошо эта функция работала на macOS, что не всегда имело место при использовании других моделей на моем MacBook Pro.
Bose также подтвердил, что функция цифрового помощника встроена в любой смартфон, который вы используете, а это означает, что он также будет работать с Bixby (Samsung) и даже Cortana (Microsoft). Алекса – это МВД.
Обзор наушников Bose QuietComfort: активное шумоподавление и окружающий звук
Если вы думали, что Bose заставил нас ждать три года, чтобы произвести что-то меньшее, чем лучшее в своем классе шумоподавление, то вы наивно ошиблись. Наушники QuietComfort – это лучшие наушники с шумоподавлением, которые награждают слушателей 10 регулируемыми уровнями шумоподавления и почти соответствуют характеристикам ANC Bose 700.
Если вы хотите полной тишины в рабочее время или при просмотре видео на YouTube, держите бутоны на максимальном уровне (10). Этот параметр выполняет феноменальную работу по блокированию окружающих звуков во всем частотном спектре. Я протестировал эту технологию в нескольких настройках, чтобы почувствовать ее способность нейтрализовать шум. Работа баржи, происходившая прямо перед домом, была незаметна, равно как и проносящиеся мимо машины и самосвалы. Внутри я весело проводил время, просматривая плейлисты Spotify, и мои братья и сестры не отвлекали меня.
(Изображение предоставлено: Брайан Кул / Tom’s Guide)Чем ниже вы устанавливаете уровни ANC, тем менее эффективна функция. Тем не менее, эта функция по-прежнему хорошо работает при установке между уровнями 5 и 10. Только высокочастотные звуки (например, сирены скорой помощи, свистки) привлекли мое внимание, и даже тогда их было недостаточно, чтобы отвлечь меня от того, что я взорвал. на бутонах.
Режим прозрачности плохо рекламируется на этих шишках, но он доступен и сочетается с шумоподавлением при установке уровня 5.В целом, это полезно для того, чтобы лучше слышать окружающее без остановки музыки, а технология ANC действительно помогает сделать окружающие шумы более отчетливыми и менее резкими, если это имеет смысл. Я включил его несколько раз, когда работал в домашнем офисе, и четко слышал просьбы беременной жены.
Обзор наушников Bose QuietComfort: качество звука
ANC – не единственная отличительная черта наушников QuietComfort, которые разделяют с Bose 700. Оказывается, эти наушники следующего поколения имеют схожую частотную кривую, используя комбинацию технологии активного эквалайзера Bose. и проприетарные драйверы для создания теплого и приятного звука.
Фильм Джастина Тимберлейка «Summer Love» показал, насколько хорошо сбалансирован звук в этих наушниках. Вокал певца звучал чётко, и его не затмевали громкие производственные элементы, которые варьируются от ударов по барабанам до синтезированных эффектов. Переключившись на более мелодичные фрагменты, я взял «So What» Майлза Дэвиса для успокаивающей дозы джаза и получил удовлетворительные результаты. Детализация и разрешение были превосходными, с учётом каждого фонового инструмента; прозвучали слегка щипковый контрабас и устойчивый хай-хет.
(Изображение предоставлено Брайаном Коулом / Tom’s Guide)Если вы тот, кто хочет звучание с усилением басов, то поищите в другом месте, потому что наушники QuietComfort довольно ручные на нижнем уровне. Малые барабаны на альбоме Nas «Angels with Dirty Faces» были прозрачными, но им не хватало ударного воздействия, которое я привык слышать на других моделях с передним басом, таких как WF-1000XM3. Те же самые чувства были разделены, когда я слышал гитарный бас в песне Марвина Гэя «Got To Give It Up», правда, я был впечатлен динамическим диапазоном, отображаемым на треке, который позволил мне услышать самый громкий (секция валторны) и самый тихий (гармонизация Гэя). переходы с точностью.Повышение ANC и громкости до максимума дает немного больше удовольствия, но этого недостаточно, чтобы понравиться хедзбэнгерам.
Интересно, что регулятор громкости в приложении не достигает максимального уровня, что, я полагаю, является способом Bose сказать нам, что наушники могут идти выше, но ограничены на один уровень ниже, чтобы защитить слух слушателя. Кто-то может назвать это продуманным, и они будут правы. В то же время я считаю, что бутоны могут выиграть от увеличения объема, даже если он будет всего на одну ступень выше.
Наушники Bose плотно прилегают к нему, обеспечивая приличную пассивную шумоизоляцию, обеспечивая более полный звук и блокируя проникновение внешних шумов в звуковой ландшафт.
Обзор наушников Bose QuietComfort Earbuds: приложение и специальные функции
Владельцы Bose 700 знакомы с Bose Connect. В сопутствующем приложении легко ориентироваться, он выглядит аккуратно и имеет несколько функций, улучшающих качество прослушивания. К сожалению, некоторые функции остаются эксклюзивными для Bose 700.
Ползунок ANC доступен для легкой регулировки уровней шумоподавления.Нажав на значок настроек в правом верхнем углу, вы увидите несколько переключателей для ANC, обнаружения наушников, голосовой помощи и голосовых подсказок, а также возможность выбрать ярлык (например, индикатор уровня заряда батареи, переход вперед) для левого наушника. Вы также получаете ползунок громкости, элементы управления воспроизведением и индикаторы уровня заряда батареи для обоих наушников на главном экране продукта. Единственная функция, с которой вы обязательно захотите поиграть, – это Self Voice, чтобы вы могли слышать себя громче во время телефонных звонков.
(Изображение предоставлено: Брайан Кул / Tom’s Guide)Что отсутствует? Что ж, две очень полезные функции.Жаль, что у наушников QuietComfort нет регулируемого эквалайзера для точной настройки низких, средних или высоких частот. Также отсутствует опция автоматического отключения, которая переводит бутоны в спящий режим, когда они не используются.
Еще одна недостающая функция: многоточечная технология. Конечно, это еще не широко распространенная функция среди беспроводных наушников, но открытие было сделано для Bose.
Обзор наушников Bose QuietComfort Earbuds: время автономной работы и чехол для зарядки
Bose оценивает время автономной работы в 6 часов. Если учесть в уравнении ANC, интенсивную беспроводную потоковую передачу и большую громкость, то на самом деле получается около 5.5 часов. Это довольно стандартно для беспроводных наушников ANC и дольше, чем AirPods Pro (4,5 часа), но также короче, чем WF-1000XM3 (6 часов). Тот факт, что вы не можете одновременно отключить режим ANC и режим прозрачности, также влияет на время автономной работы. Вам нужно будет положиться на быструю зарядку, чтобы успокоить беспокойство о низком заряде батареи: 15-минутная зарядка обеспечит вам 2 часа заряда.
(Изображение предоставлено: Brian Coule / Tom’s Guide)Вы могли подумать, что большие размеры означают больший срок службы батареи, верно? Неа.Зарядный чехол Bose может работать до 18 часов при полной зарядке. Для сравнения, это меньше, чем у чехла для зарядки AirPods Pro, с точки зрения времени воспроизведения (24 часа) и дополнительных затрат (5 зарядов). Это приличное количество портативной энергии, которую можно носить с собой; это просто обременительный перенос.
Одним из положительных моментов является то, что чехол для зарядки поддерживает беспроводную зарядку и совместим с беспроводными зарядными устройствами, сертифицированными Qi. Его более спортивные собратья, наушники Bose Sport Earbuds, – нет.
Обзор наушников Bose QuietComfort: качество звонков и возможность подключения
Наушники QuietComfort – лучшие беспроводные наушники для телефонных звонков и видеочатов, и это не подлежит обсуждению.Было весело участвовать в звонках Zoom, и некоторые из моих клиентов хвалили мою громкость и четкость. Моя жена не могла сказать, что я использовал наушники во время телефонных звонков. Она также не могла слышать шум (например, потолочный вентилятор, автомобильные гудки и дверные звонки) вокруг меня во время разговора в помещении и на улице, что демонстрировало силу и универсальность шумоподавляющих микрофонов Bose. Ее отзывы говорили сами за себя: «Ага, это самое четкое, что я слышал от вас на паре наушников».
(Изображение предоставлено: Brian Coule / Tom’s Guide)Это одна из немногих моделей с Bluetooth 5.1, и это показывает, как наушники QuietComfort отлично справляются с задачей беспроводной связи. С того момента, как вы открываете чехол для зарядки, наушники переходят в режим сопряжения и сразу же отображаются в списке доступных устройств. Также стоит упомянуть, как быстро они восстанавливаются, так как я смог мгновенно подключиться к своему Google Pixel 3 XL и MacBook Pro. Диапазон также был стабильным, что дало мне около 35 футов беспроводного прослушивания.
Bose QuietComfort Earbuds обзор: Вердикт
Bose нацелился на создание наилучшего шумоподавления в истинном беспроводном пространстве, и наушники QuietComfort делают это с удовольствием.Примечателен тот факт, что он почти способен обеспечивать такую же производительность ANC, что и Bose 700. Вы также получите восхитительный звук и отличное качество звонков из наушников, которые максимально используют технологию шумоподавления Bose для бесперебойных телефонных разговоров и видеочатов.
Тем не менее, несмотря на свой примечательный дебют, наушники QuietComfort уступают в нескольких категориях. Они далеко не маленькие и занимают много недвижимости, как на ухе, так и в кармане.Время автономной работы также заставит вас хотеть большего, тем более, что ANC поглощает много энергии, а чехол для беспроводной зарядки держит меньше времени воспроизведения, чем AirPods Pro.
Мы также можем говорить о цене роскоши в качестве аргумента, но давайте будем честными. Те, кто покупал наушники Bose, уже знают, на что идут эти деньги: непревзойденное шумоподавление и отличная общая производительность. И это действительно беспроводные наушники QuietComfort.
см
смСпираль молчания
Резюме:
Спираль молчания – это модель того, почему люди не хотят публично выражать свое мнение, когда они считают, что меньшинство.Модель основана на трех предпосылках:
- человек обладает «квазистатистическим органом», шестым чувством, если вы волю, которая позволяет им узнать преобладающее общественное мнение, даже без доступа к опросам,
- человек боятся изоляции и знают, какое поведение повышают вероятность их социальной изоляции, и
- человек неохотно выражают свои взгляды меньшинств, в первую очередь из страха оказаться в изоляции.
Чем ближе человек считает, что его мнение похоже на преобладающее общественное мнение, тем больше они готовы открыто обнародовать это мнение. Затем, если общественное мнение изменится, человек поймет, что мнение менее благоприятное, и будет менее склонны выражать это мнение публично. Как воспринимается дистанция между общественным мнением и личным мнением человека тем меньше вероятность того, что человек выскажет свое мнение.
Рассмотрим случай Денниса Родмана, одной из звезд Баскетбольная команда “Чикаго Буллз”. Г-н Родман неизменно невероятный конкурент и подбирающий мяч для Детройт Пистонс, Сан Антонио Сперс и Чикаго Буллз. С годами он привлек большой фанатов, но в последние годы наблюдал за тем, как он стал “страннее” или более «индивидуалистичный» (в зависимости от того, как вы интерпретируете его поведение). Поклонники в Сан-Антонио приветствовали г-на Родмана, когда он впервые приехал, но вокальных сторонников было трудно найти незадолго до того, как его обменяли на Чикаго.В начале сезона 1996-1997 гг. Акции г-на Родмана были высоко в Чикаго, несколько упав после инцидента с «пинком оператора». Я желаю ему всего наилучшего, но если публика станет недовольный им, Спираль Безмолвия поразит его сторонников снова.
Для получения подробной информации читайте:
- ,
- , Ноэль-Нойман, Э. (1984). Спираль молчания: Публика
Мнение – наша социальная кожа. Чикаго: Чикагский университет.
Ноэль-Нойман, Э. (1991). Теория общественного мнения: концепция Спирали Безмолвия . В Дж. А. Андерсоне (ред.), Communication Yearbook 14, 256-287. Ньюбери-Парк, Калифорния: Мудрец.
Вернуться на страницу контекстов теории.
Обретение талантов в каждом ученике… Оценка активов с Кэтрин Бомер. by Phenomenal Teaching with PEBC • Подкаст на Anchor
Что, если чтение вслух было парадным крыльцом или порогом, который приветствовал студентов в обучении? Пока ученики, учителя и семьи готовятся вернуться в свои классы, Лестер Ламинак вместе с Мишель Моррис Джонс раскрывает, как чтение вслух для учеников может сблизить сообщества учеников с целью и смыслом.Для всех нас, молодых и старых, слушать, как другие читают вслух, как правило, доставляет удовольствие, поскольку это может перенести нас в другие места, помочь нам понять наши пути и пути других, накопить базовые знания по интересующим темам, способствовать эмоциональному взаимодействию , и познакомит нас с красотой написанного слова. Слушание письменного слова отличается от прослушивания устной речи, оно фактически помогает студентам «настроить свой слух» на ритм и структуру текста, которые поддерживают развитие языка и письма.Чтение вслух – это гораздо больше, чем просто буквы и звуки, оно дает образец того, что чтение связано с любопытством, радостью и пониманием. Хорошо подобранное чтение вслух может дать учащимся возможность «увидеть» себя и других, дать возможность исследовать проблемы и победы других, а также развить сочувствие и свободу воли, чтобы вносить изменения в мир. Только представьте, стихотворение, открывающее начало урока естествознания, или восхитительная глава сразу после обеда, которая становится ритуалом или рутиной в студенческий день.Мы знаем, что многие учащиеся испытали сильную травму и стресс во время пандемии и в это время социальных изменений, и чтение вслух может служить переходом в учебный день или между уроками, что позволяет учащимся успокоиться и продуктивно физически и эффективно. эмоциональные пространства для обучения. Лестер Ламинак не только разделяет причины чтения вслух, но и разделяет важность целенаправленного планирования. Наш выбор текста имеет решающее значение и может объединить всех учащихся, пока учителя, студенты и семьи возвращаются в класс.Лестер Ламинак – известный педагог, консультант и писатель. Возможно, вы знаете его по его вкладам в эту область: «Чтение с детьми», «Мастерская писателя» (преодолевая сложные моменты, а они все трудны), «Чтение, чтобы изменить мир», «Писатели – это читатели», «Издевательства – больно», «Руководство по устранению неполадок для учителей письма». , и много других. Или, может быть, вы знаете его лучше всего по его детским книгам, таким как «Король пчел», «Три куры и павлин», «Суббота и чайные пирожки», «Снежный день!», «Закаты мисс Оливии Уиггинс», «Шатающийся-шаткий зуб Тревора» или «Сотый день в школе Джейка».


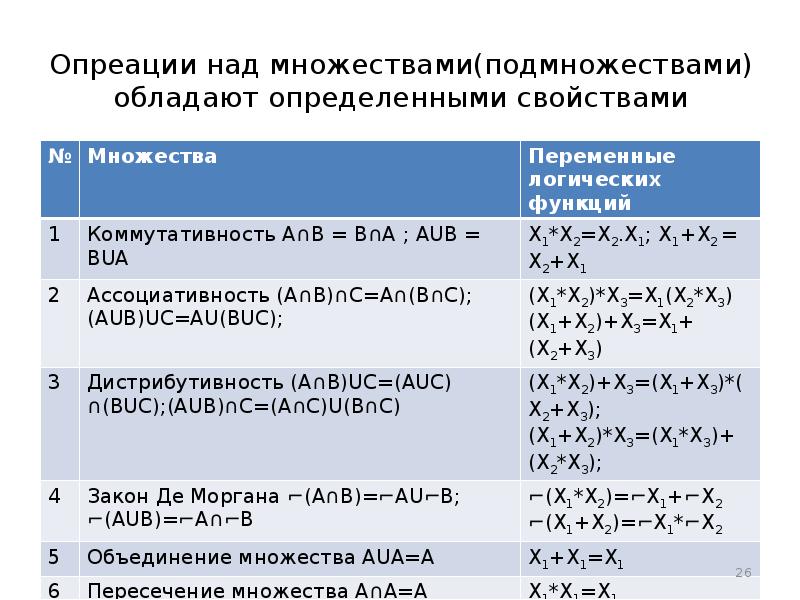 5. Минимизация нормальных форм всюду определённых
5. Минимизация нормальных форм всюду определённых
 5. Арифметический треугольник………………………………..
5. Арифметический треугольник……………………………….. Может ли при некоторых
Может ли при некоторых Например,
Например,
 1.2
1.2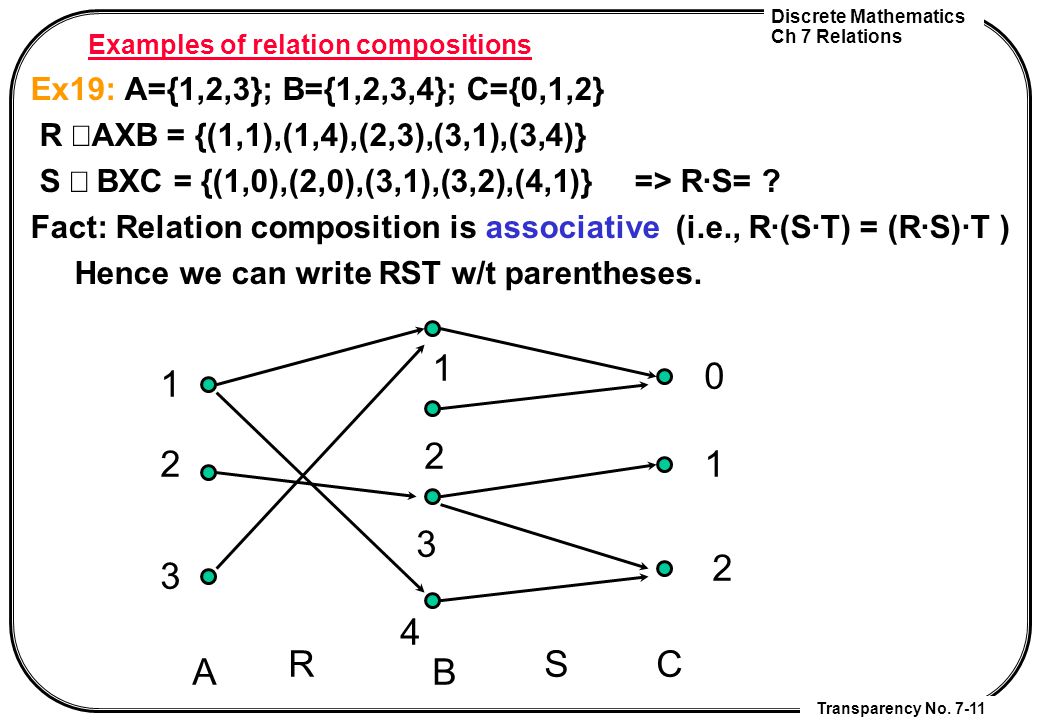 1.2
1.2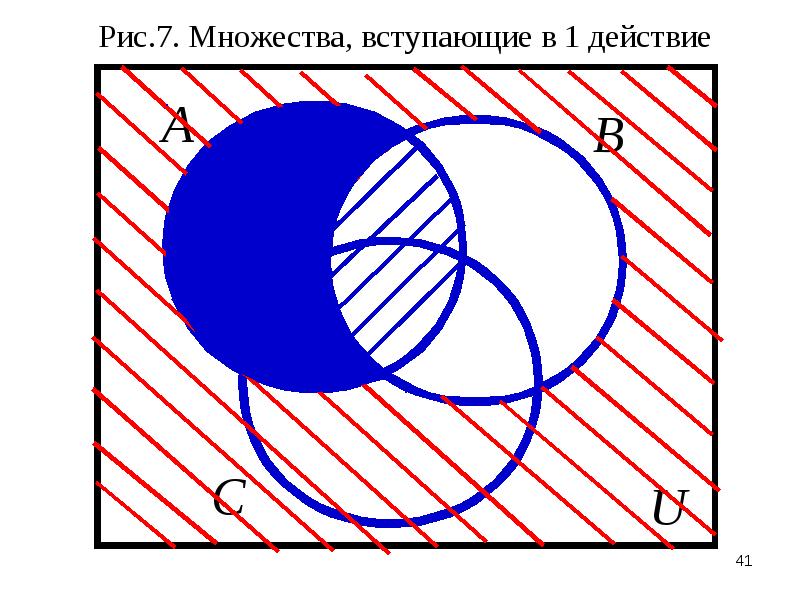
 И. Баврин. – Люберцы: Юрайт, 2015. – 208 c.
И. Баврин. – Люберцы: Юрайт, 2015. – 208 c. М. Ерусалимский. – СПб.: Лань, 2018. – 476 c.
М. Ерусалимский. – СПб.: Лань, 2018. – 476 c. – 448 c.
– 448 c. С. Спирина. – М.: Академия, 2018. – 240 c.
С. Спирина. – М.: Академия, 2018. – 240 c.
 Дискретная математика и комбинаторика. – Пер. с англ. — М. : Издатель- Издательский дом “Вильямс”, 2004. — 960 с.
Дискретная математика и комбинаторика. – Пер. с англ. — М. : Издатель- Издательский дом “Вильямс”, 2004. — 960 с. ru || mediafire.com
ru || mediafire.com О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001, 288 стр. SBN 5-93972-076-5
О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001, 288 стр. SBN 5-93972-076-5 В анализе графов и автоматов особое внимание уделено алгебраическим методам.
В анализе графов и автоматов особое внимание уделено алгебраическим методам. Книгу, без сомнения, можно рекомендоватьвсем изучающим дискретную математику и информатику. Она раскрывает тайну одного феномена американского образования – как превращать малограмотных школьников в прекрасных математиков.
Книгу, без сомнения, можно рекомендоватьвсем изучающим дискретную математику и информатику. Она раскрывает тайну одного феномена американского образования – как превращать малограмотных школьников в прекрасных математиков. : Лаборатория Базовых Знаний, 2003. — 288 с: ил. – серия “Технический университет”
: Лаборатория Базовых Знаний, 2003. — 288 с: ил. – серия “Технический университет”  Изложение, где это возможно, носит строгий математический характер. Доказательства утверждений проводятся на конструктивном уровне. Дается большое количество примеров и упражнений, результаты которых, как правило, используются в дальнейшем. ля студентов, аспирантов и научных работников, занимающихся вопросами компьютерной математики и ее приложениями.
Изложение, где это возможно, носит строгий математический характер. Доказательства утверждений проводятся на конструктивном уровне. Дается большое количество примеров и упражнений, результаты которых, как правило, используются в дальнейшем. ля студентов, аспирантов и научных работников, занимающихся вопросами компьютерной математики и ее приложениями. В двух следующих главах обсуждаются методы нахождения кратчайших путей в графах и задача отыскания максимального потока в сети. В последней главе рассматривается применение комбинаторного понятия матроида для решения некоторого класса оптимизационных задач. Книга предназначена для программистов, желающих расширить свои знания в области комбинаторных алгоритмов, а также пополнить свои практические знания теоретическими. От читателя требуются элементарные сведения из математики, а также знакомство с языком программирования Паскаль
В двух следующих главах обсуждаются методы нахождения кратчайших путей в графах и задача отыскания максимального потока в сети. В последней главе рассматривается применение комбинаторного понятия матроида для решения некоторого класса оптимизационных задач. Книга предназначена для программистов, желающих расширить свои знания в области комбинаторных алгоритмов, а также пополнить свои практические знания теоретическими. От читателя требуются элементарные сведения из математики, а также знакомство с языком программирования Паскаль Излагаются основы теории автоматов. Рассматриваются дискретные экстремальные задачи и методы их решения.Книга предназначена для инженеров, специализирующихся в области автоматического управления, вычислительной техники, систем передачи информации, а также студентов и аспирантов соответствующих специальностей.
Излагаются основы теории автоматов. Рассматриваются дискретные экстремальные задачи и методы их решения.Книга предназначена для инженеров, специализирующихся в области автоматического управления, вычислительной техники, систем передачи информации, а также студентов и аспирантов соответствующих специальностей. И. Дискретная математика. Математика для менеджера в примерах и упражнениях. – М.: Логос, 2000. – 240 с.
И. Дискретная математика. Математика для менеджера в примерах и упражнениях. – М.: Логос, 2000. – 240 с.  Рассматриваются вопросы, связанные с математической логикой, теорией алгебраических систем, комбинаторикой, теорией графов. Приводится ряд практических задач и даются алгоритмы их решения.
Рассматриваются вопросы, связанные с математической логикой, теорией алгебраических систем, комбинаторикой, теорией графов. Приводится ряд практических задач и даются алгоритмы их решения.
 Материал книги доступно изложен и проверен на нескольких поколениях студентов, содержит самые необходимые сведения для будущих инженеров-системотехников, программистов, кибернетиков и других специальностей. Дается описание некоторых алгоритмов и приведены отлаженные Паскаль-программы для наиболее важных из них. Эти программы могут служить основой для выполнения лабораторных работ по курсу. Для студентов, аспирантов и других читателей, интересующихся отдельными разделами дискретной математики.
Материал книги доступно изложен и проверен на нескольких поколениях студентов, содержит самые необходимые сведения для будущих инженеров-системотехников, программистов, кибернетиков и других специальностей. Дается описание некоторых алгоритмов и приведены отлаженные Паскаль-программы для наиболее важных из них. Эти программы могут служить основой для выполнения лабораторных работ по курсу. Для студентов, аспирантов и других читателей, интересующихся отдельными разделами дискретной математики.  В это издание включено много новых материалов, в связи с чем изменилась структура книги: появились новые главы и параграфы. Увеличено число упражнений. Текст дополнен алфавитным указателем и библиографическими рекомендациями.
В это издание включено много новых материалов, в связи с чем изменилась структура книги: появились новые главы и параграфы. Увеличено число упражнений. Текст дополнен алфавитным указателем и библиографическими рекомендациями.  ru || mediafire.com
ru || mediafire.com
 Книга хорошо дополняет учебник Алферова и др. “Основы криптографии”.
Книга хорошо дополняет учебник Алферова и др. “Основы криптографии”.
