Дисперсия для чего нужна: Зачем нужна дисперсия? : Вероятность, статистика

Для чего нужна дисперсия?

Для чего нужна дисперсия?

Дисперсия характеризует разброс случайной величины вокруг ее математического ожидания. Оно используется для оценки масштаба возможного отклонения случайной величины от ее математического ожидания. …

Что такое дисперсия случайной величины?

Дисперсия – это мера разброса значений случайной величины X относительно ее математического ожидания M(X) (см. … Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около M(X): если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см.

Что называют стандартным отклонением и дисперсией измерения?

Квадратный корень из дисперсии называется стандартным отклонением. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Как считается среднее квадратическое отклонение?

Среднее квадратичное отклонение, формула Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим. Среднее квадратичное отклонение принято обозначать греческой буквой сигма σ: 1.

Как вычислить среднее квадратическое отклонение в Excel?

Статистические функции в Excel

1. Среднее значение: =СРЗНАЧ(диапазон)
2. Квадратическое отклонение: =КВАДРОТКЛ(диапазон)
3. Дисперсия: =ДИСП(диапазон)
4. Дисперсия для генеральной совокупности: =ДИСПР(диапазон)
5. Среднеквадратическое отклонение: =СТАНДОТКЛОН(диапазон)
6. Коэффициент корреляции: =КОРРЕЛ(диапазон 1;диапазон 2)

Как найти функцию распределения дискретной случайной величины?

Функция распределения дискретной случайной величины: вычисление Чтобы вычислить функцию распределения дискретной случайной величины F(х), требуется сложить вероятности всех тех значений, которые меньше или равны граничному значению х.

Как найти оценку математического ожидания?

Формула среднего случайной величины Для непрерывной случайной величины (заданной плотностью вероятностей f(x)), формула вычисления математического ожидания Х выглядит следующим образом: M(X)=∫+∞−∞f(x)⋅xdx.

Что такое дисперсия измерений?

называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.

Какое явление называется дисперсией?

Дисперсией света называется зависимость показателя преломления n вещества от частоты ν (длины волн λ) света или зависимость фазовой скорости световых волн от их частоты. … Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму (рис. 10.

Чем можно объяснить дисперсией света?

Дисперсия света представляет собой явление зависимости абсолютного значения преломления вещества от частоты (длины волны) света. Это же явление описывается зависимостью фазовой скорости световых волн от частоты. … Такого же эффекта можно добиться с помощью дифракционной решетки, которая разлагает свет по длинам волн.

Что Ньютон назвал дисперсией?

Зависимость показателя преломления света от его цвета Ньютон назвал дисперсией. … Абсолютный показатель преломления: Дисперсией называется зависимость показателя преломления среды от частоты световой волны.

Что называется дисперсией вещества?

Дисперсия вещества определяется интенсивностью разложения света данным веществом. … Явления, соответствующие непрерывному уменьшению скорости распространения света в веществе и возрастанию показателя преломления при уменьшении длины волны, составляют область нормальной дисперсии.

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т. е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

 

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН. В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. 

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Поделиться в социальных сетях:

Дисперсия в статистике: понимание того, как она используется

Что такое дисперсия?

Область статистики используется во всех секторах и отраслях, чтобы помочь людям лучше понять и предсказать потенциальные результаты. В финансах инвесторы часто обращаются к статистике, чтобы получить представление о том, как можно распределить доходы от определенных активов или групп активов. Этот диапазон возможных доходов от инвестиций называется дисперсией. Другими словами, дисперсия относится к диапазону потенциальных результатов инвестиций на основе исторической волатильности или доходности.

Существует два важных способа измерения дисперсии — альфа и бета, — которые рассчитывают доходность с поправкой на риск и доходность относительно эталона соответственно. Рассматривая дисперсию возможных доходов от инвестиций и значений, таких как альфа и бета, инвесторы могут получить представление о риске, присущем конкретной ценной бумаге или инвестиционному портфелю.

Ключевые выводы

• Дисперсия относится к диапазону потенциальных результатов инвестиций на основе исторической волатильности или доходности.
• Дисперсия может быть измерена с помощью альфа и бета, которые рассчитывают доходность с поправкой на риск и доходность относительно эталонного индекса соответственно.
• Вообще говоря, чем выше дисперсия, тем рискованнее инвестиция, и наоборот.

Понимание дисперсии

Дисперсия часто интерпретируется как мера степени неопределенности и, следовательно, риска, связанного с конкретной ценной бумагой или инвестиционным портфелем.

У инвесторов есть тысячи потенциальных ценных бумаг, в которые они могут инвестировать, и множество факторов, которые следует учитывать при выборе места для инвестирования. Одним из факторов, стоящих на первом месте в их списке соображений, является профиль риска инвестиций. Дисперсия является одним из многих статистических показателей, позволяющих получить перспективу.

Большинство фондов указывают свой профиль риска в информационных бюллетенях или проспектах, которые можно легко найти в Интернете. Тем временем информацию об отдельных акциях можно найти через Morningstar и аналогичные компании, занимающиеся рейтингом акций.

Когда дело доходит до финансовой статистики, инвесторы часто обращаются к таким показателям, как корреляция, когда обсуждают диверсификацию и изменение портфелей с течением времени. Однако, согласно S&P Dow Jones Indices, показатель, известный как рассредоточение активов, имеет высокую квалификацию в качестве дополнительного инструмента. Это и понятно, поскольку дисперсия возможной доходности актива дает представление о волатильности и риске, связанных с владением этим активом. Чем более изменчива доходность актива, тем более он рискован или волатилен.

Например, актив, историческая доходность которого в любой данный год колеблется от +10% до -10%, может считаться более волатильным, чем актив, историческая доходность которого колеблется от +3% до -3%, поскольку его доходность более разбросана.

Измерение дисперсии

Бета

Статистический показатель измерения первичного риска, бета, измеряет дисперсию доходности ценной бумаги по отношению к определенному ориентиру или рыночному индексу, чаще всего к американскому индексу S&P 500. Бета-показатель 1,0 указывает на то, что инвестиции движутся в унисон с ориентиром.

Бета, превышающая 1,0, указывает на то, что ценная бумага, вероятно, испытает более сильные движения, чем рынок в целом — можно ожидать, что акция с бета 1,3 испытает движения, в 1,3 раза превышающие рыночные, то есть, если рынок вырастет на 10%, бета-версия 1.3 выросла на 13%. Оборотная сторона заключается в том, что, если рынок пойдет вниз, эта ценная бумага, скорее всего, упадет больше, чем рынок, хотя нет никаких гарантий масштаба движений.

Бета менее 1,0 означает менее рассредоточенную доходность по отношению к рынку в целом. Например, ценная бумага с коэффициентом бета 0,87, скорее всего, будет следовать за рынком в целом: если рынок вырос на 10%, то инвестиции с более низким коэффициентом бета вырастут только на 8,7%.

Альфа

Альфа — это статистический показатель, который измеряет доходность портфеля с поправкой на риск, то есть насколько больше или меньше возврат инвестиций по отношению к индексу или бета.

Доход выше, чем бета, указывает на положительную альфу, обычно приписываемую успеху управляющего портфелем или модели. Отрицательная альфа, с другой стороны, указывает на отсутствие успеха у управляющего портфелем в преодолении бета или, в более широком смысле, рынка.

Что такое описательная статистика?

Описательная статистика — это средство использования сводок выборки данных для описания характеристик более крупного набора данных. Например, перепись населения может включать описательную статистику о соотношении мужчин и женщин в конкретном городе.

Что такое ковариация?

Ковариация — это статистическая мера направленной связи между доходностью двух активов. Обнаружение того, что две акции с высокой или низкой ковариацией могут быть бесполезными метриками сами по себе. Некоторые инвесторы могут дополнить свой анализ анализом дисперсии доходности или корреляции, прежде чем принять решение об инвестировании.

Что такое бета?

В финансах бета — это мера волатильности ценной бумаги или портфеля по сравнению с рынком в целом. Отслеживание бета с течением времени может предоставить инвесторам полезный профиль риска для актива по сравнению с основным индексом.

Практический результат

Дисперсия относится к статистической мере диапазона потенциальных результатов инвестиций на основе их исторической волатильности или доходности. Двумя важными способами представления дисперсии являются альфа, которая рассчитывает доходность с поправкой на риск, и бета, которая описывает доходность относительно эталона.

Анализ дисперсии возможной доходности может помочь вам понять уровень риска, связанного с конкретной инвестицией, хотя важно помнить, что будущая доходность ценной бумаги может отличаться от ее прошлой доходности.

Что такое дисперсия? Определение дисперсии, дисперсия, означающее

Избранные фонды

Pro Investing от Aditya Birla Sun Vife Viritual Fund

Инвестиции сейчас

Представлены фонды

★★★★

Mirae0005

5y return

12. 27 %

Invest Now

Поиск

+

Business News ›Определения› Финансы ›Дисперсия

Предложите новое определение

Предлагаемые определения будут учитываться для включения в Economictimes. Финансы

• НАЗАД ОПРЕДЕЛЕНИЕ

• СЛЕДУЮЩЕЕ ОПРЕДЕЛЕНИЕ

Рассеивание означает распространение чего-либо. Когда мы погружаемся в статистику и обработку данных, значение дисперсии уточняется. Определение дисперсии устанавливает расширение числовых данных в статистике, которое, вероятно, будет колебаться около типичного значения. Дисперсия также известна как «изменчивость», «разброс» и «разброс».

Его можно рассчитать с помощью различных статистических данных, таких как дисперсия, диапазон, среднее значение и его отклонение, стандартное отклонение и квартили и их отклонение.

Что такое дисперсия?
Проще говоря, дисперсия помогает понять распределение любых заданных данных. С точки зрения бизнеса и финансов дисперсия означает диапазон всех возможных доходов от любых инвестиций. Его также можно использовать для расчета факторов риска в любых инвестициях.

Понять дисперсию
Когда мы инвестируем в какие-либо ценные бумаги, учитывается множество факторов. Например, неотъемлемый риск является важным фактором в инвестициях. Дисперсия помогает в измерении неопределенности, которая включает внутренние факторы риска.

У инвесторов есть много ценных бумаг, из которых они могут инвестировать, и, учитывая это, профили риска стоят на первом месте в списке. Рассеивание становится одним из лучших способов представить эти вещи в перспективе. Распределение доходности инвестиционного портфеля показывает его волатильность и риски, связанные с активом. Чем больше изменчивость возврата любой покупки, тем рискованнее и волатильнее она будет.

Чтобы лучше понять это, вы можете следовать этому примеру. Давайте рассмотрим инвестиции, годовой доход которых составляет от +15% до -20%. Этот актив окажется более волатильным, чем инвестиции, годовая доходность которых колеблется от +6% до -3%. Почему? Происходит это потому, что дисперсия первой инвестиции распространяется более широко.

Для измерения дисперсии
Ниже перечислены несколько методов измерения дисперсии.

Бета
Основная статистика измерения риска называется бета. Это относится к дисперсии доходности актива по отношению к каким-либо конкретным критериям или маркетинговым индексам. Наиболее часто используемый рыночный индекс в составе американского индекса S&P 500.

Если значение бета равно 1,0, это означает, что инвестиции движутся в соответствии с установленными критериями.

Если значение бета меньше 1,0, это означает, что доход по всему рынку менее рассеян. Например, актив со значением бета 0,78, вероятно, будет отставать от рынка. Если рынок вырос на 10%, то безопасность с этой более низкой бетой вырастет только до 7,8%.

Если значение бета больше 1,0, актив, вероятно, претерпит более значительные изменения, чем общий рыночный индекс. Например, инвестиции со значением бета 1,6 будут двигаться в 1,6 раза быстрее, чем рыночный индекс. Если рынок поднимется на 10%, акции вырастут на 16%. Риск заключается в том, что если рынок падает, актив также падает.

Alpha
Альфа-метод является одним из статистических показателей доходности любого портфеля с поправкой на риск. Это относится к тому, насколько возврат инвестиций будет больше или меньше по отношению к рыночному индексу и значению бета.

Инвестиционный доход, превышающий значение бета, указывает на положительное значение альфа. Это предполагает прибыль или успех модели портфеля. Альфа будет иметь отрицательное значение, если значение бета меньше, чем доход от инвестиций. Это указывает на то, что модель портфеля убыточна или менее успешна, чем рынок в целом в самом широком смысле.

Формула CAPM
Полная форма CAPM означает модель ценообразования основных средств. Он распознает любой доход от инвестиций с помощью уравнения, которое включает в себя как значение альфа, так и бета. Формула CAPM сделана так, что уже предполагает, что оценка любого портфеля полностью диверсифицирована. Его единственное внимание сосредоточено на рыночном (систематическом) риске для определения ожидаемой доходности актива.

Уравнение формулы САРМ:

Rp = Rf + β(Rm – Rf) + α

где,

Rp — реализованный доход.

Rf – безрисковая ставка.

Rm – рыночная доходность.

Формулу можно изменить, чтобы получить значение α.

α = Rp – Rf – β(Rm – Rf)
В этих случаях значение альфы находится по разнице между реализованным доходом модели и оцененным доходом от модели, т.е. требуемым доходом.

Какая польза от дисперсии?
Одним из наиболее важных факторов для любого инвестора является решение, в какой портфель инвестировать будет его фактор риска или волатильность. Чтобы понять и оценить это, лучшим методом является использование дисперсии. Это дает всем инвесторам необходимое представление о том, в какие активы инвестировать, о риске, связанном с портфелем, и о том, следует ли удерживать активы

Что вызывает дисперсию?
Дисперсия в статистике возникает из-за нерегулярного поведения наблюдаемых данных, технических ошибок в методах измерения данных и некоторых других природных явлений. Все эти аспекты в совокупности сочетаются с рассеянием или дисперсией данных в любом заданном наборе.

Каковы три меры дисперсии?
Дисперсия может быть рассчитана только в относительном или абсолютном выражении. Наиболее часто используемыми методами дисперсии являются диапазон, дисперсия и стандартное отклонение.

• Диапазон относится к разнице между наибольшим и наименьшим значением спреда.
• Дисперсия может быть рассчитана путем сложения квадрата разницы между каждым значением в спреде и средним значением. Затем разделите его на общее количество значений в предоставленном или принятом во внимание наборе данных.
• Стандартное отклонение относится к квадратному корню из значения дисперсии.

Что означает дисперсия в статистике?
Дисперсия относится к диапазону распределения данных об ожидаемом значении. Он показывает отношение распределения от стандартного или центрального значения.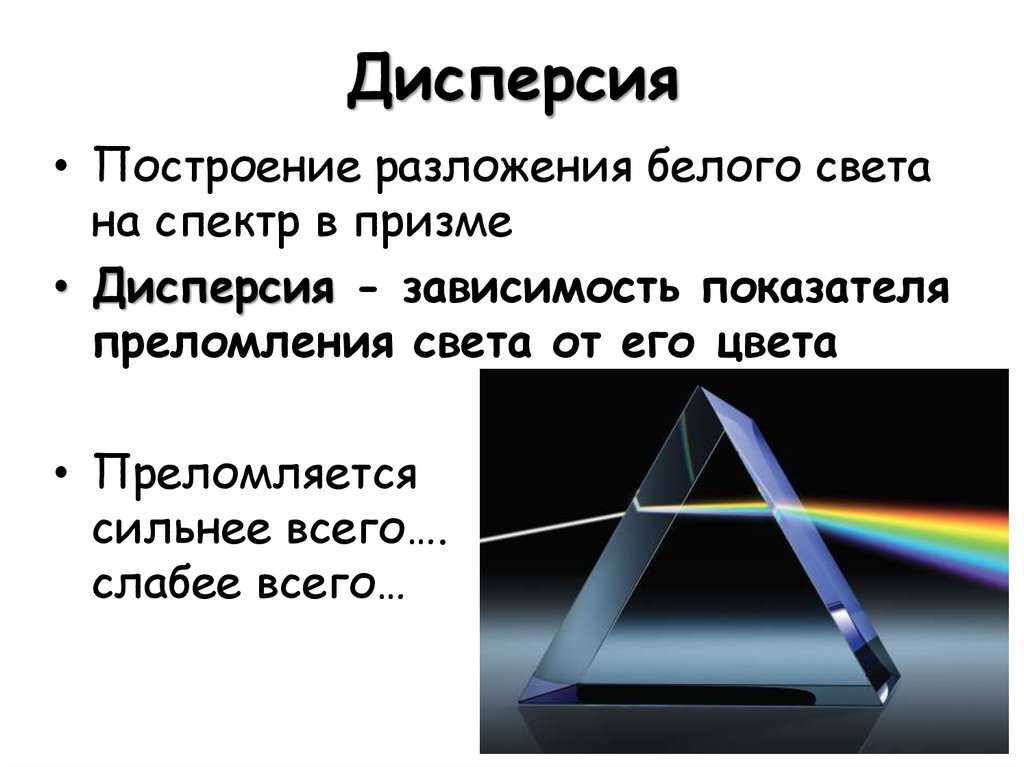 Это существенный фактор при оценке качества, изменчивости и доходности данных при любом статистическом наблюдении.

Отказ от ответственности: этот контент создан внешним агентством. Высказанные здесь взгляды принадлежат соответствующим авторам/организациям и не отражают точку зрения Economic Times (ET). ET не гарантирует, не ручается и не одобряет какое-либо его содержание, а также не несет за него никакой ответственности. Пожалуйста, примите все необходимые меры, чтобы убедиться, что любая предоставленная информация и контент являются правильными, обновленными и проверенными. Настоящим ET отказывается от любых и всех гарантий, явных или подразумеваемых, в отношении отчета и любого его содержания.

Прочтите больше новостей на

• DispersionCapMcapital Asset Pricing ModelDispersionthe
• Что представляет собой определение DispersionDispersion

• . может усугубить проблему: коктейль CSEA из выбросов от петард и сжигания стерни в соседних штатах еще больше ухудшает качество воздуха.