Для чего нужен ноль: Отгорание нуля

Отгорание нуля

Какие бывают последствия отгорания нуля?

Приходилось ли вам слышать о том, что у кого-то сгорела дорогостоящая аппаратура. Возможно, тебе лично пришлось испытать такую неприятность. Почему такое произошло? Причина оказалась в том, что на проводнике в какой-то момент, присутствовало не 220 В, а 380 В. Как такое возможно? Кого винить в произошедшем? Кто будет покрывать убытки?

Были такие случаи, когда пьяный электрик во время профилактических работ в контактных соединениях перепутал проводники, вместо проводника нуль подсоединил фазу, а между фазой и фазой напряжение составляет 380 Вольт.

Но чаще всего, 380В может поступить в наши обители с неожиданной стороны. Проблема кроется в отгорании нуля. Что это за таинственное отгорание нуля? Как оно происходит? Как защититься от нежданного “гостя”?

Для чего нужен нулевой проводник?

Отгорание нуля это лексикон электриков, на техническом языке — обрыв нуля. Проводник нуль используется в трехфазной схеме звезда. Есть еще другая схема, схема треугольник. У такой схемы присутствуют три фазных проводника: А, В, С, но отсутствует четвертый проводник, нулевой. В основном используется в промышленных целях.

В схеме звезда четыре проводника, три фазных и нулевой. Нашему населению достается именно схема звезда и другого быть быть не может. Итак, в многоквартирный дом приходят не два проводника, как некоторые могут полагать, а четырехжильный или пятижильный провод, с защитным заземлением РЕ. Но пока во внимание заземление мы намерено брать не будем, на данный момент он нас не интересует.

Мощный силовой кабель приходит в водный распределительный щит. С главного щита идет распределение по подъездам, а с подъезда по этажам, с этажей по квартирам. Трехфазная схема распределяется равномерно по этажам. Если в подъезде 36 квартир, три фазы будут распределены следующим образом: фаза А – 12 квартир, фаза В – 12 квартир, фаза С – 12 квартир. Распределено равномерно, для баланса работы трехфазной схемы.

Но вот только жители не согласовывают включение и выключение энергопотребителей, да и такого на практике быть не может. Получается так, что один стояк может оказаться сильно загруженным, а другой остается мало задействованным. Что происходит в системе? Произошел перекос  в трехфазной схеме или  дисбаланс. Поставщику электроэнергии никогда не добиться равенства потребления электроэнергии с подобной схемой. Понятно, почему. Люди не роботы, действовать подобно бездушным изобретениям по заданным алгоритмам не могут.

Представим себе, как кипит жизнь в многоэтажном доме. Одни что — то включают, другие выключают. В общем и целом, потребление электроэнергии, чаще всего, происходит более или менее одинаково. Но бывает хороший перекос: по стояку фазы А “густо” разбирают энергию, а по фазе С “пусто”. С этим все понятно. Давайте немного углубимся в трехфазную схему звезда.

Переменные токи каждой фазы в трех одинаковых нагрузках сдвинуты по фазе ровно на одну треть и в идеале компенсируют друг друга, поэтому нагрузка в такой схеме называется трехфазной сосредоточенной нагрузкой.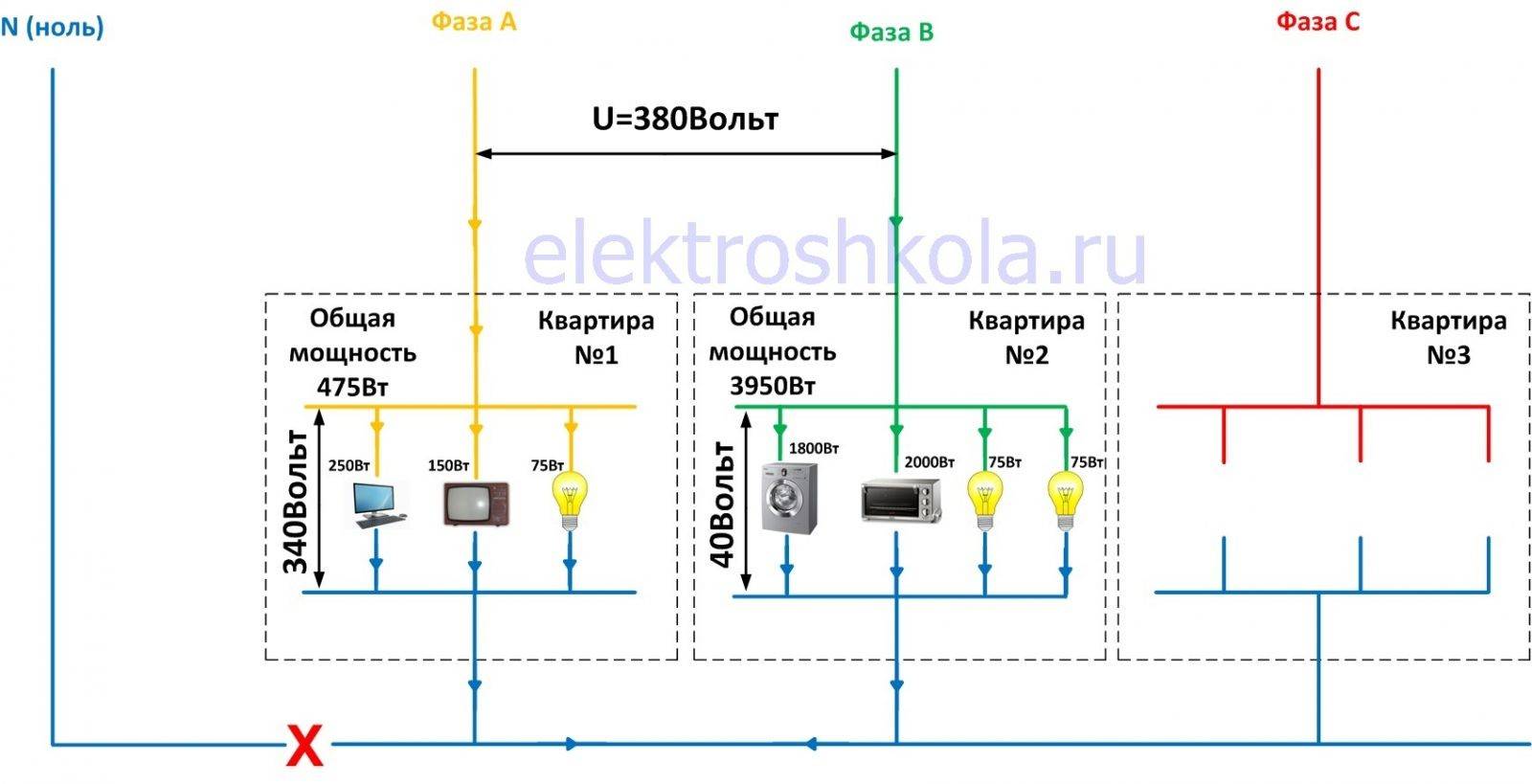 В средней точке ровна  нулю. При равномерной нагрузке трех фаз, например, работают станки на производстве, потребление энергии одинаково по всем фазам. Нуль остается невостребованным, нет дисбаланса. В связи с чем, сечение нулевого проводника гораздо меньше чем по фазе. Нет смысла тратить дорогой металл на то, в чем нет необходимости, там, где появляются незначительные токи. Но у нас в доме приборы работают не от трехфазной схемы, а от однофазной — это все в корне меняет.

Как отгорает нуль?

Тенденция отгорания нуля началась в эпоху 90-х годов. Эпоха экономического преобразования. На рынке появилось большое количество электротехники. Современная аппаратура: компьютеры, телевизоры, радиоприемники, DVD проигрыватели и многое другое. Характер таких устройств несколько отличается от классических бытовых потребителей. Дело в том, что такие приборы выбрасывают в сеть дополнительные импульсные токи, которые не компенсируются в средней точке. Когда включаются приборы , имеющие различные величины сопротивлений, на нулевом проводе может скопится равный или превышающий ток одной из фаз. Это те условия, которые могут создать отгорание нуля, из-за перегрузки на нулевой проводник.

Отгорание происходит в слабых местах, например, в плохо обжатом контакте. Такой перекос может из-за отгорания нуля  создать катастрофические последствия: скачек напряжения до 380 Вольт. Большая часть дорогостоящей аппаратуры может сгореть. Но вот спросить будет не с кого.

Как защитить аппаратуру во время отгорания нуля?

Для защиты бытовой техники от подобных неприятностей, поможет реле контроля напряжения.

реле напряжения

Надежная работа любых бытовых электроприборов от простой лампочки до посудомоечной машины зависит от стабильности электросети. Резкое повышение напряжения или его падение ниже допустимого предела, приводят к быстрому выходу из строя телевизоров, компьютеров, холодильников, стиральных машин и т.п. Это может привести к перегреву обмоток электродвигателей бытовых приборов и последующему выходу их из строя.

Реле напряжения отключает напряжение, если его значение выходит за допустимые пределы. Тем самым защищает все подключённые к нему устройства и приборы. То есть реле напряжения — это защита по напряжению. Для установки реле защиты и другим электромонтажным работам в Нижнем Новгороде, можно обратится за помощью к электрикам профессионалам.

Итак, подведем итог: отгорание нуля в наше время не редкость. Причины мы выяснили, следствия отгорания нуля понятны, как защитить аппаратуру узнали. Осталось приобрести надежное реле напряжения.

Советую не покупать реле напряжения Ресанта, время срабатывания 1 секунда, за такую медлительность все погорит. Приобретать прибор лучше со временем срабатывания по отсечке 0,2 секунды. Такой прибор стоит недешево, но без него ущерб может возрасти во много раз. Ставить прибор или надеяться на авось, решать вам.

Отгорание нуля. Видео.

Что такое модульно-штыревое заземление?

Оцените качество статьи:

flex – CSS | MDN

flex: none;


flex: 2;


flex: 10em;
flex: 30px;
flex: auto;
flex: content;


flex: 1 30px;


flex: 2 2;


flex: 2 2 10%;


flex: inherit;
flex: initial;
flex: unset;

Значения

<'flex-grow'>

Определяет flex-grow для флекс элемента. Смотри <number> для большей информации. Негативные значения считаются недействительными. Значение по умолчанию  0, если не указано.

<'flex-shrink'>

Определяет flex-shrink для флекс элемента. Смотри <number> для большей информации. Негативные значения считаются недействительными. Значение по умолчанию  1, если не указано.

<'flex-basis'>

Определяет flex-basis для флекс элемента. Любое корректное значение для высоты(height) и ширины(width) – корректно и для данного свойства. Предпочтительный размер 0 должен иметь единицу измерения, чтобы не восприниматься как гибкий. Значение по умолчанию   0%, если не указано.

none

Размер элемента устанавливается в соответствии с его свойствами width и height. Он полностью негибкий: не сжимается и не увеличивается по отношению к гибкому контейнеру. Эквивалентно значению “flex: 0 0 auto“.

Формальный синтаксис

none | (en-US) [ (en-US) <'flex-grow'> <'flex-shrink'>? (en-US) || (en-US) <'flex-basis'> ] (en-US)

#flex-container {
	display: -webkit-flex;
	display: flex;
	-webkit-flex-direction: row;
	flex-direction: row;
}

#flex-container > .flex-item {
	-webkit-flex: auto;
	flex: auto;
}

#flex-container > .raw-item {
	width: 5rem;
}

<div>
    <div>Flex box (click to toggle raw box)</div>
    <div>Raw box</div>
</div>

Результат

BCD tables only load in the browser

Стерофундин изотонический

_{Стерофундин изотонический является лекарственным препаратом, отпускаемым по рецепту. Информация на данной странице предназначена исключительно для специалистов здравоохранения — для медицинских и фармацевтических работников. Полная информация по применению препарата Стерофундин изотонический содержится в инструкции по медицинскому применению.}

 

1000 мл раствора содержит:

Концентрация электролитов:

Физико-химические характеристики: теоретическая осмолярность 309 мОсм/л, рН от 5,1 до 5,9
Описание: прозрачный бесцветный раствор без видимых механических включений
Фармакотерапевтическая группа: регидратирующее средство
Код АТХ:

 B05BB01

Стерофундин изотонический является изотоническим раствором электролитов с концентрацией электролитов, адаптированной к концентрации электролитов плазмы крови. Он применяется для коррекции потери внеклеточной жидкости (т. е. потери воды и электролитов в соразмерных количествах). Введение раствора направлено на восстановление и поддержание осмотического статуса во внеклеточном и внутриклеточном пространстве.

Анионный состав представлен сбалансированной комбинацией хлоридов, ацетатов и малатов, приближенной по молярной концентрации к анионному составу плазмы крови, что способствует коррекции метаболического ацидоза.

Замещение потерь внеклеточной жидкости при изотонической дегидратации у пациентов с ацидозом или угрозой его развития.

Стерофундин изотонический вводится капельно в периферические и центральные вены. Доза зависит от возраста, массы тела, клинического и биологического состояния пациента и сопутствующей терапии.

Рекомендуемые дозы

• Пожилым, взрослым и детям с 11 лет от 500 мл до 3 л/сутки, что соответствует 1–6 ммоль натрия/кг массы тела/сутки и 0,03–0,17 ммоль калия/кг массы тела/сутки;
• Детям до 11 лет от 20 мл до 100 мл/кг массы тела/сутки, что соответствует 3–14 ммоль натрия/кг массы тела/сутки и 0,08–0,40 калия/кг массы тела/сутки.

Скорость введения

Максимальная скорость введения определяется потребностями больного в жидкости и электролитах, массой тела, клиническим состоянием и биологическим статусом больного. Для детей скорость введения в среднем составляет 5 мл/кг массы тела/ч, однако она зависит от возраста:

• для детей до 1 года 6–8 мл/кг массы тела/ч;
• для детей с 1 года до 2 лет 4–6 мл/кг массы тела/ч;
• для детей с 2 до 11 лет 2–4 мл/кг массы тела/ч.

Продолжительность применения

Стерофундин изотонический может вводиться настолько долго, насколько это требуется для восстановления водно-электролитного баланса.

Зачем нужен бандаж при беременности и как правильно носить дородовой бандаж

м. Авиамоторная

ОРТЕКА Авиамоторная 14

г.Москва, ул. Авиамоторная, д. 14

м. Алтуфьево

ОРТЕКА Алтуфьево

г. Москва, ул. Лескова, дом 2

м.

Смоленская

ОРТЕКА на Арбате

г. Москва ул. Денежный переулок, д. 30

м. Аэропорт

ОРТЕКА Аэропорт

г. Москва ул. Черняховского, д. 4

м. Бабушкинская

ОРТЕКА Бабушкинская

г. Москва ул. Менжинского, д. 38, корпус 1, стр. 2

м. Беляево

ОРТЕКА Беляево

г. Москва, ул. Профсоюзная, д. 104, корп. 47

м. Братиславская

ОРТЕКА Братиславская

г. Москва, ул. Братиславская, д. 13/1

м. ВДНХ

ОРТЕКА ВДНХ

г. Москва, ул. Кибальчича, д. 2. корп. 1

м. Варшавская

ОРТЕКА Варшавская

г. Москва, Варшавское шоссе, д. 87

м. Водный стадион

ОРТЕКА Водный стадион

г. Москва, Головинское шоссе, 5, корп.1

Выездной Семейный ортопед Москва 1

г. Москва, Проезд Черепановых, д.8

м. Добрынинская

ОРТЕКА Добрынинская

г. Москва, ул. Люсиновская, д. 2, корп. 1

м. Домодедовская

ОРТЕКА Домодедовская

г. Москва ул. Каширское шоссе, владение 106А

м. Кантемировская

ОРТЕКА Кантемировская

Москва, Пролетарский проспект, д.25

м. Каширская

ОРТЕКА Каширская

г. Москва, Каширское шоссе, д. 26Г

м. Коломенская

ОРТЕКА Коломенская

г. Москва, ул. Новинки, д. 1

м. Красные ворота

ОРТЕКА Красные Ворота г Москва Хоромный тупик д 2/6

г Москва, Хоромный тупик, д 2/6

м. Кузьминки

ОРТЕКА Кузьминки

г. Москва Волгоградский проспект, д. 84, корп. 1

м. Курская

ОРТЕКА Курская 2

г. Москва, ул. Земляной Вал, д.27 стр. 1

м. Лермонтовский проспект

ОРТЕКА Лермонтовский проспект

г. Москва, Лермонтовский проспект, 10 к1

м. Алексеевская

ОРТЕКА МОСКВА Алексеевская Мира 97

г Москва, пр-кт Мира, д 97

м. Бульвар Дмитрия Донского

ОРТЕКА МОСКВА Бульвар Дмитрия Донского Дмитрия Донского 6

г Москва, б-р Дмитрия Донского, д 6

м. Перово

ОРТЕКА МОСКВА Перово

г Москва, ул Владимирская 2-я, д 45

м. ЦСКА

ОРТЕКА МОСКВА ТЦ Авиапарк

г.Москва, Ходынский бульвар , д.4

м. Киевская

ОРТЕКА МОСКВА ТЦ Европейский

г Москва, пл Киевского Вокзала, д 2

м. Фрунзенская

ОРТЕКА МОСКВА Фрунзенская Комсомольский 25

г Москва, Комсомольский пр-кт, д 25 к 1

м. Академическая

ОРТЕКА МСК Академическая

г. Москва, ул. Дмитрия Ульянова, д. 24, стр. 1

м. Новопеределкино

ОРТЕКА МСК Новопеределкино Боровское 36

г Москва, Боровское шоссе, д 36

м. Проспект Мира

ОРТЕКА МСК Проспект Мира Мира 45

г Москва, пр-кт Мира, д 45

ОРТЕКА МСК Строгино Маршала Катукова 11

г Москва, ул Маршала Катукова, д 11 к 1 стр 3

м. Сходненская

ОРТЕКА МСК Сходненская Химкинский 23

г Москва, Химкинский б-р, д 23

ОРТЕКА МСК ТЦ Афимолл

г Москва, Пресненская наб. д.2

ОРТЕКА МСК ТЦ Европолис Ростокино

г. Москва, проспект Мира, д.211 к.2

м. Щёлковская

ОРТЕКА МСК Щелковская Уральская 1

г. Москва, ул. Уральская, д. 1

ОРТЕКА МСК Щукинская Маршала Василевского 15

г Москва, ул Маршала Василевского, д 15

м. Марксистская

ОРТЕКА Марксистская

г. Москва, ул. Марксистская, дом 1, корпус 1

м. Маяковская

ОРТЕКА Маяковская

г. Москва, ул. 3-я Тверская- Ямская, д. 15/14

м. Медведково

ОРТЕКА Медведково

Москва, ул. Грекова, д.10

м. Менделеевская

ОРТЕКА Менделеевская

г. Москва, ул. Новослободская, д. 33

м. Войковская

ОРТЕКА Метрополис

Москва, Ленинградское шоссе, д. 16 А, стр 4

м. Митино

ОРТЕКА Митино

г. Москва, ул. Дубравная, д. 35

м. Раменки

ОРТЕКА Мичуринский

г. Москва, Мичуринский проспект, д. 20

м. Молодежная

ОРТЕКА Молодежная

г. Москва ул. Ярцевская, д. 32

м. Бабушкинская

ОРТЕКА Москва Бабушкинская Енисейская 17

Москва, ул. Енисейская , д. 17, корпус 1

ОРТЕКА Москва Жулебино Авиаконструктора Миля 8

г Москва, ул Авиаконструктора Миля, д 8 к 1

м. Сокольники

ОРТЕКА Москва Сокольники

г. Москва, ул. Стромынка, д.1

м. Саларьево

ОРТЕКА Москва ТЦ Саларис

Москва, поселение Московский, Киевское шоссе , 23-й км, д. 1

м. Улица Академика Янгеля

ОРТЕКА Москва Улица Академика Янгеля

г. Москва ул. Академика Янгеля , д. 2

м. Новогиреево

ОРТЕКА Новогиреево

г.Москва, Зеленый проспект, д. 79А

м. Новокосино

ОРТЕКА Новокосино

г. Москва, ул. Новокосинская, д. 35

м. Новокузнецкая

ОРТЕКА Новокузнецкая

г. Москва, ул. Пятницкая, д. 31/2 стр. 5

м. Октябрьская

ОРТЕКА Октябрьская

г. Москва, Крымский Вал, д.6

м. Октябрьское поле

ОРТЕКА Октябрьское поле

г. Москва, ул. Народного Ополчения, д. 45

м. Отрадное

ОРТЕКА Отрадное

г. Москва, улица Декабристов, д. 22

м. Первомайская

ОРТЕКА Первомайская

г. Москва, Первомайская улица, 77

м. Улица 1905 года

ОРТЕКА Пресненский Вал

г. Москва, ул. Пресненский вал, д. 4, стр. 29

м. Проспект Вернадского

ОРТЕКА Проспект Вернадского

Москва, ул. Удальцова, д.71 к.3

м. Профсоюзная

ОРТЕКА Профсоюзная

г. Москва, ул. Профсоюзная, д. 15

м. Рязанский проспект

ОРТЕКА Рязанский проспект

г. Москва Рязанский проспект д.40/2

м. Семёновская

ОРТЕКА Семеновская

г.Москва, улица Щербаковская, д. 3

м. Улица Скобелевская

ОРТЕКА Скобелевская

г. Москва, ул. Скобелевская, 4

м. Славянский бульвар

ОРТЕКА Славянский бульвар

г. Москва, Славянский б-р, д 5 к 1

м. Сокол

ОРТЕКА Сокол 2

г. Москва, Ленинградский проспект, д. 74, корп. 1

м. Сокол

ОРТЕКА Сокол 3

г. Москва, Ленинградский проспект, д.75, корп.1А

м. Таганская

ОРТЕКА Таганская

г. Москва ул. Большие Каменщики, д. 3, стр. 3

м. Охотный ряд

ОРТЕКА Тверская

г.Москва, ул. Тверская, д.9

м. Тёплый Стан

ОРТЕКА Теплый стан

Москва, Новоясеневский проспект, д1к2

м. Тимирязевская

ОРТЕКА Тимирязевская

г. Москва, ул. Яблочкова, д.16

м. Университет

ОРТЕКА Университет

г. Москва, Ломоносовский проспект, д. 23

м. Филевский Парк

ОРТЕКА Филевский парк

г. Москва, ул. Минская, д.14, к.1

м. Цветной бульвар

ОРТЕКА Цветной бульвар

г.Москва, ул. Садово-Самотечная, д. 24/27

м. Южная

ОРТЕКА Южная

г.Москва, ул.Сумская, 2/12

О функциях камеры на iPhone

Узнайте о фотографических стилях, QuickTake, сверхширокоугольной камере и других функциях камеры iPhone.

Сохраните свой образ с помощью фотографических стилей

Фотографические стили на моделях iPhone 13 позволяют настроить внешний вид изображений в программе «Камера». Выберите предустановленный стиль «Насыщенный контраст», «Яркий», «Теплый» или «Холодный» и при необходимости выполните более точную настройку, отрегулировав параметры «Тон» и «Теплота». Задайте стиль один раз, чтобы использовать настройки предпочитаемого стиля при каждой фотосъемке в режиме «Фото».

 

Настройка фотографического стиля

При первом открытии приложения «Камера» нажмите «Настроить», чтобы выбрать стиль фотографии. Прокрутите список стилей и нажмите «Использовать [название стиля]», выбрав понравившуюся настройку. 

Обязательно настройте стиль до начала фотосъемки. Вы не сможете добавить фотографический стиль к фотографии, после того как ее уже сделали.

Изменение фотографического стиля

Хотите изменить заданный фотографический стиль? Просто откройте программу «Камера», нажмите стрелку  и нажмите «Фотографические стили» . Стандартный — это реалистичный сбалансированный стиль по умолчанию, который нельзя изменить, но можно смахнуть влево, чтобы просмотреть другие готовые стили, которые можно изменить. Нажмите «Настроить» , чтобы отрегулировать тон и теплоту для выбранного стиля. 

Съемка крупным планом макрофото и макровидео

iPhone 13 Pro и iPhone 13 Pro Max могут снимать макрофото с помощью новой сверхширокоугольной камеры, обновленного объектива и системы автофокуса, позволяющей получать потрясающие крупные планы с резким фокусом на расстоянии всего 2 см. Кроме того, iPhone 13 Pro и iPhone 13 Pro Max могут снимать макровидео, даже замедленное и таймлапс.

Макросъемка в режимах «Фото» и «Видео» производится автоматически — просто поднесите iPhone к объекту и камера автоматически переключится на широкоугольную камеру, если та не была выбрана раньше, при этом кадрирование сохранится. Для съемки макровидео в замедленном режиме или в режиме «Таймлапс», выберите сверхширокоугольную камеру (0,5x) и поднесите устройство близко к объекту съемки.

Вы можете наблюдать переключение между приложением «Камера» и сверхширокоугольной камерой по мере перемещения iPhone к объекту съемки или от него. Чтобы отключить автоматическое переключение в режим маросъемки, перейдите в «Настройки» > «Камера» и отключите параметр «Автомакро». Для съемки макрофото и макровидео при отключенном автоматическом переключении в режим «Макро», выберите сверхширокоугольную камеру (0,5x) и поднесите устройство ближе к объекту съемки.

Снимайте видео с помощью QuickTake

Вы можете использовать QuickTake для записи видео не выходя из режима фото. Функция QuickTake доступна на iPhone XS, iPhone XR и более поздних моделях.

Удерживайте кнопку затвора для съемки видео

По умолчанию приложение «Камера» открывается в режиме фотосъемки. Нажмите кнопку затвора , чтобы сделать снимок. Затем нажмите стрелку , чтобы настроить параметры, например вспышку, Live Photos, таймер и т. д.

Если необходимо снять видеоролик QuickTake, просто нажмите и удерживайте кнопку затвора *. Чтобы остановить запись, отпустите кнопку.

В iOS 14 вы можете удерживать одну из кнопок громкости, чтобы записать видео QuickTake. Если у вас включен параметр «Кнопка увелич. громк. для серий», вы можете использовать кнопку уменьшения громкости для съемки видео QuickTake.

Проведите вправо, чтобы продолжать съемку

Чтобы продолжать съемку видео, не удерживая кнопку затвора , сдвиньте ее вправо, затем отпустите. Когда идет съемка видео, кнопка затвора отображается справа. Чтобы сделать фото во время записи видео, нажмите кнопку затвора . Чтобы завершить съемку, нажмите кнопку записи.

Проведите влево для перехода в режим серийной съемки

Сдвиньте кнопку затвора влево и удерживайте ее, чтобы сделать серию снимков, затем отпустите, чтобы прекратить съемку.

В iOS 14 можно снимать фотографии в режиме серийной съемки, нажав кнопку увеличения громкости. Просто зайдите в «Настройки» > «Камера» и включите функцию «Кнопка увелич. громк. для серий».

* Чтобы снимать видеоролики с настраиваемым разрешением, стереозвуком и функцией усиления звука, переключитесь в режим видеосъемки.

Используйте средства автоматического усовершенствования фотографий

Благодаря функции обнаружения сцены, поддерживаемой моделями iPhone 12 и более поздними, камера интеллектуально определяет, что вы фотографируете, и применяет особые настройки, чтобы подчеркнуть нюансы сцены. Чтобы отключить эту функцию, перейдите в раздел «Настройки» > «Камера» и выключите «Обнаружение сцены».

Регулируйте фокус и экспозицию

Перед тем как сделать снимок, камера автоматически устанавливает фокус и экспозицию, а функция распознавания лиц уравновешивает экспозицию для многих лиц. Вы можете использовать управление компенсацией экспозиции, чтобы точно установить и зафиксировать экспозицию для предстоящих снимков.

Просто коснитесь стрелки , затем коснитесь  и отрегулируйте уровень экспозиции. Экспозиция фиксируется до следующего открытия приложения «Камера».

Управление компенсацией экспозиции доступно на моделях iPhone 11, iPhone 11 Pro и более поздних с iOS 14 или более поздней.

Делайте зеркальные селфи

В iOS 14 можно делать зеркальное селфи, на котором снимок будет таким, каким вы его видите в кадре. Чтобы включить функцию зеркальной фронтальной камеры, перейдите в «Настройки» > «Камера», затем включите функцию.

Зеркальная фронтальная камера для фотографий и видео доступна на iPhone XS, iPhone XR и более поздних моделях. Если у вас модель от iPhone 6s до iPhone X, функция зеркального отражения фотографий спереди позволяет делать только фотографии.

Фотографируйте еще быстрее

Вы можете использовать функцию «Более быстрое срабатывание затвора», чтобы изменить способ обработки изображений: это позволяет делать больше фотографий, быстро нажимая кнопку спуска затвора . Чтобы отключить эту функцию, перейдите в раздел «Настройки» > «Камера» и отключите параметр «Более быстрое срабатывание затвора».

Функция «Более быстрое срабатывание затвора» доступна на моделях iPhone XS, iPhone XR и более поздних с iOS 14 или более поздней.

Улучшайте селфи и фотографии с использованием сверхширокоугольного объектива

Функция коррекции объектива автоматически делает более естественными селфи, сделанные на фронтальную камеру, или фотографии, снятые со сверхширокоугольным (0,5x) объективом. Чтобы отключить эту функцию, перейдите в раздел «Настройки» > «Камера» и выключите функцию «Коррекция объектива».

Функция коррекции объектива доступна на iPhone 12 и более поздних моделях.

Камера на iPhone способна на большее

• Вам нужно делать фотографии в условиях низкой освещенности? Узнайте, как использовать ночной режим на поддерживаемых моделях iPhone.
• Записывайте важные для вас моменты с движением и звуком с помощью функции Live Photos.

Дата публикации: 12 ноября 2021 г.

Можно ли стать чемпионом, если в последнем туре нужна ничья, а ты в меньшинстве проигрываешь 0:2 к 96-й минуте? Ответ — в лиге Парагвая – 07.12.2021

Мы не так часто заглядываем в южноамериканские чемпионаты — особенно за пределы высших лиг Бразилии и Аргентины. Но последний тур парагвайской Примеры не оставил нам выбора: чемпион определился в последнем туре — благодаря голу на 101-й минуте.

К последнему туру ситуация была максимально интригующей: на первом месте шел «Серро Портеньо», на 2 очка отставал «Гуарани». Но в последнем туре «Гуарани» дома играл как раз против «Серро» — и в случае победы брал чемпионство в клаусуре.

Сюжет завертелся в самом начале. Полузащитника «Серро Портеньо» выгнали с поля за грубую игру — влетел в голень сопернику. Судья посмотрел повтор на мониторе и показал прямую красную.

В большинстве «Гуарани» забили два мяча — в быстрых атаках на 36-й и 51-й минутах. И такой счет держался аж до добавленного времени.

Что могло пойти не так, когда ты к 90-й минуте ведешь 2:0 и играешь в большинстве? Как выяснилось, вообще все.

Защитник «Гуарани» получил мелкую травму и лежал за пределами поля. Вратарь команды Гаспар Сервио втащил его на поле — чтобы потянуть время.

За это кипер получил вторую желтую карточку. Судья заодно удалил и травмированного защитника Роберто Фернандеса — тот жестко что-то высказывал арбитру и тоже заслужил вторую желтую. Так «Гуарани» остались в меньшинстве — и без вратаря. В ворота пришлось встать защитнику Маркосу Касересу — замен не осталось.

К концу разборок добавленные 6 минут почти истекли, но арбитр накинул еще пять. Касерес сделал пару неплохих сэйвов, после которых брал мяч и тянул время секунд по 20−30.

«Серро» давил, «Гуарани» играл на отбой — и не отбился. Гости в оставшиеся две минуты умудрились забить необходимые два гола. Ничейный (но по факту чемпионский) гол на счету капитана Хуана Патиньо.

Судья удалил Патиньо (защитник получил вторую желтую за снятую футболку, первая — за толчок вратаря «Гуарани», который втаскивал травмированного защитника на поле), но ему было уже все равно. Радость у игроков и болельщиков «Серро» отнять уже не получилось — у «Гуарани» просто не осталось времени еще раз все перевернуть.

Тренер «Серро Портеньо» Франсиско Арсе не сдержал слез: в июле его сын Алекс разбился в аварии:

«Вы помогли мне выжить. “Серро” помог мне встать на ноги. Спасибо всем: моему штабу, руководству, фанатам. Я люблю вас всем сердцем! “Серро” всегда был для меня домом. Я обязан клубу многим: и как футболист, и как тренер. Но поддержка последних месяцев — это самое важное. На все воля божья. И сегодня случилось настоящее чудо! Кто-то свыше помог нам. И мы это заслужили, потому что сделали многое, чтобы завоевать чемпионство».

D-димер

D-димер – это белковый фрагмент, который образуется при растворении кровяного сгустка, возникающего при свертывании крови. Он является маркером тромбообразования, так как при этом процессе вместе с возникновением тромбов запускается и их растворение с образованием D-димеров.

Синонимы русские

Фрагмент расщепления фибрина.

Синонимы английские

D-dimer, Fragment D-dimer, Fibrin degradation fragment.

Метод исследования

Иммунотурбидиметрия.

Единицы измерения

Мкг FEU /мл (микрограмм фибриноген-эквивалентных единиц на миллилитр).

Какой биоматериал можно использовать для исследования?

Венозную кровь.

Как правильно подготовиться к исследованию?

• Исключить из рациона жирную пищу за 24 часа до исследования.
• Исключить физическое и эмоциональное перенапряжение за 30 минут до исследования.
• Не курить в течение 30 минут до исследования.

Общая информация об исследовании

D-димер – белковый фрагмент, который образуется в результате распада кровяного сгустка. При повреждении сосуда или ткани в организме запускается процесс свертывания крови – образования тромбов, в состав которых входит особый белок фибрин. Он “скрепляет” между собой компоненты тромба и удерживает тромб там, где он образовался.

Тромбы могут возникать не только в месте повреждения тканей или сосудов, но и внутри сосудов при наличии предрасполагающих к этому факторов: повреждение внутренней выстилки сосудов различными эндогенными и экзогенными веществами и антителами, нарушение локальной гемодинамики – застой крови, наличие турбулентных потоков. Тромбы в сосудах встречаются при целом ряде заболеваний: варикозная болезнь вен нижних конечностей, мерцательная аритмия, осложненное течение инфекционных заболеваний, осложнения после проведенного хирургического вмешательства. Организм при тромбозе запускает механизмы, способствующие разрушению тромбов, в ходе их работы фибрин начинает разрушаться плазминогеном и образуются D-димеры. Таким образом, количество D-димеров в крови указывает на активность процессов разрушения тромбов и косвенно позволяет оценить активность тромбообразования. Наиболее часто данный тест используют для диагностики синдрома диссеминированного внутрисосудистого свертывания (ДВС), а также для мониторинга терапии тромбозов антикоагулянтами (например, гепарином).

Количество D-димеров может быть повышено при беременности, обычно оно постепенно нарастает к III триместру. До недавнего времени высокие показатели считались признаком угрозы развития тромботических осложнений при беременности, однако исследования последних лет показали, что четкой связи между уровнем D-димера и патологией беременности нет.

Анализ на D-димер в подавляющем большинстве случаев используется в качестве вспомогательного теста, и диагноз ставится с учетом клинической картины и результатов других исследований.

Для чего используется исследование?

• Для диагностики ДВС-синдрома.
• Для диагностики тромбоза глубоких вен.
• Для дополнительной оценки выраженности тромбообразования и мониторинга проводимой антикоагулянтной терапии при тромбоэмболии легочных артерий, инсульте.

Когда назначается исследование?

• При симптомах тромбоза глубоких вен:
  • выраженной боли в ногах (ноге),
  • выраженных отеках ног (ноги),
  • бледности кожи в зоне тромбоза.
• При подозрении на тромбоэмболию сосудов легких:
  • внезапно возникшей одышке,
  • затруднении дыхания,
  • кашле,
  • кровохаркании (крови в мокроте),
  • резкой боли в грудной клетке,
  • учащении сердцебиения.
• При ДВС, когда на фоне основного заболевания возникают следующие симптомы:
  • одышка,
  • синюшность кожных покровов,
  • кровоточивость десен,
  • тошнота, рвота,
  • сильные боли в мышцах и животе,
  • боль в области сердца,
  • сниженное мочеотделение.
• При контроле за терапией антикоагулянтами.

Что означают результаты?

Референсные значения: 0 – 0,55 мкг FEU /мл.

Для беременных:

Неделя беременности	Референсные значения
До 13-й	0 – 0,55 мкг FEU /мл
13-21-я	0,2 – 1,4 мкг FEU /мл
21-29-я	0,3 – 1,7 мкг FEU /мл
29-35-я	0,3 – 3 мкг FEU /мл
Больше 35-й	0,4 – 3,1 мкг FEU /мл

Резкое повышение концентрации D-димера может указывать на большое количество тромбов в кровяном русле, что чаще всего обусловлено венозной тромбоэмболией или ДВС-синдромом. При этом результаты исследования не позволяют установить локализацию тромбоза. Нормальный уровень D-димера означает, что, скорее всего, у пациента нет острой формы заболевания, вызывающего тромбообразование.

Умеренное повышение концентрации D-димера часто наблюдается при:

• недавно перенесенных хирургических операциях,
• травмах (не обширных),
• сердечно-сосудистых заболеваниях,
• онкологических заболеваниях,
• заболеваниях печени,
• нормально протекающей беременности, особенно на поздних сроках.

Zero: умопомрачительная математика, стоящая за этим, объяснение

Компьютер, на котором вы сейчас читаете эту статью, работает с двоичным кодом – строками из нулей и единиц. Без нуля не было бы современной электроники. Без нуля нет исчисления, что означает отсутствие современной техники или автоматизации. Без нуля большая часть нашего современного мира буквально разваливается.

Открытие человечеством нуля «полностью изменило правила игры … эквивалентно изучению нами языка», – говорит Андреас Нидер, когнитивист из Тюбингенского университета в Германии.

Но на протяжении большей части нашей истории люди не понимали числа ноль. Это не врожденное для нас. Пришлось это изобрести. И мы должны продолжать учить этому следующее поколение.

Другие животные, такие как обезьяны, эволюционировали, чтобы понять элементарную концепцию «ничто». И ученые только что сообщили, что даже крошечный мозг пчелы может вычислить ноль. Но только люди захватили ноль и превратили его в инструмент.

Так что давайте не принимать ноль как должное. Ничего особенного.Вот почему.

Что вообще такое ноль?

Getty Images

Наше понимание нуля становится глубоким, если учесть этот факт: мы не часто или, возможно, никогда не встречаем ноль в природе.

У таких чисел, как «один», «два» и «три» есть аналог. Мы видим одну вспышку света. Мы слышим два гудка из автомобильного гудка. Но ноль? Это требует от нас осознания того, что отсутствие чего-либо – вещь сама по себе.

«Z ero находится в уме, но не в сенсорном мире», – говорит Роберт Каплан, профессор математики из Гарварда и автор книги по нулю. Даже в пустом космосе, если вы видите звезды, это означает, что вы купаетесь в их электромагнитном излучении. В самой темной пустоте всегда есть что-то. Возможно, истинный ноль – то есть абсолютное ничто – мог существовать до Большого взрыва. Но мы никогда не узнаем.

Тем не менее, ноль не обязательно должен существовать, чтобы быть полезным.Фактически, мы можем использовать понятие нуля, чтобы получить все остальные числа во Вселенной.

Каплан провел меня через мысленное упражнение, впервые описанное математиком Джоном фон Нейманом. Это обманчиво просто.

Представьте себе коробку, в которой ничего нет. Математики называют эту пустую коробку «пустым множеством». Это физическое представление нуля. Что внутри пустой коробки? Ничего такого.

Теперь возьмите еще одну пустую коробку и поместите ее в первую.

Сколько вещей сейчас в первой коробке?

В нем один объект.Затем поместите еще одну пустую коробку внутри первых двух. Сколько предметов в нем сейчас? Два. Вот как «мы выводим все счетные числа из нуля… из ничего», – говорит Каплан. Это основа нашей системы счисления. Ноль – это абстракция и реальность одновременно. «Это ничто», – сказал Каплан. (На этом этапе истории вы можете захотеть еще раз ударить по бонгу.)

Затем он выразил это в более поэтических терминах. «Ноль – это далекий горизонт, манящий нас, как горизонты в картинах», – говорит он.«Это объединяет всю картину. Если вы посмотрите на ноль, вы ничего не увидите. Но если вы посмотрите сквозь него, вы увидите мир. Это горизонт ».

Если у нас есть ноль, у нас есть отрицательные числа. Ноль помогает нам понять, что мы можем использовать математику для размышлений о вещах, не имеющих аналогов в физическом жизненном опыте; мнимых чисел не существует, но они имеют решающее значение для понимания электрических систем. Ноль также помогает нам понять его противоположность, бесконечность, во всех ее крайних странностях. (Знаете ли вы, что одна бесконечность может быть больше другой?)

Почему ноль так чертовски полезен в математике

Zero оказывает двойное влияние на нашу математику сегодня.Первый: это важная цифра-заполнитель в нашей системе счисления. Два: само по себе полезное число.

Первые случаи использования нуля в истории человечества восходят к примерно 5000 лет назад, в древнюю Месопотамию. Там он использовался для обозначения отсутствия цифры в строке чисел.

Вот пример того, что я имею в виду: подумайте о числе 103. Ноль в данном случае означает «в столбце десятков ничего нет». Это заполнитель, который помогает нам понять, что это число сто три, а не 13.

Хорошо, вы могли подумать: «Это базовое». Но древние римляне этого не знали. Вы помните, как римляне записывали свои числа? Римскими цифрами 103 – это CIII. Число 99 – XCIX. Вы пытаетесь добавить CIII + XCIX. Это абсурд. Обозначение заполнителя – это то, что позволяет нам легко складывать, вычитать и иным образом манипулировать числами. Заполнитель – это то, что позволяет нам решать сложные математические задачи на листе бумаги.

Если бы ноль оставался просто цифрой-заполнителем, он сам по себе был бы важным инструментом.Но около 1500 лет назад (а может быть, даже раньше) в Индии ноль стал отдельным числом, ничего не означающим. Древние майя в Центральной Америке также независимо разработали ноль в своей системе счисления на заре нашей эры.

В седьмом веке индийский математик Брахмагупта написал то, что считается первым письменным описанием арифметики нуля:

Когда к числу прибавляется ноль или вычитается из числа, число остается неизменным; и число, умноженное на ноль, становится равным нулю.

Ноль медленно распространился по Ближнему Востоку, прежде чем достичь Европы и мысли математика Фибоначчи в 1200-х годах, который популяризировал «арабскую» систему счисления, которую все мы используем сегодня.

Оттуда полезность нуля взорвалась. Подумайте о любом графике, на котором математическая функция начинается с 0,0. Этот теперь повсеместный метод построения графиков был впервые изобретен только в 17 веке после нулевого распространения в Европе. В том же веке появилась совершенно новая область математики, которая зависит от нуля: исчисление.

Вы, возможно, помните из математики в средней школе или колледже, что простейшая функция в исчислении – это получение производной. Производная – это просто наклон линии, которая пересекается с единственной точкой на графике.

Для расчета наклона отдельной точки обычно требуется точка сравнения: подъем за пробегом. Когда Исаак Ньютон и Готфрид Лейбниц изобрели исчисление, открыли то, что вычисление этого наклона в одной точке включает в себя все ближе, ближе и ближе – но на самом деле никогда – деление на ноль.

«Все бесконечные процессы [в математике] вращаются вокруг, танцуют вокруг, понятие нуля», – говорит Роберт Каплан. Ого.

Почему ноль так глубок, как человеческая идея?

Мы не рождены с пониманием нуля. Мы должны этому научиться, а это требует времени.

Элизабет Брэннон, нейробиолог из Университета Дьюка, изучает, как люди и животные представляют числа в своем сознании. Она объясняет, что даже когда дети младше 6 лет понимают, что слово «ноль» означает «ничего», им все равно трудно понять лежащую в основе математику.«Когда вы спрашиваете [ребенка], какое число меньше, ноль или единица, они часто думают, что единица является наименьшим числом», – говорит Брэннон. «Трудно понять, что ноль меньше единицы».

В экспериментах Браннон часто играет в игру с 4-летними детьми. Она положит пару карточек на стол или экран. И на каждой карте будет несколько объектов. Например, одна карта будет иметь две точки. У другого будет три. Вот пример того, что они могут увидеть.

Тенденции в когнитивной науке

Она просто попросит детей выбрать карточку с наименьшим количеством предметов.Когда пустая карточка сочетается с карточкой с одним предметом на ней, менее половины детей получат правильный ответ.

Часто обезьяны лучше распознают ноль, чем маленькие дети. Тенденции в когнитивной науке

Так что же заставит все щелкнуть?

Андреас Нидер, когнитивист из Германии, предполагает, что есть четыре психологических шага, чтобы понять ноль, и каждый шаг когнитивно сложнее предыдущего.

Многие животные могут пройти первые три шага. Но последняя стадия, самая трудная, «предназначена для нас, людей», – говорит Нидер.

Первый – это простое сенсорное переживание включения и выключения стимула. Это простая способность замечать, как мигает свет. Или включается и выключается шум.

Второй – понимание поведения. На этом этапе животные не только могут распознать отсутствие стимула, но и могут на него отреагировать. Когда у человека заканчивается еда, он знает, что нужно пойти и найти еще.

На третьем этапе распознается, что ноль или пустой контейнер меньше единицы. Это сложно, хотя удивительное количество животных, в том числе медоносные пчелы и обезьяны, могут распознать этот факт. Это понимание, «что ничто не имеет количественной категории», – говорит Нидер.

Четвертый этап – принять отсутствие стимула и рассматривать его как символ и логический инструмент для решения проблем. По его словам, ни одно животное, кроме человека, «каким бы умным оно ни было», не понимает, что ноль может быть символом.

Но даже хорошо образованные люди могут немного споткнуться, думая о нуле. Исследования показали, что взрослым требуется на несколько секунд больше времени, чтобы распознать число ноль, по сравнению с другими числами. И когда эксперимент Браннона по выбору карты с наименьшим числом повторяется со взрослыми, им требуется немного больше времени на выбор между нулем и единицей, чем при сравнении нуля с большим числом.

Это говорит о том, что ноль, даже для взрослых, требует дополнительных усилий мозга для обработки.

Что еще ничего не могу понять?

Getty Images / EyeEm

Мы не можем родиться с способностью понимать ноль. Но наша способность изучать это может иметь глубокие эволюционные корни, как показывает нам некоторая новая наука.

Четвертый шаг в представлении о нуле – это представление о нуле как о символе – может быть уникальным для людей. Но удивительное количество животных может перейти к третьему шагу: признать, что ноль меньше единицы.

На это способны даже пчелы.

Скарлетт Ховард, аспирантка Королевского Мельбурнского технологического института, недавно опубликовала эксперимент в Science , который почти идентичен тому, который Брэннон проводил с детьми. Пчелы выбирали чистую страницу от 60 до 70 процентов времени. И они были значительно лучше в различении большого числа, например, шести, от нуля, чем они могли отличить единицу от нуля. Прямо как дети.

Это впечатляет, учитывая, что «у нас есть большой мозг млекопитающих, но у пчел такой маленький мозг весит меньше миллиграмма», – говорит Ховард.Ее исследовательская группа надеется понять, как пчелы производят эти вычисления в уме, с целью однажды использовать эти идеи для создания более эффективных компьютеров.

В аналогичных экспериментах исследователи показали, что обезьяны могут распознавать пустое множество (и часто лучше, чем 4-летние люди). Но тот факт, что пчелы могут это делать, просто удивителен, учитывая, как далеко они находятся от нас на эволюционных деревьях жизни. «Последний общий предок между нами и пчелами жил около 600 миллионов лет назад, а это вечность с точки зрения эволюции», – говорит Нидер.

Мы, люди, могли понять ноль как число только 1500 лет назад. Эксперименты над пчелами и обезьянами показывают нам, что это не просто результат нашей изобретательности. Возможно, это также кульминационный момент эволюции.

Насчет нуля все еще остаются большие загадки. Во-первых, Нидер говорит, что «мы почти ничего не знаем» о том, как мозг это физически обрабатывает. И мы не знаем, сколько животных могут постичь идею ничто как количества.

Но математика ясно показала нам, что, когда мы ничего не исследуем, мы обязательно что-то найдем.

ноль

Ноль показывает, что суммы нет.

Пример: 6-6 = 0 (разница между шестью и шестью равна нулю)

Он также используется как «заполнитель», чтобы мы могли правильно писать числа.

Пример: 502 (пятьсот два) можно принять за 52 (пятьдесят два) без нуля в разряде десятков.

Ноль – это особенное число …

Он находится на полпути между -1 и +1 на числовой прямой:

.

изображения / числовая строка.js? режим = int

Ноль не является ни отрицательным, ни положительным. Но это четное число.

Идея

Идея ноль , хотя и естественна для нас сейчас, не была естественной для первых людей … если нечего считать, как мы можем это подсчитать?

Пример: можно посчитать собак, но нельзя считать пустое место:

Две собаки		Zero Dogs? Ноль кошек?

Пустой участок травы – это просто пустой участок травы!

Ноль как заполнитель

Но около 3000 лет назад людям нужно было различать такие числа, как 4 и 40. Без нуля они выглядят одинаково!

Итак, ноль теперь используется как «заполнитель»: он показывает, что «в этом месте нет числа», например:

502

То есть 5 сотен, , без десятков , и 2 единицы

Значение нуля

Затем люди начали думать о нуле как о фактическом числе .

Пример:

«У меня было 3 апельсина, потом я съел 3 апельсина, теперь у меня ноль апельсинов…! “

Идентификатор добавки

И у нуля есть особое свойство: когда мы добавляем его к числу, мы возвращаем это число без изменений

Пример:

7 + 0 = 7

Складывая от 0 до 7, получаем 7

Также 0 + 7 = 7

Это делает его аддитивным идентификатором , который является просто особым способом сказать «добавьте 0, и мы получим , идентичный (тот же самый) номер, с которого мы начали».

Особые свойства

Вот некоторые из свойств нуля:

Имущество	Пример
а + 0 = а	4 + 0 = 4
а – 0 = а	4 – 0 = 4
а × 0 = 0	6 × 0 = 0
0 / а = 0	0/3 = 0
a / 0 = undefined (деление на ноль не определено)	7/0 = не определено
0 a = 0 (a положительно)	0 4 = 0
0 0 = неопределенный	0 0 = неопределенный
0 a = undefined (a отрицательно)	0 -2 = не определено
0! = 1 (“!” – факториальная функция)	0! = 1

Кто изобрел ноль? – ИСТОРИЯ

Это может показаться очевидным элементом любой системы счисления, но ноль – удивительно недавнее событие в истории человечества.Фактически, этот вездесущий символ «ничего» даже не попал в Европу вплоть до XII века. Истоки Зеро, скорее всего, восходят к «плодородному полумесяцу» древней Месопотамии. Шумерские писцы использовали пробелы для обозначения отсутствий в числовых столбцах еще 4000 лет назад, но первое зарегистрированное использование символа нуля датируется примерно третьим веком до нашей эры. в древнем Вавилоне. Вавилоняне использовали систему счисления, основанную на значении 60, и разработали особый знак – два небольших клина – для различения величин так же, как современные десятичные системы используют нули для различения десятых, сотен и тысячных долей.Подобный тип символа возник независимо в Америке примерно в 350 году нашей эры, когда майя начали использовать нулевой маркер в своих календарях.

Эти ранние системы подсчета видели только ноль в качестве заполнителя, а не число со своим собственным уникальным значением или свойствами. Полное осознание нулевой важности не было достигнуто до седьмого века нашей эры в Индии. Там математик Брахмагупта и другие использовали маленькие точки под числами, чтобы показать нулевой заполнитель, но они также рассматривали ноль как имеющий нулевое значение, называемое «шунья».Брахмагупта также был первым, кто показал, что вычитание числа из самого себя дает ноль. Из Индии ноль попал в Китай и обратно на Ближний Восток, где его подхватил математик Мохаммед ибн-Муса аль-Ховаризми около 773. Именно аль-Ховаризми первым синтезировал индийскую арифметику и показал, как ноль мог функционировать в алгебраических уравнениях, и к девятому веку ноль вошел в арабскую систему счисления в форме, напоминающей овальную форму, которую мы используем сегодня.

Ноль продолжал мигрировать еще несколько столетий, прежде чем наконец достиг Европы примерно в 1100-х годах.Такие мыслители, как итальянский математик Фибоначчи, помогли внедрить ноль в мейнстрим, и позже он занял видное место в работах Рене Декарта, наряду с изобретением сэра Исаака Ньютона и Готфридом Лейбницем математического анализа. С тех пор концепция «ничего» продолжала играть роль в развитии всего, от физики и экономики до инженерии и вычислений.

Нулевые факты для детей

Краткие сведения для детей
Кардинал	0, ноль, “oh”, ноль, ноль, ноль, o,
Порядковый номер	0-я (нулевая, нулевая)
Делители	все остальные номера (кроме себя)
Двоичный	0 2
Тройной	0 3
Четвертичный	0 4
Пятидесятилетний	0 5
Сеньарный	0 6
восьмеричный	0 8
Двенадцатеричный	0 12
Шестнадцатеричный	0 16
Vigesimal	0 20
База 36	0 36
Арабский	٠,0
бенгальский	০
Деванагари	०
китайский	零, 〇
Японский	零, 〇
кхмерский	០
Тайский	๐

Ноль (0) – специальный номер.Если есть ноль вещей, значит, нет вообще ничего. Например, если у человека нет головных уборов, это означает, что у него нет шляп.

Символ

Символ числа ноль – «0». Это аддитивная идентичность общих чисел. Это означает, что если число будет добавлено к 0, то это число останется неизменным.

Математика с нулем

• При добавлении числа к нулю получается это число. Например, добавление нуля к трем дает три. В символах:

 3 + 0 = 3
 

• Вычитание нуля из числа всегда дает это число.Например, вычитание нуля из трех дает три. В символах:

 3 - 0 = 3
 

• Вычитание положительного числа из нуля всегда делает это число отрицательным (или, если отрицательное число вычитается из нуля, оно делает число положительным). В символах:

 0 - 3 = −3
 

• Умножение числа на ноль всегда дает ноль. Например, умножение сорока трех на ноль дает ноль. В символах:

 43 × 0 = 0
 

• При делении нуля на число всегда получается ноль.Например, деление нуля на сорок три дает ноль. В символах:

 0 ÷ 43 = 0
 

 43 ÷ 0 имеет неопределенный ответ.
 

• В частности, ноль, деленный на ноль, не дает ответа. В символах:

 0 ÷ 0 нет ответа.
 

Следующая таблица включает все вышеперечисленные примеры вместе с другими операциями в сжатой, обобщенной форме (где x представляет любое число).

Эксплуатация	Правило	Пример
Дополнение	x + 0 = x	3 + 0 = 3
Вычитание	x – 0 = x	3 – 0 = 3
Умножение	х × 0 = 0	5 × 0 = 0
Отдел	0 ÷ x = 0, когда x ≠ 0	0 ÷ 5 = 0
	x ÷ 0 не определено	5 ÷ 0 не определено
Возведение в степень	0 x = 0, когда x ≠ 0	0 5 = 0
	x 0 = 1, когда x ≠ 0	5 0 = 1
Корень	√0 = 0
Логарифм	журнал b (0) не определено
Факториал	0! = 1
Синус	sin 0º = 0
Косинус	cos 0º = 1
Касательная	tan 0º = 0
Производная	0 ‘= 0
Интегральный	∫ 0 d x = 0 + C

История нуля

Идея нуля впервые возникла в разное время в Вавилоне, Индии и Центральной Америке.Некоторые места и страны не знали о нуле, что, возможно, усложняло им заниматься математикой. Например, год после 1 года до н.э. – это 1 год нашей эры (нулевого года нет). В Индии нулевое значение было теоретизировано в седьмом веке математиком Брахмагуптой.

На протяжении сотен лет идея нуля передавалась из страны в страну, из Индии и Вавилона в другие места, такие как Греция, Персия и арабский мир. Европейцы узнали о нуле от арабов и перестали использовать римскую математику.Вот почему числа называют «арабскими цифрами».

Место нуля как число

Ноль почти никогда не используется в качестве порядкового номера. Это означает, что он не используется как 1, 2 или 3 для обозначения порядка или места чего-либо, например 1-го, 2-го или 3-го. Исключение составляют многие языки программирования.

Еще кое-что о нуле:

Любое число, разделенное само по себе, равно единице, кроме случая, когда это число равно нулю. В символах:

0 ÷ 0 = «не число.«

Во времени, ноль означает «сейчас». Например, когда человек отсчитывает время до начала чего-то, например, бега или взлетающей ракеты, счет будет: «три, два, один, ноль (или идут )». Ноль – это точное время старта гонки или момент взлета ракеты в небо.

0 как число

0 – это целое число, которое предшествует положительному числу 1 и следует за −1. В большинстве (если не во всех) системах счисления 0 был идентифицирован до того, как была принята идея «отрицательных целых чисел».В иероглифах это означает «мужественный».

Ноль – это число, которое означает количество нулевого размера; то есть, если количество братьев равно нулю, это означает то же самое, что и отсутствие братьев, а если что-то имеет нулевой вес, это не имеет веса. Если разница между количеством штук в двух стопках равна нулю, это означает, что в двух стопках есть равное количество штук. Перед началом подсчета результат можно принять равным нулю; то есть количество предметов, подсчитанных до того, как будет подсчитан первый предмет, и подсчет первого предмета приводит к единице.И если нет предметов для подсчета, окончательным результатом остается ноль.

В то время как все математики принимают ноль за число, некоторые нематематики сказали бы, что ноль не является числом, утверждая, что нельзя иметь ноль чего-либо. Другие говорят, что если у кого-то сальдо в банке равно нулю, то на этом счете есть определенное количество денег, а именно их нет. Это последняя точка зрения, которую принимают математики и большинство других.

Обычно между 1 г. до н.э. и 1 г. н.э. не было нулевого года.В частности, почти все историки исключают нулевой год из пролептических григорианского и юлианского календарей (то есть из обычного календаря, используемого в англоязычных странах), но астрономы включают его в те же самые календари. Однако фраза Year Zero может использоваться для описания любого события, которое считается настолько важным, что кто-то может захотеть начать отсчет лет с нуля.

0 в виде числа

Современная цифра 0 обычно записывается как круг или (закругленный) прямоугольник.В шрифтах старого стиля с текстовыми цифрами 0 обычно имеет ту же высоту, что и строчная буква x.

На семисегментных дисплеях калькуляторов, часов и т. Д. 0 обычно записывается шестью линейными сегментами, хотя на некоторых исторических моделях калькуляторов он был написан четырьмя линейными сегментами. Четырехсегментный 0 встречается нечасто.

Число , число , ноль (как в приведенном выше примере с «нулевыми братьями») не совпадает с числом , числом или числом , нулем , используемым в системах счисления с использованием позиционного обозначения.Последовательные позиции цифр имеют более высокие значения, поэтому цифра ноль используется для пропуска позиции и присвоения соответствующего значения предыдущим и последующим цифрам. В другой позиционной системе счисления нулевая цифра не всегда необходима. Так называемая биективная нумерация – возможный пример системы без нулей.

Цифровая цифра ноль

0 ( ноль ) также используется как числовая цифра, используемая для представления этого числа в цифрах. Он используется для хранения места этой цифры, потому что правильное размещение цифр влияет на значение числа.

Примеры:

• В цифре 10, которая означает один умноженный на десять и ноль единиц (или единиц).
• В цифре 100, что означает один умноженный на сотню плюс ноль десятков плюс ноль единиц.

Разделение нуля и буквы O

Цифра 0 и буква O круглые, но разной ширины. На компьютере разница важна. Во-первых, компьютер не будет выполнять арифметические операции с буквой O, потому что он не знает, что это должен быть ноль.

Овальный ноль и круглая буква O стали использоваться вместе на современных символьных дисплеях. Ноль с точкой в ​​центре, кажется, начался как выбор на контроллерах IBM 3270 (проблема заключается в том, что он выглядит как греческая буква тета). Ноль с косой чертой, похожий на букву O с проведенной внутри нее диагональной линией, используется в графических наборах ASCII старого стиля, которые были взяты из колеса набора текста по умолчанию на хорошо известном телетайпе ASR-33. Этот формат вызывает проблемы, потому что он выглядит как символ, представляющий пустой набор, а также для некоторых скандинавских языков, которые используют Ø как букву.

Правило, в котором есть буква O с косой чертой и ноль без косой черты, использовалось в IBM и некоторых других ранних производителях мэйнфреймов; это даже большая проблема для скандинавов, потому что это выглядит как две их буквы одновременно. На некоторых компьютерах Burroughs / Unisys ноль отображается с обратной косой чертой. И еще одно соглашение, распространенное в ранних линейных принтерах, оставляло ноль без каких-либо дополнительных точек или косых черт, но добавляло хвост или крючок к букве O, чтобы она напоминала перевернутую Q или прописную прописную букву O.

Немецкий номерной знак с нулями

Буквы, используемые на некоторых европейских номерных знаках автомобилей, делают два символа разными. Это достигается за счет того, что ноль должен быть скорее яйцевидным, а буква О – более круглой, но, прежде всего, разрезанием нуля в верхней правой части, чтобы круг больше не замыкался (как в немецких таблицах). Выбранный стиль букв называется fälschungserschwerende Schrift (сокр .: FE Schrift ), что означает «шрифт, который труднее подделать».Но те, которые используются в Соединенном Королевстве, не заставляют букву o и цифру 0 отличаться друг от друга, потому что никогда не может быть ошибки, если буквы расположены правильно.

При написании бумаги совсем не обязательно, чтобы 0 (ноль) и O (буква O) выглядели по-разному. Или вы можете добавить косую черту к нулю, чтобы показать разницу.

Нули функции

Функции объяснены в статье о функциях (математика). Если функция f ( x ) = 0, то x называется нулем (или корнем) функции f .Например, если функция f ( x ) равна x ² -1, то нули функции равны +1 и -1, потому что f (+1) = (+1) ² – 1 = 0 и f (−1) = (−1) ² – 1 = 0.

Нули функции используются, потому что это еще один способ поговорить о решении уравнения, что является основной целью в алгебре. Если мы хотим решить уравнение типа x ² = 1, то мы можем вычесть правую часть уравнения из обеих частей, в данном случае 1.Все, что мы получаем в левой части, в данном случае x ² – 1, можно назвать функцией f (x). Правая часть должна быть равна нулю, потому что мы вычитали ее из себя. Итак, f (x) = 0. Нахождение нулей этой функции аналогично решению этого уравнения. В предыдущем абзаце нули этой функции равны +1 и -1, поэтому они являются решениями этого уравнения. Мы получили это уравнение, вычитая одно и то же из обеих частей, поэтому у нас также есть решения уравнения, с которого мы начали, в данном случае x ² = 1.В более общем плане, если бы мы могли найти нули функций, мы могли бы решить любое уравнение.

Связанные страницы

Образы для детей

• Задняя сторона эпи-ольмекской стелы C из Трес-Сапотеса, второй старейшей обнаруженной даты с помощью длинного счета. Цифры 7.16.6.16.18 переводятся на сентябрь 32 г. до н.э. (юлианский). Символы вокруг даты считаются одним из немногих сохранившихся примеров эпи-ольмекского письма.

• Пример древнегреческого символа нуля (нижний правый угол) из папируса 2-го века

• Это изображение нуля, выраженное китайскими счетными прутьями, на основе примера, предоставленного A History of Mathematics .Пустое пространство используется для обозначения нуля.

• Число 605 кхмерскими цифрами из Самборской надписи (сакская эра 605 соответствует 683 году нашей эры). Самый ранний известный материал, использующий ноль как десятичное число.

Что такое ноль (0)? – Определение с сайта WhatIs.com

В математике ноль, обозначенный числовым символом 0, равняется обоим:

1. В позиционной системе счисления – индикатор разряда, означающий «нет единиц этого кратного».«Например, в десятичном числе 1041 одна единица находится в разряде тысяч, нет единиц в разряде сотен, четыре единицы – в разряде десятков и одна единица – в разряде 1–9.

2. Независимое значение на полпути между +1 и -1.

В письме за пределами математики, в зависимости от контекста, различные денотативные или коннотативные значения нуля включают «полный провал», «отсутствие», «ноль» и «абсолютно ничего». («Ничто» – еще более абстрактное понятие, чем «ноль», и их значения иногда пересекаются.)

Обозначение заполнителей в позиционных числах найдено на каменных табличках древнего (3000 г. до н.э.) Шумера. Тем не менее, у греков не было понятия о числе, подобном нулю. С точки зрения современного использования ноль иногда связывают с индийским математиком Арьябхатой, который примерно в 520 году нашей эры изобрел позиционную десятичную систему счисления, которая содержала слово «кха» для обозначения заполнителя. К 876 году, судя по существующей табличке с надписью с этой датой, кха стал символом «0». Между тем, несколько позже Арьябхаты, другой индиец, Брахмагупта, разработал концепцию нуля как фактического независимого числа, а не просто заполнителя, и написал правила для сложения и вычитания нуля из других чисел.Индийские сочинения были переданы аль-Хорезми (от имени которого мы получили термин «алгоритм»), а затем Леонардо Фибоначчи и другим, которые продолжали развивать концепцию и число.

Различные арифметические операции, которые включают ноль, иногда были предметом споров, например, результат деления нуля на ноль. Ответ в том, что это невозможно. Хотя первые математики пытались вывести из этой операции какой-то результат, более поздние решили, что эта проблема просто не принесет никаких плодов.Это рассматривается как еще один случай, когда язык позволяет нам задать вопрос, который действительно не имеет смысла.

С другой стороны, от нуля до нулевой степени есть три возможных ответа. По некоторым очевидным причинам ответ равен 1. Но в других контекстах ответ может быть либо «неопределенным» (невозможно вычислить), либо «неопределенным / несуществующим».

Как мы обнаружили число ноль

Из всех существующих чисел в ноле есть что-то особенное.Мы можем найти реальные примеры других чисел, будь то 1 доллар, 99 красных воздушных шаров, 100 лет одиночества или что-то еще, что мы хотим свести в таблицу. Но трудно найти примеры ничто – даже предполагаемый космический вакуум нарушается слабыми порывами атомов водорода.

Возможно, поэтому ноль – изобретение сравнительно недавнее. Хотя оно появлялось в разных формах в разных местах, понятие «ничто» как число существует не более чем несколько тысяч лет назад. А иногда кажется, что его вообще не существовало.И египтяне, и римляне, похоже, не использовали ноль.

Тем не менее, сегодня для нас очень важно ноль. Эта концепция играет фундаментальную роль в исчислении, поскольку мы вычисляем производные, сходящиеся к нулю. Он также используется в системах координат на графиках, которые начинаются в точке (0, 0).

Древние цивилизации нашли применение и в нуле, сначала как компонент числовых систем, а затем как математический инструмент. Считается, что шумеры первыми осознали идею «ничто» (хотя только позже они придумали символ для нуля).Точно так же майя независимо развили идею нуля. Позже концепция небытия распространилась с Ближнего Востока в Индию, Китай и другие страны.

Европейские цивилизации довольно поздно подошли к игре в ничто, включив ноль в свои культуры только после того, как математик Фибоначчи принес индо-арабскую систему счисления в Европу после путешествий по Ближнему Востоку и Африке. Там, как и везде, ноль окажется революционной концепцией, вдохновляющей мыслителей Средневековья и Возрождения на фундаментальные идеи о математике и мире.

Считая до нуля

Обнаружение нуля, похоже, произошло не сразу, а скорее поэтапно. Ученые считают, что это началось с концепции «ничто» в качестве заполнителя при подсчете. Вот как вавилоняне использовали нули около 4000 лет назад. При подсчете они разделили свои числа на столбцы, как мы это делаем сегодня, – концепция, называемая позиционной нотацией. Для нас у числа 115 есть три столбца с разрядами – единицы, десятки и сотни. Пять в столбце единиц, один в столбце десятков и один в столбце сотен.Чтобы написать, скажем, 105, нам нужно показать, что в столбце десятков нет ничего, что-то было выполнено с нулем сегодня.

Хотя вавилоняне использовали другую систему счисления, чем мы, они считали почти так же, используя позиционную систему счисления. Когда им нужно было показать, что в колонне ничего нет, вавилоняне пришли к идее просто оставить там место – ничего в прямом смысле слова. Это наш первый реальный пример признания концепции «ничто».

Вавилонские клинописи.(Предоставлено: Josell7 / CC BY-SA 4.0 / Wikimedia Commons)

Более 1000 лет спустя, при Империи Селевкидов, вавилоняне, похоже, начали использовать глифы в форме клиньев вместо пробелов – одни из первых графических представлений нуля. . Но даже в этом случае вавилоняне, похоже, не расширили свою концепцию нуля, чтобы включить его в качестве действительного числа. Например, каменная табличка с математическими суммами включает вычисление «20–20», но оставляет пустой ответ – неопределенную сумму.

Майя применяли ноль почти таким же образом. При написании дат им требовалось, чтобы в столбцах при необходимости ставили ноль. Например, дата, которая соответствует началу того, что они считали нынешней эрой мира, была записана 13.0.0.0.0 в нотации майя и соответствовала 3114 году до нашей эры. Поскольку майя не контактировали с Евразией долгое время после того, как эти символы были написаны, ясно, что майя изобрели концепцию нуля независимо.

Числа майя.(Предоставлено:! Оригинал: Neuromancer2K4, вектор: Брайан Дерксен / CC BY-SA 3.0 / Wikimedia Commons)

Майя, похоже, использовали несколько разных символов для нуля, хотя оболочка была наиболее распространенной. Глиф оболочки также, кажется, использовался для обозначения концепции ничего более общего. Переведенный стих в тексте майя, оплакивающий павшего лидера, частично гласит: «Ни пирамиды, ни жертвенника, ни земли / пещеры». Тот же символ оболочки, который обозначает ноль в их системе счисления, появляется здесь в более абстрактном смысле и ничего не означает.

Ноль в движении

Из Вавилона ноль начал медленно распространяться в другие регионы мира. Он появляется в Греции примерно в четвертом веке до нашей эры, вероятно, принесен Александром Македонским после того, как он завоевал Вавилонскую империю в 331 году до нашей эры. Здесь мы начинаем видеть следы современного овала, который мы сегодня используем для обозначения нуля. Греческие астрономы, такие как Птолемей, использовали полый круг при вычислении тригонометрических фигур, часто добавляя черту или линию сверху. Это, как утверждает Роберт Каплан в своей книге «Ничто из сущего: естественная история нуля», указывает на то, что они, вероятно, думали о нуле как о чем-то более близком к знаку препинания между действительными числами, чем о числе как таковом.

Чтобы по-настоящему оценить место нуля в числовой прямой, мы должны отправиться в Индию. Там исследователи видят первое твердое доказательство того, что ноль, который индейцы называют «сунья», используется в математических расчетах. Это знак того, что математики считали ноль уникальной числовой единицей. Вероятно, первым, кто совершил этот логический скачок, был человек по имени Брахмагупта, основоположник индийской математики. В своем математическом трактате Brahmasphutasiddhanta, написанном в 628 году нашей эры, Брахмагупта дает правила для выполнения вычислений с нулем, которые отражают то, что мы понимаем сегодня.

«Когда к числу прибавляется ноль или вычитается из числа, число остается неизменным; и число, умноженное на ноль, становится нулем », – пишет он.

Это представляет собой глубокий логический скачок, – утверждает нейробиолог Андреас Нидер в статье 2016 года.

«Для мозга, который эволюционировал для обработки сенсорных стимулов (чего-то), представление пустых множеств (ничего) как значимой категории требует абстракции высокого уровня. Это требует способности представлять концепцию, выходящую за рамки того, что воспринимается », – пишет он.

Кхмерские цифры из самборских надписей, датируемых 683 годом нашей эры, найденные на территории современной Камбоджи. Некоторые говорят, что эта система счисления включает в себя самое раннее использование нуля. (Кредит: Paxse / CC BY-SA 3.0 / Wikimedia Commons)

Истинное происхождение нуля все еще является предметом споров среди историков и математиков. Например, цифра ноль могла появиться на территории нынешней Камбоджи даже раньше, чем в Индии, утверждает Амир Акзель. Математик предпринял долгие годы поисков истоков нуля и в итоге оказался в сарае недалеко от древнего города Ангкор-Ват.Там, на табличке, датируемой седьмым веком нашей эры, есть то, что, по его мнению, является первым настоящим нулем. Как он пишет в своей книге «В поисках нуля: одиссея математика по раскрытию происхождения чисел», это переместит первый истинный ноль из Индии в Камбоджу и отодвинет нашу временную шкалу числа примерно на 200 лет.

Где бы он ни был впервые обнаружен, наш нынешний ноль – тот, который мы пишем полым овалом – не попадал в западный мир до 13 века. Именно тогда Фибоначчи, наиболее известный сегодня благодаря одноименному набору чисел, познакомил Европу с индо-арабским нулем в своем тексте Liber Abaci.Книга, опубликованная в 1202 году, принесла на континент нашу современную систему счисления, включая ее основополагающий ноль. Числа прижились, и математики перенесли ноль в эпоху Возрождения и далее.

В Европе, как и везде, где был открыт или введен ноль, похоже, что это число никогда не выходило из моды. Когда ничего не появляется, оно остается.

Нулевой фактор – ChiliMath

Я могу понять, почему многим из нас трудно принять тот факт, что значение нулевого факториала равно единице.Это звучит как абсурдное заявление о том, что это никак не может быть правдой. У нас есть общее восприятие нуля как дурной славы, потому что в нем есть что-то такое, что может заставить любое число, связанное с ним, исчезнуть или вести себя неправильно.

Например, большое число, такое как 1000, умноженное на ноль, становится равным нулю. Он исчезает! С другой стороны, хорошее число, такое как 5, деленное на ноль, становится неопределенным. Это плохо себя ведет. Так что можно скептически относиться к тому, почему ноль «внезапно» становится единицей, хорошим числом, после обработки его с помощью какой-либо специальной операции.

Есть и другие способы показать, почему утверждение верно. Для этого мы будем использовать определение самого факториала. Честно говоря, с помощью этого метода обоснование простое и требует небольшой математики.

---

Простое «доказательство», почему нулевой факторный коэффициент равен единице

Пусть n будет целым числом, где n! определяется как произведение всех целых чисел меньше n, включая само n.

Это означает, что сначала вы начинаете записывать целое число n, а затем вести обратный отсчет, пока не дойдете до целого числа 1.

Общая формула факториала может быть записана в полностью развернутой форме как

или в частично развернутом виде как

Мы знаем с абсолютной уверенностью, что 1! = 1 , где n = 1. Если мы подставим это значение n во вторую формулу, которая является частично развернутой формой n !, мы получим следующее:

Чтобы уравнение было истинным, мы должны заставить значение нулевого факториала равняться 1 и никакому другому.