Добротность колебательного контура. Как измерить добротность в радиолюбительских условиях.
«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы, который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания» – авторитетно учит нас Википедия.
Да уж. Напустили тумана ироды – без поллитры не разберёшься. А ведь придётся, раз впряглись.
Для начала возьмём ёжика. Хорошее животное! Хотя выдающимся умом не обладает, но думаю, что и оно в курсе, что
“quality factor” – это показатель качества колебательного контура и в первую очередь, конструктивного качества катушки индуктивности.
Теперь возьмём женщину в теле – добротную женщину. Таких женщин рисовали художники 18-го, 19-го веков, а поэты писали: «Её
выпуклости меня восхищают, её впуклости сводят с ума».
Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный
конденсатор с низким током утечки, и катушку индуктивности – крепкую, добротную и красивую, словно выпавшую из картины
венецианского мастера в Пушкинском музее.
Приведём эквивалентную схему колебательного контура.
Здесь L и C – собственные индуктивность и ёмкость компонентов, входящих в состав колебательного
контура,
rL – сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,
Rш – сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности,
а также потерями, вызванные наличием токов утечки в конденсаторе.
Рис.1
При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.
По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо учитывать и суммировать со значением основной ёмкости С.
Теперь давайте разберёмся, что такое “скорость затухания собственных колебаний в системе” и, каким боком она связана с добротностью.
Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Конденсатор С зарядится до уровня, равного напряжению питания.
Теперь перещёлкнем переключатель в правое по схеме положение.
Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса
колебательного контура, равной fо= 1/2π√LС.
Поскольку у нас ни с какой стороны не вечный двигатель – свободные колебания затухают, причём скорость затухания зависит от потерь
в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.
Число колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в е
Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность колебательного контура, генератор сигналов в этом случае не нужен.
Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.
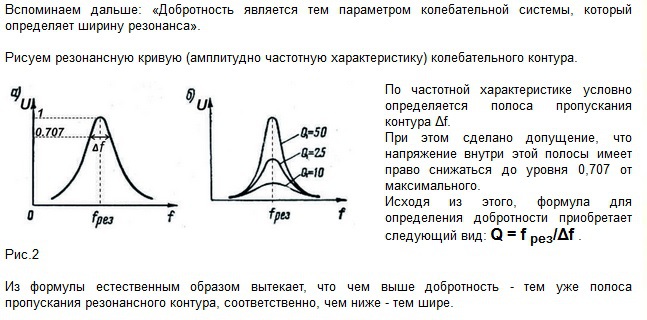
Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».
Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид:
Q = f рез/Δf .
Рис.2
Из формулы естественным образом вытекает, что чем выше добротность – тем уже полоса пропускания резонансного контура, соответственно, чем ниже – тем шире.
А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?
1. Если речь идёт о низких (звуковых) частотах, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления)
к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не
вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления
катушки.
В виду того, что конденсаторы на данных частотах практически не
вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления
катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую
манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт
добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих
существенных потерь в работу колебательного контура.
2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к
тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными
методами, как в случае НЧ обойтись не удастся.

В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с контуром.
Спаяем пару резисторов.
Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному
напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.
В нашем случае Q = 250 x V2/V1 .
Рис.3
Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню
килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать
это значение как минимум на порядок.
Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе
отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.
Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле:
Q = Q0x Rш/(Rш+Rо) , где
Q
Rш – шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
Rо – эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте,
значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.
А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.
Расчет добротности контура
⇐ ПредыдущаяСтр 8 из 10Следующая ⇒
8. По резонансным кривым, снятым экспериментально, определите частоты f1 и f2, соответствующие границам полосы пропускания контура и их разность Df = f2 – f1. Результаты измерений занесите в табл. 2.
Таблица 2
| Сопротивление контура, Ом | R1 | R2 |
| U0 РЕЗ, В | ||
| 0,7U0 РЕЗ, В | ||
| fРЕЗ,МГц | ||
| f1, МГц | ||
| f2, МГц | ||
| Df, МГц | ||
| Q1 = | ||
| E0, В | ||
| Q2 = | ||
| QСР = (Q1 + Q2)/2 | ||
| QТЕОР = Q = |
9. Вычислите значения добротности Q1 и Q2 по формулам (10) и (12) для различных значений сопротивлений контура. Результаты занесите в табл. 2.
Вычислите значения добротности Q1 и Q2 по формулам (10) и (12) для различных значений сопротивлений контура. Результаты занесите в табл. 2.
10. Определите среднее арифметическое значение добротности при различных фиксированных значениях сопротивлений контура:
QСР = (Q1 + Q2)/2.
11. Оцените относительную погрешность определения добротности по косвенным измерениям:
dQ1 = = + + ,
dQ2 = = + ,
где DfРЕЗ, Df1, Df2,DU0 РЕЗ, DE0 – ошибки в определении соответствующих значений fРЕЗ, f1, f2, U0 РЕЗ, E0.
Вычислите теоретическое значение добротности контура по формуле (9) и сравните его с результатами расчета по формулам (10) и (12). Объясните возможные причины расхождения результатов измерений и расчета.
Контрольные вопросы
1. Какие колебания называются вынужденными?
2. В чем заключается явление резонанса?
3. От чего зависит добротность контура?
4. Перечислите методы определения добротности контура.
5. Дайте определение полосы пропускания контура.
6. Чему равна частота вынуждающей э. д. с. в момент резонанса?
7. Каким образом снимается резонансная кривая в данной работе?
Список литературы
3. Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.
4. Селезнёв В.А., Тимофеев Ю.П.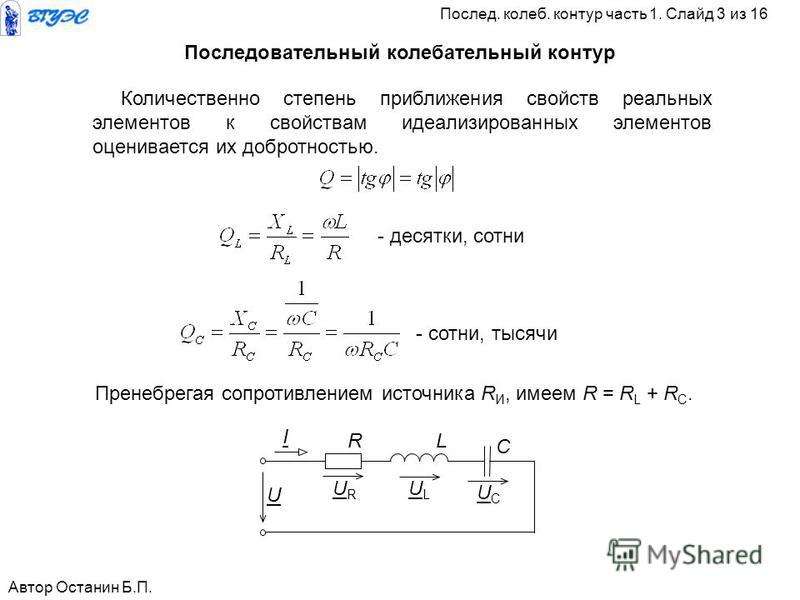 Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.
Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.
Работа 129
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ
С ПОМОЩЬЮ ОСЦИЛЛОГРАФА
Цель работы. Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.
Введение
На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор емкостью C, катушку индуктивностью L и активное сопротивление R.
Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э. д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.
Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления R = 0 при сообщении конденсатору заряда q0.
Вначале энергия электрического поля конденсатора емкостью C равна:
WC = q02/2C = CU02/2,
где U0 = q0/С – максимальнаяразность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток:
I(t) = – dq(t)/dt, (1)
где dq(t) – изменение заряда на обкладках конденсатора.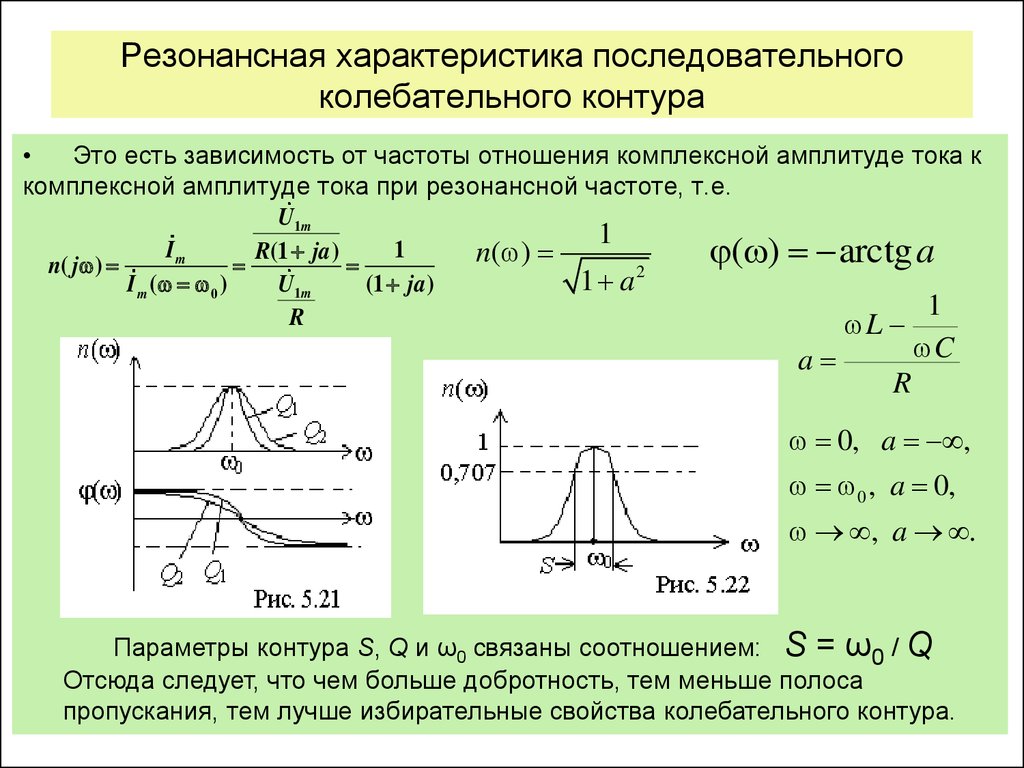 Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq < 0).
Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq < 0).
Энергия электрического поля конденсатора уменьшается, переходя в энергию магнитного поля, создаваемого током в катушке. Возрастание тока (dI > 0) в катушке индуктивностью L приводит к появлению в ней электродвижущей силы (э. д. с.) самоиндукции E(t), препятствующей изменению тока (E < 0):
E(t) = – L(dI/dt).
При полном разряде конденсатора его электрическое поле исчезает, а ток в контуре, наоборот, достигает максимального значения I0. Максимального значения достигает и энергия магнитного поля в катушке:
WL = LI02/2.
С этого момента начинается перезарядка конденсатора под действием э. д. с. самоиндукции. Ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. Энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растет, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В тот момент времени мгновенные значения электрического тока и энергии магнитного поля обращаются в нуль. Далее процесс повторяется в обратном порядке. В контуре устанавливаются незатухающие электромагнитные колебания.
д. с. самоиндукции. Ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. Энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растет, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В тот момент времени мгновенные значения электрического тока и энергии магнитного поля обращаются в нуль. Далее процесс повторяется в обратном порядке. В контуре устанавливаются незатухающие электромагнитные колебания.
Интервал времени между двумя последовательными максимальными значениями колеблющейся величины называется периодом колебаний T.
Заметим, что описанные выше колебания происходили бы бесконечно долго лишь при отсутствии испускания таким контуром электромагнитного излучения.
Если колебательный контур содержит активное сопротивление R, то при протекании по нему тока часть общей энергии контура W выделяется в виде тепла:
Q = WR = I2Rt.
При этом уменьшаются с течением времени амплитудные значения тока в контуре и разности потенциалов на обкладках конденсатора. Колебания затухают.
Временная зависимость разности потенциалов на обкладках конденсатора U(t) = j1 – j2 наблюдается в данной работе на экране осциллографа. Эту зависимость можно получить теоретическим путем, используя закон Ома для участка цепи, содержащей э. д. с. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде:
IR =j1 – j2 + E = U – L(dI/dt). (2)
Преобразуем это уравнение, используя формулу (1) и соотношение q = CU. Тогда уравнение (2) примет вид:
LC(d2U/dt2) + RC(dU/dt) + U = 0. (3)
Разделив обе части уравнения (3) на LC и введя обозначения
R/2L = b, 1/LC = w02,
где w0 называется собственной циклической (круговой) частотой контура, а b – коэффициентом затухания, получим дифференциальное уравнение:
d2U/dt2 + 2b(dU/dt) + w02U = 0, (4)
решение которого дает искомую зависимость U(t).
Следует отметить, что аналогичные дифференциальные уравнения могут быть получены для различного рода механических, электромеханических и других колебательных систем, в которых отсутствуют внешние вынуждающие воздействия, а силы сопротивления при малых скоростях движения (скоростях изменения параметра системы, совершающей колебания) линейно зависят от скорости.
При этом энергия, внесенная в сиcтему извне, непрерывно уменьшается в процессе колебаний, переходя, в конечном счете, в тепловую энергию. Уравнение (4) есть линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для частного случая, когда b < w0, его решение имеет вид:
U(t) = U0e–βtcos(wt + j0), (5)
где j0 – начальная фаза колебаний; w – циклическая частота затухающих колебаний:
w = = (6)
На рис. 2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.
2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.
Выражение (5) описывает затухающий колебательный процесс (рис. 2б) с периодом колебаний
T = = . (7)
Амплитудой затухающих колебаний называют величину
A(t) = U0e–bt, (8)
где U0 – максимально возможное значение амплитуды напряжения:
U0= A(t = 0).
Вообще говоря, при b¹ 0 разность потенциалов U(t) не является строго периодической функцией времени: U(t) ¹ U(t + T). Периодом колебаний в этом случае принято считать минимальные промежутки времени между наибольшими значениями напряжения одного знака.
Как следует из формул (5) и (8), изменение амплитуды колебаний зависит от величины коэффициента затухания b. Согласно (8) коэффициент затухания есть физическая величина, обратная времени t, в течение которого амплитуда колебаний уменьшается в е раз:
Согласно (8) коэффициент затухания есть физическая величина, обратная времени t, в течение которого амплитуда колебаний уменьшается в е раз:
U0/A(t) = e при t = t= 1/b.
Таким образом, характер колебательного процесса определяется соотношениями между электрическими параметрами контура R, L и C. Так, при b = 0 в контуре устанавливаются свободные незатухающие гармонические (колеблющаяся величина изменяется со временем по закону синуса или косинуса) колебания (рис. 2а):
U(t) = U0cos(w0t + j0)
с периодом T0 = 2p/w0 = 2p (формула У.Томсона).
При критическом сопротивлении (см. формулы (6) и (7))
R = RКР = 2
b = w0, и период колебаний становится бесконечным. В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).
В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).
При R < RКР (т. е. при b < w0) в контуре реализуется затухающий колебательный процесс (рис. 2б).
При R > RКР (b > w0) циклическая частота wи период колебаний Т становятся мнимыми величинами. Это соответствует апериодическому процессу разряда конденсатора на большое активное сопротивление (рис. 2г).
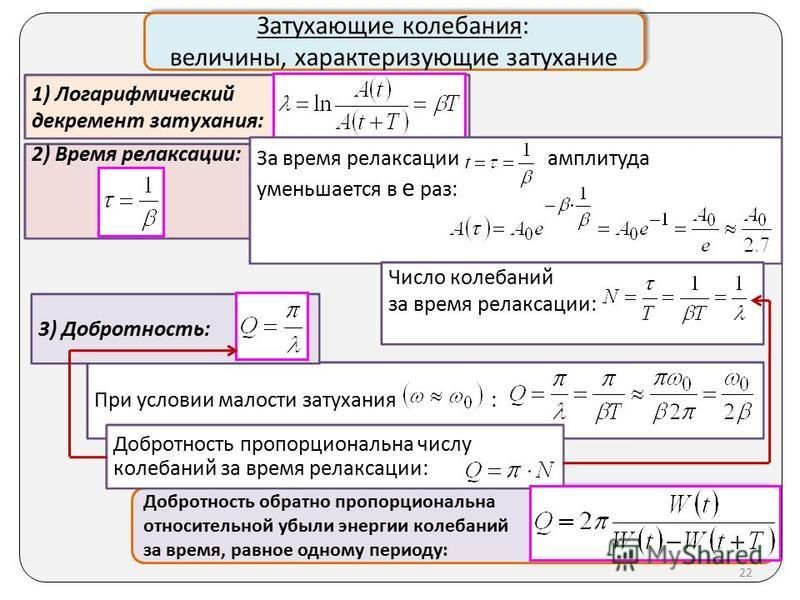
Для характеристики затухающих колебаний наряду с коэффициентом затухания b используются и другие параметры: логарифмический декремент d и добротность контура Q.
Логарифмический декремент вводится как натуральный логарифм отношения амплитуд колебаний, разделенных во времени на период Т (рис. 2):
d = ln = ln = bT = T/t = 1/N, (9)
т. е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N = t/T).
е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N = t/T).
Из соотношения между d и b
d = bT = RT/(2L) (10)
при малых затуханиях (b << w0): T » T0 = 2p можно, зная d, определить коэффициент затухания b:
b = d/T0 = d/(2p ). (11)
Добротность контура Q – важный параметр, характеризующий быстроту потери энергии, запасенной в контуре. Добротность контура показывает, во сколько раз амплитуда вынужденных колебаний напряжения на конденсаторе при резонансе превышает амплитуду внешней прикладываемой электродвижущей силы, и определяется формулой:
Q = w0/2b.
Для колебаний при малых b частота затухающих колебаний ω приблизительно равна собственной частоте колебаний w0 (см. формулу (6)) и тогда, учитывая формулу (9), величина добротности:
формулу (6)) и тогда, учитывая формулу (9), величина добротности:
Q = w0/2b ≈ w/2b = 2p/2βT = p/d. (12)
Для колебательного контура:
b = R/2L, и w0 = 1/ .
Добротность в этом случае:
Q = w0/2b = = r/R. (13)
Физическую величину r = называют волновым или характеристическим сопротивлением колебательного контура.
Из соотношения (13) следует, что контур, имеющий большое активное сопротивление, обладает малой добротностью и интенсивно теряет электромагнитную энергию, колебания быстро затухают.
Все рассмотренные процессы относятся к колебательному контуру с сосредоточенными параметрами R, L и C. В реальных колебательных контурах нельзя выделить ни одного участка цепи, не обладающего активным сопротивлением, индуктивностью и емкостью, т. е. параметры R, L и С не являются сосредоточенными, а распределены по участкам цепи, что усложняет анализ колебательных процессов. При этом также необходимо учитывать входные электрические параметры измерительных приборов.
е. параметры R, L и С не являются сосредоточенными, а распределены по участкам цепи, что усложняет анализ колебательных процессов. При этом также необходимо учитывать входные электрические параметры измерительных приборов.
⇐ Предыдущая12345678910Следующая ⇒
Поиск по сайту:
Методы измерения электрического колебательного контура
Эффект резонанса находит своё применение в решении различных технических задач. Одной из таких задач была симуляция резонанса вибростенда электрическим колебательным контуром. Подбор элементов для колебательного контура осуществляется с целью добиться резонанса на заданной частоте с заданной добротностью. Резонансная частота и добротность определяются по нижеприведённым формулам. Для подтверждения расчетной частоты резонанса или добротности требуются практические методы с использованием измерительных приборов. Преимущество виртуальной лаборатории ZETLab в том, что она содержит в себе широкий спектр программ для различных измерений, которые можно использовать для проверки теоретических расчетов.
Принципиальная схема последовательного колебательного контура
Параметры схемы, приведённой на рисунке 1, вычисляются по следующим формулам:
Резонансная частота электрического колебательного контура
Добротность электрического колебательного контура
Примечание: в формулы для расчета подставляются не паспортные данные элементов (по которым их возможно выбирали), а реальные, которые были измерены с помощью соответствующих измерительных приборов.
Теоретический расчет
R=16 Ом,
L=18 мГн,
C=1,75 мкФ
Резонансная частота
Добротность
Программа «Измерение АЧХ (8 каналов)»
График АЧХ электрического резонансного контура
Измерение добротности по графику АЧХ
По графику АЧХ колебательного контура определяем частоту резонанса курсорными измерениями: f0 = 847 Гц.
Добротность электрического колебательного контура обратно пропорциональна разности относительных частот, соответствующих значениям относительного напряжения 1/√2 (относительно резонансной частоты и резонансного напряжения):
Кроме того добротность может быть вычислена как отношение напряжения в пике резонанса к входному напряжению.
На частоте менее 10% от резонансной частоты напряжение на конденсаторе будет составлять более 99% от входного напряжения. Соответственно ошибка, которую внесёт метод вычисления добротности, составит менее 1%.
Программа «Измерение АЧХ-ФЧХ (4 канала)»
Как известно из радиотехники, полосу пропускания колебательного контура можно найти из частотных характеристик, отмечая граничные частоты, по уровню 1/v2 от максимума модуля амплитудной характеристики для последовательного колебательного контура или максимума сопротивления для параллельного контура. Можно также измерить полосу пропускания резонатора по фазово-частотной характеристике электрического импеданса как разность между частотами, соответствующими сдвигу фаз ±45° от фазы в точке резонанса. Отношение резонансной частоты к ширине полосы пропускания есть добротность колебательной системы.
Гафики измеренных АЧХ и ФЧХ
f0 = 845,3 Гц
Измерение добротности по АЧХ
АЧХ: f2=898,5 Гц ФЧХ: f2=903,3 Гц
АЧХ: f1=739 Гц ФЧХ: f1=738 Гц
Измерение добротности по ФЧХ
Модальный анализ
Измерение резонанса с помощью программы «Модальный анализ»
Затухающие колебания на выходе электрического колебательного контура
Если на вход системы подать дельта-импульс, то на выходе будет импульсная характеристика системы. Дельта-импульс эмулируется радио-импульсом высокой частоты с 0 периодов (полуволна).
Дельта-импульс эмулируется радио-импульсом высокой частоты с 0 периодов (полуволна).
Характеристики колебательного контура:
τ — время релаксации колебаний — время, в течение которого амплитуда колебаний уменьшится в e раз.
λ — логарифмический декремент затухания — логарифм отношения двух последовательных амплитуд колебаний.
Q — добротность контура — отношение энергии запасённой в контуре к убыли энергии за один период колебаний умноженное на 2π.
Взаимный узкополосный спектр, передаточная функция h2
Вычисления по взаимному узкополосному спектру:
Вычисления по переходной характеристике:
Взаимный узкополосный спектр генератора и измерительного канала
Корреляционная функция (белый шум и радиоимпульс)
Корреляционная функция сигнала генератора и выхода колебательного контура
U1=48,922 мВ·g
U2=24,297 мВ·g
U3=12,513 мВ·g
U4=6,498 мВ·g
Узкополосный спектр
Применяя те же самые формулы, что и для АЧХ находим характеристики системы:
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Проведение виброиспытаний на системе с резонансом
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Узкополосный спектр широкополосного шума с усреднением за 600 секунд
Результаты, полученные в ходе испытаний:
Формула добротности»Заметки по электронике
Коэффициент добротности или добротность является мерой производительности катушки, конденсатора, катушки индуктивности с точки зрения его потерь и полосы пропускания резонатора.
 Простые формулы могут связывать переменные.
Простые формулы могут связывать переменные. Q, учебник по фактору качества Включает:
Q, основы фактора качества
Индуктор Q
RLC-сеть Q
Коэффициент добротности или добротность катушки индуктивности или настроенной схемы часто используется для определения ее характеристик в резонаторной схеме, и он широко используется в разработке радиочастот и во многих других областях проектирования электронных схем.
Добротность, или добротность, представляет собой безразмерное число, описывающее демпфирование в цепи. Он также обеспечивает индикацию полосы пропускания резонатора относительно его центральной частоты.
Концепция коэффициента добротности Q для настроенных цепейЗначения коэффициента добротности часто указываются в кавычках и могут использоваться для определения характеристик катушки индуктивности, конденсатора или настроенной цепи.
Добротность или добротность используется во многих радиочастотных схемах или элементах, чтобы указать их характеристики в генераторе или другой форме резонансного контура.
Существует несколько простых формул, которые связывают потери и полосу пропускания с добротностью, и их можно легко использовать для определения различных аспектов соответствующей цепи.
Как появилась добротность
Концепция Q, фактора качества была впервые предложена инженером по имени К. С. Джонсон из инженерного отдела компании Western Electric Company в США.
Джонсон оценивал производительность и качество различных катушек. В ходе своих исследований он разработал концепцию Q.
Интересно, что он выбрал букву Q потому, что были взяты все остальные буквы алфавита, а не из-за термина добротность, хотя, оглядываясь назад, выбор буквы Q для добротности не мог быть лучше.
Основы добротности
Коэффициент качества — понятие, применимое во многих областях физики и техники. Он обозначается буквой Q и может называться добротностью.
Коэффициент добротности — это безразмерный параметр, показывающий потери энергии в резонансном элементе, который может быть чем угодно: механическим маятником, элементом механической конструкции или электронной схемой, такой как резонансная цепь.
Хотя добротность элемента связана с потерями, она напрямую связана с шириной полосы резонатора по отношению к его центральной частоте.
Q указывает потери энергии по отношению к количеству энергии, хранящейся в системе. Таким образом, чем выше добротность, тем меньше скорость потери энергии и, следовательно, колебания будут уменьшаться медленнее, т. е. они будут иметь низкий уровень затухания и будут звучать дольше.
В электронных схемах потери энергии в цепи вызваны сопротивлением. Хотя это может произойти в любом месте цепи, основная причина сопротивления возникает внутри катушки индуктивности.
Определение коэффициента качества
Определение коэффициента качества часто необходимо для более точного понимания того, что представляет собой эта величина на самом деле. Часто полезно иметь краткую форму слов, объясняющих, что это такое.
Коэффициент добротности, определение добротности:
Для электронных схем добротность определяется как отношение энергии, запасенной в резонаторе, к энергии, подводимой к нему за период, чтобы поддерживать постоянную амплитуду сигнала на частоте, при которой сохраняется энергия постоянна во времени.
Из этого видно, что накопленная и потерянная энергия в основном стоит за Q или цепью.
Ом также может быть определено для индуктора, где это отношение его индуктивного реактивного сопротивления к его сопротивлению на определенной частоте, и это является мерой его эффективности.
Точно так же Q также часто используется с конденсаторами, и это также важно для варакторных диодов, где потери в диоде могут иметь большое влияние на работу любого резонансного контура, управляемого напряжением, использующего диоды.
Влияние добротности
При работе с радиочастотными цепями важно учитывать добротность по многим причинам. Обычно высокий уровень добротности полезен, но в некоторых приложениях может потребоваться определенный уровень добротности.
Некоторые из соображений, связанных с добротностью в радиочастотных цепях, резюмируются ниже:
Полоса пропускания: С увеличением добротности или добротности полоса пропускания настроенного контурного фильтра уменьшается.
 По мере уменьшения потерь настроенная цепь становится более четкой, поскольку энергия лучше сохраняется в цепи.
По мере уменьшения потерь настроенная цепь становится более четкой, поскольку энергия лучше сохраняется в цепи.Видно, что по мере увеличения добротности полоса пропускания по уровню 3 дБ уменьшается, а общий отклик настроенной схемы увеличивается. Во многих случаях для обеспечения требуемой степени селективности требуется высокая добротность.
Широкая полоса пропускания: Во многих радиочастотных приложениях требуется работа с широкой полосой пропускания. Некоторым формам модуляции требуется широкая полоса пропускания, а другим приложениям требуются фиксированные фильтры для обеспечения широкополосного покрытия.
Хотя может потребоваться сильное подавление нежелательных сигналов, существуют конкурирующие требования к широкой полосе пропускания. Соответственно, во многих приложениях необходимо определить требуемый уровень добротности, чтобы обеспечить общую производительность, необходимую для удовлетворения требований широкой полосы пропускания и адекватного подавления нежелательных сигналов.

Фазовый шум генератора: Любой генератор генерирует так называемый фазовый шум. Это включает в себя случайные сдвиги в фазе сигнала. Это проявляется в виде шума, который распространяется от основной несущей.
Как и следовало ожидать, этот шум нежелателен и поэтому должен быть сведен к минимуму. Конструкция генератора может быть адаптирована для уменьшения этого несколькими способами, главным из которых является увеличение добротности схемы настроенного генератора.
- Общие паразитные сигналы: Для удаления паразитных сигналов часто используются настроенные схемы и фильтры. Чем острее фильтр и выше уровень добротности, тем лучше схема сможет удалить паразитные сигналы.
Звонок: По мере увеличения добротности резонансного контура потери уменьшаются. Это означает, что любое колебание, возникающее в цепи, будет затухать дольше. Другими словами, схема будет иметь тенденцию «звонить» больше.

Это на самом деле идеально подходит для использования в схеме генератора, поскольку его легче настроить и поддерживать генерацию, поскольку в настроенной схеме теряется меньше энергии.
Формулы добротности
Базовая формула Q или коэффициента добротности основана на потерях энергии в катушке индуктивности, цепи или другом компоненте.
Исходя из приведенного выше определения добротности, добротность может быть математически выражена в следующей формуле добротности:
Q=EStoredELost за цикл
Где:
Q = добротность контура
E накопленная = сохраненная энергия
E Потеря за цикл = энергия, потерянная за каждый цикл
Если посмотреть на полосу пропускания ВЧ-резонансного контура, это переводится в формулу добротности:
Q=F0F-3дБ
Где:
Q = добротность контура
F 0 = центральная частота настроенного контура
F -3 дБ – смещение частоты от центральной частоты, при котором отклик падает на 3 дБ.
В любой радиочастотной или другой цепи каждый отдельный компонент может вносить вклад в добротность или добротность сети цепи в целом. Добротность компонентов, таких как катушки индуктивности и конденсаторы, часто указывается как имеющая определенную добротность или добротность.
Коэффициент добротности и демпфирование
Одним из важных аспектов добротности во многих схемах является демпфирование. Коэффициент добротности Q определяет качественное поведение простых генераторов с демпфированием и влияет на другие схемы, такие как отклик в фильтрах и т. д.
Существуют три основных режима, которые можно учитывать при рассмотрении демпфирования и добротности.
С недостаточным демпфированием (Q > 1/2) : Система с недостаточным демпфированием — это система, в которой коэффициент добротности больше половины. Те системы, в которых добротность составляет чуть более половины, могут колебаться один или два раза при приложении ступенчатого импульса до того, как колебание исчезнет.
 По мере увеличения добротности затухание падает и колебания будут поддерживаться дольше.
По мере увеличения добротности затухание падает и колебания будут поддерживаться дольше.В теоретической системе, где добротность бесконечна, колебание будет поддерживаться бесконечно без необходимости добавления каких-либо дополнительных стимулов. В осцилляторах некоторый сигнал возвращается, чтобы обеспечить дополнительный стимул, но высокая добротность обычно дает гораздо более чистый результат. В сигнале присутствуют более низкие уровни фазового шума.
С избыточным демпфированием (Q < 1/2): Система с избыточным демпфированием имеет коэффициент добротности менее 1/2. В этом типе системы потери высоки, и система не имеет перерегулирования. Вместо этого система будет экспоненциально затухать, асимптотически приближаясь к установившемуся значению после подачи ступенчатого импульса.
По мере уменьшения добротности или добротности системы медленнее реагируют на ступенчатый импульс.
Критически демпфированная (Q = 1/2) : Система с критическим демпфированием имеет коэффициент добротности 0,5, и, как и система с избыточным демпфированием, выходной сигнал не колеблется и не выходит за пределы установившегося выходного сигнала.
 Система будет приближаться к стационарной асимптоте за самое короткое время без какого-либо выброса.
Система будет приближаться к стационарной асимптоте за самое короткое время без какого-либо выброса.
Во многих резонансных ВЧ системах требуются высокие уровни добротности. Для фильтров требуется достаточная избирательность, но не слишком большая, а для генераторов высокие уровни добротности приводят к улучшению стабильности и снижению фазового шума. Во многих системах коэффициент добротности не должен быть слишком высоким, так как это может привести к тому, что полоса пропускания фильтра будет слишком узкой, а генераторы не смогут отслеживать сигнал в требуемом диапазоне. Однако уровни добротности должны быть скорее высокими, чем низкими.
Добротность или добротность является ключевым аспектом резонансных и фильтрующих схем, особенно в ВЧ-проектировании. Q также может быть важным в других областях, включая общий дизайн электронных схем, а также некоторые аспекты звукового дизайна, включая громкоговорители и тому подобное.
Базовое понимание Q поможет лучше понять некоторые элементы схемотехники и работы в различных областях.
Больше основных концепций и руководств по электронике:
Напряжение
Текущий
Сила
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ-шум
Сигналы
Вернуться в меню основных понятий электроники . . .
Добротность в электротехнике и электронике
Добротность в Электротехника и электроника
В настроенной цепи соотношение между реактивным сопротивлением и сопротивлением называется добротностью … или добротностью …0009
Противоположность коэффициенту мощности называется добротностью или добротностью катушки или ее добротностью.
Коэффициент добротности = 1/ Коэффициент мощности = 1/Cosθ= Z/R … (где коэффициент мощности Cosθ = R/Z)
Если R слишком мало по отношению к реактивному сопротивлению
Тогда добротность = Z/R = ωL /R = 2πfL / R … (ωL/R = 2πf)
Кроме того, добротность может быть определена как отношение между запасенной энергией и энергией, рассеиваемой за цикл в цепи
Q = 2π x (запасенная энергия/потеря мощности)
В резонаторе Q — это отношение между накопленной в резонаторе энергией и энергией, подаваемой генератором для поддержания постоянной амплитуды сигнала.
Полезно знать * 1 :
В электрических системах и цепях накопленная энергия представляет собой сумму накопленных энергий в катушках индуктивности и конденсаторах без потерь. А потерянная энергия представляет собой сумму энергий, рассеянных в резисторах (тепло, свет и т. д.) за цикл
Принимая во внимание, что;
Конденсатор поглощает реактивную мощность и сохраняет энергию в виде электрического поля
Катушка индуктивности поглощает реактивную мощность и сохраняет энергию в виде магнитного поля
И
Резистор поглощает реальную мощность и рассеивает ее в виде тепла и света
Коэффициент добротности в чисто емкостных (C) и чисто индуктивных (L) цепях
Как мы знаем, мощность в чисто емкостных и индуктивных цепях равна нулю. Таким образом, коэффициент мощности цепи также равен нулю. Но коэффициент добротности цепи является обратным коэффициенту мощности, поэтому коэффициент добротности как в чисто емкостных, так и в индуктивных цепях бесконечен (∞).
Коэффициент добротности в последовательной цепи RL
В последовательной цепи RL полное сопротивление (Z) = индуктивное реактивное сопротивление = X L = 2πfL, поэтому добротность «Q» L /R → = 2πf r L /R
Коэффициент добротности в последовательной RC-цепи
В последовательной RC-цепи полное сопротивление (Z) = емкостное реактивное сопротивление = X Добротность «Q»
= Z/ R → = X C /R → = (1/2πf r C) /R → = 1 / 2πf r CR.
, где
z = наносимость = сопротивление в цепях переменного тока (z = x L 2 -x C 2 ω)
R = сопротивление ω
C = CAPACITANE в FARADS
99 = индуктивность в ХеннериX L = индуктивное сопротивление в Ом
X C = емкостное реактивное сопротивление в Ом
f r = резонансная частота в Гц = частота резонанса / коэффициент добротности контура
Q = F R / B
Q = F R / (F 2 – F 1 )
, где
F R = Resonance Chiteary в HERTZ
99999999999999999. разность между верхней и нижней частотами в непрерывном наборе частот = B = (f 2 – f 1 )
разность между верхней и нижней частотами в непрерывном наборе частот = B = (f 2 – f 1 )
Коэффициент добротности в последовательной цепи RLC (резонансная цепь входа напряжения)
В идеале последовательная цепь RLC (Также в настроенном радиочастотном приемнике (TRF)) Коэффициент добротности равен
Q = (1/R) x (√ (L/C) = ω 0 L/R
Из приведенного выше уравнения видно, что чем больше последовательное сопротивление, тем меньше добротность Контур, т. е. чем больше теряется энергии и тем шире полоса пропускания
Полезно знать* 2 : Высокая добротность резонансного контура имеет узкую полосу пропускания по сравнению с низкой добротностью
Добротность в a Параллельная цепь RLC (резонансная цепь тока на входе)
«Добротность» в параллельной цепи RLC является обратной величиной «добротности» в последовательной цепи RLC
Q = R x (√ (C /L) = R /ω 0 L
Где
R = сопротивление в Ом
C = емкость в фарадах
L = индуктивность в Генри
9
5 Из приведенного выше уравнения видно, что чем ниже сопротивление, тем больше добротность цепи, т.
 е. меньше потерь энергии и более узкая полоса пропускания, и было бы полезно определить полосу пропускания в схемах проектирования фильтров. Цепь со сложным импедансом
е. меньше потерь энергии и более узкая полоса пропускания, и было бы полезно определить полосу пропускания в схемах проектирования фильтров. Цепь со сложным импедансом Как мы обсуждали выше, «В настроенной цепи соотношение между реактивным сопротивлением и сопротивлением называется добротностью или добротностью… Или
Противоположность коэффициенту мощности называется добротностью или добротностью катушки.
Коэффициент добротности = 1/ Коэффициент мощности=1/Cosθ= Z/R … (где коэффициент мощности Cosθ = R/Z)”
Эти для; мы также можем определить коэффициент добротности цепи со сложным импедансом, если мы знаем коэффициент мощности цепи, где
коэффициент мощности = Cosθ = R/Z … или…
Тангенс фазового угла (θ) между током и напряжением.
Полезно знать * 3 :
Высокая добротность резонансного контура имеет узкую полосу пропускания по сравнению с низкой добротностью
Низкая добротность дает широкую полосу пропускания (широкая полоса пропускания)
A высокая добротность дает узкую полосу (маленькая полоса пропускания )
Показать полную статью
Связанные статьи
Q
Q Такие слова, как «качество», подразумевают «хорошесть» и
может ввести в заблуждение при использовании в технических контекстах. Коэффициент качества, Q,
Резонансная система считается высокой, если система теряет мало энергии за
времени по сравнению с энергией системы. Качели, которые качают сотни
раз после одиночного толчка будет “высокая Q” по сравнению с замахом
комплект, который останавливается после нескольких качаний из-за чрезмерного трения в подшипниках.
Катушки индуктивности и конденсаторы с малыми потерями создают схемы с высокой добротностью.
как и пружинно-массовые механические системы с низким коэффициентом трения, и такие компоненты
в целом качественно. Но не всегда хорошо иметь высокий Q. Далее
когда ваш автомобиль попадает в выбоину, поблагодарите свои амортизаторы за то, что они дали вашему автомобилю
подвеска ужасно низкая добротность. Настроенные цепи в вашем радио должны иметь только
нужное количество Q, не слишком много и не слишком мало. Слишком много Q и некоторые
пропущен спектр модуляции; слишком мало и другие сигналы или чрезмерно
шум получает
через. Хотя высокая добротность не всегда желательна, обычно это действительно так.
Коэффициент качества, Q,
Резонансная система считается высокой, если система теряет мало энергии за
времени по сравнению с энергией системы. Качели, которые качают сотни
раз после одиночного толчка будет “высокая Q” по сравнению с замахом
комплект, который останавливается после нескольких качаний из-за чрезмерного трения в подшипниках.
Катушки индуктивности и конденсаторы с малыми потерями создают схемы с высокой добротностью.
как и пружинно-массовые механические системы с низким коэффициентом трения, и такие компоненты
в целом качественно. Но не всегда хорошо иметь высокий Q. Далее
когда ваш автомобиль попадает в выбоину, поблагодарите свои амортизаторы за то, что они дали вашему автомобилю
подвеска ужасно низкая добротность. Настроенные цепи в вашем радио должны иметь только
нужное количество Q, не слишком много и не слишком мало. Слишком много Q и некоторые
пропущен спектр модуляции; слишком мало и другие сигналы или чрезмерно
шум получает
через. Хотя высокая добротность не всегда желательна, обычно это действительно так.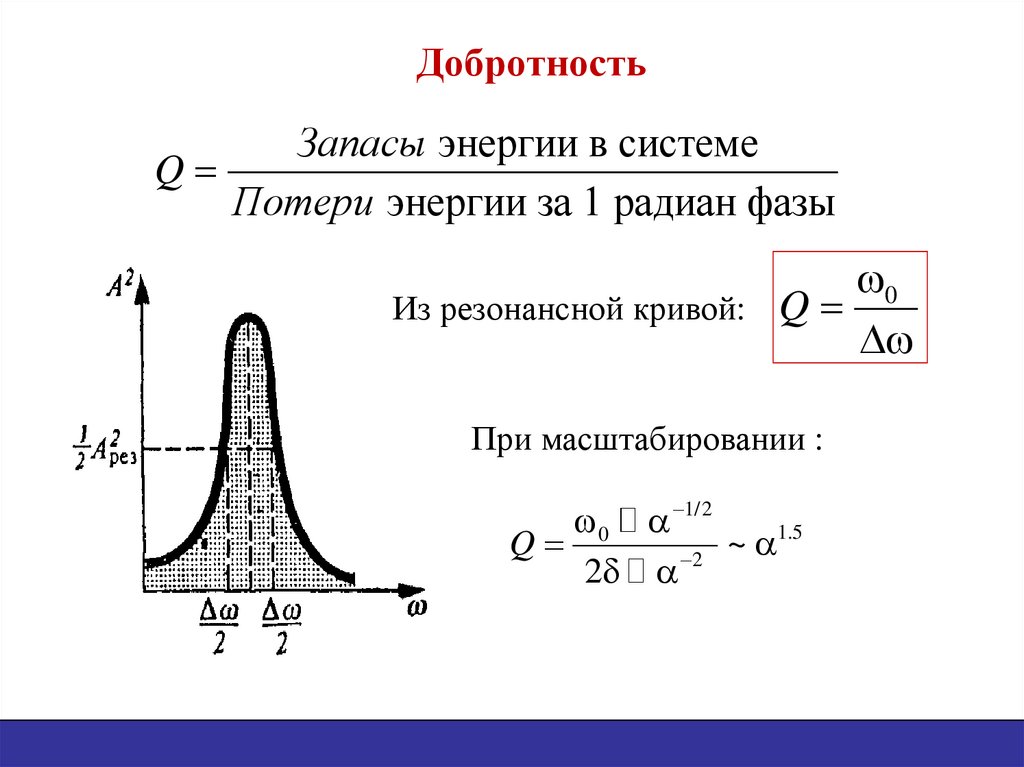 лучше всего иметь компоненты с высокой добротностью, такие как катушки индуктивности и конденсаторы или пружины, и
подшипники, которые преднамеренно демпфируются резисторами, приборными панелями или другими устройствами с потерями, чтобы
дизайнер сохраняет хороший контроль над значением Q.
лучше всего иметь компоненты с высокой добротностью, такие как катушки индуктивности и конденсаторы или пружины, и
подшипники, которые преднамеренно демпфируются резисторами, приборными панелями или другими устройствами с потерями, чтобы
дизайнер сохраняет хороший контроль над значением Q.
Простым определением Q может быть отношение полной энергии в системе к энергии, теряемой за цикл. Теперь это разумное и легко запоминающееся определение, но это произвольное определение, которое мы можем «возиться с», и есть изменение, которое упрощает математику. Давайте дать определение отношения полной энергии в системе к потерянной энергии на радиан. Какая? Зачем использовать часть цикла? Ну, есть 2 пи радиана за цикл и при использовании радианов из множества полезных значений Q выпадает несколько 2 пи. уравнения. Это делает Q примерно в 6 раз выше, чем это было бы с наше первоначальное более простое определение. Есть два эквивалентных способа сказать это:
Q = (2 pi) (общая запасенная энергия) / (потеря энергии за цикл)
Q = (общая накопленная энергия) / (потеря энергии на радиан)
Если вы чувствуете, что скоро забудете о 2 пи
лет, просто постарайтесь запомнить, что «циклы в секунду» или «Гц» обычно не используются в
эти типы вычислений, потому что радианы более удобны с математической точки зрения. Всякий раз, когда в формулах, включающих импедансы, появляются «частота» или «циклы», старайтесь мыслить последовательно.
“радианы”.
Всякий раз, когда в формулах, включающих импедансы, появляются «частота» или «циклы», старайтесь мыслить последовательно.
“радианы”.
Представьте себе “параллельную” настроенную схему, в которой катушка индуктивности, конденсатор и резистор соединены параллельно. Сначала рассмотрим числитель, полная накопленная энергия. Можно написать уравнение для мгновенная энергия в конденсаторе как функция синусоидального напряжения и в индукторе как функция синусоидального тока; квадрат каждого и добавить чтобы получить итог. Или можно сократить путь! В какой-то момент вся энергия будет в конденсаторе (когда напряжение находится на пике). Энергия в конденсатор «половина C V в квадрате»:
ш = (С х В 2 ) / 2
, где V — пиковое напряжение.
В уравнении Q знаменатель представляет собой энергию, потерянную в резисторе в течение одного
радиан, который представляет собой ватты (джоули в секунду), деленные на частоту в радианах. (Если вы теряете мощность X в секунду, вы теряете частоту X/радиан за одну секунду.
время в радианах.) Мощность, теряемая в резисторе, равна квадрату среднеквадратичного напряжения.
деленное на сопротивление («v-квадрат на R»). Ну и среднеквадратичное напряжение
в 0,707 раз больше пикового напряжения для синусоиды, и когда вы возведете 0,707 в квадрат, вы
получите 0,5, что дает «0,5 В в квадрате на R», где V — пиковое напряжение. К
получаем мощность, потерянную на радиан, мы делим на w (радиан
частота).
(Если вы теряете мощность X в секунду, вы теряете частоту X/радиан за одну секунду.
время в радианах.) Мощность, теряемая в резисторе, равна квадрату среднеквадратичного напряжения.
деленное на сопротивление («v-квадрат на R»). Ну и среднеквадратичное напряжение
в 0,707 раз больше пикового напряжения для синусоиды, и когда вы возведете 0,707 в квадрат, вы
получите 0,5, что дает «0,5 В в квадрате на R», где V — пиковое напряжение. К
получаем мощность, потерянную на радиан, мы делим на w (радиан
частота).
Уравнение Q принимает вид:
(CV 2 ) / 2 (0,5) V 2 / wR p = wR p C
Q = wR p C
Посмотрите, как аккуратно стало!
Используя формулу резонанса, w = 1 / (LC) 1/2 , легко показать, что:
Q = R p (C/L) 1/2 = R p / X c = Р p / X l
Q = R p / wL
, где X — реактивное сопротивление катушки индуктивности или конденсатора (они
равны по величине при
резонанс). Небольшой нижний индекс “p” напоминает нам, что это
параллельное сопротивление.
Небольшой нижний индекс “p” напоминает нам, что это
параллельное сопротивление.
Аналогичное упражнение можно выполнить для случая последовательно настроенной схемы. но не должно быть большим сюрпризом увидеть эти результаты:
Q = wL / R с
Q = 1/R s (L/C) 1/2 = X c / R s = X l / R s
Q = X / R s
Для конденсатора с последовательным сопротивлением:
Q = 1/ wCR с
В параллельном баке большой шунтирующий резистор дает высокую добротность, а в
последовательный бак низкий последовательный резистор дает высокую добротность (обратите внимание на R в числителе в
в одном и знаменателе в другом). В параллельном баке с низким реактивным сопротивлением «замыкает».
вне» резистор, делающий добротность высокой, а в последовательном баке высокое реактивное сопротивление
делает небольшой последовательный резистор несущественным (обратите внимание на C/L в одном и L/C в
Другой).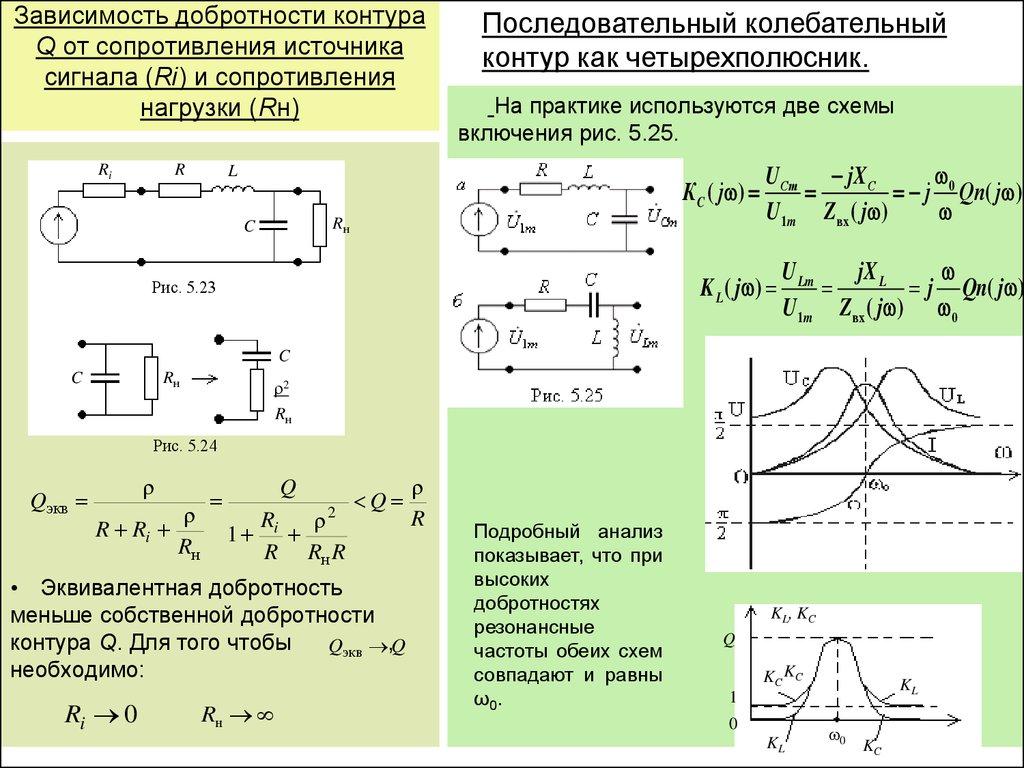

 По мере уменьшения потерь настроенная цепь становится более четкой, поскольку энергия лучше сохраняется в цепи.
По мере уменьшения потерь настроенная цепь становится более четкой, поскольку энергия лучше сохраняется в цепи.

 По мере увеличения добротности затухание падает и колебания будут поддерживаться дольше.
По мере увеличения добротности затухание падает и колебания будут поддерживаться дольше. Система будет приближаться к стационарной асимптоте за самое короткое время без какого-либо выброса.
Система будет приближаться к стационарной асимптоте за самое короткое время без какого-либо выброса.