Правило Лопиталя
Производные позволяют не только исследовать функции на возрастание, убывание или выпуклость. Ещё с их помощью можно находить пределы, раскрывая неопределенности.
20.1Раскрытие неопределенности 0/0
Правило Лопиталя позволяет раскрывать неопределенности с помощью дифференцирования. Существует много разных версий этого правила — для начала, я сформулирую ту, которую проще доказывать.
Теорема 1. (Правило Лопиталя для неопределенности 0/0 в конечной точке). Пусть функции f и g определены на интервале (a,b),
limx→a+f(x)=0,limx→a+g(x)=0,
существуют производные f′(x) и g′(x) для всех x∈(a,b), g′(x) не обращается в ноль на (a,b), и существует предел
limx→a+f′(x)g′(x)=:L.
Тогда существует предел
limx→a+f(x)g(x),
и он равен L.
Иными словами, теорема 1 позволяет раскрывать
неопределенность 0/0 путём дифференцирования числителя и знаменателя дроби.
20.1.1Теорема Коши
Для доказательства теоремы 1 нам понадобится вспомогательное утверждение, известное как теоремы Коши.
Теорема 2. (Коши). Пусть функции f и g непрерывны на отрезке [a,b] и дифференцируемы на интервале (a,b). Пусть g′(x)≠0 при всех x∈(a,b). Тогда существует такая точка c∈(a,b), что
f(a)−f(b)g(a)−g(b)=f′(c)g′(c)
H(x)=f(x)−f(a)−f(b)g(a)−g(b)(g(x)−g(b)).
Это похоже на то, как мы доказывали теорему Лагранжа, только вместо линейной функции вычитаем функцию g(x) с подходящим коэффициентом. Заметим, что
H(a)=f(b)=H(b).
Применим к H теорему Ролля.
Существует такая точка c∈(a,b), что
H′(c)=0. Запишем производную H:
H′(x)=f′(x)=f(a)−f(b)g(a)−g(b)g′(x).
Следовательно
0=H′(c)=f′(c)−f(a)−f(b)g(a)−g(b)g′(c).
Вопрос 1. А почему при определении функции H можно делить на (g(a)−g(b)), почему эта штука не обращается в ноль?
Узнать ответ
Верный ответ. Если бы она обращалась в ноль, то g(a) было бы равно g(b) и функция g удовлетворяла бы условиям теоремы Ролля, а значит нашлась бы точка на интервале (a,b), в которой производная g обнуляется. А это ей запрещено условием нашей теоремы.
20.1.2Доказательство правила Лопиталя
Доказательство теоремы 1. До- или переопределяя функции f и g в точке a, можно считать, что
f(a)=g(a)=0.
limx→a+f(x)g(x)=limx→a+f(x)−f(a)g(x)−g(a)=…
Применим теорему Коши к отрезку [a,x]. Существует такая точка c(x)∈(a,x), что дробь под знаком предела равна f′(c(x))/g′(c(x)). (Теорема Коши для фиксированного отрезка даёт фиксированную точку c, а в нашем случае для каждого x свой отрезок, поэтому точка c зависит от x.)
Можно продолжить равенство:
…=limx→a+f′(c(x))g′(c(x))=…
Заметим, что c(x)→a+ при x→a+ и c(x)≠a, поскольку c(x)∈(a,x) (по теореме о двух милиционерах). Значит, можно использовать теорему о пределе сложной функции (см. упражнение 2 в лекции 13). Имеем:
…=limc→a+f′(c)g′(c)=L.
∎
20.2Другие версии и примеры
Конечно, можно доказать утверждение, аналогичное теореме 1 с
пределом слева, а также с двусторонним пределом (в этом случае требуется, что
f и g были дифференцируемы в проколотой окрестности точки a).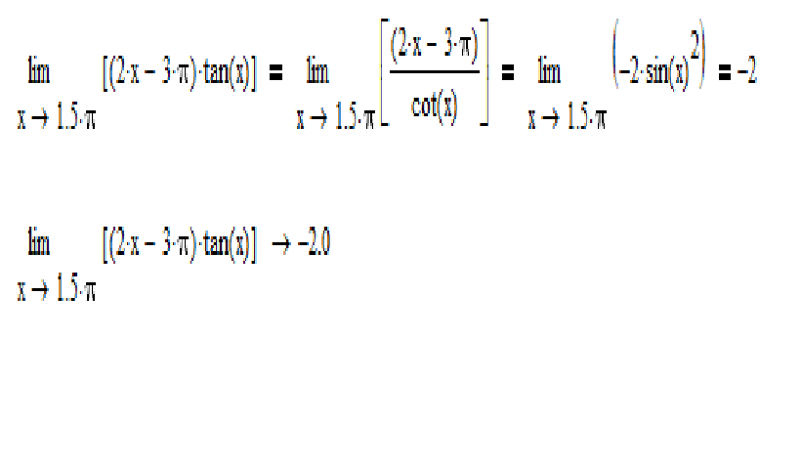
Доказательства полностью аналогичны.
20.2.1Предел в бесконечности
Теорема 3. Пусть функции f и g определены на луче (a,+∞),
limx→+∞f(x)=0,limx→+∞g(x)=0,
существуют производные f′(x) и g′(x) для всех x∈(a,+∞), g′(x) не обращается в ноль на (a,+∞) и существует предел
limx→+∞f′(x)g′(x)=:L.
Тогда существует предел
limx→+∞f(x)g(x).
и он равен L.
Доказательство. Пусть t=1/x. Тогда при x→+∞, t→0+. По теореме о пределе сложной функции (похожая была в домашнем задании),
limx→+∞f(x)g(x)=limt→0+f(1/t)g(1/t)=…(20.1)
Рассмотрим функции
~f(t):=f(1/t),~g(t):=g(1/t).
Равенство (20.1) можно продолжить:
limt→0+~f(t)~g(t)=…
Применим теорему 1 к получившемуся пределу и интервалу
(0,1/a) (можно считать, что a>0).
Для вычисления производных f(1/t) и
g(1/t) применим теорему о производной сложной функции.
…=limt→0+~f′(t)~g′(t)=limt→0+f′(1/t)⋅(−1t2)g′(1/t)⋅(−1t2)=limt→0+f′(1/t)g′(1/t=…
…=limt→0+~f′(t)~g′(t)==limt→0+f′(1/t)⋅(−1t2)g′(1/t)⋅(−1t2)==limt→0+f′(1/t)g′(1/t=…
…=limx→+∞f′(x)g′(x).
∎
Аналогично можно разобрать случай x→−∞ и x→∞.
20.2.2Примеры раскрытия неопределенности 0/0
Пример 1. Найдём предел
limx→0sinxx+x2.
Перед нами неопределенность 0/0, производная знаменателя не обнуляется вблизи нуля, продифференцируем числитель и знаменатель. Имеем:
limx→0cosx1+2x.
Теперь неопределенности нет, этот предел существует и равен 1 (в силу
непрерывности косинуса и теоремы о пределе частного).
Пример 2. Найдём предел
limx→01−cosxsin(x2).(20.2)
Снова неопределенность 0/0. Производная знаменателя не обнуляется вблизи нуля. Продифференцируем числитель и знаменатель.
limx→0sinx2xcosx2.(20.3)
Снова получили неопределенность 0/0. Можно попробовать к новому пределу также применить правило Лопиталя.
limx→0cosx2cosx2+4x2sinx2.
Теперь неопределенности нет, и в силу непрерывности косинуса и синуса и арифметики пределов, предел равен 1/2. Значит, правило Лопиталя применимо для вычисления предела (20.3), он существует и равен 1/2. Значмт, правило Лопиталя применимо для вычисления предела (20.2), он существует и равен 1/2.
Пример 3. Найдём предел
limx→0sinxx.
В принципе, можно было бы формально применить правило Лопиталя и получить
верный ответ, но тут возникает логическая ошибка.
Дело в том, что это первый
замечательный предел. При доказательстве дифференцируемости синуса и
вычислении его производной мы воспользовались тем, что этот предел
существует и равен 1. (Это мы доказывали на семинарах из геометрических
соображений.) Чтобы воспользоваться правилом Лопиталя сейчас, нам нужно
продифференцировать синус, но сделать мы это можем только если уже как-то
доказали, что данный предел равен 1.
20.2.3Раскрытие неопределенности ∞/∞
Вместо условия, что f и g одновременно стремятся к нулю, можно использовать условие, что они одновременно стремятся к бесконечности. Доказательство этого утверждения довольно громоздкое, и мы его приводить не будем, а вот пример разберём.
Пример 4. Найдём предел
limx→+∞lnx√x.
Это неопределенность вида ∞/∞, производная знаменателя не обращается в ноль. Попробуем продифференцировать числитель и знаменатель. Имеем:
limx→+∞1/x1/(2√x)=limx→+∞2√x=0.
Предел существует и равен нулю, значит, правило Лопиталя применимо, исходный предел также существует и равен нулю.
20.3Заключение
Правило Лопиталя часто (хотя и не всегда) позволяет раскрывать неопределенности вида 0/0 или ∞/∞ без особых раздумий — если после первого дифференцирования снова получили неопределенность, не беда — можно продифференцировать ещё раз, и так пока не получим какой-нибудь конкретный предел. (Главное не забывать проверить, что условия соответствующих теорем применимы.) Студенты его очень любят. А я нет. Потому что на практике вместо правило Лопиталя быстрее использовать другую штуку — разложение функций в ряд Тейлора. Об этом мы поговорим в следующий раз.
← Предыдущая глава Следующая глава →
Математический анализ. Дифференциальное исчисление
Математический анализ. Дифференциальное исчисление
ОглавлениеПРЕДИСЛОВИЕГЛАВА 1. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ 2. Определение непрерывности функции в точке «на языке приращений». § 2. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ 2. Связь между непрерывностью и дифференцируемостью функции в точке. 3. Производная и дифференциал. 4. Односторонние и бесконечные производные. § 3. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧ 2.  Геометрические приложения производной.3. Применения производной в физических задачах. Механический смысл производной. § 4. ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАЦИЙ 2. Дифференцирование произведения. 3. Дифференцирование частного. § 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ 2. Инвариантность формы записи дифференциала. § 6. ДИФФЕРЕНЦИРОВАНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Дифференцирование обратной функции. 3. Дифференцирование обратных тригонометрических функций. 4. Дифференцирование показательной и логарифмической функций. 5. Дифференцирование гиперболических функций. 6. Сводка правил и формул дифференцирования. 7. Логарифмическое дифференцирование. § 7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. Механический смысл второй производной. 3. Натуральная степень бинома (формула Ньютона). 4. Свойства производной n-го порядка. 5. Дифференциалы высшего порядка. ГЛАВА 2. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 1. СВЯЗЬ МЕЖДУ ХОДОМ ИЗМЕНЕНИЯ ФУНКЦИИ И ЕЕ ПРОИЗВОДНОЙ 2.  Экстремумы функции.§ 2. ТЕОРЕМА ЛАГРАНЖА И ЕЕ СЛЕДСТВИЯ 2. Теорема 2 (теорема Ролля). 3. Теорема Лагранжа. 4. Условие постоянства функции. § 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ 2. Исследование функций на экстремум с помощью первой производной. 3. Использование второй производной для исследования функций на экстремум. 4. Нахождение наибольшего и наименьшего значений функции на данном отрезке. § 4. ВЫПУКЛЫЕ ФУНКЦИИ 2. Достаточные условия выпуклости. 3. Точки перегиба. § 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ И РЕШЕНИЮ УРАВНЕНИЙ 2. Приближенное решение уравнений. § 6. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ФУНКЦИЙ 2. Правило Лопиталя. § 7. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ § 8. КРИВЫЕ НА ПЛОСКОСТИ 2. Жордановы кривые. 3. Связь между различными видами уравнений линий. 4. Дифференцирование параметрически заданных функций. 5. Полярное уравнение кривой. 6. Производная второго порядка для параметрически заданной функции.  7. Построение кривых, заданных параметрическими уравнениями. 8. Построение кривых, заданных полярными уравнениями. ОТВЕТЫ |
Я., Куницкая Е.С., Мордкович А.Г. Математический анализ. Дифференциальное исчисление. М.: Просвещение, 1978. — 161 с.
– Доказательство правила L’Hospitals
Это ответ на запрос Долдрамса, но слишком длинный для комментария.
Теорема:
Если производная функции $\hspace{.04 in}f$ всюду неотрицательна, то $\hspace{.04 in}f$ не убывает.
$\implies$
Если $\hspace{.04 in}f$ дифференцируемо и $\:\hspace{.04 in}f'(x) = 0\:$ для всех $\;\; x\: \in \: (a,b) \;\;$, $\;\;$, то $\hspace{.04 in}f$ является константой.
Доказательство:
Предположим, что $\hspace{.04 in}f$ дифференцируемо и $\:\hspace{.04 in}f'(x) = 0\:$ для всех $\:\: x\: \in \: ( а, б) \;\;$.
Пусть $\;\; g \: : \: (a,b) \to \mathbb{R} \;\;$ определяется выражением $\: g(x) = -(\hspace{0,05 in}f(x)) \; $.
Для всех $\:\: x\: \in \: (a,b) \:\:$,
$g'(x) \: = \: (g(x))’ \: = \: (-(\hspace{.
05 in}f(x)))’ \: = \: -((\ hspace{0,05 дюйма}f(x))’) \: = \: -(\hspace{0,05 дюйма}f'(x)) = -0 = 0 \;\;\;$.
Для всех элементов $x$ и $y$ из $(a,b)$, $\;\;$[$\;\; \hspace{.04 in}f(x) \leq \hspace{.04 in}f(y) \: \text{ и } \: g(x) \leq g(y)$
$\ подразумевает \;\;\hspace{0,04 дюйма}f(x) \leq \hspace{0,04 дюйма}f(y) \: \text{ и } \: -\hspace{-0,04 дюйма}( \hspace{0,05 дюйма}f(x)) = g(x) \leq g(\hspace{0,03 дюйма}y) = -(\hspace{0,05 дюйма}f(\hspace{0,03 дюйма}y ))$
$\подразумевает \;\; \hspace{0,04 дюйма}f(x) \leq \hspace{0,04 дюйма}f(\hspace{0,03 дюйма}y) \: \text{ и } \: \hspace{0,04 дюйма}f(\ hspace{.03 in}y) \leq \hspace{.04 in}f(x) \;\; \подразумевает\;\; \hspace{0,04 дюйма}f(x) = \hspace{0,04 дюйма}f(\hspace{0,03 дюйма}y) \;\;$]$\;\;$.
Если $\hspace{0,04 in}f$ и $g$ неубывают, то $\hspace{0,04 in}f$ является константой.
Если выполнено первое предложение (основного) следствия теоремы,
, то верно второе предложение этой теоремы. $\:$ Следовательно, теорема верна.
Теорема: $\;\;\;$ Если $\:\operatorname{Dom}(\hspace{.05 in}f\hspace{.02 in})\:$ интервал, то
Если производная функции $\hspace{.04 in}f$ всюду неотрицательна, то $\hspace{.04 in}f$ не убывает.
$\implies$
Если производная функции $\hspace{.04 in}f$ везде строго положительна,
, то $\hspace{.04 in}f$ — строго возрастающая функция.
.
Доказательство:
Предположим, что верно первое предложение стрелки теоремы, а затем предположим, что производная от $\hspace{.04 in}f$ везде строго положительна, и что входы $x$ и $y$ такой, что $\: x< y\:$ и $\: \hspace{.04 in}f(x) \leq \hspace{.04 in}f(\hspace{.03 in}y) \ ;$. $\;\;\;$ Для всех элементов $z$ из $[x,y]$, $\: \hspace{.04 in}f(x) \leq \hspace{.04 in}f(z) \leq \hspace{0,04 дюйма}f(\hspace{0,03 дюйма}y) = \hspace{0,04 дюйма}f(x) \;$.
$\hspace{0,04 in}f$ постоянно на $[x,y]$. $\;\;\;$ Для $\: w = \frac{x+z}2 \:$ и $h$ такие, что $\: 0 < |h| < \frac{y-x}2 \:$, $\:$ $\;\; w+h \: \in \: [x,y] \;\;\;$.
Для $\: w = \frac{x+z}2 \:$ и $h$ таких, что $\: 0 < |h| < \frac{y-x}2 \:$, $\:$ $\: \frac{\hspace{0,04 дюйма}f(w+h)-\hspace{0,04 дюйма}f(w)}h = \ frac{\hspace{0,04 дюйма}f(w+0)-\hspace{0,04 дюйма}f(w+0)}h = \frac{0-0}h = \frac0h = 0 \;\;$ .
Поскольку $\: x< y\:$, $\: 0 < \frac{y-x}2 \:$, $\:$, поэтому $\;\; \hspace{04 дюйма}f'(w) \; "=" \displaystyle\lim_{h\to 0} \frac{\hspace{0,04 дюйма}f(w+h)-\hspace{0,04 дюйма}f(w)}h \; "=" \displaystyle\lim_{h\to 0} \: 0 \; "=" 0 \;\;$,
, что противоречит предположению второго предложения стрелки теоремы.
Это противоречие показывает, что второе предложение стрелки теоремы следует
из предположения в начале этого доказательства. $\:$ Следовательно, теорема верна.
Теорема:
Если $x$ находится внутри $\operatorname{Dom}(\hspace{.05 in}f\hspace{.02 in})$ и $x$ является локальным слабым
существует экстремум $\hspace{.04 in}f$ и $\hspace{.04 in}f'(x)$, тогда $\: \hspace{.04 in}f'(x) = 0 \; $.
Доказательство:
Предположим, $\epsilon$ таков, что $\:0<\epsilon \:$ и $\: (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\ hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon) \subseteq \operatorname{Dom}(\hspace{0,05 дюйма}f\hspace{0,02 дюйма}) \:$ и $x$ слабо
максимизирует $\hspace{0,04 дюйма}f$ на интервале $\:(x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{ -0,04 дюйма}\эпсилон)\;$.
$\;\;\;$ Для всех $h$, $\: \big|\hspace{-0,04 дюйма}\pm\hspace{-0,04 дюйма}|h|\big| = |ч| \;$.
Для всех $h$, если $\: 0<|\hspace{.02 in}h\hspace{.01 in}|<\epsilon \:$, то $\:h\neq 0\:$ и $\ ;\; x\hspace{-0,02 дюйма}\pm\hspace{-0,01 дюйма}|h| \: \in \: (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon) \subseteq \operatorname{ Дом}(\hspace{0,05 дюйма}f\hspace{0,02 дюйма}) \;\;$.
Для всех $h$, если $\: 0<|\hspace{.02 in}h\hspace{.01 in}|<\epsilon \:$, то $\:\: \frac{\hspace{.04 in}f(x+|h|)-f(x)}{|h|} \leq \frac{\hspace{0,04 дюйма}f(x)-\hspace{0,04 дюйма}f(x)}{ |h|} = \frac{0-0}{|h|} = \frac0{|h|} = 0 \;\;$.
Для всех $h$, если $\: 0<-|\hspace{.02 in}h\hspace{.01 in}|<\epsilon \:$, то $0 = \frac0{|h|} = \frac {0-0}{|h|} = \frac{\hspace{0,04 дюйма}f(x)-\hspace{0,04 дюйма}f(x)}{|h|} = \frac{\hspace{ 0,04 дюйма}f(x)-\hspace{0,04 дюйма}f(x+(-|h|))}{|h|} \leq \frac{-(\hspace{0,04 дюйма}f(x+( -|h|))-f(x))}{|h|} = \frac{--(\hspace{.
04 in}f(x+(-|h|))-f(x))}{ -|h|} = \frac{\hspace{0,04 дюйма}f(x+(-|h|))-f(x)}{-|h|} \;\;$.
Для всех $h$, если $\: 0 < |h| < \epsilon \:$, тогда $\: \frac{\hspace{0,04 дюйма}f(x+|h|)-f(x)}{|h|} \leq 0\leq \frac{\hspace{. 04 in}f(x+(-|h|))-f(x)}{-|h|} \;$.
Если $\; \displaystyle\lim_{h\to 0} \frac{\hspace{0,04 in}f(x+h)-f(x)}h \;$ существует, тогда $\;\; \displaystyle\lim_{h\to 0} \frac{\hspace{0,04 дюйма}f(x+h)-f(x)}h \; “=” 0 \;\;\;$.
Если $\hspace{.04 in}f'(x)$ существует, то $\: \hspace{.04 in}f'(x) = 0 \;$.
Теперь предположим, что $\epsilon$ таков, что $\:0<\epsilon \:$ и $x$ слабо минимизирует $\hspace{0,04 in}f$ на интервале $\:(x\hspace{-0,04 in }-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon)\;$.
Пусть $g$ задается как $\:g(y) = -(\hspace{.05 in}f(y))\;$. $\;\;\;$ Для всех $\: y\in (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 in}\эпсилон) \:$,
$-(г(х)) \; “=” –(\hspace{0,05 дюйма}f(x)) \; “=” \hпробел{0,04 дюйма}f(x) \; \leq\; \hspace{04 дюйма}f(y) \; “=” –(\hspace{0,05 дюйма}f(y)) \; “=” -(г(у)) \;\;\;$.
Для всех $\: y\in (x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\hspace{-0,04 дюйма}\epsilon) \: $, $\:$ $\: g(y) \leq g(x) \;$. $\;\;\;$ $x$ слабо максимизирует $g$ на $\:(x\hspace{-0,04 дюйма}-\hspace{-0,04 дюйма}\epsilon,x\hspace{-0,04 дюйма}+\ hspace{-0,04 дюйма}\эпсилон)\;$.
Согласно предыдущей части этого доказательства, если $g'(x)$ существует, то $\:g'(x) = 0 \;$. $\;\;\;$ Если $\hspace{.04 in}f'(x)$ существует, то
$\hspace{0,04 дюйма}f'(x) \: = \: (\hspace{0,05 дюйма}f(x))’ \: = \: -\hspace{-0,04 дюйма}-\hspace{ -0,04 дюйма}((\hspace{0,05 дюйма}f(x))’) \: = \: -((-(\hspace{0,05 дюйма}f(x)))’) \: = \: -((g(x))’) \: = \: -(g'(x)) \: = \: -0 \: = \: 0 \;\;\;$.
В обоих случаях получено, что “если $\hspace{.04 in}f'(x)$ существует, то $\:\hspace{.04 in}f'(x) = 0\:$”. $\;\;$ Следовательно, теорема верна.
реальный анализ – Доказательство правила Лопиталя для $\frac{\infty}{\infty}$
Задавать вопрос
спросил
Изменено 6 лет, 8 месяцев назад
Просмотрено 10 тысяч раз
$\begingroup$
Прошу доказать правило Лопиталя для неопределенной формы $\frac{\infty}{\infty}$ с использованием правила для формы $\frac{0}{0}$.