Доплеровское смещение | это… Что такое Доплеровское смещение?
Источник волн перемещается налево. Тогда слева частота волн становится выше (больше), а справа — ниже (меньше).
Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, тот услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Для волн, распространяющихся в какой-либо среде (например, звука) нужно принимать во внимание движение как источника так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, имеет значение только[1] относительное движение источника и приёмника.
Эффект был впервые описан Кристианом Доплером в 1842 году.
Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью. В этом случае в лабораторной системе регистрируется черенковское излучение, имеющее непосредственное отношение к эффекту Доплера.
Содержание
|
Сущность явления
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется — длина волны увеличивается.
где f0 — частота, с которой источник испускает волны, c — скорость распространения волн в среде, v — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).
Частота, регистрируемая неподвижным приёмником
| (1) |
Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника.
u — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).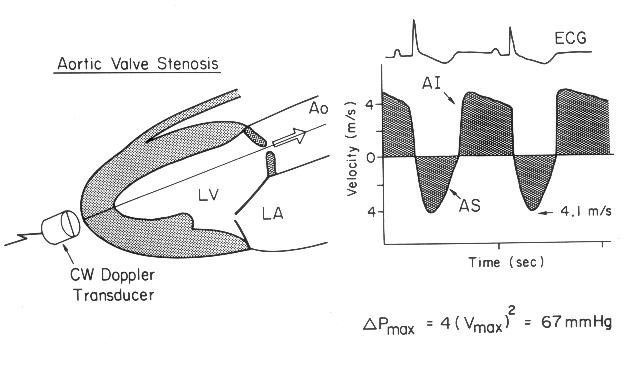
Подставив значение частоты из формулы (1) в формулу (2), получим формулу для общего случая.
| (3) |
Релятивистский эффект Доплера
В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительности.Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя.
где
Как наблюдать эффект Доплера
Не меняющий своего местоположения микрофон записывает звук, издаваемый сиренами двух движущихся влево полицейских машин. Снизу можно видеть частоту каждого из двух звуков, принимаемую микрофоном.
Поскольку явление характерно для любых колебательных процессов, то его очень легко наблюдать для звука. Частота звуковых колебаний воспринимается на слух как высота звука. Надо дождаться ситуации, когда быстро движущийся автомобиль будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте.
Надо дождаться ситуации, когда быстро движущийся автомобиль будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте.
Применение
Доплеровский радар
Радар, который измеряет изменение частоты сигнала, отражённого от объекта. По изменению частоты вычисляется радиальная составляющая скорости объекта (проекция скорости на прямую, проходящую через объект и радар). Доплеровские радары широко применяются в самых разных областях: для определения скорости летательных аппаратов, кораблей, автомобилей, гидрометеоров (например, облаков) и других объектов.
Доказательство вращения Земли вокруг Солнца с помощью эффекта Допплера.
Астрономия
- по смещению линий спектра определяют скорость движения звёзд
С помощью ЭД по спектру небесных тел определяется их лучевая скорость. Изменение длин волн световых колебаний приводит к тому, что все спектральные линии в спектре источника смещаются в сторону длинных волн, если лучевая скорость его направлена от наблюдателя (красное смещение), и в сторону коротких, если направление лучевой скорости – к наблюдателю (фиолетовое смещение). Если скорость источника мала по сравнению со скоростью света (300000км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и деленной на длину волны этой же линии в неподвижном источнике.
Изменение длин волн световых колебаний приводит к тому, что все спектральные линии в спектре источника смещаются в сторону длинных волн, если лучевая скорость его направлена от наблюдателя (красное смещение), и в сторону коротких, если направление лучевой скорости – к наблюдателю (фиолетовое смещение). Если скорость источника мала по сравнению со скоростью света (300000км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и деленной на длину волны этой же линии в неподвижном источнике.
- по увеличению ширины линий спектра определяют температуру звезд
Неинвазивное измерение потока жидкости
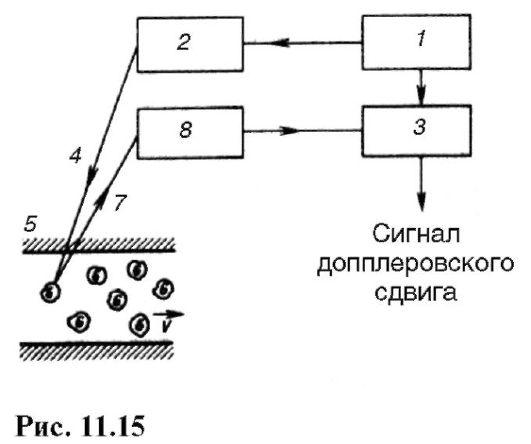
С помощью эффекта Доплера измеряют скорость потока жидкостей. Преимущество этого метода заключается в том, что не требуется помещать датчики непосредственно в поток. Скорость определяется по рассеянию ультразвука на неоднородностях среды (частицах взвеси, каплях жидкости, не смешивающихся с основным потоком, пузырьках газа).
Автосигнализации
Для обнаружения движущихся объектов вблизи и внутри автомобиля
Примечания
- ↑ В первом приближении. На самом деле скорость света через прозрачную среду зависит от скорости движения этой среды. См. опыт Физо.
См. также
- Красное смещение
- Фиолетовое смещение
- Эффект Черенкова
Ссылки
- Применение эффекта Доплера для измерения течений в океане
Доплеровское смещение | это… Что такое Доплеровское смещение?
Источник волн перемещается налево. Тогда слева частота волн становится выше (больше), а справа — ниже (меньше).
Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена.
Для волн, распространяющихся в какой-либо среде (например, звука) нужно принимать во внимание движение как источника так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, имеет значение только[1] относительное движение источника и приёмника.
Эффект был впервые описан Кристианом Доплером в 1842 году.
Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью.
Содержание
|
Сущность явления
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется — длина волны увеличивается.
где f0 — частота, с которой источник испускает волны, c — скорость распространения волн в среде, v — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).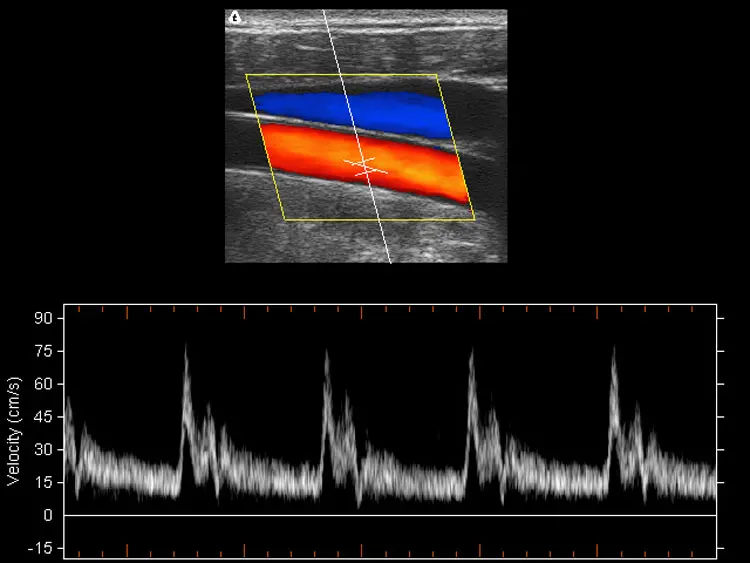
Частота, регистрируемая неподвижным приёмником
| (1) |
Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника.
| (2) |
u — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).
Подставив значение частоты из формулы (1) в формулу (2), получим формулу для общего случая.
| (3) |
Релятивистский эффект Доплера
В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительности.Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя.
где с — скорость света, v — относительная скорость приёмника и источника (положительная в случае их удаления друг от друга).
Как наблюдать эффект Доплера
Не меняющий своего местоположения микрофон записывает звук, издаваемый сиренами двух движущихся влево полицейских машин. Снизу можно видеть частоту каждого из двух звуков, принимаемую микрофоном.
Поскольку явление характерно для любых колебательных процессов, то его очень легко наблюдать для звука. Частота звуковых колебаний воспринимается на слух как высота звука. Надо дождаться ситуации, когда быстро движущийся автомобиль будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте.
Применение
Доплеровский радар
Радар, который измеряет изменение частоты сигнала, отражённого от объекта. По изменению частоты вычисляется радиальная составляющая скорости объекта (проекция скорости на прямую, проходящую через объект и радар). Доплеровские радары широко применяются в самых разных областях: для определения скорости летательных аппаратов, кораблей, автомобилей, гидрометеоров (например, облаков) и других объектов.
Доплеровские радары широко применяются в самых разных областях: для определения скорости летательных аппаратов, кораблей, автомобилей, гидрометеоров (например, облаков) и других объектов.
Доказательство вращения Земли вокруг Солнца с помощью эффекта Допплера.
Астрономия
- по смещению линий спектра определяют скорость движения звёзд
С помощью ЭД по спектру небесных тел определяется их лучевая скорость. Изменение длин волн световых колебаний приводит к тому, что все спектральные линии в спектре источника смещаются в сторону длинных волн, если лучевая скорость его направлена от наблюдателя (красное смещение), и в сторону коротких, если направление лучевой скорости – к наблюдателю (фиолетовое смещение). Если скорость источника мала по сравнению со скоростью света (300000км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и деленной на длину волны этой же линии в неподвижном источнике.
- по увеличению ширины линий спектра определяют температуру звезд
Неинвазивное измерение потока жидкости
С помощью эффекта Доплера измеряют скорость потока жидкостей. Преимущество этого метода заключается в том, что не требуется помещать датчики непосредственно в поток. Скорость определяется по рассеянию ультразвука на неоднородностях среды (частицах взвеси, каплях жидкости, не смешивающихся с основным потоком, пузырьках газа).
Преимущество этого метода заключается в том, что не требуется помещать датчики непосредственно в поток. Скорость определяется по рассеянию ультразвука на неоднородностях среды (частицах взвеси, каплях жидкости, не смешивающихся с основным потоком, пузырьках газа).
Автосигнализации
Для обнаружения движущихся объектов вблизи и внутри автомобиля
Примечания
- ↑ В первом приближении. На самом деле скорость света через прозрачную среду зависит от скорости движения этой среды. См. опыт Физо.
См. также
- Красное смещение
- Фиолетовое смещение
- Эффект Черенкова
Ссылки
- Применение эффекта Доплера для измерения течений в океане
Доплеровское смещение | это… Что такое Доплеровское смещение?
Источник волн перемещается налево. Тогда слева частота волн становится выше (больше), а справа — ниже (меньше).
Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, тот услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Его легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, тот услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Для волн, распространяющихся в какой-либо среде (например, звука) нужно принимать во внимание движение как источника так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, имеет значение только[1] относительное движение источника и приёмника.
Эффект был впервые описан Кристианом Доплером в 1842 году.
Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью. В этом случае в лабораторной системе регистрируется черенковское излучение, имеющее непосредственное отношение к эффекту Доплера.
Содержание
|
Сущность явления
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется — длина волны увеличивается.
Если удаляется — длина волны увеличивается.
где f0 — частота, с которой источник испускает волны, c — скорость распространения волн в среде, v — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).
Частота, регистрируемая неподвижным приёмником
| (1) |
Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника.
| (2) |
u — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).
Подставив значение частоты из формулы (1) в формулу (2), получим формулу для общего случая.
| (3) |
Релятивистский эффект Доплера
В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительности. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя.
Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя.
где с — скорость света, v — относительная скорость приёмника и источника (положительная в случае их удаления друг от друга).
Как наблюдать эффект Доплера
Не меняющий своего местоположения микрофон записывает звук, издаваемый сиренами двух движущихся влево полицейских машин. Снизу можно видеть частоту каждого из двух звуков, принимаемую микрофоном.
Поскольку явление характерно для любых колебательных процессов, то его очень легко наблюдать для звука. Частота звуковых колебаний воспринимается на слух как высота звука. Надо дождаться ситуации, когда быстро движущийся автомобиль будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте.
Применение
Доплеровский радар
Радар, который измеряет изменение частоты сигнала, отражённого от объекта. По изменению частоты вычисляется радиальная составляющая скорости объекта (проекция скорости на прямую, проходящую через объект и радар). Доплеровские радары широко применяются в самых разных областях: для определения скорости летательных аппаратов, кораблей, автомобилей, гидрометеоров (например, облаков) и других объектов.
Доказательство вращения Земли вокруг Солнца с помощью эффекта Допплера.
Астрономия
- по смещению линий спектра определяют скорость движения звёзд
С помощью ЭД по спектру небесных тел определяется их лучевая скорость. Изменение длин волн световых колебаний приводит к тому, что все спектральные линии в спектре источника смещаются в сторону длинных волн, если лучевая скорость его направлена от наблюдателя (красное смещение), и в сторону коротких, если направление лучевой скорости – к наблюдателю (фиолетовое смещение). Если скорость источника мала по сравнению со скоростью света (300000км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и деленной на длину волны этой же линии в неподвижном источнике.
Если скорость источника мала по сравнению со скоростью света (300000км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и деленной на длину волны этой же линии в неподвижном источнике.
- по увеличению ширины линий спектра определяют температуру звезд
Неинвазивное измерение потока жидкости
С помощью эффекта Доплера измеряют скорость потока жидкостей. Преимущество этого метода заключается в том, что не требуется помещать датчики непосредственно в поток. Скорость определяется по рассеянию ультразвука на неоднородностях среды (частицах взвеси, каплях жидкости, не смешивающихся с основным потоком, пузырьках газа).
Автосигнализации
Для обнаружения движущихся объектов вблизи и внутри автомобиля
Примечания
- ↑ В первом приближении. На самом деле скорость света через прозрачную среду зависит от скорости движения этой среды. См. опыт Физо.
См. также
- Красное смещение
- Фиолетовое смещение
- Эффект Черенкова
Ссылки
- Применение эффекта Доплера для измерения течений в океане
сущность метода и его преимущества
ГлавнаяСтатьиДопплер-ультразвуковое исследование
Допплерография – это современный высокоинформативный метод ультразвуковой диагностики заболеваний сосудов, основанный на использовании эффекта Доплера. Целью УЗДГ является определение объема и скорости кровотока, а так же наличия препятствий для него.
Целью УЗДГ является определение объема и скорости кровотока, а так же наличия препятствий для него.
Из истории метода
Изменение (или сдвиг) частоты и длины звуковых и ультразвуковых волн, отражающихся от подвижных объектов относительно неподвижного регистратора, называется эффектом Доплера. Сдвиг частоты прямо пропорционален скорости движущихся объектов. Движение, направленное в сторону датчика, проявляется увеличением частоты, движение от датчика – снижением. Явление было названо в честь австрийского ученого-физика К. Доплера (К.Doppler), впервые описавшего его в 1842 г.
В медицинской диагностике эффект Доплера применяется с ультразвуковым и с лазерным излучением, но более широкое распространение получили ультразвуковые методы.
Первые сообщения об использовании эффекта Доплера в медицине относятся к 1956 году, когда впервые был проведен анализ скорости кровотока на основе отражения звуковых волн от эритроцитов. Вначале использовались простейшие приборы с непрерывным излучением, которые выдавали информацию в виде звуковых сигналов через встроенные динамики.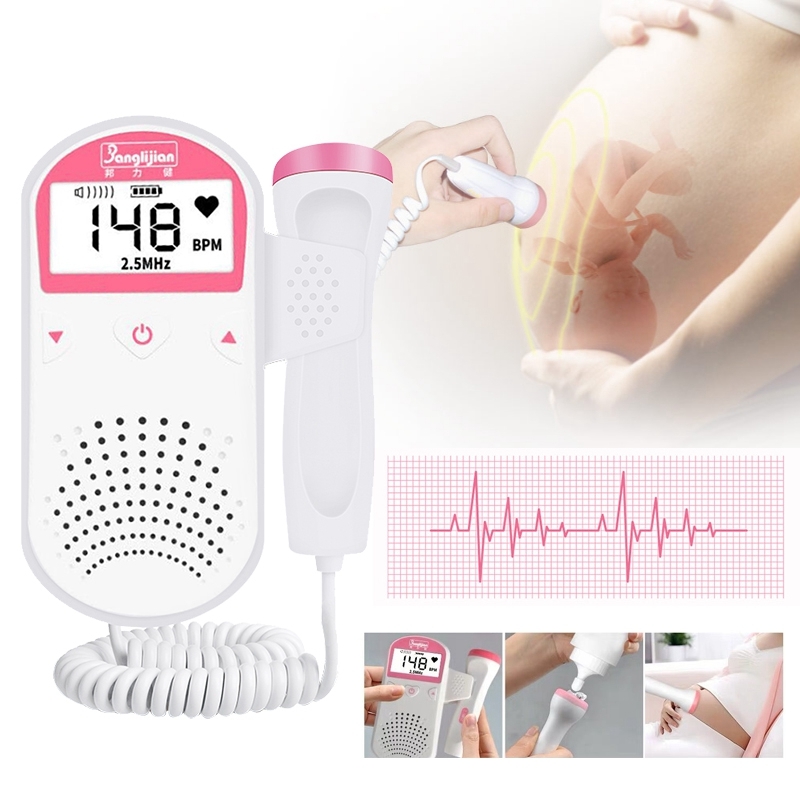 В ходе дальнейшего усовершенствования элементарной базы достигались все новые уровни технических решений:
В ходе дальнейшего усовершенствования элементарной базы достигались все новые уровни технических решений:
- в 1966 г разработаны допплеровские системы с выделением направления,
- в 1967 – импульсные системы,
- 1971 г – допплеровская визуализация,
- 1974 г – дуплексные системы эхо-импульсного типа,
- 1979-82 – цветовое допплеровское картирование (ЦДК или CFM) в режиме реального времени,
- 1994 г – допплеровская тканевая визуализация (энергетический допплер).
Суть метода допплерографии
Допплерография – это метод УЗИ диагностики, основанный на эффекте Доплера: изменение частоты УЗ-волн, отраженных от движущихся эритроцитов. Допплеровский сдвиг частоты позволяет судить о скорости и направлении кровотока. В результате передачи серии ультразвуковых импульсов в ткани на экране монитора получают график, демонстрирующий изменение скорости кровотока с течением времени на заданной глубине (допплеровский спектр или частотный спектр эхо-сигналов, поступающих от кровотока).
Такой спектральный (или импульсный) режим позволяет на основе оценки кровотока вычислить ряд важных параметров. Метод УЗ-допплерографии (или «слепой допплер») позволяет оценить лишь одну функцию – проходимость сосуда, на основе графика кровотока. Поскольку отсутствует визуализация сосудов, нельзя уточнить причину выявленного нарушения его проходимости.
Моно режим УЗДГ считается устаревшим. Это был первый этап развития УЗ-допплерографии, когда исследователю приходилось на глаз выставлять глубину сканирования в предполагаемом местонахождении сосуда. Графический спектр кровотока получался в слепую, без визуального подтверждения, откуда он получен.
Усовершенствованный и более информативный метод – дуплексное ультразвуковое сканирования (УЗДС). Современный УЗИ-сканер выполняет одновременно две функции (дуплекс):
- анатомическое исследование сосудов,
- качественное и количественное исследование кровотока.
УЗДС дает информацию о состоянии сосуда и окружающих тканей в В-режиме (серый спектр) и позволяет оценить гемодинамические явления с использованием эффекта Доплера.
Дуплексное сканирование отображает сосуд в двух плоскостях – вдоль и поперек. Двухмерная визуализация сосудов позволяет оценивать их проходимость и причины ее нарушения (стеноз, наличие тромбов и бляшек, извитость хода, аномалии развития), а так же скорость и направление кровотока.
Технологический режим, при котором дуплексное сканирование проходит с использованием цветного допплеровского картирования, называется триплексным сканированием. Цветовой режим дает информацию о качественном состоянии кровотока, его характере (равномерный или турбулентный, с множественными завихрениями), а спектральный режим – количественную, или информацию о скорости кровотока.
Цветовой режим дает более точную оценку проходимости сосудов. Исследуется состояние как венозных, так и артериальных сосудов. Красный цвет на мониторе показывает кровоток, направленный в сторону датчика, синий – направление кровотока от датчика.
В режиме триплексного сканирования способен работать любой стационарный сканер среднего или экспертного класса, произведенный ведущими мировыми фирмами в течение последних 10 лет.
Преимущество метода
УЗ-допплерография, позволяющая проводить наблюдения в режиме реального времени, является неинвазивным и безопасным методом исследования параметров циркуляции крови и состояния сосудов. Преимущество УЗДГ в том, что он позволяет получить результат безболезненно и без побочных эффектов для пациента, без лучевой нагрузки и практически без прямых противопоказаний. Его можно применять и у детей.
Допплерография исследует так же скорость сокращения сердечной мышцы и движения сердечных клапанов. В отличие от ангиографии, метод УЗДГ совершенно безвреден, поскольку не нуждается во введении контрастных веществ.
Преимущества допплерографии особенно очевидны в акушерской практике. Метод позволяет изучать состояние кровотока плода, маточных артерий и пуповины, а так же регистрировать ЧСС плода.
Дуплексное сканирование широко используется в сосудистой хирургии.
Метод способствует ранней диагностике заболеваний и предупреждению развития осложнений. Может выполняться повторно неоднократно, что может быть необходимо для оценки динамики заболевания на фоне терапии.
Может выполняться повторно неоднократно, что может быть необходимо для оценки динамики заболевания на фоне терапии.
Смотреть все статьи
Прецизионный хирургический микроскоп Leica M530 OHX для нейрохирургии и пластической реконструктивной хирургии
SMART-технологии в анестезиологии и интенсивной терапии
Как выбрать микроскоп для лаборатории
Как выбрать дефибриллятор?
Дуплексное сканирование
- Что такое дуплексное сканирование
- На чем основано дуплексное сканирование
- Цели дуплексного сканирования
- Применение дуплексного сканирования в диагностике различных органов
- Безопасность дуплексного сканирования
- Дуплексное сканирование сосудов
- Что такое дуплексное сканирование сосудов
- Показания для проведения дуплексного сканирования артерий ног и рук
- Функциональные пробы при дуплексном сканировании артерий
- Показания для дуплексного сканирования брюшной аорты и ее ветвей
- Дуплексное сканирование почечных артерий и вен
- Дуплексное сканирование сосудов малого таза
- Дуплексное сканирование сосудов семенного канатика
- Дуплексное сканирование сосудов полового члена
- Дуплексное сканирование вен ног и рук
- Дуплексное сканирование сосудов шеи и головы
- Дуплексное сканирование сосудов при беременности
- Наша аппаратура
- другие виды.
 ..
..
Что такое дуплексное сканирование
Дуплексным сканированием называют режим работы аппарата узи при котором одновременно получают черно-белое изображение и изображение сосудов с движущейся кровью. В некоторых аппаратах для оценки подвижности тканей ипользуют также детекцию движения тканей- тканевой допплер. В основном же, под термином дуплексное сканирование понимают изображение потока крови.
На чем основано дуплексное сканирование
При дуплексном сканировании используется допплеровский эффект. Этот эффект состоит в том, что ультразвуковая волна, отражаясь от поверхности движущейся частицы, меняет свою частоту. В том случае, если движение частицы совпадает с направлением распространения ультразвукового луча или находится под углом к нему (не превышая 60 градусов) можно определить сдвиг частоты отраженного сигнала и вычислить скорость движения. Так как кровь состоит плазмы и форменных элементов (эритроциты, лейкоциты, тромбоциты), то отражение от множества частиц создает допплеровский сдвиг. Допплеровский сдвиг можно закодировать в виде графика скорости крови с сосуде и в виде визуального представления кровотока с различной скоростью. В этом случае скорость кодируется различными оттенками цвета. Отображение кровотока при помощи цвета на фоне черно – белой картинки обычного узи называют дуплексным сканированием. Также в некоторых случаях используют термин цветовое допплеровское кодирование.
Допплеровский сдвиг можно закодировать в виде графика скорости крови с сосуде и в виде визуального представления кровотока с различной скоростью. В этом случае скорость кодируется различными оттенками цвета. Отображение кровотока при помощи цвета на фоне черно – белой картинки обычного узи называют дуплексным сканированием. Также в некоторых случаях используют термин цветовое допплеровское кодирование.
Цели дуплексного сканирования
Дуплексное сканирование прежде всего позволяет увидеть кровеносные сосуды в тех местах, где их невозможно обранужить при обычном узи. Например в полости черепа дуплексное сканирование является основным методом, позволяющим диагностировать нарушения мозгового кровотока в артериях и венах. До появления дуплексного сканирования сосудистые исследования в головном мозге производились при помощи слепого ультразвукового допплерографического исследования. Исследователь не видел сосуд, а направлял датчик в место предполагаемой проекции сосуда и при помощи специального аппарата регистрировал звуки (скорость кодировалась в звук различной громкости). С появлением дуплексного сканирования стало возможным точно визуализировать расположение сосудов и изучать их характеристики.
С появлением дуплексного сканирования стало возможным точно визуализировать расположение сосудов и изучать их характеристики.
Применение дуплексного сканирования в диагностике различных органов
Дуплексное сканирование может выступать самостоятельным методом диагностики – как,например, в случаях исследования сосудов головного мозга,позвоночных артерий, глубоких вен и артерий. Гораздо чаще дуплексное сканирование является очень ценным дополнением к многим видам ультразвукового исследования. В современной узи диагностике практически всегда возникает необходимость в проведении дополнительного дуплексного исследования.
Например при узи щитовидной железы дуплексное сканирование позволяет оценить характер кровоснабжения органа и заподозрить такие состояния как хронический аутоиммунный тиреоидит или дииффузный токсический зоб. Узловые образования при узи щитовидной железы обязательно исследуются при помощи дуплексного сканирования. Это позволяет заподозрить злокачественные процессы. При узи сосудов шеи дуплексное сканирование применяют как вспомогательное для оценки невидимых для обычного узи атеросклеротических бляшек и тромбов.
При узи сосудов шеи дуплексное сканирование применяют как вспомогательное для оценки невидимых для обычного узи атеросклеротических бляшек и тромбов.
В исследовании брюшной полости дуплексное сканирование позволяет отличать сосуды от полостных структур. При помощи дуплексного сканирования оцениваются подозрительные на опухоли образования. Иногда применение этой методики является решающим в оценке данных, полученных при узи. Применяется дуплексное сканирование при исследовании брюшной аорты, позволяя выявлять расслаивающие аневризмы и атеросклеротические бляшки. При узи печени дуплексное сканирование используется для различения сосудов желчевыводящей системы и кровеносных сосудов и для оценки направления движения крови по воротной вене, а также при оценке порто-кавальных анастомозов, если у пациента цирроз печени или портальная гипертензия.
Дуплексное сканирование незаменимо в узи почек при поиске почечных артерий и вен, а также для исследования внутрипочечных сосудов. Часто задачей дуплексного сканирования является определение жизнеспособности и нормального функционирования почки.
Часто задачей дуплексного сканирования является определение жизнеспособности и нормального функционирования почки.
При диагностике обструктивных поражений почек дуплексное сканирование применяется для оценки проходимость мочеточников, ориентируясь на выбросы мочи из устья мочеточника в стенке мочевого пузыря.
Очень большое значение дуплексное сканирование имеет в эхокардиографии. Оно позволяет замечать места патологических сбросов крови в клапанах или сильные сужения.
При помощи этой методики делают заключение о тяжести тех или иных клапанных пороков и о дефектах сердечной межжелудочковой и межпредсердной перегородки.
Дуплексное сканирование используется при трансвагинальном узи для оценки кровоснабжения узлов в матке и полипов эндометрия при узи матки. Кровоснабжение различных кист также имеет важное диагностическое значение. При гидротубации дуплексное сканирование позволяет наблюдать движение жидкости по маточным трубам.
Трансректальное узи делается обязательно с применением дуплексного сканирования. Оно дает возможность наблюдать геометрию (форму) сосудов, равномерность распределения сосудистого рисунка в предстательной железе. При аденоме (доброкачественной гиперплазии) предстательной железы перераспределение плостности сосудов можно наблюдать на ранних стадиях.
Оно дает возможность наблюдать геометрию (форму) сосудов, равномерность распределения сосудистого рисунка в предстательной железе. При аденоме (доброкачественной гиперплазии) предстательной железы перераспределение плостности сосудов можно наблюдать на ранних стадиях.
Дуплексное сканирование конечно же применяется и при узи беременных. При помощи этого метода исследования можно проследить ход пуповины, визуализировать пороки сердца плода и оценить кровоток в головном мозге.
Во время проведения узи органов мошонки дуплексное сканирование прежде всего используется для проведения пробы Вальсальвы при подозрении на варикоцеле. Также при помощи дуплексного сканирования диагностируется такое экстренное состояниие, как перекрут яичка. Оценка кровоснабжения яичек при дуплексном сканировании используется для диагностики опухолей.
Дуплексное сканирование вен и артерий дополняет черно – белое узи. Именно благодаря дуплексному сканированию возможна диагностика клапанной несостоятельности поверхностных, коммуникантных и глубоких вен вен ног. Также дуплексное сканирование вен применяется и для нижней полой вены, подвздошных вен, яремных, подключичных вен.
Также дуплексное сканирование вен применяется и для нижней полой вены, подвздошных вен, яремных, подключичных вен.
Кроме дуплексного сканирования используется также режим триплексного сканирования. При этом режиме аппарат узи одновременно получает данные в режиме черно-белого узи, цветового допплеровского кодирования и спектрального допплера. В некотрых случаях применение триплексного режима является предпочтительным. Так, при помощи дуплексного сканирования фиксируется зона интереса, которую потом тестируют при помощи импульсного допплера.
Безопасность дуплексного сканирования
Дуплексное сканирование обычно не несет никакой угрозы здоровью пациента. Однако все же допплеровское излучение обладает большой энергией и применение его нужно сводить к минимуму у беременных. Также при большой мощности излучения существует вероятность повреждения сетчатки глаза, если применяется глазничный доступ при дуплексном сканировании глазной и надблоковой артерий.
В современных аппаратах высокого класса – Medison Accuvix – применены специальные дорогостящие фильтры, которые делают невозможным превышение безопасного уровня мощности допплеровского сигнала.
Что такое дуплексное сканирование сосудов
Дуплексное сканирование сосудов – исследование, которое позволяет регистрировать показания в двух режимах – в обычном В-режиме (черно-белом) и в режиме цветового допплера (ЦДК). Если при этом еще используют импульсный допплер, то такое исследование называют триплексным. Дуплексное сканирование позволяет видеть кровоток и измерять его скоростные характеристики, направление, равномерность. Дуплексное сканирование сосудов используют для диагностики артерий и вен рук и ног, шеи, головного мозга, сосудов брюшной полости, сосудов полового члена, сосудов малого таза, предстательной железы, семенных канатиков и яичек у мужчин, матки и яичников у женщин. Также производят дуплексное сканирование при беременности для определения кровотока в пуповине, маточной артерии, сердце и аорте плода, в сосудах головного мозга плода.
Показания для проведения дуплексного сканирования артерий ног и рук
- Наличие признаков ухудшения кровоснабжения конечностей (ишемии) – онемение, зябкость, парестезии (искажения чувствительности)
- Травматическое повреждение артерий конечностей
- Признаки аневризмы артериальных сосудов
- Боли при ходьбе
- Наследственная предрасположенность к артериальным тромбозам
- Изменение цвета конечности
Какие артерии можно исследовать
Дуплексному сканированию доступны подключичная артерия, подмышечная, плечевая, лучевая и локтевая артерии на верхнем поясе конечностей. В нижнем поясе конечностей исследуются общая и наружная подвздошная артерии, общая глубокая и поверхностная бедренные, подколенная,передняя и задняя большеберцовые и малоберцовые артерии, а так же дорсальная артерия стопы. Эти сосуды исследуют в стандартных точках – местах наиболее поверхностного их расположения.
В нижнем поясе конечностей исследуются общая и наружная подвздошная артерии, общая глубокая и поверхностная бедренные, подколенная,передняя и задняя большеберцовые и малоберцовые артерии, а так же дорсальная артерия стопы. Эти сосуды исследуют в стандартных точках – местах наиболее поверхностного их расположения.
Строение артерий
Артериальные сосуды состоят из трех слоев, хорошо различимых при проведении ангиосканирования: внутренний слой-интима, средний-медиа и наружный-адвентиция.
Интима покрыта клетками, которые называются эндотелием. Эти клетки имеют очень важную роль в обеспечении текучести крови,транспорте питательных веществ в ткани из просвета сосуда,формировании иммунных реакций, в регуляции сосудистого тонуса(напряжении стенки артерий),восстановлении поврежденных сосудов при травмах или окклюзиях (закупорке просвета сосуда).
Медиа содержит мышечные волокна и волокна эластина и коллагена. Мышечные волокна регулируют ширину просвета артерий, а эластические и коллагеновые обеспечивают сохранение формы сосуда и амортизируют измения вызванные колебаниями артериального давления в различные фазы сердечного цикла.
Мышечные волокна регулируют ширину просвета артерий, а эластические и коллагеновые обеспечивают сохранение формы сосуда и амортизируют измения вызванные колебаниями артериального давления в различные фазы сердечного цикла.
Наружный слой-адвентиция содержит также много эластиновых и коллагеновых волокон и играет роль каркаса для сосуда. Также в адвентиции содержится много мелких сосудов диаметром до 1 мм, назначение которых питать стенку крупного кровеносного сосуда. Многие нарушения внутреннего просвета сосуда начинаются именно с внутреннего слоя. Атеросклеротические бляшки развиваются именно на поврежденном эндотелии. Воспалительные заболевания-васкулиты также протекают с изменениями внутреннего слоя сосуда. Тромботические массы также откладываются в местах повреждения интимы. При ультразвуковом исследовании артериальных сосудов доступны визуализации участки интимы, на которых можно выявить развитие повреждений, тромбов, бляшек.
Что исследуют при узи артерий
Повреждение интимы сосуда – ее неравномерность, утолщение, прерывистость – служат ранними предвестниками развития тяжелых поражений сосудов. Однако, хорошо визуализировать структуру сосудистой стенки представляется возможным не во всех артериях. На качество изображения влияет глубина залегания исследуемого сосуда. В глубоко лежащих арериях ограничиваются проведением исследования в режиме цветного допплера – он позволяет хорошо визуализировать наличие кровотока, судить о направлении движения крови по сосуду, дает сведения о характере -ламинарный или турбулентный, и, самое важное, позволяет выявить участки сужения сосудов, вызванные наличием тромбов или атеросклеротических бляшек или сдавлением сосуда извне.
Однако, хорошо визуализировать структуру сосудистой стенки представляется возможным не во всех артериях. На качество изображения влияет глубина залегания исследуемого сосуда. В глубоко лежащих арериях ограничиваются проведением исследования в режиме цветного допплера – он позволяет хорошо визуализировать наличие кровотока, судить о направлении движения крови по сосуду, дает сведения о характере -ламинарный или турбулентный, и, самое важное, позволяет выявить участки сужения сосудов, вызванные наличием тромбов или атеросклеротических бляшек или сдавлением сосуда извне.
Очень важную информацию дает применение спектрального допплера. При помощи этого вида исследований получают важные данные о скоростных параметрах кровотока в той или иной артерии, а так же судят о типе кровотока по характерной графике. Во время узи артерий у здорового человека кровток называется магистральным. При проведении исследования в режиме спектрального допплера легко выявляются участки со сниженным кровотоком и дается количественная оценка степени нарушения кровообращения в данном сегменте. Кровоток в этом случае может быть магистральным измененным или коллатеральным (при тяжелых поражениях). Помимо исследования ширины просвета сосуда, состояния его стенки, характера кровотока и геометрии ультразвуковое ангиосканирование артерий рук и ног всегда дополняется функциональными пробами.
Кровоток в этом случае может быть магистральным измененным или коллатеральным (при тяжелых поражениях). Помимо исследования ширины просвета сосуда, состояния его стенки, характера кровотока и геометрии ультразвуковое ангиосканирование артерий рук и ног всегда дополняется функциональными пробами.
Функциональные пробы при дуплексном сканировании артерий
Функциональные пробы позволяют выявить отклонения в регуляции тонуса сосудов и помогают в диагностике как местных сосудистых изменений, так и общих нарушений в организме. При помощи функциональных проб исследуют механизмы регуляции опосредуемые метаболическими изменениями в работающей конечности – например в работающей конечности сосуды раширяются и скорость прохождения крови по ним возрастает. Обеспечивают такое измение несколько регуляторных механизмов. Поскольку самая важная функция сосудов конечностей – обеспечение адекватного кровотока при разных физиологических условиях,нарушение механизмов регуляции ведет к сбою в работе артерий. При дуплексном сканировании функциональные пробы являются обязательный элементом исследования. В покое часто не удается выявить нарушения кровообращения, которые могут служить сигналами для принятия нетложных мер по спасению конечности. Самые распространенные функциональные пробы выявляют вклад метаболических, мышечных и эндотелиальных факторов регуляции. Обычно пациенту предлагают совершать в течение некоторого времени физическую нагрузку в исследуемой конечности. После выполнения нагрузки фиксируют показатели артериального кровотока и сравнивают их с показателями, измеренными до исследования. В норме происходит изменение показателей от 10 до 40%. Также применяется проба с напряжением конечности – показатели кровотока также измеряются до и во время напряжения. Существует проба с нитроглицерином. Испльзуют свойство нитроглицерина расслаблять мускулатуру артерий среднего и мелкокого калибра.
При дуплексном сканировании функциональные пробы являются обязательный элементом исследования. В покое часто не удается выявить нарушения кровообращения, которые могут служить сигналами для принятия нетложных мер по спасению конечности. Самые распространенные функциональные пробы выявляют вклад метаболических, мышечных и эндотелиальных факторов регуляции. Обычно пациенту предлагают совершать в течение некоторого времени физическую нагрузку в исследуемой конечности. После выполнения нагрузки фиксируют показатели артериального кровотока и сравнивают их с показателями, измеренными до исследования. В норме происходит изменение показателей от 10 до 40%. Также применяется проба с напряжением конечности – показатели кровотока также измеряются до и во время напряжения. Существует проба с нитроглицерином. Испльзуют свойство нитроглицерина расслаблять мускулатуру артерий среднего и мелкокого калибра.
Лодыжечно–плечевой индекс
Лодыжечно–плечевой индекс измеряют во время дуплексного сканирования сосудов для оценки состояния артериального кровоснабжения ног. В норме артериальное давление на руках (на плечевой артерии) ниже, чем давление в артериях голени на 20-30 мм. рт. ст. При заболеваниях, сопровождающихся снижением артериального кровоснабжения эта разница уменьшается и даже может возникать ситуация, когда давление на руках больше, чем давление на голени. Например при атеросклеротическом поражении сосудов ног или артериальном тромбозе. Напротив, слишком большое увеличение артериального давления на голени по сравнению с плечом может возникать при увеличении жесткости сосудистой стенки (например при кальцификации). Лодыжечно – плечевой индекс является соотношением систолического артериального давления в артериях голени (обычно это задняя большеберцовая артерия) к систолическом артериальному давлению плечевой артерии. Измерения на плечевой артерии производят обычным способом – так как измеряют артериальное давление. Измерение же давления в задней большеберцовой артерии определяют с использованием дуплексного сканирования. Нормальное значение лодыжечно – плечевого индекса – 0.
В норме артериальное давление на руках (на плечевой артерии) ниже, чем давление в артериях голени на 20-30 мм. рт. ст. При заболеваниях, сопровождающихся снижением артериального кровоснабжения эта разница уменьшается и даже может возникать ситуация, когда давление на руках больше, чем давление на голени. Например при атеросклеротическом поражении сосудов ног или артериальном тромбозе. Напротив, слишком большое увеличение артериального давления на голени по сравнению с плечом может возникать при увеличении жесткости сосудистой стенки (например при кальцификации). Лодыжечно – плечевой индекс является соотношением систолического артериального давления в артериях голени (обычно это задняя большеберцовая артерия) к систолическом артериальному давлению плечевой артерии. Измерения на плечевой артерии производят обычным способом – так как измеряют артериальное давление. Измерение же давления в задней большеберцовой артерии определяют с использованием дуплексного сканирования. Нормальное значение лодыжечно – плечевого индекса – 0. 9-1. 3. Если значение 0. 41-0. 9, то это свидетельствует об умеренном нарушении кровоснабжения конечности. Если коэффициент ниже, чем 0. 4 – это говорит о тяжелых нарушениях. Лодыжечно – плечевой индекс измеряют дважды: в покое и после 5 минутной физической нагрузки. Считается, что изменения лодыжечно – плечевого индекса сигнализируют о высокой вероятности инсульта и инфаркта миокарда.
9-1. 3. Если значение 0. 41-0. 9, то это свидетельствует об умеренном нарушении кровоснабжения конечности. Если коэффициент ниже, чем 0. 4 – это говорит о тяжелых нарушениях. Лодыжечно – плечевой индекс измеряют дважды: в покое и после 5 минутной физической нагрузки. Считается, что изменения лодыжечно – плечевого индекса сигнализируют о высокой вероятности инсульта и инфаркта миокарда.
Оценка функции эндотелия
Во время дуплексного сканирования сосудов конечностей можно оценить функцию эндотелия. Выявление нарушений факторов эндотелиальной регуляции позволяет судить о патологии не только одного исследуемого сегмента но и о функционировании эндотелиальной системы организма в целом. В последнее время в медицине все больше внимания уделяют изучению влияния эндотелиальной системы на многие функции органзма. В эндотелии сосудов вырабатываются очень мощные факторы-местные гормоны, влияющие на тонус сосудов и соответственно на артериальное давление. Нормальное функционирование эндотелия обеспечивает адекватную циркуляцию крови по сосудам. Атеросклеротические поражения в первую очередь развиваются на поврежденном эндотелии. Общий вес клеток эндотелия в организме взрослого составляет около 2 кг. Для сравнения-вес щитовидной железы – около 30 г. Влияние гормонов щитовидной железы на организм человека известно всем. Не менее значимым влиянием обладают и вещества, вырабатываемые эндотелием. Суммарно выработка вазоактивных веществ сосудистым эндотелием превосходит по количеству продукцию всех желез внутренней секреции. Методика осуществления функциональной пробы состоятельности эндотелиального фактора регуляции сосудистой системы проста и не занимает много времени. Выявленные отклонения помогут быстро разработать тактику и стратегию лечения нарушений на ранних стадиях, когда возможна коррекция патологии минимальными усилиями. Например оценка регуляторного потенциала эндотелиальных клеток способна правильно подобрать терапию гипертонической болезни, эректильной дисфункции и нарушений жирового обмена.
Атеросклеротические поражения в первую очередь развиваются на поврежденном эндотелии. Общий вес клеток эндотелия в организме взрослого составляет около 2 кг. Для сравнения-вес щитовидной железы – около 30 г. Влияние гормонов щитовидной железы на организм человека известно всем. Не менее значимым влиянием обладают и вещества, вырабатываемые эндотелием. Суммарно выработка вазоактивных веществ сосудистым эндотелием превосходит по количеству продукцию всех желез внутренней секреции. Методика осуществления функциональной пробы состоятельности эндотелиального фактора регуляции сосудистой системы проста и не занимает много времени. Выявленные отклонения помогут быстро разработать тактику и стратегию лечения нарушений на ранних стадиях, когда возможна коррекция патологии минимальными усилиями. Например оценка регуляторного потенциала эндотелиальных клеток способна правильно подобрать терапию гипертонической болезни, эректильной дисфункции и нарушений жирового обмена.
Показания для дуплексного сканирования брюшной аорты и ее ветвей
- Острые и хронические заболевания органов брюшной полости и забрюшинного пространства
- Подозрение на врожденную патологию сосудов
- Признаки аневризмы
- Наличие патологических объемных образований
Исследованию доступна брюшная аорта от диафрагмы до разделения на подвздошные артерии, такие ее крупные ветви как чревный ствол и верхняя брыжеечная артерия. Основная патология, выявляемая при дуплексном сканировании – аневризмы и атеросклеротические поражения. Реже тромбозы.
Основная патология, выявляемая при дуплексном сканировании – аневризмы и атеросклеротические поражения. Реже тромбозы.
Дуплексное сканирование почечных артерий и вен
Проводится при таких состояниях
- Подозрение на почечную артериальную гипертензию
- Визуализация дополнительных ветвей почечной артерии при вазоренальном конфликте, синдроме Фрейли
- Подозрение на тромбоз почечных вен
- Подозрение на синдром мезентериального пинцета
- Оценка особенностей кровоснабжения почки перед оперативным вмешательством
- Гематурия (кровь в моче)
- Оценка степени и диагностика нефроангиосклероза
- Дифференциальная диагностика обструктивной и необструктивной нефропатии
- Диагностика начальных стадий пиелонефрита
Дуплексное сканирование почечных артерий относится к технически сложным исследованиям. При проведении дуплексного сканирования сосудов почек очень важна подготовка пациента, так как газы, содержащиеся в кишечники делают невозможным визуализацию почечных артерий. При дуплексном сканировании сосудов почек определяют количество почечных артерий, место их отхождения от аорты, взаимоотношения с нижней полой веной и верхней брыжеечной артерией. Исследуются и сравниваются скорости кровотока в аорте и почечных артериях. Изменение соотношения скоростей представляют важный диагностический материал, который позволяет заподозрить стеноз (сужение) устья артерий. В почке артерия делится на сегментарные ветви, межолевые, дуговые и внутридольковые артерии. При дуплексном сканировании проводится визуальная оценка распределения кровотока в почки и измеряются скоростные характеристики и коэффициенты, которые сравниваются с данными противоположной стороны.
При дуплексном сканировании сосудов почек определяют количество почечных артерий, место их отхождения от аорты, взаимоотношения с нижней полой веной и верхней брыжеечной артерией. Исследуются и сравниваются скорости кровотока в аорте и почечных артериях. Изменение соотношения скоростей представляют важный диагностический материал, который позволяет заподозрить стеноз (сужение) устья артерий. В почке артерия делится на сегментарные ветви, межолевые, дуговые и внутридольковые артерии. При дуплексном сканировании проводится визуальная оценка распределения кровотока в почки и измеряются скоростные характеристики и коэффициенты, которые сравниваются с данными противоположной стороны.
Дуплексное сканирование сосудов малого таза
В клинической практике у мужчин широко применяют дуплексное сканирование сосудов предстательной железы при простатите, подозрении на абсцесс железы, при аденоме и раке простаты. Также проводят дуплексное сканирование вен простатического сплетения. У женщин дуплексное сканирование применяют при диагностике кист яичников, для оценки нормальной функции яичников, кровоснабжения патологических объемных образований в стенке и полости полости матки.
Дуплексное сканирование сосудов семенного канатика
Применяют при диагностике варикоцеле – состояния, при котором расширены вены семенного канатика. Чаще левого. При дуплексном сканировании вен семенного канатика применяют пробу Вальсальвы – сильное натуживание на высоте вдоха. При этом регистирурют возникновение обратного кровотока в венах семенного канатика. Также исследуют левую почечную вену при признаках варикоцеле. Дело в том, что яичковая вена впадает в левую почечную вену и сдавление ее может привести к развитию варикоцеле.
Дуплексное сканирование сосудов полового члена
Показанием служит нарушение потенции у мужчин. Проводят дуплексное сканирование пещеристых и дорсальных артерий, а также соответствующих вен до и после применения сосудорасширяющих препаратов. Дуплексное сканирование сосудов полового члена позволяет диагностировать васкулогенную форму эректильной дисфункции.
Дуплексное сканирование вен ног и рук
Дуплексное сканирование вен ного является в настоящее время основным диагностическим инструментом для исследования состояния трех венозных систем ног: системы глубоких вен, системы поверхностных вен и коммуникантных вен. Дуплексное сканирование позволяет регистрировать направление кровотока венах, наличие и степень снижения кровотока, измерять площадь сужения сосуда, диагностировать наличие тромбов и определять состоятельность клапанов вен.
Дуплексное сканирование позволяет регистрировать направление кровотока венах, наличие и степень снижения кровотока, измерять площадь сужения сосуда, диагностировать наличие тромбов и определять состоятельность клапанов вен.
Дуплексное сканирование сосудов шеи и головы
Показания к дуплексному сканированию сосудов головы и шеи
- Признаки нарушения мозгового кровообращения
- Головная боль
- Шум в ушах
- Нарушения координации
- Изменение поля зрения
- Черепно-мозговая травма
- Перенесенный инсульт
- Подозрение на сосудистые аномалии
- Остеохондроз шейного отдела позвоночника
Преимущество дуплексного сканирования сосудов шеи и головы является возможность проводить измерения в динамике и использовать функциональные пробы.
Дуплексное сканирование сосудов при беременности
Применяют для диагностики динамики развития плода, для оценки гемодинамики плода, кровотока в маточных и пупочных артериях.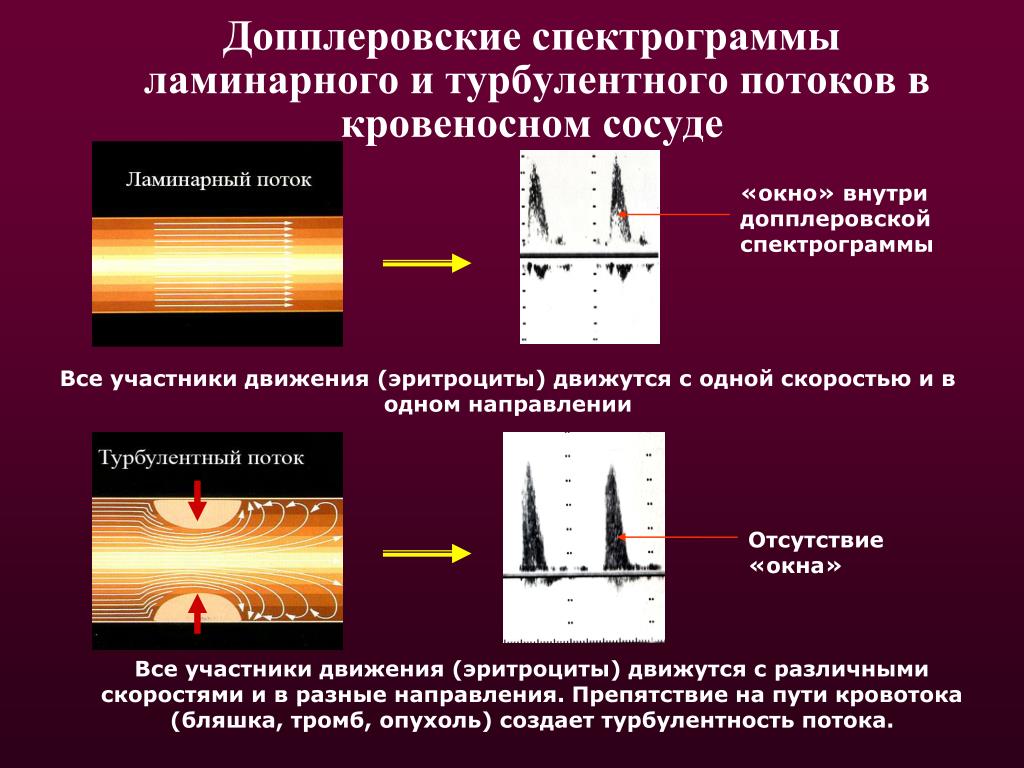 В некоторых случаях проводят дуплексное сканирование сосудов головного мозга плода.
В некоторых случаях проводят дуплексное сканирование сосудов головного мозга плода.
Читайте по теме:
- Дуплексное сканирование брюшной аорты и ее висцеральных ветвей
Мы вполняем все виды узи-диагностики:
- 3D и 4D узи при беременности
- Данные фетометрии в различных сроках
- Узи-диагностика синдрома Дауна и других хромосомных аномалий
- Оценка правильного развития плода по УЗИ
Узи при беременности
- Гидротубация (эхогидротубация): исследование проходимости маточных труб (ультразвуковая гистеросальпингоскопия)
- Трансвагинальное
- Яичников
- Матки
- Молочных желез
Женское УЗИ
- Дуплексное сканирование
- Сосудов головного мозга
- Сосудов шеи (дуплексное ангиосканирование магистральных артерий головы)
- Вен нижних конечностей
УЗИ сосудов
- Трансректальное (трузи): предстательной железы
- Мошонки (яичек)
- Сосудов полового члена
Мужское УЗИ
- Аппендицит
- Брюшной полости
- Желчного пузыря
- Желудка
- Кишечника
- Мочевого пузыря
- Мягких тканей
- Поджелудочной железы
- Печени
- Почек
- Суставов
- Щитовидной железы
- Эхокардиография (узи сердца)
УЗИ органов
- Варикоз: УЗИ-диагностика варикозного расширения вен
- Гипертония: УЗИ-диагностика гипертонии
- Тромбоз: УЗИ-диагностика тромбоза вен
- Узи диагностика хронического панкреатита
- при камнях в почках
- при холецистите
УЗИ-диагностика заболеваний
- Тазобедренных суставов у новорожденных (при подозрении на дисплазию тазобедренного сустава)
Детское УЗИ
Эффект доплера доплеровский сдвиг частоты.
 В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительности
В случае электромагнитных волн формулу для частоты выводят из уравнений специальной теории относительностиЭффект Доплера для упругих волн обусловлен постоянством скорости распространения упругой волны в среде, служащей некоторой выделенной системой отсчета. Для электромагнитных волн такой выделенной системы отсчета (среды) не существует и объяснение эффекта Доплера для электромагнитных волн может быть дано только в рамках специальной теории относительности.
Пусть источник S приближается со скоростью к неподвижному приемнику Р . При этом источник испускает в направлении приемника электромагнитные импульсы с частотой (собственная частота). Промежуток времени между двумя последовательными импульсами в системе отсчета, связанной с источником, равен . Поскольку источник движется, то соответствующий промежуток времени в неподвижной системе отсчета, связанной с приемником, вследствие эффекта замедления хода движущихся часов будет больше, а именно
, (40.1)
Расстояние между смежными импульсами в системе отсчета, связанной с приемником, будет равно
. (40.2)
(40.2)
Тогда частота следования импульсов , воспринимаемых приемником, окажется равной , или
. (40.3)
Полученная формула (40.3) соответствует продольному эффекту Доплера , который является следствием двух явлений: замедления хода движущихся часов и “уплотнения” (или разряжения) импульсов, связанного с изменением расстояния между источником и приемником. Если источник приближается (как в рассмотренном случае), то частота принимаемой электромагнитной волны увеличивается (), если же удаляется, то (в этом случае знак скорости меняется на противоположный).
Если скорость много меньше скорости света, то (40.3) с точностью до членов можно заменить приближенной формулой (нерелятивистское приближение):
. (40.4)
В общем случае, когда вектор скорости источника образует угол с направлением на приемник (линией визирования), скорость в формуле (40.3) следует заменить ее проекцией на линию визирования и тогда частота принимаемых электромагнитных волн определяется выражением
. (40.5)
(40.5)
Из последнего выражения следует, что если источник движется перпендикулярно к направлению на приемник (), то наблюдается поперечный эффект Доплера:
, (40.6)
при котором воспринимаемая приемником частота оказывается всегда меньше собственной частоты источника (). Поперечный эффект является прямым следствием замедления хода движущихся часов и значительно слабее продольного.
Продольный эффект Доплера используется в локации для определения скорости движения объекта. Учет доплеровского смещения частоты может потребоваться при организации связи с подвижными объектами. С помощью эффекта Доплера были открыты двойные звезды. В 1929 г. американский астроном Э. Хаббл обнаружил, что линии в спектре излучения далеких галактик смещены в сторону больших длин волн (космологическое красное смещение). Красное смещение возникает в результате эффекта Доплера и свидетельствует о том, что далекие галактики удаляются от нас, причем скорость разлета галактик пропорциональна расстоянию до них:
где – постоянная Хаббла.
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается. Если удаляется – длина волны увеличивается.
Частота волны в общем виде, зависит только от того, с какой скоростью двигается приемник
Как только волна пошла от источника, скорость ее распространения определяется только свойствами среды, в которой она распространяется, – источник же волны никакой роли больше не играет. По поверхности воды, например, волны, возбудившись, далее распространяются лишь в силу взаимодействия сил давления, поверхностного натяжения и гравитации. Акустические же волны распространяются в воздухе (и иных звукопроводящих средах) в силу направленной передачи перепада давлений. И ни один из механизмов распространения волн не зависит от источника волны. Отсюда и эффект Доплера .
Для того чтоб был более понятным, рассмотрим пример на машине с сиреной.
Предположим для начала, что машина стоит. Звук от сирены доходит до нас потому, что упругая мембрана внутри нее периодически воздействует на воздух, создавая в нем сжатия – области повышенного давления, – чередующиеся с разряжениями. Пики сжатия – «гребни» акустической волны – распространяются в среде (воздухе), пока не достигнут наших ушей и не воздействуют на барабанные перепонки. Так вот, пока машина стоит, мы так и будем слышать неизмененный тон ее сигнала.
Но как только машина тронется с места в вашу сторону, добавится новый эффект . За время с момента испускания одного пика волны до следующего машина проедет некоторое расстояние по направлению к вам. Из-за этого источник каждого следующего пика волны будет ближе. В результате волны будут достигать ваших ушей чаще, чем это было, пока машина стояла неподвижно, и высота звука, который вы воспринимаете, увеличится. И, наоборот, если машина с звуковым сигналом поедет в обратном направлении, пики акустических волн будут достигать ваших ушей реже, и воспринимаемая частота звука понизится.
Имеет важное значение в астрономии, гидролокации и радиолокации. В астрономии по доплеровскому сдвигу определенной частоты испускаемого света можно судить о скорости движения звезды вдоль линии ее наблюдения. Наиболее удивительный результат дает наблюдение доплеровского сдвига частот света удаленных галактик: так называемое красное смещение свидетельствует о том, что все галактики удаляются от нас со скоростями примерно до половины скорости света, возрастающими с расстоянием. Вопрос о том, расширяется ли Вселенная подобным образом или красное смещение обусловлено чем-то иным, а не «разбеганием» галактик, остается открытым.
В формуле мы использовали.
Источник волн перемещается налево. Тогда слева частота волн становится выше (больше), а справа – ниже (меньше), другими словами, если источник волн догоняет испускаемые им волны, то длина волны уменьшается. Если удаляется – длина волны увеличивается.
Эффе́кт До́плера – изменение частоты и длины волн , регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.
Сущность явления
Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью . В этом случае в лабораторной системе регистрируется черенковское излучение , имеющее непосредственное отношение к эффекту Доплера.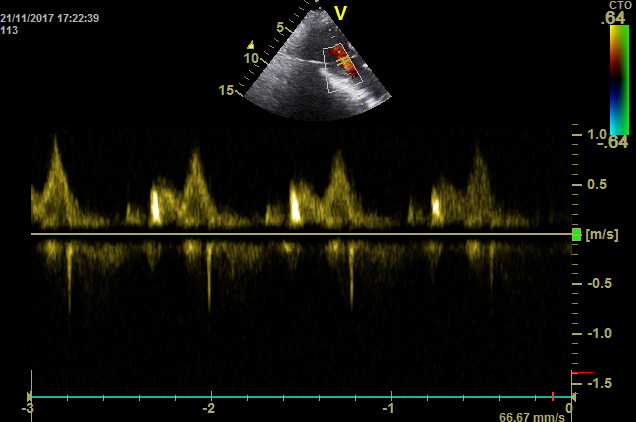
Математическое описание
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется – длина волны увеличивается:
где – частота, с которой источник испускает волны, – скорость распространения волн в среде, – скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).
Частота, регистрируемая неподвижным приёмником
где – скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).
Подставив вместо в формуле (2) значение частоты из формулы (1), получим формулу для общего случая:
где – скорость света , – скорость источника относительно приёмника (наблюдателя), – угол между направлением на источник и вектором скорости в системе отсчёта приёмника.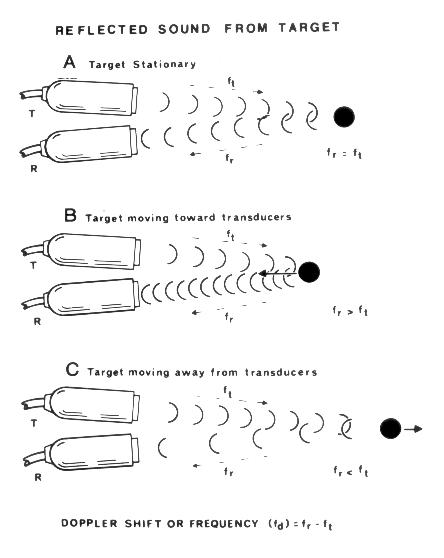 Если источник радиально удаляется от наблюдателя, то , если приближается – .
Если источник радиально удаляется от наблюдателя, то , если приближается – .
Релятивистский эффект Доплера обусловлен двумя причинами:
- классический аналог изменения частоты при относительном движении источника и приёмника;
Последний фактор приводит к поперечному эффекту Доплера, когда угол между волновым вектором и скоростью источника равен . В этом случае изменение частоты является чисто релятивистским эффектом, не имеющим классического аналога.
Как наблюдать эффект Доплера
Поскольку явление характерно для любых волн и потоков частиц, то его очень легко наблюдать для звука. Частота звуковых колебаний воспринимается на слух как высота звука . Надо дождаться ситуации, когда быстро движущийся автомобиль или поезд будет проезжать мимо вас, издавая звук, например, сирену или просто звуковой сигнал. Вы услышите, что когда автомобиль будет приближаться к вам, высота звука будет выше, потом, когда автомобиль поравняется с вами, резко понизится и далее, при удалении, автомобиль будет сигналить на более низкой ноте .
Применение
- Доплеровский радар – радар , который измеряет изменение частоты сигнала, отражённого от объекта. По изменению частоты вычисляется радиальная составляющая скорости объекта (проекция скорости на прямую, проходящую через объект и радар). Доплеровские радары могут применяться в самых разных областях: для определения скорости летательных аппаратов, кораблей, автомобилей, гидрометеоров (например, облаков), морских и речных течений , а также других объектов.
- Астрономия
- По смещению линий спектра определяют лучевую скорость движения звёзд , галактик и других небесных тел. С помощью эффекта Доплера по спектру небесных тел определяется их лучевая скорость . Изменение длин волн световых колебаний приводит к тому, что все спектральные линии в спектре источника смещаются в сторону длинных волн, если лучевая скорость его направлена от наблюдателя (красное смещение), и в сторону коротких, если направление лучевой скорости – к наблюдателю (фиолетовое смещение).
 Если скорость источника мала по сравнению со скоростью света (300 000 км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и делённой на длину волны этой же линии в неподвижном источнике.
Если скорость источника мала по сравнению со скоростью света (300 000 км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и делённой на длину волны этой же линии в неподвижном источнике. - По увеличению ширины линий спектра определяют температуру звёзд
- По смещению линий спектра определяют лучевую скорость движения звёзд , галактик и других небесных тел. С помощью эффекта Доплера по спектру небесных тел определяется их лучевая скорость . Изменение длин волн световых колебаний приводит к тому, что все спектральные линии в спектре источника смещаются в сторону длинных волн, если лучевая скорость его направлена от наблюдателя (красное смещение), и в сторону коротких, если направление лучевой скорости – к наблюдателю (фиолетовое смещение).
- Неинвазивное измерение скорости потока. С помощью эффекта Доплера измеряют скорость потока жидкостей и газов. Преимущество этого метода заключается в том, что не требуется помещать датчики непосредственно в поток. Скорость определяется по рассеянию ультразвука на неоднородностях среды (частицах взвеси , каплях жидкости, не смешивающихся с основным потоком, пузырьках газа).
- Охранные сигнализации. Для обнаружения движущихся объектов
- Определение координат. В спутниковой системе Коспас-Сарсат координаты аварийного передатчика на земле определяются спутником по принятому от него радиосигналу, используя эффект Доплера.
Искусство и культура
- В 6-ой серии 1-го сезона американского комедийного телесериала «The Big Bang Theory » доктор Шелдон Купер идёт на Хэллоуин , для которого надел костюм, символизирующий эффект Доплера.
 Однако все присутствующие (кроме друзей) думают, что он – зебра .
Однако все присутствующие (кроме друзей) думают, что он – зебра .
Примечания
См. также
Ссылки
- Применение эффекта Доплера для измерения течений в океане
Wikimedia Foundation . 2010 .
Смотреть что такое “Эффект Доплера” в других словарях:
эффект Доплера – доплеровский эффект Изменение частоты, возникающее при перемещении передатчика относительно приемника или наоборот. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва … Справочник технического переводчика
эффект Доплера – Doplerio reiškinys statusas T sritis fizika atitikmenys: angl. Doppler effect vok. Doppler Effekt, m rus. эффект Доплера, m; явление Доплера, n pranc. effet Doppler, m … Fizikos terminų žodynas
эффект Доплера – Doppler io efektas statusas T sritis automatika atitikmenys: angl. Doppler effect vok. Doppler Effekt, m rus. доплеровский эффект, m; эффект Доплера, m pranc. effet Doppler, m ryšiai: sinonimas – Doplerio efektas … Automatikos terminų žodynas
доплеровский эффект, m; эффект Доплера, m pranc. effet Doppler, m ryšiai: sinonimas – Doplerio efektas … Automatikos terminų žodynas
эффект Доплера – Doplerio efektas statusas T sritis Energetika apibrėžtis Spinduliuotės stebimo bangos ilgio pasikeitimas, šaltiniui judant stebėtojo atžvilgiu. atitikmenys: angl. Doppler effect vok. Dopplereffekt, m rus. доплеровский эффект, m; эффект Доплера, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
эффект Доплера – Doplerio efektas statusas T sritis Standartizacija ir metrologija apibrėžtis Matuojamosios spinduliuotės dažnio pokytis, atsirandantis dėl reliatyviojo judesio tarp pirminio ar antrinio šaltinio ir stebėtojo. atitikmenys: angl. Doppler effect vok … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Под эффектом
Доплера понимают изменение частоты, регистрируемой
приемником волны, связанное с движением
источника и приемника. Впервые теоретически
этот эффект в акустике и оптике был
обоснован австрийским физиком К. Доплером
в 1842 г.
Доплером
в 1842 г.
Рассмотрим
вывод формулы, определяющей частоту
упругой волны, воспринимаемой приемником,
на примере двух частных случаев. 1.
В среде находятся неподвижные источник
и приемник звуковых волн .
Испускаемые источником волны частоты
и длины волны
,
двигаясь со скоростью ,
достигают приемника и создают в нем
колебания такой же частоты
(рис. 6.11,а). 2.
Источник и испускаемая им волна движутся
вдоль оси Ох. Приемник движется к ним
навстречу. Отметим, что скорость волны
зависит только от свойств среды и не
зависит от движения приемника и источника.
Поэтому движение источника при постоянной
частоте
излучаемых им колебаний приведет к
изменению только длины волны. Действительно,
источник за период колебаний
пройдет расстояние
,
а по закону сложения скоростей волна
отойдет от
источника на расстояние
,
и поэтому ее длина волны
будет меньше (рис.6.11,б).
По
отношению к приемнику волна в соответствии
с законом сложения скоростей будет
двигаться со скоростью
и для неизменной длины волны частота колебаний, воспринимаемых источником,
изменится и будет равна
.
Если источник и приемник будут удаляться друг от друга, то тогда в формуле для частоты нужно изменить знаки. Следовательно, единая формула для частоты колебаний, воспринимаемой приемником, при движении источника и приемника по одной прямой, будет выглядеть следующим образом:
. (6.36)
Из этой формулы следует, что для наблюдателя, находящегося, например на станции, частота звукового сигнала приближающегося поезда (υ ПР =0, υ ИСТ >0)
будет больше, а при удалении от станции меньше. Если, например, взять скорость звука υ=340 м/с, скорость поезда υ=72 км/ч и частоту звукового сигнала ν 0 =1000 Гц (такая частота хорошо воспринимается человеческим ухом, причем ухо различает звуковые волны с разностью частот, большей 10 Гц), тогда частота сигнала, воспринимаемого ухом будет изменяться в пределах
=
Если
источник и приемник движутся со
скоростями, направленными под углом к
соединяющей их прямой, то тогда для
расчета частоты
,
воспринимаемой приемником, нужно брать
проекции их скоростей на эту прямую
(рис. 6.11,в):
6.11,в):
. (6.37)
Эффект Доплера наблюдается и для электромагнитных волн. Но в отличие от
упругих волн, ЭМВ могут распространяться в отсутствии среды, в вакууме. Следовательно, для ЭМВ не имеет значения скорость движения источника и приемника относительно среды. Для ЭМВ необходимо рассматривать относительную скорость движения источника и приемника, учитывать при этом преобразования Лоренца и замедление хода времени в движущейся системе отсчета.
Рассмотрим продольный эффект Доплера. Выведем формулу для частоты ЭМВ, фиксируемой приемником, в частном случае – источник и приемник движутся навстречу друг другу в направлении соединяющей их прямой. Пусть имеются две И.С.О. – неподвижная И.С.О. К (в ней находится неподвижный приемник ЭМВ) и движущаяся относительно нее вдоль совпадающих осей координат Ох и Ох′ И.С.О. К ′ (в ней находится неподвижный источник ЭМВ) (рис. 6.12,а).
Рассмотрим,
что наблюдается в И.С.О. К и К” .
1. И.С.О. К ′ .
Источник ЭМВ неподвижен и находится в
начале оси координат Ох ′
(рис. 6.12,а). Он излучает в И.С.О. К ′
ЭМВ с периодом
,
частоты
и длины волны
.
Приемник движется, но его движение не влияет на изменение частоты принимаемого сигнала. Это связано с тем, что, согласно второму постулату С.Т.О., скорость ЭМВ относительно приемника будет всегда равна с, и поэтому частота принимаемой приемником волны в И.С.О. К” будет также равна ,
2.
И.С.О. К .
Приемник ЭМВ неподвижен, а источник
ЭМВ движется в направлении оси Ох со скоростью
.
Поэтому для источника необходимо учесть
релятивистский эффект замедления
времени. Это означает, что период волны,
излучаемой источником в этой инерциальной
системе отсчета, будет больше периода
волны в И.С.О.
().
Для длины волны , излучаемой источником в направлении приемника, можно записать
Это
выражение позволяет для периода Т и частоты
воспринимаемой приемником ЭМВ в И. С.О. К, записать следующие формулы:
С.О. К, записать следующие формулы:
,
(6.38)
где учтено, что скорость ЭМВ относительно приемника в И.С.О. К равна с .
В случае удаления источника и приемника необходимо в формуле (6.38) изменить знаки. При этом фиксируемая приемником частота излучения будет уменьшаться по сравнению с частотой волны, излучаемой источником, т.е. наблюдается красное смещение спектра видимого света.
Как видно, в выражение (6.38) не входит скорость источника и приемника по отдельности, входит только скорость их относительного движения.
Для
ЭМВ также наблюдается поперечный
эффект Доплера ,
который связан с эффектом замедления
времени в движущейся инерциальной
системе отсчета. Возьмем момент времени,
когда скорость источника ЭМВ будет
перпендикулярна линии наблюдения (рис.
6.12,б), тогда движение источника к приемнику
не происходит и поэтому длина излучаемой
им волны не изменяется (
).
Остается только релятивистский эффект
замедления времени
,
. (6.39)
(6.39)
Для
поперечного эффекта Доплера изменение
частоты будет существенно меньше, чем
для продольного эффекта Доплера.
Действительно, отношение частот,
найденных по формулам (6.38) и (6.39), для
продольного и поперечного эффектов
будет значительно меньше единицы:
.
Поперечный эффект Доплера был подтвержден экспериментально, что еще раз доказало справедливость специальной теории относительности.
Приведенные здесь доводы в пользу формулы (6.39) не претендуют на строгость, но они дают правильный результат. В общем случае, для произвольного угла между линией наблюдения и скоростью движения источника , можно записать следующую формулу
, (6.40) где угол – это угол между линией наблюдения и скоростью движения источника см. (рис. 6.12, б).
Поперечный
эффект Доплера отсутствует для упругих
волн в среде. Это связано с тем, что, для
определения частоты волны, воспринимаемой
приемником, берутся проекции скоростей
на прямую, соединяющую источник и
приемник см. (рис. 6.11,в), а замедление
времени для упругих волн отсутствует.
(рис. 6.11,в), а замедление
времени для упругих волн отсутствует.
Эффект Доплера находит широкое практическое применение, например для измерения скоростей движения звезд, галактик по доплеровскому (красному) смещению линий в спектрах их излучения; для определения скоростей движущихся целей в радиолокации и гидролокации; для измерения температуры тел по доплеровскому уширению линий излучения атомов и молекул и т.д.
1
Юшкевич Р.С., Дегтярева Е.Р.
В статье даётся вывод формул к эффекту Доплера без использования закона сложения скоростей, но с использованием принципа постоянства скорости света только относительно источника света. Определена пространственная граница возможности приёма электромагнитных волн. Рассмотрена зависимость скорости света от расстояния. Определен коэффициент для вычисления скорости света.
Для объяснения эффекта допускаем, что свет, идущий от источника света, связан с источником и распространяется от него со скоростью с = 3 · 10 8 м/с относительно источника. Для приемника скорость света относительно источника будет складываться со скоростью источникаv .
Для приемника скорость света относительно источника будет складываться со скоростью источникаv .
Чтобы определить зависимость частоты света ν от скорости v , рассмотрим распространение света от двух источников, один из которых Ѕ движется по направлению от приемника со скоростью v , а другой S 0 покоится.
Рис. 1.
Одинаковые источники излучают свет одинаковой частоты ν 0 . Свет относительно источников распространяется с одинаковой скоростью с , поэтому и длина излучаемой волны λ 0 будет одинакова. К приемнику от движущегося источника свет подойдет со скоростью с- v и длина волны λ 0 будет принята за время Т = (период), а от покоящегося источника – за время Т 0 = . Периоды есть величины обратные частотам колебаний и . Подставим значения Т и Т 0 в полученные равенства
разделив их почленно, получаем
,
получаем [с. 181].
(1)
В случае, когда источник и приемник сближаются, надо знак v заменить на противоположный, получим . Отметим, что с- v и c – это скорости света соответственно относительно приемника и источника света.
Теперь рассмотрим случай, когда источник света движется перпендикулярно направлению на приемник. Учитывая, что свет связан с источником, распространяется относительно его со скоростью с и сносится с ним со скоростью v , чтобы он попал на приемник его надо направить под некоторым углом α так, что sinα = . В этом случае составляющая скорости света, совпадающая с направлением на приемник А будет , составляющая v на это направление равна 0. Чтобы не повторять предыдущие рассуждения, воспользуемся формулой (1), с- v заменим на , а скорость с относительно источника останется неизменной. В результате получаем:
что соответствует результату, полученному в опытах Айвса [с. 181].
Рис. 2.
2.
При переходе света от источника к приемнику меняется его частота от ν 0 до ν. Из формулы с=λν следует, что должна меняться и длина волны. Если от источника света шла волна длиной λ 0 , то приемник получит ее другой, допустим λ . Получить значение λ можно, воспользовавшись тем, что λ и ν величины обратно пропорциональные . Подставив значение ν из формулы (1), получим
Для большей уверенности получим эту формулу другим способом.
Любой приемник света может быть и излучателем, значит, он имеет такую же светонесущую среду, как и источник, и свет в ней распространяется со скоростью с . Свет, переходя из среды источника в среду приемника, получает скорость с относительно приемника.
Волна длиной λ 0 от источника к границе раздела сред источника и приемника подходит со скоростью с – v и границу пройдет за время C самого начала входа волны в сферу среды приемника ее начало приобретает скорость с относительно приеника и за время Т пройдет путь λ = сТ. Подставив значение Т , получаем:
Подставив значение Т , получаем:
Рис. 3.
В первой половине ХХ в. американский ученый Хаббл в спектрах далеких звезд обнаружил смещение спектральных линий в сторону красной части спектра по сравнению с лабораторными спектрами – «красное смещение». Это означало, что длина принимаемой волны λ больше, чем λ 0 и чем дальше звезда, тем больше «красное смещение».
В формулу (2) входят четыре величины λ, λ 0 , с и v . Кo времени открытия «красного смещения» скорость света с постулатом Эйнштейна была закреплена постоянной относительно любой системы отсчета, значит, и λ 0 , связанная со скоростью света с и источником излучения, оказалась постоянной. В формуле (2) переменная величина λ , оказалась связанной со скоростью источникаv . Увеличение λ вызывает и увеличение v .
«Красное смещение» наблюдается у звезд, расположенным по всем направлениям, поэтому был признан факт расширения Вселенной.
В астрономии связь между λ и v определяется другой формулой
(3)
для удаляющегося источника излучения.
Для одного и того же явления и одних и тех же величин двумя формулами устанавливается разная зависимость! Чтобы разобраться с этим, сравним результаты, которые дают эти формулы при различных v . Ограничений на значение скорости v формулы не требуют. Для удобства длины волн обозначим λ 3 и λ 2 соответственно обозначению формул (3) и (2 ), в которые они входят. При v =0 :
При 0v сравним делением:
Если v «с , то и λ 3 ≈ λ 2 . При этих двух условиях результаты практически не противоречат друг другу.
При v = с; λ 2 превращается в бесконечность, при этом формула (1) дает . Получается, что световая волна от источника к приемнику не попадает, она со скоростью с от источника будет двигаться к приемнику и вместе с источником будет с такой же скоростью уходить от него с – с = 0 .
Третье сравнение требует сделать вывод, какая же формула правильно отражает действительность. Происхождение формулы (2) рассмотрено в начале статьи. Теперь рассмотрим, как получается формула (3).
Рис. 4.
Представим, что источник света окружен средой, в которой свет распространяется к приемнику со скоростью с . Источник света в точке А начал излучать волну. Время излучения одной волны обозначим Т (период). С момента появления начала волны оно начинает перемещаться к приемнику в окружающей среде со скоростью с и за время Т удалится от точки А на расстояние сТ . Но за это же время источник, двигаясь от приемника окажется в точке С , пройдя расстояние АС = v Т , где и окажется конец волны. Расстояние от С до В и будет длиной волны λ = сТ + v Т = (с + v )Т
Если источник не движется, то v = 0 и длина волны будет λ 0 = сТ. Разделив λ на λ 0 , получим:
Разделив λ на λ 0 , получим:
В начале статьи мы рассмотрели среду, которая обеспечивает скорость света с, она либо связана с источником, либо с приемником света. Первая – дает формулы (1) и (2). Вероятность того, что вторая, от далеко расположенного приемника света, на скорость света больше влияла, чем среда источника света, ничтожно мала. Остается среда, не связанная ни с источником ни с приемником света, которая действует подобно воздуху (веществу) на распространение звука. Но отрицательный результат опытов Майкельсона по обнаружению «эфирного ветра» доказал, что такой среды в природе нет. Остается сделать предпочтение формуле (2). Ранее отмечалось, что при удалении источника света со скоростью v = с волна не достигнет приемника, и сигнал не будет получен.
Хабл ввел закон, носящий его имя [с. 120]
v = НD ,
где v – скорость удаления источника света, D – расстояние между источником и приемником, Н – коэффициент пропорциональности, называемой постоянной Хабла.
.
1 Мпк = 10 6 пк; 1пк (парсек) = 3,26 светового года = 3 . 10 13 км.
Найдем расстояние, при котором v = с: ;
D – это радиус сферы, ограничивающей прием прямого электромагнитного излучения из просторов Вселенной. Из прилегающих к этой сфере зон во внутренней ее части электромагнитные излучения могут приходить только в виде радиоволн. В природе не наблюдается какого-либо приоритетного направления в распределения звезд, поэтому радиоизлучение должно приходить со всех сторон равномерно.
Рассмотрим вариант, когда v >с. В этом случае формулы (1) и (2) дают: и .
Это означает, что волна должна приходить с направления, противоположного тому, где находиться излучатель.
При v = 2с имеем
.
Волна придет без «красного смещения». Определенная в статье граница возможного приема электромагнитного излучения будет верной, если верен закон Хаббла и «красное смещение» вызвано исключительно удалением излучателя. Если же обнаружатся другие факторы, уменьшающие скорость света относительно приемника (а они могут быть), то граница приема волн может быть приближена.
Если же обнаружатся другие факторы, уменьшающие скорость света относительно приемника (а они могут быть), то граница приема волн может быть приближена.
Обратимся теперь к формулам (1) и (2). В них c-v есть скорость света относительно приёмника, обозначим её с 1 =с-v откуда v=c-c 1 .В формулах v представляет разность скоростей света независимо от природы её возникновения. Принято считать, что это результат удаления источника света. Но эта разность скоростей может возникнуть и за счет уменьшения скорости света с увеличением расстояния. Свет это поток квантов энергии и, возможно, что скорость их может уменьшаться.
Предположим, что скорость света с увеличением расстояния от источника света уменьшается, образно говоря «свет стареет».
Известно, что скорость света уменьшается при переходе из оптически менее плотной среды в более плотную. Вызвано это тем, что, что меняются условия для прохождения света. Уменьшение скорости характеризуется показателем преломления n; , где с – скорость света в вакууме а с 1 – скорость в другой среде.
Если по предположению, скорость света уменьшается с увеличением расстояния от источника света, то, значит, меняются и условия его прохождения, что также можно характеризовать показателем преломления n. Получаем, что уменьшенная скорость света будет .
В статье «Опыт Физо» (ж. «Современные наукоёмкие технологии» №2, 2007г.) для определения скорости света в движущейся среде показатель преломления n был использован в виде , где часть показателя, определяемая излучающим атомом, а определяется условиями прохождения света в среде.
Применим такое представление показателя преломления и для вакуума. Если мы приняли предположение, что в вакууме скорость света уменьшается, а вакуум является однородной средой, то уменьшение скорости света должно зависеть только от расстояния и пропорционально ему. Поэтому можно записать ,где D -расстояние до источника света, μ – коэффициент пропорциональности постоянная величина. Скорость принимаемого света будет
Разность между начальной и уменьшенной скоростями света будет
Здесь выражена зависимость между уменьшением скорости света и расстоянием D . Связь между этими же величинами выражает и закон Хабла где v – скорость удаления звезды, что для приёмника света есть разность с-с 1 .
Связь между этими же величинами выражает и закон Хабла где v – скорость удаления звезды, что для приёмника света есть разность с-с 1 .
Сравним значения v , которые дают эти два уравнения для предельных значений расстояния D.
Если , то из первого уравнения получаем: , n =1 (для малых расстояний) и . Из закона Хаббла также получаем .
Если это совпадение не случайно, можно предположить, что кванты световой энергии связаны с излучателем, на это же указывает и связь светонесущей среды с источником света.
Чтобы определить скорость с 1 , надо решить относительно n уравнение:
и через n найти скорость с 1 .
Для малых значений D можно использовать закон Хаббла.
В статье имеется явное противоречие. Основываясь на понятии о расширении Вселенной, получен вывод о существовании границы возможного приема электромагнитных волн, а, основываясь на естественном уменьшении скорости света, такая граница отсутствует. Получается, что обнаружение такой границы будет являться доказательством расширения Вселенной.
Получается, что обнаружение такой границы будет являться доказательством расширения Вселенной.
В статье также без убедительных оснований принято предположение о зависимости скорости света от расстояний. Основания для этого предположения будут обнаружены при рассмотрении процесса излучения квантов света атомом.
СПИСОК ЛИТЕРАТУРЫ:
- Зисман Г.А., Тодес О.М., Курс общей физики т.3. – М.: «Наука», 1972г.
- Воронцов – Вельяминов Б.А. Астрономия 10. – М.: «Просвещение», 1983г.
Библиографическая ссылка
Юшкевич Р.С., Дегтярева Е.Р. ЭФФЕКТ ДОПЛЕРА И СКОРОСТЬ СВЕТА // Фундаментальные исследования. – 2008. – № 3. – С. 17-24;
URL: http://fundamental-research.ru/ru/article/view?id=2764 (дата обращения: 04.03.2019).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
5.6 Эффект Доплера. Астрономия 2e
Цели обучения
К концу этого раздела вы сможете:
- Объясните, почему спектральные линии фотонов, которые мы наблюдаем от объекта, изменяются в результате движения объекта к нам или от нас
- Опишите, как мы можем использовать эффект Доплера для определения скорости движения астрономических объектов в пространстве
Последние два раздела познакомили вас со многими новыми концепциями, и мы надеемся, что благодаря им вы увидели появление одной важной идеи. Астрономы могут узнать об элементах в звездах и галактиках, расшифровав информацию в их спектральных линиях. Однако есть один усложняющий фактор в обучении расшифровке сообщения звездного света. Если звезда движется к нам или от нас, ее линии будут находиться в немного другом месте в спектре, чем у покоящейся звезды. И большинство объектов во Вселенной имеют некоторое движение относительно Солнца.
Астрономы могут узнать об элементах в звездах и галактиках, расшифровав информацию в их спектральных линиях. Однако есть один усложняющий фактор в обучении расшифровке сообщения звездного света. Если звезда движется к нам или от нас, ее линии будут находиться в немного другом месте в спектре, чем у покоящейся звезды. И большинство объектов во Вселенной имеют некоторое движение относительно Солнца.
Движение влияет на волны
В 1842 году Кристиан Доплер впервые измерил влияние движения на волны, наняв группу музыкантов, чтобы они играли на открытом железнодорожном вагоне, когда он двигался по рельсам. Затем он применил то, что узнал, ко всем волнам, включая свет, и указал, что если источник света приближается или удаляется от наблюдателя, то световые волны будут, соответственно, сгущаться или распространяться. Общий принцип, теперь известный как эффект Доплера, показан на рис. 5.22.
Рисунок
5.22
Эффект Допплера.
(a) Источник S создает волны, гребни которых (1, 2, 3 и 4) омывают неподвижного наблюдателя. (b) Теперь источник S движется к наблюдателю A и удаляется от наблюдателя C . Гребень 1 волны возник, когда источник находился в положении S1, гребень 2 — в положении S2 и так далее. Наблюдатель A видит волны, сжатые этим движением, и видит синее смещение (если волны светлые). Наблюдатель C видит волны, растянутые движением, и видит красное смещение. Наблюдатель B , чья линия зрения перпендикулярна движению источника, не видит изменений в волнах (и чувствует себя обделенным).
(b) Теперь источник S движется к наблюдателю A и удаляется от наблюдателя C . Гребень 1 волны возник, когда источник находился в положении S1, гребень 2 — в положении S2 и так далее. Наблюдатель A видит волны, сжатые этим движением, и видит синее смещение (если волны светлые). Наблюдатель C видит волны, растянутые движением, и видит красное смещение. Наблюдатель B , чья линия зрения перпендикулярна движению источника, не видит изменений в волнах (и чувствует себя обделенным).
В части (а) рисунка источник света (S) неподвижен относительно наблюдателя. Источник испускает серию волн, гребни которых мы обозначили цифрами 1, 2, 3 и 4. Световые волны равномерно распространяются во всех направлениях, как рябь от брызг в пруду. Гребни разделены расстоянием λ, где λ — длина волны. Наблюдатель, находящийся в направлении нижней части изображения, видит световые волны, идущие красиво и равномерно на расстоянии одной длины волны. Наблюдатели, находящиеся в любом другом месте, увидят то же самое.
Наблюдатели, находящиеся в любом другом месте, увидят то же самое.
С другой стороны, если источник света движется относительно наблюдателя, как видно в части (б), ситуация более сложная. Между моментом появления одного гребня и готовностью к выходу следующего источник немного сместился к нижней части страницы. С точки зрения наблюдателя A , это движение источника уменьшило расстояние между гребнями — он сжимает гребни вместе, мог бы сказать этот наблюдатель.
В части (b) мы показываем ситуацию с точки зрения трех наблюдателей. Источник виден в четырех позициях, S 1 , S 2 , S 3 и S 4 , каждая из которых соответствует излучению одного гребня волны. Наблюдателю A волны кажутся более близкими друг к другу, с меньшей длиной волны и, следовательно, с большей частотой. (Помните, что все световые волны распространяются со скоростью света через пустое пространство, несмотря ни на что. Это означает, что движение не может влиять на скорость, а только на длину волны и частоту. Когда длина волны уменьшается, частота должна увеличиваться. Если волны короче, за каждую секунду сможет пройти больше.)
Это означает, что движение не может влиять на скорость, а только на длину волны и частоту. Когда длина волны уменьшается, частота должна увеличиваться. Если волны короче, за каждую секунду сможет пройти больше.)
Для других наблюдателей ситуация иная. Посмотрим на ситуацию с точки зрения наблюдателя C , расположенного напротив наблюдателя A на рисунке. Для нее источник удаляется от ее местоположения. В результате волны не сжимаются, а распространяются движением источника. Гребни приходят с увеличенной длиной волны и уменьшенной частотой. Для наблюдателя B в направлении, перпендикулярном движению источника, никакого эффекта не наблюдается. Длина волны и частота остаются такими же, как и в части (а) рисунка.
Из этого рисунка видно, что эффект Доплера создается только движением к наблюдателю или от него, движением, называемым радиальной скоростью. Движение вбок такого эффекта не дает. Наблюдатели между A и B заметят некоторое укорочение световых волн для той части движения источника, которая находится вдоль их луча зрения. Наблюдатели между B и C заметят удлинение световых волн вдоль их луча зрения.
Наблюдатели между A и B заметят некоторое укорочение световых волн для той части движения источника, которая находится вдоль их луча зрения. Наблюдатели между B и C заметят удлинение световых волн вдоль их луча зрения.
Возможно, вы слышали эффект Доплера со звуковыми волнами. Когда свисток поезда или полицейская сирена приближается к вам, а затем удаляется, вы заметите уменьшение высоты (именно так человеческие чувства интерпретируют частоту звуковой волны) звуковых волн. По сравнению с волнами в состоянии покоя, они изменились от немного более частых при приближении к вам до немного менее частых при удалении от вас.
Изменение цвета
Когда источник волн приближается к вам, длина волны немного уменьшается. Если задействованные волны представляют собой видимый свет, то цвета света немного меняются. По мере уменьшения длины волны они смещаются в сторону синего конца спектра: астрономы называют это blueshift (поскольку конец спектра действительно фиолетовый, термин, вероятно, должен быть violetshift , но синий является более распространенным цветом). Когда источник удаляется от вас и длина волны увеличивается, мы называем изменение цвета красным смещением . Поскольку эффект Доплера впервые был использован для видимого света в астрономии, термины «синее смещение» и «красное смещение» стали общепринятыми. Сегодня астрономы используют эти слова для описания изменений длин волн радиоволн или рентгеновских лучей так же удобно, как используют их для описания изменений в видимом свете.
Когда источник удаляется от вас и длина волны увеличивается, мы называем изменение цвета красным смещением . Поскольку эффект Доплера впервые был использован для видимого света в астрономии, термины «синее смещение» и «красное смещение» стали общепринятыми. Сегодня астрономы используют эти слова для описания изменений длин волн радиоволн или рентгеновских лучей так же удобно, как используют их для описания изменений в видимом свете.
Чем больше движение к нам или от нас, тем больше доплеровский сдвиг. Если относительное движение происходит полностью вдоль луча зрения, формула для доплеровского смещения света равна
.Δλλ=vcΔλλ=vc
, где λ — длина волны, испускаемая источником, Δλ — разница между λ и длиной волны, измеренной наблюдателем, c — скорость света, а v — относительная скорость наблюдателя и источника в Поле зрения. Переменная v считается положительным, если скорость является скоростью отступления, и отрицательным, если это скорость приближения. Решая это уравнение для скорости, находим v = c × Δλ/λ.
Решая это уравнение для скорости, находим v = c × Δλ/λ.
Если звезда приближается к нам или удаляется от нас, длины световых волн в ее непрерывном спектре кажутся соответственно укороченными или удлиненными, как и темные линии. Однако, если только ее скорость не достигает десятков тысяч километров в секунду, звезда не кажется заметно более синей или красной, чем обычно. Таким образом, доплеровский сдвиг нелегко обнаружить в непрерывном спектре и нельзя точно измерить в таком спектре. Однако длины волн линий поглощения можно точно измерить, а их доплеровский сдвиг обнаружить относительно просто.
Пример 5.6
Эффект Доплера
Мы можем использовать уравнение эффекта Доплера для расчета радиальной скорости объекта, если нам известны три вещи: скорость света, исходная (несмещенная) длина волны излучаемого света и разница между длиной волны излучаемого света и длиной волны мы наблюдаем. Для конкретных линий поглощения или излучения мы обычно точно знаем, какую длину волны имеет линия, в наших лабораториях на Земле, где источник света не движется. Мы можем измерить новую длину волны с помощью наших инструментов в телескопе, и поэтому мы знаем разницу в длине волны из-за доплеровского сдвига. Поскольку скорость света является универсальной константой, мы можем вычислить лучевую скорость звезды.
Для конкретных линий поглощения или излучения мы обычно точно знаем, какую длину волны имеет линия, в наших лабораториях на Земле, где источник света не движется. Мы можем измерить новую длину волны с помощью наших инструментов в телескопе, и поэтому мы знаем разницу в длине волны из-за доплеровского сдвига. Поскольку скорость света является универсальной константой, мы можем вычислить лучевую скорость звезды.
Особая линия излучения водорода первоначально испускается с длиной волны 656,3 нм из газового облака. В наш телескоп мы наблюдаем, что длина волны эмиссионной линии составляет 656,6 нм. С какой скоростью движется это газовое облако к Земле или от нее?
Раствор
Поскольку свет смещается в сторону большей длины волны (красное смещение), мы знаем, что это газовое облако удаляется от нас. Скорость можно рассчитать по формуле доплеровского сдвига:
ν=c×Δλλ=(3,0×108 м/с)(0,3нм656,3нм)=(3,0×108м/с)(0,3×10–9m656,3×10–9 м)=140 000 м/с=140 км/сν=c×Δλλ=(3,0×108 м/с)(0,3 нм656,3 нм)=(3,0×108 м/с)(0,3×10–9м656. 3×10–9 м)=140 000 м/с=140 км/с
3×10–9 м)=140 000 м/с=140 км/с
Проверьте свои знания
Предположим, что спектральная линия водорода, обычно с длиной волны 500 нм, наблюдается в спектре звезды с длиной волны 500,1 нм. С какой скоростью звезда движется к Земле или от нее?
Отвечать:
Поскольку свет смещается в сторону большей длины волны, звезда удаляется от нас:
10–9m500×10–9м)=60000м/с.ν=c×Δλλ=(3,0×108м/с)(0,1мм500нм)=(3,0×108м/с)(0,1×10-9м500×10-9м)=60000 РС. Его скорость
60 000 м/с.
Теперь вы можете спросить: если все звезды движутся и движение изменяет длину волны каждой спектральной линии, не станет ли это катастрофой для астрономов, пытающихся выяснить, какие элементы присутствуют в звездах? В конце концов, именно длина волны (или цвет) сообщает астрономам, какие линии принадлежат какому элементу. И мы сначала измеряем эти длины волн в контейнерах с газом в наших лабораториях, которые не двигаются. Если теперь каждая линия в спектре звезды смещается в результате ее движения на другую длину волны (цвет), то как мы можем быть уверены, какие линии и какие элементы мы наблюдаем в звезде, скорость которой нам неизвестна?
Если теперь каждая линия в спектре звезды смещается в результате ее движения на другую длину волны (цвет), то как мы можем быть уверены, какие линии и какие элементы мы наблюдаем в звезде, скорость которой нам неизвестна?
Мужайтесь. Эта ситуация звучит хуже, чем есть на самом деле. Астрономы редко судят о наличии элемента в астрономическом объекте по одной линии. Именно паттерн линий, уникальных для водорода или кальция, позволяет нам определить, являются ли эти элементы частью звезды или галактики, которую мы наблюдаем. Эффект Доплера не изменяет рисунок линий данного элемента — он лишь немного сдвигает весь рисунок в сторону более красных или голубых длин волн. Смещенный паттерн по-прежнему довольно легко распознать. Лучше всего то, что когда мы распознаем шаблон знакомого элемента, мы получаем бонус: величина смещения шаблона может позволить нам определить скорость объектов в поле нашего зрения.
Подготовка астрономов включает в себя большую работу по обучению расшифровке света (и другого электромагнитного излучения). Умелый «декодер» может узнать температуру звезды, какие в ней элементы и даже ее скорость в направлении к нам или от нас. Это действительно впечатляющий объем информации о звездах, находящихся на расстоянии световых лет.
Умелый «декодер» может узнать температуру звезды, какие в ней элементы и даже ее скорость в направлении к нам или от нас. Это действительно впечатляющий объем информации о звездах, находящихся на расстоянии световых лет.
Эффект Доплера
Эффект ДоплераДэниел А. Рассел , Аспирантура по акустике, Пенсильванский государственный университет
Весь текст и изображения на этой странице принадлежат Дэниелу А. Расселу © 2014 и не могут использоваться на других веб-страницах или в отчетах без разрешения.
Содержание этой страницы было первоначально опубликовано 23 июля 1997 г. . HTML-код был изменен для обеспечения совместимости с HTML5 12 сентября 2014 года.
Внезапное изменение высоты звука автомобильного гудка, когда автомобиль проезжает мимо (движение источника) или высоты звука магнитофона на тротуаре, когда вы проезжаете мимо в своей машине (движение наблюдателя), впервые было объяснено в 1842 году Кристианом Допплером. . Его Эффект Доплера — это сдвиг частоты и длины волны, возникающий в результате движения источника относительно среды, приемника, движущегося относительно среды, или даже самой движущейся среды.
. Его Эффект Доплера — это сдвиг частоты и длины волны, возникающий в результате движения источника относительно среды, приемника, движущегося относительно среды, или даже самой движущейся среды.
Воспринимаемая частота ( f ´) связана с фактической частотой ( f 0 ) и относительными скоростями источника ( v с ), наблюдателя ( v 8 o ) , а скорость ( v ) волн в среде на $$ f’=f_O\biggl ( \frac{v\pm v_o}{v \pm v_s}\biggr ) $$ Выбор использования знака плюс (+) или минус (-) сделан в соответствии с соглашением, согласно которому, если относительное движение источника и наблюдателя таково, что они движутся навстречу друг другу, воспринимаемая частота ( f ´) на выше фактической частоты ( f 0 ). Точно так же, если относительное движение источника и наблюдателя таково, что они движутся от друг от друга, воспринимаемая частота ( f ´ ) на ниже фактической частоты ( f 0 ). Хотя эффект Доплера впервые был обнаружен для звуковых волн, он справедлив для всех типов волн, включая световые и другие электромагнитные волны (хотя для электромагнитных волн — из-за теории Эйнштейна или теории относительности — имеет значение только относительная скорость, и не имеет значения, является ли источник или наблюдатель движется). Эффект Доплера для световых волн обычно описывается с точки зрения цвета, а не частоты. Красное смещение возникает, когда источник и наблюдатель удаляются друг от друга, а синее смещение возникает, когда источник и наблюдатель движутся навстречу друг другу. Красное смещение света от далеких галактик доказывает, что Вселенная расширяется. Анимация ниже иллюстрирует это явление для движущегося источника звуковых волн и неподвижного наблюдателя. Анимация слева показывает стационарный источник звука. Звуковые волны производятся с постоянной частотой f 0 , а волновые фронты распространяются симметрично от источника с постоянной скоростью v , которая является скоростью звука в среде. Фильм, показывающий, как могут быть созданы круговые волны (с точки зрения движения частиц и волн), смотрите здесь. На анимации слева тот же источник звука излучает звуковые волны с постоянной частотой в той же среде. Однако теперь источник звука движется вправо со скоростью v с = 0,7 v (0,7 Маха). Волновые фронты создаются с той же частотой, что и раньше. Однако, поскольку источник движется, центр каждого нового волнового фронта теперь немного смещается вправо. В результате волновые фронты начинают сгущаться с правой стороны (перед) и расходиться дальше с левой стороны (сзади) от источника. Наблюдатель перед источником будет слышать более высокую частоту f ´ > f 0 , а наблюдатель за источником услышит более низкую частоту f ´ < f 0 . Теперь источник движется со скоростью звука в среде ( v с = c , или 1,0 Маха). Скорость звука в воздухе на уровне моря составляет около 340 м/с или около 750 миль в час. Волновые фронты перед источником теперь все сгруппированы в одной точке. В результате наблюдатель перед источником ничего не обнаружит, пока источник не прибудет. Фронт давления будет довольно интенсивным (ударная волна) из-за того, что все волновые фронты складываются вместе, и будет восприниматься не как высота звука, а как «удар» звука при прохождении стены давления. На рисунке справа показана пуля, летящая со скоростью 1,01 Маха. Вы можете видеть фронт ударной волны прямо перед пулей. Пилоты реактивных самолетов, летящие со скоростью 1 Маха, сообщают, что существует заметная «стена» или «барьер», который необходимо преодолеть, прежде чем достичь сверхзвуковой скорости.
Стационарный источник звука
 Расстояние между волновыми фронтами равно длине волны. Все наблюдатели будут слышать одну и ту же частоту, которая будет равна фактической частоте источника.
Расстояние между волновыми фронтами равно длине волны. Все наблюдатели будут слышать одну и ту же частоту, которая будет равна фактической частоте источника. Источник движется с v
с < c (0,7 Маха)
Источник, движущийся с v
с = c (1 Маха – преодоление звукового барьера) Эта «стена» возникает из-за интенсивного фронта давления, и полет в пределах этого фронта давления создает очень турбулентную и упругую езду. Чак Йегер.0249
Эта «стена» возникает из-за интенсивного фронта давления, и полет в пределах этого фронта давления создает очень турбулентную и упругую езду. Чак Йегер.0249
Источник движется с v
с > c (1,4 Маха – сверхзвук)Источник звука преодолел барьер скорости звука и движется со скоростью, в 1,4 раза превышающей скорость звука (1,4 Маха). Поскольку источник движется быстрее, чем создаваемые им звуковые волны, он фактически опережает распространяющийся волновой фронт. Источник звука пройдет мимо неподвижного наблюдателя до того, как наблюдатель действительно услышит создаваемый им звук.
При просмотре анимации обратите внимание на четкое формирование конуса Маха , угол которого зависит от отношения скорости источника к скорости звука.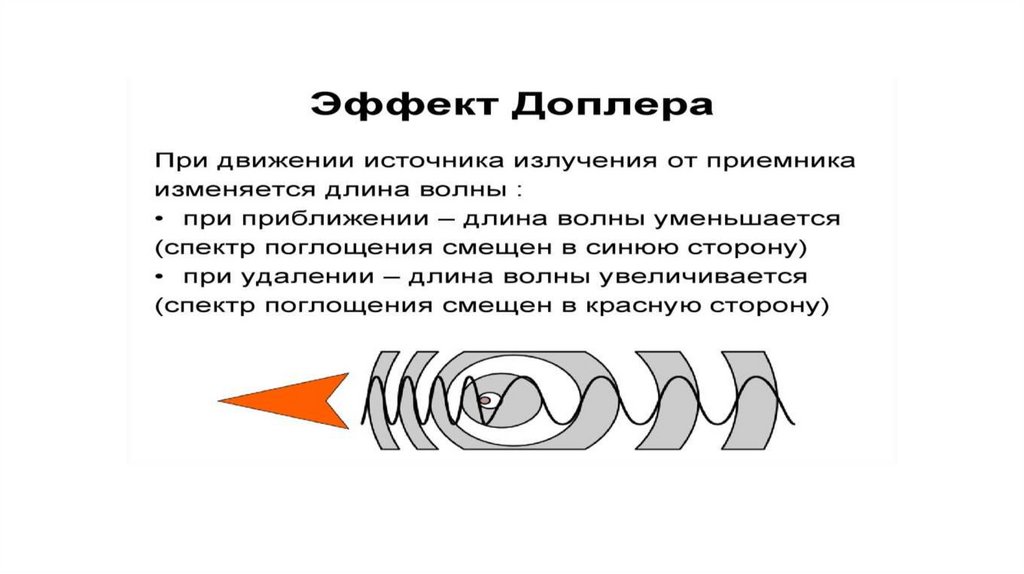 Именно этот интенсивный фронт давления на конус Маха вызывает ударную волну , известную как звуковой удар , когда сверхзвуковой самолет пролетает над головой. Ударная волна распространяется со скоростью звука v , а поскольку она складывается из всех объединенных волновых фронтов, звук, слышимый наблюдателем, будет достаточно интенсивным. Сверхзвуковой самолет обычно производит два звуковых удара, один из носа самолета, а другой из его хвоста, что приводит к двойному удару. На рисунке справа показана пуля, летящая со скоростью 2,45 Маха. Конус Маха и фронты ударных волн очень заметны.
Именно этот интенсивный фронт давления на конус Маха вызывает ударную волну , известную как звуковой удар , когда сверхзвуковой самолет пролетает над головой. Ударная волна распространяется со скоростью звука v , а поскольку она складывается из всех объединенных волновых фронтов, звук, слышимый наблюдателем, будет достаточно интенсивным. Сверхзвуковой самолет обычно производит два звуковых удара, один из носа самолета, а другой из его хвоста, что приводит к двойному удару. На рисунке справа показана пуля, летящая со скоростью 2,45 Маха. Конус Маха и фронты ударных волн очень заметны.
На картинке слева показан фронт ударной волны, созданный T-38 Talon , двухмоторным высотным сверхзвуковым учебно-тренировочным самолетом.
На этом снимке показан звуковой удар, созданный автомобилем команды THRUST SSC, когда он побил рекорд наземной скорости (а также преодолел звуковой барьер на суше). Нажмите на изображение, чтобы загрузить увеличенную версию изображения.
Эта веб-страница получила рейтинг «пять звезд» () от группы опытных учителей Schoolzone.
Объяснение: эффект Доплера
Рябь в пруду помогает проиллюстрировать движение волн и эффект Доплера. Flickr/Доун Эллнер, CC BY
Джиллиан Изоарди, Квинслендский технологический университет,
Автор
- Джиллиан Изоарди
Преподаватель факультета оптической физики и инженерии Технологического университета Квинсленда.
Заявление о раскрытии информации
Джиллиан Изоарди не работает, не консультирует, не владеет акциями и не получает финансирование от какой-либо компании или организации, которые могли бы извлечь выгоду из этой статьи, и не раскрыла никаких соответствующих связей, помимо своей академической должности.
Партнеры
Технологический университет Квинсленда предоставляет финансирование в качестве члена The Conversation AU.
Посмотреть всех партнеров
Когда машина скорой помощи проезжает с ревущей сиреной, вы слышите, как меняется тон сирены: по мере приближения сирена звучит выше, чем когда она удаляется от вас. Это изменение является обычной физической демонстрацией эффекта Доплера.
Эффект Доплера описывает изменение наблюдаемой частоты волны при относительном движении между источником волны и наблюдателем. Впервые он был предложен в 1842 году австрийским математиком и физиком Кристианом Иоганном Допплером. Наблюдая за далекими звездами, Доплер описал, как цвет звездного света менялся при движении звезды.
Чтобы объяснить, почему возникает эффект Доплера, нам нужно начать с нескольких основных особенностей волнового движения. Волны бывают разных форм: рябь на поверхности пруда, звуки (как в случае с сиреной выше), свет и толчки при землетрясении демонстрируют периодическое волновое движение.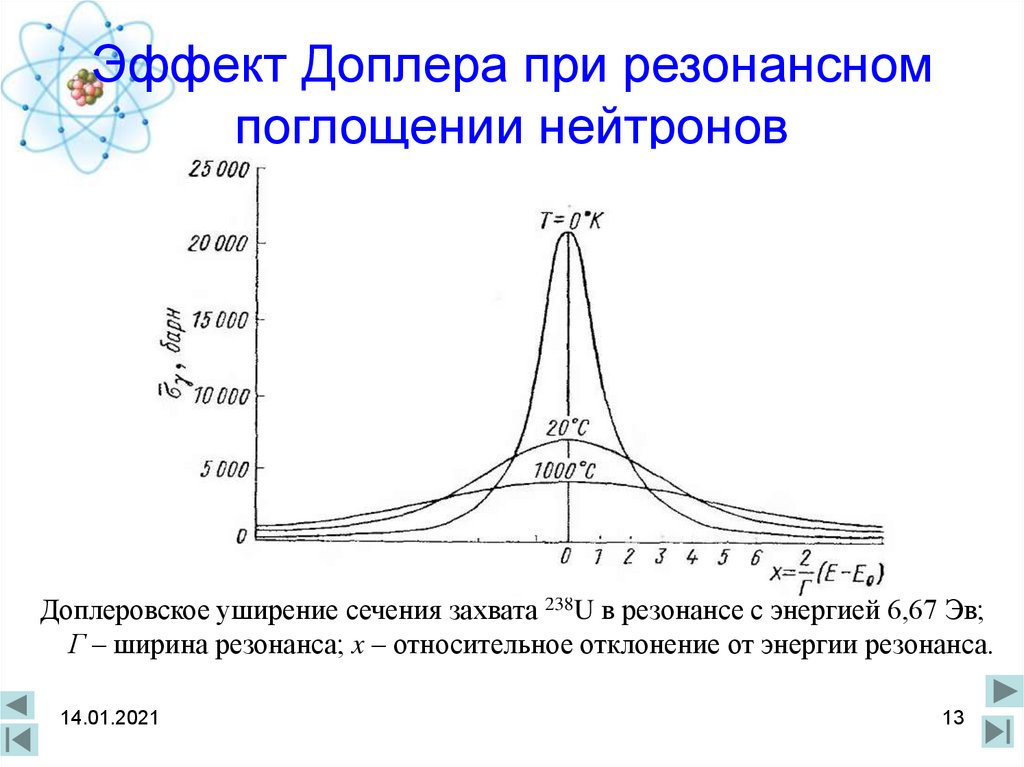
Двумя общими характеристиками, используемыми для описания всех типов волнового движения, являются длина волны и [частота](http://encyclopedia2.thefreedictionary.com/Frequency+(wave+motion). Если вы считаете, что волна имеет пики и впадины, длина волны — это расстояние между последовательными пиками, а частота — это количество пиков, которые проходят контрольную точку за заданный период времени.0005 Снимок движущейся волны, показывающий длину волны. Джиллиан Изоарди
Когда нам нужно подумать о том, как волны распространяются в двух- или трехмерном пространстве, мы используем термин волновой фронт для описания связи всех общих точек волны.
Таким образом, объединение всех волновых пиков, исходящих из точки, где в пруд брошен камешек, создаст серию круглых волновых фронтов (рябь), если смотреть сверху.
Волновые фронты, выходящие из центрального источника. Джиллиан Изоарди Рассмотрим стационарный источник, излучающий волны во всех направлениях с постоянной частотой. Форма волновых фронтов, исходящих от источника, описывается серией концентрических, равномерно расположенных «оболочек». Любой человек, стоящий рядом с источником, встретит каждый волновой фронт с той же частотой, на которой он был испущен.
Форма волновых фронтов, исходящих от источника, описывается серией концентрических, равномерно расположенных «оболочек». Любой человек, стоящий рядом с источником, встретит каждый волновой фронт с той же частотой, на которой он был испущен.
Но если источник волны движется, картина волновых фронтов будет выглядеть по-другому. За время между испусканием одного волнового пика и следующим источник сместится так, что оболочки перестанут быть концентрическими. Волновые фронты будут группироваться (сближаться) перед источником, когда он движется, и будут разнесены (дальше друг от друга) позади него.
Теперь человек, стоящий перед движущимся источником, будет наблюдать более высокую частоту, чем раньше, когда источник движется к ним. И наоборот, кто-то позади источника будет наблюдать более низкую частоту пиков волны по мере того, как источник удаляется от него.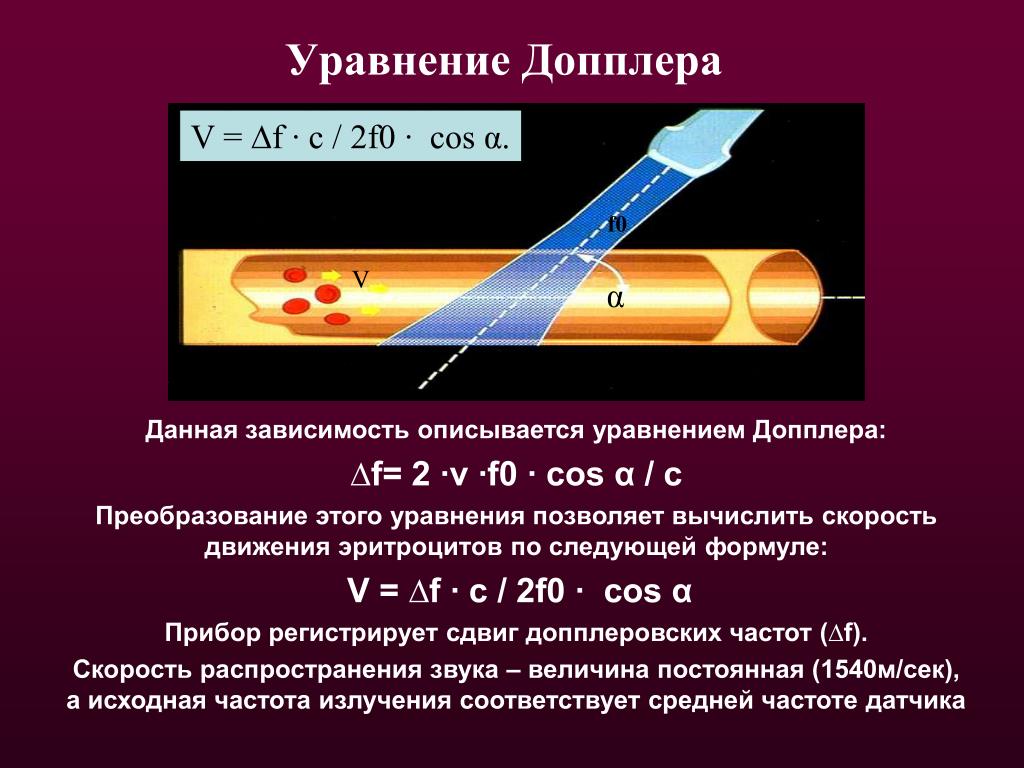
Это показывает, как движение источника влияет на частоту, воспринимаемую неподвижным наблюдателем. Аналогичное изменение наблюдаемой частоты происходит, если источник неподвижен, а наблюдатель движется к нему или от него.
На самом деле, любое относительное движение между ними вызовет доплеровский сдвиг/эффект наблюдаемой частоты.
Так почему же мы слышим изменение высоты звука проходящих сирен? Высота звука, которую мы слышим, зависит от частоты звуковой волны. Высокая частота соответствует высокому тону. Таким образом, в то время как сирена производит волны постоянной частоты, по мере приближения к нам наблюдаемая частота увеличивается, и наше ухо слышит более высокий тон.
После того, как он прошел мимо нас и удаляется, наблюдаемая частота и высота тона падают. Истинный тон сирены находится где-то между тем, что мы слышим, когда она приближается к нам, и тем, что мы слышим, когда она удаляется.
Для световых волн частота определяет цвет, который мы видим. Самые высокие частоты света находятся в синей части видимого спектра; самые низкие частоты появляются на красном конце этого спектра.
Если звезды и галактики удаляются от нас, видимая частота излучаемого ими света уменьшается, а их цвет смещается в сторону красного конца спектра. Это известно как красное смещение.
Звезда, летящая к нам, будет иметь синее смещение (более высокая частота). Это явление впервые привело Кристиана Доплера к документированию одноименного эффекта и в конечном итоге позволило Эдвину Хабблу в 1919 г.29, чтобы предположить, что Вселенная расширяется, когда он заметил, что все галактики оказались смещенными в красную сторону (то есть удалялись от нас и друг от друга).
Эффект Доплера имеет множество других интересных применений, помимо звуковых эффектов и астрономии. Доплеровский радар использует отраженные микроволны для определения скорости удаленных движущихся объектов. Он делает это, посылая волны с определенной частотой, а затем анализируя отраженную волну на предмет изменений частоты.
Он делает это, посылая волны с определенной частотой, а затем анализируя отраженную волну на предмет изменений частоты.
Он применяется при наблюдении за погодой для характеристики движения облаков и погодных условий, а также имеет другие применения в авиации и радиологии. Он даже используется в полицейских детекторах скорости, которые по сути представляют собой небольшие доплеровские радары.
Медицинская визуализация также использует эффект Доплера для мониторинга кровотока через сосуды в организме. Ультразвуковая допплерография использует высокочастотные звуковые волны и позволяет нам измерять скорость и направление кровотока, чтобы предоставить информацию о тромбах, закупоренных артериях и сердечной функции у взрослых и развивающихся плодов.
Наше понимание эффекта Доплера позволило нам больше узнать о Вселенной, частью которой мы являемся, измерить окружающий мир и заглянуть внутрь собственного тела. Дальнейшее развитие этих знаний, в том числе о том, как обратить вспять эффект Доплера, может привести к созданию технологий, о которых раньше читали только в научно-фантастических романах, таких как плащи-невидимки.
См. другие пояснительные статьи на The Conversation.
- Эффект Допплера
- Физика
- объяснитель
- Астрофизика
17.8: Эффект Доплера – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4736
- OpenStax
- OpenStax
Цели обучения
- Объяснить изменение наблюдаемой частоты при приближении или удалении движущегося источника звука от неподвижного наблюдателя
- Объясните изменение наблюдаемой частоты по мере того, как наблюдатель движется к стационарному источнику звука или от него
Характерный звук проезжающего мимо мотоцикла является примером эффекта Доплера . В частности, если вы стоите на углу улицы и наблюдаете, как машина скорой помощи со звуком сирены проезжает с постоянной скоростью, вы заметите два характерных изменения в звуке сирены. Во-первых, громкость звука увеличивается по мере приближения машины скорой помощи и уменьшается по мере ее удаления, что и ожидалось. Но, кроме того, высокий звук сирены резко меняется на более низкий звук. Когда машина скорой помощи проезжает, частота звука, слышимого стационарным наблюдателем, изменяется с постоянной высокой частоты на постоянную более низкую частоту, даже если сирена излучает постоянную частоту источника. Чем ближе проезжает скорая помощь, тем резче сдвиг. Кроме того, чем быстрее движется машина скорой помощи, тем больше смещение. Мы также слышим этот характерный сдвиг частоты для проезжающих автомобилей, самолетов и поездов.
В частности, если вы стоите на углу улицы и наблюдаете, как машина скорой помощи со звуком сирены проезжает с постоянной скоростью, вы заметите два характерных изменения в звуке сирены. Во-первых, громкость звука увеличивается по мере приближения машины скорой помощи и уменьшается по мере ее удаления, что и ожидалось. Но, кроме того, высокий звук сирены резко меняется на более низкий звук. Когда машина скорой помощи проезжает, частота звука, слышимого стационарным наблюдателем, изменяется с постоянной высокой частоты на постоянную более низкую частоту, даже если сирена излучает постоянную частоту источника. Чем ближе проезжает скорая помощь, тем резче сдвиг. Кроме того, чем быстрее движется машина скорой помощи, тем больше смещение. Мы также слышим этот характерный сдвиг частоты для проезжающих автомобилей, самолетов и поездов.
Эффект Доплера — это изменение наблюдаемой частоты звука из-за движения либо источника, либо наблюдателя. Хотя этот эффект менее известен, он легко заметен для стационарного источника и движущегося наблюдателя. Например, если вы проедете в поезде мимо стационарного звукового сигнала, вы услышите, как частота звукового сигнала смещается с высокой на низкую, когда вы проходите мимо. Фактическое изменение частоты из-за относительного движения источника и наблюдателя называется доплеровским сдвигом . Эффект Доплера и доплеровский сдвиг названы в честь австрийского физика и математика Кристиана Иоганна Доплера (1803–1853), который проводил эксперименты как с движущимися источниками, так и с движущимися наблюдателями. Допплер, например, заставил музыкантов играть в движущемся открытом вагоне поезда, а также играть стоя рядом с железнодорожными путями, когда поезд проезжал мимо. Их музыку наблюдали как в поезде, так и вне его, и измеряли изменения частоты.
Например, если вы проедете в поезде мимо стационарного звукового сигнала, вы услышите, как частота звукового сигнала смещается с высокой на низкую, когда вы проходите мимо. Фактическое изменение частоты из-за относительного движения источника и наблюдателя называется доплеровским сдвигом . Эффект Доплера и доплеровский сдвиг названы в честь австрийского физика и математика Кристиана Иоганна Доплера (1803–1853), который проводил эксперименты как с движущимися источниками, так и с движущимися наблюдателями. Допплер, например, заставил музыкантов играть в движущемся открытом вагоне поезда, а также играть стоя рядом с железнодорожными путями, когда поезд проезжал мимо. Их музыку наблюдали как в поезде, так и вне его, и измеряли изменения частоты.
Что вызывает доплеровский сдвиг? На рисунке \(\PageIndex{1}\) показаны звуковые волны, излучаемые стационарными и движущимися источниками в неподвижной воздушной массе. Каждое возмущение распространяется сферически от точки, в которой излучается звук.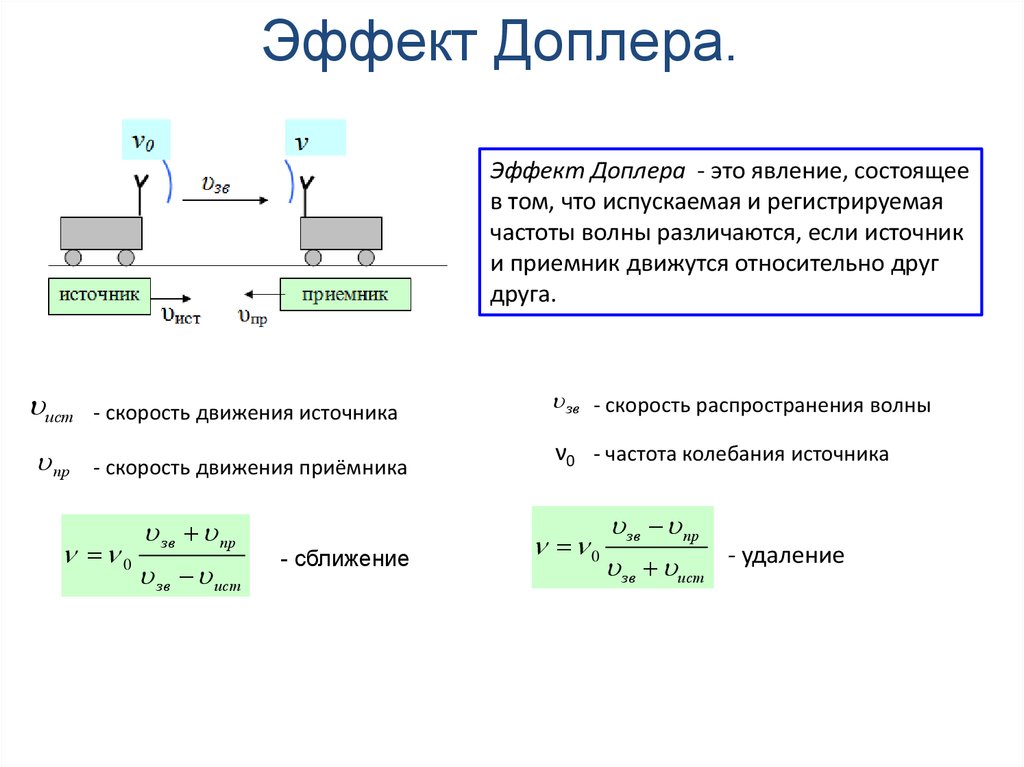 Если источник неподвижен, то центр всех сфер, представляющих сжатие воздуха в звуковой волне, находится в одной точке, и неподвижные наблюдатели с обеих сторон слышат ту же длину волны и частоту, что и источник (случай а). Если источник движется, ситуация иная. Каждое сжатие воздуха движется по сфере из точки, в которой он был выпущен, но точка выброса движется. Эта движущаяся точка выброса заставляет сжатия воздуха быть ближе друг к другу с одной стороны и дальше друг от друга с другой. Таким образом, длина волны меньше в направлении движения источника (справа в случае б) и длиннее в противоположном направлении (слева в случае б). Наконец, если наблюдатели перемещаются, как в случае (с), частота, с которой они получают сжатия, изменяется. Наблюдатель, движущийся к источнику, принимает их с более высокой частотой, а человек, удаляющийся от источника, принимает их с более низкой частотой.
Если источник неподвижен, то центр всех сфер, представляющих сжатие воздуха в звуковой волне, находится в одной точке, и неподвижные наблюдатели с обеих сторон слышат ту же длину волны и частоту, что и источник (случай а). Если источник движется, ситуация иная. Каждое сжатие воздуха движется по сфере из точки, в которой он был выпущен, но точка выброса движется. Эта движущаяся точка выброса заставляет сжатия воздуха быть ближе друг к другу с одной стороны и дальше друг от друга с другой. Таким образом, длина волны меньше в направлении движения источника (справа в случае б) и длиннее в противоположном направлении (слева в случае б). Наконец, если наблюдатели перемещаются, как в случае (с), частота, с которой они получают сжатия, изменяется. Наблюдатель, движущийся к источнику, принимает их с более высокой частотой, а человек, удаляющийся от источника, принимает их с более низкой частотой.
 (а) Когда источник, наблюдатели и воздух неподвижны, длина волны и частота одинаковы во всех направлениях и для всех наблюдателей. (б) Звуки, излучаемые источником, движущимся вправо, распространяются от точек, в которых они излучались. Длина волны уменьшается, и, следовательно, частота увеличивается в направлении движения, так что наблюдатель справа слышит более высокий звук. Противоположное верно для наблюдателя слева, где длина волны увеличивается, а частота уменьшается. в) Тот же эффект возникает при движении наблюдателей относительно источника. Движение к источнику увеличивает частоту, поскольку наблюдатель справа проходит через большее количество гребней волны, чем если бы он оставался неподвижным. При движении от источника частота уменьшается, поскольку наблюдатель слева проходит через меньшее количество гребней волны, чем если бы он оставался неподвижным.
(а) Когда источник, наблюдатели и воздух неподвижны, длина волны и частота одинаковы во всех направлениях и для всех наблюдателей. (б) Звуки, излучаемые источником, движущимся вправо, распространяются от точек, в которых они излучались. Длина волны уменьшается, и, следовательно, частота увеличивается в направлении движения, так что наблюдатель справа слышит более высокий звук. Противоположное верно для наблюдателя слева, где длина волны увеличивается, а частота уменьшается. в) Тот же эффект возникает при движении наблюдателей относительно источника. Движение к источнику увеличивает частоту, поскольку наблюдатель справа проходит через большее количество гребней волны, чем если бы он оставался неподвижным. При движении от источника частота уменьшается, поскольку наблюдатель слева проходит через меньшее количество гребней волны, чем если бы он оставался неподвижным. Мы знаем, что длина волны и частота связаны соотношением v = f\(\lambda\), где v — фиксированная скорость звука. Звук движется в среде и имеет в этой среде одинаковую скорость v независимо от того, движется источник или нет. Таким образом, f, умноженное на \(\lambda\), является константой. Поскольку наблюдатель справа в случае (b) получает более короткую длину волны, частота, которую он принимает, должна быть выше. Точно так же наблюдатель слева получает более длинную волну и, следовательно, слышит более низкую частоту. То же самое происходит и в случае (с). Наблюдатель, движущийся к источнику, принимает более высокую частоту, а наблюдатель, удаляющийся от источника, принимает более низкую частоту. В общем, относительное движение источника и наблюдателя друг к другу увеличивает принимаемую частоту. Относительное движение врозь снижает частоту. Чем больше относительная скорость, тем больше эффект.
Таким образом, f, умноженное на \(\lambda\), является константой. Поскольку наблюдатель справа в случае (b) получает более короткую длину волны, частота, которую он принимает, должна быть выше. Точно так же наблюдатель слева получает более длинную волну и, следовательно, слышит более низкую частоту. То же самое происходит и в случае (с). Наблюдатель, движущийся к источнику, принимает более высокую частоту, а наблюдатель, удаляющийся от источника, принимает более низкую частоту. В общем, относительное движение источника и наблюдателя друг к другу увеличивает принимаемую частоту. Относительное движение врозь снижает частоту. Чем больше относительная скорость, тем больше эффект.
Эффект Доплера возникает не только для звука, но и для любой волны, когда существует относительное движение между наблюдателем и источником. Доплеровские сдвиги возникают, например, в частоте звуковых, световых и водных волн. Доплеровские сдвиги можно использовать для определения скорости, например, когда ультразвук отражается от крови при медицинской диагностике. Относительные скорости звезд и галактик определяются сдвигом частот света, получаемого от них, и многое говорят о происхождении Вселенной. На современную физику глубоко повлияли наблюдения доплеровских сдвигов.
Относительные скорости звезд и галактик определяются сдвигом частот света, получаемого от них, и многое говорят о происхождении Вселенной. На современную физику глубоко повлияли наблюдения доплеровских сдвигов.
Рассмотрим двух стационарных наблюдателей X и Y на рисунке \(\PageIndex{2}\), расположенных по обе стороны от стационарного источника. Каждый наблюдатель слышит одну и ту же частоту, и эта частота является частотой, создаваемой стационарным источником.
Рисунок \(\PageIndex{2}\): Неподвижный источник излучает звуковые волны с постоянной частотой f s , с постоянной длиной волны \(\lambda_{s}\) со скоростью звука v. Два стационарные наблюдатели X и Y по обе стороны от источника наблюдают частоту fo = f s , с длиной волны \(\lambda_{o} = \lambda_{s}\). Теперь рассмотрим стационарного наблюдателя X с источником, удаляющимся от наблюдателя с постоянной скоростью v s < v (рис. \(\PageIndex{3}\)). В момент времени t = 0 источник посылает звуковую волну, обозначенную черным цветом. Эта волна движется со скоростью звука v. Положение звуковой волны на каждом временном интервале периода T с показано пунктирными линиями. Через один период источник переместился \(\Delta\)x = v s T s и испускает вторую звуковую волну, которая движется со скоростью звука. Источник продолжает двигаться и производить звуковые волны, на что указывают кружки с номерами 3 и 4. Обратите внимание, что по мере того, как волны удаляются, они остаются центрированными в соответствующей точке происхождения.
Эта волна движется со скоростью звука v. Положение звуковой волны на каждом временном интервале периода T с показано пунктирными линиями. Через один период источник переместился \(\Delta\)x = v s T s и испускает вторую звуковую волну, которая движется со скоростью звука. Источник продолжает двигаться и производить звуковые волны, на что указывают кружки с номерами 3 и 4. Обратите внимание, что по мере того, как волны удаляются, они остаются центрированными в соответствующей точке происхождения.
 Пунктирные линии используются для отображения положения волн в каждый период времени. Наблюдатель слышит длину волны \(\lambda_{o} = \lambda_{s} + \Delta x = \lambda_{s} + v_{s}T_{s}\).
Пунктирные линии используются для отображения положения волн в каждый период времени. Наблюдатель слышит длину волны \(\lambda_{o} = \lambda_{s} + \Delta x = \lambda_{s} + v_{s}T_{s}\).Используя тот факт, что длина волны равна произведению скорости на период, а период обратно пропорционален частоте, мы можем вывести наблюдаемую частоту:
\[\begin{align} \lambda_{o} & = \lambda_{s} + \Delta x \\ vT_{o} & = vT_{s} + v_{s} T_{s} \\ \dfrac {v}{f_{o}} & = \dfrac{v}{f_{s}} + \dfrac{v_{s}}{f_{s}} = \dfrac{v + v_{s}}{f_ {s}} \\ f_{o} & = f_{s} \left(\dfrac{v}{v}{v + v_{s}}\right) \ldotp \end{align}\]
При перемещении источника вдали от наблюдателя наблюдаемая частота ниже частоты источника.
Теперь рассмотрим источник, движущийся с постоянной скоростью v s , движущийся к неподвижному наблюдателю Y, также показанному на рисунке \(\PageIndex{3}\). Длина волны определяется Y как \(\lambda_{o} = \lambda_{s} – \Delta x = \lambda_{s} – v_{s} T_{s}\). Снова, используя тот факт, что длина волны равна произведению скорости на период, а период обратно пропорционален частоте, мы можем вывести наблюдаемую частоту:0005
\[\begin{split} \lambda_{o} & = \lambda_{s} – \Delta x \\ vT_{o} & = vT_{s} – v_{s} T_{s} \\ \dfrac {v}{f_{o}} & = \dfrac{v}{f_{s}} – \dfrac{v_{s}}{f_{s}} = \dfrac{v – v_{s}}{f_ {s}} \\ f_{o} & = f_{s} \left(\dfrac{v}{v – v_{s}}\right) \ldotp \end{split}\]
Когда источник движется, а наблюдатель неподвижен, наблюдаемая частота равна
\[f_{o} = f_{s} \left(\dfrac{v}{v \mp v_{s}}\right), \label{17. 18} \]
18} \]
где f o – частота, наблюдаемая неподвижным наблюдателем, f с — частота, создаваемая движущимся источником, v — скорость звука, v с — постоянная скорость источника, верхний знак соответствует источнику, приближающемуся к наблюдателю, а нижний знак — источнику. отходит от наблюдателя.
Что произойдет, если наблюдатель движется, а источник неподвижен? Если наблюдатель движется к стационарному источнику, наблюдаемая частота выше, чем частота источника. Если наблюдатель удаляется от стационарного источника, наблюдаемая частота ниже частоты источника. Рассмотрим наблюдателя X на рисунке \(\PageIndex{4}\), поскольку наблюдатель движется к стационарному источнику со скоростью v или . Источник излучает тон с постоянной частотой f с и постоянным периодом T с . Наблюдатель слышит первую волну, излучаемую источником. Если бы наблюдатель был неподвижен, то время прохождения одной длины волны звука должно быть равно периоду источника T с .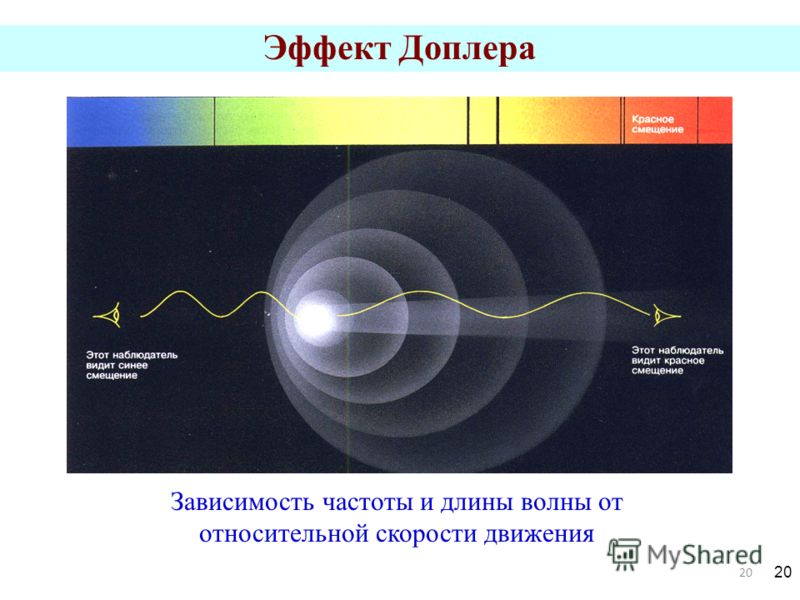 Поскольку наблюдатель движется к источнику, время прохождения одной длины волны меньше T с и равно наблюдаемому периоду T o = T с − \(\Delta\)t. В момент времени t = 0 наблюдатель начинает с начала длины волны и движется ко второй длине волны по мере того, как длина волны удаляется от источника. Длина волны равна расстоянию, пройденному наблюдателем, плюс расстояние, пройденное звуковой волной до встречи с наблюдателем:
Поскольку наблюдатель движется к источнику, время прохождения одной длины волны меньше T с и равно наблюдаемому периоду T o = T с − \(\Delta\)t. В момент времени t = 0 наблюдатель начинает с начала длины волны и движется ко второй длине волны по мере того, как длина волны удаляется от источника. Длина волны равна расстоянию, пройденному наблюдателем, плюс расстояние, пройденное звуковой волной до встречи с наблюдателем:
\[\begin{split} \lambda_{s} & = vT_{o} + v_{o} T_{o} \\ vT_{s} & = (v + v_{o}) T_{o} \ \ v \left(\dfrac{1}{f_{s}}\right) & = (v + v_{o}) \left(\dfrac{1}{f_{o}}\right) \\ f_{ o} & = f_{s} \left(\dfrac{v + v_{o}}{v}\right) \ldotp \end{split}\]
Рисунок \(\PageIndex{4}\): Стационарный источник излучает звуковую волну с постоянной частотой f s , с постоянной длиной волны \(\lambda_{s}\), движущуюся со скоростью звука v. Наблюдатель X движется к источнику с постоянной скоростью v o , а на рисунке показано начальное и конечное положение наблюдателя X. Наблюдатель X наблюдает частоту выше частоты источника. Сплошные линии показывают положение волн при t = 0. Пунктирные линии показывают положение волн при t = T o .
Наблюдатель X наблюдает частоту выше частоты источника. Сплошные линии показывают положение волн при t = 0. Пунктирные линии показывают положение волн при t = T o .Если наблюдатель удаляется от источника (рисунок \(\PageIndex{5}\)), можно найти наблюдаемую частоту:
\[\begin{split} \lambda_{s} & = vT_{o} – v_{o} T_{o} \\ vT_{s} & = (v – v_{o}) T_{o} \\ v \left(\dfrac{1}{f_{s}}\right) & = (v – v_{o}) \left(\dfrac{1}{f_{o}}\right) \\ f_{o} & = f_{s} \left(\dfrac{v – v_{o} }{v}\right) \ldotp \end{split}\]
Рисунок \(\PageIndex{5}\): Неподвижный источник излучает звуковую волну с постоянной частотой f s , с постоянной длиной волны \(\lambda_{s}\), движущуюся со скоростью звука v. Наблюдатель Y удаляется от источника с постоянной скоростью v o , а на рисунке показано начальное и конечное положение наблюдателя Y. Наблюдатель Y наблюдает с частотой ниже частоты источника. Сплошные линии показывают положение волн при t = 0. Пунктирные линии показывают положение волн при t = T или .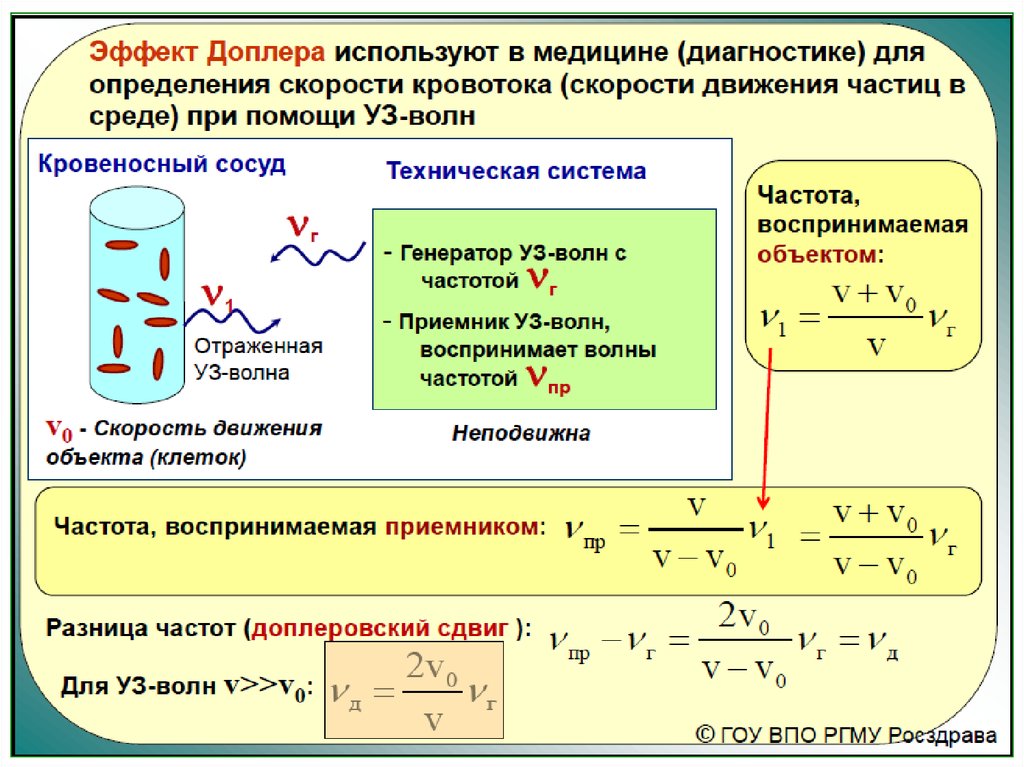
Уравнения для наблюдателя, движущегося к стационарному источнику или от него, можно объединить в одно уравнение:
\[f_{o} = f_{s} \left(\dfrac{v \pm v_{o}}{v }\right), \label{17.19}\]
где f o – наблюдаемая частота, f s – частота источника, v – скорость звука, v o – скорость наблюдателя , верхний знак соответствует наблюдателю, приближающемуся к источнику, а нижний знак — наблюдателю, удаляющемуся от источника. Уравнение \ref{17.18} и Уравнение \ref{17.19} можно обобщить в одном уравнении (верхний знак соответствует приближению) и дополнительно проиллюстрировать в таблице \(\PageIndex{1}\), где f o — наблюдаемая частота, f s — частота источника, v — скорость звука, v o — скорость наблюдателя, v s — скорость источника, верхний знак — приближение, нижний — удаление.
\[f_{o} = f_{s} \left(\dfrac{v \pm v_{o}}{v \mp v_{s}}\right), \label{17.20}\]
| Доплеровский сдвиг \(f_{o} = f_{s} \left(\dfrac{v \pm v_{o}}{v \mp v_{s}}\right)\) | Стационарный наблюдатель | Наблюдатель движется к источнику | Наблюдатель удаляется от источника |
|---|---|---|---|
| Стационарный источник | $$f_{o} = f_{s} \номер $$ | $$f_{o} = f_{s} \left(\dfrac{v + v_{o}}{v} \right) \nonumber $$ | $$f_{o} = f_{s} \left(\dfrac{v – v_{o}}{v}\right) \nonumber $$ |
| Источник движется к наблюдателю | $$f_{o} = f_{s} \left(\dfrac{v}{v – v_{s}}\right) \nonumber $$ | $$f_{o} = f_{s} \left(\dfrac{v + v_{o}}{v – v_{s}}\right) \nonumber $$ | $$f_{o} = f_{s} \left(\dfrac{v – v_{o}}{v – v_{s}}\right) \nonumber $$ |
| Источник удаляется от наблюдателя | $$f_{o} = f_{s} \left(\dfrac{v}{v+v_{s}}\right) \nonumber $$ | $$f_{o} = f_{s} \left(\dfrac{v + v_{o}}{v + v_{s}}\right) \nonumber $$ | $$f_{o} = f_{s} \left(\dfrac{v – v_{o}}{v + v_{s}}\right) \nonumber $$ |
Примечание
Эффект Доплера связан с движением, и это видео поможет визуализировать эффекты движущегося наблюдателя или источника. На видео показаны движущийся источник и неподвижный наблюдатель, а также движущийся наблюдатель и неподвижный источник. Также обсуждается эффект Доплера и его применение к свету.
На видео показаны движущийся источник и неподвижный наблюдатель, а также движущийся наблюдатель и неподвижный источник. Также обсуждается эффект Доплера и его применение к свету.
Пример \(\PageIndex{1}\): расчет доплеровского сдвига
Предположим, поезд с рупором 150 Гц движется со скоростью 35,0 м/с в неподвижном воздухе в день, когда скорость звука составляет 340 м. /с.
- Какие частоты наблюдает человек, стоящий на обочине пути при приближении поезда и после его прохождения?
- Какую частоту наблюдает машинист, едущий в поезде?
Стратегия
Чтобы найти наблюдаемую частоту в (а), мы должны использовать f obs = f s \(\left(\dfrac{v}{v \mp v_{s}}\right)\), потому что источник движется. Знак «минус» используется для приближающегося поезда, а знак «плюс» — для удаляющегося поезда. В (b) есть два доплеровских смещения — одно для движущегося источника и другое для движущегося наблюдателя.
Решение
- Введите известные значения в f o = f s \(\left(\dfrac{v}{v – v_{s}}\right)\): $$f_{o } = f_{s} \left(\dfrac{v}{v – v_{s}}\right) = (150\; Гц) \left(\dfrac{340\; м/с}{340\; м /с – 35,0\; м/с}\right) \ldotp$$Рассчитайте частоту, наблюдаемую неподвижным человеком при приближении поезда: $$f_{o} = (150\; Гц)(1,11) = 167\; Гц \ldotp$$Используйте то же уравнение со знаком плюс, чтобы найти частоту, слышимую неподвижным человеком при удалении поезда: $$f_{o} = f_{s} \left(\dfrac{v}{v + v_ {с}}\справа) = (150\; Гц) \слева(\dfrac{340\; м/с}{340\; м/с + 35,0\; м/с}\справа) \ldotp$$Рассчитать вторая частота: $$f_{o} = (150\; Гц)(0,907) = 136\; Гц \ldotp$$
- Определить известные:
- Кажется разумным, что инженер получит ту же частоту, что и рупор, потому что относительная скорость между ними равна нулю.
- Относительно среды (воздуха) скорости v с = v o = 35,0 м/с.

- Первое доплеровское смещение для движущегося наблюдателя; второй для движущегося источника.
Используйте следующее уравнение:
\[f_{o} = \left[ f_{s} \left(\dfrac{v \pm v_{o}}{v}\right) \right] \left(\dfrac{v}{v \ mp v_{s}}\right) \ldotp\]
Величина в квадратных скобках представляет собой частоту, сдвинутую Доплером из-за движущегося наблюдателя. Фактор справа — это эффект движущегося источника. Поскольку машинист движется в направлении к звуковому сигналу, мы должны использовать знак плюс для v obs ; однако, поскольку рупор также движется в направлении от инженера, мы также используем знак плюс для v с . Но поезд везет машиниста и гудок с одинаковой скоростью, поэтому v s = v o . В результате все, кроме f s , сокращается, что дает
\[f_{o} = f_{s} \ldotp\]
Значение
Для случая, когда источник и наблюдатель не движутся вместе , рассчитанные числа действительны, когда источник (в данном случае поезд) находится достаточно далеко, чтобы движение происходило почти вдоль линии, соединяющей источник и наблюдателя. В обоих случаях сдвиг значителен и легко заметен. Обратите внимание, что сдвиг составляет 17,0 Гц для движения вперед и 14,0 Гц для движения назад. Сдвиги не симметричны.
В обоих случаях сдвиг значителен и легко заметен. Обратите внимание, что сдвиг составляет 17,0 Гц для движения вперед и 14,0 Гц для движения назад. Сдвиги не симметричны.
Для машиниста, едущего в поезде, мы можем ожидать, что частота не изменится, поскольку источник и наблюдатель движутся вместе. Это соответствует вашему опыту. Например, нет доплеровского сдвига частоты разговоров водителя и пассажира на мотоцикле. Люди, разговаривающие, когда ветер перемещает воздух между ними, также не наблюдают в своем разговоре доплеровского сдвига. Важным моментом является то, что источник и наблюдатель не движутся друг относительно друга.
Упражнение 17.9
Опишите ситуацию в вашей жизни, когда вы могли бы положиться на доплеровский сдвиг, чтобы помочь вам, когда вы ведете машину или идете рядом с транспортным потоком.
Эффект Доплера и сдвиг Доплера имеют множество важных применений в науке и технике. Например, доплеровский сдвиг в ультразвуке можно использовать для измерения скорости кровотока, а полиция использует доплеровский сдвиг в радаре (микроволне) для измерения скорости автомобиля. В метеорологии доплеровский сдвиг используется для отслеживания движения грозовых облаков; такой «доплеровский радар» может определить скорость и направление дождя или снега на погодном фронте. В астрономии мы можем исследовать свет, излучаемый далекими галактиками, и определять их скорость относительно нашей. По мере того, как галактики удаляются от нас, их свет смещается в сторону более низкой частоты и, следовательно, в сторону большей длины волны — так называемое красное смещение. Такая информация от далеких-далеких галактик позволила нам оценить возраст Вселенной (с момента Большого взрыва) примерно в 14 миллиардов лет.
В метеорологии доплеровский сдвиг используется для отслеживания движения грозовых облаков; такой «доплеровский радар» может определить скорость и направление дождя или снега на погодном фронте. В астрономии мы можем исследовать свет, излучаемый далекими галактиками, и определять их скорость относительно нашей. По мере того, как галактики удаляются от нас, их свет смещается в сторону более низкой частоты и, следовательно, в сторону большей длины волны — так называемое красное смещение. Такая информация от далеких-далеких галактик позволила нам оценить возраст Вселенной (с момента Большого взрыва) примерно в 14 миллиардов лет.
Эта страница под названием 17.8: Эффект Доплера распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Эффект Доплера
- Доплеровский сдвиг
- источник@https://openstax.
 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1
Происхождение: Хаббл: Инструменты: эффект Доплера и красное смещение
Физика
101: Красное смещение и расширяющаяся Вселенная
Перл Теслер
На всей территории наша вселенная , вспыхивает свет со звезд, отскакивая от планет, ныряя в черные дыры, блуждая в туманности, и вообще в разные стороны. Тем временем, немного его действительно проявляется здесь, на земле.
свет, который приходит сюда, кажется, несет одно и то же сообщение: вселенная расширяется.
Как
Может ли свет с ночного неба сказать нам, что Вселенная растет
по размеру? Основная подсказка исходит от чего-то, называемого красным смещением.
Красное смещение это световая версия феномена, с которым мы постоянно сталкиваемся со звуком. Вы когда-нибудь замечали, как звук полицейской сирены кажется, внезапно падает, когда автомобиль приближается к вам? Когда приближается сирена ты, волны звука сжимаются вместе, и ты слышишь их как более высокий тон. Когда машина проезжает мимо, звуковые волны от удаляющейся сирены растянуты в стороны. Вы слышите эти растянутые волны как более низкие.
| Подписаться автомобиль чтобы увидеть демонстрацию доплеровского удара Shockwave. |
Это
видимое изменение высоты (или частоты) звука называется
Доплеровский сдвиг. Свет от далеких звезд и галактик можно сместить
во многом таким же образом.
Свет от далеких звезд и галактик можно сместить
во многом таким же образом.
Нравится звук, свет — это волна, которую можно описать с точки зрения ее частоты, количество волновых пиков, проходящих каждую секунду. Так же, как космическая полицейская машина, звезда, приближающаяся к вам, имеет свои световые волны сжаты вместе. Вы видите эти световые волны как имеющие более высокое частота, чем обычно. Поскольку синий находится на высокочастотном конце видимого спектра, мы говорим, что свет от приближающегося звезда смещена в сторону синего или синего цвета.
Аналогично,
если звезда удаляется от вас, любой свет, который она излучает, растягивается.
Вы видите, что эти растянутые световые волны имеют более низкую частоту.
Поскольку красный цвет находится на низкочастотном конце видимого спектра,
мы говорим, что свет от удаляющейся звезды смещается в сторону красного,
или с красным смещением.
| Представьте себе вы двигаетесь влево с этой стрелкой. Излучаемый свет от галактик, движущихся к вам, будет раздавлено, что сделает длина волны короче, а свет голубее. На земле мы воспринимаем свет от удаляющихся от нас галактик (как кажется почти все галактики такие) . . . . как несколько растянутый, с более длинными волнами, которые делают его более красным. |
величина сдвига зависит от скорости звезды, относительной
тебе. Чтобы движущийся объект создавал заметное красное смещение
или blueshift требует довольно серьезных скоростей. Чтобы получить просто
изменение частоты света на 1%, звезда должна двигаться
1864 мили в секунду. Чтобы синяя лампочка выглядела красной,
должны улетать от вас на 3/4 скорости света.
Чтобы синяя лампочка выглядела красной,
должны улетать от вас на 3/4 скорости света.
Учеба свет от галактик по всей нашей Вселенной, астрономы заметил кое-что удивительное: почти все это с красным смещением. На самом деле, это не только красное смещение, галактики, которые дальше вдали больше смещены в красную сторону, чем ближе. Так вроде нет только все галактики во вселенной удаляются от нас, дальние удаляются от нас быстрее всех.
Вкл. На первый взгляд кажется, что это ставит нас в эпицентре крупного космологического Исход. . .какой он наш
Покажи себе, почему всегда кажется что мы центр вселенной.  (требуется Ударная волна
Вспышка) (требуется Ударная волна
Вспышка) |
дыхание? На самом деле, мы не находимся в центре расширения. В расширяющаяся вселенная, любой, стоящий где-либо во вселенной, видеть все как удаляющееся или с красным смещением.
Что больше всего загадок астрономов в настоящее время заключается не в том, что Вселенная расширяется, но скорость этого расширения, по-видимому, увеличивается. С использованием данные космического телескопа Хаббл, астрономы надеются получить выяснить вероятную судьбу нашей Вселенной: будет ли она расширяться навсегда, или расширение обратится вспять и заставит вселенную рухнуть обратно в другой Большой Хлопнуть? Следите за обновлениями.
Для более
подробно рассмотрим, как астрономы могут использовать красное смещение для определения
скорость и другие свойства небесных объектов, ознакомьтесь с этим
презентация от NOVA “Runaway
Сайт “Вселенная”.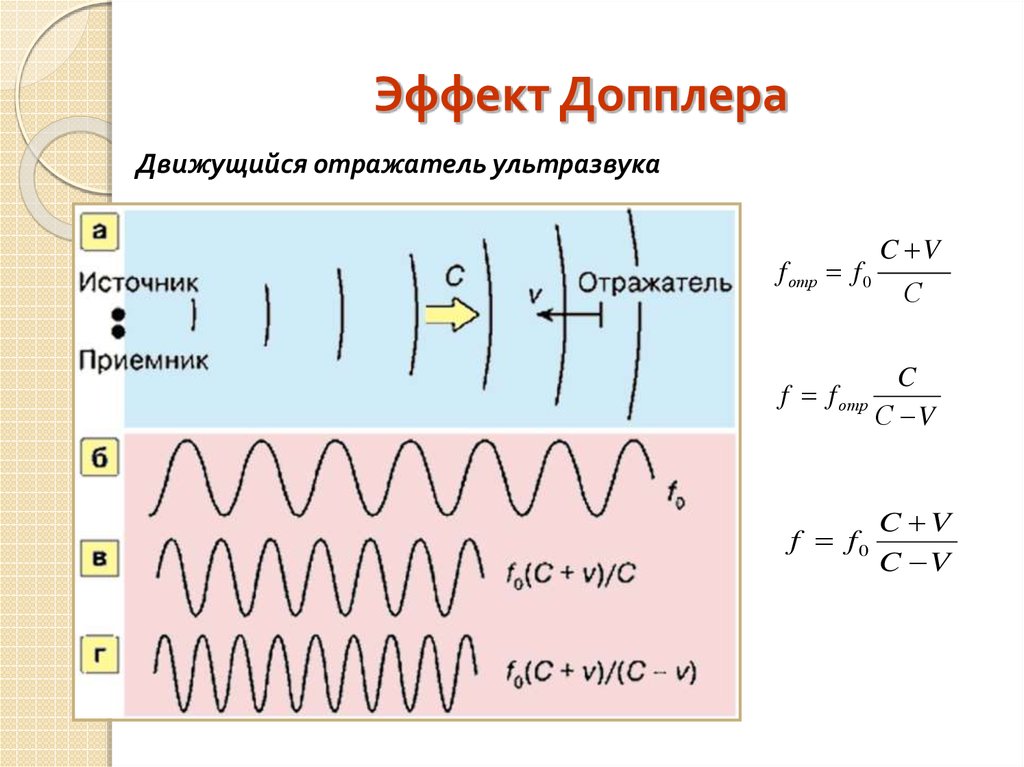
Эффект Доплера
Эффект ДоплераДвижущийся наблюдатель
Предположим, что стационарный источник генерирует звук
волны с частотой f 0 = 240 Гц (средний C) и
длина волны λ 0 = v/f 0 . Стационарный
наблюдатель на определенном расстоянии от источника услышит звук
с шагом f 0 . 240 раз каждую секунду
барабанная перепонка наблюдателя будет вдавливаться и вытягиваться из-за давления
гребень и впадина давления достигают уха. Период времени
между двумя последовательными гребнями T = 1/f 0 = (1/240)
с. Предположим, что наблюдатель садится на мотоцикл и начинает
отъезжая от источника. Предположим, что в момент времени t 1 гребень давления достигает уха в положении x. Следующий
гребень будет в позиции x в момент времени t 1 + T. Но
уха уже нет. Наблюдатель переехал.
Гребень должен пройти дополнительное расстояние, прежде чем он достигнет
ухо. Для этого требуется дополнительный интервал времени ∆t. Время
интервал между последовательными гребнями, достигающими уха
наблюдатель теперь равен T’ = T + ∆t.
Время
интервал между последовательными гребнями, достигающими уха
наблюдатель теперь равен T’ = T + ∆t.
Пока наблюдатель проехал
расстояние ∆x = v набл. (T + ∆t),
волна прошла расстояние ∆x + λ 0 = v(T + ∆t).
Приравнивая два выражения для ∆x, получаем
v набл. T + v набл. ∆t = vT + v∆t – λ 0 ,
и, используя λ 0 = v/f 0 = vT, мы имеем
v набл. T + v набл. ∆t = v∆t или ∆t = v набл. T/(v
– v обс ).
T’ = T + v набл. T/(v – v наб. ) = vT/(v – v обс ),
f’ = 1/T’ = f 0 (v – v наб )/v.
Наблюдатель слышит звук высотой f’ < f 0 .
Период увеличился, кажущееся частота волны уменьшилась, высота тона уменьшилась. наблюдатель слышит ноту ниже среднего C. Это пример Эффект Доплера .
Скорость является вектором. Пусть v obs — компоненты
скорость наблюдателя вдоль направления скорости звука
достигая наблюдателя. Тогда v obs положительный, если
наблюдатель удаляется от источника и v obs отрицательно, если наблюдатель движется к источнику. С этим знаком
соглашение
f’ = f 0 (v – v obs )/v также дает
частота f’, слышимая наблюдателем, движущимся к источнику.
Пусть v obs — компоненты
скорость наблюдателя вдоль направления скорости звука
достигая наблюдателя. Тогда v obs положительный, если
наблюдатель удаляется от источника и v obs отрицательно, если наблюдатель движется к источнику. С этим знаком
соглашение
f’ = f 0 (v – v obs )/v также дает
частота f’, слышимая наблюдателем, движущимся к источнику.
Если наблюдатель движется к источнику, то временной интервал между последовательными
гребни, достигающие уха, будут короче T. Предположим, что в момент времени t 1 гребень давления достигает уха в положении x. Следующий герб будет
в позиции x во время t 1 + T. Но он достигнет уха до того, как достигнет позиции x,
потому что наблюдатель движется к источнику. Наблюдатель слышит
нота выше среднего C.
Кажущаяся частота звуковой волны
достижение наблюдателя
f’ = f 0 (v – v наб )/v=
f = f 0 (v + |v наб |)/об.
f’ > f 0 , наблюдатель слышит звук более высокой частоты.
Обычно мы не замечаем эффекта Доплера при передвижении пешком, потому что скорость звука намного больше, чем наша скорость. Но передвигаться на мотоцикле при скорости 55 миль/ч = 24,6 м/с по направлению к источнику имеем f = f 0 (340 + 24,6)/340 = 1,07 f 0 . При удалении от источника имеем f = f 0 (340 – 24,6)/340 = 0,93 ф 0 . Когда мы проезжаем мимо источника, поэтому воспринимаемая высота звука изменяется примерно на 14%, что является заметным сдача.
Движущиеся источники
Воспринимаемая высота звуковой волны также изменяется, если наблюдатель
неподвижен, а источник движется. Пусть v s будет
компоненты скорости источника вдоль направления скорости
звука, достигающего наблюдателя. Тогда v s положительно
если источник движется к наблюдателю и v с есть
отрицательно, если источник удаляется от наблюдателя. Кажущаяся частота звуковой волны, достигающей наблюдателя
это
Кажущаяся частота звуковой волны, достигающей наблюдателя
это
f’ = f 0 v/(v – v с ).
На рисунке справа кольца обозначают последовательные гребни звуковая волна. Интервал времени между выбросами последовательных гребней есть Т. Чем больше кольцо, тем раньше время выброса. Все кольца расширяются с той же скоростью, что и скорость звука в среде. Если наблюдатель неподвижен, то интервал времени между приход последовательных колец в ухо – Т.
На следующем рисунке источник движется к наблюдатель. Центр каждого кольца находится в положении источника в то время, когда он испускает гребень. Поскольку источник движется к вправо, центр последовательных колец перемещается вправо. Если наблюдатель неподвижен, то интервал времени между приход последовательных колец в ухо меньше, чем T.
За время T волна проходит расстояние λ 0 и источник проходит расстояние ∆x.
λ 0 /v = ∆x/v с .
Длина волны у наблюдателя λ’ =
λ 0 – ∆x =
λ 0 – λ 0 v с /v
= λ 0 (v – v с )/v.
f’ = v/λ’ = (v/λ 0 )[v/(v
– v с )] = f 0 v/(v – v с ).
На следующем рисунке источник удаляется от наблюдатель. Поскольку источник движется влево, центр последовательных колец движется влево. Если наблюдатель стационарно, то интервал времени между приходами последовательных кольца в ухе больше Т.
Видимая частота звуковой волны, достигающей наблюдателя
это
f’ = f 0 v/(v – v s ) = f 0 v/(v + |v s |).
Щелкните здесь, чтобы получить интерактивную визуализацию звуковых волн вблизи
цилиндрический динамик.
Сравните звуковые волны с разными длинами волн, возникающие, когда динамик находится в
покоя и во время движения.
Всякий раз, когда источник и наблюдатель движутся с
относительно друг друга, длина волны звука, достигающего уха, будет
быть доплеровским сдвигом. Но формула доплеровского сдвига зависит от
кто движется, источник или наблюдатель. Если источник движется
к наблюдателю со скоростью, близкой к скорости звука, то
Длина волны звука, достигающего уха, становится очень короткой, и
высота становится очень высокой. В формуле f’ = f 0 v/(v – v s ), в знаменателе получается
очень маленький. Когда v s = v , знаменатель равен нулю, поэтому f’
становится бесконечным. Звуковой удар
производится в месте нахождения наблюдателя.
Но формула доплеровского сдвига зависит от
кто движется, источник или наблюдатель. Если источник движется
к наблюдателю со скоростью, близкой к скорости звука, то
Длина волны звука, достигающего уха, становится очень короткой, и
высота становится очень высокой. В формуле f’ = f 0 v/(v – v s ), в знаменателе получается
очень маленький. Когда v s = v , знаменатель равен нулю, поэтому f’
становится бесконечным. Звуковой удар
производится в месте нахождения наблюдателя.
Если и источник, и наблюдатель находятся в движении, то кажущаяся частота звуковой волны, достигающей наблюдателя, равна
f’ = f 0 (v – v обс )/(v – v s )
где v обс и v с являются
не скорости, а составляющие скорости наблюдателя и
скорость источника в направлении скорости звука, достигающего
Наблюдатель.
f’ увеличивается, если источник и наблюдатель
приближаются друг к другу и уменьшаются, если они удаляются друг от друга.
Ссылка:
- Доплеровский сдвиг и звуковой удар
Проблема:
В поезде есть свисток, который издает звук частотой 400 Гц. Вы неподвижны и вы слышите свист, но высота звука 440 Гц. С какой скоростью движется поезд к вам или от вас?
Решение:
- Рассуждение:
Шаг выше, поэтому поезд движется к вам.
Его скорость относительно вас находится из f = f 0 v/(v-v с ). - Детали расчета:
Имеем (v-v s ) = f 0 v/f = (400/с)(340 м/с)/(440/с) = 309 м/с.
Следовательно, v с = 340 м/с-309 м/с = 31 м/с = 69 миль в час.
v s положительный, поезд движется в направлении звук, к вам.
Проблема:
Два орла летят прямо навстречу друг другу, первый со скоростью 15,0 м/с, второй
секунда на скорости 20,0 м/с. Оба визжат, первый излучает частоту
3200 Гц, а второй излучающий на частоте 3800 Гц. какая
какие частоты они получают, если скорость звука равна 330 м/с?
какая
какие частоты они получают, если скорость звука равна 330 м/с?
Решение:
- Рассуждение:
И источник, и наблюдатель находятся в движении, поэтому f = f 0 (v – v наб )/(v – v с ). - Детали расчета:
(i) Первый орел — источник, второй — наблюдатель. затем v с = 15 м/с, v обс = -20 м/с, f 0 = 3200/с.
Второй орел слышит визг с частотой f = 3200/с*(330 + 20)/(330 – 15) = 3556/с.
(i) Второй орел — источник, первый — наблюдатель. затем v с = 20 м/с, v обс = -15 м/с, f 0 = 3800/с.
Второй орел слышит визг с частотой f = 3800/с*(330 + 15)/(330 – 20) = 4229 с.
Эффект Доплера — явление, наблюдаемое для всех волн. Это
назван в честь австрийского ученого
Кристиан Доплер (1803-1853). Всякий раз, когда источник, генерирующий волну, движется
относительно наблюдателя или наблюдатель движется относительно источника, частота
волны в месте нахождения наблюдателя сдвинута относительно частоты
источника.

 также
также ..
.. Если скорость источника мала по сравнению со скоростью света (300 000 км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и делённой на длину волны этой же линии в неподвижном источнике.
Если скорость источника мала по сравнению со скоростью света (300 000 км/с), то лучевая скорость равна скорости света, умноженной на изменение длины волны любой спектральной линии и делённой на длину волны этой же линии в неподвижном источнике. Однако все присутствующие (кроме друзей) думают, что он – зебра .
Однако все присутствующие (кроме друзей) думают, что он – зебра .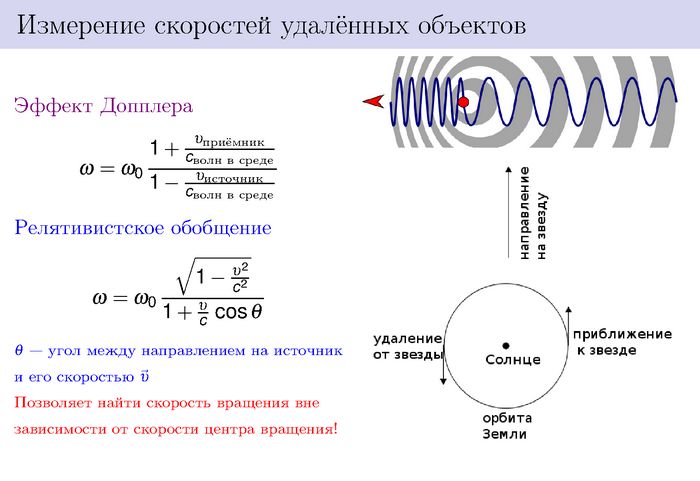
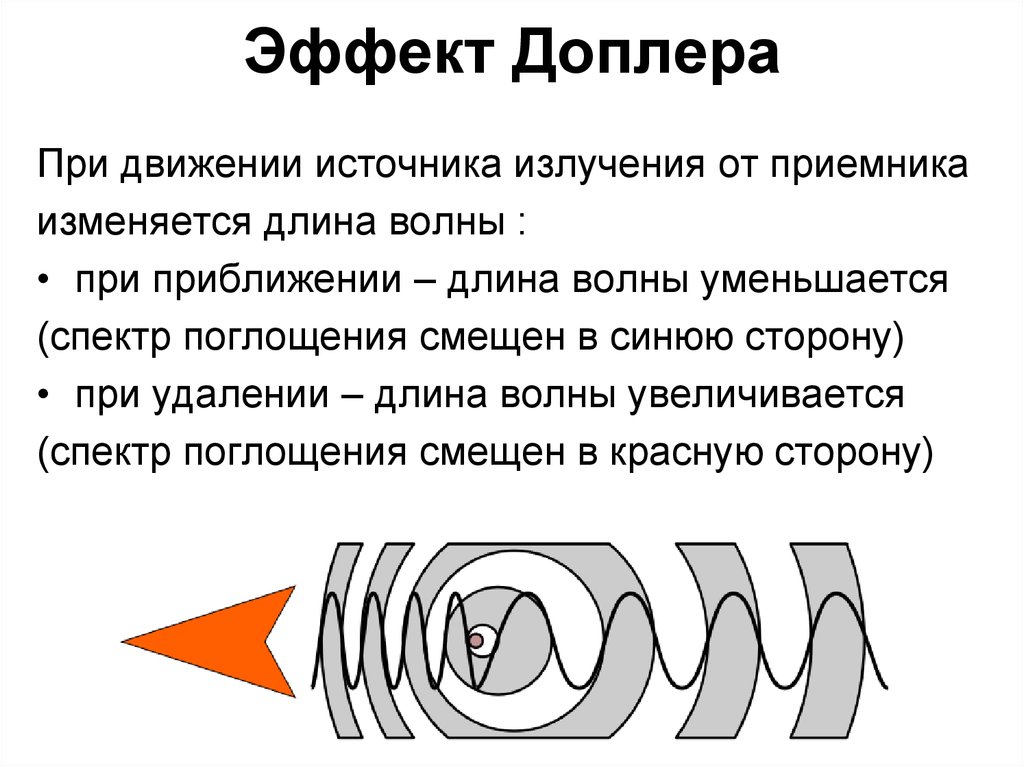 org/details/books/university-physics-volume-1
org/details/books/university-physics-volume-1