Равнопеременное движение. Ускорение. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Равнопеременное движение. Ускорение.
| Равнопеременное движение. Ускорение. | ||
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. | ||
Обозначим: – вектор начальной скорости, – изменение скорости, а Δt – промежуток времени. Пусть Δt1= Δt2=Δt3=…, тогда по определению | ||
Следовательно,
Т. | ||
Если t0=0, то | ||
УСКОРЕНИЕ – физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло. | ||
Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ – м/с2. | Например, ускорение равно 5 м/с2 – это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения. | |
В случае не равнопеременного движения: | ||
| тогда мгновенное ускорение | ||
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает. | Условие р.у.д. –. | |
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается. | Условие р.з.д. – . | |
Графики равнопеременного движения. | ||
или – в проекциях; или – через модули. | ||
Линейная функция. График – прямая. | ||
Движения, совпадающие с направлением координатной оси: 1. равноускоренноес начальной скоростью 2. равноускоренное без начальной скорости 3. равнозамедленное
4. равнозамедленное 5. 6. равноускоренное с начальной скоростью | ||
Перемещение при равнопеременном движении. | ||
Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению. | ||
Решение основной задачи механики для р.у.д. : | ||
Графики перемещения и координаты. | ||
Функции и – квадратичные. График – парабола! | ||
Теги:
конспект
Прямолинейное равноускоренное движение. Ускорение 9 класс онлайн-подготовка на Ростелеком Лицей
Введение
Тема урока «Неравномерное прямолинейное движение, прямолинейное равноускоренное движение. Ускорение». Для описания такого движения мы введем важную величину – ускорение.
Ускорение». Для описания такого движения мы введем важную величину – ускорение.
Неравномерное движение
На предыдущих занятиях обсуждался вопрос о прямолинейном равномерном движении, т. е. таком движении, когда скорость остается величиной постоянной. А что, если скорость изменяется? В этом случае говорят в том, что движение неравномерное, то есть скорость от точки к точке меняется. Важно понимать, что скорость может увеличиваться, тогда движение будет ускоренным, или уменьшаться (рис. 1) (в этом случае мы будем говорить о движении замедленном).
Рис. 1. Движение с изменением скорости
В общем случае изменение скорости можно характеризовать величиной уменьшения или увеличения скорости.
Средняя скорость
Когда мы говорим о неравномерном движении, то, помимо понятия «мгновенная скорость», которым мы будем часто пользоваться, крайнюю важность приобретает и понятие «средняя скорость». Более того, именно это понятие позволит нам дать корректное определение мгновенной скорости.
Более того, именно это понятие позволит нам дать корректное определение мгновенной скорости.
Что же такое средняя скорость? Это можно понять на простом примере. Представьте себе, что вы едете на автомобиле из Москвы в Санкт-Петербург и проезжаете 700 км за 7 часов. Какова была ваша скорость во время этого перемещения? Если автомобиль проехал 700 км за 7 часов, то его скорость составляла 100 км/ч. Но это не значит, что спидометр в каждый момент времени показывал 100 км/ч, так как где-то автомобиль стоял в пробке, где-то он разгонялся, где-то он обгонял или вообще останавливался. В этом случае можно сказать, что мы искали не мгновенную скорость, а какую-то другую.
Именно для таких ситуаций в физике и вводится понятие средней скорости (а также средней путевой скорости). Сегодня мы рассмотрим и одну, и другую и выясним, какой пользоваться удобнее и практичнее.
Средней скоростью называют отношение модуля полного перемещения тела ко времени, за которое это перемещение совершено: .
Представим пример: вы вышли в магазин за покупками и вернулись домой, модуль вашего перемещения равен нулю, но ведь скорость не была равна нулю, поэтому понятие средней скорости в данном случае неудобно.
Перейдем к более практичному понятию – средняя путевая скорость. Средняя путевая скорость – отношение полного пути, которое пройдено телом, к полному времени, за которое этот путь пройден: .
Это понятие удобное, ведь путь – скалярная величина, он может только нарастать. Часто понятия средней скорости и средней путевой скорости путают, и мы также часто будем под средней скоростью иметь в виду среднюю путевую скорость.
Существует множество интересных задач на нахождение средней скорости, самые интересные из которых мы вскоре рассмотрим.
Определение мгновенной скорости через среднюю скорость движения
Для того чтобы описать неравномерное движение, мы вводим понятие мгновенной скорости, называя ее скоростью в данной точке траектории в данный момент времени. Но такое определение не будет корректным, потому что мы знаем всего два определения скорости: скорость равномерного прямолинейного движения и средняя скорость, которой мы пользуемся в случае, когда хотим найти отношение полного пути к полному времени. Эти определения в данном случае не подходят. Как же корректно найти мгновенную скорость? Здесь можно воспользоваться понятием средней скорости.
Но такое определение не будет корректным, потому что мы знаем всего два определения скорости: скорость равномерного прямолинейного движения и средняя скорость, которой мы пользуемся в случае, когда хотим найти отношение полного пути к полному времени. Эти определения в данном случае не подходят. Как же корректно найти мгновенную скорость? Здесь можно воспользоваться понятием средней скорости.
Посмотрим на рисунок, на котором изображен произвольный участок криволинейной траектории с точкой А, в которой нам нужно найти мгновенную скорость (рис. 2). Для этого рассмотрим участок , который содержит точку А, и нарисуем вектор перемещения на этом участке. Средней скоростью на этом участке будет отношение перемещения ко времени . Будем уменьшать этот участок и найдем аналогичным образом среднюю скорость уже для меньшего участка. Совершая таким образом предельный переход от к и т. д., мы приходим к очень маленькому перемещению за очень маленький промежуток времени.
Рис. 2. Определение мгновенной скорости через среднюю скорость
Безусловно, сначала средние скорости будут сильно отличаться от мгновенной скорости в точке А, но, чем ближе мы будем приближаться к точке А, тем меньше за это время будут меняться условия движения, тем больше движение будет походить на равномерное движение, для которого мы знаем, что такое скорость.
Итак, при устремлении промежутка времени к нулю средняя скорость практически совпадает со скоростью в данной точке траектории, и мы переходим к мгновенной скорости. Мгновенная скорость в данной точке траектории – это отношение малого перемещения, которое совершает тело ко времени, за которое оно произошло.
Интересно, что в английском языке для понятия скорости существует два отдельных определения: speed (модуль скорости), отсюда спидометр; velocity, первая буква которого – v, отсюда обозначение вектора скорости.
Мгновенная скорость имеет направление. Вспомним, что когда мы говорили о мгновенной скорости, то рисовали перемещения , и т. тд. (рис. 2). По отношению к участку криволинейной траектории они являются секущими. Если ближе приближаться к точке А, они станут касательными (рис. 3). Мгновенная скорость на участке траектории всегда направлена по касательной к траектории.
тд. (рис. 2). По отношению к участку криволинейной траектории они являются секущими. Если ближе приближаться к точке А, они станут касательными (рис. 3). Мгновенная скорость на участке траектории всегда направлена по касательной к траектории.
Рис. 3. При уменьшении участка секущие приближаются к касательной
Например, в дождь, когда проезжающая мимо машина забрызгивает нас каплями, они летят именно по касательной к окружности, а данной окружностью является колесо автомобиля (рис. 4).
Рис. 4. Движения капель
Другой пример: если к жгуту привязать камень и раскрутить, то, когда камень оторвется, он тоже полетит по касательной к траектории, по которой движется жгут.
Другие примеры мы рассмотрим при изучении равноускоренного движения.
Мгновенная скорость
Для характеристики неравномерного движения вводится новая физическая величина – мгновенная скорость. Мгновенная скорость – это скорость тела в данный момент времени или в данной точке траектории.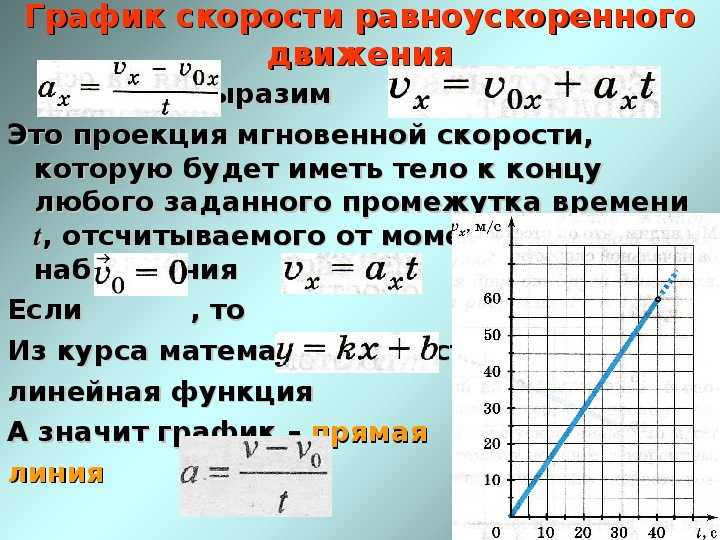 Прибор, который показывает мгновенную скорость, есть на любом транспортном средстве: в автомобиле, поезде и т. д. Это прибор, который называется спидометр (от англ. speed – «скорость»).
Прибор, который показывает мгновенную скорость, есть на любом транспортном средстве: в автомобиле, поезде и т. д. Это прибор, который называется спидометр (от англ. speed – «скорость»).
Обращаем ваше внимание на то, что мгновенная скорость определяется как отношение перемещения ко времени, в течение которого это перемещение произошло. Если перемещение будет уменьшаться, стремиться к точке, то в этом случае можно говорить о мгновенной скорости: .
Обратите внимание, что и – это координаты тела (рис. 5). Если промежуток времени будет очень маленьким, то и изменение координаты произойдет очень быстро, а изменение скорости на малом промежутке будет незаметным. Скорость на данном промежутке мы характеризуем мгновенной скоростью.
Рис. 5. К вопросу об определении мгновенной скорости
Ускорение
Таким образом, неравномерное движение имеет смысл характеризовать изменением скорости от точки к точке, тем, как быстро это происходит. Это изменение скорости характеризуется величиной, которая называется ускорением. Обозначается ускорение , это векторная величина.
Это изменение скорости характеризуется величиной, которая называется ускорением. Обозначается ускорение , это векторная величина.
Ускорение – физическая величина, которая характеризует быстроту изменения скорости. По сути скорость изменения скорости – это есть ускорение. Поскольку это вектор, значение проекции ускорения может быть отрицательным и положительным.
Ускорение измеряется в и находится по формуле: . Ускорение определяется как отношение изменения скорости ко времени , в течение которого это изменение произошло.
Важный момент – это разность векторов скоростей. Обратите внимание, что разность мы обозначим (рис. 6).
Рис. 6. Вычитание векторов скорости
В заключение отметим, что проекция ускорения на ось точно так же, как любая векторная величина, может иметь отрицательные и положительные значения в зависимости от направления. Важно отметить, что, куда направлено изменение скорости, туда будет направлено ускорение (рис. 7). Особое значение это приобретает при криволинейном движении, когда изменяется не только значение скорости, но и направление.
Рис. 7. Проекция вектора ускорения на ось
Список литературы
- Кикоин И.К., Кикоин А.К. Физика: учебник для 9 класса средней школы. – М.: Просвещение.
- Слободянюк А.И. Физика 10. Часть 1. Механика. Электричество.
- Физика. Механика. 10 класс / Под ред. Мякишева Г.Я. – М.: Дрофа.
- Филатов Е.Н. Физика 9. Часть 1. Кинематика. – ВШМФ: Авангард.
Домашнее задание
- Чем отличается средняя скорость от мгновенной?
- Начальная скорость велосипедиста 36 км/ч, затем он замедлил движение до 18 км/ч. Он тормозил на протяжении 10 секунд. С каким ускорением двигался велосипедист и куда оно было направлено?
- Мальчик вышел из пункта В и направился в пункт С, при этом пройдя 400 м, и оттуда вернулся в пункт А. Чему равна средняя путевая скорость, если расстояние от пункта А до пункта В равно 150 метров, а на всю дорогу мальчик потратил 12 минут?
3.
 4 Ускорение – биомеханика движения человека
4 Ускорение – биомеханика движения человека В повседневном разговоре ускорить означает ускорить. Пожалуй, самая распространенная демонстрация ускорения происходит, когда вы нажимаете на педаль газа в своем автомобиле. Ускоритель в автомобиле фактически может заставить его ускориться. Чем больше
СРЕДНЕЕ УСКОРЕНИЕ
Среднее ускорение равно скорости изменения скорости {v}}}{\Delta\mathbf{t}} = \frac{\overrightarrow{\mathbf{v_f}}-\overrightarrow{\mathbf{v_i}}}{\mathbf{t_f-t_i}}[/latex ]
где [латекс]\overrightarrow{\mathbf{a}}[/латекс] – среднее ускорение, [латекс]\overrightarrow{\mathbf{v}}[/латекс] – скорость, а
Поскольку ускорение представляет собой скорость в м/с, деленную на время в с, стандартными единицами измерения ускорения являются м/с 2 , метры в секунду в квадрате или метры в секунду в секунду, что буквально означает, на сколько метров в секунду скорость меняется каждую секунду.
Вспомним, что скорость — это вектор: она имеет как величину, так и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но оно также может быть изменением направление . Например, если велосипедист поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение происходит, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по тому и другому.
УСКОРЕНИЕ КАК ВЕКТОР
Ускорение — это вектор, направленный в том же направлении, что и изменение скорости, [латекс]\Дельта\overrightarrow{\mathbf{v}}[/латекс]. Поскольку скорость является вектором, она может изменяться как по величине, так и по направлению. Таким образом, ускорение — это изменение либо скорости, либо направления, либо того и другого.
Имейте в виду, что хотя ускорение направлено в направлении изменения
 Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .
Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление .ПРЕДУПРЕЖДЕНИЕ О НЕПРАВИЛЬНОМ КОНЦЕПЦИИ: ЗАМЕДЛЕНИЕ VS. ОТРИЦАТЕЛЬНОЕ УСКОРЕНИЕ
Под замедлением всегда подразумевается ускорение в направлении, противоположном направлению скорости. Замедление всегда снижает скорость. Однако отрицательное ускорение равно ускорению в отрицательном направлении в выбранной системе координат . Отрицательное ускорение может быть, а может и не быть замедлением, а замедление может считаться или не считаться отрицательным ускорением. Например, рассмотрим автомобиль, показанный ниже:
 Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).
Автомобиль тоже тормозит: направление его ускорения противоположно направлению его движения. (c) Этот автомобиль движется влево, но со временем замедляется. Следовательно, его ускорение положительно в нашей системе координат, потому что оно направлено вправо. Однако автомобиль замедляется, потому что его ускорение противоположно его движению. (d) Этот автомобиль ускоряется, когда он движется влево. Он имеет отрицательное ускорение, потому что он ускоряется влево. Однако, поскольку его ускорение направлено в том же направлении, что и его движение, оно ускоряется (а не замедляется).Пример 1: Расчет ускорения: скаковая лошадь покидает ворота
Скаковая лошадь, выходящая из ворот, разгоняется из состояния покоя до скорости 15,0 м/с строго на запад за 1,80 с. Каково его среднее ускорение?
Рисунок 4. (кредит: Джон Салливан, PD Photo.org).Стратегия
Сначала мы рисуем эскиз и присваиваем задаче систему координат. Это простая задача, но ее всегда полезно визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Мы можем решить эту задачу, идентифицируя [латекс]\Delta\overrightarrow{\mathbf{v}}[/latex] и Δ t из данной информации, а затем вычисляя среднее ускорение непосредственно из уравнения:
[латекс]\overrightarrow{\mathbf{a}}_{average} = \frac{\Delta\overrightarrow{\mathbf{v}}}{\Delta\mathbf{ t}} = \frac{\overrightarrow{\mathbf{v_f}}-\overrightarrow{\mathbf{v_i}}}{\mathbf{t_f-t_i}}[/latex]
Решение
1. Определите известные [латекс]\overrightarrow{\mathbf{v_i}}=0\textbf{ м/с}[/латекс], [латекс]\overrightarrow{\mathbf{v_f }}=-15 \textbf{ м/с}[/latex], (знак минус указывает направление на запад), Δt = 1,80 с .
2. Найти изменение скорости. Поскольку лошадь движется от нуля до -15,0 м/с, изменение ее скорости равно ее конечной скорости: [латекс]\Delta\overrightarrow{\mathbf{v}} = \overrightarrow{\mathbf{v_f}} = -15,0 \textbf{м/с}[/латекс].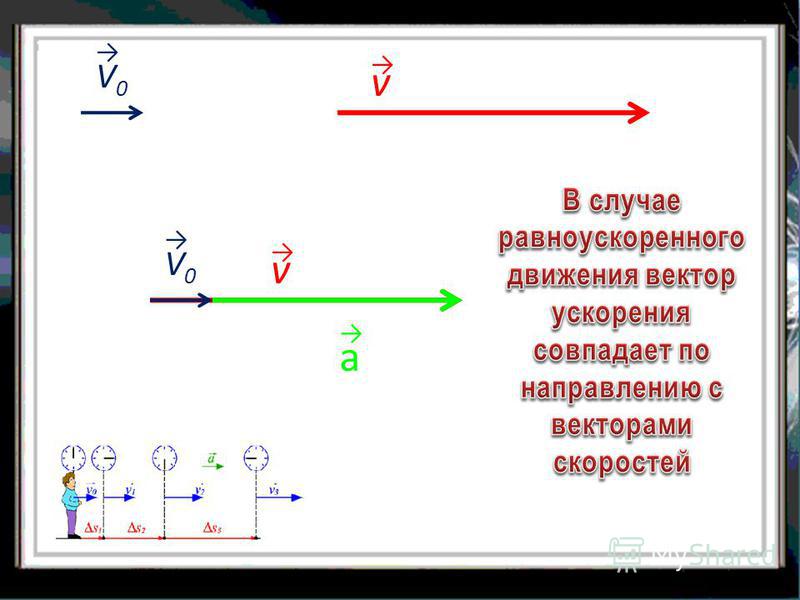 92}[/latex]
92}[/latex]
Обсуждение
Отрицательный знак ускорения означает, что ускорение направлено на запад. Ускорение 8,33 м/с 2 строго на запад означает, что лошадь увеличивает свою скорость на 8,33 м/с строго на запад каждую секунду, то есть на 8,33 метра в секунду в секунду, что мы записываем как 8,33 м/с 2 . . Это действительно среднее ускорение, потому что езда не плавная. Позже мы увидим, что ускорение такой величины потребовало бы, чтобы всадник удерживался с силой, почти равной его весу.
Мгновенное ускорение, [latex]\overrightarrow{\mathbf{a}}[/latex] , или ускорение в определенный момент времени , получается тем же процессом, который обсуждался для мгновенной скорости в предыдущем разделе. на скорости и скорости, то есть рассматривая бесконечно малый интервал времени. Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение.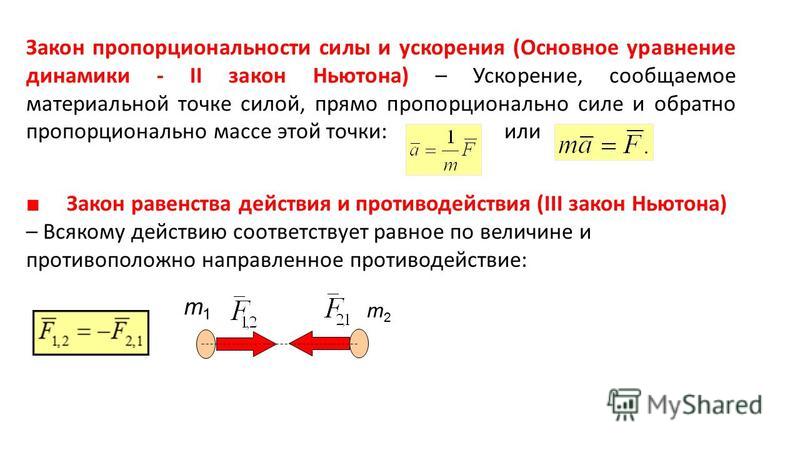 На рисунке 6 ниже показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рисунке 6 а) ускорение меняется незначительно, и среднее значение по всему интервалу почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение так, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1,8 м/с 2 ). На рисунке 6 б) ускорение резко меняется во времени. В таких ситуациях лучше рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, движение на интервалах времени от 0 до 1,0 с и от 1,0 до 3,0 с можно рассматривать как отдельные движения с ускорениями +3,0 м/с 2 и -2,0 м/с 2 соответственно.
На рисунке 6 ниже показаны графики зависимости мгновенного ускорения от времени для двух очень разных движений. На рисунке 6 а) ускорение меняется незначительно, и среднее значение по всему интервалу почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение так, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1,8 м/с 2 ). На рисунке 6 б) ускорение резко меняется во времени. В таких ситуациях лучше рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, движение на интервалах времени от 0 до 1,0 с и от 1,0 до 3,0 с можно рассматривать как отдельные движения с ускорениями +3,0 м/с 2 и -2,0 м/с 2 соответственно.
 Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя посылку на ленточном конвейере почтового отделения, которая ускоряется вперед и назад, когда она толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Среднее значение по интервалу почти такое же, как ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя посылку на ленточном конвейере почтового отделения, которая ускоряется вперед и назад, когда она толкается. В такой ситуации необходимо рассматривать небольшие промежутки времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Пожалуй, самое важное, что следует отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус означает, что она находится слева. Это легко представить для смещения и скорости. Но это немного менее очевидно для ускорения. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Решающее различие, если ускорение находится в направлении, противоположном скорости. В самом деле, отрицательное ускорение будет увеличить отрицательную скорость. Если ускорение имеет тот же знак, что и скорость, то тело ускоряется. Если ускорение имеет противоположный знак скорости, то объект замедляется.
Если ускорение имеет противоположный знак скорости, то объект замедляется.
ИССЛЕДОВАНИЯ PHET: МОДЕЛИРОВАНИЕ ДВИЖУЩЕГОСЯ ЧЕЛОВЕКА
Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка вперед-назад с помощью мыши и зарисовывайте его движение. Установите положение, скорость или ускорение, и пусть симуляция переместит человека за вас.
https://phet.colorado.edu/en/simulation/moving-man
Рисунок 13. Движущийся человек.- Ускорение — это скорость изменения скорости. В символах среднее ускорение равно
[латекс]\overrightarrow{\mathbf{a}}_{среднее} = \frac{\Delta\overrightarrow{\mathbf{v}}}{\Delta\mathbf{t}} = \frac{\overrightarrow {\mathbf{v_f}}-\overrightarrow{\mathbf{v_i}}}{\mathbf{t_f-t_i}}[/latex]
- Стандартной единицей ускорения является м/с 2 .
- Ускорение является вектором и поэтому имеет как величину, так и направление.

- Ускорение может быть вызвано либо изменением величины, либо направления скорости.
- Мгновенное ускорение [латекс]\overrightarrow{\mathbf{a}}[/латекс] — это ускорение в определенный момент времени.
- Замедление — это ускорение с направлением, противоположным направлению скорости.
- ускорение
- скорость изменения скорости; изменение скорости во времени
- среднее ускорение
- изменение скорости, деленное на время, за которое она изменяется
- мгновенное ускорение
- ускорение в определенный момент времени
- замедление
- ускорение в направлении, противоположном скорости; ускорение, приводящее к уменьшению скорости
Механика ускорения и торможения
Ниже приводится эксклюзивный отрывок из книги Развитие ловкости и быстроты, второе издание , опубликовано Human Kinetics. Весь текст и изображения предоставлены Human Kinetics.
Ускорение при старте с места (статическое) или в движении (с качения) очень важно в спорте. Ключом к ускорению при беге вперед является позиция тройного разгибания, которая характеризуется скоординированным и мощным разгибанием лодыжки, колена и бедра (2). Это мощное движение позволяет спортсмену быстро продвигать тело вперед, создавая значительные силы реакции опоры (GRF). Основываясь на третьем законе движения Ньютона (на каждое действие есть равное и противоположное противодействие), чем больше GRF спортсмен может произвести за ограниченное время, в течение которого стопа находится в контакте с землей, тем быстрее он или она должен иметь возможность толкать тело в заданном направлении. То же самое относится и к тренировкам с ХПК или боковыми движениями.
При замедлении тела или торможении положение тройного сгибания используется для снижения скорости и подготовки к ХПК. Это положение характеризуется сгибанием лодыжек, коленей и бедер. В этом случае, чем большее тормозное усилие сможет создать спортсмен, тем быстрее он сможет замедлиться и изменить положение тела, чтобы подготовиться к следующему необходимому движению.
При обучении тренировкам ХПК на скорость или ловкость следует акцентировать внимание на нескольких ключевых моментах (1, 2).
Осанка
Во время ускорения центр масс спортсмена должен находиться перед основанием опоры (т. е. ступнями). Это позволяет оптимально расположить тело для производства GRF, чтобы увеличить горизонтальную тягу. Этого наклона не следует добиваться сгибанием в талии; вместо этого тренер должен иметь возможность наблюдать воображаемую линию, пересекающую уши, вниз через туловище, бедро, колено и лодыжку опорной ноги, когда колено спортсмена полностью выпрямлено непосредственно перед тем, как стопа теряет контакт с землей. Голова спортсмена должна быть на одной линии с туловищем, а туловище на одной линии с ногами во время движений с линейным ускорением (рисунок 6.1).
При замедлении или торможении наклон вперед, наблюдаемый при ускорении вперед, не заметен. Это связано с тем, что для уменьшения импульса тела туловище должно принять более прямое положение по сравнению с нижней частью тела и больший наклон назад во время замедления. Это действие туловища перемещает центр масс назад к основанию опоры. Это позволяет нижней части тела занять лучшее положение для торможения горизонтального толчка, создаваемого во время ускорения (рис. 6.2).
Это действие туловища перемещает центр масс назад к основанию опоры. Это позволяет нижней части тела занять лучшее положение для торможения горизонтального толчка, создаваемого во время ускорения (рис. 6.2).
Движение рук
Спортсмен должен быть проинструктирован бежать с согнутыми руками примерно на 90 градусов при ускорении. Тем не менее, следует отметить, что во время замаха локоть спортсмена, скорее всего, вытянется за пределы 90 градусов из-за сил, возникающих при мощном замахе руками назад. Это мощное движение рук назад использует рефлекс растяжения и обеспечивает большую часть силы, необходимой для движения тела. Руки не должны пересекать среднюю линию тела, чтобы помочь противодействовать вращательным силам нижних конечностей. В общих чертах, чем больше длина шага спортсмена, тем больше будет размах рук, потому что скорость рук и скорость ног зависят друг от друга. Другими словами, по мере того, как увеличивается размах рук, увеличивается и длина шага (и наоборот).
При замедлении руки будут продолжать двигаться в основном в сагиттальной плоскости (т. е. качаться вперед и назад), хотя диапазон движения в плече и амплитуда маха руками будут уменьшаться, когда для замедления используются более короткие шаги телом вниз или для подготовки к смене направления. При боковом движении или в спортивном положении руки должны быть по бокам тела.
Работа ногами
Взрывной отталкивание требует синхронного разгибания бедра, колена и лодыжки для создания GRF. При выполнении упражнений на ускорение спортсмены должны быть проинструктированы держать лодыжку в положении тыльного сгибания и использовать ударно-двигательное действие (т. е. ударять по колену и вдавливать стопу в землю). Во время приземления вес спортсмена должен приходиться на подушечку стопы. Это действие минимизирует тормозные силы и максимизирует движущую силу. Угол наклона голеней спортсмена к земле будет острым (менее 9°).0 градусов) и будет немного увеличиваться с каждым последующим шагом.

 о., это характеристика движения.
о., это характеристика движения.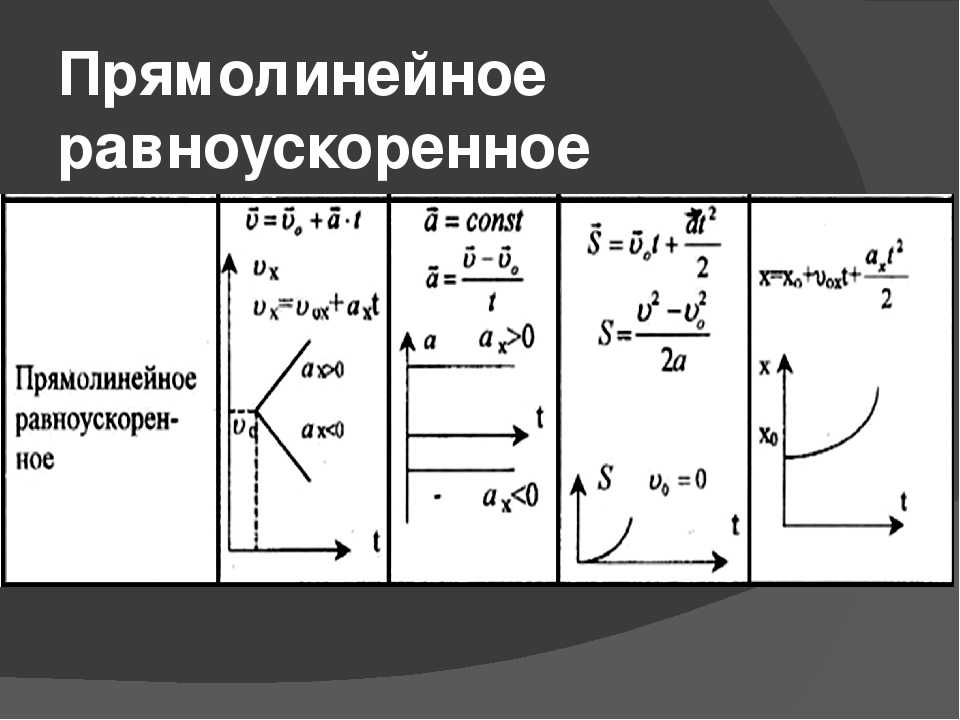
 равноускоренное без начальной скорости
равноускоренное без начальной скорости