Е как найти: Число е, формулы и онлайн калькуляторы - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Число е | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

С замечательным числом e мы впервые встречаемся, начиная изучать показательную функцию, логарифмы и производные. Поэтому для лучшего понимания мы рекомендуем вам прочитать наши статьи «Показательная функция» и «Геометрический смысл производной».

В статье «Показательная функция» мы говорили о важнейшем свойстве функции — при эта функция очень быстро растет. И не просто «быстро растет» — чем больше x, тем больше скорость ее роста, тем круче идет график. Можно сказать, что с увеличением x растут и значения показательной функции, и ее производная. А если аргументом показательной функции является время, то при такая функция является математическим выражением стремительно развивающегося процесса.

Среди показательных функций есть особенная. Называется она экспонента, ее формула . Особенность ее в том, что в каждой точке скорость роста этой функции равна значению самой функции в этой точке. Другими словами, , то есть производная функции равна ей самой.

Нарисуем несколько графиков функции при , а также при . Среди этих графиков есть такой, что касательная к нему, проведенная в точке , идет ровно под углом к положительному направлению оси OX.

Это и есть график функции . Само число e — иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приблизительно оно равно 2,718.

Логарифм по основанию e называется натуральным и обозначается . Если в уравнении или неравенстве вам встретились такие логарифмы, вы работаете с ними так же, как и с любыми другими, у которых основание больше 1.

Функция также обладает интересным свойством:

Это значит, что с ростом

x график логарифмической функции идет более и более полого, скорость роста его уменьшается, что мы и видим.

Формулы для производных функций и содержат в себе выражение :

Число e, как и число , является одной из мировых констант. Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.

Число известно людям с глубокой древности. Оно равно отношению длины окружности к ее диаметру. А вот с числом e (названным так в честь великого математика Леонарда Эйлера) человечество познакомилось намного позже. Впервые его вычислил математик Якоб Бернулли в начале XVIII века, причем сделал это, решая чисто практическую задачу о начислении процентов на банковский вклад.

В заданиях вариантов ЕГЭ вам встречались задачи, где вклад величиной x помещен в банк под p % годовых. Найти нужно было, например, каким станет вклад через два года. Рассказывая о решении таких задач, мы вывели удобные формулы:

если величину x увеличить на p процентов, получится
если величину x дважды увеличить на p процентов, получим Именно таким станет вклад через два года;

если вклад пролежит в банке n лет, его величина станет равной

Итак, если вклад поместить банк под 10% годовых, он вырастет за год в 1,1 раз, за два года — в 1,21 раза, за десять — примерно в 2,6 раза.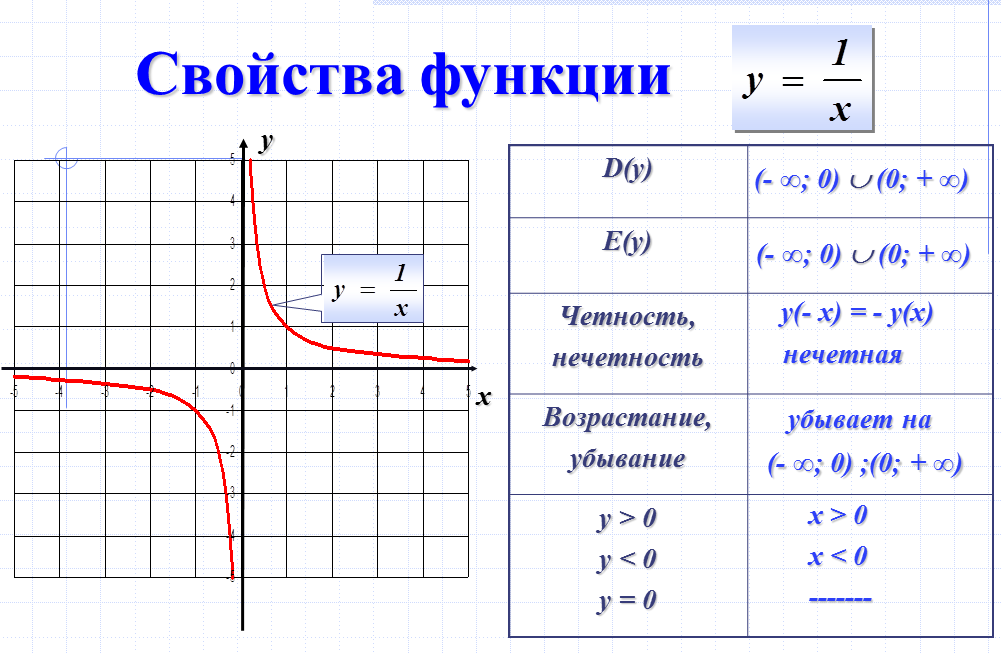 Значит, рост вклада зависит от того, сколько он пролежит в банке, то есть сколько раз начисляются проценты. А что будет через сто лет? А если найти такой банк, где процент начисляется не раз в год, а раз в день? И пусть даже каждый день начисляется совсем небольшой процент, но ведь дней-то много! Верно ли, что можно положить в такой банк один доллар под одну сотую процента в день, а через пару десятков лет забрать из банка миллион?

Давайте так и сформулируем задачу. Пусть банк начисляет каждый день по одной сотой процента. Во сколько раз вырастет вклад через 10000 дней (это двадцать семь с лишним лет)? Иными словами, чему приближенно равна величина ? И к чему будет стремиться величина , если n стремится к бесконечности?
Вот такую задачу и решал Бернулли. Если n будет очень большим, или, как говорят математики, бесконечно большим, будет стремиться к бесконечности (то есть больше миллиона, больше миллиарда, больше двух миллиардов. . . ) — то величина будет, наоборот, очень малой.

Вычисление константы Эйлера (e) – Карьера в математике

Число Эйлера, записываемое как , вероятно, является второй по известности математической константой после Пи. Но что такое число Эйлера и как его вычислить? В самом деле, почему и стали такими известными и почему они заслужили место в наших калькуляторах и в зале славы математических констант?

Что такое число Эйлера (

e ) и откуда оно взялось?

Число Эйлера имеет значение 2,718… , однако, как и Пи, это иррациональное число, а это означает, что его нельзя записать в виде дроби и что оно имеет десятичное расширение, которое будет продолжаться вечно без повторений. число Эйлера 9Число 0003 e прославилось по двум основным причинам: во-первых, оно используется во многих важных жизненных ситуациях, а во-вторых, оно обладает множеством интересных математических свойств. Это интересное и полезное число для ученых, инженеров и математиков.

Число Эйлера

e и сложные проценты

Число Эйлера было впервые обнаружено Якобом Бернулли в 17 веке, когда он изучал проблему сложных процентов.

Представьте, что у вас есть 1 фунт стерлингов и вы получаете проценты два раза в год по ставке 50%.

В конце года у вас останется 1 фунт стерлингов = 2,25 фунта стерлингов

Теперь представьте, что у вас есть 1 фунт стерлингов и вы получаете проценты 12 раз в год или каждый месяц по ставке (8,3%)

В к концу года у вас будет 1 фунт стерлингов 2,61303529

Теперь представьте, что у вас есть 1 фунт стерлингов и вы получаете проценты 365 раз в год или каждый день по ставке (0,2739….%)

В конце года в год вы получите 1 фунт стерлингов 2,714567482 фунта стерлингов

Яков Бернулли задал важный вопрос: что произойдет, если вы будете получать проценты так часто, что будете получать их непрерывно?

В самом деле, каково значение n при стремлении n к бесконечности?

Возможно, вы уже догадались об ответе, просто взглянув на наш пример, где n=365, что уже довольно близко к . Это подводит нас к наиболее известному способу вычисления:

Вычисление значения числа Эйлера

e в качестве предела:

(Продолжайте вводить все большие и большие значения до тех пор, пока не получите действительно близкое к истинному значению .) сказать, что значение было между 2 и 3. Несколько лет спустя Леонарду Эйлеру, одному из величайших математиков в истории, удалось вычислить значение , с точностью до 18 знаков после запятой. Эйлер также открыл следующее:

Вычисление числа Эйлера

e с использованием бесконечного ряда:

(Если вам интересно, 5! означает и является функцией факториала)

Чем больше членов вы вычисляете ближе вы получите к истинному значению . Вы получите точное значение только в том случае, если будете бесконечно складывать последовательность.

Никто точно не знает, как Эйлер вычислял до 18 знаков после запятой, однако можно предположить, что он использовал приведенную выше последовательность. Именно Эйлер назвал константу ‘’. Удивительно, но историки совершенно уверены, что он не назвал его в честь себя, а то, что он выбрал первую букву своей фамилии, было чистой случайностью.

Непрерывные дроби и

Эйлер также смог представить в виде «непрерывной дроби». Есть много разных способов представить e в виде бесконечной цепной дроби. Вот один из них:

Вычисление числа Эйлера e как цепной дроби:

Другие способы вычисления

Выше были перечислены три основных способа вычисления. Однако есть много других менее известных представлений, таких как:

Если вы посетите страницу Wolfram Mathworld e , вы сможете просмотреть огромную коллекцию различных способов вычислений, некоторые из которых действительно очень сложны. На этой же странице также приводится коллекция мнемоник, которые помогут вам запомнить цифры . Любимый должен быть:

«Это позволяет тупице запоминать количество цифр» (10 цифр)

Подсчитайте буквы в каждом слове, и вы получите: 2,718281828

Где число Эйлера

e используется в реальном мире?

Сложные проценты — не единственное практическое применение для . На самом деле число Эйлера, функция и натуральный логарифм по основанию часто встречаются в реальных процессах. Основная причина этого заключается в том, что экспоненциальную функцию можно использовать для описания роста и распада.

Примеры:

Рост населения
Как изменяется температура при нагревании или охлаждении материалов

Радиоактивный распад частиц

Уникальное математическое свойство

Функция обладает особым математическим свойством, которое имеет важные последствия для вычислений с участием , что делает работу с математикой намного проще, чем со многими другими функциями. Это одна из причин, которая так часто используется для моделирования реального мира.

Функция является единственной функцией, где она равна своей производной ( обозначает любое число, и это просто означает, что свойство также выполняется для кратных ). Когда вы дифференцируете , он остается неизменным: . Это также означает, что при интегрировании она останется неизменной, кроме константы интегрирования. Это уникальное свойство упрощает многие расчеты с участием

Не забывайте о

Никакое обсуждение числа Эйлера и не будет полным без упоминания одного из самых известных уравнений в математике, называемого уравнением Эйлера:

for – равно квадратному корню из минус 1 и называется мнимым числом.)

Уравнение Эйлера показывает, что оба и связаны друг с другом. Это действительно удивительно, учитывая, что это происходит из рассмотрения свойств круга и возникает из ситуаций, которые не имеют ничего общего с кругами, такими как сложные проценты. Уравнение Эйлера показывает, что — это больше, чем просто полезное число, которое ученые могут использовать для моделирования реального мира — это увлекательное число само по себе с точки зрения математики.

Авторы изображений:

Leonhard_Euler, автор Якоб Эмануэль Хандманн [общественное достояние], через Wikimedia Commons , через Wikimedia Commons

Статья Хейзел Льюис

Объяснение числа Эйлера (e), как оно используется в финансах

Что такое число Эйлера (е)?

Термин число Эйлера (e) относится к математическому выражению основания натурального логарифма. Это представлено неповторяющимся числом, которое никогда не заканчивается. Первые несколько цифр числа Эйлера — 2,71828. Число обычно обозначается буквой e и обычно используется в задачах, связанных с экспоненциальным ростом или затуханием. Вы также можете интерпретировать число Эйлера как основу экспоненциальной функции, значение которой всегда равно ее производной. Другими словами, e — единственное возможное число, такое что

e ^x увеличивается со скоростью e ^x для каждого возможного x.

Ключевые выводы

Число Эйлера — важная константа, которая встречается во многих контекстах и является основой для натуральных логарифмов.
Иррациональное число, представленное буквой е, число Эйлера равно 2,71828…, где цифры продолжаются бесконечно в ряду, который никогда не заканчивается и не повторяется (аналогично числу пи).
Число Эйлера используется везде, от объяснения экспоненциального роста до радиоактивного распада.
В финансах число Эйлера используется для расчета того, как богатство может расти за счет сложных процентов.
Не путайте число Эйлера с константой Эйлера, которая является еще одним иррациональным и неограниченным числом, начинающимся с 0,57721.

Понимание числа Эйлера (e)

Как отмечалось выше, число Эйлера используется для выражения основания натурального логарифма. E — это ряд чисел, начинающихся с 2,71828. Как и число Пи, оно не имеет конца, что означает, что оно продолжается и продолжается. Это также иррациональное число, что означает, что его нельзя представить в виде дроби. Вы можете использовать его для расчета снижения или роста определенного фактора с течением времени, например сложных процентов.

Представьте, что вы даете деньги взаймы под 100% процентную ставку, начисляемую каждый год. Через год ваши деньги удвоятся. Но что, если бы процентная ставка была снижена вдвое и начислялась бы в два раза чаще? При 50% каждые шесть месяцев ваши деньги вырастут на 225% за год.

По мере того, как интервал становится меньше, общая доходность становится немного выше. Если проценты рассчитываются n раз в год по ставке 100%/n, общее накопленное богатство в конце первого года будет немного больше, чем в 2,7 раза больше первоначальных инвестиций, если n

достаточно большой.

История числа Эйлера (e)

Хотя обычно он ассоциируется со швейцарским математиком Леонардом Эйлером и назван в его честь, он был впервые обнаружен в 1683 году математиком Якобом Бернулли. Он пытался определить, как будет расти богатство, если проценты будут начисляться чаще, а не ежегодно.

Самая важная работа, связанная с числом, была выполнена Леонардом Эйлером лишь несколько десятилетий спустя. В своей книге Introductio in Analysin Infinitorum (1748 г.) Эйлер доказал, что это иррациональное число, цифры которого никогда не повторяются. Он также доказал, что число можно представить в виде бесконечной суммы обратных факториалов:

е знак равно 1 + 1 1 + 1 2 + 1 1 × 2 × 3 + 1 1 × 2 × 3 × 4 + . . . + 1 н ! e = 1 + \ frac { 1 }{ 1 } + \ frac { 1 }{ 2 } + \ frac { 1 }{ 1 \ times 2 \ times 3 } + \ frac {1 }{ 1 \ times 2 \ times 3 \times 4 } + … + \frac { 1 }{ n! } e=1+11+21+1×2×31+1×2×3×41+…+n!1

Эйлер использовал букву e для показателей степени, но теперь эта буква широко ассоциируется с его именем. Он обычно используется в широком спектре приложений, включая рост популяции живых организмов и радиоактивный распад тяжелых элементов, таких как уран, учеными-ядерщиками. Его также можно использовать в тригонометрии, вероятности и других областях прикладной математики.

Число Эйлера (e) не следует путать с постоянной Эйлера, которая обозначается строчной гаммой (γ). Также известная как постоянная Эйлера-Маскерони, последняя связана с гармоническим рядом и имеет значение приблизительно 0,57721…9.0005

Число Эйлера (e) в финансах: сложные проценты

Сложные проценты были провозглашены чудом финансов, когда проценты начисляются не только на первоначальные суммы инвестиций или депозитов, но и на ранее полученные проценты. Непрерывное начисление процентов достигается, когда проценты реинвестируются в течение бесконечно малой единицы времени. Хотя в реальном мире это практически невозможно, эта концепция имеет решающее значение для понимания поведения многих различных типов финансовых инструментов, от облигаций до контрактов на деривативы. 9{rt} \\&\textbf{где:} \\&\text{FV} = \text{Будущая стоимость} \\&\text{PV} = \text{Текущая стоимость баланса или суммы} \\&e = \text{Константа Эйлера} \\&r = \text{Процентная ставка начисляется} \\&t = \text{Время в годах} \\\end{выровнено} FV=PVertwhere:FV=Будущая стоимостьPV=Текущая стоимость баланса или сумма=Константа Эйлера=Процентная ставка начисляетсяt=Время в годах

Таким образом, если бы у вас было 1000 долларов с выплатой 2% годовых с непрерывным начислением сложных процентов, через три года у вас было бы: 9{ 12 \ умножить на 3 } = \ $ 1061,78 1000 долларов США (1 + 12,02) 12 × 3 = 1061,78 долларов США

Здесь разница составляет всего несколько центов, но по мере того, как наши суммы становятся больше, процентные ставки становятся выше, а количество времени увеличивается, непрерывное начисление процентов с использованием константы Эйлера становится все более и более ценным по сравнению с дискретным начислением процентов.

Почему число Эйлера важно?

Число Эйлера часто появляется в задачах, связанных с ростом или уменьшением, где скорость изменения определяется текущим значением измеряемого числа. Одним из примеров является биология, где ожидается удвоение популяции бактерий через определенные промежутки времени. Другим случаем является радиометрическое датирование, когда ожидается, что количество радиоактивных атомов уменьшится в течение фиксированного периода полураспада измеряемого элемента.

Как число Эйлера используется в финансах?

Число Эйлера появляется в задачах, связанных со сложными процентами. Всякий раз, когда инвестиция предлагает фиксированную процентную ставку в течение определенного периода времени, будущая стоимость этой инвестиции может быть легко рассчитана с точки зрения e.

Что такое число Эйлера?

Проще говоря, число Эйлера является основанием экспоненциальной функции, скорость роста которой всегда пропорциональна текущему значению.